- 1Department of Mathematics, University College in Al-Qunfudhah, Umm Al-Qura University, Al-Qunfudhah, Saudi Arabia
- 2Department of Mathematics, IPEIN, Carthage University, Nabeul, Tunisia
The aim of this paper is to propose some efficient and accurate numerical methods to compute the steady-state of variable coefficients space fractional Cahn-Allen equations. The approach combines an adaptive time stepping semi-implicit gradient flow method to minimize the fractional energy functional and pseudo-spectral approximation schemes. Based on the use of a preconditioned GMRES, the space fractional Cahn-Allen equation is then solved efficiently. The full methodology is supported by the numerical solution of a one-dimensional problem.
1 Introduction
During the last 2 decades, the mathematical analysis and numerical simulation of fractional partial differential equations became one of the most important hot topics in applied and computational mathematics [1–4]. One of the reasons of this growing interest is related to the fact that these new models provide a better description of some physical phenomena. Indeed, for example, for the heat equation, considering space fractional effects allows to handle anomalous diffusion [5] when the stochastic process driving the medium is a Lévy α-stable flight. Fractional PDEs are also of interest when modeling e.g., the behavior of turbulent flows [6, 7], the chaotic effects in the dynamics of conservative systems [8] but also for the transport of contaminant in groundwater flow [9, 10] or finally in mathematical finance [11]. In [12], a fast algorithm based on time two-mesh finite element scheme, which aims at solving nonlinear problems quickly, is considered to numerically solve the nonlinear space fractional Cahn-Allen equations with smooth and non-smooth solutions. In [13], different schemes has been effectively employed for finding the exact solutions and dynamics of the Cahn-Allen model and the dispersive predator-prey model. The goal of this paper is to contribute to the numerical solution to such systems, and most particularly to a space fractional Cahn-Allen equation [14] with variable coefficients. The integer order equation is usually used to describe the complex phase separation and coarsening phenomena in a solid. Here, the fractional order appears as an exponent α/2 (1 ≤ α ≤ 2) in the laplacian operator, α = 2 corresponding to the standard situation. The fractional Cahn-Allen equation can then be seen as a more general situation than the standard one. It has been introduced (see e.g., [15–17]) for studying the competing stable phases having an identical Lyapunov functional density for Lévy processes of order α/2. This allows to include the situation where the random walk has correlations, non-Gaussian or non-Markovian memory effects which cannot be described by the standard Laplacian.
A recent interesting application [18, 19] considers image segmentation techniques based on the fractional Cahn-Allen equation, with examples in medical imaging. Here, the objective of the paper is to show how the widely used pseudo-spectral approximation schemes which are well-adapted to solve constant coefficients PDEs (see e.g., [20–23]) can be adapted to the variable coefficients case for computing the steady-state of fractional Cahn-Allen equations based on the gradient flow formulation and its suitable discretization.
To this end, we introduce in Section 2 the problem setting for an example of space fractional Cahn-Allen equation (the approach could be probably extended to other kinds of equations), and we provide a few useful definitions for the pseudo-spectral approximation, in particular concerning the spectral definition of the fractional laplacian. The gradient flow formulation is also given. Section 3 is devoted to the development of numerical schemes for the gradient flow as well as an adaptive time stepping method. We also explain how to get an efficient implementation of the pseudo-spectral approximation schemes, most particularly regarding the use of a Krylov subspace iterative solver with a well-designed preconditioner. In Section 4, we analyze the full methodology in the case of a one-dimensional example. This shows that the newly designed method performs very well for various fractional orders. Finally, we conclude in Section 5.
2 Problem Setting and Definition
The problem that we propose to solve is the following: find
In the above system, u≔u(t, x) represents the concentration of one of the mixtures at time t and point x appearing in the modeling of the phase of a binary mixture. The domain of computation is a d-dimensional rectangular box:
In this paper, we consider the SFCA equation for a fractional laplacian (−Δ)α/2, 1 < α ≤ 2, with homogeneous Neumann boundary conditions [24]. Nevertheless, homogeneous Dirichlet or periodic boundary conditions can also be included. In the one-dimensional case, we introduce λj as the eigenvalues and φj,
These functions, which are explicitly defined by
form a complete set of orthogonal eigenfunctions. In the case of a homogeneous Dirichlet boundary condition, then one would get
Let us define
Then, if we assume that
with
The nonlinear term f is given by f′(u) = F(u). The choice of the potential function F, also called Helmholtz free-energy density, is related to the physical situation, e.g., the case of a convex quartic double-well potential or a non-convex logarithmic potential [25, 26]. Here, to fix the ideas, we consider the first choice with a variable space function, for x ∈ Ω, 0 < β(x) ≤ 1, generalizing the standard constant situation β = 1, and setting
leading to
Let us introduce the generalized energy functional
with (⋅,⋅)0,Ω as the L2(Ω)-norm. As in [21, 24], we define
setting
One also can prove that the energy is nonincreasing, after integration over the domain Ω, taking a test-function v = (ɛ(−Δ)α/2u + f(u)), and since κ is a positive function
3 Numerical Schemes
3.1 Minimization Algorithms
When one wants to reach the long time solution to Eq. 1, i.e., to compute the steady-state, we can directly discretize the initial boundary-value system Eq. 9 as a time-dependent problem which is a standard approach. An alternative solution consists in looking at the long-time solution to the gradient flow system Eq. 9 which cancels the energy gradient (Euler equation), based on an optimization algorithm related to the minimization of the energy functional. A standard way is to use a gradient-type method by building a sequence of minimizers u(n) which is supposed to converge towards the steady-state, hence corresponding to the long-time dynamics solution of the gradient flow, i.e., for large values of n.
Based on this point of view, we can for example build the following simple scheme
with
and where ρ(n) > 0 is the local descent step of the gradient method which is computed in such a way that the energy is indeed decaying between two successive steps n and n + 1.
Let us now make a few remarks. If one considers that the step δ(n) is a constant step, which means that we use a constant-step minimization gradient algorithm, then scheme Eq. 10 would correspond to an explicit Euler discretization in time of Eq. 1 with constant time step Δt = ρ. In the case of the computation of an optimal step, or at least an adapted gradient step ρ(n), then one gets an explicit Euler scheme with time stepping. It is well-known that the steepest descent method with constant step is not optimal and may suffer from convergence problems, therefore requiring the computation of an optimal step. To this end, we use an optimal linear search method following (the starting value ρ = 1 can be changed)
which will also be used for all the other alternative schemes below.
Concerning the stopping criterion related to Eq. 10, one possibility consists in forcing a maximal value of n. Based on the interpretation of the steepest descent step ρ(n) as a local time step Δtn, this would correspond to fixing a maximal time of computation tN for a certain a priori known value of N. Nevertheless, N is never a priori known and should be determined dynamically into the loop on n thanks to a stopping criterion. Here, we propose the following strong convergence test
for a very small value of ϵ1, where
The stability and convergence properties of the steepest descent algorithm depend on the fact that it is also fully explicit. Here we consider the following alternative scheme where we implicit the energy gradient term
which, in terms of PDEs can be rewritten as
The problem related to the above fully implicit (Euler) scheme is that we have to solve a nonlinear equation at each gradient step, leading to a higher computational cost if for example a fixed-point or Newton-type algorithm is used, most particularly in the framework of pseudo-spectral approximation schemes. Here, we consider the semi-implicit (Euler) (E, for short) scheme
which avoids any nonlinear solution and leads to solving the linear PDE formulation
where I is the identity operator. In fact, it can be seen as the formulation of the fully-implicit (Euler) scheme Eq. 15 with one iteration of the fixed-point algorithm. If one uses the decomposition of the Ginzburg–Landau free energy into a linear kinetic part and a nonlinear part related to the potential function F
setting
then Eq. 15 can also be seen as an algorithm where the kinetic energy is implicitly approximated while the potentiel energy is explicit resolved
An alternative to the semi-implicit Euler scheme is to use a semi-implicit Crank-Nicolson (CN, for brevity) scheme which writes
and is similar to Eq. 19 but evaluating the kinetic energy at the mid-point un+1/2≔(u(n+1) + u(n))/2 as well as the Neumann boundary condition. For both the E and CN schemes, the line search algorithm Eq. 11 is adapted thanks to the formulation.
3.2 Pseudo-Spectral Discretization in Space and Linear System Solution
In a practical computation, we approximate the solution u by a J-terms finite-dimensional approximation
When one uses a fast transform (cosine, sine, FFT), we can proceed to the efficient computation of the application of an operator to a given function. For example, let us consider that one wants to numerically apply the fractional laplacian of order α to a given function v, i.e., we wish to compute w≔(−Δ)α/2v, where v is a given field known by its values vj at the nodes xj≔ − L/2 + (2j + 1)h/2, for 0 ≤ j ≤ J − 1 and where h = L/J denotes the uniform spatial meshsize (L = b − a). Then, we get the practical efficient calculation of w by the cosine (dct) and inverse cosine (idct) transforms in one-dimension through the Matlab code
For all the previous schemes presented in section 3.1, and for a constant function κ, the finite-dimensional solution in space can be obtained directly thanks to the above pseudo-spectral discretization. Indeed, even for the semi-implicit schemes, the operators to invert, i.e.
However, for the more complex situation that we consider in this paper, this is no longer possible. Indeed, a variable coefficient operator cannot be inverted explicitly in the Fourier space. Let us for example consider the situation of a full space representation (no boundary condition). Then, we can use the inverse Fourier representation of the operator
where
and
The symbol of the pseudodifferential operator [27] is given here by the expression
The inner product of two vectors p and q in
where σBA is the symbol of the operator BA. The operator Dη is:
since a does not depend on x and then the infinite sum Eq. 24 reduces to only one term for η = 0. When a is x-dependent, then the asymptotic expansion is infinite and b includes an infinite number of terms. The operator B−α/2 with symbol b−α/2≔a(x,ξ)−1 is a regularizing pseudodifferential operator of order − α which is not the inverse of A. Indeed, we have: B−α/2A = I + R, where R is a pseudodifferential operator of negative order which is however usually not an infinitely smoothing operator.
Now, if we come back to Eq. 22, we see that we can rewrite it as
which can be discretized directly thanks to a FFT, fast cosine or sine transform according to the boundary conditions. Let us write the corresponding discrete operation as
where v and w denotes the given and unknown vectors, respectively, at the discretization points, I is the identity matrix of size J, κ is the diagonal matrix with the entries κ(xj), for 0 ≤ j ≤ J − 1, and [[(−Δ)α/2]]v denotes the application of the fast algorithm for evaluating Av at the discrete level. Therefore, [[A]] is a matrix-free operator given through a fast evaluation procedure (with e.g., a function call
As previously seen, using the E or CN approximations needs the resolution of a linear system. When κ is a constant function, this can be trivially done thanks to the explicit inversion of the operator through the inverse of its symbol. For a function κ depending on x, then the process for solving one of the linear systems is to use an iterative solver instead of a direct method. Among them, fixed-point methods [28] (Jacobi, Gauss-Seidel, successive approximation) can be used. Nevertheless, it is well-known that they are not robust since their convergence rate strongly depends on the spectral radius of the iteration matrix. More efficient methods are based on Krylov subspace iterative solvers [28, 29]. We choose here the Generalized Minimal Residual (GMRES) method [29] which is extremely robust (other methods, like e.g., BiCGStab, have been tested but are proved to be less efficient within the framework of this paper; we do not report the results for the sake of conciseness). This method can solve matrix-free linear systems by calling an argument which is the function
where [[Bn]] is the discretization of the operator with symbol
where
4 Computational Aspects and Numerical Example
4.1 Computational Aspects
In the following, we call E and CN the semi-implicit Euler and Crank-Nicolson schemes Eqs 16, 20, respectively, without any preconditioner for the GMRES. When the preconditioner
where
Let us introduce the discrete L2-norm as:
The converged solution for a method m, the fractional PDE of order α/2, a number of spatial grid points J and a number of iterations
Therefore, representing
4.2 A One-Dimensional Example
To illustrate the methods, we consider an example in dimension one. The computational domain is
The parameter ɛ is fixed to 10–2 and β is the function
Concerning the variable function κ, we consider
Therefore, κm = 1 while κ oscillates. The number of grid points is set to J = 2p, for
Let us first report on Figure 1 (left) the computed solutions
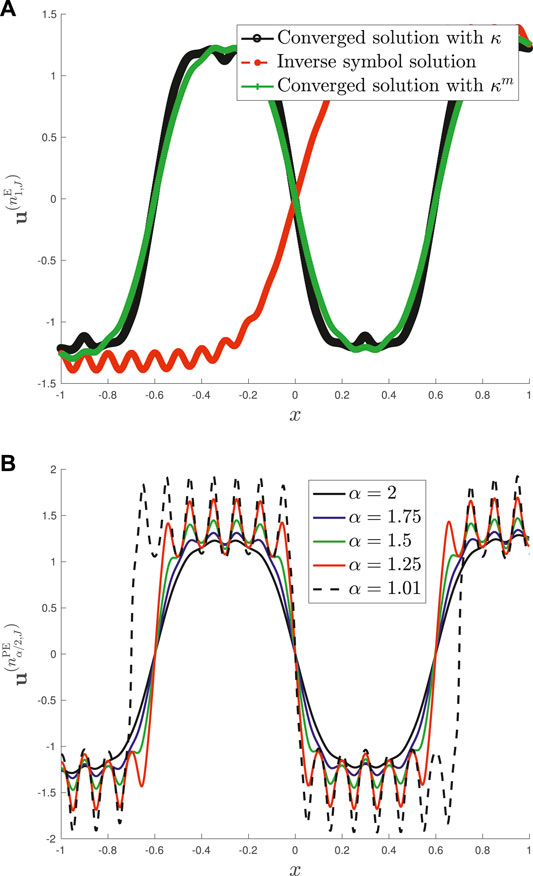
FIGURE 1. 1d case: (A) (α = 2): converged solutions for 1) the variable coefficients case with the unpreconditioned Euler scheme and variable function κ, 2) with the direct inversion of the operator by using the variable function κ and 3) with the Euler scheme by using the average constant κm. (B): converged solutions for various values of the fractional order α.
We analyze now the behavior of the global iterative method on Figure 2. The spatial discretization parameter is J = 210 for the same function cases as before, but with α = 1.5 and α = 1.9. On Figure 2, we report the residual history for the E, PE, CN and PCN methods, the preconditioner being based on the inverse of the operator with average symbol κm. As it can be seen, the semi-implicit Euler iterative scheme converges faster than the CN method, while preconditioning helps a lot for both methods by dividing the number of iterations by a factor 5–6 (α = 1.5) to 20 (α = 1.9). When α is close to 1, the preconditioner effect is less visible while it is more important for α close to 2. This can be understood by the fact that the condition number is then larger as α increases, leading to a need for preconditioning (−Δ)α/2. In addition, the preconditioner helps a lot for the convergence when refining the spatial discretization thanks to J, i.e. to get a higher accuracy. As a conclusion, and from other simulations in different configurations (not reported here for the sake of conciseness), it appears that the PE method always provides the best convergence rate.
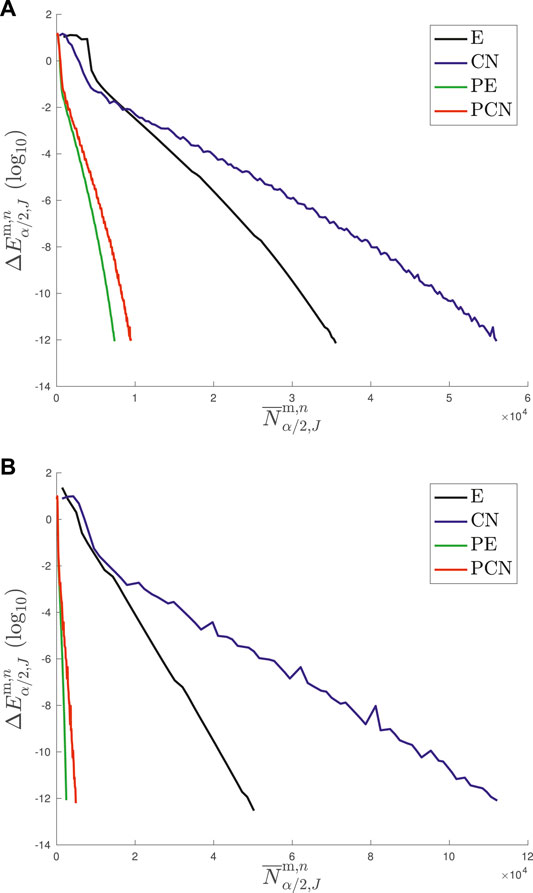
FIGURE 2. 1d case: (A) (α = 1.5) and (B) (α = 1.9): energy residual history of the E, PE, CN and PCN methods.
5 Conclusion
In this paper, we introduced some full discretizations of the gradient flow formulation of space fractional Cahn-Allen equations with variable coefficients in space. To this end, we use an Euler or Crank-Nicolson time discretization of the gradient flow formulation, with adaptive time stepping. In addition, a Fourier-based pseudo-spectral discretization scheme in space allows for an efficient and robust computation of each time step, in conjunction with a GMRES solver accelerated by a spectral preconditioner. Some simulations in dimension one show that the method based on the Euler scheme with the spectral preconditioner performs the best. This conclusion should extend to 2D/3D problems since all the ingredients here can be adapted and higher-dimensional grids are cartesian extensions of the one-dimensional case. In some future works, we will address more numerical examples in 2D and an extension of the method to the fractional Cahn-Hillard equation [30, 31] that is used for example in [32] as fractional inpainting model.
Data Availability Statement
The original contributions presented in the study are included in the article/Supplementary Materials, further inquiries can be directed to the corresponding authors.
Author Contributions
SA and CC developed the theoretical formalism, performed the analytic calculations and performed the numerical simulations. Authors contributed equally to the final version of the manuscript.
Funding
The authors would like to thank the Deanship of Scientific Research at Umm Al-Qura University for supporting this work by Grand code 18-SCI-1-01-0017.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Karniadakis GE, Hesthaven JS, Podlubny I. Special Issue on "Fractional PDEs: Theory, Numerics, and Applications". J Comput Phys (2015) 293:1–3. doi:10.1016/j.jcp.2015.04.007
3. Baleanu D, Diethelm K, Scalas E, Trujillo JJ. Fractional Calculus, Models and Numerical Methods. Series on Complexity, Nonlinearity and Chaos, 3. Boston, Mass: World Scientific (2012).
4. Herrmann R. Fractional Calculus, An Introduction for Physicists. GigaHedron, Germany: World Scientific (2011).
5. Metzler R, Klafter J. The Random Walk's Guide to Anomalous Diffusion: a Fractional Dynamics Approach. Phys Rep (2000) 339(1):1–77. doi:10.1016/s0370-1573(00)00070-3
6. Carreras BA, Lynch VE, Zaslavsky GM. Anomalous Diffusion and Exit Time Distribution of Particle Tracers in Plasma Turbulence Model. Phys Plasmas (2001) 8:5096–103. doi:10.1063/1.1416180
7. Shlesinger MF, West BJ, Klafter J. Lévy Dynamics of Enhanced Diffusion: Application to Turbulence. Phys Rev Lett (1987) 58:1100–3. doi:10.1103/physrevlett.58.1100
8. Zaslavsky GM, Stevens D, Weitzner H. Self-similar Transport in Incomplete Chaos. Phys Rev E (1993) 48:1683–94. doi:10.1103/physreve.48.1683
9. Meerschaert MM, Benson DA, Wheatcraft SW. Subordinated Advection-Dispersion Equation for Contaminant Transport. Water Resour Res (2001) 37:1543–50. doi:10.1029/2000WR900409
10. Benson DA, Wheatcraft SW, Meerschaert MM. The Fractional-Order Governing Equation of Lévy Motion. Water Resour Res (2000) 36:1413–23. doi:10.1029/2000wr900032
11. Scalas E, Gorenflo R, Mainardi F. Fractional Calculus and Continuous-Time Finance. Phys A: Stat Mech Appl (2000) 284:376–84. doi:10.1016/s0378-4371(00)00255-7
12. Yin B, Liu Y, Li H, He S. Fast Algorithm Based on TT-M FE System for Space Fractional Allen-Cahn Equations with Smooth and Non-smooth Solutions. J Comput Phys (2019) 379:351–72. doi:10.1016/j.jcp.2018.12.004
13. Ullah MS, Harun-Or-Roshid , Ali MZ, Noor NFM. Novel Dynamics of Wave Solutions for Cahn-Allen and Diffusive Predator-Prey Models Using MSE Scheme. Partial Differ Equations Appl Maths (2021) 3:100017. doi:10.1016/j.padiff.2020.100017
14. Allen SM, Cahn JW. A Microscopic Theory for Antiphase Boundary Motion and its Application to Antiphase Domain Coarsening. Acta Metal (1979) 27:1085–95. doi:10.1016/0001-6160(79)90196-2
15. Algahtani OJJ. Comparing the Atangana-Baleanu and Caputo-Fabrizio Derivative with Fractional Order: Allen Cahn Model. Chaos Solitons Fractals (2016) 89:552–9. doi:10.1016/j.chaos.2016.03.026
16. Nec Y, Nepomnyashchy AA, Golovin AA. Front-type Solutions of Fractional Allen-Cahn Equation. Phys D: Nonlinear Phenomena (2008) 237(24):3237–51. doi:10.1016/j.physd.2008.08.002
17. Lee S, Lee D. The Fractional Allen-Cahn Equation with the Sextic Potential. Appl Maths Comput (2019) 351:176–92. doi:10.1016/j.amc.2019.01.037
18. Benes M, Chalupecky V, Mikula K. Geometrical Image Segmentation by the Allen-Cahn Equation. Appl Numer Maths (2004) 51(2-3):187–205.
19. Lee D, Lee S. Image Segmentation Based on Modified Fractional Allen-Cahn Equation. Math Probl Eng (2019) 2019:3980181. doi:10.1155/2019/3980181
20. Zhai S, Gui D, Zhao J, Feng X. High Accuracy Spectral Method for the Space-Fractional Diffusion Equations. JMS (2014) 47(3):274–86. doi:10.4208/jms.v47n3.14.03
21. Bueno-Orovio A, Kay D, Burrage K. Fourier Spectral Methods for Fractional-In-Space Reaction-Diffusion Equations. Bit Numer Math (2014) 54(4):937–54. doi:10.1007/s10543-014-0484-2
22. Zhai S, Weng Z, Feng X. Fast Explicit Operator Splitting Method and Time-step Adaptivity for Fractional Non-local Allen-Cahn Model. Appl Math Model (2016) 40(2):1315–24. doi:10.1016/j.apm.2015.07.021
23. Alzahrani SS, Khaliq AQM. Fourier Spectral Exponential Time Differencing Methods for Multi-Dimensional Space-Fractional Reaction-Diffusion Equations. J Comput Appl Maths (2019) 361:157–75. doi:10.1016/j.cam.2019.04.001
24. Lischke A, Pang G, Gulian M, Song F, Glusa C, Zheng X, et al. What Is the Fractional Laplacian? A Comparative Review with New Results. J Comput Phys (2020) 404:109009. doi:10.1016/j.jcp.2019.109009
25. Choi J-W, Lee HG, Jeong D, Kim J. An Unconditionally Gradient Stable Numerical Method for Solving the Allen-Cahn Equation. Physica A: Stat Mech its Appl (2009) 388:1791–803. doi:10.1016/j.physa.2009.01.026
26. Dai S, Du Q. Motion of Interfaces Governed by the Cahn--Hilliard Equation with Highly Disparate Diffusion Mobility. SIAM J Appl Math (2012) 72(6):1818–41. doi:10.1137/120862582
29. Saad Y, Schultz MH. GMRES: a Generalized Minimal Residual Algorithm for Solving Nonsymmetric Linear Systems. SIAM J Sci Stat Comput (1986) 7(3):856–69. doi:10.1137/0907058
30. Ainsworth M, Mao Z. Analysis and Approximation of a Fractional Cahn--Hilliard Equation. SIAM J Numer Anal (2017) 55(4):1689–718. doi:10.1137/16m1075302
31. Weng Z, Zhai S, Feng X. A Fourier Spectral Method for Fractional-In-Space Cahn-Hilliard Equation. Appl Math Model (2017) 42:462–77. doi:10.1016/j.apm.2016.10.035
Keywords: nonlinear pseudodifferential equation, fractional derivative, dynamics, gradient flow, pseudo-spectral method
Citation: Alzahrani SM and Chokri C (2022) Preconditioned Pseudo-Spectral Gradient Flow for Computing the Steady-State of Space Fractional Cahn-Allen Equations With Variable Coefficients. Front. Phys. 10:844294. doi: 10.3389/fphy.2022.844294
Received: 27 December 2021; Accepted: 04 March 2022;
Published: 08 April 2022.
Edited by:
Valentina De Simone, University of Campania Luigi Vanvitelli, ItalyReviewed by:
Harun-Or Roshid, Pabna University of Science and Technology, BangladeshYang Liu, Inner Mongolia University, China
Copyright © 2022 Alzahrani and Chokri . This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Saleh Mousa Alzahrani , c2FsemFocmFuaUB1cXUuZWR1LnNh; Chniti Chokri , Y2hva3JpLmNobml0aUBpcGVpbi5ybnUudG4=
 Saleh Mousa Alzahrani 1*
Saleh Mousa Alzahrani 1* Chniti Chokri
Chniti Chokri