- Mathematical Science Department Faculty of Science Princess Nourah Bint Abdulrahman University, Riyadh, Saudi Arabia
In this study, the timelike-ruled and developable surfaces are constructed in Minkowski 3-space
1 Introduction
In spatial kinematics, the movement of an oriented line over a curve forms a ruled surface. The oriented lines are named generators (rulings), and each curve that intersects all the generators is called A directrix (or base curve). The theory of ruled surfaces is mentioned by researchers and mathematicians because of its applications in screw systems, iterative methods for displacement analysis of spatial mechanisms, and computer aided design (CAD) [1–4]. Because many researchers have already studied and determined numerous characteristics of ruled surfaces, as in [24, 25], this study is limited to the Minkowski 3 space. Developable surfaces define a subset of ruled surfaces, such that every point from the same ruling shares a common tangent plane. Rulings define the principal curvature lines of zero normal curvature in addition to the Gaussian curvature, which is zero at each point on the surface. Because the inner metric of a surface locates the Gaussian curvature, all the angles and lengths on the surface remain invariant under bending. This feature is what makes ruled and developable surfaces important in manufacturing. Hence, both ruled and developable surfaces have been considered in engineering, architecture, design, etc. (see [5–10])].
A suitable method to study the motion of an oriented line in space starts from the relationship among this space, dual numbers, and dual vector calculus. Dual numbers were first introduced by W. Clifford; subsequently E. Study utilized it as an instrument for the purpose of differential line geometry and kinematics. He devoted special care to the impersonation of oriented lines by dual unit vectors and defined the mapping, which was later named after him. The E. Study map indicates that the set of all oriented lines in Euclidean 3-space
Kose introduced a novel method for determining developable ruled surfaces using dual-vector calculus [14]. They demonstrated that a ruled surface can be obtained from coordinates and first derivatives of the base curve. Further Yildz et al. applied this method using an orthotomic concept [15]. In the course of time, this method has been extended and presented in the dual Lorentzian 3-space
However, to the best of the authors’ knowledge, no literature exists regarding the fact that a timelike-ruled surface can be obtained from coordinates and the first derivatives of the base curve. Hence, this study attempts to address this need. The remainder of this paper is organized as follows: In Section 2, we present some basic concepts dealing with the dual Lorentzian 3-space
2 Basic Concepts
We begin with basic concepts on the theory of dual numbers, dual Lorentzian Vectors, and the E. Study map (see [1–5, 16–21]): A directed (non-null) line L in Minkowski 3-space
The six components
A dual number A is a number a + ɛa*, where a, a* in
joining with Lorentzian scalar product
leads to what is named the dual Lorentzian 3-space
If a is spacelike, we have
If a is timelike, we have
Therefore, A is the spacelike dual unit vector in case ⟨A, A⟩ = 1 and the timelike dual-unit vector in case ⟨A, A⟩ = −1. The hyperbolic and Lorentzian dual unit spheres are
and
respectively.
Theorem 1. : [17–19, 22, 23]. There is a one-to-one correspondence between spacelike (resp. timelike) oriented lines at Minkowski 3-space
where a and a* are the normed Pl ücker coordinates of the line.
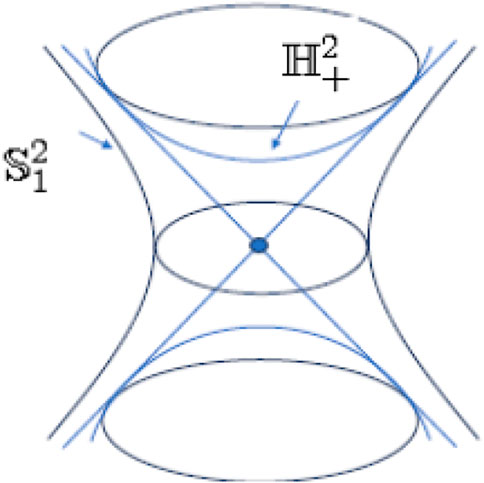
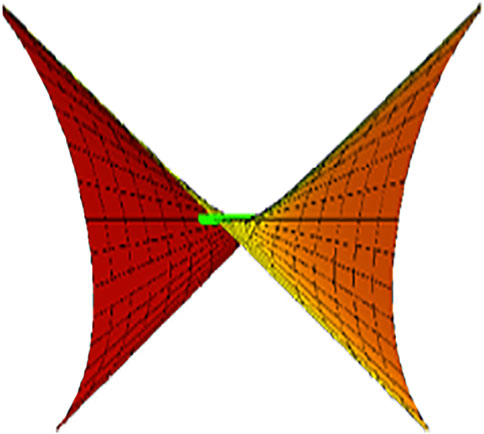
Using Theorem 1, we obtain the following map (E. Study’s map), where the dual unit spheres are shaped as a pair of conjugate hyperboloids. The ring shaped hyperboloid represents the set of spacelike lines, the common asymptotic cone represents the set of null (lightlike) lines, the oval shaped hyperboloid forms the set of timelike lines, and opposite points of each hyperboloid perform a pair of obverse vectors on a line (see Figure 1). Applying to the E. Study map, the differentiable curve on
2.1 Timelike-Ruled Surface as a Curve at
Let y(t) be the regular curve at the Minkowski 3-space
Here y = y(t) is its directrix or base curve, and t is the motion parameter. The E. Study map is adopted to write Eq. 2 using the dual vector function as
Because the spherical image x, is the timelike unit vector, the timelike dual vector X and unit magnitude, as is observed from the computation
Therefore, the timelike-ruled surface is presented using the dual curve at the surface of the dual hyperbolic unit sphere. The dual arc length of
Hence, the distribution parameter is expressed as
Here, and in what follows, the prime symbol denotes derivatives with respect to parameter “t.”
The Gaussian curvature K (t, v) is related to the distribution parameter λ(t) of the timelike-ruled surface [5] as follows:
If K (t, v) equals zero everywhere, this means that λ equals zero everywhere; therefore, M is referred to as developable. At Eq. 5: (a) in case λ(t) = 0, therefore M is the timelike developable ruled surface (b) if x′ = 0, therefore M is the timelike cylindrical ruled surface.
3 Timelike-Ruled and Developable Surfaces
In this section, we develop a procedure to construct timelike-ruled and developable surfaces using the E. Study’s map. Dual coordinates
where Θ = ϑ + ɛϑ∗ and Ψ = ψ + ɛψ* defines the dual hyperbolic and space-like angles with ϑ*,
If we separate the real and dual parts of Eq. 6, in the same order, we obtain:
and
Thus, we arrive at
It is clear that: (a) if λ(t) = 0, then M is the timelike developable ruled surface (b) if ψ(t) and ϑ(t) are constants; that is, x′ = 0, then M is a time-like cylinder.
Becauseɛ2 = ɛ3 = … = 0, the Plucker coordinates of X are:
Here, the normal question appears when curve y(t) = (y1(t), y2(t), y3(t)) is provided, will the timelike ruled surface considering its base curve be defined as the curve y(t)? The answer is affirmative and can be stated as follows: Because x* = y ×x, we obtain a system of linear equations in yi for i = 1, 2, 3:
The matrix of the coefficients of unknowns y1, y2, and y3 is the skew-adjoint matrix
and thus, its rank is 2 with ϑ ≠ 0, and ψ ≠ 2πk (k is the integer). This augmented matrix
is of rank 2. Thus, infinite solutions of the system are expressed as
Because it is possible to choose y1(t), we use y1(t) = ψ*(t). Then, Eq. 12 will be reduced to
From Eq. 13, we have
Notably, ϑ*(t) has two values; using the minus sign resulted in the reciprocal of the timelike-ruled surface obtained using the plus sign. Therefore, in this study, we chose a lower sign. Into Eq. 2 we substitute from Eqs 13, 14 and obtain:
where
Theorem 2. : Let y(t) be a regular curve in Minkowski 3-space
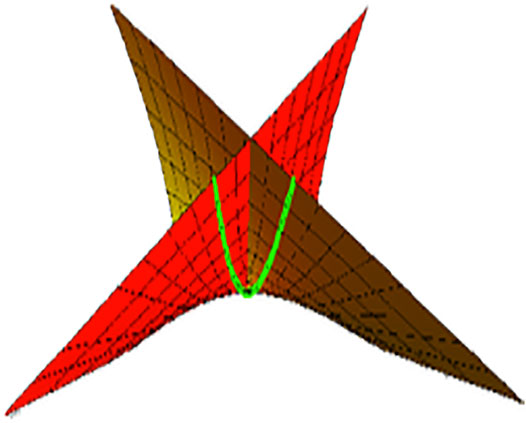
Example 1. : Let y(t) = (t, t2, t2) be the curve at Minkowski 3-space
The distribution parameter is
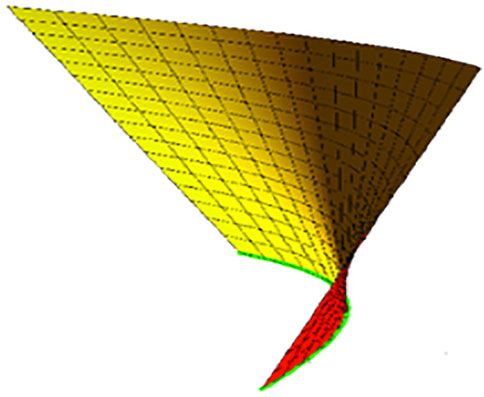
Function ϑ(t) can control the shape of the surface. If we take ϑ(t) = t, then
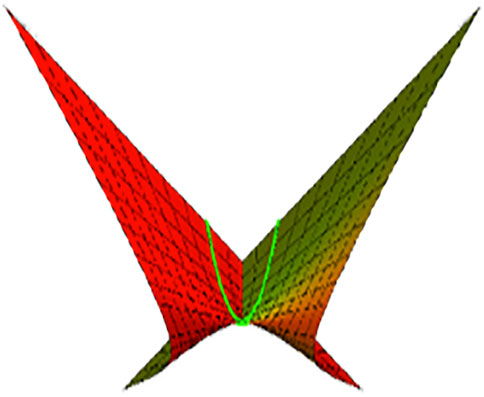
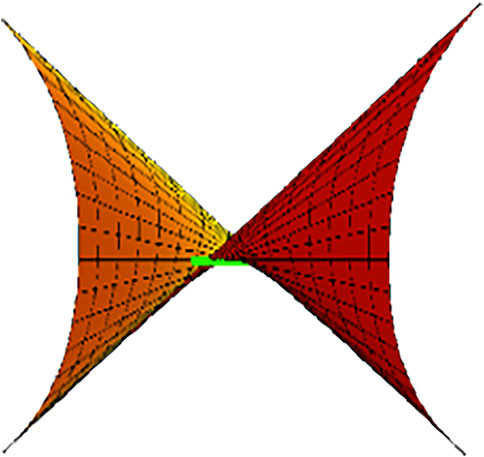
Example 2. : Let y(t) = (t, t, 1) be the null curve at Minkowski 3-space
The distribution parameter is
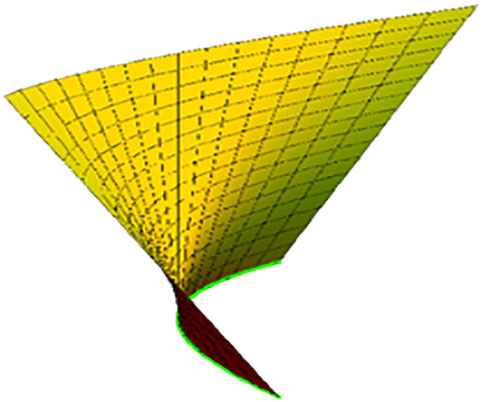
If we take ϑ(t) = t, then for -1 ≤ t ≤ 1 and −6 ≤ v ≤ 6, the timelike-ruled surface is illustrated in Figure 4. For ϑ(t) = −t, 1 ≤ t ≤ 1 and −6 ≤ v ≤ 6, the surface is illustrated in Figure 5.
3.1 Timelike Developable Surfaces
In this subsection, the challenge of constructing developable timelike surfaces from a timelike-ruled surfaces is analyzed. Therefore, the normal question that is raised here is: what is the condition of y (t, v) to a timelike developable ruled surface in Minkowski 3-space
or equivalently
If we
which leads to the linear differential equation of first order
Here, it is necessary to determine ϑ(t). The solution to (19) leads to coth ϑ. It contains the integral constant and we have several infinitely timelike developable ruled surfaces, that is every timelike developable surface has a base curve y(t); From Eqs.(13) and, (14), we have
Example 3. : In Example 1, clearly
and
we substitute these values into Eq. 19 and solve this differential equation
Because coth ϑ = c, we have:
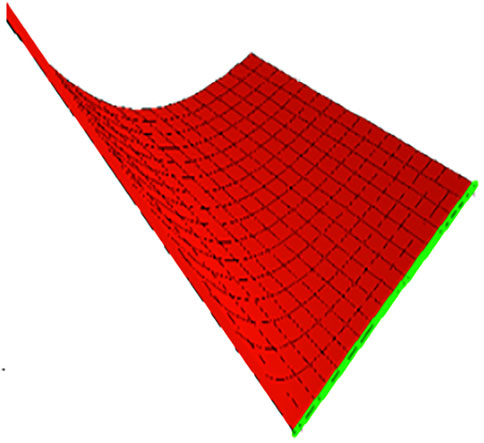
If we choose the plus sign, then the family of timelike developable ruled surface is presented as
If
Example 4. : From the curve in Example 2,
Then, combining Eq. 20 and (Eq. 22), we have:
The solution of this differential equation gives
Because f(t) = − coth ϑ, then we have:
If we choose the plus sign, then the family of timelike developable ruled surface is introduced as
If we consider
4 Conclusion
In this study, a general method to determine timelike-ruled and developable surfaces in Minkowski 3-space
Data Availability Statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Author Contributions
The author confirms being the sole contributor of this work and has approved it for publication.
Funding
Princess Nourah bint Abdulrahman University Researchers Supporting Project number (PNURSP2022R27), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia.
Conflict of Interest
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Acknowledgments
The author expresses their sincere gratitude to Prof. Rashad A. Abdel-Baky for his productive consultations. The author expresses her gratitude to Princess Nourah Bint Abdulrahman University Researchers Supporting Project number (PNURSP2022R27), Princess Nourah Bint Abdulrahman University, Riyadh, Saudi Arabia.
References
2. Karger A, Novak J. Space Kinematics and Lie Groups. New York: Gordon and Breach Science Publishers (1985).
3. McCarthy JM. Scalar and Dual Formulations of Curvature Theory of Line Trajectories. ASME J Mech Trans Auto Des. (1987) 109/101.
5. Mancewicz MJ, Frey WH. Developable Surfaces: Properties Representations and Methods of Design Doctoral dissertation. Kalamazoo College: General Motors R&D Publication (1992). p. 7637.
6. Bodduluri RMC, Ravani B. Design of Developable Surfaces Using Duality between Plane and point Geometries. Computer-aided Des (1993) 25(10):621–32. doi:10.1016/0010-4485(93)90017-i
7. Zhao H, Wang G. A New Method for Designing a Developable Surface Utilizing the Surface Pencil through a Given Curve. Prog Nat Sci (2008) 18(1):105–10. doi:10.1016/j.pnsc.2007.09.001
8. Li CY, Wang RH, Zhu CG. Approach for Designing a Developable Surface through a Given Line of Curvature. Computer-Aided Des (2013)(45) 621–7. doi:10.1016/j.cad.2012.11.001
9. Wang J, Jiang P, Guo Y, Meng J. Developable Surface Pencil Pairs with Special Pairs as Common Asymptotes. Appl Math Comput (2019) 362:124583. doi:10.1016/j.amc.2019.124583
10. Köse Ö. Contributions to the Theory of Integral Invariants of a Closed Ruled Surface. Mechanism Machine Theor (1997) 32(2):261–77. doi:10.1016/s0094-114x(96)00034-1
11. Abdel-Baky RA, Al-Solamy FR. A New Geometrical Approach to One-Parameter Spatial Motion. J Eng Math (2008) 60:149–72. doi:10.1007/s10665-007-9139-5
12. Abdel-Baky RA, Al-Ghefari RA. On the One-Parameter Dual Spherical Motions. Comp Aided Geometric Des (2011) 28:23–37. doi:10.1016/j.cagd.2010.09.007
13. Al-Ghefari RA, Abdel-Baky RA. Kinematic Geometry of a Line Trajectory in Spatial Motion. J Mech Sci Technol (2015) 29(9):3597–608. doi:10.1007/s12206-015-0803-9
15. Yıldız OG, Karakus SO, Hacısalihoglu HH. On the Determination of a Developable Spherical Orthotomic Ruled Surface. Bull Math Sci (2015) 5:137–46.
16. H Abdel-All N, Abdel-Baky RA, Hamdoon FM. Ruled Surfaces with Timelike Rulings. App Math Comp (2004)(147) 241–53. doi:10.1016/s0096-3003(02)00664-1
17. Alluhaibi N, Abdel-Baky RA. On Kinematic Geometry of Hyperbolic Dual Spherical Motions and Euler–Savary’s Equation. Int J Geometric Methods Mod Phys (2019) 16(No. 12). doi:10.1142/s0219887819501974
18. Alluhaibi N, Abdel-Baky RA. On the One-Parameter Lorentzian Spatial Motions. Int J Geometric Methods Mod Phys (2019) 16(No. 12):1950197. doi:10.1142/s0219887819501974
19. Abdel-Baky RA, Unlütürk Y. A New Construction of Timelike-Ruled Surfaces with Constant Disteli-axis. Honam Math J (2020) 42(3):551–68.
21. Lopez R. Differential Geometry of Curves and Surfaces in Lorentz-Minkowski Space. arxiv.org/abs/0810.3351v1 2008.
22. Uğurlu HH, Çalişkan A. Study Mapping for Directed Space-like and Time-like in Minkowski 3-Space R13. Math Comput Appl (1996) 1(2):142–8.
24. Turgut A, Hacisalioğlu H. Timelike-ruled over the Surfaces in Minkowski 3-Space-II. Turkish J Math (1998) 22(1):33–46.
Keywords: plucker coordinate, distribution paramater, E. study map, timelike-ruled, developable surface
Citation: Mofarreh F (2022) Timelike-Ruled and Developable Surfaces in Minkowski 3-Space
Received: 18 December 2021; Accepted: 14 February 2022;
Published: 16 June 2022.
Edited by:
Josef Mikes, Palacký University, CzechiaReviewed by:
Alberto Molgado, Autonomous University of San Luis Potosí, MexicoAndreas Gustavsson, University of Seoul, South Korea
Copyright © 2022 Mofarreh. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Fatemah Mofarreh, ZnlhbG1vZmFycmFoQHBudS5lZHUuc2E=
 Fatemah Mofarreh
Fatemah Mofarreh