- 1SLAC National Accelerator Laboratory, Stanford Institute for Materials and Energy Sciences, Menlo Park, CA, United States
- 2Department of Physics, Stanford University, Stanford, CA, United States
- 3Department of Materials Science and Engineering, Stanford University, Stanford, CA, United States
Building upon the recent progress on the intriguing underlying physics for the newly discovered infinite-layer nickelates, in this article we review an examination of valence charge and spin excitations via multi-orbital Hubbard models as way to determine the fundamental building blocks for Hamiltonians that can describe the low energy properties of infinite-layer nickelates. We summarize key results from density-functional approaches, and apply them to the study of x-ray absorption to determine the valence ground states of infinite-layer nickelates in their parent form, and show that a fundamental d9 configuration as in the cuprates is incompatible with a self-doped ground state having holes in both
1 Introduction
The discovery of experimental superconductivity in infinite-layer nickelates [1], 20 years after they were theoretically proposed [2], has unveiled new territory to probe the unknowns of unconventional superconductivity. The comparison between the superconducting nickelates to the cuprates has proven to be a rich area of inquiry. Significant progress has been made in the last 2 years, but many mysteries about this novel superconducting family remain unsolved. As pointed out early on [3], the bandstructure for LaNiO2 while being primarily 3d9 Ni near the Fermi level has additional small Fermi pockets of largely axial character involving Ni
Thus there already is a rich amount of information from which an estimate for a fundamental low energy model Hamiltonian can be obtained and used to model the phase diagram of infinite-layer nickelates. In this article we review efforts to combine density functional approaches with cluster exact diagonalization to determine such a model. Specifically we utilize x-ray absorption (XAS) as a tool to determine valence charge states in the undoped and doped infinite-layer nickelates, arriving at a low-energy 2-orbital model Hamiltonian. We then perform calculations on finite-sized clusters to determine the dynamic spin structure factor in undoped and doped systems. Our results yield a consistent description of charge valence and spin excitation states in the infinite-layer nickelates, indicating that a 2-orbital model likely contains the fundamental ingredients needed to explore superconductivity and the rich phase diagram in these compounds.
2 Methods
2.1 Density Functional Theory
The electronic structure of the infinite-layer nickelates RNiO2 have been evaluated using density functional theory (DFT) in the generalized gradient approximation (GGA) for the exchange-correlation functional as implemented in Quantum Espresso [9, 10]. The band structure near the Fermi energy that was obtained for NdNiO2 is shown in Figures 1A, B.
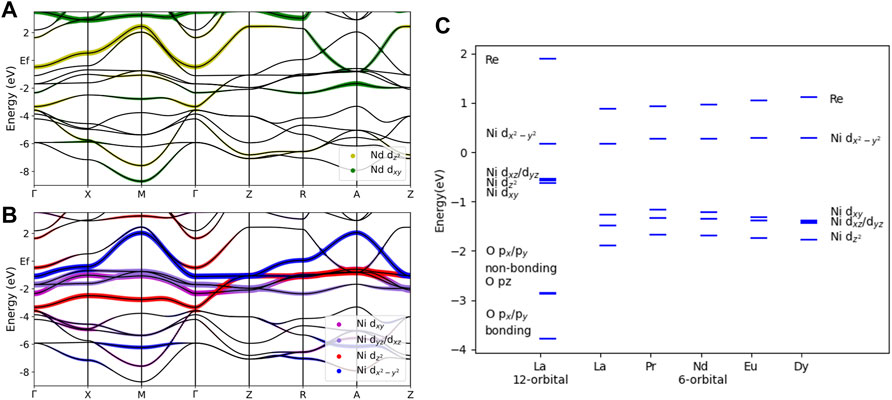
FIGURE 1. (A) DFT calculated band structure and projected Nd 5d orbital content for infinite-layer nickelate NdNiO2. (B) DFT calculated band structure and projected Ni 3d orbital content for NdNiO2. (C) Atomic energy level diagram for infinite-layer nickelates RNiO2, where R = La, Pr, Nd, Eu, and Dy. On-site energies are obtained by 6-orbital and 12-orbital Wannier downfolding from DFT calculated band structures. All energy levels are relative to the Fermi level of the corresponding material.
To obtain a microscopic Hamiltonian and understand the atomic energy levels, we downfolded the bandstructure as implemented in Wannier90 [11] to obtain the tight-binding model parameters
2.2 X-Ray Absorption from Multi-Orbital Hubbard Hamiltonians
We focus on the Ni L-edge (2p → 3d) XAS utilizing a cluster model for monovalent NiO2 containing five Ni 3d orbitals and six O 2p orbitals in a square-planar geometry, and three Ni 2p orbitals per unit cell in the atomic core, with hybridization parameters obtained from Wannier downfolding as described in the previous section. We evaluate the XAS κ for the absorption of a photon having momentum and polarization ki, ei, respectively, as
Here, Z is the partition function, E{i,ν}, |{i, ν}⟩ are the energies and eigenstates of the initial (ground state) and XAS final states, respectively, obtained from exact diagonalization of the multi-orbital Hubbard model in the cluster Hilbert space. The multi-orbital Hubbard model can be compactly written as
Here i, j denote sites, σ, σ′ denote spin, and μ, ν, μ′, ν′ denote orbital indices. The operators
2.3 Dynamic Spin Structure Factor
The dynamic spin structure factor has been shown to be an accurate approximation of the RIXS cross section of both Mott insulators and doped systems [6, 13]. The dynamical spin structure factor is defined as
where the spin density operator is given by
where ck
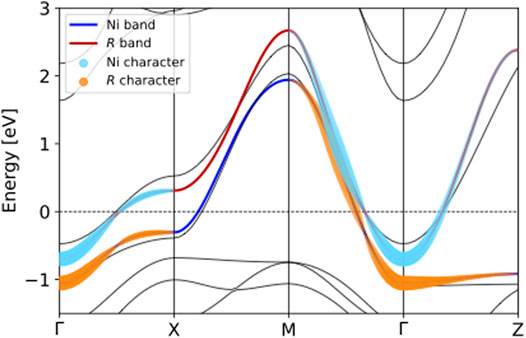
FIGURE 2. Hybridization of the 2-orbital model for NdNiO2, as described in Eq. 4, showing subdominant Ni and R band character, respectively.
We evaluate the dynamic spin structure factor, S (q, ω), for the 2-orbital nickelate model using exact diagonalization (ED) on an 8-site (diamond-shaped) Betts cluster [15] with periodic boundary conditions, which suffers from finite-size effects but is sufficient for determining the magnon spectrum on the antiferromagnetic Brillouin zone boundary at (π/2, π/2). We take the value of the Hubbard U = 8 eV so that we get a reasonable estimate of J ∼ 80 meV. The eigenvalues and eigenvectors of the ED calculations were found using the Implicitly Restarted Lanczos Method from the ARnoldi PACKage (ARPACK), as implemented in SciPy Linalg library ([16], RRID: SCR_008058). The biconjugate gradient stabilized method was used to calculate S (q, ω).
3 Results
3.1 X-Ray Absorption Spectroscopy
3.1.1 Single-Site
The single site XAS is simulated using techniques mentioned in Sec. 2.2, where the Hilbert space is determined using only the 3d (valence) and 2p (core) orbitals of the Ni transition metal ion, without ligand 2p orbitals, and with open boundary conditions. The eigenenergies are obtained by diagonalizing the Hamiltonian and the XAS cross section is evaluated using Eq. (1).
We first calculate the multiplet XAS of the d9 electronic configuration of the Ni ion where the Slater-Condon, spin orbit coupling and crystal-field splitting parameters are taken from Ref. [17]. The results are plotted in Figure 3. Since the single site calculation does not include ligand orbitals in the Hilbert space, direct measurements of crystal field splitting of d orbitals energy levels are used without hybridization parameters obtained by Wannier downfolding from Ref. [18]. Although hybridization with ligands is not considered in this single-site calculation, it can still capture the difference in XAS between high-spin and low-spin ground state as described below. The Coulomb interaction for d9 ions is less relevant and the spectral lineshape is dominated by the spin orbit coupling of the core levels, showing a single peak for both the L3 and L2 edges with light polarization along the x-direction, and no absorption with light polarization along the z-direction, due to the orbital
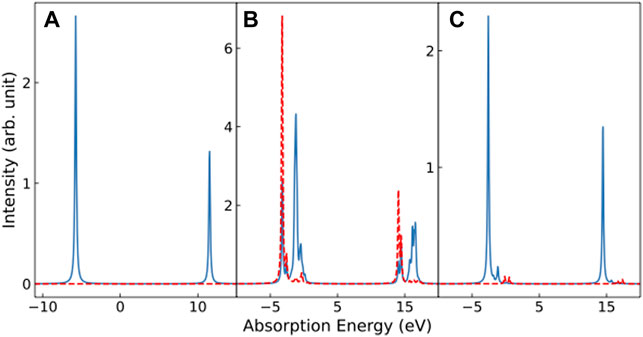
FIGURE 3. Multiplet XAS calculations for the single-site nickel ion. The absorption energy is measured with respect to the ground state of d9 ion. The solid line is the spectra measured with x-polarized light, and the dashed line is the spectra measured with z-polarized light. From left to right are spectra of (A) the d9 ion, (B) the d8 high-spin ion, and (C) the d8 low-spin ion.
We also simulated doped spectra as a linear combination of the d8 and d9 spectra, with the results plotted in Figure 4. Clearly, the high-spin d8 state produces spectra with a wide energy spread and additional multiplet peaks. A better comparison to experiment [17] can be made if the d8 ion is in the low-spin configuration, producing a less pronounced shoulder in addition to the main absorption peak from the dominant d9 configuration.
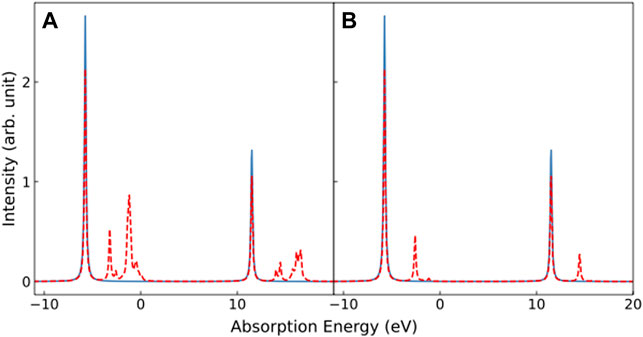
FIGURE 4. XAS spectra for the undoped d9 ion (solid line) and with 20% of the hole-doped d8 ion (dashed line) calculated for x-polarization. Panel (A) shows the results for doping with the d8 high-spin state, and panel (B) shows the results for doping with the d8 low-spin state.
3.1.2 Two-Site
The two-site XAS is simulated with a two-site, multi-orbital Hubbard model as described in Sec. 2.2 with periodic boundary conditions in contrast to section Sec. 3.1.1, with 11 orbitals for each site (unit cell NiO2) in the initial state that includes six oxygen 2p orbitals and the five nickel 3d orbitals, and 14 orbitals for one of the cells in the final state, which includes an additional three core-level nickel 2p orbitals for the target atom. The eigenenergies and eigenstates are obtained by exact diagonalization of the model Hamiltonian and the XAS spectra are calculated using Eq. (1). Including the oxygen ligand orbitals in the model allows hybridization and charge transfer effects between oxygen 2p and Nickel 3d orbitals. The Ni-O hybridization will affect not only the effective energy levels of the Nickel 3d orbitals, but this also changes the effective band character, with oxygen ligand p orbital contributions to the valance and conduction bands, which will result in changes to the XAS lineshape compared to the single-site calculation in Sec. 3.1.1.
We performed multiplet calculations for a two-site, two-hole (nominally d9 nickel) and a two-site, three-hole (doped NiO2 planes) cluster using effective parameters described in Sec. 3.1.1, and hopping parameters (tpd, tpdz, tpdxy, tpdxz, tpdyz are 1.2, 0.3, 0.7, 0.8 and 0.8 eV, respectively) obtained by Wannier downfolding as described in Sec. 2.1. The inclusion of hybridization parameters allow us to modulate the strength of electron hopping between each orbital and the onsite energy, with the electrons distributed between the different orbitals based on the model Hamiltonian as described in Ref. [18]. These XAS spectra are shown in Figure 5. The two-site, two-hole XAS spectrum with x-polarization is similar to the single-site, d9 model, which was described in the previous section. When doped with one hole, the L3 and L2 edges split into three peaks due to Ni-O hybridization. These results are consistent with both the single-site calculation and the experimental results [17].
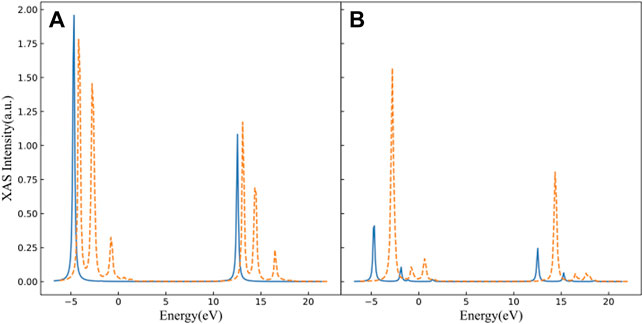
FIGURE 5. Multiplet calculations for two-site, two-hole (solid, blue line) and two-site, three-hole (dashed, orange) NiO2 clusters. The absorption energy is measured from the ground state of the two-site, two-hole calculation. Panel (A) shows the XAS spectra in x-polarization; and panel (B) shows the XAS spectra in z-polarization.
3.2 Spin Structure Factor
Results for the dynamical spin structure factor calculated via exact diagonalization are plotted in Figure 6, showing a comparison of the 2-orbital model with two different values of the energy difference between Ni and R orbitals
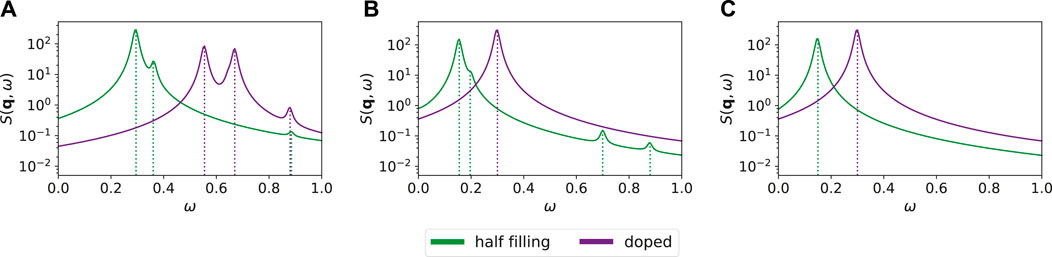
FIGURE 6. Comparison of S (q, ω) at
For the 2-orbital model, tuning the energy difference between Ni and R sites, Δ, plays a major role in the occupation of the R orbital, and hence the “self-doping” of the Ni layer. In Figure 6A, Δ ∼ 1 eV results in approximately two electrons occupying the R-sites at both overall half-filling and ∼
4 Discussion
In this paper we explored numerical simulations using DFT and ED to determine the underlying band structure, valence configuration, and dynamical spin response of model Hamiltonians aimed to describe infinite-layer nickelates. DFT for various R substituted nickelates was used to determine the parameters of an effective 2-orbital model including Ni 3
Our ED calculations are limited to small clusters and therefore the effect of long-wavelength physics remains beyond our level of investigation. This may be particularly relevant to a discussion of the root cause of superconductivity and the competition between superconductivity and other intertwined phases, such as spin and/or charge stripes that are prevalent in both cuprate phase diagrams and numerical simulations of the single-band Hubbard model [19, 20]. Reference [21] reports density matrix renormalization group (DMRG) simulations of a similar 2-orbital model, and finds Luther-Emery behavior - coexistence of long-range superconducting and charge-density wave order - away from half-filling as in the 1D Hubbard model, while the undoped model does not contain long-range antiferromagnetic order, different than single-band Hubbard and more closely in-line with infinite-layer nickelates. The spin dynamics may be investigated using t-DMRG or other techniques, such as determinant quantum Monte Carlo [22]. This remains a topic of future interest.
Data Availability Statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Author Contributions
EB performed ED calculations for S (q, ω), YH and KH performed ED calculations for XAS, CJ and EB performed DFT calculations for the nickelate bandstructure. BM, CJ, YC, and TD conceived the project. All authors contributed to the writing of the manuscript.
Funding
This work was supported by the U.S. Department of Energy (DOE), Office of Basic Energy Sciences, Division of Materials Sciences and Engineering. Computational work was performed on the Sherlock cluster at Stanford University and on resources of the National Energy Research Scientific Computing Center, supported by the U.S. DOE, Office of Science, under Contract no. DE-AC02-05CH11231.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Acknowledgments
We would like to thank Yao Wang from Clemson University for helpful discussions about exact diagonalization and the 2-orbital nickelate model.
References
1. Li D, Lee K, Wang BY, Osada M, Crossley S, Lee HR, et al. Superconductivity in an Infinite-Layer Nickelate. Nature (2019) 572:624–7. doi:10.1038/s41586-019-1496-5
2. Anisimov VI, Bukhvalov D, Rice TM. Electronic Structure of Possible Nickelate Analogs to the Cuprates. Phys Rev B (1999) 59:7901–6. doi:10.1103/PhysRevB.59.7901
3. Lee K-W, Pickett WE. Infinite-layerLaNiO2: Ni1+is notCu2+. Phys Rev B (2004) 70:165109. doi:10.1103/PhysRevB.70.165109
4. Zaanen J, Sawatzky GA, Allen JW. Band Gaps and Electronic Structure of Transition-Metal Compounds. Phys Rev Lett (1985) 55:418–21. doi:10.1103/PhysRevLett.55.418
5. Lu H, Rossi M, Nag A, Osada M, Li DF, Lee K, et al. Magnetic Excitations in Infinite-Layer Nickelates. Science (2021) 373:213–6. doi:10.1126/science.abd7726
6. Jia CJ, Nowadnick EA, Wohlfeld K, Kung YF, Chen C-C, Johnston S, et al. Persistent Spin Excitations in Doped Antiferromagnets Revealed by Resonant Inelastic Light Scattering. Nat Commun (2014) 5:3314. doi:10.1038/ncomms4314
7. Le Tacon M, Ghiringhelli G, Chaloupka J, Sala MM, Hinkov V, Haverkort MW, et al. Intense Paramagnon Excitations in a Large Family of High-Temperature Superconductors. Nat Phys (2011) 7:725–30. doi:10.1038/nphys2041
8. Dean MPM, Dellea G, Springell RS, Yakhou-Harris F, Kummer K, Brookes NB, et al. Persistence of Magnetic Excitations in La2−xSrxCuO4 from the Undoped Insulator to the Heavily Overdoped Non-superconducting Metal. Nat Mater (2013) 12:1019–23. doi:10.1038/nmat3723
9. Giannozzi P, Baseggio O, Bonfà P, Brunato D, Car R, Carnimeo I, et al. QuantumESPRESSO toward the Exascale. J Chem Phys (2020) 152:154105. doi:10.1063/5.0005082
10. Perdew JP, Burke K, Ernzerhof M. Generalized Gradient Approximation Made Simple. Phys Rev Lett (1996) 77:3865–8. doi:10.1103/PhysRevLett.77.3865
11. Mostofi AA, Yates JR, Pizzi G, Lee Y-S, Souza I, Vanderbilt D, et al. An Updated Version of Wannier90: A Tool for Obtaining Maximally-Localised Wannier Functions. Comp Phys Commun (2014) 185:2309–10. doi:10.1016/j.cpc.2014.05.003
12. de Groot F, Kotani A. Advances in Condensed Matter Science. Boca Raton: CRC Press (2008). doi:10.1201/9781420008425 Core Level Spectroscopy of Solids.
13. Jia C, Wohlfeld K, Wang Y, Moritz B, Devereaux TP. Using RIXS to Uncover Elementary Charge and Spin Excitations. Phys Rev X (2016) 6:021020. doi:10.1103/PhysRevX.6.021020
14. Been E, Lee W-S, Hwang HY, Cui Y, Zaanen J, Devereaux T, et al. Electronic Structure Trends across the Rare-Earth Series in Superconducting Infinite-Layer Nickelates. Phys Rev X (2021) 11:011050. doi:10.1103/physrevx.11.011050
15. Betts DD, Lin HQ, Flynn JS. Improved Finite-Lattice Estimates of the Properties of Two Quantum Spin Models on the Infinite Square Lattice. Can J Phys (1999) 77:353–69. doi:10.1139/p99-041
16. Virtanen P, Gommers R, Oliphant TE, Haberland M, Reddy T, Cournapeau D, et al. SciPy 1.0: Fundamental Algorithms for Scientific Computing in Python. Nat Methods (2020) 17:261–72. doi:10.1038/s41592-019-0686-2
17. Rossi M, Lu H, Nag A, Li D, Osada M, Lee K, et al. Orbital and Spin Character of Doped Carriers in Infinite-Layer Nickelates. Phys Rev B (2021) 104:L220505. doi:10.1103/PhysRevB.104.L220505
18. Hepting M, Li D, Jia CJ, Lu H, Paris E, Tseng Y, et al. Electronic Structure of the Parent Compound of Superconducting Infinite-Layer Nickelates. Nat Mater (2020) 19:381–5. doi:10.1038/s41563-019-0585-z
19. Arovas DP, Berg E, Kivelson S, Raghu S. The Hubbard Model (2021). arXiv e-prints , arXiv:2103.12097.
20. Huang EW, Wang WO, Ding JK, Liu T, Liu F, Huang X-X, et al. Intertwined States at Finite Temperatures in the Hubbard Model. J Phys Soc Jpn (2021) 90:111010. doi:10.7566/JPSJ.90.111010
21. Peng C, Jiang H-C, Moritz B, Devereaux TP, Jia C. Superconductivity in a Minimal Two-Band Model for Infinite-Layer Nickelates (2021). arXiv e-printsarXiv:2110.07593.
Keywords: nickelate, superconductor, exact diagonalization, dynamic spin structure factor, spectroscopy, x-ray absorption spectroscopy, XAS
Citation: Been EM, Hsu KH, Hu Y, Moritz B, Cui Y, Jia C and Devereaux TP (2022) On the Nature of Valence Charge and Spin Excitations via Multi-Orbital Hubbard Models for Infinite-Layer Nickelates. Front. Phys. 10:836959. doi: 10.3389/fphy.2022.836959
Received: 16 December 2021; Accepted: 17 January 2022;
Published: 28 February 2022.
Edited by:
Antia Botana, Arizona State University, United StatesReviewed by:
Atsushi Fujimori, Waseda University, JapanFranca Manghi, University of Modena and Reggio Emilia, Italy
Copyright © 2022 Been, Hsu, Hu, Moritz, Cui, Jia and Devereaux. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Thomas P. Devereaux, dHBkQHN0YW5mb3JkLmVkdQ==
 Emily M. Been
Emily M. Been Kuan H. Hsu
Kuan H. Hsu Yi Hu
Yi Hu Brian Moritz
Brian Moritz Yi Cui3
Yi Cui3 Thomas P. Devereaux
Thomas P. Devereaux