Ab Initio Wavefunction Analysis of Electron Removal Quasi-Particle State of NdNiO2 With Fully Correlated Quantum Chemical Methods

The discovery of superconductivity in hole-doped infinite-layer NdNiO₂ — a transition metal (TM) oxide that is both isostructural and isoelectronic to cuprate superconductors—has lead to renewed enthusiasm in the hope of understanding the origin of unconventional superconductivity. Here, we investigate the electron-removal states in infinite-layered Ni¹⁺ oxide, NdNiO₂, which mimics hole doping, with the state-of-the-art many-body multireference quantum chemistry methods. From the analysis of the many-body wavefunction we find that the hole-doped d⁸ ground state of NdNiO₂ is very different from the d⁸ ground state in isostructural cuprate analog CaCuO₂, although the parent d⁹ ground states are for the most part identical. We show that the doped hole in NdNiO₂ mainly localizes on the Ni 3$d_{x^2-y^2}$ orbital to form a closed-shell singlet, and this singlet configuration contributes to ∼40% of the wavefunction. In contrast, in CaCuO₂ the Zhang-Rice singlet configurations contribute to ∼65% of the wavefunction. With the help of the quantum information concept of entanglement entropy, we quantify the different types of electronic correlations in the nickelate and cuprate compounds, and find that the dynamic radial-type correlations within the Ni d manifold are persistent in hole-doped NdNiO₂. As a result, the d⁸ multiplet effects are stronger and the additional hole foot-print is more three-dimensional in NdNiO₂. Our analysis shows that the most commonly used three-band Hubbard model employed to express the doped scenario in cuprates represents ∼90% of the d⁸ wavefunction for CaCuO₂, but such a model grossly approximates the d⁸ wavefunction for NdNiO₂ as it only stands for ∼60% of the wavefunction.

1 Introduction

For more than 3 decades, understanding the mechanism of superconductivity observed at high critical temperature (HTC) in strongly correlated cuprates [1] has been the “holy grail” of many theoretical and experimental condensend matter researchers. In this context, the observation of superconductivity in nickelates LnNiO₂, Ln = {La, Nd and Pr} [2–4] upon doping with holes is remarkable. These superconducting nickelates are isostructural as well as isoelectronic to HTC cuprate superconductors and thus enable the comparison of the essential physical features that may be playing a crucial role in the mechanism driving superconductivity.

LnNiO₂ family of compounds are synthesized in the so-called infinite-layer structure, where NiO₂ and Ln layers are stacked alternatively [2]. The NiO₂ planes are identical to the CuO₂ planes in HTC cuprates which host much of the physics leading to superconductivity [5]. A simple valence counting of the these nickelates reveals a 1+ oxidation state for Ni (2- for O and 3+ for Ln) with nine electrons in the 3d manifold. In the cuprates, the Cu²⁺ oxidation state gives rise to the same 3d⁹ electronic configuration. Contrary to many nickel oxides where the Ni atom sits in an octahedral cage of oxygens, in the infinite-layered structure, square planar NiO₄ plaques are formed without the apical oxygens. The crystal field due to square-planar oxygen coordination stabilizes the $d_{z^2}$ orbital of the e_g manifold, making its energy close to the t_2g orbitals (the 3d orbitals split to 3-fold t_2g and 2-fold e_g sub-shells in an octahedral environment). With d⁹ occupation, a half-filled $d_{x^2-y^2}$-orbital system is realized as in cuprates. In fact, recent resonant inelastic X-ray scattering (RIXS) experiments [6] as well as the ab initio correlated multiplet calculations [7] confirm that the Ni¹⁺ d-d excitations in NdNiO₂ are similar to the Cu²⁺ ions in cuprates [8].

Several electronic structure calculations based on density-functional theory (DFT) have shown that in monovalent nickelates the Ni 3$d_{x^2-y^2}$ states sit at the Fermi energy level [9–11]. These calculations further show that the nickelates are more close to the Mott-Hubbard insulating limit with a decreased Ni 3d- O 2p hybridization compared to cuprates. The latter are considered to be charge transfer insulators [12] where excitations across the electronic band gap involves O 2p to Cu 3d electron transfer. Correlated wavefunction-based calculations [7] indeed find that the contribution from the O 2p hole configuration to the ground state wavefunction in NdNiO₂ is four times smaller than in the cuprate analogue CaCuO₂. X-ray absorption and photoemission spectroscopy experiments [13, 14] confirm the Mott behavior of nickelates.

In the cuprate charge-transfer insulators, the strong hybridization of the Cu 3$d_{x^2-y^2}$ and O 2p orbitals result in O 2p dominated bonding and Cu 3$d_{x^2-y^2}$ -like antibonding orbitals. As a consequence, the doped holes primarily reside on the bonding O 2p orbitals, making them singly occupied. The unpaired electrons on the Cu $d_{x^2-y^2}$ and the O 2p are coupled antiferromagnetically resulting in the famous Zhang-Rice (ZR) spin singlet state [15]. In the monovalent nickelates, it is unclear where the doped-holes reside. Do they form a ZR singlet as in cuprates? Instead, if the holes reside on the Ni site, do they form a high-spin local triplet with two singly occupied Ni 3d orbitals and aligned ferromagnetically or a low-spin singlet with either both the holes residing in the Ni 3$d_{x^2-y^2}$ orbital or two singly occupied Ni 3d orbitals but aligned anti-parallel. While Ni L-edge XAS and RIXS measurements [6] conclude that an orbitally polarized singlet state is predominant, where doped holes reside on the Ni 3$d_{x^2-y^2}$ orbital, O K-edge electron energy loss spectroscopy [14] reveal that some of the holes also reside on the O 2p orbitals. On the other hand, calculations based on multi-band d − p Hubbard models show that the fate of the doped holes is determined by a subtle interplay of Ni onsite (U_dd), Ni d - O 2p inter-site (U_dp) Coulomb interactions and the Hund’s coupling along with the charge-transfer gap [16, 17]. However, with the lack of extensive experimental data, it is difficult to identify the appropriate interaction parameters for a model Hamiltonian study, let alone identifying the model that best describes the physics of superconducting nickelates.

Despite the efforts to discern the similarities and differences between the monovalent nickelates and superconducting cuprates, there is no clear understanding on the nature of doped holes in NdNiO₂. Particularly, there is no reliable parameter-free ab initio analysis of the hole-doped situation. In this work, we investigate the hole‐doped ground state in NdNiO₂ and draw parallels to the hole‐doped ground state of cuprate analogue CaCuO₂. We use fully ab initio many-body wavefunction-based quantum chemistry methodology to compute the ground state wavefunctions for the hole‐doped NdNiO₂ and CaCuO₂. We find that the doped hole in NdNiO₂ mainly localizes on the Ni 3$d_{x^2-y^2}$ orbital to form a closed-shell singlet, and this singlet configuration contributes to ∼40% of the wavefunction. In contrast, in CaCuO₂ the Zhang-Rice singlet configurations contribute to ∼65% of the wavefunction. The persistent dynamic radial-type correlations within the Ni d manifold result in stronger d⁸ multiplet effects than in CaCuO₂, and consequently the additional hole foot-print is more three-dimensional in NdNiO₂. Our analysis shows that the most commonly used three-band Hubbard model to express the doped scenario in cuprates represents 90% of the d⁸ wavefunction for CaCuO₂, but such a model grossly approximates the d⁸ wavefunction for the NdNiO₂ as it only stands for ∼60% of the wavefunction.

In what follows, we first describe the computational methodology we use in this work where we highlight the novel features of the methods and provide all the computational details. We then present the results of our calculations and conclude with a discussion.

2 The Wavefunction Quantum Chemistry Method

Ab initio configuration interaction (CI) wavefunction-based quantum chemistry methods, particularly the post Hartree-Fock (HF) complete active space self-consistent field (CASSCF) and the multireference perturbation theory (MRPT), are employed. These methods not only facilitate systematic inclusion of electron correlations, but also enable to quantify different types of correlations, static vs. dynamic [18]. These calculations do not use any ad hoc parameters to incorporate electron-electron interactions unlike other many-body methods, instead, they are computed fully ab initio from the kinetic and Coulomb integrals. Such ab initio calculations provide techniques to systematically analyze electron correlation effects and offer insights into the electronic structure of correlated solids that go substantially beyond standard DFT approaches, e.g., see Refs. [7, 19–22] for the 3d TM oxides and Refs. [23–27] for 5d compounds.

2.1 Embedded Cluster Approach

Since strong electronic correlations are short-ranged in nature [28], a local approach for the calculation of the N and N ± 1 –electron wavefunction is a very attractive option for transition metal compounds. In the embedded cluster approach, a finite set of atoms, we call quantum cluster (QC), is cut out from the infinite solid and many-body quantum chemistry methods are used to calculate the electronic structure of the atoms within the QC. The cluster is “embedded” in a potential that accounts for the part of the crystal that is not treated explicitly. In this work, we represent the embedding potential with an array of point charges (PCs) at the lattice positions that are fitted to reproduce the Madelung crystal field in the cluster region [29]. Such procedure enables the use of quantum chemistry calculations for solids involving transition-metal or lanthanide ions, see Refs. [23, 30, 31].

2.2 Complete Active Space Self-Consistent Field

CASSCF method [18] is a specific type of multi-configurational (MC) self-consistent field technique in which a complete set of Slater determinants or configuration state functions (CSFs) that is used in the expansion of the CI wavefunction is defined in a constrained orbital space, called the active space. In the CASSCF(n,m) approach, a subset of n active electrons are fully correlated among an active set of m orbitals, leading to a highly multi-configurational (CAS) reference wavefunction. CASSCF method with a properly chosen active space guarantees a qualitatively correct wavefunction for strongly correlated systems where static correlation [18] effects are taken into account.

We consider active spaces as large as CAS(24,30) in this work. Because the conventional CASSCF implementations based on deterministic CI space (the Hilbert space of all possible configurations within the active space) solvers are limited to active spaces of 18 active electrons in 18 orbitals, we use the full configuration interaction quantum Monte Carlo (FCIQMC) [32–34] and density matrix renormalization group (DMRG) theory [35, 36] algorithms to solve the eigenvalue problem defined within the active space.

2.3 Multireference Perturbation Theory

While the CASSCF calculation provides a qualitatively correct wavefunction, for a quantitative description of a strongly correlated system, dynamic correlations [18] (contributions to the wavefunction from those configurations related to excitations from inactive to active and virtual, and active to virtual orbitals) are also important and must be accounted for. A natural choice is variational multireference CI (MRCI) approach where the CI wavefunction is extended with excitations involving orbitals that are doubly occupied and empty in the reference CASSCF wavefunction [18]. An alternative and computationally less demanding approach to take into account the dynamic correlations is based on perturbation theory in second- and higher-orders. In multireference perturbation theory (MRPT) MC zeroth-order wavefunction is employed and excitations to the virtual space are accounted by means of perturbation theory. If the initial choice of the MC wavefunction is good enough to capture the large part of the correlation energy, then the perturbation corrections are typically small. The most common variations of MRPT are the complete active space second-order perturbation theory (CASPT2) [37] and the n-electron valence second-order perturbation theory (NEVPT2) [38] which differ in the type of zeroth-order Hamiltonian H₀ employed.

3 The Ab Initio model

Before we describe the ab initio model we consider, let us summarize the widely used and prominent model Hamiltonian to study the nature of doped hole in HTC cuprates and also employed for monovalent nickelates lately. It is the three-band Hubbard model [39] with three orbital degrees of freedom (bands) which include the d orbital of Cu with x²−y² symmetry and the in-plane oxygen p orbitals aligned in the direction of the nearest Cu neighbours. These belong to the b₁ irreducible representation (irrep) of the D_4h point group symmetry realized at the Cu site of the CuO₄ plaque, the other Cu d orbitals belong to a₁ $(d_{z^2})$, b₂ (d_xy) and e (d_xz,yz) irreps. The parameters in this Hamiltonian include the most relevant hopping and Coulomb interactions within this set of orbitals. More recently, the role of the Cu 3d multiplet structure on the hole‐doped ground state is also studied [40]. While this model explains certain experimental observations, there is still a huge debate on what is the minimum model to describe the low-energy physics of doped cuprates. Nevertheless, this model has also been employed to investigate the character of the doped hole in monovalent nickelates [16, 17, 41].

Within the embedded cluster approach described earlier, we consider a QC of five NiO₄ (CuO₄) plaques that includes five Ni (Cu) atoms, 16 oxygens and 8 Nd (Ca) atoms, see Figure 1. The 10 Ni (Cu) ions neighbouring to the cluster are also included in the QC, however, these are considered as total ion potentials (TIPs). The QC is embedded in point charges that reproduce the electrostatic field of the solid environment. We used the crystal structure parameters for the thin film samples reported in Refs. [2, 42–44].

FIGURE 1

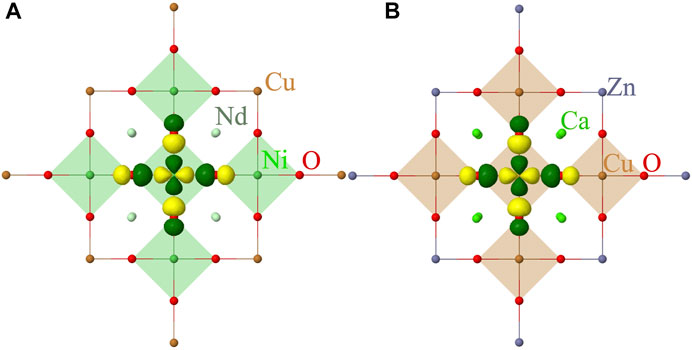
FIGURE 1. Quantum cluster of five NiO₄ (A) and CuO₄ (B) plaques considered in our calculations. The point-charge embedding is not shown. The symmetry adapted localized 3$d_{x^2-y^2}$ and the oxygen Zhang-Rice-like 2p orbitals, the basis in which the wavefunction in Table 3 is presented are shown in yellow and green color.

We used effective core potentials [45] and correlation consistent basis sets of triple-ζ quality with additional polarization functions—[4s3p3d1f]—for Ni (Cu) [46] and double-ζ quality—[ 3s2p1d ]—for oxygens [47]. For the eight Nd (Ca) atoms large core effective potentials [48–50] and associated [3s2p2d] basis functions were used. In the case of Nd, the f-electrons were incorporated in the core. Cu¹⁺ (Zn²⁺) total ion potentials (TIPs) with [2s1p] functions were used for the 10 Ni¹⁺ (Cu²⁺) [51, 52] peripheral ions of the QC.

To investigate the role of different interactions in the d⁸ ground state, two different active spaces were considered. In the first active space, CAS-1 in Table 1, only the orbitals in the b₁ and a₁ irreps are active. These are $d_{x^2-y^2}$ and $d_{z^2}$-like orbitals respectively, and the corresponding double-shell 4d orbitals of each of the five Ni (Cu) atoms. CAS-1 also contains the symmetry-adapted ZR-like composite O 2p and the double-shell 3p-like orbitals, numbers 1–20 and 21–24 in Figure 2. At the mean-field HF level of theory, there are 16 electrons within this set of orbitals, resulting in CAS(16,22) active space. In the second active space, CAS-2, orbitals of b₂ and the e irreps from the central Ni (Cu) d manifold are also included. These are the 3d_xy, 3d_xz,yz-like orbitals and the corresponding 4d orbitals and the six electrons, numbers 25–30 in Figure 2, resulting in a CAS(24,30) active space. The latter active space takes into account the d⁸ multiplet effects within the 3d manifold explicitly.

TABLE 1

TABLE 1. The different active spaces (CAS) considered in this work. NEL is number of active electrons and NORB is the number of active orbitals. The numbers in parenthesis indicate the orbital numbers in Figure 2.

FIGURE 2

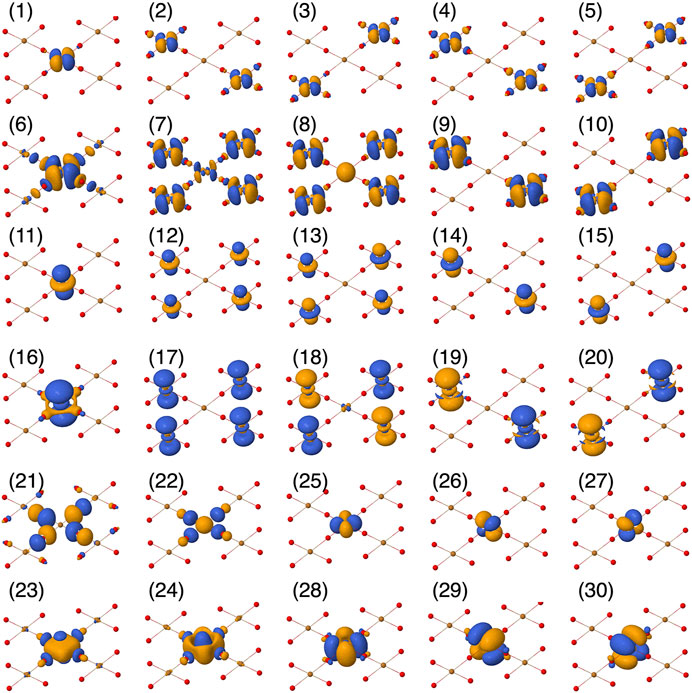
FIGURE 2. Active orbital basis used in the CASSCF calculations, plotted using Jmol [54].

The two active spaces considered in this work not only describe all the physical effects included in the above mentioned three-band Hubbard model but go beyond. More importantly, we do not have any ad-hoc input parameters for the calculation as all the physical interactions are implicitly included in the ab initio Hamiltonian describing the actual scenario in the real materials. We employed OpenMolcas [53] quantum chemistry package for all the calculations.

4 Results

4.1 Ground State of the d⁸ Configuration

Starting from the electronic structure of the parent compounds, where each Ni (Cu) is in the d⁹ configuration, we compute the electron-removal (in the photoemission terminology) d⁸ state to investigate the hole-doped quasiparticle state. Since the parent compounds in d⁹ configuration have strong nearest neighbour antiferromagnetic (AF) correlations [7], the total spin of our QC in undoped case, with five Ni (Cu) sites, in the AF ground state is S_QC = 3/2. By introducing an additional hole (or removing an electron) from the central Ni (Cu) in our QC, the S_QC values range from 0 to 3. To simplify the analysis of the distribution of the additional hole, we keep the spins on the four neighbouring Ni (Cu) sites parallelly aligned in all our calculations and from now on we only specify the spin multiplicity of the central Ni (Cu)O₄ plaque. The multiplet structure of the d⁸ configuration thus consists of only spin singlet and triplet states, spanned by the four irreps of the 3d manifold. The active spaces we consider in this work allow us to compute accurately the excitations only within the b₁ and a₁ irreps [55] and we address the full multiplet structure elsewhere.

When computing the local excitations, a local singlet state on the central Ni (Cu) corresponds to a total spin on the cluster S_QC = 2. However, a local triplet state, with central spin aligned parallel to the neighboring spins, corresponds to S_QC = 3 and do not satisfy the AF correlations. To avoid the spin coupling between the central d⁸ Ni (Cu) with the neighbouring d⁹ Ni (Cu) ions, we replace the latter with closed shell, Cu (Zn) d¹⁰, ions and freeze them at the mean-field HF level. Such a simplification is justified, as the local excitation energy we compute is an order of magnitude larger than the exchange interaction [7].

In Table 2, the relative energies of the lowest local spin singlets ¹A_1g, ¹B_1g and spin triplet ³B_1g states are shown. These are obtained from CASSCF + CASPT2 calculations with CAS(12,14) active space (CAS-3 in Table 1) which includes the 3d and 4d orbitals of the central Ni (Cu) ion and the in-plane O 2p and 3p orbitals in the b₁ irrep. In the CASPT2 calculation, the remaining doubly occupied O 2p, the central Ni (Cu) 3s and 3p orbitals and all the unoccupied virtual orbitals are correlated.

TABLE 2

TABLE 2. Relative energies (in eV) of the electron removal d⁸ states in NdNiO₂ and the iso-structural CaCuO₂ obtained from CAS(12,14)SCF and CASSCF + CASPT2 calculations.

It can be seen that the ground state is of ¹A_1g symmetry and the lowest triplet excited state, with ³B_1g symmetry, is around 1.88 and 2.5 eV for NdNiO₂ and CaCuO₂ respectively. The AF magnetic exchange in these two compounds is 76 and 208 meV respectively [7], and thus we expect that our simplification of making the neighbouring d⁹ ions closed shell do not over/underestimate the excitation energies. At the CASSCF level, the ¹A_1g-³B_1g excitation energy is 1.35 eV in NdNiO₂ while it is 2.26 eV in CaCuO₂. Interestingly, the inclusion of dynamical correlations via the CASPT2 calculation, the ¹A_1g in NdNiO₂ is stabilized by 0.53 eV compared to ³B_1g state. However, in CaCuO₂, the ¹A_1g state is stabilized by only 0.24 eV. This indicates that the dynamical correlations are more active in the ¹A_1g state in NdNiO₂ than in CaCuO₂. We note that the hole excitations within the 3d orbitals in the irreps b₂ and e, calculated with this limited active space (CAS-3) results in energies lower than the ³B_1g and ¹B_1g states. However, an accurate description of those states requires an enlarged active space that includes not only the same symmetry oxygen 2p and 3p orbitals from the central NiO₄ plaque but also the 3d, 4d manifold of the neighbouring Ni (Cu) ions, making the active space prohibitively large. Here, we concentrate on the analysis of the ¹A_1g ground state and address the complete d⁸ multiplet spectrum elsewhere.

4.2 Wavefunction of the d⁸ Ground State

The ¹A_1g ground wavefunction in terms of the weights of the four leading Slater determinants (SD) (in the case of CaCuO₂) is shown in Table 3. The wavefunctions corresponding to the CASSCF calculations with the active spaces CAS-1 and CAS-2 are shown. The basis in which the wavefunctions are represented is constructed in two steps: 1) A set of natural orbitals are generated by diagonalising the CASSCF one-body reduced density matrix. 2) To obtain a set of atomic-like symmetry-adapted localized orbital basis, we localize the Ni (Cu) 3d and O 2p orbitals on the central NiO₄ (CuO₄) plaque through a unitary transformation. Such partial localization within the active space keeps the total energy unchanged. The resulting 3$d_{x^2-y^2}$ and the ZR-like oxygen 2p orbital basis is shown in Figure 1. FCIQMC calculation was performed in this partial localized basis to obtain the wavefunction as a linear combination of SDs. 10 million walkers were used to converge the FCIQMC energy to within 0.1 mHartree.

TABLE 3

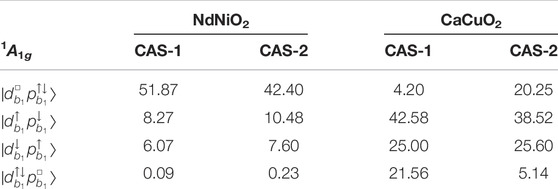
TABLE 3. Ni and Cu 3d^{8 1}A_1g ground state wavefunction: Weights (%) of the leading configurations in the wavefunction computed for NdNiO₂ and CaCuO₂ with active spaces CAS-1 and CAS-2 (see Table 1). $d_{b_1}$ and $p_{b_1}$ are the localized Ni (Cu) $3d_{x^2-y^2}$ and the oxygen 2p ZR-like orbitals (see Figure 1) in the b₁ irrep respectively. Arrows in the superscript indicate the spin of the electrons and a □ indicates two holes.

From Table 3 it can be seen that the electron-removal d⁸ ground state wavefunction for the two compounds is mostly described by the four configurations spanned by the localized 3$d_{x^2-y^2}$ $(d_{b_1})$ and the symmetry-adapted ZR-like oxygen 2p $(p_{b_1})$ orbitals that are shown in Figure 1. Let us first discus the wavefunction obtain from the CAS-1 active space. For NdNiO₂, the dominant configuration involves two holes on 3$d_{x^2-y^2}$, $|d_{b_1}^{\square }{p}_{b_1}^{\uparrow \downarrow }\rangle$, and contributes to ∼52% of the wavefunction, while the configurations that make up the ZR singlet, $|d_{b_1}^{\uparrow }{p}_{b_1}^{\downarrow }\rangle$ and $|d_{b_1}^{\downarrow }{p}_{b_1}^{\uparrow }\rangle$, contributes to only ∼14%. On the other hand, the d^{8 1}A_1g state in CaCuO₂ is predominantly the ZR singlet with ∼68% weight. In the CASSCF calculation with CAS-2 active space, where all the electrons in the 3d manifold are explicitly correlated, we find that the character of the wavefunction remains unchanged in NdNiO₂ but weight on the dominant configurations is slightly reduced. On the other hand, in CaCuO₂, while the contribution from the ZR singlet is slightly reduced, the contribution from $|d_{b_1}^{\square }{p}_{b_1}^{\uparrow \downarrow }\rangle$ configuration is dramatically increased at the expense of the weight on $|d_{b_1}^{\uparrow \downarrow }{p}_{b_1}^{\square }\rangle$. This demonstrates that the additional freedom provided by the d_xy and d_xz/yz orbitals for the electron correlation helps to accommodate the additional hole on the Cu ion.

We note that the four configurations shown in Table 3 encompass almost 90% of the d⁸ wavefunction (with CAS-2 active space) in CaCuO₂. Thus, the use of a three-band Hubbard model [39, 40] to investigate the role of doped holes in CuO₂ planes is a reasonable choice. However, for NdNiO₂ these configurations cover only 60% of the d⁸ wavefunction, hence a three-band Hubbard model is too simple to describe the hole-doped monovalent nickelates.

In Table 4 and Table 5, we show the first ten dominant SD configurations by weight in the d⁸ wavefunction of NdNiO₂ and CaCuO₂ respectively. Interestingly, the configurations with two holes in the out-of-plane d-orbitals $d_{z^2}$ (configuration 6) and d_xz/yz (9 and 10 configurations) is significant in NdNiO₂, while such configurations do not exist in the dominant ten for CaCuO₂. We also find the additional hole to be more delocalized on to the neighboring Ni ions in NdNiO₂ than it is in CaCuO₂, however, this observation should be taken with precaution as the oxygen environment around the neighboring Ni/Cu ions is only described at the mean-field level in our calculation setup.

TABLE 4

TABLE 4. Dominant ten Slater derterminants and their weights (in %) in the d⁸ wavefunction for NdNiO₂ (we also show the 11th which is the same as the fourth configuration in Table 3). The wavefunction is represented in the same basis as the wavefunction in Table 3. However, for convenience we use the orbital numbers from Figure 2 in the first row to express the basis. These orbitals are visually very close to the actual basis. The doubly occupied orbitals are shown as ↑↓, the singly occupied ones with ↑(↓) for spin $\frac{1}{2}$ ($\frac{-1}{2}$) and an empty box implies that the orbital is unoccupied. The red (electrons removed) and green (electrons added) colors indicate the orbitals involved in the excitation starting from the first configuration. The red box indicates that the orbital becomes empty in this particular excited configuration.

TABLE 5

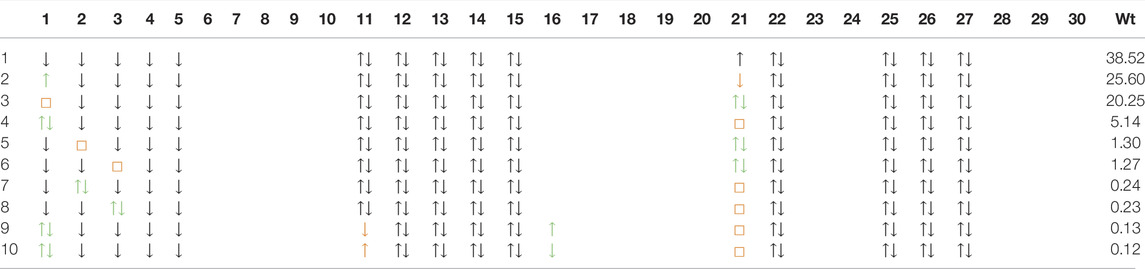
TABLE 5. Dominant ten SD configurations and their weights (in %) in the d⁸ wavefunction for CaCuO₂. See the caption of Table 4 for details of the wavefunction representation.

A more intuitive and visual understanding of the distribution of the additional hole can be obtained by plotting the difference of the d⁸ and the d⁹ ground state electron densities as shown in Figure 3. Electron density of a multi-configurational state can be computed as a sum of densities arising from the natural orbitals and corresponding (well-defined) occupation numbers. We used Multiwfn program [56] to perform this summation. The negative values of the heat map of the electron density difference (blue color) and the positive values (in red) represent respectively the extra hole density and additional electron density in d⁸ state compared to the d⁹ state. From Figure 3A/Figure 3C that show the density difference in the NiO₂/CuO₂ planes (xy-plane), we conclude the following:

1. The hole density is concentrated on the Ni site (darker blue) with b₁ ($d_{x^2-y^2}$) symmetry in NdNiO₂ whereas it is distributed evenly on the four oxygen and the central Cu ions with b₁ symmetry in CaCuO₂, a result consistent with the wavefunction reported in Table 3.

2. In NdNiO₂, the hole density is spread out around the Ni ion with larger radius, and otherwise in CaCuO₂. This demonstrates that the 3d manifold in Cu is much more localized than in Ni and therefore the onsite Coulomb repulsion U is comparatively smaller for Ni.

3. The darker red regions around the Ni site in NdNiO₂ indicate stronger d⁸ multiplet effects that result in rearrangement of electron density compared to d⁹ configuration.

4. In CaCuO₂, we see darker red regions on the oxygen ions instead, which shows that the significant presence of a hole on these ions results in noticeable electron redistribution.

FIGURE 3

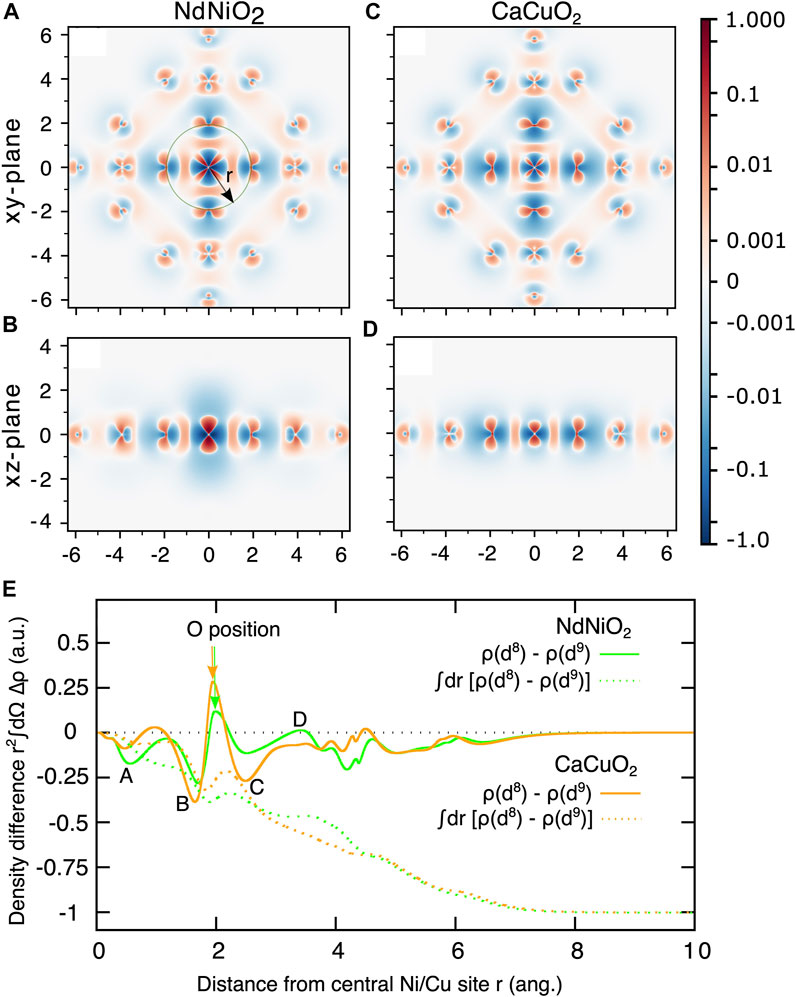
FIGURE 3. Electron density difference of the d⁸ and d⁹ ground states (ρ(d⁸)− ρ(d⁹)) for NdNiO₂ in the xy-plane (A) and xz-plane (B), and for CaCuO₂ xy-plane (C) and xz-plane (D). The coordinates of the central Ni (Cu) d⁸ ion are set to (0,0). The scale of the heat-bar is logarithmic between ±0.001 to ±1.0 and is linear between 0 and ±0.001. (E) Electron density difference integrated over a sphere centered on the central Ni(Cu) atoms (full curves) as a function of the radius r shown in (A). The result of an additional radial integration (dashed curves) as a function of the upper integration limit.

The electron density difference in the xz-plane (which is perpendicular to the NiO₂/CuO₂ planes) is quite different in the two compounds. The hole density in NdNiO₂ is spread out up to 2 Å in the z-direction, unlike in CaCuO₂, where it is confined to within 1 Å. We attribute this to the strong radial-type correlations in NdNiO₂. With the creation of additional hole on the 3$d_{x^2-y^2}$ orbital, the electron density which is spread out in the $d_{z^2}$ symmetry via the dynamical correlation between 3$d_{z^2}$ and 4$d_{z^2}$ orbitals [7], becomes more compact in the $d_{z^2}$ symmetry through the reverse breathing. Thus, we see a strong red region with 3$d_{z^2}$ profile and a blue region with expanded 4$d_{z^2}$ profile.

To obtain a quantitative understanding of the charge density differences for the two compounds, in Figure 3E we plot the electron density difference integrated over a sphere centered on the central Ni(Cu) atom as a function of the radius r shown in Figure 3A. Four features, which we marked A-D, clearly demonstrate the contrast in the charge density differences in the two compounds. From the feature A at r close to Ni (Cu), it is evident that the extent of hole density around Ni in NdNiO₂ is larger than around Cu in CaCuO₂. The features B and C that are on either side of the position of oxygen ions show that the hole density is significantly larger on oxygen atoms in CaCuO₂ than in NdNiO₂. It is interesting to note that we see a jump (feature D) in the electron density above zero at r close to the position of Nd ions in NdNiO₂, while in CaCuO₂ the curve is flat in the region of Ca ions. This shows that there is some electron redistribution happening around the Nd ions. The hole density within a solid sphere (SS) around the central Ni (Cu) atom obtained by additional integration over the radius r is also shown in Figure 3E with dashed curves. It can be seen that the total hole density within the SS of r ∼4 Å, where the neighboring Ni (Cu) ions are located, is only ∼0.5 in both the compounds, with slight differences related to the feature D. This is due to the screening of the hole with the electron density pulled in from the farther surroundings. As one would expect, a SS with r of the size of the cluster, the total hole density is one in both the compounds.

4.3 Orbital Entanglement Entropy

To analyse the different type of correlations active in the two compounds in d⁸ configuration, we compute the entanglement entropy [57–59]. While the single orbital entropy, s(1)_i, quantifies the correlation between ith orbital and the remaining set of orbitals, the mutual information, I_i,j is the two-orbital entropy between i and j [60, 61], and illustrates the correlation of an orbital with another, in the embedded environment comprising of all other orbitals. We used QCMaquis [63] embedded in OpenMolcas [54] package to compute the entropies.

In Figure 4, s(1)_i and I_i,j extracted from the d⁸ ground state CASSCF calculations with CAS-2 active space for NdNiO₂ and CaCuO₂ are shown. The orbital basis for which the entropy is computed is the same as the basis in which the wavefunction presented in Table 3 is expanded. As mentioned previously, this orbital basis is obtained from partial localization of the natural orbitals in a way that only the 3$d_{x^2-y^2}$ and the O 2p ZR-like orbitals are localized. Since a large part of electron correlation is compressed in natural orbitals, we see a tiny s(1)_i for all orbitals except for the localized 3$d_{x^2-y^2}$ and the O 2p ZR-like orbitals where it is significant. This is consistent with the wavefunction in Table 3. The mutual orbital entanglement between pairs of orbitals shows strong entanglement between the 3$d_{x^2-y^2}$ and the O 2p ZR-like orbitals for both NdNiO₂ and CaCuO₂, a consequence of the dominant weight of the configurations spanned by these two orbitals in the wavefunction. The next strongest entanglement is between the Ni/Cu 3d valence and their double-shell 4d orbitals. Such strong entanglement also observed for the undoped d⁹ ground state [7], is a result of dynamical radial correlation [18] and orbital breathing effects [63, 64]. Interestingly, the entanglement entropy in the range 0.001–0.01 (green lines) is quite similar in the two compounds, although one sees more entanglement connections in NdNiO₂. A comparison of the entropy information between NdNiO₂ and CaCuO₂ reveals that the Ni 3d and 4d-like orbitals contribute rather significantly (thicker blue lines) to the total entropy, in contrast to the Cu 3d and 4d-like orbitals, something that is also seen in the undoped compounds [7].

FIGURE 4

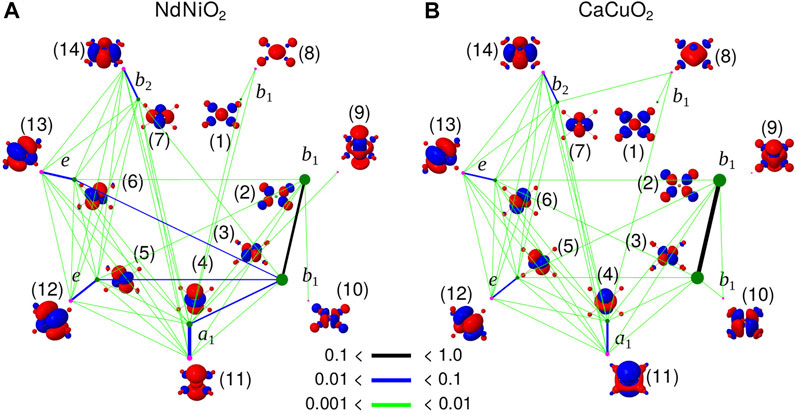
FIGURE 4. Single orbital entanglement entropy, s(i)_i (dots) and mutual orbital entanglement entropy, I_i,j (colored lines) of the orbital basis used to expand the d⁸ wavefunction in Table 3 for NdNiO₂ (A) and CaCuO₂ (B). Entanglement entropy of the orbitals centred on the central NiO₄/CuO₄ plaque are only shown. The irrep to which the orbitals belong to are also shown. The green and magenta colors represent the two different set of orbitals, occupied (at the HF level) and the corresponding double-shell (virtual), respectively. The thickness of the black, blue and green lines denote the strength of I_i,j, and the size of the dots is proportional to s (1)_i. The raw data is presented in Supplementary Tables S1, S2.

5 Conclusion and Discussion

In conclusion, our ab initio many-body quantum chemistry calculations for the electron removal (d⁸) states find a low-spin closed-shell singlet ground state in NdNiO₂ and that the additional hole is mainly localized on the Ni 3$d_{x^2-y^2}$ orbital, unlike in CaCuO₂, where a Zhang-Rice singlet is predominant. We emphasise that the d⁸ wavefunction is highly multi-configurational where the dominant closed-shell singlet configuration weight is only ∼42%. This result is consistent with the experimental evidence [6, 14] of orbitally polarized singlet state as well as the presence of holes on the O 2p orbitals. Importantly, the persistent dynamic radial-type correlations within the Ni d manifold result in stronger d⁸ multiplet effects in NdNiO₂, and consequently the additional hole foot-print is more three dimensional. In CaCuO₂, we find that the electron correlations within the d_xy and d_xz/yz orbitals changes the hole-doped wavefunction significantly. Specifically, the double hole occupation of Cu $d_{x^2-y^2}$ is significantly increased and this can influence the transport properties.

It was recently proposed that nickelates could be a legitimate realization of the single-band Hubbard model [65]. However, our analysis shows that even the three-band Hubbard model [66], which successfully describes the hole-doped scenario in cuprates, falls short to describe hole-doped nickelates and additional orbital degrees of freedom are indeed necessary for the description of the strong multiplet effects we find. Much has been discussed about the importance of rare-earth atoms for the electronic structure of superconducting nickelates, e.g. see [67]. The three-dimensional nature of the hole density we find in NdNiO₂ might also be hinting at the importance of out-of-plane Nd ions. It would be interesting to compare the hole density of NdNiO₂ with other iso-structural nickelates such as LaNiO₂ where La 5d states are far from the Fermi energy. Since the infinite-layered monovalent nickelates are thin films that are grown on substrates, one could ask the question of how the electronic structure of the undoped and doped compounds changes with varying Ni-O bond length. Would this influence the role of electronic correlations in d⁹ nickelates? We will address these in the near future.

Data Availability Statement

The data supporting the conclusions of this study can be made available upon reasonable request.

Author Contributions

VK and AA designed the project. VK and NB performed the calculations. All the authors analysed the data. VK wrote the paper with inputs from NB and AA.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

VK would like to acknowledge Giovanni Li Manni and Oskar Weser for fruitful discussions. We gratefully acknowledge the Max Plank Society for financial support.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2022.836784/full#supplementary-material

References

1. Bednorz JG, Müller KA. Possible High Tc Superconductivity in the Ba-La-Cu-O System. Z Physik B - Condensed Matter (1986) 64:189–93. doi:10.1007/bf01303701

CrossRef Full Text | Google Scholar

2. Li D, Lee K, Wang BY, Osada M, Crossley S, Lee HR, et al. Superconductivity in an Infinite-Layer Nickelate. Nature (2019) 572:624–7. doi:10.1038/s41586-019-1496-5

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Osada M, Wang BY, Goodge BH, Lee K, Yoon H, Sakuma K, et al. A Superconducting Praseodymium Nickelate with Infinite Layer Structure. Nano Lett (2020) 20:5735–40. doi:10.1021/acs.nanolett.0c01392

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Osada M, Wang BY, Goodge BH, Harvey SP, Lee K, Li D, et al. Nickelate Superconductivity without Rare‐Earth Magnetism: (La,Sr)NiO₂. Adv Mater (2021) 33:2104083. doi:10.1002/adma.202104083

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Keimer B, Kivelson SA, Norman MR, Uchida S, Zaanen J. From Quantum Matter to High-Temperature Superconductivity in Copper Oxides. Nature (2015) 518:179–86. doi:10.1038/nature14165

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Rossi M, Lu H, Nag A, Li D, Osada M, Lee K, et al. Orbital and Spin Character of Doped Carriers in Infinite-Layer Nickelates. Phys. Rev. B (2021). 104:L220505. doi:10.1103/PhysRevB.104.L220505

CrossRef Full Text | Google Scholar

7. Katukuri VM, Bogdanov NA, Weser O, van den Brink J, Alavi A. Electronic Correlations and Magnetic Interactions in Infinite-Layer NdNiO₂. Phys Rev B (2020) 102:241112. doi:10.1103/physrevb.102.241112

CrossRef Full Text | Google Scholar

8. Moretti Sala M, Bisogni V, Aruta C, Balestrino G, Berger H, Brookes NB, et al. Energy and Symmetry of d-d Excitations in Undoped Layered Cuprates Measured by CuL₃ Resonant Inelastic X-ray Scattering. New J Phys (2011) 13:043026. doi:10.1088/1367-2630/13/4/043026

CrossRef Full Text | Google Scholar

9. Lee K-W, Pickett WE. Infinite-Layer LaNiO₂: Ni¹⁺ is not Cu²⁺. Phys Rev B (2004) 70:165109. doi:10.1103/physrevb.70.165109

CrossRef Full Text | Google Scholar

10. Liu Z, Ren Z, Zhu W, Wang Z, Yang J. Electronic and Magnetic Structure of Infinite-Layer NdNiO₂: Trace of Antiferromagnetic Metal. Npj Quan Mater (2020) 5:31. doi:10.1038/s41535-020-0229-1

CrossRef Full Text | Google Scholar

11. Zhang H, Jin L, Wang S, Xi B, Shi X, Ye F, et al. Effective Hamiltonian for Nickelate Oxides Nd_1−xSr_xNiO₂. Phys Rev Res (2020) 2:013214. doi:10.1103/physrevresearch.2.013214

CrossRef Full Text | Google Scholar

12. Zaanen J, Sawatzky GA, Allen JW. Band Gaps and Electronic Structure of Transition-Metal Compounds. Phys Rev Lett (1985) 55:418–21. doi:10.1103/physrevlett.55.418

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Hepting M, Li D, Jia CJ, Lu H, Paris E, Tseng Y, et al. Electronic Structure of the Parent Compound of Superconducting Infinite-Layer Nickelates. Nat Mater (2020) 19:381–5. doi:10.1038/s41563-019-0585-z

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Goodge BH, Li D, Lee K, Osada M, Wang BY, Sawatzky GA, et al. Doping Evolution of the Mott–Hubbard Landscape in Infinite-Layer Nickelates. Proc Natl Acad Sci (2021) 118:e2007683118. doi:10.1073/pnas.2007683118

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Zhang FC, Rice TM. Effective Hamiltonian for the Superconducting Cu Oxides. Phys Rev B (1988) 37:3759–61. doi:10.1103/physrevb.37.3759

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Jiang M, Berciu M, Sawatzky GA. Critical Nature of the Ni Spin State in Doped NdNiO₂. Phys Rev Lett (2020) 124:207004. doi:10.1103/physrevlett.124.207004

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Plienbumrung T, Schmid MT, Daghofer M, Oleś AM. Character of Doped Holes in Nd_1−xSr_xNiO₂. Condensed Matter (2021) 6:33. doi:10.3390/condmat6030033

CrossRef Full Text | Google Scholar

18. Helgaker T, Jørgensen P, Olsen J. Molecular Electronic-Structure Theory. Chichester: Wiley (2000).

Google Scholar

19. Muñoz D, Illas F, de P. R. Moreira I. Accurate Prediction of Large Antiferromagnetic Interactions in High-Tc HgBa₂Ca_{n–1}Cu_nO_{2n+2+} (n=2,3) Superconductor Parent Compounds. Phys Rev Lett (2000) 84:1579–82. doi:10.1103/physrevlett.84.1579

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Hozoi L, Siurakshina L, Fulde P, van den Brink J. Ab Initio determination of Cu 3d Orbital Energies in Layered Copper Oxides. Sci Rep (2011) 1:65. doi:10.1038/srep00065

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Hozoi L, Fulde P. Computational Methods for Large Systems: Electronic Structre Approaches for Biotechnology and Nanotechnology. Hoboken: John Wiley & Sons (2011). Chap. 6.

Google Scholar

22. Bogdanov NA, van den Brink J, Hozoi L. Ab Initio Computation of d-d Excitation Energies in Low-Dimensional Ti and V Oxychlorides. Phys Rev B (2011) 84:235146. doi:10.1103/physrevb.84.235146

CrossRef Full Text | Google Scholar

23. Katukuri VM, Stoll H, van den Brink J, Hozoi L. Ab Initio Determination of Excitation Energies and Magnetic Couplings in Correlated Quasi-Two-Dimensional Iridates. Phys Rev B (2012) 85:220402. doi:10.1103/physrevb.85.220402

CrossRef Full Text | Google Scholar

24. Bogdanov NA, Maurice R, Rousochatzakis I, van den Brink J, Hozoi L. Magnetic State of Pyrochlore Cd₂Os₂O₇ Emerging from Strong Competition of Ligand Distortions and Longer-Range Crystalline Anisotropy. Phys Rev Lett (2013) 110:127206. doi:10.1103/physrevlett.110.127206

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Gretarsson H, Clancy JP, Liu X, Hill JP, Bozin E, Singh Y, et al. Crystal-field Splitting and Correlation Effect on the Electronic Structure of A₂IrO₃. Phys Rev Lett (2013) 110:076402. doi:10.1103/PhysRevLett.110.076402

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Katukuri VM, Yushankhai V, Siurakshina L, Brink JVD, Hozoi L, Rousochatzakis I. Mechanism of Basal-Plane Antiferromagnetism in the Spin-Orbit Driven Iridate Ba₂IrO₄. Phys Rev X (2014) 4:021051. doi:10.1103/physrevx.4.021051

CrossRef Full Text | Google Scholar

27. Katukuri VM, Nishimoto S, Yushankhai V, Stoyanova A, Kandpal H, Choi S, et al. Kitaev Interactions Between j= 1/2 Moments in Honeycomb Na₂IrO₃ are Large and Ferromagnetic: Insights From Ab Initio Quantum Chemistry Calculations. New J Phys (2014) 16:013056. doi:10.1088/1367-2630/16/1/013056

CrossRef Full Text | Google Scholar

28. Fulde P. Correlated Electrons in Quantum Matter. Singapore: World Scientific (2012).

Google Scholar

29. Klintenberg M, Derenzo SE, Weber MJ. Accurate crystal fields for Embedded Cluster Calculations. Comput Phys Commun (2000) 131:120–8. doi:10.1016/s0010-4655(00)00071-0

CrossRef Full Text | Google Scholar

30. Katukuri VM, Roszeitis K, Yushankhai V, Mitrushchenkov A, Stoll H, van Veenendaal M, et al. Electronic Structure of Low-Dimensional 4d⁵ Oxides: Interplay of Ligand Distortions, Overall Lattice Anisotropy, and Spin-Orbit Interactions. Inorg Chem (2014) 53:4833–9. doi:10.1021/ic402653f

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Babkevich P, Katukuri VM, Fåk B, Rols S, Fennell T, Pajić D, et al. Magnetic Excitations and Electronic Interactions in Sr₂CuTeO₆: A Spin-1/2 Square Lattice Heisenberg Antiferromagnet. Phys Rev Lett (2016) 117:237203. doi:10.1103/physrevlett.117.237203

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Booth GH, Thom AJW, Alavi A. Fermion Monte Carlo without Fixed Nodes: a Game of Life, Death, and Annihilation in Slater Determinant Space. J Chem Phys (2009) 131:054106. doi:10.1063/1.3193710

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Cleland D, Booth GH, Alavi A. Communications: Survival of the Fittest: Accelerating Convergence in Full Configuration-Interaction Quantum Monte Carlo. J Chem Phys (2010) 132:041103. doi:10.1063/1.3302277

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Guther K, Anderson RJ, Blunt NS, Bogdanov NA, Cleland D, Dattani N, et al. NECI: N-Electron Configuration Interaction with an Emphasis on State-Of-The-Art Stochastic Methods. J Chem Phys (2020) 153:034107. doi:10.1063/5.0005754

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Chan GK-L, Sharma S. The Density Matrix Renormalization Group in Quantum Chemistry. Annu Rev Phys Chem (2011) 62:465–81. doi:10.1146/annurev-physchem-032210-103338

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Sharma S, Chan GK-L. Spin-adapted Density Matrix Renormalization Group Algorithms for Quantum Chemistry. J Chem Phys (2012) 136:124121. doi:10.1063/1.3695642

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Andersson K, Malmqvist PÅ, Roos BO. Second‐order Perturbation Theory with a Complete Active Space Self‐consistent Field Reference Function. J Chem Phys (1992) 96:1218–26. doi:10.1063/1.462209

CrossRef Full Text | Google Scholar

38. Angeli C, Cimiraglia R, Evangelisti S, Leininger T, Malrieu J-P. Introduction Of N-Electron Valence States for Multireference Perturbation Theory. J Chem Phys (2001) 114:10252–64. doi:10.1063/1.1361246

CrossRef Full Text | Google Scholar

39. Emery VJ. Theory of High-Tc superconductivity in Oxides. Phys Rev Lett (1987) 58:2794–7. doi:10.1103/physrevlett.58.2794

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Jiang M, Moeller M, Berciu M, Sawatzky GA. Relevance of Cu-3d Multiplet Structure in Models of High-T_c Cuprates. Phys Rev B (2020) 101:035151. doi:10.1103/physrevb.101.035151

CrossRef Full Text | Google Scholar

41. Plienbumrung T, Daghofer M, Oleś AM. Interplay between Zhang-Rice Singlets and High-Spin States in a Model for Doped NiO₂ Planes. Phys Rev B (2021) 103:104513. doi:10.1103/physrevb.103.104513

CrossRef Full Text | Google Scholar

42. Hayward MA, Rosseinsky MJ. Synthesis of the Infinite Layer Ni(I) Phase NdNiO_2+x by Low Temperature Reduction of NdNiO₃ with Sodium Hydride. Solid State Sci (2003) 5:839–50. doi:10.1016/s1293-2558(03)00111-0

CrossRef Full Text | Google Scholar

43. Kobayashi N, Hiroi Z, Takano M. Compounds and Phase Relations in the SrO-CaO-CuO System under High Pressure. J Solid State Chem (1997) 132:274–83. doi:10.1006/jssc.1997.7442

CrossRef Full Text | Google Scholar

44. Karpinski J, Mangelschots I, Schwer H, Conder K, Morawski A, Lada T, et al. Single crystal Growth of HgBaCaCuO and Infinite Layer CaCuO₂ at High Gas Pressure. Physica C: Superconductivity (1994) 235-240:917–8. doi:10.1016/0921-4534(94)91683-7

CrossRef Full Text | Google Scholar

45. Dolg M, Wedig U, Stoll H, Preuss H. Energy-adjusted ab Initio Pseudopotentials for the First Row Transition Elements. J Chem Phys (1987) 86:866–72. doi:10.1063/1.452288

CrossRef Full Text | Google Scholar

46. Martin JML, Sundermann A. Correlation Consistent Valence Basis Sets for Use with the Stuttgart-Dresden-Bonn Relativistic Effective Core Potentials: The Atoms Ga-Kr and In-Xe. J Chem Phys (2001) 114:3408–20. doi:10.1063/1.1337864

CrossRef Full Text | Google Scholar

47. Roos BO, Lindh R, Malmqvist P-Å, Veryazov V, Widmark P-O. Main Group Atoms and Dimers Studied with a New Relativistic ANO Basis Set. J Phys Chem A (2004) 108:2851–8. doi:10.1021/jp031064+

CrossRef Full Text | Google Scholar

48. Dolg M, Stoll H, Savin A, Preuss H. Energy-adjusted Pseudopotentials for the Rare Earth Elements. Theoret Chim Acta (1989) 75:173–94. doi:10.1007/bf00528565

CrossRef Full Text | Google Scholar

49. Dolg M, Stoll H, Preuss H. A Combination of Quasirelativistic Pseudopotential and Ligand Field Calculations for Lanthanoid Compounds. Theoret Chim Acta (1993) 85:441–50. doi:10.1007/bf01112983

CrossRef Full Text | Google Scholar

50. Kaupp M, Schleyer Pv. R, Stoll H, Preuss H. Pseudopotential Approaches to Ca, Sr, and Ba Hydrides. Why Are Some Alkaline Earth MX₂ Compounds Bent? J Chem Phys (1991) 94:1360–6. doi:10.1063/1.459993

CrossRef Full Text | Google Scholar

51. Igel-Mann G. Ph.D. thesis. Stuttgart: University of Stuttgart (1987). Untersuchungen an Hauptgruppenelementen und Nebengruppenelementen mit abgeschlossener d-Schale

Google Scholar

52.University of Cologne. Energy-consistent Pseudopotentials of Stuttgart/Cologne Group (2014). Available at: http://www.tc.uni-koeln.de/cgi-bin/pp.pl?language=en,format=molpro,element=Zn,job=getecp,ecp=ECP28SDF (Accessed Sept 15, 2021).

Google Scholar

53. Fdez. Galván I, Vacher M, Alavi A, Angeli C, Aquilante F, Autschbach J, et al. OpenMolcas: From Source Code to Insight. J Chem Theor Comput. (2019) 15:5925–64. doi:10.1021/acs.jctc.9b00532

CrossRef Full Text | Google Scholar

54.Jmol. Jmol: An Open-source Java Viewer for Chemical Structures in 3D (2001). Available from: http://www.jmol.org/.

Google Scholar

55..For an accurate quantitative description of the multiplet structure spanned by the other two irreps b₁ and e, one would need to extend the active space and include the 3d and 4d manifolds of the four neighbouring Ni (Cu) atoms as well as the O 2p orbitals of the same symmetry, resulting in a gigantic 68 electrons in 74 orbitals active space.

Google Scholar

56. Lu T, Chen F. Multiwfn: A Multifunctional Wavefunction Analyzer. J Comput Chem (2012) 33:580–92. doi:10.1002/jcc.22885

PubMed Abstract | CrossRef Full Text | Google Scholar

57. Boguslawski K, Tecmer P, Legeza Ö, Reiher M. Entanglement Measures for Single- and Multireference Correlation Effects. J Phys Chem Lett (2012) 3:3129–35. doi:10.1021/jz301319v

PubMed Abstract | CrossRef Full Text | Google Scholar

58. Boguslawski K, Tecmer P, Barcza G, Legeza Ö, Reiher M. Orbital Entanglement in Bond-Formation Processes. J Chem Theor Comput. (2013) 9:2959–73. doi:10.1021/ct400247p

PubMed Abstract | CrossRef Full Text | Google Scholar

59. Boguslawski K, Tecmer P. Orbital Entanglement in Quantum Chemistry. Int J Quan Chem. (2015) 115:1289–95. doi:10.1002/qua.24832

CrossRef Full Text | Google Scholar

60. Legeza Ö, Sólyom J. Optimizing the Density-Matrix Renormalization Group Method Using Quantum Information Entropy. Phys Rev B (2003) 68:195116. doi:10.1103/physrevb.68.195116

CrossRef Full Text | Google Scholar

61. Rissler J, Noack RM, White SR. Measuring Orbital Interaction Using Quantum Information Theory. Chem Phys (2006) 323:519–31. doi:10.1016/j.chemphys.2005.10.018

CrossRef Full Text | Google Scholar

62. Keller S, Dolfi M, Troyer M, Reiher M. An Efficient Matrix Product Operator Representation of the Quantum Chemical Hamiltonian. J Chem Phys (2015) 143:244118. doi:10.1063/1.4939000

PubMed Abstract | CrossRef Full Text | Google Scholar

63. Gunnarsson O, Andersen OK, Jepsen O, Zaanen J. Density-functional Calculation of the Parameters in the Anderson Model: Application to Mn in CdTe. Phys Rev B (1989) 39:1708–22. doi:10.1103/physrevb.39.1708

PubMed Abstract | CrossRef Full Text | Google Scholar

64. Bogdanov NA, Li Manni G, Sharma S, Gunnarsson O, Alavi A. Enhancement of Superexchange Due to Synergetic Breathing and Hopping in Corner-Sharing Cuprates. Nat Phys (2021) 18:190–5. doi:10.1038/s41567-021-01439-1

CrossRef Full Text | Google Scholar

65. Kitatani M, Si L, Janson O, Arita R, Zhong Z, Held K. Nickelate Superconductors – a Renaissance of the One-Band Hubbard Model. npj Quan Mater (2020) 5:59. doi:10.1038/s41535-020-00260-y

CrossRef Full Text | Google Scholar

66. Eskes H, Sawatzky GA. Single-, Triple-, or Multiple-Band Hubbard Models. Phys Rev B (1991) 44:9656–66. doi:10.1103/physrevb.44.9656

PubMed Abstract | CrossRef Full Text | Google Scholar

67. Nomura Y, Arita R. Superconductivty in Infinite-Layer Nickelates. Rep. Prog. Phys. (2021) 85:052501. doi:10.1088/1361-6633/ac5a60

CrossRef Full Text | Google Scholar