
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Phys., 01 November 2022
Sec. Soft Matter Physics
Volume 10 - 2022 | https://doi.org/10.3389/fphy.2022.836287
 Heiko G. Kurz1
Heiko G. Kurz1 Martin Kretschmar2
Martin Kretschmar2 Thomas Binhammer3
Thomas Binhammer3 Tamas Nagy2
Tamas Nagy2 Detlev Ristau1,4,5
Detlev Ristau1,4,5 Manfred Lein6
Manfred Lein6 Uwe Morgner1,4,5
Uwe Morgner1,4,5 Milutin Kovačev1,4*
Milutin Kovačev1,4*We use high-order harmonic spectroscopy to study ionization dynamics in a macroscopic target with tunable density, spanning over six orders of magnitude. In an in situ pump-probe experiment, the target is prepared at different densities with varying degrees of laser-induced ionization. High-order harmonic radiation is generated in the pre-ionized target, and a steepening in the decrease of the harmonic yield is observed for increasing pre-ionization, allowing not only to identify the contributing quantum paths during high-order harmonic generation but also in determining the amount of ionization within the target. The measurements allow probing of ionization dynamics in laser-induced plasma with high spatio-temporal resolution and are specifically of interest for the optimization of the harmonic generation process in high-density targets with number densities of up to 1022 cm−3.
High-order harmonic generation (HHG) [1] requires laser intensities comparable to the inner atomic electric fields in order to induce tunnel ionization [2, 3]. These intensities are typically within the range from I ≈ 1013 to 1015 W/cm2. However, by applying strong electric fields onto a macroscopic ensemble the target’s composition is affected, changing it from usually being purely neutral into a mixture of neutral particles, ions, and free electrons which can severely influence the HHG process. The presence of free electrons, for example, may shift the phase-matching conditions by inducing an additional phase term via a change in the refractive index, deteriorating the conversion efficiency [4, 5]. Furthermore, the fast variation of the electron density during the driver pulse leads to transient phase-matching conditions, which may result in blue-shifting or spectral broadening of the harmonic radiation [6–9]. Much effort has been carried out in order to minimize the plasma effects on HHG, searching for optimum conditions for the nonlinear frequency conversion [10–18, 20].
However, plasma formation not only has negative impacts on HHG but it also opens possibilities for the generation of extreme ultraviolet radiation that differs from conventional gas targets, such as wakefield acceleration [20] or HHG from relativistic oscillating mirrors [25, 24, 23, 21]. Even methods for the spatial separation of different spectral components of harmonic radiation during the HHG process have been applied [25]. The plasma itself can also be used as a medium for HHG, enhancing the emission process at the whole, as in the case of laser-ablated plasmas as the target medium [28, 26]. Furthermore, plasmas give rise to amplify single-harmonic orders through atomic [33, 32, 31, 30, 28] or fano-shaped resonances [33].
Additional benefits arise from a pre-ionized target with a low free electron density, where the source of HHG no longer lies within the neutral particle but in the ion. Within these ionic targets, enhancing the harmonic cutoff becomes accessible due to the higher ionic potential [36, 34]. The range of an ionic Coulomb potential, however, is large compared with the short-ranged character of a neutral atom so that the effect of neighboring ions on the electron along its excursion in the continuum is not negligible. An ionic background medium, therefore, provides a source of perturbation for electronic trajectories during HHG, where the electron is deflected by neighboring ions within the target and misses its parent ion so that the recombination step is inhibited.
In a theoretical work, V. Strelkov et. al. [36] simulated the emission of harmonic radiation from a neutral argon atom surrounded by an ionized background medium in order to study the influence of neighboring ions on the emission process. The numerical calculations were performed for the single-atom response, considering a single-ionized target. Figure 1 depicts the calculated yield of harmonic orders in the plateau region from [36] for an intensity of a driving pulse of Ipump = 2 × 1014 W/cm2 and an ionized background medium. The pulse duration has been set to 50 fs at a wavelength of 800 nm. The contributions of short (blue circles) and long (red squares) trajectories have been distinguished in the calculations due to the fact that the emission via the two quantum paths features a severe difference in the slope as the target’s density increases. Although the signal originating from the short trajectories is less affected by surrounding ions, particularly for densities with ρ < 1019 cm−3, the contribution via the long trajectory decreases rapidly. The origin of the trajectory-dependent emitted harmonic yield lies in the inequality of excursion times τex between the two quantum paths [4, 38–40]. Since the long trajectory has a larger excursion time, the electron wavepacket is spreading more severely, thus accumulating a higher phase contribution induced by the long-ranging Coulomb potential of neighboring ions [36]. Increasing the density of the ionized medium, therefore, leads to larger distortions, and the effect of separation becomes pronounced. Both contributions, however, feature a linear decrease in the high-density regime (dashed lines in Figure 1), where the slopes are well distinguishable. Additionally, the calculations by V. Strelkov et. al. indicate that the difference between the slopes decreases as the medium becomes less ionized, approaching the same intermediate value for a neutral medium.
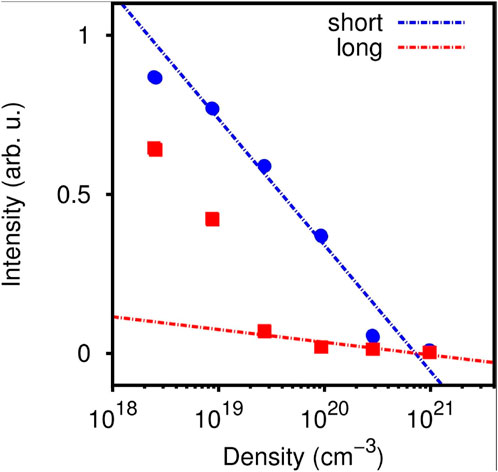
FIGURE 1. Simulated signal of harmonic radiation as a function of the density of argon ions (single-ionized). The data have been collected from Strelkov et al. [36]. Only the experimentally relevant middle group contributions are shown. The signal of the long trajectory (red squares) shows a decrease in the low-density regime, contrarily to the short trajectory (blue dots) which drops at a significantly higher density. Additionally, a linear approximation to the high-density regime is depicted (dashed lines).
Detecting these microscopic effects in a macroscopic ensemble, however, is nontrivial not only because the amount of ionization in the target has to be controlled but also following the deflection of electronic trajectories is challenging as well. Moreover, the density regime where the linear dependence of the harmonic yield becomes observable is beyond ρ > 2 × 1019 cm−3, exceeding the available density supported by conventional setups such as gas jets or gas cells, resulting in a need for a high-density target to observe these effects. In order to match the experimental requirements of a high-density target in this work, we apply a liquid–water droplet in a vacuum as a target for HHG in an in situ pump-probe setup [45, 44, 43, 42, 40], giving access to densities of up to ρ0 = 3.34 × 1022 cm−3. Our approach is complemented by making use of high-order harmonic spectroscopy which is capable of observing the electronic motion and its dynamic interaction with strong laser fields with unprecedented precision since the information is imprinted onto the emitted radiation in an in situ process [52, 51, 50, 49, 48, 47, 45]. Our observations demonstrate ionization dynamics which allow for estimates on the degree of ionization of the target medium. These measurements, therefore, contribute to the optimization of high-harmonic generation in high-density targets which have been investigated recently [18, 19, 45].
Two time-delayed, intense laser pulses with a duration of 40 fs and variable energy of up to 1 mJ each are focused collinearly by the same lens (f = 500 mm) reaching a size in the focal region of about 90 microns in diameter. Intensity control is realized via attenuation through the combination of two thin-film polarizers in reflection and a half-wave plate in each arm. The droplets are prepared by using a capillary nozzle containing a piezoelectric aperture in order to induce hydrodynamic instability for a controlled water jet breakup. The deterministic series of water droplets are characterized via imaging to a diameter of about 15 µm [, 44, 42]. The droplet is expanded by the pump pulse through a laser-induced optical breakdown (LIB) [53–55], initiating a rapid decrease in its density but not contributing to HHG due to the high initial density and the ps-scale delay in the expansion [54, 56]. An additional tuning of the pump pulse intensity allows in controlling the laser-induced ionization. Hence, a target can be generated whose composition reaches from consisting mainly of neutral particles to being dominated by ions, controlled by the intensity of the pump pulse. Depending on the time delay t, which reaches from 0 ns to 15 ns, different target densities become accessible for HHG with the probe pulse, and the droplet’s internal composition can be studied in situ via high-order harmonic spectroscopy. It should be noted that the derived density calculations depend on the water droplet expansion upon LIB by the pump pulse. The estimates take into account the ionic mass, the ionization potential, and the density of liquid water.
The high-order harmonic spectra have been recorded as a function of the pump-probe time delay and the intensity of the pump pulse using an XUV grazing-incidence spectrometer (LHT 30, Horiba-Jobin-Yvon, 500 lines/mm) with an attached micro-channel plate. A model from plasma physics [57] describing the ion velocities is used to derive the mapping of the delay t onto the density evolution
where
with the volume at time zero
Here, M denotes the ionic mass, Z the degree of ionization (set to be Z = 1),
Figure 2A depicts the harmonic spectrum as a function of the density evolution of the target for intensities of the pump- and probe-pulse of Ipump = 7.2 × 1014 W/cm2 and Iprobe = 9.5 × 1014 W/cm2, respectively. The signal increases toward a maximum around a density of ρ ≈ 1019 cm−3, where optimum conversion efficiencies for higher orders are also observed. Further increase in the density results in a decreasing signal.
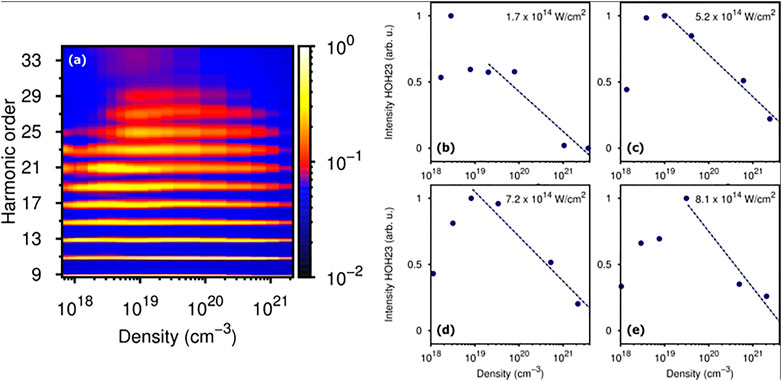
FIGURE 2. (A) Measured spectra of harmonic radiation as a function of the density of the target at an intensity of the pump pulse of Ipump = 7.2 × 1014 W/cm2 and an intensity of the probe pulse of Iprobe = 9.5 × 1014 W/cm2. (B) to (E) outlines the signal of the 23rd harmonic order with different intensities of the pump pulse. The dashed lines indicate the linear fit to the high-density regime. The slopes of the fits decrease from (B) −0.131 via (C) −0.138 and (D) −0.147 to (E) −0.185.
For more detailed insights into the density-dependent evolution of the harmonic yield and to study the influence of ionization on the HHG process, Figures 2B–E show outlines of the 23rd harmonic order’s yield (blue dots) for different intensities of the pump pulse. The signal increases for all intensities as a function of the density due to the larger number of emitters contributing to HHG until a maximum of around ρ ≈ 1019 cm−3 is reached. From there on, the high-density regime is reached and the signal drops. The blue-dashed line indicates the linear fit to the high-density regime, where a steepening in the slope is observed with the increasing intensity of the pump pulse.
The decreasing signal in the high-density regime in Figures 2B–E can be attributed to a perturbation of the electron on its excursion in the continuum, which is induced by adjacent particles. Since the mean inter-particle distance in the target is reduced as the density is increased, approaching the maximum electronic displacement during HHG, the possibility for a perturbation of electronic trajectories by neighboring particles increases, suppressing the harmonic yield [43]. However, the steepening of the linear fit’s slope as a function of the pump pulse’s intensity is observed, indicating that an additional change in the composition of the target medium is induced. At higher pump intensities, a larger fraction of the molecules within the droplet is ionized [55, 59–61], providing a long-ranging ionic Coulomb field. When the probe pulse interacts with the prepared target to drive the HHG process, the electrons are not only perturbed along their trajectories by neutral particles but also experience an additional deflection by the ionic Coulomb fields. Consequently, the recombination step is perturbed even more and the harmonic yield decreases; the more rapid, the higher the number of ions induced by the pump pulse is within the target, resulting in a steepening of the slope in the high-density regime.
The inherent sensitivity of the HHG process to the presence of residing ions in the high-density regime enables us to elucidate the ionization dynamics explaining the behavior of the target in terms of generation efficiency within the macroscopic ensemble by analyzing the slope of the harmonic signal. To this end, Figure 3 compares the slope of the harmonic signal versus the pump intensity, averaged over the orders 21–25, with the calculations by V. Strelkov et al. [36] for an ionized (dashed blue line for the short trajectory and dashed red line for the long trajectory) and a neutral background medium (dashed green line). In the latter case, the slopes of long and short trajectories are non-distinguishable and, therefore, deliver a single, intermediate value. At low intensities, the mean slopes are close to the calculated value for a neutral medium, which suggests that the target’s composition is dominated by neutral particles. It should be noted that data for the lower intensity of the pump pulse are close to the threshold intensity for LIB such that the expansion process of the droplet may differ from the model used previously. The mean slope becomes more negative as a function of Ipump, resulting in a better agreement between the measurement and the simulation for the short trajectory. Considering that the short trajectory has been selected in the experiment, the convergence of the measurement toward the theoretical value is consistent with the assumption that a larger amount of ionization is induced by the pump pulse, affecting the HHG process.
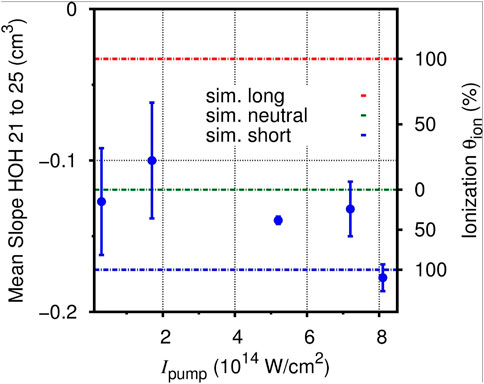
FIGURE 3. Mean slopes (blue dots) of the linear fits to the experimental data on orders 21–25 as a function of the intensity of the pump pulse. The horizontal lines indicate the slopes obtained from the simulations of [36] for the long (red) and short (blue) trajectories in an ionic background medium and the case of a neutral background medium (green). The comparison with the simulation allows the conversion of the mean slopes into the amount of ionization within the target.
Considering that the ionization fraction in the simulation of a neutral background is 0% (dashed green line in Figure 3), while it is 100% for the value of the short trajectory (dashed blue line in Figure 3), the measurements deliver a degree of ionization reaching from θion < 10% to θion ≈ 100%, indicating that the target can be prepared in different extents of ionization. Additionally, the measurement’s convergence toward the theoretical prediction of the short trajectory confirms that the long trajectory can be neglected (dashed red line in Figure 3) since the short quantum path has been selected in the experiment. The intensity of the probe pulse, however, is high enough to lead to additional ionization within the target; otherwise, no harmonic radiation would be emitted. A contribution of the HHG driving pulse to θion, therefore, has to be considered. Its impact on the measurement is estimated by a comparison with experimental pump-probe results of LIB in water using low-intensity probe pulses that do not lead to further ionization.
A measurement by Sarpe-Tudoran et al. [56] applied two 35 fs pulses with 780 nm to a water jet. The pump intensity was set to 1.5 times the threshold intensity for LIB (ILIB ≈ 1.4 × 1014 W/cm2). Its result is an ionization degree of θion ≈ 3.6%. A comparable experiment by Brown et al. [55] indicated an ionization fraction of θion ≈ 6%. Both results are in reasonable agreement with our findings in Figure 3. Hence, we deduce that although the probe pulse is intense enough to induce severe ionization, the generated ions are screened by their associated electrons, resulting in no additional perturbation of other molecules generating harmonic radiation. This shows that in situ high-order harmonic spectroscopy is able to map laser-induced ionization dynamics important for the understanding of generation efficiencies in macroscopic targets.
Using liquid water droplets in an in situ pump-probe experiment, we have demonstrated the influence of a pre-ionized target on the HHG process. The density of the target was decreased using an intense pump pulse which triggers a laser-induced-breakdown-based expansion. Additionally, the amount of laser-induced ionization within the target was controlled via the intensity of the pump pulse. The harmonic radiation was generated in the pre-ionized target by applying a second, time-delayed probe pulse. Our findings indicate that an ionic background medium can severely distort the electron along its excursion in the continuum and, thus, verify the theoretical prediction by V. Strelkov et al. [36]. We have shown that ionization induced by the pump pulse can be a major contribution for the distortion of electronic trajectories and is able to significantly reduce the conversion efficiency of HHG. Moreover, by applying different intensities of the pump pulse, we show laser-induced ionization dynamics allowing estimates on the harmonic generation efficiency within the target by high-order harmonic spectroscopy. Our measurements open new routes to probe ionization dynamics in laser-induced plasmas with high spatio-temporal resolution and are specifically of interest for the optimization of the HHG process in high-density targets [33, 32, 31, 30, 29, 62, 28, 26].
The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.
The authors contributed to manuscript writing (HK, MaKr, ML, and MiKo) and editing (TB, TN, DR, and UM).
We are grateful for the financial support from DFG project no. KO 3798/1-1 and the Air Force Office of Scientific Research under Grant No. FA9550-12-1-0482. This research was supported by Germany’s Excellence Strategy within the Cluster of Excellence PhoenixD (EXC 2122, Project ID 390833453).
Author TB is employed by NeoLASE GmbH.
The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
1. Corkum P. Plasma perspective on strong field multiphoton ionization. Phys Rev Lett (1993) 71:1994–7. doi:10.1103/physrevlett.71.1994
2. Krausz F, Ivanov M. Attosecond physics. Rev Mod Phys (2009) 81:163–234. doi:10.1103/revmodphys.81.163
3. Keldysh L. Quantum transport equations for high electric fields. Soviet Phys - JETP (1965) 20:1307–14.
4. Salières P, L’Huillier A, Lewenstein M. Coherence control of high-order harmonics. Phys Rev Lett (1995) 74:3776–9. doi:10.1103/physrevlett.74.3776
5. Altucci C, Starczewski T, Mevel E, Wahlstrom CG, Carre B, L’Huillier A. Influence of atomic density in high-order harmonic generation. J Opt Soc Am B (1996) 13:148–56. doi:10.1364/josab.13.000148
6. Zhong F, Deng J, Hu X, Li Z, Zhang Z, Xu Z. The effect of ionization of gases on the high harmonic splitting. Phys Lett A (2000) 278:35–43. doi:10.1016/s0375-9601(00)00746-5
7. Wang Y, Liu Y, Yang X, Xu Z. Spectral splitting in high-order harmonic generation. Phys Rev A (Coll Park) (2000) 62:063806. doi:10.1103/physreva.62.063806
8. Holler M, Zair A, Schapper F, Auguste T, Cormier E, Wyatt A, et al. Ionization effects on spectral signatures of quantum-path interference in high-harmonic generation. Opt Express (2009) 17:5716–22. doi:10.1364/oe.17.005716
9. Heyl CM, Güdde J, Höfer U, L’Huillier A. Spectrally resolved maker fringes in high-order harmonic generation. Phys Rev Lett (2011) 107:033903. doi:10.1103/physrevlett.107.033903
10. L’Huillier A, Lewenstein M, Salieres P, Balcou P, Ivanov MY, Larsson J, et al. High-order harmonic-generation cutoff. Phys Rev A (Coll Park) (1993) 48:R3433–6. doi:10.1103/physreva.48.r3433
11. Wahlström C-G, Larsson J, Persson A, Starczewski T, Svanberg S, Salieres P, et al. High-order harmonic generation in rare gases with an intense short-pulse laser. Phys Rev A (Coll Park) (1993) 48:4709–20. doi:10.1103/physreva.48.4709
12. Balcou P, Salieres P, L’Huillier A, Lewenstein M. Generalized phase-matching conditions for high harmonics: The role of field-gradient forces. Phys Rev A (Coll Park) (1997) 55:3204–10. doi:10.1103/physreva.55.3204
13. Constant E, Garzella D, Breger P, Mevel E, Dorrer C, Le Blanc C, et al. Optimizing high harmonic generation in absorbing gases: Model and experiment. Phys Rev Lett (1999) 82:1668–71. doi:10.1103/physrevlett.82.1668
14. Hergott J-F, Kovacev M, Merdji H, Hubert C, Mairesse Y, Jean E, et al. Extreme-ultraviolet high-order harmonic pulses in the microjoule range. Phys Rev A (Coll Park) (2002) 66:021801. doi:10.1103/physreva.66.021801
15. Kazamias S, Douillet D, Weihe F, Valentin C, Rousse A, Sebban S, et al. Global optimization of high harmonic generation. Phys Rev Lett (2003) 90:193901. doi:10.1103/physrevlett.90.193901
16. Bahabad A, Murnane M, Kapteyn HC. Quasi-phase-matching of momentum and energy in nonlinear optical processes. Nat Photon (2010) 4:570–5. doi:10.1038/nphoton.2010.122
17. Boutu W, Auguste T, Caumes JP, Merdji H, Carré B. Scaling of the generation of high-order harmonics in large gas media with focal length. Phys Rev A (Coll Park) (2011) 84:053819. doi:10.1103/PhysRevA.84.053819
18. Popmintchev T, Chen MC, Popmintchev D, Arpin P, Brown S, Alisauskas S, et al. Bright coherent ultrahigh harmonics in the kev x-ray regime from mid-infrared femtosecond lasers. Science (2012) 336:1287–91. doi:10.1126/science.1218497
19. Heyl CM, Coudert-Alteirac H, Miranda M, Louisy M, Kovacs K, Tosa V, et al. Scale-invariant nonlinear optics in gases. Optica (2016) 3:75–81. doi:10.1364/optica.3.000075
20. Quéré F, Thaury C, Monot P, Dobosz S, Martin P, Geindre JP, et al. Coherent wake emission of high-order harmonics from overdense plasmas. Phys Rev Lett (2006) 96:125004. doi:10.1103/physrevlett.96.125004
21. Tsakiris G, Eidmann K, Meyer-ter Vehn J, Krausz F. Route to intense attosecond pulses. New J Phys (2006) 8:1367.
22. Dromey B, Zepf M, Gopal A, Lancaster K, Wei MS, Krushelnick K, et al. High harmonic generation in the relativistic limit. Nat Phys (2006) 2:456–9. doi:10.1038/nphys338
23. Rödel C, an der Brugge D, Bierbach J, Yeung M, Hahn T, Dromey B, et al. Harmonic generation from relativistic plasma surfaces in ultrasteep plasma density gradients. Phys Rev Lett (2012) 109:125002. doi:10.1103/physrevlett.109.125002
24. Heissler P, Horlein R, Mikhailova JM, Waldecker L, Tzallas P, Buck A, et al. Few-cycle driven relativistically oscillating plasma mirrors: A source of intense isolated attosecond pulses. Phys Rev Lett (2012) 108:235003. doi:10.1103/physrevlett.108.235003
25. Wheeler J, Borot A, Monchoce S, Vincenti H, Ricci A, Malvache A, et al. Attosecond lighthouses from plasma mirrors. Nat Photon (2012) 6:829–33. doi:10.1038/nphoton.2012.284
26. Ditmire T, Hutchinson MHR, Key MH, Lewis CLS, MacPhee A, Mercer I, et al. Amplification of xuv harmonic radiation in a gallium amplifier. Phys Rev A (Coll Park) (1995) 51:R4337–40. doi:10.1103/physreva.51.r4337
27. Ganeev R, Suzuki M, Baba M, Kuroda H. High-order harmonic generation from laser plasma produced by pulses of different duration. Phys Rev A (Coll Park) (2007) 76:023805. doi:10.1103/physreva.76.023805
28. Tudorovskaya M, Lein M. High-order harmonic generation in the presence of a resonance. Phys Rev A (Coll Park) (2011) 84:013430. doi:10.1103/physreva.84.013430
29. Ganeev R, Hutchison C, Zair A, Witting T, Frank F, Okell WA, et al. Enhancement of high harmonics from plasmas using two-color pump and chirp variation of 1 khz ti:sapphire laser pulses. Opt Express (2012) 20:90–100. doi:10.1364/oe.20.000090
30. Ganeev R, Witting T, Hutchison C, Frank F, Tudorovskaya M, Lein M, et al. Isolated sub-fs xuv pulse generation in mn plasma ablation. Opt Express (2012) 20:25239. doi:10.1364/oe.20.025239
31. Ganeev R, Witting T, Hutchison C, Strelkov VV, Frank F, Castillejo M, et al. Comparative studies of resonance enhancement of harmonic radiation in indium plasma using multicycle and few-cycle pulses. Phys Rev A (Coll Park) (2013) 88:033838. doi:10.1103/physreva.88.033838
32. Haessler P, Strelkov V, Elouga Bom LB, Khokhlova M, Gobert O, Hergott JF, et al. Phase distortions of attosecond pulses produced by resonance-enhanced high harmonic generation. New J Phys (2013) 15:013051. doi:10.1088/1367-2630/15/1/013051
33. Rothhardt J, Hadrich S, Demmler S, Krebs M, Fritzsche S, Limpert J, et al. Enhancing the macroscopic yield of narrow-band high-order harmonic generation by fano resonances. Phys Rev Lett (2014) 112:233002. doi:10.1103/physrevlett.112.233002
34. Gibson E, Paul A, Wagner N, Tobey R, Backus S, Christov IP, et al. High-order harmonic generation up to 250 ev from highly ionized argon. Phys Rev Lett (2004) 92:033001. doi:10.1103/physrevlett.92.033001
35. Gaudiosi D, Reagan B, Popmintchev T, Grisham M, Berrill M, Cohen O, et al. High-order harmonic generation from ions in a capillary discharge. Phys Rev Lett (2006) 96:203001. doi:10.1103/physrevlett.96.203001
36. Strelkov V, Platonenko V, Becker A. High-harmonic generation in a dense medium. Phys Rev A (Coll Park) (2005) 71:053808. doi:10.1103/physreva.71.053808
37. Lewenstein M, Balcou P, Ivanov MY, L’Huillier A, Corkum PB. Theory of high harmonic generation by low-frequency laser fields. Phys Rev A (Coll Park) (1994) 49:2117–32. doi:10.1103/physreva.49.2117
38. Bellini M, Lynga C, Tozzi A, Gaarde MB, Hansch TW, L'Huillier A, et al. Temporal coherence of ultrashort high-order harmonic pulses. Phys Rev Lett (1998) 81:297–300. doi:10.1103/physrevlett.81.297
39. Lyngå C, Gaarde MB, Delfin C, Bellini M, Hansch TW, L’ Huillier A, et al. Temporal coherence of high-order harmonics. Phys Rev A (Coll Park) (1999) 60:4823–30. doi:10.1103/physreva.60.4823
40. Düsterer S, Schwoerer H, Ziegler W, Ziener C, Sauerbrey R. Optimization of euv radiation yield from laser-produced plasma. Appl Phys B: Lasers Opt (2001) 73:693–8. doi:10.1007/s003400100730
41. Flettner A, Pfeifer T, Walter D, Winterfeldt C, Spielmann C, Gerber G. High-harmonic generation and plasma radiation from water microdroplets. Appl Phys B (2003) 77:747–51. doi:10.1007/s00340-003-1329-x
42. Kurz HG, Steingrube DS, Ristau D, Lein M, Morgner U, Kovacev M. High-order-harmonic generation from dense water microdroplets. Phys Rev A (Coll Park) (2013) 87:063811. doi:10.1103/physreva.87.063811
43. Kurz H, Kretschmar M, Binhammer T, Nagy T, Ristau D, Lein M, et al. Revealing the microscopic real-space excursion of a laser-driven electron. Phys Rev X (2016) 6:031029. doi:10.1103/physrevx.6.031029
44. Luu TT, Yin Z, Jain A, Gaumnitz T, Pertot Y, Ma J, et al. Extreme–ultraviolet high–harmonic generation in liquids. Nat Commun (2018) 9(1):3723. doi:10.1038/s41467-018-06040-4
45. Itatani J, Levesque J, Zeidler D, Niikura H, Pepin H, Kieffer JC, et al. Tomographic imaging of molecular orbitals. Nature (2004) 432:867–71. doi:10.1038/nature03183
46. Uiberacker M, Uphues T, Schultze M, Verhoef AJ, Yakovlev V, Kling MF, et al. Attosecond real-time observation of electron tunnelling in atoms. Nature (2007) 446:627–32. doi:10.1038/nature05648
47. Smirnova O, Mairesse Y, Patchkovskii S, Dudovich N, Villeneuve D, Corkum P, et al. High harmonic interferometry of multi-electron dynamics in molecules. Nature (2009) 460:972–7. doi:10.1038/nature08253
48. Wörner H, Bertrand D, Kartashov JB, Corkum P, Villeneuve D. Following a chemical reaction using high-harmonic interferometry. Nature (2010) 466:604–7. doi:10.1038/nature09185
49. Shafir D, Soifer H, Bruner BD, Dagan M, Mairesse Y, Patchkovskii S, et al. Resolving the time when an electron exits a tunnelling barrier. Nature (2012) 485:343–6. doi:10.1038/nature11025
50. Schultze M, Ramasesha K, Pemmaraju C, Sato S, Whitmore D, Gandman A, et al. Attosecond band-gap dynamics in silicon. Science (2014) 346:1348–52. doi:10.1126/science.1260311
51. Vampa G, Hammond T, Thire N, Schmidt B, Legare F, McDonald C, et al. All-optical reconstruction of crystal band structure. Phys Rev Lett (2015) 115:193603. doi:10.1103/physrevlett.115.193603
52. Harth A, Guo C, Cheng YC, Losquin A, Miranda M, Mikaelsson S, et al. Compact 200 kHz HHG source driven by a few-cycle OPCPA. J Opt (2018) 20:014007. doi:10.1088/2040-8986/aa9b04
53. Feng Q, Moloney J, Newell A, Wright E, Cook K, Kennedy P, et al. Theory and simulation on the threshold of water breakdown induced by focused ultrashort laser pulses. IEEE J Quan Electron (1997) 33:127–37. doi:10.1109/3.552252
54. Schaffer C, Nishimura N, Glezer E, Kim A, Mazur E. Dynamics of femtosecond laser-induced breakdown in water from femtoseconds to microseconds. Opt Express (2002) 10:196–203. doi:10.1364/oe.10.000196
55. Brown MS, Erickson T, Frische K, Roquemore WM. Hot electron dominated rapid transverse ionization growth in liquid water. Opt Express (2011) 19:12241–7. doi:10.1364/oe.19.012241
56. Sarpe-Tudoran C, Assion A, Wollenhaupt M, Winter M, Baumert T. Plasma dynamics of water breakdown at a water surface induced by femtosecond laser pulses. Appl Phys Lett (2006) 88:261109. doi:10.1063/1.2217158
57. Puell H. Heating of laser produced plasmas generated at plane solid targets 1. theory. Z für Naturforschung A-Astrophysik, Physik Physikalische Chem A (1970) 25:1807–15.
58. Salières P, Antoine P, de Bohan A, Lewenstein M. Temporal and spectral tailoring of high-order harmonics. Phys Rev Lett (1998) 81:5544–7. doi:10.1103/physrevlett.81.5544
59. Augst S, Strickland D, Meyerhofer D, Chin S, Eberly J. Tunneling ionization of noble gases in a high-intensity laser field. Phys Rev Lett (1989) 63:2212–5. doi:10.1103/physrevlett.63.2212
60. Bauer D. Plasma formation through field ionization in intense laser-matter interaction. Laser Part Beams (2003) 21:489–95. doi:10.1017/s0263034603214026
61. Petretti S, Saenz A, Castro A, Decleva P. Water molecules in ultrashort intense laser fields. Chem Phys (2013) 414:45–52. doi:10.1016/j.chemphys.2012.01.011
Keywords: high-order harmonic generation, spectroscopy, ionization, droplets, water, pump-probe, high-density target
Citation: Kurz HG, Kretschmar M, Binhammer T, Nagy T, Ristau D, Lein M, Morgner U and Kovačev M (2022) High-order harmonic spectroscopy in an ionized high-density target. Front. Phys. 10:836287. doi: 10.3389/fphy.2022.836287
Received: 15 December 2021; Accepted: 13 October 2022;
Published: 01 November 2022.
Edited by:
Miha Ravnik, University of Ljubljana, SloveniaReviewed by:
Nektarios Papadogiannis, Hellenic Mediterranean University, GreeceCopyright © 2022 Kurz, Kretschmar, Binhammer, Nagy, Ristau, Lein, Morgner and Kovačev. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Milutin Kovačev, a292YWNldkBpcW8udW5pLWhhbm5vdmVyLmRl
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.