Investigation of Micron-Scale Radiotherapy Dose Deposition in the Lung: Effect of Magnetic Field and Nanoparticles—a Monte Carlo Simulation

MRI-Linacs couple magnetic resonance imaging (MRI) with a linear accelerator (Linac) to enable MR-guided radiotherapy. The magnetic field is known to cause inhomogeneities in the pattern of dose deposition at centimeter-scale air-tissue interfaces such as pockets of digestive gas but has not been studied at the micrometer scale of lung alveoli. Nanoparticle radio-enhancement is a novel therapy enhancing the dose deposition pattern where nanoparticles are delivered to the radiation target, with proposed application to lung cancer treatment through inhalation of nebulized nanoparticles. This study reports the first investigation of the effect of a magnetic field on the pattern of dose deposition at the micrometer air-tissue interfaces of alveoli in the lung, and the impact of incorporating nanoparticles. Monte Carlo simulations investigated a single alveolus model irradiated with mono-energetic, uni-directional electrons and a multi-alveoli model irradiated with a realistic beam at depth. The magnetic field was found to produce field-strength dependent hot- and cold-spot dose inhomogeneities in the tissue surrounding a micrometer air cavity irradiated with low energy (100 keV) electrons. The most affected regions exhibited a dose increase of 37.30 ± 1.29% and a decrease of 31.58 ± 1.01% with the application of a 1.5 T magnetic field. The addition of nanoparticles to the interior surface layer of the alveolus air cavity increased energy deposit by a constant ratio dependent on the nanoparticle concentration regardless of magnetic field strength. A similar but less pronounced effect was observed for a multi-alveolus model irradiated at depth by a 6 MV photon beam. This result warrants further investigation into the biological impact of micrometer-scale dose inhomogeneity on tumor response and normal tissue complication probability.

Introduction

Lung cancer is the leading cause of cancer-related death in both men and women, accounting for over 1.8 million deaths worldwide in 2020 [1]. Despite ongoing technological advancements in medicine, the 5-years survival of lung cancer remains relatively poor at 21.80% which is significantly lower compared to other common cancer sites such as prostate, breast, and colorectal [2]. Therefore, each year, novel technologies and techniques are introduced with the intent to improve lung cancer treatment. Radiotherapy is an important treatment modality in lung cancer and targeted radio-enhancement by metallic nanoparticles (NPs) has shown early promising results [3]. Some NPs exhibit magnetic resonance imaging (MRI) contrast, indicating application on recently developed MRI-Linac radiotherapy treatment systems [4, 5]. However, the fundamental behavior of dose enhancement by NPs in the lung under the influence of the magnetic field of an MRI-Linac treatment system remains unknown.

MRI-Linacs enable imaging during radiotherapy (RT) delivery. This advancement is desirable for treating the lung as online imaging with superior soft-tissue contrast allows adaptive modification of RT treatment plans due to inter- and intra-fraction movement. This gives MRI-Linacs the advantage in treating the tumor with better accuracy, thus sparing surrounding healthy tissue [6]. In the current market, there are two commercially available MRI-Linac treatment systems: the ViewRay MRIdian with a 0.35 T magnet [7]; and Elekta Unity with a 1.5 T magnet [8]. Both systems use the perpendicular configuration wherein the Linac treatment beam is delivered perpendicularly to the direction of the magnetic field. However, there are additional treatment planning considerations regarding this setup as treatments are delivered in the presence of a magnetic field. Typically, when tissue is irradiated with high-energy photons, a cascade of secondary electrons is produced which deposit their energy along the beam path. With the presence of a magnetic field, secondary electrons experience a Lorentz force and are then deflected in a helical manner. This causes local increase and decrease of dose known as hot and cold spots at tissue-air interfaces in the body such as the lung [9, 10], with the dose distortion dependent on the strength of the magnetic field being used [11].

NP radio-enhancement is an emerging field in RT delivering high atomic number NPs that can selectively target cancer cells. Upon irradiation, this causes higher energy deposition and biological damage within the cell by producing additional low-energy secondary electrons [3]. The administration of NPs is usually through IV injection. However, pulmonary administration of NPs (via inhalation) is an attractive strategy for diagnostic and therapeutic purposes given that the lung has a large surface area for drug absorption and has an extensive vasculature with a weak anatomical barrier that does not hinder access to the body [12–14]. The utilization of NPs that provide magnetic contrast with the MRI-Linac treatment system presents a promising technique for delivering an enhanced dose more precisely to the target volume. Dufort et al [15] investigated radio-enhancement with nebulized gadolinium-based NPs in a mouse lung tumor model where it was found out that the mean survival time following RT was extended to 112 days compared to 77 days without integration of NPs. On the other hand, gold NPs exhibit the same mechanisms for the physical enhancement of energy deposit and are the most extensively studied in the literature. Several in vivo and in vitro studies of gold NPs (AuNPs) have shown that radiobiological damage and tumor response were enhanced due to gold’s high electronic density [16–19]. Furthermore, Monte Carlo (MC) simulation and theoretical work have identified changes in the local patterns of radiation damage due to NPs which may give rise to enhanced biological damage [20–24].

The dose distortion in the lung due to the presence of a magnetic field needs to be understood and accounted for in radiotherapy planning and to date, this has only been investigated at the centimeter scale using homogeneous tissue composition [10]. Thus, this study investigates dose deposition around the micrometer tissue inhomogeneities in the lung. Of particular interest is the influence of a magnetic field on the dose deposition by low-energy electrons at air-tissue interfaces, specifically in the alveolar structure of the lung, and how this dose deposition is affected by the presence of NPs.

Methods and Materials

Two sets of MC simulations were carried out using a model of a single alveolus (Alveolus Irradiated With Mono-Energetic Electrons) and a multi-stage simulation with a microscale model containing multiple alveoli at depth (Multiple-Alveoli Irradiated With a Realistic Photon Source).

MC simulations were performed on a Linux computer with 32 CPU cores [AMD Opteron(tm) Processor 6282 SE] and 336 GB of RAM, and were carried out using TOPAS version 3.6.1 (www.topasmc.org) [25]. The simulation time of Alveolus Irradiated With Mono-Energetic Electrons took around several minutes and Multiple-Alveoli Irradiated With a Realistic Photon Source to about a couple of days to complete.

Pre-defined TOPAS materials for water, air, tungsten, and gold were utilized. For the homogeneous lung equivalent material, it was defined with the same composition as water but with a lower density of $0.27\text{ g}/{\text{cm}}^3$ and a mean excitation energy of 75.3 eV. AuNPs were envisaged to be inhaled in nebulized form, evenly reaching the inner surface of the alveolus and adhering to or being absorbed into the surface layer. Tissue containing AuNPs in the water shell around the alveolus was defined as a single TOPAS material consisting of water with a percentage of gold added. The mass percentage of gold was set to 1, 5, and 10% having overall mean excitation energies of 76.6, 82.1, and 89.7 eV, respectively. Consequently, the density of the water shell was adjusted accordingly to 1.01 $\text{g}/{\text{cm}}^3$, 1.05 $\text{g}/{\text{cm}}^3$, and 1.10 $\text{g}/{\text{cm}}^3$. Following intravenous injection of NPs, concentrations in the target of up to 1% are achievable, but less experimental data exists for inhaled nebulized nanoparticles, so higher concentrations were investigated to allow for uneven distribution and localized clumping.

All physical processes in the simulations used the g4em-penelope physics module (See Geant4 physics reference manual for details [26]). Furthermore, the threshold for the production cut lower edge was set to 100 eV and range cut values appropriate for the simulation geometry were chosen: 0.05 mm for the initial stage of the second simulations; 1.00 nm for the second and intermediate stage, and 0.50 nm in the third stage of the single alveolus and multi-alveoli model simulations. This means that secondary particles are generated if their energy is over 100 eV, and particles are stopped and the remaining energy is deposited locally when they have less energy than needed to travel the range cut distance through the medium in which they are generated. Additionally, the max step size was set to 1/3 of the energy deposition scoring voxel size.

Alveolus Irradiated With Mono-Energetic Electrons

The alveolus model was constructed based on morphological findings [27]. As shown in Figure 1A, the alveolus model is a $220\times 220\times 220 {\text{μm}}^3$ of lung material. At the center, the spherical air cavity has a radius of ${\text{r}}_{\text{a}}=99.50\text{ μm}$ which is then encapsulated with a water shell $0.50 \text{μm}$ thick. The water shell represents the blood-gas-barrier of the alveolus which is an important target for biological damage. Overall, the alveolus has a total radius of ${\text{r}}_{\text{T}}=100\text{ μm}$.

FIGURE 1

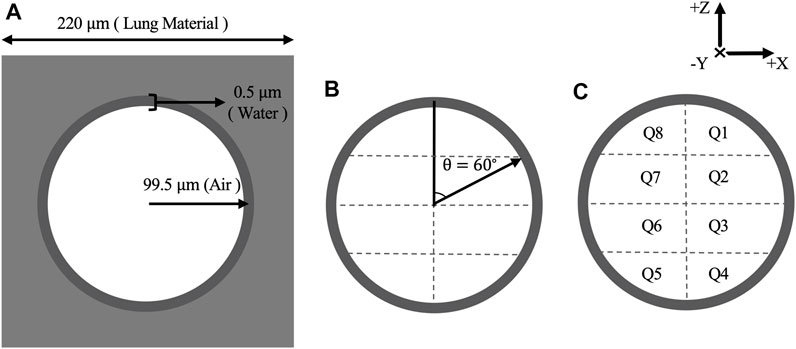
FIGURE 1. (A) Schematic diagram of alveolus model with corresponding measurements (not to scale) and materials. (B) Water shell divided into 16 quadrants with equal volume by setting $\mathit{\theta }={60}^{\circ }$ from the zenith point. (C) Quadrant labels for retracing energy deposition (only the front “A” quadrants are shown; “B” quadrants are on the reverse surface).

The alveolus was irradiated with a monoenergetic 100 keV electron source which was found to have a sufficient range to traverse the alveolus model and to exhibit curvature of the electron tracks within the air cavity. The number of histories generated upon irradiation was $1\times {10}^8$ using a beam size of $200\times 200{\text{ μm}}^2$. This source was placed immediately on the model’s surface in the positive x-axis. Furthermore, a uniform magnetic field was set perpendicularly to the beam direction pointing to the positive y-axis. The magnetic field was then varied at 0.00, 0.35, 1.50, 3.00, and 7.00 T to demonstrate the dependency of dose distortion with increasing magnetic field strength, similarly to that previously reported at a larger scale [11].

The integration of NPs was achieved by replacing the material in the water shell with an atomic mix of gold and water as detailed above. The concentration of AuNPs was varied to observe the effect of NPs on the energy deposition in the water shell. A high upper concentration was simulated to consider possible maximum effects in the event of clumping of nebulized NPs.

To obtain the energy deposition in the model, two approaches were used. The first approach was a grid of $200\times 200\times 200$ voxels set in the parallel world in TOPAS so no physical geometrical boundaries were created in the simulation. This grid was used to reconstruct a visual energy deposition map of the entire model. In the second approach, 16 TOPAS energy scorers were defined in the water shell. This was done by dividing the water shell into 16 quadrants of equal volume, setting $\text{θ}={60}^{\circ }$ from the zenith point of the alveolus, as depicted in Figure 1B. Each quadrant was then assigned an identifier (e.g., Q1A, Q1B, Q2A, Q2B) where A stands for quadrants located in the negative y-direction and B in the positive y-direction, as shown in Figure 1C. This naming scheme facilitates retracing of the energy depositions in the model to a specific quadrant. When comparing the energy deposition in the alveolus with varying magnetic field strength, the energy deposition in adjacent “A” and “B” quadrants was found to be symmetrical due to the symmetry of the model irradiation (data not shown). To aid analysis, the energy deposition of adjacent quadrants was added, Q1 = Q1A + Q1B—reducing the number of quadrants to 8. The energy deposit in each quadrant was summed across all histories, with uncertainty given by the standard error for the sum calculated by multiplying the standard deviation by the square root of the number of histories.

Multiple-Alveoli Irradiated With a Realistic Photon Source

Figure 2A shows a geometric chest model filled with water with dimensions of $30\times 20\times 30{\text{ cm}}^3$. At the center, two lung volumes were placed 15 cm apart on the x-axis, filled with lung equivalent material and each having dimensions of $10\times 15\times 30{\text{ cm}}^3$. In the lung on the positive x-axis, a $5 \times 5 \times 5 {\text{cm}}^3$ intermediate volume filled with lung equivalent material was constructed, as seen in Figure 2B, where the range cut was reduced to 1 nm for improved geometric accuracy. Moreover, in Figures 2A,C transition volume of $6\times 6\times 6{\text{ mm}}^3$ was placed at the center which then encapsulates the alveoli model, with the range cut reduced further to 0.5 nm.

FIGURE 2

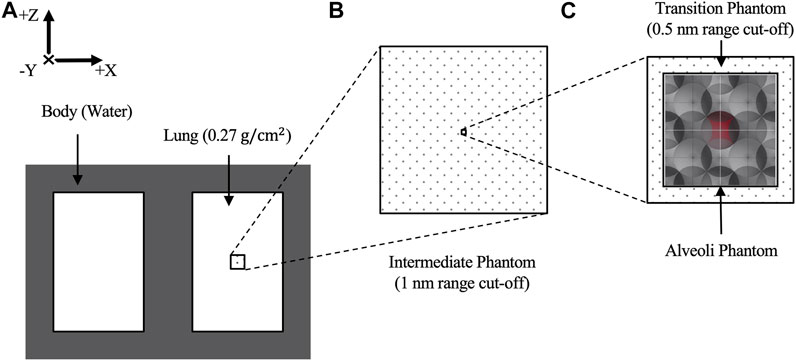
FIGURE 2. (A) Schematic layout of generic chest phantom consisting of a body and lungs. (B) The right lung contains an intermediate volume where the phase space “2” was collected. Within the intermediate volume, (C) a transition volume encases the alveoli model. The central alveolus, shaded in red, has 16 energy deposition scorers attached to its water shell.

The alveoli model consisted of multiple alveolar air cavities with water shells arranged in face-centered-cubic configuration surrounded with water as adapted from Hombrink et al [28]. However, to achieve the same overall density as the surrounding lung, the dimension of each alveolus was modified and adopted the same parameters as in Alveolus Irradiated With Mono-Energetic Electrons. Eight face-centered-cubic blocks were stacked together to obtain a more realistic representation of the alveoli having a comparable size to a CT pixel with a dimension of $5.61\times 5.61\times 5.61{\text{ mm}}^2.$ NPs were introduced by filling the alveoli’s water shell with a mix of water and 10% NPs.

A semi-realistic simulation was carried out using a realistic 6 MV beam spectrum with and without a perpendicular 7.00 T magnetic field and the region of interest simulated at depth in the lung to replicate a conventional MRI-Linac setup. It is well established that a photon source requires longer computing time and more histories to have a good statistic in the simulation. Hence, the simulation was divided into a three-step process that utilizes two phase space scorers “1” and “2,” and the range cut-off was adjusted in each geometry depending on the required geometric accuracy, ensuring that a precise energy deposition within the thin water shell is obtained in the alveoli model while earlier simulation stages can run faster.

In the first step, a phase space scoring plane “1” was placed in front of the Elekta Precise 6 MV photon source (www-nds.iaea.org/phsp/phsp.htmlx) that was collimated with a $1\times 1{\text{ cm}}^2$ tungsten collimator. The phase space “1” file was then used as the particle source in the second step and was placed at a distance of 1 m in the positive x-axis from the surface of the chest phantom. The TOPAS sequential time feature was used to call the phase space file several times to achieve $1\times {10}^8$ primary particles. All particles that passed through all 6 surfaces of the intermediate volume were recorded and stored by the phase space scorer “2.”

The phase space file “2” was used to produce primary particles for the third step, the detailed simulation recording energy deposition in the alveoli model, and iterated 2,400 times to achieve good statistics. Fewer particles were recorded in the phase space file “2” when the magnetic field was present, thought to be due to the somewhat reduced path length of secondary particles. Therefore, the number of primary particles was adjusted so that the energy deposition in the central alveolus with and without the magnetic field (and without NPs) was made uniform with a difference of less than 1%. The energy deposit in each quadrant was summed across all histories from phase space file 2, with error bars in the results representing the standard error for the sum.

All geometries stated above were enclosed by a world geometry having a dimension of $200\times 200\times 200{\text{ cm}}^3$ and, at the center, a $100\times 100\times 100{\text{ cm}}^3$ cubic magnetic field geometry pointing in the positive y-axis was defined.

Results

Alveolus Irradiated With Mono-Energetic Electrons

Figure 3 shows the energy deposition in the alveolus model irradiated with mono-energetic 100 keV electrons in the presence of varying magnetic field strength. With the introduction of a magnetic field, dose distortion was observed around the air cavity and is characterized by the presence of a hot spot (concentrated energy deposit) and an opposing cold spot (reduced energy deposit). The hot spot is found to be concentrated towards the upper left while the opposing cold spot is located across at the lower left, as seen in the “Side View.” Within the air cavity, little to no energy deposition was observed.

FIGURE 3

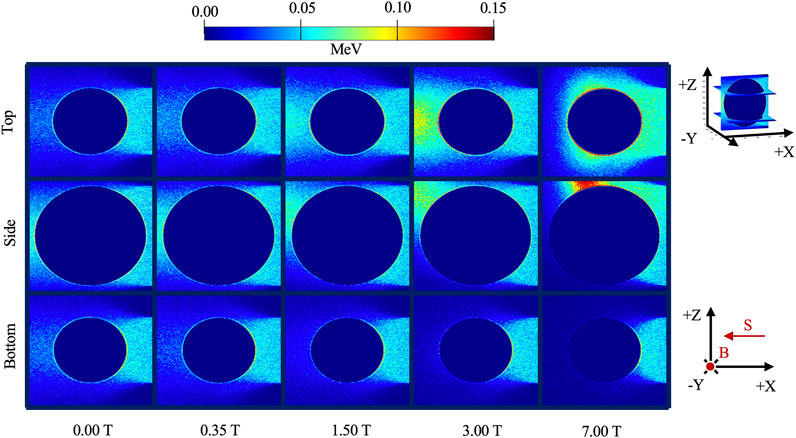
FIGURE 3. Energy deposition in the alveolus model irradiated with 100 keV electrons in the presence of varying magnetic field strength. The side view was acquired in the 100th slice along the y-axis while the top and bottom views were acquired at the 30th and 170th slice along the z-axis, respectively (shown by the insert). B designates the direction of the magnetic field and S is the direction of the electron beam source.

As the magnetic field was increased, the hot spot rotated in a clockwise direction in the “Side View” and increased in intensity, as shown by the moving bright intensity in the immediate periphery of the alveolus. This rotation and concentration are attributed to the increased Lorentz force at higher magnetic field strength.

Figure 4 shows quantitatively how the energy deposition in the water shell of the alveolus is distorted with the presence of a magnetic field, as described qualitatively in Figure 3. At 0.00 T, quadrants Q1–Q4, closer to the beam source, received a higher deposition than quadrants Q5–Q8, with higher energy deposition in the more central quadrants (Q2, Q3, Q6, and Q7) where the beam has traversed less lung material. As the magnetic field was increased, a gradual increase of energy deposition at the top quadrants (Q1, Q2, Q7, and Q8) was observed. This is in contrast with the bottom quadrants (Q3, Q4, Q6, and Q5) where an increase of magnetic field strength decreases the energy deposition. At 7.00 T, energy deposition peaks occurred at the adjacent quadrants of Q1 and Q8. Furthermore, when comparing the energy deposition with and without the presence of the magnetic field, 0.00 and 7.00 T, the greatest increase in deposition is located at Q8 with 148.35%, and the greatest decrease in a deposition is located at Q5 with 86.80%. For the 1.50 T field as used in the Elekta Unity system, there is an increase of 37.30 ± 1.29% in Q8 and a decrease of 31.58 ± 1.01% in Q5.

FIGURE 4

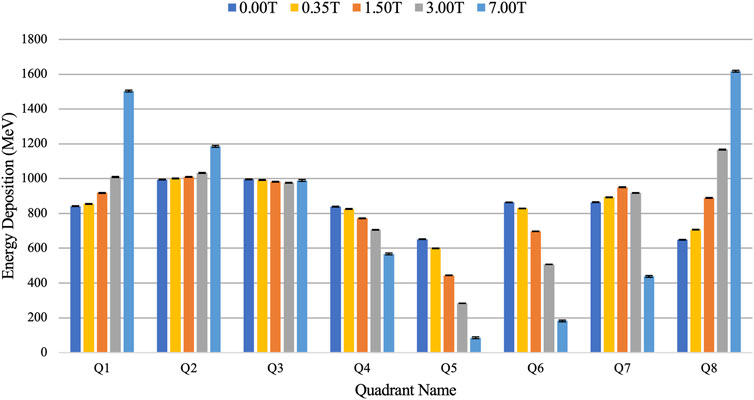
FIGURE 4. Comparison of energy deposition in each quadrant of the water shell of the alveolus model with varying magnetic field strength.

With the integration of NPs, similar behaviors were observed where the energy deposition, in the side view, is still seen to concentrate on the far side of the cavity and rotates in a clockwise direction with increasing magnetic field strength. Qualitatively, no apparent distinction of the energy deposition pattern with the integration of NPs can be seen as compared to Figure 3 (data not shown). In Figure 5, it can be seen quantitatively that increasing the NPs concentration increases the energy deposition in the alveolus. Furthermore, the relative increase in energy deposition with respect to the NP concentration was found to be the same regardless of the magnetic field strength imposed. A mean increase of energy deposition across all quadrants of the water shell was found to be: 0.57% ± 0.16 for 1% gold; 2.61% ± 0.07 for 5% gold; and 5.51% ± 0.23 for 10% gold.

FIGURE 5

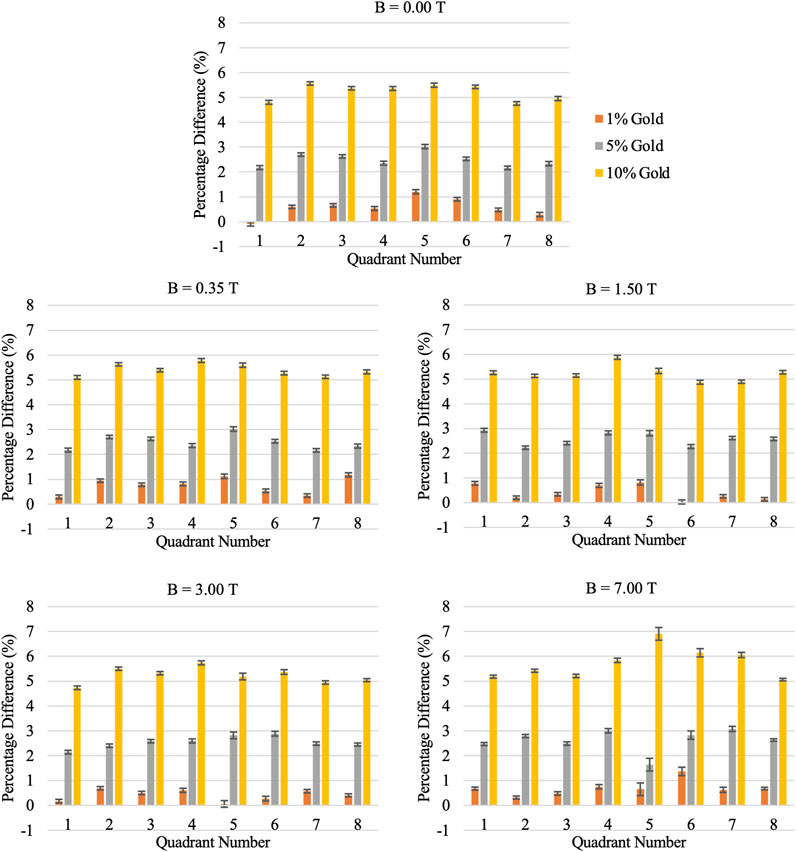
FIGURE 5. Percentage difference in energy deposition in alveolus water shell with and without integration of nanoparticles at varying magnetic field strength.

Multiple-Alveoli Irradiated With a Realistic Photon Source

The energy deposition in the water shell of the central alveolus of the multiple alveoli model irradiated with a realistic 6 MV photon source at varying magnetic field strength is shown in Figure 6. The energy deposition across all simulations was made uniform at the central alveolus with a difference of less than 1% to examine the energy deposition pattern at varying magnetic fields. It was observed that in the presence of a magnetic field, the energy deposition was distorted in a similar pattern to Figure 4 with observed increases in Q1-3 and decreases in Q5-7 though with some uncertainty in some quadrants shown by overlapping error bars.

FIGURE 6

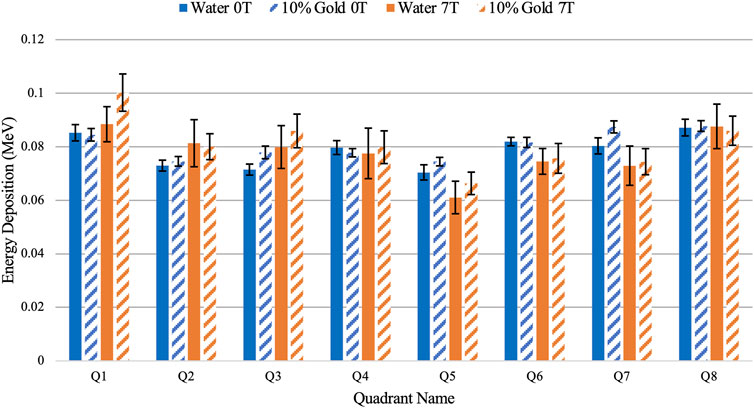
FIGURE 6. Comparison of energy deposition in the water shell of the central alveolus between water and 10% concentration of nanoparticles using the multiple alveoli model at 0.00 and 7.00 T.

The uncertainty in energy deposition in this simulation, shown by the error bars in each quadrant, is greater than the 5.51% expected to increase when nanoparticles are included. However, the same pattern of increased energy deposit in Q1-3 and decreased energy deposit in Q5-7 is seen when the magnetic field was applied with nanoparticles included. Additionally, an increase in total energy deposition across the whole water shell was found with the integration of nanoparticles. Although the difference is minimal at 0.00 T, at a higher magnetic field strength, a 3.87% ± 0.01 distinguishable increase of energy deposition was observed.

Discussion

Alveolus Irradiated With Mono-Energetic Electrons

This study shows that on the micrometer scale of the alveoli in the lung, the influence of a magnetic field on a directional low energy electron flux results in hot spots in the dose deposition in the tissue surrounding the air cavity. This finding is directly in line with a previous simulation study on a much larger scale with a 2 cm diameter spherical air cavity, wherein electrons are diverted by the magnetic field at right angles, thereby causing a hot spot at the upper left corner of the air cavity at the expense of inducing a cold spot at the lower left [10]. The hot and cold spots are produced as electrons traveling through the air cavity with few scatter interactions are deflected by the Lorentz force, as seen in the “Side View” in Figure 3, as a concentration of energy deposit toward the upper left at the expense of that in the lower left. The behavior of the electron paths due to the influence of the magnetic field is shown in Supplementary Figure S1.

To counterbalance the dose inhomogeneity surrounding an air cavity, a four-sided irradiation technique has been used to cancel out the hot and cold spots, making the dose around the air cavity desirably flat [10]. However, more research is needed to determine whether this still holds true for complex geometries such as utilizing the multi-alveoli model.

As the magnetic field was increased, the hot spot moved in a clockwise direction as more electrons are deflected by the Lorenz force to travel across the upper boundary. Due to differing path lengths across the cavity, electrons are constricted to a smaller surface area thereby causing the hot spot to increase in magnitude. Concurrently, fewer electrons traverse to the lower-left corner of the alveolus and the cold spot also increases in magnitude.

With the integration of nanoparticles in the alveolus, the same behavior was observed where hot and cold spots become apparent as the magnetic field was turned on. However, the presence of nanoparticles produced an increase in energy deposition in all quadrants of the alveolus surface in proportion to the density of nanoparticle/water compound simulated and not dependent on magnetic field strength. At higher magnetic field strength, a further radio-enhancement was not observed. Although the deflected electrons caused localized dose enhancement to a certain quadrant, the NP radio-enhancement observed in the entire alveolus model remains the same as the magnitude of the hot spot is compensated by the opposing cold spot. Further, highly localized ionizations occur where electrons interact with high-Z material capable of activating a nonlinear avalanche of electron emission through impact ionization and subsequent Auger cascades [3]. The secondary electrons produced by these events have been found to have a mean effective range of about 0.5 $\text{μm}$ for a 2 nm AuNP irradiated with 50 keV mono-energetic electrons [29], which is within the dimension of the water shell of the alveolus model. The mean effective range is important for the transport of energy deposition in increasing the cell kill probability when NPs are situated beside a nucleus containing the DNA [30]. Furthermore, secondary electrons can also propagate to ionize and excite nearby surrounding molecules and NPs, thereby depositing an increased localized dose and increasing biological damage within the immediate nanoscale vicinity [3]. This effect may be more important at higher field strengths where the hot spot is concentrated into a smaller area.

Multiple-Alveoli Irradiated With a Realistic Photon Source

The pattern of increase and decrease in energy deposition in opposing quadrants in Figure 6 being similar to that seen in Figure 4 implies that using a realistic photon source, energy distortion may be observed clinically on the micrometer scale within the lung in the presence of a magnetic field. Although the primary photons are unaffected by the magnetic field, the secondary electrons experience the Lorentz force and any overall degree of directionality in the electron flux perpendicular to the magnetic field will lead to dose distortion around air cavities. The effect is dependent on the relative size of the air cavity and the energy of the electrons, with low-energy electrons of the order of 100 keV exhibiting curvatures demonstrating the effect in cavities the size of the alveoli. Further investigation is needed to assess the biological importance of this micrometer-scale dose inhomogeneity on tumor control and radiation side-effects in normal tissue.

With the integration of nanoparticles, the single alveolus model displayed a concentration-dependent increase in energy deposits that was not affected by the magnetic field. In the multiple alveoli model, there was evidence of an overall increase in energy deposit in the nanoparticle-doped water shell of the order of a few percent, in line with previous Monte Carlo simulations with MV photons [31]. For the clinical radiotherapy applications, it will be important to track where nanoparticles are concentrated following nebulization at the time of radiation delivery. In previous work by Lin et al., a 4% dose increase was observed in the inner wall of the vessels when AuNPs were attached homogenously to the lumen, potentially contributing to the disruption of the functionality of the blood vessels in the tumor [32]. The evidence for these effects in a clinical scenario could be strengthened by more detailed simulation, using a refined linear accelerator model to produce the initial photon beam with gantry angles and a patient model imported from an actual patient radiotherapy plan. Additionally, large substructures such as vessels and bronchial structures should also be accounted for which have been found to cause micrometer-scale dose perturbation in the lungs using 6 and 18 MV photon beams with varying field sizes [33].

An understanding of the actual physical dose delivered and inhomogeneities at the local scale in the lung is vital to modeling the biological response to radiation and improving our understanding of the mechanisms of immune response and development of side effects following radiation treatment and to safe implementation of dose enhancement techniques such as nanoparticle radio-enhancement [15, 34]. An increasing number of studies using other nanoparticles such as gadolinium-based, hafnium oxide, and superparamagnetic iron oxide nanoparticles have also shown potential clinical translation for radio-enhancement and MRI contrast agent for which the in-depth physical mechanisms of dose deposition should also be investigated [4].

Conclusion

A beam of low-energy electrons of 100 keV can form hot and cold spots in energy deposition around an air cavity on the scale of an alveolus in a magnetic field representative of those used in current MRI-Linacs. The integration of nanoparticles, evenly distributed on the inner surface of the alveolus, maintains this hot and cold spot effect with a local enhancement of energy deposited in the nanoparticle-doped layer. The proportion of dose enhancement was found to be independent of the magnetic field strength, despite the changing pattern of dose distribution. Simulation of a semi-realistic photon treatment beam provides evidence that this effect may be observed in a clinical scenario. The inhomogeneity of dose induced by a magnetic field which is further amplified with the integration of nanoparticles has relevance to biological response to dose and safe dose limits when treating the lung in radiotherapy.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

DM, HB, and ZK contributed to the conception and design of the study. DM performed the simulation, analysis, creation of the figures, and wrote the first draft of the manuscript. HB served as an advisor of this study. Hence, all data acquired were approved by HB. AM provided technical assistant in building the simulation code. All authors contributed to manuscript revision, read, and approved the submitted version.

Funding

The authors acknowledge funding from the Cancer Institute NSW Translational Program Grant (2019/TPG2165).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The handling editor declared a past co-authorship with the authors ZK and HB.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

This work was made possible with the support from the Department of Science and Technology—Science Education Institute, The Republic of the Philippines and ACRF Image X Institute, The University of Sydney.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2022.835016/full#supplementary-material

References

1. Ferlay J EM, Lam F, Colombet M, Mery L, Piñeros M. Global Cancer Observatory: Cancer Today. Lyon, France: International Agency for Research on Cancer (2020).

Google Scholar

2. Howlader N, Noone AM, Krapcho M, Miller D, Brest A, Yu M, et al. editors. SEER Cancer Statistics Review. Bethesda, MD: National Cancer Institute (1975–2017). https://seer.cancer.gov/csr/1975_2017/.

PubMed Abstract | Google Scholar

3. Kuncic Z, Lacombe S. Nanoparticle Radio-Enhancement: Principles, Progress and Application to Cancer Treatment. Phys Med Biol (2018) 63(2):02TR01. doi:10.1088/1361-6560/aa99ce

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Schuemann J, Bagley AF, Berbeco R, Bromma K, Butterworth KT, Byrne HL, et al. Roadmap for Metal Nanoparticles in Radiation Therapy: Current Status, Translational Challenges, and Future Directions. Phys Med Biol (2020) 65(21):21RM02. doi:10.1088/1361-6560/ab9159

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Byrne HL, Le Duc G, Lux F. Enhanced MRI-Guided Radiotherapy with Gadolinium-Based Nanoparticles: Preclinical Evaluation with an MRI-Linac. Cancer Nano (2020) 11(9). doi:10.1186/s12645-020-00065-5

CrossRef Full Text | Google Scholar

6. Pollard JM, Wen Z, Sadagopan R, Wang J, Ibbott GS. The Future of Image-Guided Radiotherapy Will Be MR Guided. Bjr (2017) 90(1073):20160667. doi:10.1259/bjr.20160667

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Klüter S. Technical Design and Concept of a 0.35 T MR-Linac. Clin Translational Radiat Oncol (2019) 18:98–101. doi:10.1016/j.ctro.2019.04.007

CrossRef Full Text | Google Scholar

8. Raaymakers BW, Jürgenliemk-Schulz IM, Bol GH, Glitzner M, Kotte ANTJ, van Asselen B, et al. First Patients Treated with a 1.5 T MRI-Linac: Clinical Proof of Concept of a High-Precision, High-Field MRI Guided Radiotherapy Treatment. Phys Med Biol (2017) 62(23):L41–L50. doi:10.1088/1361-6560/aa9517

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Raaymakers BW, Raaijmakers AJE, Kotte ANTJ, Jette D, Lagendijk JJW. Integrating a MRI Scanner with a 6 MV Radiotherapy Accelerator: Dose Deposition in a Transverse Magnetic Field. Phys Med Biol (2004) 49(17):4109–18. doi:10.1088/0031-9155/49/17/019

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Raaijmakers AJE, Raaymakers BW, Lagendijk JJW. Integrating a MRI Scanner with a 6 MV Radiotherapy Accelerator: Dose Increase at Tissue-Air Interfaces in a Lateral Magnetic Field Due to Returning Electrons. Phys Med Biol (2005) 50(7):1363–76. doi:10.1088/0031-9155/50/7/002

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Raaijmakers AJE, Raaymakers BW, Lagendijk JJW. Magnetic-field-induced Dose Effects in MR-Guided Radiotherapy Systems: Dependence on the Magnetic Field Strength. Phys Med Biol (2008) 53(4):909–23. doi:10.1088/0031-9155/53/4/006

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Labiris NR, Dolovich MB. Pulmonary Drug Delivery. Part I: Physiological Factors Affecting Therapeutic Effectiveness of Aerosolized Medications. Br J Clin Pharmacol (2003) 56(6):588–99. doi:10.1046/j.1365-2125.2003.01892.x

CrossRef Full Text | Google Scholar

13. Zarogoulidis P, Zarogoulidis K, Domvri K, Goldberg W, Karamanos E, Schmidt N, et al. Inhaled Chemotherapy in Lung Cancer: Future Concept of Nanomedicine. Ijn (2012) 7:1551–72. doi:10.2147/ijn.s29997

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Azarmi S, Roa WH, Löbenberg R. Targeted Delivery of Nanoparticles for the Treatment of Lung Diseases. Adv Drug Deliv Rev (2008) 60(8):863–75. doi:10.1016/j.addr.2007.11.006

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Dufort S, Bianchi A, Henry M, Lux F, Le Duc G, Josserand V, et al. Nebulized Gadolinium-Based Nanoparticles: a Theranostic Approach for Lung Tumor Imaging and Radiosensitization. Small (2015) 11(2):215–21. doi:10.1002/smll.201401284

PubMed Abstract | CrossRef Full Text | Google Scholar

16. McMahon Sj HW, Brun E. Energy Dependence of Gold Nanoparticle Radiosensitization in Plasmid DNA. J Phys Chem C (2011). doi:10.1021/jp206854s

CrossRef Full Text | Google Scholar

17. Porcel ELS, Usami N. Nano-Sensitization under Gamma Rays and Fast Ion Radiation. J Phys Conf Ser (2012). doi:10.1088/1742-6596/373/1/012006

CrossRef Full Text | Google Scholar

18. Bobyk L, Edouard M, Deman P, Vautrin M, Pernet-Gallay K, Delaroche J, et al. Photoactivation of Gold Nanoparticles for Glioma Treatment. Nanomedicine: Nanotechnology, Biol Med (2013) 9(7):1089–97. doi:10.1016/j.nano.2013.04.007

CrossRef Full Text | Google Scholar

19. Hainfeld JF, Smilowitz HM, O’Connor MJ, Dilmanian FA, Slatkin DN. Gold Nanoparticle Imaging and Radiotherapy of Brain Tumors in Mice. Nanomedicine (2013) 8(10):1601–9. doi:10.2217/nnm.12.165

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Byrne H, McNamara A, Kuncic Z. Impact of Nanoparticle Clustering on Dose Radio-Enhancement. Radiat Prot Dosimetry (2019) 183(1-2):50–4. doi:10.1093/rpd/ncy218

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Butterworth KT, McMahon SJ, Currell FJ, Prise KM. Physical Basis and Biological Mechanisms of Gold Nanoparticle Radiosensitization. Nanoscale (2012) 4(16):4830–8. doi:10.1039/c2nr31227a

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Lechtman E, Mashouf S, Chattopadhyay N, Keller BM, Lai P, Cai Z, et al. A Monte Carlo-Based Model of Gold Nanoparticle Radiosensitization Accounting for Increased Radiobiological Effectiveness. Phys Med Biol (2013) 58(10):3075–87. doi:10.1088/0031-9155/58/10/3075

PubMed Abstract | CrossRef Full Text | Google Scholar

23. McNamara AL, Kam WWY, Scales N, McMahon SJ, Bennett JW, Byrne HL, et al. Dose Enhancement Effects to the Nucleus and Mitochondria from Gold Nanoparticles in the Cytosol. Phys Med Biol (2016) 61(16):5993–6010. doi:10.1088/0031-9155/61/16/5993

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Brown JMC, Hanna GG, Lampe N, Villagomez-Bernabe B, Nicol JR, Coulter JA. Towards Photon Radiotherapy Treatment Planning with High Z Nanoparticle Radiosensitisation Agents: the Relative Biological Effective Dose (RBED) Framework. Cancer Nano (2018) 9(1):9. doi:10.1186/s12645-018-0043-7

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Perl J, Shin J, Schümann J, Faddegon B, Paganetti H. TOPAS: an Innovative Proton Monte Carlo Platform for Research and Clinical Applications. Med Phys (2012) 39(11):6818–37. doi:10.1118/1.4758060

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Geant4 . Physics Reference Manual: Penelope Models (2021). Available from: https://geant4-userdoc.web.cern.ch/UsersGuides/PhysicsReferenceManual/html/electromagnetic/introduction/penelope.html (Accessed January, 2022).

Google Scholar

27. Maina JN, West JB. Thin and strong! the Bioengineering Dilemma in the Structural and Functional Design of the Blood-Gas Barrier. Physiol Rev (2005) 85(3):811–44. doi:10.1152/physrev.00022.2004

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Hombrink G, Wilkens JJ, Combs SE, Bartzsch S. Simulation and Measurement of Microbeam Dose Distribution in Lung Tissue. Physica Med (2020) 75:77–82. doi:10.1016/j.ejmp.2020.06.003

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Grumezescu AM. Nanobiomaterials In Medical Imaging : Applications of Nanobiomaterials. Applications of Nanobiomaterials. Amsterdam ; Bostonxxvi: Elsevier/WA, William Andrew is an imprint of Elsevier (2016). p. 491.

Google Scholar

30. Chithrani BD, Ghazani WCW. Determining the Size and Shape Dependence of Gold Nanoparticle Uptake into Mammalian Cells. Nano Lett (2006) 6:662–8. doi:10.1021/nl052396o

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Byrne HL, Gholami Y, Kuncic Z. Impact of Fluorescence Emission from Gold Atoms on Surrounding Biological Tissue-Implications for Nanoparticle Radio-Enhancement. Phys Med Biol (2017) 62(8):3097–110. doi:10.1088/1361-6560/aa6233

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Lin Y, Paganetti H, McMahon SJ, Schuemann J. Gold Nanoparticle Induced Vasculature Damage in Radiotherapy: Comparing Protons, Megavoltage Photons, and Kilovoltage Photons. Med Phys (2015) 42(10):5890–902. doi:10.1118/1.4929975

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Liang L, Larsen EW, Chetty IJ. An Anatomically Realistic Lung Model for Monte Carlo‐based Dose Calculations. Med Phys (2007) 34(3):1013–25. doi:10.1118/1.2437284

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Hales RB. The Impact of Gadolinium-Based MR Contrast on Radiotherapy Planning for Oropharyngeal Treatment on the MR Linac. Med Phys (2021).

Google Scholar