- ISIS Neutron and Muon Source, Rutherford Appleton Laboratory, Science and Technology Facilities Council, UKRI, Chilton, Didcot, United Kingdom
Lattice dynamics in organic ferroelectric PhMDA (2-phenylmalondialdehyde C9H8O2) has been investigated using inelastic neutron scattering (INS) spectroscopy and first principles based calculations. Most of the prominent features of the INS spectrum originated from the normal modes of hydrogen bonded malondialdehyde (MDA) units rather than from phenyl rings. It is also found that carbon-hydrogen bonds in the MDA unit are tighter than these in phenyl rings. From the calculated splitting of LO (longitudinal optical) and TO (transverse optical) normal modes, it is predicted that hydrogen bonds in MDA units, which hold the solid state structure, contribute more to the ferroelectric polarisation of PhMDA. Any distortion of H-ions in these hydrogen bonds thus affects ferroelectric properties of this material.
1 Introduction
Organic ferroelectrics, particularly those exhibiting ferroelectric properties at room temperature, are important functional materials [1–4], for potential technological applications in flexible electronics, energy harvesting, or medical devices. These materials are low cost, thin, soft and generally metal-free; making them attractive for commercial use. To design and improve these materials for particular applications, it is important to understand their microscopic properties. Lattice dynamics gives information about inter-atomic forces, intrinsic polarisations and thermodynamic properties, which are important for understanding ferroelectric properties of these materials [5–7].
Hydrogen bonds play an important role inorganic ferroelectric materials. Here the polar phase is stabilised by energy-lowering chemical bonds which form non-centrosymmetric arrangements of constituent ions. Dynamics of hydrogen bonds determine the strength of the bulk polarisation. In croconic acid, the strongest room temperature organic ferroelectric material known so far, strong and flexible hydrogen bonds support a Jahn-Teller type distortion at room temperatures leading to strong polarisation [8]. Dynamics of these hydrogen bonds in a number of organic ferroelectrics was investigated previously using inelastic neutron scattering (INS) spectroscopy [9–12]. In the present article, we focus on the investigation of lattice dynamics of another hydrogen-bonded organic ferroelectrics, PhMDA (2-phenylmalondialdehyde C9H8O2)) using neutron spectroscopy, complemented with calculations based on the density functional theory (DFT).
The structure of PhMDA has been reported using X-ray diffraction [2, 4]. First principles DFT has been used to focus on the mechanism of proton transfer across hydrogen bonds [13]. No investigation has been reported on lattice dynamics, or normal modes of vibrations so far, although this is important to understand ferroelectric properties of materials. In the current article, we present experimental vibrational spectra of PhMDA using INS spectroscopy and microscopic lattice dynamics analysis employing first principles DFT calculations to understand the atomistic origin of its ferroelectric polarisations.
2 Methods
2.1 Experiments
INS experiments are performed on TOSCA [14] spectrometer at the ISIS Pulsed Neutron and Muon Source at 10 K [15]. About 2.4 g of commercially available PhMDA powder bought from Sigma Aldrich is used in this experiment. TOSCA is a high resolution time-of-flight, indirect geometry spectrometer having energy resolution ΔE/E less than 1% with energy transfer range up to 8,000 cm−1. The sample is wrapped in a thin aluminum foil and placed in a flat aluminum container sealed by indium wire under vacuum.
2.2 Calculations
Calculations are performed using plane wave pseudo-potential electronic-structure calculations as implemented in the CASTEP code [16] with optimized norm-conserving pseudopotentials [17] generated with the Perdew–Burke–Ernzerhof (PBE) [18] functional within the generalized-gradient approximation (GGA). Dispersion corrections are included in the PBE functional (PBE + D) as proposed by Tkatchenko and Scheffler (TS) [19]. The initial atomic structure is taken from the reported experimental structure obtained from XRD measurements and available in Cambridge Crystallographic data center (CCDC) as entry number 796168 [4]. Full-geometry optimizations using both PBE and PBE + D functionals with a force tolerance of 1.0 × 10−3 eV/Å are performed with the Broyden-Fletcher-Goldfarb-Shanno (BFGS) algorithm. A plane-wave cutoff of 1,000 eV and a Brillouin-zone (BZ) sampling of 8 × 2 × 8 k-points equivalent to 16 points when symmetry-reduced are used with self-consistent single-point energy minimizations tolerance of 2.5 × 10–7 eV. The tolerance of atomic forces minimization is 1.0 × 10–3 eV/Å.
Normal mode frequencies and eigenvectors are determined by lattice dynamics calculations at the Γ-point of the resulting ground state structure by diagonalisation of dynamical matrices using the density-functional perturbation theory (DFPT) and linear-response methods [20]. INS spectra are obtained from calculated eigenenergies and eigenvectors and using the abINS algorithm in Mantid [21].
Intensity of a particular INS mode is related to the dynamic structure factor S (Q, E). For a crystal containing N atoms in the unit cell, the structure factor of single-quantum excitation of normal mode m with energy Em at temperature T [24] is:
where, ei,m is the eigenvector of atom i in mode m, Q is the momentum-transfer vector, Mi is the mass of atom i and W (Q, T) is the Debye-Waller (DW) factor at temperature T. At very low temperatures, the DW term is approximated as zero. For an inverted-geometry INS spectrometer like TOSCA, Q2 is proportional to E. A powder averaging has been applied in this calculation following standard methodology [21–23].
3 Results and Discussions
The unit cell of PhMDA consists of four molecular units as shown in Figure 1. In each unit a malondialdehyde (MDA) molecule is attached with a six-member phenyl-ring through C=C bond. Single crystal X-ray diffraction (XRD) found the crystal structure as orthorhombic having space group Pna21, space group number 33 [4]. The phenyl-ring molecular units are connected by hydrogen bonding in a zig-zag manner through MDA units to make the solid state structure. The a and b -lattice parameters obtained for the ground state geometry by cell optimised PBE + D calculations compared within 1%. The calculated c-lattice parameter, however, underestimated by 2.6%. This difference primarily comes from the differences in of lengths hydroxyl and hydrogen bonds. The positions of H obtained from X-ray diffraction may have contributed in this discrepancy. Due to larger differences, 7.8%, 13.2% and 3.8% for a, b and c lattice parameters, respectively, when the unit cell is optimised without dispersion corrections (PBE), it is not used in subsequent calculations.
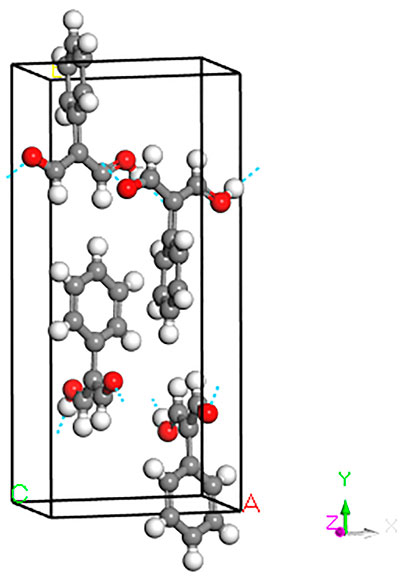
FIGURE 1. Unit cell of PhMDA as obtained after full geometry optimisation on the experimental structure [4]. See text for more details. Gray: C, white: H, red: O.
Lattice dynamics calculations show that there are 225 optic modes in four different symmetries, A1, A2, B1 and B2. All these modes are Raman-active, however, modes with A1, B1, B2 symmetry only are IR-active. All 57 modes with A2 symmetry are IR-inactive. As there is no selection rule, INS spectroscopy is capable of giving almost complete information of normal modes in this material.
The experimentally obtained INS spectrum is compared with the DFT simulated one in Figure 2. Frequencies of important normal modes and molecular unites responsible for these vibrations are labeled in this figure. Both spectra agree relatively well showing that the calculations using DFT within harmonic approximation can explain almost all vibrational transitions. Although INS experiments are done on powdered sample and DFT calculations are done on a periodic structure, which resembles with the single crystal structure of the material, this agreement shows that the powdered sample retains its local and medium range order of atomic arrangements. The long range order of the atomic structure may be affected more in the powdered sample reflecting the differences between experimental and simulated INS in the low energy modes of collective vibrations.
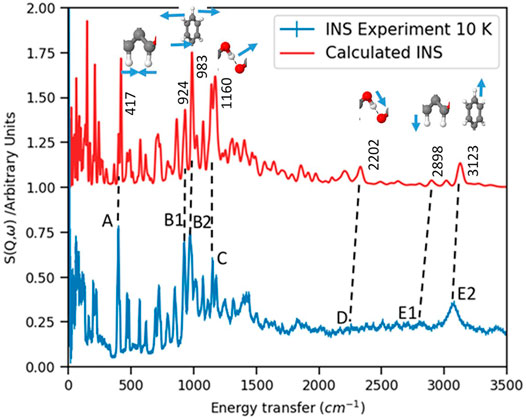
FIGURE 2. INS spectrum is compared with DFT calculations. Important peaks are labeled by frequencies of normal modes along with structures of functional groups responsible for those modes. The direction of vibrations of respective atoms are indicated by small arrows. See text for more details.
The vibrational peaks below 400 cm−1 are collective vibrations and dominated by oxygens in MDA units. The sharp peak around 400 cm−1, labeled as A is Figure 2, is due to a wagging motion of two dangling hydrogens in MDA units, which are not hydrogen-bonded. In practice there are four modes ranging between 400, −, 417 cm−1 due to the C-C=C bending modes in MDA. These IR-active modes are clearly visible in INS spectroscopy because these are associated with the motion of hydrogens. However, calculations show that these low energy modes are of low intensities, so may be not be visible in IR spectrum.
The next most intense peaks observed in the INS spectrum are located at 924 cm−1 and 972 cm−1, labeled as B1 and B2 in Figure 2. These are antisymmetric librational modes of non-hydrogen bonded hydrogens in MDA and the wagging motion of the phenyl-ring and its associated hydrogen atoms, respectively. Corresponding calculated modes are within 1.5% of that of experimental frequencies. Calculations show that these IR-active modes also may not be visible in the IR spectrum due to their low intensities.
The out-of plane bending motion of O-H–O hydrogen bond in MDA chains, observed at 1,151 cm−1 are of relatively lower intensities than the wagging modes at 972 cm−1 mentioned above. This peak is denoted at C in Figure 2. These modes are observed in other hydrogen bonded ferroelectrics, such as croconic acid [8, 11] and CBDC [12], around 1,000 − 1,100 cm−1. The relative INS intensities of these modes are increasingly stronger from CBDC to PhMDA to croconic acid. The vibration of hydrogen bonds in MDA chain along with wagging motion of dangling hydroxyl ions associated with MDA units is observed around 1,230 cm−1. This peak appears just above the peak denoted as C.
The O-H stretching modes around 2,200 cm−1, marked as D in Figure 2, are not visible in the INS spectrum. These modes can be visible in IR spectrum due to their moderately high intensities. The clearly visible modes in INS around 3,100 cm−1, marked as E2 in Figure 2, are C-H stretching modes associated with phenyl rings in the PhMDA crystal. The C-H stretching modes related with MDA are observed in a little bit lower energy transfer region, i.e., around 2,800 cm−1, which is labeled as E1 in Figure 2. This predicts that C-H bonds in MDA unit are tighter than these are in phenyl rings. These C-H stretching modes may not be visible in IR spectroscopy due to their very low intensities as obtained from lattice dynamics simulations.
Lattice dynamics plays an important role in understanding the particular vibrational mode or modes responsible for ferroelectric properties in materials. The LO-TO splitting of normal modes is a measure of their contribution to the dynamical effective charge responsible for ferroelectricity [6, 7]. In PhMDA it is found that OH stretching modes around 2,200 cm−1 exhibit LO-TO splitting of about 100 cm−1. Although this is not huge in comparison to the giant LO-TO splitting of about 700 cm−1 found in inorganic ferroelectric BaTiO3 [6], this is the maximum LO-TO splitting obtained from calculations. The LO-TO-splitting for the mode at 1,230 cm−1 is about 50 cm−1. On the other hand, the LO-TO splitting for C-H stretching modes (E1 and E2) and O-H–O bending mode (C) are negligible.
A comparatively large LO-TO splitting of modes around 2,200 cm−1, which is associated with hydrogen bonded MDA chain, indicates that these modes couple strongly with electric fields and contribute more to the dynamical effective charge responsible for ferroelectric polarisation. Any distortion of the H-ion in the hydrogen bond as well as hydroxyl ions in MDA molecular units are thus sensitive to long range Coulomb interaction and ferroelectric properties of this material. This observation is consistent with previously reported findings [13].
4 Conclusions
Lattice dynamics of hydrogen bonded organic ferroelectric PhMDA (2-phenylmalondialdehyde C9H8O2) has been investigated using inelastic neutron scattering (INS) spectroscopy. Calculations are performed using first principles DFT simulations. The calculated and the experimental INS spectra compared well within harmonic approximations. Most of the prominent features of this INS spectrum are originated from the normal modes of hydrogen bonded MDA units rather than from phenyl rings. It is also found that CH bonds in the MDA unit are tighter than these in phenyl rings. Calculations predict that O-H stretching modes around 2,200 cm−1 exhibit maximum LO-TO splitting in this material. This finding implies that any distortion of H-ion in these hydrogen bonds should affect ferroelectric properties of the material. This insight can be used to design and synthesize materials with stronger ferroelectricity in real life applications.
Data Availability Statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Author Contributions
SM has planned the research, performed experiments and computations, analysed results and written the manuscript.
Conflict of Interest
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Acknowledgments
The ISIS Facility is acknowledged for the provision of beam time under the grant RB1320543, and the United Kingdom Science and Technology Facilities Council e-Science Department for continued access to the SCARF cluster at the Rutherford Appleton Laboratory. Some of the computations have been performed on the United Kingdom Supercomputing Facility ARCHER under the auspices of the Materials Chemistry Consortium (EPSRC grant EP/L000202).
References
1. Horiuchi S, Tokunaga Y, Giovannetti G, Picozzi S, Itoh H, Shimano R, et al. Nature (2010) 463:789–792. doi:10.1038/nature08731
2. Horiuchi S, Kobayashi K, Kumai R, Ishibashi S. Proton Tautomerism for strong Polarization Switching. Nat Commun (2017) 8:14426. doi:10.1038/ncomms14426
4. Horiuchi S, Kumai R, Tokura Y. Hydrogen-Bonding Molecular Chains for High-Temperature Ferroelectricity. Adv Mater (2011) 23:2098–103. doi:10.1002/adma.201100359
5.K Rebe, CH Ahn, and JM Triscone, editors. Physics of Ferroelectrics: A Modern Perspective. Berlin, Germany: Spinger-Verlag Berlin Heidelberg (2007).
6. Zhong W, King-Smith RD, Vanderbilt D. Giant LO-TO Splittings in Perovskite Ferroelectrics. Phys Rev Lett (1994) 72:3618–21. doi:10.1103/physrevlett.72.3618
8. Mukhopadhyay S, Gutmann MJ, Jiménez-Ruiz M, Jochym DB, Wikfeldt KT, Refson K, et al. Mechanism of Enhancement of Ferroelectricity of Croconic Acid with Temperature. Phys Chem Chem Phys (2017) 19:32216–25. doi:10.1039/c7cp06039d
9. Fernandez-Alonso F, Gutmann MJ, Mukhopadhyay S, Jochym DB, Refson K, Jura M, et al. Hydrogen Bonding in the Organic Ferroelectric Croconic Acid: Insights from Experiment and First-Principles Modelling. J Phys Soc Jpn (2013) 82:SA001. doi:10.7566/jpsjs.82sa.sa001
10. Mukhopadhyay S, Gutmann MJ, Jura M, Jochym DB, Jimenez-Ruiz M, Sturniolo S, et al. Ferroelectric Behaviour in Solid Croconic Acid Using Neutron Scattering and First-Principles Density Functional Theory. Chem Phys (2013) 427:95–100. doi:10.1016/j.chemphys.2013.10.008
11. Mukhopadhyay S, Gutmann M, Fernandez-Alonso F. Hydrogen-bond Structure and Anharmonicity in Croconic Acid. Phys Chem Chem Phys (2014) 16:26234–9. doi:10.1039/c4cp03713h
12. Mukhopadhyay S. Identification of normal Modes Responsible for Ferroelectric Properties in Organic Ferroelectric CBDC. J Phys Commun (2019) 3:113001. doi:10.1088/2399-6528/ab5431
13. Stroppa A, Sante DD, Horiuchi S, Tokura Y, Vanderbilt D, Picozzi S. Phys Rev B (2011) 84:014101. doi:10.1103/physrevb.84.014101
14.Tosca. Tosca (2021). Available from: https://www.isis.stfc.ac.uk/Pages/tosca.aspx (Accessed December 12, 2021).
16. Clark SJ, Segall MD, Pickard CJ, Hasnip PJ, Probert MIJ, Refson K, et al. First Principles Methods Using CASTEP. Z Kristallogr (2005) 220:567–70. doi:10.1524/zkri.220.5.567.65075
17. Rappe AM, Rabe KM, Kaxiras E, Joannopoulos JD. Optimized Pseudopotentials. Phys Rev B (1990) 41:1227–30. doi:10.1103/physrevb.41.1227
18. Perdew JP, Burke K, Ernzerhof M. Generalized Gradient Approximation Made Simple. Phys Rev Lett (1996) 77:3865–8. doi:10.1103/physrevlett.77.3865
20. Refson K, Tulip PR, Clark SJ. Variational Density-Functional Perturbation Theory for Dielectrics and Lattice Dynamics. Phys Rev B (2006) 73:155114. doi:10.1103/physrevb.73.155114
21. Dymkowski K, Parker SF, Fernandez-Alonso F, Mukhopadhyay S. AbINS: The Modern Software for INS Interpretation. Physica B: Condensed Matter (2018) 551:443–8. doi:10.1016/j.physb.2018.02.034
22.Abins v1. Abins V1 (2021). Available from: https://docs.mantidproject.org/v3.9.1/algorithms/Abins-v1.html (Accessed December 12, 2021).
23. Mitchell PCH, Parker SF, Ramirez-Cuesta AJ, Tomkinson J. Vibrational Spectroscopy with Neutrons. London: World Scientific Pub (2005).
Keywords: inelastic neutron scattering, organic ferroelectrics, lattice dynamics, electronic structure, neutron spectroscopy, phMDA
Citation: Mukhopadhyay S (2022) Lattice Dynamics in Organic Ferroelectrics Using Neutron Spectroscopy and Ab-Initio Modeling. Front. Phys. 10:834902. doi: 10.3389/fphy.2022.834902
Received: 14 December 2021; Accepted: 22 February 2022;
Published: 08 March 2022.
Edited by:
Rogelma M. S. Ferreira, Federal University of the Recôncavo of Bahia, BrazilReviewed by:
Wei Liu, University of Science and Technology of China, ChinaMarie Plazanet, UMR5588 Laboratoire Interdisciplinaire de Physique (LIPhy), France
Copyright © 2022 Mukhopadhyay. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Sanghamitra Mukhopadhyay, c2FuZ2hhbWl0cmEubXVraG9wYWRoeWF5QHN0ZmMuYWMudWs=
 Sanghamitra Mukhopadhyay
Sanghamitra Mukhopadhyay