
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
MINI REVIEW article
Front. Phys. , 11 February 2022
Sec. Condensed Matter Physics
Volume 10 - 2022 | https://doi.org/10.3389/fphy.2022.834882
This article is part of the Research Topic Advances in Superconducting Infinite-Layer and Related Nickelates View all 16 articles
The family of rare earth (RE) nickelate perovskites RENiO3 has emerged over the past two decades as an important platform for quantum matter physics and advanced applications. The parent compounds from this family are strongly correlated insulators or metals, in most cases with long-range spin order. In the past few years, carrier doping has been achieved using different approaches and has been proven to be a powerful tuning parameter for the microscopic properties and collective macroscopic states in RENiO3 compounds. In particular, a series of recent studies has shown that carrier doping can be responsible for dramatic but reversible changes in the long-range electronic and magnetic properties, underscoring the potential for use of nickelates in advanced functional devices. In this review, we discuss the recent advancements in our description, understanding and application of electron-doped rare earth nickelates. We conclude with a discussion of the developments and outlook for harnessing the quantum functional properties of nickelates in novel devices for sensing and neuromorphic computation.
Functional materials exhibit properties that can be harnessed for novel technological applications. Control over selected electronic, magnetic, optical, and/or structural properties is often achieved by stabilizing one particular phase of matter over other competing phases or by tuning the material across phase boundaries. A significant fraction of functional materials is found among transition metal oxides (TMOs) characterized by perovskite structures with chemical formula ABO3. The advantage of the perovskite structure is its flexibility to accommodate atoms of various sizes and its tolerance to stoichiometry variations, making their physical properties highly tunable.
One of the most common ways to modify the physical properties of perovskite-type TMOs is via carrier doping [1]. The latter is typically achieved by partial substitution of atoms with different valence; by creating charged atomic vacancies; or by ion intercalation. Carrier control has been shown to induce emergent properties in the perovskite TMOs including colossal magnetoresistance, unconventional high-temperature superconductivity, quantum criticality, and charge/spin density wave orders [2–6].
This review focuses on the TMO family of rare earth nickelates (RENiO3; RE = rare earth ion), which have for many years attracted the attention of the scientific community owing to their highly tunable electronic properties. The electronic, magnetic, optical, and structural tunability of these systems not only leads to potential applications but also provides new opportunities to realize and understand quantum matter phenomena.
Before discussing the physical properties of doped RENiO3, we review the complex electronic properties of undoped nickelates. RENiO3 has a distorted GdFeO3-perovskite-like structure where the Ni-O-Ni bond angle can be continuously varied by rare earth substitution. The bond angle has been shown to have a profound impact on their electronic properties [7, 8]. In the rare earth series (except La), RENiO3 first undergo a metal (or semiconductor) to insulator transitions and subsequently a paramagnet to antiferromagnet transition. The transition points vary with the size of the rare earth atoms and are concurrent for RE = Nd, Pr. In terms of local electronic configuration, Ni has a nominal electron filling d7 (Ni3+). However, a series of experimental and theoretical studies have identified RENiO3 as a negative charge transfer insulator, with the electronic ground state exhibiting a significant projection onto a 3d8L configuration (L denotes a ligand hole in oxygen orbital) [9–12]. Therefore, RENiO3 has rather unique ground state properties among charge transfer insulators.
Upon entering the insulating state, a disproportionated state emerges where neighboring Ni-O6 octahedra alternately compress and expand, forming a 3D period-2 checkerboard arrangement. In the antiferromagnetically ordered phase, the Ni spins are close to S = 1/2 and order at the wavevector (1/4, 1/4, 1/4) in the pseudocubic cell [13–16]. Since RENiO3 could be hardly synthesized in single crystalline form until recently [17], most earlier studies focused on polycrystalline RENiO3 with varying chemical compositions. Since the development of epitaxial synthesis in the last two decades, many studies of RENiO3 have focused on thin films, whose physical properties can be altered not only via chemical composition, but also by strain, dimensionality, and superlattice engineering [18].
Due to strong on-site Coulomb interactions, the electronic properties of RENiO3 are extremely sensitive to the electron filling of the Ni-O bands. Therefore, carrier doping is another effective and well-established practice of controlling the physical properties of RENiO3. In the following, we will review the recent progress on carrier-doped nickelates. We will focus on recent advances in understanding the physics of rare earth nickelates as a function of carrier doping and the potential functional applications enabled by the latter.
It has been recently demonstrated that pseudocubic RENiO3 can conduct and incorporate large amounts of dopant ions such as hydrogen, alkali (Li, Na) or alkali-earth metals [19–22]. The ion dopants have been shown to preferentially bond with oxygen and can undergo frequent diffusive hopping to nearby sites via the Grotthuss mechanism [22, 23]. In presence of an external bias (chemical/electrical), the ions will diffuse in and out of the RENiO3 scaffolding with a relatively high ionic conductivity [20, 24].
The incorporation of interstitial ions with low electron affinity adds extra electrons to the conduction states and can dramatically alter the ground state of RENiO3. It has been shown that the incorporated ion concentration can be as high as ∼1:1 ion:Ni ratio [20–22, 25]. Recent studies report that the properties of ion-intercalated nickelates change dramatically: 1) Doping induces a reversible giant resistance switching by eight orders of magnitude at room temperature [19, 20], with accompanying changes from a metallic or semiconducting state (∼100 meV) to a large bandgap insulating state (∼3 eV) [19, 26]. 2) The doping process alters the nickel valence state from Ni3+ to Ni2+ and is independent of temperature, a fundamental departure from thermally-driven insulator-metal transitions previously noted in perovskite nickelates. 3) The ligand holes are getting filled upon doping. 4) The lattice constants can increase significantly (∼10%, depending on the ion species) upon ion intercalation [27]. 5) The (1/4, 1/4, 1/4) antiferromagnetic order breaks down after some critical doping [28]. Many exciting applications have been proposed and realized in these interstitially-doped nickelates, e.g., electronic devices (phase-change transistor) [19, 29–31], fuel cells [22], bio-electronic interfaces [32, 33], electric field sensor [21], as well as artificial cognitive systems [28, 34, 35].
Most of these studies focused on SmNiO3 for its large resistive switching, faster intercalation dynamics, and facile synthesis. The study by Chen et al. examined the hydrogenation of RENiO3 for RE = La, Nd, Sm, Eu [26]. They showed that for rare earth ions with larger atomic numbers, the resistivity could be tuned over a more extensive range with faster kinetics. This general trend unveils the role of the structure in ionic doping. With the decrease of RE radius, the tolerance factor further deviates from 1, and the structure becomes less stable. Thus, the smaller RE compounds are more prone to incorporate and retain interstitial ions. However, the structural changes during the intercalation process cannot alone explain the very large changes in resistivity. From a structural point of view, the expansion of lattice upon intercalation tends to straighten the Ni-O-Ni bonds and should stabilize the metallic state over the insulating state [36, 37]. Therefore, the electronic contribution must be accounted for to explain the colossal resistive switching effect.
In a semiconductor, carrier doping is generally realized by injecting electron/hole carriers into the conduction/valence band so that electrical conductivity increases proportionally to the number of mobile carriers. Carrier doping in RENiO3 by ion intercalation (and oxygen vacancies as will be discussed in the following section) defies this simple notion as the resistance increases by orders of magnitude. Such a phenomenon is sometimes called antidoping [38]. The large increase of the resistance and the bandgap cannot be explained simply by a Fermi level shift as described in the rigid-band model. The physical origin of the antidoping has recently been unveiled by Ref. [38]. A prerequisite of an antidoping system is the existence of partially filled intermediate side bands consisting of trapped holes (electrons) inside the conduction-to-valence bandgap. The intermediate side bands in RENiO3 are represented by 3d8L states consisting of hybridized trapped ligand holes and Ni orbitals. Upon electron doping, the electrons fill the available trapped hole states in the intermediate band and thus significantly alter the Ni-O hybridization. Instead of the shift in the Fermi level, the doping alters the band structure where the density of state of the intermediate side band diminishes and restores the pure O-2p and Ni-3d character of the conduction and valence band. This mechanism increases the effective band gap and leads to extraordinary resistive switching [1].
This interpretation was supported by the DFT calculations in electron doped SmNiO3 and YNiO3 by two different groups [38–40]. As shown in Figure 1, in the undoped compound, the intermediate band is composed of Ni-3d and O-2p states with a gap size of ∼0.5 eV. Upon doping, the doped electrons selectively fill the ligand hole states, transferring the unoccupied intermediate in-gap density of states to the valence band below. The gap is widened to 2–3 eV with no oxygen ligand holes, suggesting a positive charge transfer system upon doping.
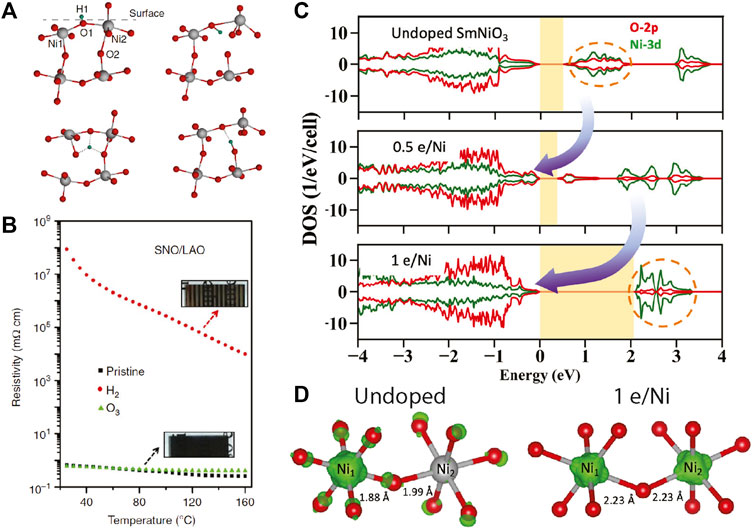
FIGURE 1. (A) The diffusive ionic intercalation process exemplified by hydrogen. The proton (H+, in green) mainly bonds with oxygen and undergoes diffusive rotation and transfer onto neighboring oxygen ions [35]. (B) Resistivity versus temperature for the pristine (black), hydrogen-intercalated (red), and ozone-annealed (green) SmNiO3 thin films grown on LaAlO3 substrates (SNO/LAO). The resistivity increases by eight orders of magnitude upon doping [19]. (C) Density of states of undoped and electron-doped SmNiO3. (D) The squared modulus of the unoccupied intermediated band wavefunctions (green isosurfaces) [dashed-circles in (D)] [38].
Similar to ion-intercalated nickelates, creating oxygen vacancies is an alternative chemical route to introduce carriers into nickelates via charge compensation. Since Ni3+ is chemically less stable than Ni2+, the synthesis of stoichiometric RENiO3 polycrystalline ceramics requires high temperatures and high oxygen pressures. Failure to meet the synthesis criteria (whether undoped compound or intentionally oxygen-deficient compounds) often results in cation and oxygen off-stoichiometry issues, manifested by substantial deviations and broadening in the metal-insulator transition temperature and its reproducibility [41–44].
Recently, with the development of the topotactic reduction technique, high-quality RENiO3 thin films with precise-controlled oxygen vacancy concentration could be produced [45, 46]. Studies have shown that the oxygen vacancies can induce novel forms of electronic symmetry breaking including unconventional superconductivity in the infinite-layer nickelates RENiO2 (where Ni is in a 1+ state [45]). Such precise control over the oxygen concentration provides another avenue to tune the physical properties of RENiO3-x in the small x limit.
Studies of oxygen-deficient films have shown phenomena similar to other electron-doped RENiO3, in particular the dramatic increase of the resistance similar to the colossal resistive switching achieved via ionic intercalation [46, 47]. Moreover, oxygen-deficient RENiO3 can be used as an ionic voltage-driven switch. By applying a bias voltage, the oxygen vacancies can be driven toward the electrode to realize a high resistance state. With a reversed bias voltage, the oxygen vacancies redistribute and are pushed away from the electrode, and the device returns to the low resistance state [46]. Numerous intermediate states can be achieved by controlling the strength of the electric field. Although the local oxygen defect concentration can be modified by the electric field, it has been shown that the oxygen vacancies do not aggregate into clusters segregating the undoped/doped domains [47].
Unlike ion intercalation, doping through oxygen vacancies more severely alters the local crystal structure. Depending on the density and distribution of the oxygen vacancies, the Ni local symmetry can be lowered to square pyramidal, square planar and tetrahedral, which leads to a dramatic change in the crystal field splitting (Figure 2A). DFT calculations on these Ni-O local electronic structures have shown a smaller contribution from unoccupied Ni-3d and O-2p 3d8L hybridized states. These states are transferred from the bottom of the conduction band to the top of the valence band. The unoccupied states with Ni2+ are also pushed up in energy, resulting in a 2–3 eV bandgap that characterizes the insulating nature of the doped nickelates [46, 48, 49]. Such a transfer of electronic states was also observed experimentally, where the low-energy density of states near the Fermi energy is continuously shifted to the high energy states in response to the doping changes [50].
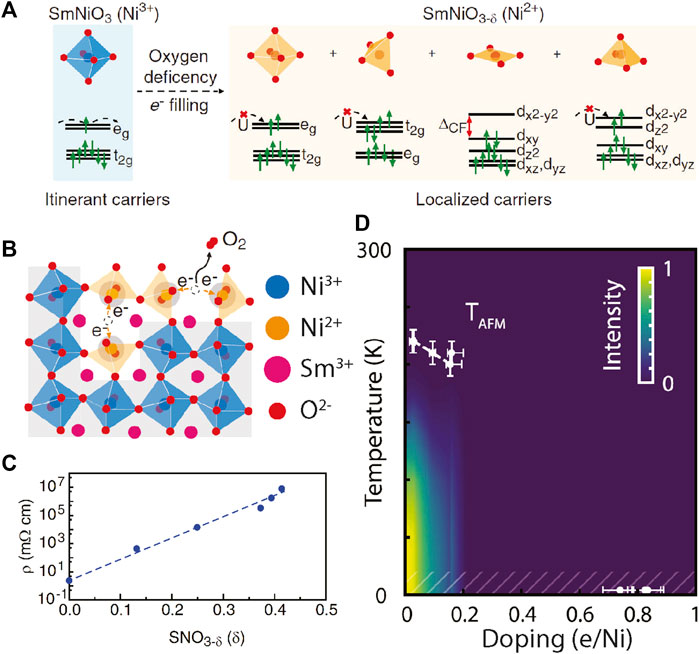
FIGURE 2. (A) Illustration of how oxygen vacancies modify the local crystal field splitting of Ni 3d orbitals, together with the doping effect, leading to opening of the bandgap and resistive switching [46]. (B) Oxygen vacancy formation changes the local symmetry from octahedral to lower-than-cubic. (C) Electrical resistivity at room temperature as a function of oxygen deficiency level in SNO3-x. The resistance can be tuned over eight orders of magnitude. (D) Temperature-doping plot of the magnetic phase diagram in SmNiO3−x. The magnitude of the antiferromagnetic order parameter is color coded in the background [47].
The introduction of oxygen vacancies has been shown to also modify the magnetic properties of RENiO3. The latter were recently explored in SmNiO3-x and NdNiO3-x [47]. Despite the fact that doping linearly suppresses the strength of the (1/4, 1/4, 1/4) antiferromagnetic state, the magnetic properties (correlation length, transition temperature, etc.) are remarkably robust to substantial levels of carrier doping up to a doping threshold of x∼0.1 where magnetic order collapses without an accompanying structural transition (Figure 2D).
There is also evidence of emergent magnetic order in oxygen-deficient nickelates. The parent compound of LaNiO3 stands out as the only member in the RENiO3 family that remains metallic and paramagnetic down to low temperature. The recent reports on the synthesis of the bulk LaNiO3 single crystals have shown an unexpected antiferromagnetic order below 157K with ordering wave vector consistent to (1/4, 1/4, 1/4) as in other RENiO3 [51]. However, it was inconclusive whether this antiferromagnetic order in LaNiO3 discovered by Ref. [51] is intrinsic or resulted from extrinsic oxygen defects, as other studies have shown that magnetic order (ferro- and antiferro-magnetic) could arise upon intentional introduction of the oxygen vacancies [52, 53].
Carrier doping can further be obtained by A-site substitution of the 3+ rare earth ions by other divalent (typically Sr2+, Ca2+) or tetravalent elements (Th4+, Ce4+). Divalent doping adds holes while tetravalent doping adds electrons into RE1-xAxNiO3, changing the formal valence of Ni to (3+x) and (3-x), respectively. Studies have shown that the metal-to-insulator transition temperature is rapidly suppressed upon cation substitution (x < 0.1) [54–58], despite the type of dopants.
The goal of cation doping is to separate the genuine electronic carrier doping effect from steric contribution arising from the change of the A-site ionic radius. In the seminal study by García-Muñoz Ref. [54], by accounting for the size changes of the dopants, they have found that both electron and hole doping suppress the insulating phases by cationic doping (Sr, Ca, Th, Ce) with asymmetric suppression rates for the metal-insulator transition temperature (TMI): hole doping is more effective than electron doping to suppress TMI with the rate:
Since both doping routines lead to a suppression of TMI, the doped carriers are more likely to create a new in-gap state rather than causing a rigid-band shift [54]. The origin of the electron-hole asymmetry is naturally attributed to the hybridization of Ni-O bands. Such a trend is in contrast with the tendency towards strong insulating state upon electron doping via ion intercalation or oxygen removal as described in the previous sections. A possible explanation is that the latter doping processes alter the material at a very local scale, drastically altering the electronic potential in the vicinity of the added (or missing) atom and reducing the local symmetry and potentially the bonding environment. Conversely, cation substitution largely preserves the coordination, leading to a less drastic alteration of the local environment. For carriers introduced in a high symmetry environment, the wavefunction can be more extended in space and thus lead to more delocalized, itinerant states, promoting metallic behavior. Charge compensation mechanism studies and local structure analysis should be carried out in future to better understand the doping processes. The magnetic properties of the cation doped RENiO3 are yet to be explored.
It is worth mentioning that there are also other methods of doping the RENiO3, such as electrostatic gating [59, 60], ionic liquid gating [61–63], and fluorine substitution [64], which are capable of changing the charge carrier density, resistance level, and transition temperature of RENiO3.
Carrier doping has historically been a powerful tuning parameter in the exploration of the rich physics of strongly correlated quantum material. We have summarized recent studies of carrier doping effects in the rare earth nickelates RENiO3 and the resulting unconventional phenomena, including giant resistive switching, the antidoping mechanism, the fast and reversible switching of the Ni valence and ligand electronic state, the doping evolution of the coupled electronic and magnetic ground state, and emergent quantum states (superconductivity). These phenomena would not be possible without convergent advances in highly controlled synthesis and doping protocols, and in characterization methods and theoretical modelling.
Doped nickelates also represent a promising platform for new functional devices owing to their high sensitivity to external perturbations. A wide range of proof-of-principle applications has been reported based on their novel electronic transport, magnetic, optical, catalytical, and energy storage/conversion properties. Based on these, major areas of application could be electronic/magnetic switching applications such as multistate switching memory devices for neuromorphic computing [28, 29, 34, 35, 63], optical and photonic modulation technologies [65], and high-density hydrogen storage [22].
At the same time, further studies are necessary to develop a deeper mechanistic understanding of the physics of doped nickelates and their practical applications across multiple scales. A major outstanding question is how the local atomic defects contribute to macroscopic transport properties. First principles calculations incorporating defects in large unit cells are necessary to understand how atomic-scale dopants influence the electronic band structure. At a higher scale, spatial cluster simulations can be helpful to understand the percolative nature of electronic conduction and its variable-range hopping nature. Despite limited studies on the magnetic properties in doped nickelates, more research efforts are needed to produce a unified picture of the magnetic properties and their nanoscale underpinnings. Moreover, a broader canvassing of the doping-temperature phase diagram could possibly unveil new collective states of matter, for example superconductivity at the far end of the electron doping axis (Ni d9 configuration). On the application front, there are many opportunities that can be harnessed by a deeper understanding of the properties of doped nickelates. As an example, various open questions remain to be answered to assess the applicability of doped nickelates for non-Von Neuman architecture computation such as dynamics of multi-state switching; energy landscapes as a function of electron doping and percolation transport physics in inhomogeneous doped films.
All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.
Work at MIT (JL and RC) was supported by the Air Force Office of Scientific Research Young Investigator Program under grant FA9550-19-1-0063. SR acknowledges AFOSR FA9550-19-1-0351 for support.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
We acknowledge Robert Green for many invaluable discussions.
1. Zunger A, Malyi OI. Understanding Doping of Quantum Materials. Chem Rev (2021) 121:3031–60. doi:10.1021/acs.chemrev.0c00608
2. Ramirez AP. Colossal Magnetoresistance. J Phys Condens Matter (1997) 9:8171–99. doi:10.1088/0953-8984/9/39/005
3. Keimer B, Kivelson SA, Norman MR, Uchida S, Zaanen J. From Quantum Matter to High-Temperature Superconductivity in Copper Oxides. Nature (2015) 518:179–86. doi:10.1038/nature14165
4. Janod E, Tranchant J, Corraze B, Querré M, Stoliar P, Rozenberg M, et al. Resistive Switching in Mott Insulators and Correlated Systems. Adv Funct Mater (2015) 25:6287–305. doi:10.1002/adfm.201500823
5. Dagotto E. Complexity in Strongly Correlated Electronic Systems. Science (2005) 309:257–62. doi:10.1126/science.1107559
6. Sleight AW. Bismuthates: BaBiO3 and Related Superconducting Phases. Physica C: Superconductivity its Appl (2015) 514:152–65. doi:10.1016/j.physc.2015.02.012
7. Catalano S, Gibert M, Fowlie J, Íñiguez J, Triscone J-M, Kreisel J. Rare-earth Nickelates RNiO3: Thin Films and Heterostructures. Rep Prog Phys (2018) 81:046501. doi:10.1088/1361-6633/aaa37a
8. Catalan G. Progress in Perovskite Nickelate Research. Phase Transitions (2008) 81:729–49. doi:10.1080/01411590801992463
9. Zaanen J, Sawatzky GA, Allen JW. Band Gaps and Electronic Structure of Transition-Metal Compounds. Phys Rev Lett (1985) 55:418–21. doi:10.1103/physrevlett.55.418
10. Bisogni V, Catalano S, Green RJ, Gibert M, Scherwitzl R, Huang Y, et al. Ground-state Oxygen Holes and the Metal-Insulator Transition in the Negative Charge-Transfer Rare-Earth Nickelates. Nat Commun (2016) 7:13017. doi:10.1038/ncomms13017
11. Johnston S, Mukherjee A, Elfimov I, Berciu M, Sawatzky GA. Charge Disproportionation without Charge Transfer in the Rare-Earth-Element Nickelates as a Possible Mechanism for the Metal-Insulator Transition. Phys Rev Lett (2014) 112:106404. doi:10.1103/physrevlett.112.106404
12. Medarde M, Fontaine A, García-Muñoz JL, Rodríguez-Carvajal J, de Santis M fnm, Sacchi M, et al. RNiO3 Perovskites (R=Pr,Nd): Nickel Valence and the Metal-Insulator Transition Investigated by x-ray-absorption Spectroscopy. Phys Rev B Condens Matter (1992) 46:14975–84. doi:10.1103/physrevb.46.14975
13. Scagnoli V, Staub U, Bodenthin Y, García-Fernández M, Mulders AM, Meijer GI, et al. Induced Noncollinear Magnetic Order of Nd3+ in NdNiO3 Observed by Resonant Soft X-ray Diffraction. Phys Rev B (2008) 77:115138. doi:10.1103/physrevb.77.115138
14. Frano A, Schierle E, Haverkort MW, Lu Y, Wu M, Blanco-Canosa S, et al. Orbital Control of Noncollinear Magnetic Order in Nickel Oxide Heterostructures. Phys Rev Lett (2013) 111:106804. doi:10.1103/physrevlett.111.106804
15. Hepting M, Green RJ, Zhong Z, Bluschke M, Suyolcu YE, Macke S, et al. Complex Magnetic Order in Nickelate Slabs. Nat Phys (2018) 14:1097–102. doi:10.1038/s41567-018-0218-5
16. Gaecía-Muñoz JL, Rodríguez-Carvajal J, Lacorre P. Sudden Appearance of an Unusual Spin Density Wave at the Metal-Insulator Transition in the Perovskites RNiO3 (R = Pr, Nd). Epl (1992) 20:241–7. doi:10.1209/0295-5075/20/3/009
17. Klein YM, Kozłowski M, Linden A, Lacorre P, Medarde M, Gawryluk DJ. RENiO3 Single Crystals (RE = Nd, Sm, Gd, Dy, Y, Ho, Er, Lu) Grown from Molten Salts under 2000 Bar of Oxygen Gas Pressure. Cryst Growth Des (2021) 21:4230–41. doi:10.1021/acs.cgd.1c00474
18. Middey S, Chakhalian J, Mahadevan P, Freeland JW, Millis AJ, Sarma DD. Physics of Ultrathin Films and Heterostructures of Rare-Earth Nickelates. Annu Rev Mater Res (2016) 46:305–34. doi:10.1146/annurev-matsci-070115-032057
19. Shi J, Zhou Y, Ramanathan S. Colossal Resistance Switching and Band gap Modulation in a Perovskite Nickelate by Electron Doping. Nat Commun (2014) 5:4860. doi:10.1038/ncomms5860
20. Sun Y, Kotiuga M, Lim D, Narayanan B, Cherukara M, Zhang Z, et al. Strongly Correlated Perovskite Lithium Ion Shuttles. Proc Natl Acad Sci USA (2018) 115:9672–7. doi:10.1073/pnas.1805029115
21. Zhang Z, Schwanz D, Narayanan B, Kotiuga M, Dura JA, Cherukara M, et al. Perovskite Nickelates as Electric-Field Sensors in Salt Water. Nature (2017) 553:68–72. doi:10.1038/nature25008
22. Zhou Y, Guan X, Zhou H, Ramadoss K, Adam S, Liu H, et al. Strongly Correlated Perovskite Fuel Cells. Nature (2016) 534:231–4. doi:10.1038/nature17653
23. Kreuer K-D. Proton Conductivity: Materials and Applications. Chem Mater (1996) 8:610–41. doi:10.1021/cm950192a
24. Sidik U, Hattori AN, Rakshit R, Ramanathan S, Tanaka H. Catalytic Hydrogen Doping of NdNiO3 Thin Films under Electric Fields. ACS Appl Mater Inter (2020) 12:54955–62. doi:10.1021/acsami.0c15724
25. Chen J, Mao W, Ge B, Wang J, Ke X, Wang V, et al. Revealing the Role of Lattice Distortions in the Hydrogen-Induced Metal-Insulator Transition of SmNiO3. Nat Commun (2019) 10:694–8. doi:10.1038/s41467-019-08613-3
26. Chen J. Self-limited Kinetics of Electron Doping in Correlated Oxides. Appl Phys Lett (2015) 107:031905. doi:10.1063/1.4927322
27. Zaluzhnyy IA. Proton Distribution Visualization in Perovskite Nickelate Devices Utilizing Nanofocused X Rays. Phys Rev Mater (2021) 5:095003. doi:10.1103/physrevmaterials.5.095003
28. Zuo F, Panda P, Kotiuga M, Li J, Kang M, Mazzoli C, et al. Habituation Based Synaptic Plasticity and Organismic Learning in a Quantum Perovskite. Nat Commun (2017) 8:240. doi:10.1038/s41467-017-00248-6
29. Shi J, Ha SD, Zhou Y, Schoofs F, Ramanathan S. A Correlated Nickelate Synaptic Transistor. Nat Commun (2013) 4:2676–9. doi:10.1038/ncomms3676
30. Oh C, Heo S, Jang HM, Son J. Correlated Memory Resistor in Epitaxial NdNiO3 Heterostructures with Asymmetrical Proton Concentration. Appl Phys Lett (2016) 108:122106. doi:10.1063/1.4944842
31. Ramadoss K. Proton-Doped Strongly Correlated Perovskite Nickelate Memory Devices. IEEE Electron Device Lett (2018) 39:1500–3. doi:10.1109/led.2018.2865776
32. Zhang HT, Zuo F, Li F, Chan H, Wu Q, Zhang Z, et al. Perovskite Nickelates as Bio-Electronic Interfaces. Nat Commun (2019) 10:1651–7. doi:10.1038/s41467-019-09660-6
33. Sun Y, Nguyen TNH, Anderson A, Cheng X, Gage TE, Lim J, et al. In Vivo Glutamate Sensing inside the Mouse Brain with Perovskite Nickelate-Nafion Heterostructures. ACS Appl Mater Inter (2020) 12:24564–74. doi:10.1021/acsami.0c02826
34. Zhang HT. Organismic materials for beyond von Neumann machines. Appl Phys Rev (2020) 7:011309. doi:10.1063/1.5113574
35. Zhang HT, Park TJ, Zaluzhnyy IA, Wang Q, Wadekar SN, Manna S, et al. Perovskite Neural Trees. Nat Commun (2020) 11:2245–9. doi:10.1038/s41467-020-16105-y
36. Catalano S, Gibert M, Fowlie J, Íñiguez J, Triscone JM, Kreisel J. Rare-earth Nickelates RNiO3: Thin Films and Heterostructures. Rep Prog Phys (2018) 81:046501. doi:10.1088/1361-6633/aaa37a
37. Torrance J, Lacorre P, Nazzal A, Ansaldo E, Niedermayer C. Systematic Study of Insulator-Metal Transitions in Perovskites RNiO3 (R=Pr,Nd,Sm,Eu) Due to Closing of Charge-Transfer gap. Phys Rev B (1992) 45:8209–12. doi:10.1103/physrevb.45.8209
38. Liu Q, Dalpian GM, Zunger A. Antidoping in Insulators and Semiconductors Having Intermediate Bands with Trapped Carriers. Phys Rev Lett (2019) 122:106403. doi:10.1103/physrevlett.122.106403
39. Kotiuga M, Rabe KM. High-density Electron Doping of SmNiO3 from First Principles. Phys Rev Mater (2019) 3:115002. doi:10.1103/physrevmaterials.3.115002
40. Malyi OI, Zunger A. Hole Antidoping of Oxides. Phys Rev B (2020) 101:235202. doi:10.1103/physrevb.101.235202
41. Preziosi D, Sander A, Barthélémy A, Bibes M. Reproducibility and Off-Stoichiometry Issues in Nickelate Thin Films Grown by Pulsed Laser Deposition. AIP Adv (2017) 7:015210. doi:10.1063/1.4975307
42. Breckenfeld E, Chen Z, Damodaran AR, Martin LW. Effects of Nonequilibrium Growth, Nonstoichiometry, and Film Orientation on the Metal-To-Insulator Transition in NdNiO3 Thin Films. ACS Appl Mater Inter (2014) 6:22436–44. doi:10.1021/am506436s
43. Nikulin IV, Novojilov MA, Kaul AR, Mudretsova SN, Kondrashov SV. Oxygen Nonstoichiometry of NdNiO3−δ and SmNiO3−δ. Mater Res Bull (2004) 39:775–91. doi:10.1016/j.materresbull.2004.02.005
44. Hauser AJ. Correlation between Stoichiometry, Strain, and Metal-Insulator Transitions of NdNiO3 Films. Appl Phys Lett (2015) 106:092104. doi:10.1063/1.4914002
45. Li D, Lee K, Wang BY, Osada M, Crossley S, Lee HR, et al. Superconductivity in an Infinite-Layer Nickelate. Nature (2019) 572:624–7. doi:10.1038/s41586-019-1496-5
46. Kotiuga M, Zhang Z, Li J, Rodolakis F, Zhou H, Sutarto R, et al. Carrier Localization in Perovskite Nickelates from Oxygen Vacancies. Proc Natl Acad Sci USA (2019) 116:21992–7. doi:10.1073/pnas.1910490116
47. Li J, Green RJ, Zhang Z, Sutarto R, Sadowski JT, Zhu Z, et al. Sudden Collapse of Magnetic Order in Oxygen-Deficient Nickelate Films. Phys Rev Lett (2021) 126:187602. doi:10.1103/physrevlett.126.187602
48. Iglesias L, Bibes M, Varignon J. First-principles Study of Electron and Hole Doping Effects in Perovskite Nickelates. Phys Rev B (2021) 104:035123. doi:10.1103/physrevb.104.035123
49. Espinosa-García WF, Dalpian GM. Influence of Defects on Antidoping Behavior in SmNiO3. Phys Rev B (2021) 104:205106. doi:10.1103/PhysRevB.104.205106
50. Jaramillo R, Ha SD, Silevitch DM, Ramanathan S. Origins of Bad-Metal Conductivity and the Insulator-Metal Transition in the Rare-Earth Nickelates. Nat Phys (2014) 10:304–7. doi:10.1038/nphys2907
51. Guo H, Li ZW, Zhao L, Hu Z, Chang CF, Kuo CY, et al. Antiferromagnetic Correlations in the Metallic Strongly Correlated Transition Metal Oxide LaNiO3. Nat Commun (2018) 9:43. doi:10.1038/s41467-017-02524-x
52. Wang BX. Antiferromagnetic Defect Structure in LaNiO3-δ Single Crystals. Phys Rev Mater (2018) 2:064404. doi:10.1103/physrevmaterials.2.064404
53. Sânchez RD. Metal-insulator Transition in Oxygen-Deficient LaNiO3-x. Perovskites. Phys Rev B-condensed Matter (1996) 54:16574–8. doi:10.1103/physrevb.54.16574
54. García-Muñoz JL, Suaaidi M, Martínez-Lope MJ, Alonso JA. Influence of Carrier Injection on the Metal-Insulator Transition in Electron- and Hole-Doped R1-xAxNiO3 Perovskites. Phys Rev B (1995) 52:13563–9. doi:10.1103/physrevb.52.13563
55. Xiang PH. Room Temperature Mott Metal-Insulator Transition and its Systematic Control in Sm1-xCaxNiO3 Thin Films. Appl Phys Lett (2010) 97:032114. doi:10.1063/1.3467199
56. Wang L, Chang L, Yin X, Rusydi A, You L, Zhou Y, et al. Localization-driven Metal-Insulator Transition in Epitaxial Hole-Doped Nd1-XSrXNiO3 Ultrathin Films. J Phys Condens Matter (2017) 29:025002–6. doi:10.1088/0953-8984/29/2/025002
57. Wang BX. Synthesis and Characterization of Bulk Nd1-xSrxNiO2 and Nd1-xSrxNiO3. Phys Rev Mater (2020) 4:084409. doi:10.1103/physrevmaterials.4.084409
58. Yang H, Wen Z, Cui Y, Chen Y, Zhao Y. The Preparation, Structure, and Metal-Insulator Transition in Bulk Nd1−xCaxNiO3 (X = 0 ∼ 0.3). J Supercond Nov Magn (2021) 34:2339–47. doi:10.1007/s10948-021-05929-4
59. Ha SD, Vetter U, Shi J, Ramanathan S. Electrostatic Gating of Metallic and Insulating Phases in SmNiO3 Ultrathin Films. Appl Phys Lett (2013) 102:183102. doi:10.1063/1.4804142
60. Son J. Probing the Metal-Insulator Transition of NdNiO3 by Electrostatic Doping. Appl Phys Lett (2011) 99:192107. doi:10.1063/1.3659310
61. Asanuma S. Tuning of the Metal-Insulator Transition in Electrolyte-Gated NdNiO3 Thin Films. Appl Phys Lett (2010) 97:142110. doi:10.1063/1.3496458
62. Scherwitzl R, Zubko P, Lezama IG, Ono S, Morpurgo AF, Catalan G, et al. Electric-field Control of the Metal-Insulator Transition in Ultrathin NdNiO3 Films. Adv Mater (2010) 22:5517–20. doi:10.1002/adma.201003241
63. Zhang HT. Beyond Electrostatic Modification: Design and Discovery of Functional Oxide Phases via Ionic-Electronic Doping. Adv Phys X (2019) 4:1523686. doi:10.1080/23746149.2018.1523686
64. Onozuka T, Chikamatsu A, Katayama T, Hirose Y, Harayama I, Sekiba D, et al. Reversible Changes in Resistance of Perovskite Nickelate NdNiO3 Thin Films Induced by Fluorine Substitution. ACS Appl Mater Inter (2017) 9:10882–7. doi:10.1021/acsami.7b00855
Keywords: rare earth nickelate, carrier doping, resistive switching (RS), antidoping, hydrogenation, oxygen vancany, ion intercalation/de-intercalation
Citation: Li J, Ramanathan S and Comin R (2022) Carrier Doping Physics of Rare Earth Perovskite Nickelates RENiO3. Front. Phys. 10:834882. doi: 10.3389/fphy.2022.834882
Received: 13 December 2021; Accepted: 11 January 2022;
Published: 11 February 2022.
Edited by:
Matthias Hepting, Max Planck Institute for Solid State Research, GermanyReviewed by:
Chun-Gang Duan, East China Normal University, ChinaCopyright © 2022 Li, Ramanathan and Comin. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Jiarui Li, amlhcnVpbGlAbWl0LmVkdQ==; Riccardo Comin, cmNvbWluQG1pdC5lZHU=
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.