Efficient Solution of Emissivity for the Area Blackbody Based on the Multiple Reflection Method

At present, the Monte Carlo method is the only method to evaluate the area blackbody emissivity, so it needs to be compared and verified with other calculation methods. In particular, the efficiency of Monte Carlo is low when the micro-cavity structure of the area blackbody is more complex for higher emissivity. An efficient algorithm for calculating emissivity of the area blackbody based on the multiple reflection method was put forward in this article. A multiple reflected light path that radiated into the inner micro-cavity structure of the area blackbody was simulated. The ratio of the outgoing light intensity to the incident light intensity was obtained by setting a threshold of the outgoing light intensity, and then the area blackbody emissivity was calculated. The simulation results showed that, compared with the Monte Carlo method, the results of the emissivity calculation were similar, and calculation efficiency was increased more than 100 times under the same micro-cavity structure. A practical area blackbody was made based on the simulation results from the proposed multiple reflection method, and the emissivity measurement experiments were carried out and compared to the cavity blackbody at the same temperature. The results showed that the emissivity was near one and stable for the NIR (Near Infrared) spectrum range when the temperature was higher than 280°C. Thus, the feasibility of the multiple reflection method for calculating the area blackbody emissivity was verified. The multiple reflection method proposed in this article provided one more design path for developing area blackbodies with more complex micro-cavity structures.

1 Introduction

In recent years, with the rapid development of infrared radiation metrology, spectral detection technology, and thermal imaging technology, it is significant to develop the blackbody radiation source for calibration [1–4]. Cavity blackbody has been maturely developed and applied to calibrate a small infrared instrument, but it cannot meet the calibration requirements for a large aperture area source infrared detection instrument; so, the demand for the area blackbody is becoming stronger. But, the emissivity calculation method of the cavity blackbody does not apply to area blackbodies; therefore, the solution of emissivity for the area blackbody is very important [5].

In the development of the blackbody, it is important to evaluate and measure its radiation capability. Buckley proposed the integral equation method in the 1930s and then gradually improved it by Sparrow and Bedford et al [6]. The integral equation method assumes that the reflection occurring on the inner wall of the blackbody cavity is ideal diffuse reflection and then establishes the emissivity integral model of each to solve in parallel. In the case that the reflection of the cavity surface is regarded as an ideal diffuse reflection, the integral equation method can be used in the theory to solve the emissivity of the blackbody cavity with any shape. However, it is difficult to meet the ideal diffuse reflection conditions in reality, especially in the area blackbody evaluation, this method has a large error with the actual situation, and the calculation process is complex [7].

The Monte Carlo method is commonly used to calculate the emissivity of the blackbody cavity. Prokhorov A V used the Monte Carlo method to analyze the radiation on the surface of the concentric circular trapezoidal groove and the emission and reflection characteristics of normal and directional angles [8]. C Monte proposed the evaluation standard of cavity emissivity of vacuum terahertz blackbody based on the Monte Carlo method [9]. The heat transfer simulation of a blackbody at low temperature was proposed by Prokhorov A V, but it was also limited to the cavity [10]. Pahl R J proposed a new fast convergence Monte Carlo method but was also used for the blackbody cavity structure [11]. Yikun Zhao calculated and compared the emissivity of two blackbody cavities by the Monte Carlo method and pointed out that the emissivity of the V-shaped cavity was higher [12]. Futao Sun used the Monte Carlo method to calculate the effective emissivity of a cylindrical isothermal cavity, analyzed some factors affecting the effective emissivity of the cavity, and discussed the influence of the spectral emissivity of the cavity wall material on the effective emissivity of the cavity, providing a theoretical basis for the design and calculation of blackbody cavities [13]. JiuLi Shen used the Monte Carlo method to calculate the effective emissivity of the conical blackbody cavity. When the distance from the detector to the cavity orifice is 15 times the cavity radius, the effective emissivity of the conical blackbody cavity is larger [14]. Tingting Xing established a cylindrical blackbody cavity model based on the Monte Carlo method and calculated the effective emissivity of the blackbody cavity model. The results show that when the length–diameter ratio is large, the aperture ratio is small, and the emissivity of the cavity material is large, the effective emissivity of the blackbody cavity is large [15]. Shimizu Y designed a high-precision 100 mm × 80 mm polydimethylsiloxane area blackbody in the room temperature range, and the emissivity is not less than 0.998 [16]. Olschewski F designed a stratospheric balloon-borne, in which the blackbody emissivity of the micro-cone low temperature (−40 to 20°C) surface with a size of 5 mm × 5 mm and a height of 9 mm reaches 0.99 [17]. Bae JiYong designed a small area blackbody emissivity of 0.99 for infrared remote sensing calibration [18]. Chang Anbang’s master thesis used the Monte Carlo method to evaluate the emissivity of the V-groove area blackbody, but it also needs other theories to verify it [19]. Yuan S, Naveh D, Watanabe K, Taniguchi T, and Xia F reconstructed unknown spectra from their corresponding photo response vectors by the wavelength and bias-dependent responsivity matrix from the spectra of a tunable blackbody source [20].

In this article, the multiple reflection method integrates the secondary reflection method of Gouffe and the micro-surface element method of DeVos. The basic theory of multiple reflections is deduced and simulated for comparison to the Monte Carlo method. An area blackbody is made according to theoretical calculation of the multiple reflection method, and emissivity is measured by a cavity blackbody under the same temperature to verify its applicability.

2 Multiple Reflection Theory

The multiple reflection method divides the inner wall of the cavity into infinite micro-faces. The directional radiation intensity of each micro-face is composed of the directional radiation intensity of the micro-face itself and the directional radiation intensity reflected by other micro-faces to the micro-face.

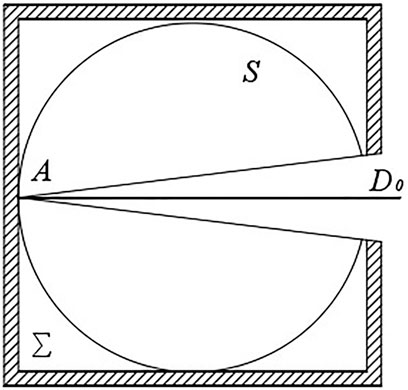
As shown in Figure 1, it is assumed that a beam of light vertically enters D₀ at the opening of the blackbody cavity, and the residual light absorbed by the bottom micro-plane element A will reflect the inner surface of the cavity, and a part of it will escape from D₀ at the opening. Therefore, it can be considered that the ratio of the product of the inner surface S of the spherical cavity and the D₀ area at the opening to the reflectivity ρ is equal to the ratio of the total beam energy to the energy of the escaped beam.

FIGURE 1

FIGURE 1. Circular blackbody cavity diagram.

When only one reflection is considered, the absorption rate of the blackbody cavity α₁ is calculated as:

$\begin{array}{c}{\alpha }_1=1-\rho \frac{D_0}{\text{π}{l}^2}\end{array},(1)$

where ρ represents the reflectivity of the inner wall of the cavity in the formula, D₀ represents the area at the opening and l represents the bottom micro-plane element A radius.

However, since there will not be only one reflection in practice, there will still be residual energy continuing to reflect in the inner wall of the cavity. The energy e₁ is left in the cavity after the first reflection for the next reflection, and the same can be said for the energy e₂ that escapes from the opening after a secondary reflection:

$\begin{array}{c}{e}_1=\rho \left(1-\frac{D_0}{\text{π}{l}^2}\right)\end{array};(2)$

$\begin{array}{c}{e}_2={\rho }^2\left(1-\frac{D_0}{\text{π}{l}^2}\right)\frac{D_0}{\mathrm{\Sigma }}\end{array},(3)$

where ∑ represents the cavity inner wall surface area.

The energy of the beam that finally escapes from the opening e consists of two parts: the energy carried by the beam that escapes directly from a single reflection and the energy that escapes from the opening after multiple reflections:

$e=\rho \frac{D_0}{\text{π}{l}^2}+{\rho }^2\left(1-\frac{D_0}{\text{π}{l}^2}\right)\frac{D_0}{\mathrm{\Sigma }}[1+\rho \left(1-\frac{D_0}{\mathrm{\Sigma }}\right)+{\rho }^2{\left(1-\frac{D_0}{\mathrm{\Sigma }}\right)}^2+\dots ].=\rho \frac{D_0}{\text{π}{l}^2}+\frac{{\rho }^2\left(1-\frac{D_0}{\text{π}{l}^2}\right)\frac{D_0}{\mathrm{\Sigma }}}{1-\rho \left(1-\frac{D_0}{\mathrm{\Sigma }}\right)}.(4)$

When the total incident energy is set to 1, the reflectivity ρ₀ is the total energy escaping from the opening e. Thus, the emissivity of the black cavity ε can be obtained by subtracting the reflectivity ρ₀ by the total incident energy:

$\begin{array}{c}\epsilon =1-{\rho }_{\text{0}}=1-e=1-\frac{{\rho }^2\left(1-\frac{D_0}{\pi l^2}\right)\frac{D_0}{\mathrm{\Sigma }}}{1-\rho \left(1-\frac{D_0}{\mathrm{\Sigma }}\right)}\end{array}-\rho \frac{D_0}{\pi l^2}.(5)$

The multiple reflection method can simulate a more realistic optical path motion trajectory, and then a better calculation of radiant energy can be obtained. It is more concise and clear than the calculation process of the integral equation and avoids the error caused by randomness. The multiple reflection method can be used to verify the calculation results of the Monte Carlo method.

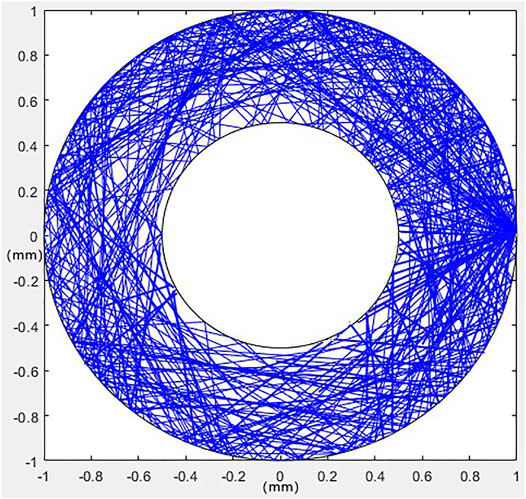
A planar concentric cavity is used for simulating the multiple reflection method. The emissivity of the surface is specified as 0.9, and the radii of the two concentric circles are 1 and 0.5 mm, respectively. When the light intensity is less than 10⁻¹⁰ (i.e., 10 reflections on the surface), it is considered to be completely absorbed. The incident position is located on the inner wall on the right side of the big circle. The simulation results are shown in Figure 2.

FIGURE 2

FIGURE 2. Planar concentric cavity simulation with 1,000 rays.

3 Simulation

In the design of the area blackbody, surfaces with concentric V-shaped slots are often used because they have a higher effective emissivity than other slotted (e.g., rectangular-slotted) surfaces [21]. Emissivity tends to be uniform regardless of whether the material itself is diffuse or specular reflecting. This type of a radiating surface was usually used and evaluated by the Monte Carlo method.

3.1 V-Groove Model Construction

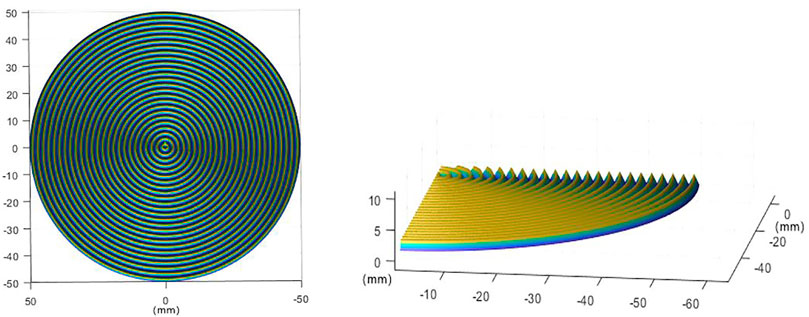
To compare with calculation results of the Monte Carlo method, the same circular V-groove area blackbody model with a diameter of 50 mm is constructed in this article according to Ref. [19], as shown in Figure 3.

FIGURE 3

FIGURE 3. V-slot model drawing.

The parameters of the V-groove model are shown in Table 1:

TABLE 1

TABLE 1. V-groove model parameters.

For the multiple reflection simulation, the amount of light is input, and the light enters the V-groove. The intensity of the light gradually decays through multiple reflections (as shown in Figure 4). The emissivity of the surface coating is 0.93. When the intensity of the light is less than 10⁻⁵ (i.e., after five reflections at the inner wall) [22], it is considered to be completely absorbed, and the light with less than five times reflections is emitted. Finally, the emissivity is calculated according to Eq. 5.

FIGURE 4

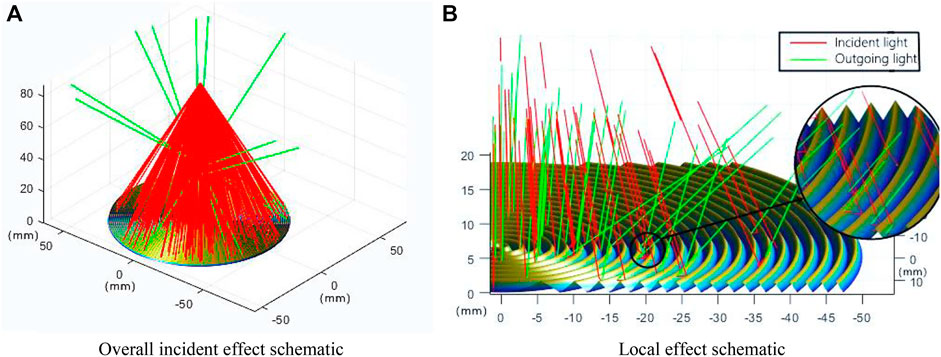
FIGURE 4. Light reflection path inside the V-groove simulated by the multiple reflection method (point light resource height is 20 cm). (A) Overall incident effect schematic and (B) local effect schematic.

3.2 The Amount of Incident Rays

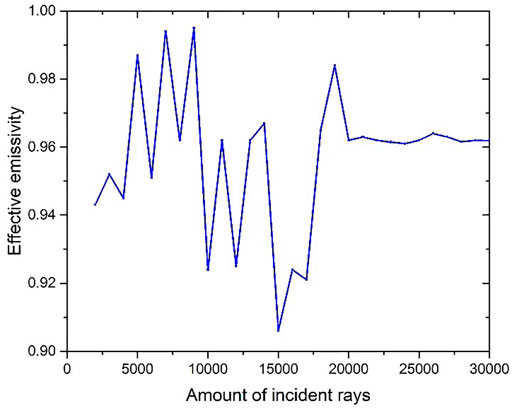
The number of incident rays is an important factor in the emissivity of an area blackbody. It is important to select several incident rays that tend to stabilize the emissivity for the simulation to avoid the chance of sample size problems affecting the emissivity calculation. Repeatedly increasing the number of incident rays in simulation, the 13th (middle) V-groove was selected for simulation. The emissivity was calculated according to Eq. 5, and the results are shown in Figure 5.

FIGURE 5

FIGURE 5. Emissivity stability varies with the amount of incident rays.

As can be seen from Figure 5, when the number of incident rays is less, the calculated emissivity fluctuates widely and cannot avoid the influence of chance on the emissivity calculation due to the small number of incident rays. However, when the number of incident rays exceeds 20,000, the emissivity calculation results tend to be smooth. So, the number of incident rays in the emissivity simulation experiment is chosen to be 20,000.

3.3 Emissivity Simulation

This simulation uses the established V-groove area blackbody model to simulate the local emissivity in the radius direction of the bottom surface of this blackbody at an incident of 20,000 rays. The model has an overall radius of 50 mm; each V-groove is 2-mm wide and is divided into areas of 10 mm length along the radius (i.e., five adjacent V-grooves are divided into one area, making a total of five areas), and the local emissivity in each area is simulated by varying the angle of incidence of the incident light. A total of five simulations were carried out for each of these areas, and the results of the simulated localized emissivity were matched to the five V-grooves in the area. Figure 6A shows the simulation process for the 20–30 mm area:

FIGURE 6

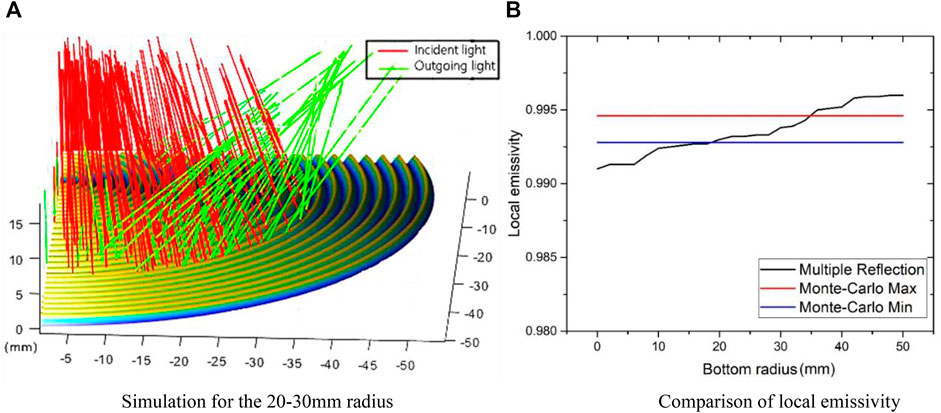
FIGURE 6. Simulation results obtained by the multiple reflection method with the bottom radius. (A) Simulation for 20–30 mm radius and (B) comparison of local emissivity.

As shown in Figure 6A, the red light is the incident light, and the green light is the reflected light passing through the area blackbody. After the light has been reflected by the V-groove area blackbody, the vast majority of the light has been absorbed (i.e., the light intensity is less than 0.1% of the initial intensity) and only some of the light can be returned by reflection. But, the reflected intensity of the high emissivity coating is also substantially attenuated, and thus the emissivity of the area blackbody is improved.

According to the aforementioned steps, the five regions were simulated five times according to the order of the radius length from small to large, so that the local emissivity value of each V-shaped groove can be obtained.

The emissivity calculated by the multiple reflection method has been obtained through several simulations. Then, it is compared with the emissivity calculated using the Monte Carlo method (2,000,000 incident lines). The reliability of the method is verified.

The maximum and minimum local effective emissivity values calculated using the Monte Carlo method are 0.9946 and 0.9928, respectively. The minimum local effective emissivity is higher than 0.99. The simulation results shown in Figure 6B are obtained by using the two methods[19].

As can be seen from Figure 6B, the local emissivity calculated by using the multiple reflection method fluctuates in the range from 0.9928–0.9946 in the 15–35 mm area. The local emissivity of the edge area fluctuates outside the range, but there is no large gap. The overall trend shows a positive correlation. Therefore, the calculation results obtained by the two methods are close.

4 Area Blackbody Performance Experiment

4.1 Experimental Environment

In this article, an experiment was carried out to verify the feasibility of the multiple reflection method. The experimental conditions are shown in Table 2:

TABLE 2

TABLE 2. Experimental conditions.

The local emissivity of the area blackbody is first measured using a spectrometer and other equipment. Then, a blackbody model is created based on the dimensions of the experimental area blackbody, and the theoretical emissivity is calculated using the multiple reflection method.

4.2 Emissivity Measurement and Calculation

Due to the complexity of the area blackbody and the limitations of infrared radiation measurement accuracy, no equipment can be used for the direct measurement of the area blackbody emissivity. So, a comparative experimental method is used to measure the area blackbody emissivity. The cavity blackbody is used as the standard because the effective cavity blackbody emissivity has been relatively well. The area blackbody emissivity is obtained by the ratio of radiation intensity measured using the spectrometer at the same temperature.

The Ocean Optics NIRQuest512 micro-spectrometer and thermocouples are used for this experiment, and the experimental scenario is shown in Figure 7.

FIGURE 7

FIGURE 7. Experimental scenario (measured cavity blackbody and area blackbody radiation intensity with wavelength at the same temperature).

First, the standard cavity blackbody and the area blackbody to be measured were fixed in parallel and adjusted to the same temperature. The thermocouple is fixed on the surface of the area blackbody to monitor the temperature. The radiation intensities of the cavity blackbody and the area blackbody are measured using the spectrometer at the same distance. At 420°C, the cavity blackbody and the area blackbody at the radius of 30 mm are tested. The data are collated as shown in Figure 8:

FIGURE 8

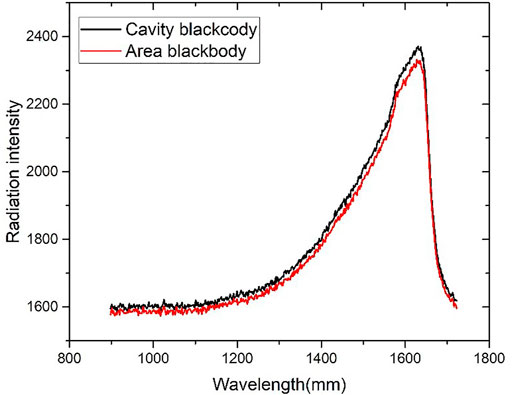
FIGURE 8. Experiment results at 420°C (cavity blackbody and area blackbody radiation intensity with wavelength).

Since the emissivity of the cavity blackbody is close to 1, the measured radiation intensity is divided by the radiation intensity of the cavity blackbody, and the average value is the local emissivity of the area blackbody at that position. Keep the temperature constant, and change the position of the fiber by adjusting the three-dimensional optical platform. Repeat the aforementioned steps to measure the emissivity of different positions of the area blackbody.

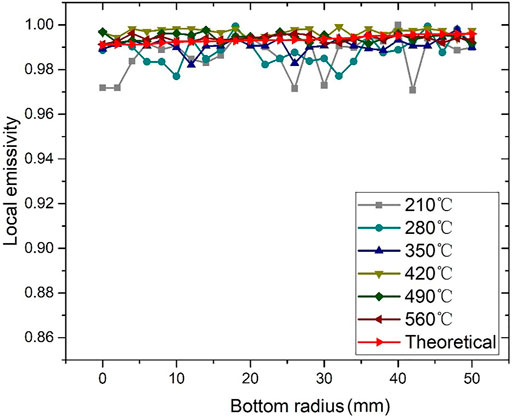
Afterward, the temperature was changed, and the aforementioned steps were repeated to measure the emissivity at different temperatures and different radius positions. A total of six different temperatures were chosen for this experiment, namely 210, 280, 350, 420, 490, and 560°C. The emissivity at each temperature and position was collated to give the following Figure 9.

FIGURE 9

FIGURE 9. Comparison of theoretical and measured emissivity.

The dimensions of the area blackbody used for this emissivity measurement experiment are as follows:

The area blackbody model was constructed from Table 3. The multiple reflection method used in Section 3.3 is applied to the simulation model of the area blackbody. The model is divided into different areas in order of radius from small to large. Then, the local emissivity of different positions on the area blackbody model is obtained by the simulation calculation for each area. The results of the simulation are shown in Figure 9.

TABLE 3

TABLE 3. Dimensions of the area blackbody.

4.3 Discussion of Experimental Results

The measured emissivity was obtained by comparison with the cavity blackbody at different temperatures, and the theoretical emissivity was then calculated based on the multiple reflection method. The theoretical emissivity is around 0.993, with maximum fluctuations not exceeding 0.003. The average of the theoretical and measured emissivity is collated as shown in Figure 9:

As can be seen from Figure 9, the radiation intensity on the surface of the blackbody is relatively uniform, with fewer fluctuations, and is closer to the theoretical emissivity. This leads to the conclusion that the theoretical values obtained using the emissivity calculation method based on the multiple reflection method coincide with the measured values, which proves the feasibility of the method.

5 Conclusion

The multiple reflection method is proposed to calculate the area blackbody emissivity in this article. This method integrates the secondary reflection method of Gouffe and the micro-surface element method of DeVos. The emissivity calculated by the multiple reflection method is similar to that calculated by the Monte Carlo method, and the two algorithms are verified against each other. However, the efficiency of the multiple reflection method is greatly improved. The measured emissivity results in the experiment are equivalent to the theoretical results, which proves the feasibility of the multiple reflection method. This efficient method of calculating the area blackbody emissivity provides a theoretical basis for the area blackbody design of higher emissivity.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author Contributions

JX: conceptualization, resources, validation, supervision, and funding acquisition; DL: writing—original draft, software, formal analysis, data curation, and experiment; SC: methodology, investigation, writing—reviewing and editing, and project administration.

Funding

This work was supported by the National Natural Science Foundation of China (No. 61975028).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Liu X, Qiao S, Ma Y. Highly Sensitive Methane Detection Based on Light-Induced Thermoelastic Spectroscopy with a 2.33 Μm Diode Laser and Adaptive Savitzky-Golay Filtering. Opt Express (2022) 30(2):1304–13. doi:10.1364/OE.446294

CrossRef Full Text | Google Scholar

2. Ma Y, Hu Y, Qiao S, Lang Z, Liu X, He Y, et al. Quartz Tuning forks Resonance Frequency Matching for Laser Spectroscopy Sensing. Photoacoustics (2022) 25:100329. doi:10.1016/j.pacs.2022.100329

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Liu XN, Ma YF. Sensitive Carbon Monoxide Detection Based on Light-Induced Thermoelastic Spectroscopy with a Fiber-Coupled Multipass Cell. Chin Opt Lett (2022) 20:031201. doi:10.3788/COL202220.031201

CrossRef Full Text | Google Scholar

4. Ma Y, Hong Y, Qiao S, Lang Z, xiaonan L. H-shaped Acoustic Micro-resonator Based Quartz-Enhanced Photoacoustic Spectroscopy. Opt Lett (2022). doi:10.1364/OL.449822

CrossRef Full Text | Google Scholar

5. Wijethunge D, Zhang L, Tang C, Du A. Tuning Band Alignment and Optical Properties of 2D van der Waals Heterostructure via Ferroelectric Polarization Switching. Front Phys (2020) 15(6):7. doi:10.1007/s11467-020-0987-z

CrossRef Full Text | Google Scholar

6. Sparrow EM, Jonsson VK. Radiant Emission Characteristics of Diffuse Conical Cavities. J Opt Soc Am (1963) 53(7):816–8. doi:10.1364/JOSA.53.000816

CrossRef Full Text | Google Scholar

7. Cai LL, Tian HX, Wu F, Dong J. Calculate on Effective Emissivity of High-Temperature Blackbody Cavity. Acta Metrologica Sinica (2016). doi:10.3969/j.issn.1000-1158.2016.06.11

CrossRef Full Text | Google Scholar

8. Prokhorov AV, Hanssen LM, Mekhontsev SN, et al. Radiation Properties of IR Calibrators with V-Grooved Surfaces. Proc SPIE - Int Soc Opt Eng (2006) 6205:620505. doi:10.1117/12.667557

CrossRef Full Text | Google Scholar

9. Monte C, Gutschwager B, Adibekyan A, Hollandt J. A Terahertz Blackbody Radiation Standard Based on Emissivity Measurements and a Monte-Carlo Simulation. J Infrared Milli Terahz Waves (2014) 35(8):649–58. doi:10.1007/s10762-014-0056-1

CrossRef Full Text | Google Scholar

10. Prokhorov AV, Martin JE. Monte Carlo Simulation of the Radiative Heat Transfer from a Blackbody to a Cryogenic Radiometer. Proc SPIE - Int Soc Opt Eng (1996) 160–8. doi:10.1117/12.257153

CrossRef Full Text | Google Scholar

11. Pahl RJ, Shannon MA. Analysis of Monte Carlo Methods Applied to Blackbody and Lower Emissivity Cavities. Appl Opt (2002) 41(4):691–9. doi:10.1364/AO.41.000691

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Zhao Y, Wang J, Feng G, Cao B. Comparative Study on Radiation Properties of Blackbody Cavity Model Based on Monte Carlo Method. Int J Thermophys (2020) 41(6). doi:10.1007/s10765-020-02648-1

CrossRef Full Text | Google Scholar

13. Sun FT. Calculation of the Effective Emissivities of Blackbody Cavity by the Monte-Carlo Method. J Astronautic Metrology Meas (2010) 30(2). doi:10.3969/j.issn.1000-7202.2010.02.007

CrossRef Full Text | Google Scholar

14. Shen JL, Xing TT, Fei WU. Research on the Effective Emissivity of Conical Blackbody Cavity Based on Monte-Carlo Method. Acta Metrologica Sinica (2018) 39(3). doi:10.3969/j.issn.1000-1158.2018.03.14

CrossRef Full Text | Google Scholar

15. Xing TT, Shen JL, Cai LL. Research on Effective Emissivity of Blackbody Cavity High Temperature Sensor Based on Monte-Carlo Method. Transducer Microsystem Tech (2017) 36(6), 7–9. doi:10.13873/j.1000-9787(2017)06-0007-03

CrossRef Full Text | Google Scholar

16. Shimizu Y, Koshikawa H, Imbe M, Yamaki T, Amemiya K. Large-area Perfect Blackbody Sheets Having Aperiodic Array of Surface Micro-cavities for High-Precision thermal Imager Calibration. Opt Express (2020) 28(15):22606. doi:10.1364/OE.397136

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Olschewski F, Monte C, Adibekyan A, Reiniger M, Gutschwager B, Hollandt J, et al. A Large-Area Blackbody for In-Flight Calibration of an Infrared Interferometer Deployed on Board a Long-Duration Balloon for Stratospheric Research. Atmos Meas Tech (2018) 11(8):4757–62. doi:10.5194/amt-2017-41710.5194/amt-11-4757-2018

CrossRef Full Text | Google Scholar

18. Bae JY, Choi W, Hong S-J, Kim S, Kim E, Lee C-H, et al. Design, Fabrication, and Performance Evaluation of Portable and Large-Area Blackbody System. Sensors (2020) 20(20):5836. doi:10.3390/s20205836

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Chang'anbang . Design, Development, and Testing of Surface Blackbody Radiation Source. Harbin: Harbin University of Technology (2019). doi:10.27061/d.cnki.ghgdu.2019.002260

CrossRef Full Text | Google Scholar

20. Yuan S, Naveh D, Watanabe K, Taniguchi T, Xia F. A Wavelength-Scale Black Phosphorus Spectrometer. Nat Photon (2021) 15:601–7. doi:10.1038/s41566-021-00787-x

CrossRef Full Text | Google Scholar

21. Mekhontsev SN, Sapritsky VI, Prokhorov AV, Khromchenko VB, Samoilov ML. Modeling, Design, and Characterization of Medium-Background Blackbodies for Full-Aperture Calibration of Spaceborne Infrared Systems and Imagers. Beijing: International Society for Optics and Photonics (1998). doi:10.1117/12.318101

CrossRef Full Text | Google Scholar

22. Fang Qian-qian 方., Fang Wei 方., Wang Kai 王. Calculation of Effective Emissivity of Blackbody Cavities by Monte-Carlo Method. 中国光学 (2012) 5(2):167–73. doi:10.3788/co.20120502.0167

CrossRef Full Text | Google Scholar