Periodic Flow of Non-Newtonian Fluid Over a Uniformly Heated Block With Thermal Plates: A Hybrid Mesh-Based Study

In this work, we analyze the characteristics of periodic flows in non-isothermal viscous fluid over a heated block in the presence of thermal plates at Reynolds number $\left(Re=100\right)$. The unsteady, incompressible Navier–Stokes (NS) equations with suitable initial and boundary data in 2D are executed by the finite element technique using a highly refined hybrid mesh. The temporal discretization is performed by an implicit stable backward differencing in time and a stable choice of finite elements from the finite element library for spatial discretization. The discrete nonlinear system arising from this discretization is linearized by Newton’s method and then solved through a direct linear solver PARDISO. For this forced convective study, the range of dimensionless parameters, namely, the Prandtl number $\left(Pr\right)$ and power law index $\left(n\right)$, are varied from 1 to 10 and 0.6 to 1.4 with a low Grashof number varying as $\left(1\le Gr\le 10\right)$ to produce a forced convection regime, respectively. For the authentication, we have compared our results with the literature at a similar configuration. After simulation, the results accomplished in the velocity profile, pressure, isotherm contours, drag and lift coefficients (trajectory motion), average Nusselt number $\left(N{u}_{avg}\right)$, etc. are considered. For convergence of solution at low shear rate $\left(n<1\right)$, crosswind stabilization (CWS) function has been incorporated. It is observed that $N{u}_{avg}$ becomes oscillatory for the shear-thinning case $\left(n<1\right)$, while for the shear-thickening cases $\left(n>1\right)$, it converges to a single value. Furthermore, the drag $\left(C_D\right)$ and lift $\left(C_L\right)$ coefficients are more pronounced for shear-thinning cases $\left(n<1\right)$ as compared with shear-thickening cases $\left(n>1\right).$

Introduction

Thermal flow over a stationary heated cylinder does not have many physical applications such as thermal processing of electronic cooling, fibrous suspensions, and others, moreover, use in a specific region of heat transfer for space economy. For more appropriate settings of visco-thermal flows, most excessive mixtures of fluid flow (emulsions, suspensions of paper pulps, foams, etc.) and most expensive systems of molecular polymers (blends, melts, etc.) have revealed shear-thickening or shear-shinning characteristics in the literature for a decade. In general, the geometrical configuration is categorized for the heated cylinder with thermal plates flowing toward the upstream direction. Yang et al. [1] analyzed the characteristics of thermal flow over the heated rectangular cylinder by the implementation of an arbitrary Lagrangian–Eulerian kinematic (ALEK) descriptive technique. Also, the effects of periodic flow with time state and average Nusselt number are presented. The influence of fluid flow in a heated pipe filled with nanomaterial is considered by Kamyar et al. [2]. Valipour et al. [3] depicted the influence of flow pattern and energy exchange over the square block by capitalizing of the finite volume scheme (FVS). Mostafa et al. [4] examined the flow visualization of thermal flow around the elliptic cylinder based on a large Reynolds number. They also analyzed the effects of fluid forces over the block. Kumar et al. [5] analyzed the influence of forced convection flow of generalized Newtonian fluid over the confined semiheater. Furthermore, hydrodynamic forces and Nusselt number are described by fluent. The forced convection thermal flow over the blocks embedded in a permeable medium was considered by Sayehvand et al. [6], and also, the results of a blind and porous medium channel were compared. Thermal flow around the block in the channel for large Reynolds number $\left(Re\right)$ is studied numerically using the finite volume approach [7, 8]. Also, the effects of fluid forces and Nusselt number in the given domain are examined. Dyakova et al. [9] examined the characteristics of power law fluid flow in a channel under thermal consideration. Also, they compared their results with the experimental data of other researchers for configuration of code. The characteristics of thermal flow in a channel have been highlighted in [10–12].

Computational elucidation of the generalized Newtonian fluid flow behaviors, thus, becomes a famous topic from the perception of both academics and the application. Considerations in this field have been continuing for over a decade, which contained Newtonian or non-Newtonian models, linear or nonlinear viscoelastic models, etc. Particularly, the viscous models preserved the general form of Navier–Stokes (NS) for Newtonian fluid because it depends on shear rate. Puente et al. [13] examined the effects of viscous fluid flow in a permeable channel as imposed binary constituency mixture in the domain. Despite the nonlinearity of the work, the methodology gives us stability and accuracy of outcomes. Two dimensionally, the incompressible flow of power law fluid around the obstacle in the range of large Reynolds number $\left(Re\right)$ is considered by Ehsan et al. [14]. SIMPLEC algorithm for a finite volume scheme with a non-uniform computational mesh is studied. Laidoudi et al. [15] analyzed the effects of power law fluid separation over the block by embedded thermal buoyancy solved using finite volume method (FVM)-based computational solver ANSYS. The typical grid was generated by the GAMBIT package. Nguyen et al. [16] analyzed the effects of non-Newtonian fluid in a three-dimensional pump and compared their results with the literature for code configuration. Siddiki et al. [17] investigated the characteristics of power law fluid in a channel by implementing the LBM numerical scheme. In addition, they found the intensities and recirculation in the bifurcated channel. The characteristics of the planar flow of viscous fluid in the channel (T-shape) were analyzed by Borzenko et al. [18]. Also, they described the influence of the kinematic and dynamic viscosity of fluid flow with slip boundary conditions on the walls of the channel. FEM computation emphasizing the character of flow behavior index $\left(n\right)$ and Reynolds number $\left(Re\right)$ on the domains is engrossed in [19–21]. Also, the results of fluid forces in numerous cases and graphically are described. Akyildiz et al. [22] investigated the characteristics of the periodic flow of power law fluid in a slip wall channel. Chen and Shu [23] implemented a famous numerical approach LBM for analyzing the flow pattern of a generalized Newtonian fluid. Furthermore, they solved two remarkable cases for checking the accuracy of the proposed scheme. X. J. Yang [24] probed the numerical solution of power law fluid by adopting Leibniz derivative-based simulation. Moreover, they also addressed the novelty of nonlinear viscous fluid. In the abovementioned literature review, it is clarified that the power law fluid is analyzed in many physical configurations.

Wu et al. [25] imposed a fancy numerical scheme (LBM) for control of the flow pattern over the cylinder in a channel. Also, the effects of fluid forces over the block with a high Reynolds number$\left(Re\right)$ were examined. Therefore, such experimental and computational simulations on this field have been engrossed in [26–36], and quite fascinating phenomena such as drag depletion and vortex shedding frequency under a particular condition have been carried out. The pioneering work was discussed, and the fluctuation of hydrodynamic forces due to high $Re$ by was studied using FEM computation based on CFD characteristics. Wang et al. [37] addressed the features of unsteady viscous fluid flow in the triangular arrangement of circular obstacles. In addition, they constructed the effects of vortex shedding, motion trajectories, and vibration amplitudes. Mahmood et al. [38] studied the flow pattern over the cylinder against several materials by the implementation of FEM computation. They examined pressure stagnation that appeared at the right upper corner of the square cavity. B. E. Abali [39] considered a characteristic of viscous fluid flow by implementing finite element-based simulation. Moreover, they exhibited the tenacity of the execution in open-source packages.

Furthermore, such numerical approaches in this field have been studied in [40–45]. Mahmood et al. [41, 42] examined the features of viscous fluid flow in a channel-driven cavity based on FEM computation. Also, the effects of shape function for quadratic and linear profiles were described. The variations of a hybrid computational mesh based on FEM for the physical configuration of the problem are presented. Also, the characteristics of fluid forces over the square block are discussed.

In most of the relevant studies available in the literature, the drag and lift coefficients have been computed in isothermal problems; however, in the present study, a non-isothermal flow regime is developed and the impact of forced convection on $C_D$ and $C_L$ has been investigated. The rest of the manuscript is organized as follows: mathematical modeling and geometric configuration are defined in Section 2, while Section 3 discloses the computational scheme with a weak formulation of the problem, results and discussions are defined in Section 4, and the manuscript is concluded in Section 5.

Physical Problem and Mathematical Modeling

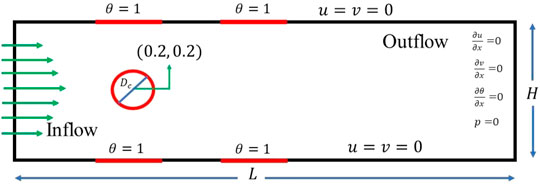
We consider two-dimensional, unsteady, incompressible, viscous fluid flow over the circular heated obstacle with thermal plates installed at the walls of the channel. The physical domain with height $H=0.41$ and length $L=2.2$ with a diameter of block $(D_c=0.1)$ placed at $C\left(x,y\right)=C\left(0.2,0.2\right)$ is considered. The domain specifications are revealed in Figure 1, and the free stream flow is in the $x-$direction.

FIGURE 1

FIGURE 1. Schematic figure of the flow problem.

The average velocity $\left(u_{\text{mean}}\right)$ and length (diameter of a cylinder$D_c$) scales are implemented for nondimensionalized governing equations, respectively.

The following assumptions are made for analysis:

• The characteristics of unsteady and non-isothermal fluid flow depending on the shear rate are studied

• The influence of parabolic inlet flow is studied, and the body force effects are neglected

• Boundary condition (no-slip) is assumed on the surface of the block as well as both symmetric walls of the channel

The governing equations of unsteady, non-isothermal, and viscous incompressible fluid flow over an endlessly long heated circular block are the classical continuity, momentum, and energy equations. The dimensionless form of the governing equations is defined as follows [45]:

$\nabla .\mathbf{u}=0,(1)$

${\mathbf{u}}_t+\mathbf{u}.\nabla \mathbf{u}+\nabla p=\frac{1}{Re}\nabla .\mathbf{\tau }+\mathbf{f,}(2)$

${\theta }_t+\mathbf{u}.\nabla \theta =\frac{1}{RePr}{\nabla }^2\theta ,(3)$

where $\mathbf{u}=[u, v]$ and the vector $\mathbf{f}={\left[0, \theta \raisebox{1ex}{$Gr$}\!\left/ \!\raisebox{-1ex}{$R{e}^2$}\right.\right]}^{\text{'}}$ is the source term for the 2D case and $\mathit{\tau }=\mu {\dot{\mathit{\gamma }}}^n$ that describes the nonlinear viscosity fluid. These equations have been nondimensionalized by utilizing the characteristics scaling variables $\begin{array}{l}{D}_c,u_{\text{mean}},{\rho }^2\text{, and }{T}_0\\ \end{array}$ for length, average velocity, pressure, and temperature, respectively. The dimensionless parameters such as Reynolds, Grashof, and Prandtl numbers for this problem are defined as follows:

Here, $\upsilon$ and $\alpha$ are the kinematic viscosity and thermal diffusivity, and the gravitational acceleration and volumetric expansion are defined as $g$ and $\beta$. Also, $n$ is the power law index, and the thermal conductivity parameter is defined as $k$. Here, the average velocity is $u_{\text{mean}}=\frac{2}{3}{u}_{\max },$ where $u_{\max }=1.5$ is the maximum velocity.

The boundary conditions for thermal flow field are described as follows:

• At the inlet region: $u_{in}=4u_{\text{mean}}y(H-y)/H^2,v=0,\theta =0$

• At the outlet region: ${\varphi }_x=0,\varphi =u,v,\theta ,p=0$

• At the surface of the cylinder: $u=0,v=0,\theta =1$

• At the surface of heaters (plates): $u=0,v=0,\theta =1$

• The other surfaces of the channel have no-slip conditions for velocity with $\theta =0$

The computational solution of governing Eqs. 1–3 is found along with the implementation of a specific boundary condition flow domain by capitalizing variables $\mathbf{u},p,\text{ and }\theta .$ The local Nusselt $\left(N{u}_{\text{local}}\right)$ number is used to quantify thermal flow taken from the surface of heaters. Therefore, the computational grid is more refined near the cylinder to acquire the $N{u}_{\text{avg}}$. These terms can be post-processed to conclude the quantities of interest defined as follows [45]:

• Drag coefficient:

$C_D=\frac{2F_d}{\rho u_{\text{mean}}^2{D}_c}.$

• Lift coefficient:

$C_L=\frac{2F_l}{\rho u_{\text{mean}}^2{D}_c}.$

• Local Nusselt number:

$N{u}_{\text{local}}=-\frac{\partial \theta }{\partial n_s}.$

• Average Nusselt number:

$N{u}_{\text{avg}}=\frac{1}{S}{\displaystyle \underset{s}{\int }N{u}_{\text{local}}dS}.$

The dimensional net drag $\left(F_d\right)$ and lift $\left(F_l\right)$ forces act on the surface of the block in the flow and normal direction. Where $"S"\text{ and "}{n}_s\text{"}$ are the surfaces of the thermal regime and normal direction of the surface, it is appropriate to postulate that the drag coefficient is the function of $Re$, whereas the average Nusselt number depends on the $Pr.$ This work endeavors to exhibit and develop a more efficient functional relationship for a block.

Numerical Procedure

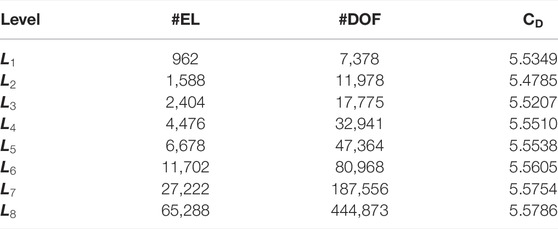
A complex discretization of a given domain is shown in Figure 2. The overall dimension of the computational domain is $\left(L,H\right)=\left(2.2, 0.41\right)$ and adopting $\left(P_2/P_1/P_1\right)$ elements based on the 2^nd- and 1^st-order polynomial shape functions for the approximate solution. The unstructured hybrid mesh used for computations consists of 65,288 elements and 444,873 degrees of freedom at an extra-fine level, while the details of several meshing levels are provided in Table 1.

FIGURE 2

FIGURE 2. Hybrid grid structure at a fine level.

TABLE 1

TABLE 1. Degrees of freedom and grid convergence for various levels.

A mathematical formulation consisting of governing equations is attained and handled with FEM computation. For the enlargement of finite element method discretization, the elements are capitalized triangular and quadratic in shape. The finite element method formulations attain the nonlinear algebraic equations by the implementation of the Newton–Raphson (N-R) iterative scheme. For validation of code, we compute the lift coefficient of the benchmark problem for the present work at $n=1$ and zero temperature and then compare with the results of the work of Turek et al. [46], as shown in Figure 3.

FIGURE 3

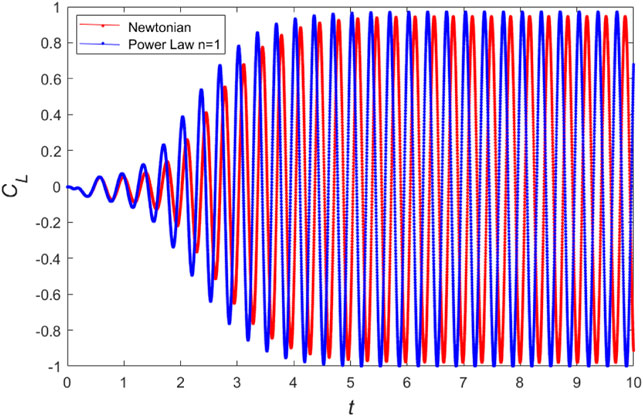
FIGURE 3. Lift comparison test for Newtonian fluid $(n=1)$ [46].

Weak Formulation

To solve the system of Equations 1–3, the underlying methodology is based on the finite element method. The first step is to transfer the model equation into the so-called weak formulations. Introducing the tested and tried spaces, we proceed as follows:.

Let $W={\left[H^1\left(\mathrm{\Omega }\right)\right]}^3$ be the test subspaces for $\text{u,v},\theta$, and $Q=L^2\left(\mathrm{\Omega }\right)$ is the test space for pressure. The weak form of the abovementioned equations is given as

$Re{\displaystyle \underset{\mathrm{\Omega }}{\int }\left(u_t+u{u}_x+v{u}_y\right)}wd\mathrm{\Omega }+Re{\displaystyle \underset{\mathrm{\Omega }}{\int }{p}_x}wd\mathrm{\Omega }-{\displaystyle \underset{\mathrm{\Omega }}{\int }\nabla .\mathbf{\tau }}wd\mathrm{\Omega }=0,(5)$

$R{e}^2{\displaystyle \underset{\mathrm{\Omega }}{\int }\left(v_t+u{v}_x+v{v}_y\right)}wd\mathrm{\Omega }+R{e}^2{\displaystyle \underset{\mathrm{\Omega }}{\int }{p}_y}wd\mathrm{\Omega }-Re{\displaystyle \underset{\mathrm{\Omega }}{\int }\nabla .\mathbf{\tau }}wd\mathrm{\Omega }-Gr{\displaystyle \underset{\mathrm{\Omega }}{\int }\theta w}d\mathrm{\Omega }=0,(6)$

${\displaystyle \underset{\mathrm{\Omega }}{\int }\left(u_x+v_y\right)}qd\mathrm{\Omega }=0,(7)$

$PrRe{\displaystyle \underset{\mathrm{\Omega }}{\int }\left({\theta }_t+u{\theta }_x+v{\theta }_y\right)}wd\mathrm{\Omega }-{\displaystyle \underset{\mathrm{\Omega }}{\int }{\nabla }^2\theta }wd\mathrm{\Omega }=0.(8)$

For numerical approximation, we compute the continuous solutions with the discrete ones in the finite-dimensional subspaces.

$\begin{array}{l}u\approx u_{\hslash }\in W_{\hslash },\\ v\approx v_{\hslash }\in W_{\hslash },\\ \theta \approx {\theta }_{\hslash }\in W_{\hslash },\\ p\approx p_{\hslash }\in Q_{\hslash }.\end{array}(9)$

Using Eq. 9 in Eqs. 5–8, the following discrete version is obtained:

$Re{\displaystyle \underset{\mathrm{\Omega }}{\int }\left(u_{{\hslash }_t}+u_{\hslash }{u}_{{\hslash }_x}+v_{\hslash }{u}_{{\hslash }_y}\right)}{w}_{\hslash }d\mathrm{\Omega }+Re{\displaystyle \underset{\mathrm{\Omega }}{\int }{p}_{{\hslash }_x}}{w}_{\hslash }d\mathrm{\Omega }-{\displaystyle \underset{\mathrm{\Omega }}{\int }\nabla .{\mathbf{\tau }}_{\hslash }}{w}_{\hslash }d\mathrm{\Omega }=0,(10)$

$R{e}^2{\displaystyle \underset{\mathrm{\Omega }}{\int }\left(v_{{\hslash }_t}+u_{\hslash }{v}_{{\hslash }_x}+v_{\hslash }{v}_{{\hslash }_y}\right)}{w}_{\hslash }d\mathrm{\Omega }+R{e}^2{\displaystyle \underset{\mathrm{\Omega }}{\int }{p}_{{\hslash }_y}}{w}_{\hslash }d\mathrm{\Omega }-{\displaystyle \underset{\mathrm{\Omega }}{\int }\nabla .{\mathbf{\tau }}_{\hslash }}{w}_{\hslash }d\mathrm{\Omega }-Gr{\displaystyle \underset{\mathrm{\Omega }}{\int }{\theta }_{\hslash }{w}_{\hslash }}d\mathrm{\Omega }=0,(11)$

${\displaystyle \underset{\mathrm{\Omega }}{\int }\left(u_{{\hslash }_x}+v_{{\hslash }_y}\right)}{w}_{\hslash }d\mathrm{\Omega }=0,(12)$

$RePr{\displaystyle \underset{\mathrm{\Omega }}{\int }\left({\theta }_{{\hslash }_t}+u_{\hslash }{\theta }_{{\hslash }_x}+v_{\hslash }{\theta }_{{\hslash }_y}\right)}{w}_{\hslash }d\mathrm{\Omega }-{\displaystyle \underset{\mathrm{\Omega }}{\int }{\nabla }^2{\theta }_{\hslash }}{w}_{\hslash }d\mathrm{\Omega }=0.(13)$

Basis functions are defined for the discrete solution as follows:

$\begin{array}{l}{u}_{\hslash }\approx {\displaystyle \sum _{k=1}^{\text{ndof}}{u}_k{\phi }_k(\mathrm{x},\mathrm{y})},\\ v_{\hslash }\approx {\displaystyle \sum _{k=1}^{\text{ndof}}{v}_k{\phi }_k(\mathrm{x},\mathrm{y})},\\ p_{\hslash }\approx {\displaystyle \sum _{k=1}^{\text{ndof}}{p}_k{\psi }_k(\mathrm{x},\mathrm{y})},\\ {\theta }_{\hslash }\approx {\displaystyle \sum _{k=1}^{\text{ndof}}{\theta }_k{\phi }_k(\mathrm{x},\mathrm{y})},\end{array}(14)$

where $\text{ndof}$ denotes the number of degrees of freedom. Equations 10–13 give rise to

$Re{\displaystyle \underset{\mathrm{\Omega }}{\int }\left(u_{{\hslash }_t}+u_{\hslash }{u}_{{\hslash }_x}+v_{\hslash }{u}_{{\hslash }_y}\right)}{w}_{\hslash }d\mathrm{\Omega }+Re{\displaystyle \underset{\mathrm{\Omega }}{\int }{p}_{{\hslash }_x}}{w}_{\hslash }d\mathrm{\Omega }+{\displaystyle \underset{\mathrm{\Omega }}{\int }\nabla .{\mathbf{\tau }}_{\hslash }{w}_{\hslash }}d\mathrm{\Omega }=0,(15)$

$R{e}^2{\displaystyle \underset{\mathrm{\Omega }}{\int }\left(v_{{\hslash }_t}+u_{\hslash }{v}_{{\hslash }_x}+v_{\hslash }{v}_{{\hslash }_y}\right)}{w}_{\hslash }d\mathrm{\Omega }+R{e}^2{\displaystyle \underset{\mathrm{\Omega }}{\int }{p}_{{\hslash }_y}}{w}_{\hslash }d\mathrm{\Omega }+{\displaystyle \underset{\mathrm{\Omega }}{\int }\nabla .{\mathbf{\tau }}_{\hslash }}{w}_{\hslash }d\mathrm{\Omega }-Gr{\displaystyle \underset{\mathrm{\Omega }}{\int }{\theta }_{\hslash }{w}_{\hslash }}d\mathrm{\Omega }=0,(16)$

${\displaystyle \underset{\mathrm{\Omega }}{\int }\left(u_{{\hslash }_x}+v_{{\hslash }_y}\right)}{w}_{\hslash }d\mathrm{\Omega }=0,(17)$

$RePr{\displaystyle \underset{\mathrm{\Omega }}{\int }\left({\theta }_{{\hslash }_t}+u_{\hslash }{\theta }_{{\hslash }_x}+v_{\hslash }{\theta }_{{\hslash }_y}\right)}{w}_{\hslash }d\mathrm{\Omega }+{\displaystyle \underset{\mathrm{\Omega }}{\int }{\nabla }^2{\theta }_{\hslash }{w}_{\hslash }}d\mathrm{\Omega }=0.(18)$

In the matrix form,

$\left[\begin{array}{cccc}M+Re.L_{\hslash }+N\left(u_{\hslash },v_{\hslash },{\theta }_{\hslash }\right)& 0& Re.B_1& 0\\ 0& R{e}^2.L_{\hslash }+N_{\hslash }\left(u_{\hslash },v_{\hslash },{\theta }_{\hslash }\right)& R{e}^2.B_2& -Gr.M_{\hslash }\\ B_1^T& B_2^T& 0& 0\\ 0& 0& 0& Pr.Re.L_{\hslash }+N_{\hslash }\left(u_{\hslash },v_{\hslash },{\theta }_{\hslash }\right)\end{array}\right]\left[\begin{array}{c}\underset{¯}{U}\\ \underset{¯}{V}\\ \underset{¯}{P}\\ \underset{¯}{\theta }\end{array}\right]=\left[\begin{array}{c}{\text{F}}_1\\ {\text{F}}_2\\ {\text{F}}_3\\ {\text{F}}_4\end{array}\right],(19)$

which can be written as

$\mathbf{A\xi }=\mathbf{F}\mathbf{.}$

All parameters have their usual meanings, and to compute the solution, this complex system is iterated till a particular convergence criterion is met. The nonlinear iterations are stopped when the residual is dropped by 10^–6.

Results and Discussion

In this manuscript, we have considered the governing parameters for thermal flow characteristics as follows: Grashof number (Gr) from 1 to 10, power law index (n) from 0.6 to 1.4, Prandtl number ($Pr$) varying from 1 to 10, and time dependence (t) from 0 to 10; for more efficient computation, the time step size $\Delta t=0.001$ is considered with constant Reynolds number $Re=100$.

(1) Fluid Flow

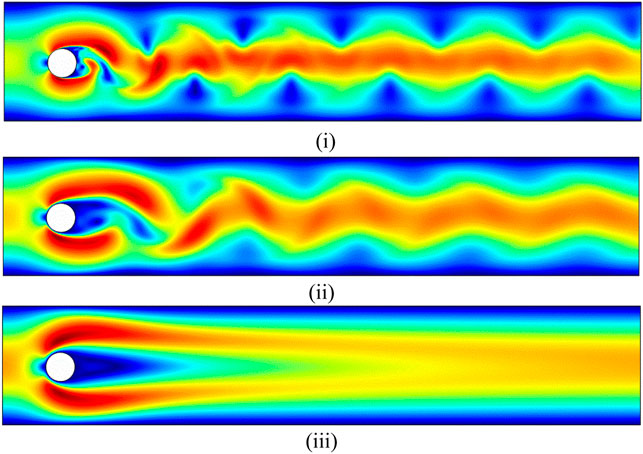
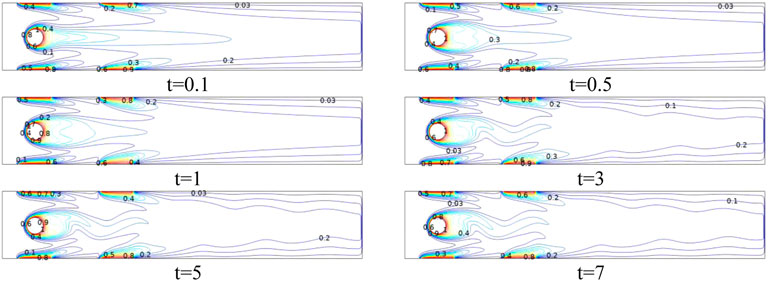
In this section, the effects of superimposed phenomena on viscous fluid flow are considered. The drag and lift coefficients, viscosity, and shear rate are provided for incompressible unsteady viscous (power law) fluid flow over a circular heated block situated in a channel with a fixed Reynolds number $Re.$ The representative velocity profile and pressure field are illustrated over the heated block for different values of the power law index $\left(n\right)$ from 0.4 to 1.6 at 5s, which is shown in Figures 4, 5. For $n=0.4,$ there were certain disparities that appeared in the flow pattern, and the CWS function has been assimilated for the sake of convergence for the shear-thinning case. For shear thinning $\left(n=0.4\right),$ wavering flow in a time step is considered in the downstream regime of the block. However, the instantaneous wake behavior is seen for Newtonian flow $\left(n=1\right),$ qualitatively close to the shear-thinning flow pattern. For instance, several vortices are found behind the circular block. The fluid flow pattern changes from Newtonian to shear thickening $\left(n=1.6\right),$ the recirculation region reduces in size, and a uniform flow behavior appears in the downstream region. Also, the pressure is maximum at the stagnation point.

FIGURE 4

FIGURE 4. Influence on velocity for $\left(i\right)n=0.6, \left(ii\right)n=1, \left(iii\right)n=1.4$ with $Pr=7$ and $Re=100$ at $t=5.$

FIGURE 5

FIGURE 5. Influence on pressure for $\left(i\right)n=0.6, \left(ii\right)n=1, \left(iii\right)n=1.4$ with $Pr=7$ and $Re=100$ at $t=5.$

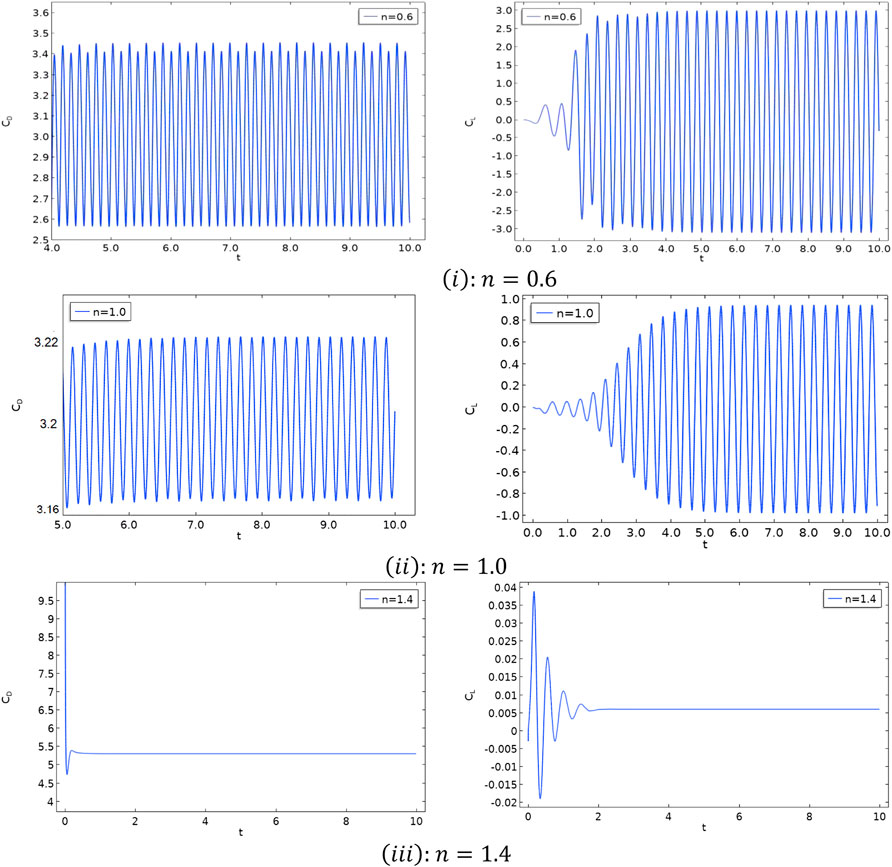
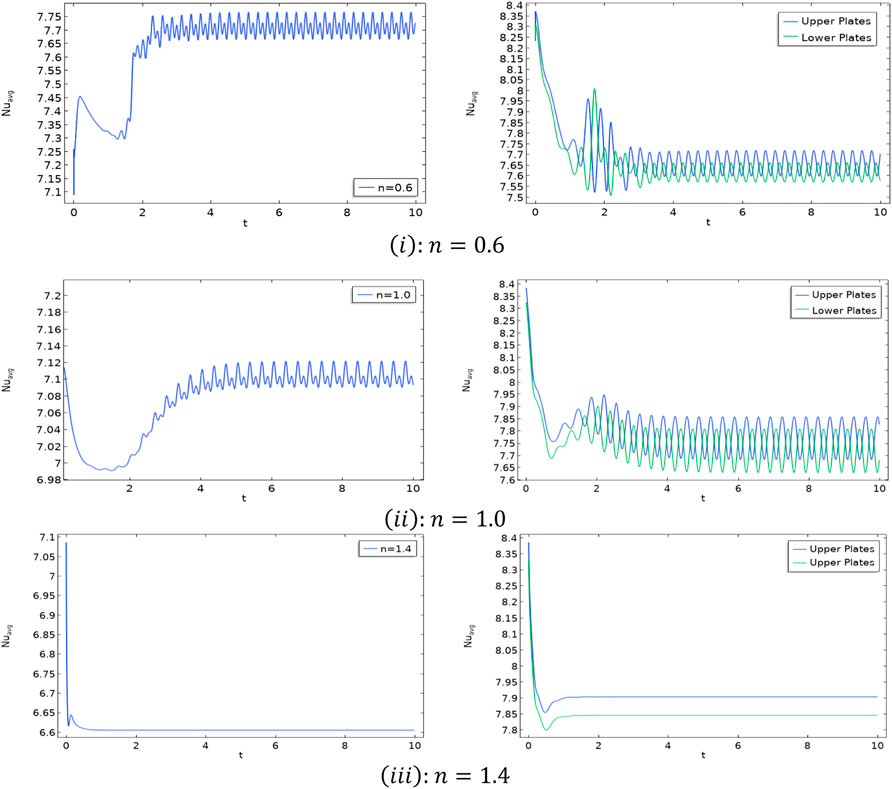
Figure 6 illustrates the effects of flow behavior index (n) on the time evaluation of $C_D$ and $C_L$ in the vicinity of a block. As noted prior, a computation was broken and said to have converged after 10 constant periodic cycles in both$\left(C_D\right)$ and $\left(C_L\right)$ time evaluation graphs. At the Reynolds number, $\left(Re=100\right),$ the frequency range of periodic oscillation of both $\left(C_D\right)$ and $\left(C_L\right)$ is increasing. Once the periodic state is attained, the drag and lift coefficients in the shear-thinning $\left(n=0.4\right)$ liquids are larger than both Newtonian and the shear-thickening $\left(n=1.6\right)$ liquids. However, both drag and lift coefficients become symmetric in shear thickening. Before 2, the lift coefficient has oscillated in this region, but increasing over time, the lift coefficient becomes constant. Figure 7 displays the drag-lift phase $\left(C_D-C_L\right)$ portrait over a time period for different values of power law index $n$. These phase plots show that one cycle of the $C_L$ is equal to two cycles of the $C_D.$ The phase curves also reveal that the values of drag coefficient increases with the raise in the values of flow behavior index $\left(n\right)$, and the lift coefficient decreases at fixed Reynolds number $Re.$ For the shear-thickening case $\left(n=1.4\right)$, both the drag and lift coefficients converge to a steady-state value.

FIGURE 6

FIGURE 6. Influence on drag and lift coefficients for different $n$ with $Pr=7$ and $Re=100$.

FIGURE 7

FIGURE 7. Impact of $n$ on the phase plot $\left(C_D-C_L\right)$ diagram.

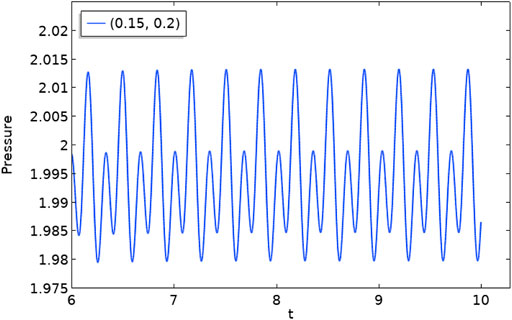
Figure 8 illustrates that the influence on the pressure profile at the stagnation position for an oscillating flow regime. The frequency of periodicity of the pressure profile is minimum when the $Re$ is lower than the critical $Re$ values, while the pressure oscillation increases with an increase in $Re=100.$

FIGURE 8

FIGURE 8. Line graph of the pressure profile for the Newtonian case $(n=1)$.

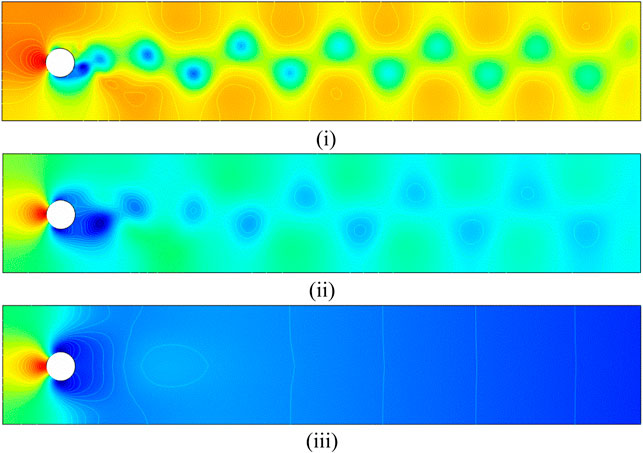
(2): Thermal Flow Behavior

In this section, the influence of the flow behavior parameter $\left(n\right),$ Prandtl number $\left(Pr\right),$ Grashof number $\left(Gr\right),$ Reynolds number $\left(Re\right)$, and periodicity on the forced convection heat transfer over the thermal surfaces is studied. It is analyzed that a wavering flow downstream of the block exists. The thermal flow field grows frequently on upstream surfaces of the heater, while it is eventually discontinuous from both top and bottom corners of it. Heat transfer distribution over the surfaces of the heater is acted by a fluid momentum. The non-isothermal flow behavior can be attained from a time-averaged isotherm, where we can study the effects of thermal clouds. The influence of Grashof variation on heat transfer characteristics of heated surfaces (cylinder and plates) in the periodic regime is considered through the time-averaged isotherm in Figures 9, 10. It has been observed that the flow shows complex patterns, especially behind the block, that do, however, exhibit periodic behavior. Non-isothermal flow for Grashof at 3 and 10 shows that the heat transfer increases with an increase in time.

FIGURE 9

FIGURE 9. Influence on isotherm for different periods with $n=1.0, Pr=5,Gr=3,$ and $Re=100.$

FIGURE 10

FIGURE 10. Influence on isotherm for different periods with $n=1.0, Pr=5,Gr=10,$ and $Re=100.$

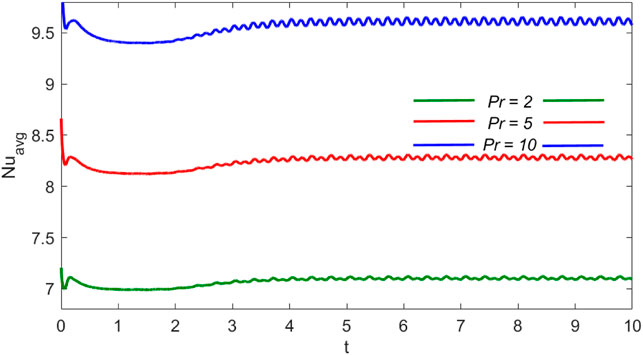
In Figure 11, the average Nusselt number $\left(N{u}_{\text{avg}}\right)$ along time (t) is comparatively elucidated for both cylinder as well as thermal plates, and also, the effects of flow characteristics parameter $\left(n\right)$ are examined. For $n=0.6$, the average Nusselt number decreases before $t=2$, then oscillating between 7.65 and 7.75 on the cylinder and 7.55 and 7.70 on plates. Similarly, for $n=1$, oscillation is steady after $t=4$, between 7.08 and 7.12 on the cylinder and 7.65 and 7.85 on plates, while for $n=1.4$, the average Nusselt number initially decreases; after a certain time, it becomes fixed on both cylinder and thermal plates. Figure 12 reveals the $N{u}_{avg}$ versus time for different Prandtl numbers over a cylinder. As expected from previous analysis, the $N{u}_{avg}$ raises due to an increase of $Pr$, while after a certain time, it becomes oscillatory at $Re=100.$

FIGURE 11

FIGURE 11. Influence of $n$ on $N{u}_{avg}$ over the cylinder (left) and plates (right) with $Pr=7$ and $Re=100$.

FIGURE 12

FIGURE 12. Influence of $Pr$ on $N{u}_{avg}$ with $n=1$ and $Re=100$.

Conclusion

Numerical simulations have been carried out to investigate the fluid flow over a uniformly heated cylindrical block in a channel with thermal plates installed at the walls of the channel. The fluid model incorporated is the Ostwald de-Waele power law rheological model that describes a wide range of shear-thinning and shear-thickening fluids. A highly refined hybrid grid is generated at the preprocessing stage to achieve high accuracy in the solution, and a code validation study is also performed. Based on the obtained results, the following conclusions are drawn:

i. The amplitude of drag and lift increases for shear-thinning cases $\left(n<1\right)$, while both drag and lift coefficients approach a constant value for shear-thickening cases $\left(n>1\right)$

ii. For $n=1$ that corresponds to the Newtonian case, the lift oscillates between [−1, +1] and drag oscillates in [3.16, 3.22], which show an excellent agreement with the reference value

iii. Average Nusselt number increases with the Prandtl number and reaches an oscillatory steady state in all cases after $\left(t\ge 5\right)$

iv. For Newtonian and shear-thinning cases, $C_D$ and $C_L$ are periodic, while for the shear-thickening case, both converge to a fixed value due to the increase in viscosity

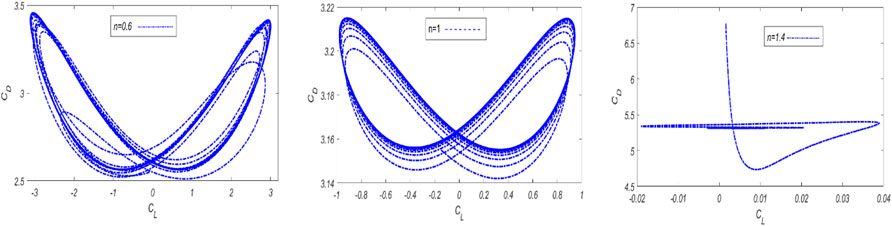
v. Phase plots of $\left(C_D-C_L\right)$ form a closed loop for the cases $(n<1)$ and $(n=1)$ showing also the limit cycle of oscillations, while for $(n>1)$, there is no oscillation in the limit cycle

This work can be extended in many directions, for instance, selecting higher values of $Re$ to get into a transitional regime between the periodic and turbulent flow and to control the fluid forces by introducing some passive control devices in the flow domain. One possible extension could be to work with turbulent models for $Re$ in the range $200<Re<300.$

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

AH has performed modeling and computed data. RM has supervised the work. IS has written the manuscript.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Yang SJ, Fu WS. Numerical Investigation of Heat Transfer from a Heated Oscillating Rectangular Cylinder in a Cross Flow. Numer Heat Trans (2010) 45:569–91.

Google Scholar

2. Kamyar A, Ong KS, Saidur R. Effects of Nanofluids on Heat Transfer Characteristics of a Two-phase Closed Thermosyphon. Int J Heat Mass Transfer (2013) 65:610–8. doi:10.1016/j.ijheatmasstransfer.2013.06.046

CrossRef Full Text | Google Scholar

3. Valipour M, Masoodi R, Rashidi S, Bovand M, Mirhosseini M. A Numerical Study on Convection Around a Square cylinder Using AL2O3-H2O Nanofluid. Therm Sci (2014) 18(4):1305–14. doi:10.2298/TSCI121224061V

CrossRef Full Text | Google Scholar

4. Mostafa M, Kamal R, Gobran M. Flow and Heat Transfer Characteristics Around an Elliptic cylinder Placed in Front of a Curved Plate. Therm Sci (2014) 18(2):465–78. doi:10.2298/TSCI120307054M

CrossRef Full Text | Google Scholar

5. Kumar A, Dhiman A, Baranyi L. CFD Analysis of Power-Law Fluid Flow and Heat Transfer Around a Confined Semi-circular cylinder. Int J Heat Mass Transfer (2015) 82:159–69. doi:10.1016/j.ijheatmasstransfer.2014.11.046

CrossRef Full Text | Google Scholar

6. Sayehvand H-O, Dehkordi K, Basiri P. Numerical Analysis of Forced Convection Heat Transfer from Two Tandem Circular Cylinders Embedded in a Porous Medium. Therm Sci (2017) 21(5):2117–28. doi:10.2298/TSCI150307081S

CrossRef Full Text | Google Scholar

7. Hassanzadeh R, Darvishyadegari M. Influence of Rotation on the Heat and Fluid Flow Around a Circular Cylinder. Int J Mod Stud Mech Eng (2018) 2018:1. doi:10.20431/2454-9711.0404002

CrossRef Full Text | Google Scholar

8. Sayehvand H-O, Yari S, Basiri P. Numerical Study of Forced Convection Heat Transfer over Three Cylinders in Staggered Arrangement Immersed in Porous media. Therm Sci (2018) 22(1):467–75. doi:10.2298/TSCI150808249S

CrossRef Full Text | Google Scholar

9. Dyakova OA, Frolov OY, Frolov OY. Investigation of the Structure of Nonisothermal Power-Law Fluid Flow in an L-Shaped Channel. Tomsk State Univ J Math Mech (2019) 2019(58):71–83. doi:10.17223/19988621/58/6

CrossRef Full Text | Google Scholar

10. Athinarayanan A, Gurunathan M, Parthasarathy R, Taler J, Oclon P, Taler D. Numerical Investigation of Heat Transfer from Flow over Square cylinder Placed in a Confined Channel Using Cu-Water Nanofluid. Therm Sci (2019) 23:1367–80. doi:10.2298/TSCI19S4367A

CrossRef Full Text | Google Scholar

11. Perumal S, Sundaresan D, Thanikodi S, Sivanraju R, Tesfil N, Ramalingam K. Heat Transfer Analysis in Counter Flow Shell and Tube Heat Exchanger Using of Design of Experiments. Belgrade, Serbia: Therm. Sci. (2020).

Google Scholar

12. Javidi Sarafan M, Alizadeh R, Fattahi A, Valizadeh Ardalan M, Karimi N. Heat and Mass Transfer and Thermodynamic Analysis of Power-Law Fluid Flow in a Porous Microchannel. J Therm Anal Calorim (2020) 141(5):2145–64. doi:10.1007/s10973-020-09679-8

CrossRef Full Text | Google Scholar

13. Puente JAA, Martins-Costa ML, Costa Mattos H. Numerical Simulation of Power-Law Fluid Flows in a Porous Channel. Braz Congr. Therm. Sci. Eng. (2012) 3:1.

Google Scholar

14. Ehsan I, Mohammad S, Mohammad Reza N, Ali J, Sharifi Tashnizi E. Power-law Fluid Flow Passing Two Square Cylinders in Tandem Arrangement. J Fluids Eng Trans ASME (2013) 135–6. doi:10.1115/1.4023853

CrossRef Full Text | Google Scholar

15. Houssem L, Bouzit M. Suppression of Flow Separation of Power-Law Fluids Flow Around a Confined Circular cylinder by Superimposed thermal Buoyancy. mech (2017) 23(2):220–7. doi:10.5755/j01.mech.23.2.14342

CrossRef Full Text | Google Scholar

16. Xin L X, Lai H. The Simulation of Non-newtonian Power-Law Fluid Flow in a Centrifugal Pump Impeller. J Appl Mech Eng (2017) 05(4):381–90. doi:10.4172/2168-9873.1000230

CrossRef Full Text | Google Scholar

17. Siddiki MN-A -A, Molla MM, Thohura S, Saha SC. Lattice Boltzmann Simulation of Non-newtonian Power-Law Fluid Flows in a Bifurcated Channel. AIP Conf Proc (2018) 1980:040023. doi:10.1063/1.5044333

CrossRef Full Text | Google Scholar

18. Borzenko EI, Dyakova OA. Power-law Fluid Flow in a T-Shaped Channel with Slip Boundary Conditions on the Solid walls. J Phys Conf Ser (2018) 1128(1):012013. doi:10.1088/1742-6596/1128/1/012013

CrossRef Full Text | Google Scholar

19. Ameur H. Pressure Drop and Vortex Size of Power Law Fluids Flow in Branching Channels with Sudden Expansion. Jafm (2018) 11(6):1739–49. doi:10.29252/jafm.11.06.28831

CrossRef Full Text | Google Scholar

20. Vishal G, Tomar J, Bharti RP. Critical Parameters for Non-newtonian Power-Law Fluid Flow across a Channel Confined Circular cylinder. New York: arXiv (2019).

Google Scholar

21. Tang M, He L, Ma R, He S, Yao G. Modeling of Yield-Power-Law Fluid Flow in an Eccentric Annulus with Fixed Horizontal Cuttings Bed. Energy Sourc A: Recovery, Utilization, Environ Effects (2019) 2019:1–16. doi:10.1080/15567036.2019.1683649

CrossRef Full Text | Google Scholar

22. Akyildiz FT, Siginer DA, Boutaous Mh. Unsteady Flow of Power Law Fluids with Wall Slip in Microducts. J Fluids Eng Trans ASME (2019) 141–8. doi:10.1115/1.4042558

CrossRef Full Text | Google Scholar

23. Chen Z, Shu C. Simplified Lattice Boltzmann Method for non‐Newtonian Power‐law Fluid Flows. Int J Numer Meth Fluids (2020) 92(1):38–54. doi:10.1002/fld.4771

CrossRef Full Text | Google Scholar

24. Yang X-J. The Vector Power-Law Calculus with Applications in Power-Law Fluid Flow. Therm Sci (2020) 24:4289–302. doi:10.2298/TSCI2006289Y

CrossRef Full Text | Google Scholar

25. Wu J, Qiu YL, Shu C, Zhao N. Flow Control of a Circular cylinder by Using an Attached Flexible Filament. Phys Fluids (2014) 26:103601–10. doi:10.1063/1.4896942

CrossRef Full Text | Google Scholar

26. Seyed-Aghazadeh B, Modarres-Sadeghi Y. An Experimental Investigation of Vortex-Induced Vibration of a Rotating Circular cylinder in the Crossflow Direction. Phys Fluids (2015) 27(6):067. doi:10.1063/1.4921683

CrossRef Full Text | Google Scholar

27. Ahmed RA. Simulation of Unsteady Flow Around a Cylinder. ejuow (2015) 3(2):28–49. doi:10.31185/ejuow.vol3.iss2.38

CrossRef Full Text | Google Scholar

28. Abbasi WS, Islam SU. Transition from Steady to Unsteady State Flow Around Two Inline Cylinders under the Effect of Reynolds Numbers. J Braz Soc Mech Sci Eng (2018) 40(3):1–12. doi:10.1007/s40430-018-1083-y

CrossRef Full Text | Google Scholar

29. Behara S, Ravikanth B, Chandra V. Flow-induced Oscillations of Three Tandem Rotating Cylinders. Phys Fluids (2018) 30:113604. doi:10.1063/1.5051773

CrossRef Full Text | Google Scholar

30. Abbasi WS, Islam S-u., Rahman H, Manzoor R. Numerical Investigation of Fluid-Solid Interaction for Flow Around Three Square Cylinders. AIP Adv (2018) 8(2):025221. doi:10.1063/1.5004631

CrossRef Full Text | Google Scholar

31. Sarwar Abbasi W, Ul Islam S, Faiz L, Rahman H. Numerical Investigation of Transitions in Flow States and Variation in Aerodynamic Forces for Flow Around Square Cylinders Arranged Inline. Chin J Aeronautics (2018) 31(11):2111–23. doi:10.1016/j.cja.2018.08.020

CrossRef Full Text | Google Scholar

32. Behara S, Chandra V, Ravikanth B, Kotteda VMK. Oscillation Responses and Wake Modes of Three Staggered Rotating Cylinders in Two- and Three-Dimensional Flows. Phys Fluids (2018) 30:103602–10. doi:10.1063/1.5049347

CrossRef Full Text | Google Scholar

33. Wang E, Xu W, Gao X, Liu L, Xiao Q, Ramesh K. The Effect of Cubic Stiffness Nonlinearity on the Vortex-Induced Vibration of a Circular cylinder at Low Reynolds Numbers. Ocean Eng (2019) 173:1. doi:10.1016/j.oceaneng.2018.12.039

CrossRef Full Text | Google Scholar

34. Abbasi WS, Islam SU, Rahman H. Proximity Effects on Characteristics of Flow Around Three Inline Square Cylinders. Math Probl Eng (2019) 2019:1–14. doi:10.1155/2019/1752803

CrossRef Full Text | Google Scholar

35. Abbasi WS, Mahmood R, Naheed A. On the Wake Interference Effects for Flow Around Tandem Bodies. J Braz Soc Mech Sci Eng (2020) 42(1):1–20. doi:10.1007/s40430-019-2137-5

CrossRef Full Text | Google Scholar

36. Chen W, Rheem C-K, Lin Y, Li Y. Experimental Investigation of the Whirl and Generated Forces of Rotating Cylinders in Still Water and in Flow. Int J Naval Architecture Ocean Eng (2020) 12:531–40. doi:10.1016/j.ijnaoe.2020.03.004

CrossRef Full Text | Google Scholar

37. Wang H, Yu G, Yang W. Numerical Study of Vortex-Induced Vibrations of Three Circular Cylinders in Equilateral-triangle Arrangement. Adv Mech Eng (2013) 5:287923. doi:10.1155/2013/287923

CrossRef Full Text | Google Scholar

38. Mahmood R, Bilal S, Majeed AH, Khan I, Sherif E-SM. A Comparative Analysis of Flow Features of Newtonian and Power Law Material: A New Configuration. J Mater Res Technol (2019) 9:1.

Google Scholar

39. Abali BE. An Accurate Finite Element Method for the Numerical Solution of Isothermal and Incompressible Flow of Viscous Fluid. Fluids (2019) 4:5–1. doi:10.3390/fluids4010005

CrossRef Full Text | Google Scholar

40. Ahmad H, Mahmood R, Hafeez MB, Majeed AH, Askar S, Shahzad H. Thermal Visualization of Ostwald-De Waele Liquid in Wavy Trapezoidal Cavity: Effect of Undulation and Amplitude. Netherlands: Case Studies in Thermal Engineering (2022).

Google Scholar

41. Mahmood R, Bilal S, Majeed AH, Khan I, Nisar KS. Assessment of Pseudo-plastic and Dilatant Materials Flow in Channel Driven Cavity: Application of Metallurgical Processes. J Mater Res Tech (2020) 9(3):3829–37. doi:10.1016/j.jmrt.2020.02.009

CrossRef Full Text | Google Scholar

42. Mahmood R, Bilal S, Majeed AH, Khan I, Nisar KS. CFD Analysis for Characterization of Non-linear Power Law Material in a Channel Driven Cavity with a Square cylinder by Measuring Variation in Drag and Lift Forces. J Mater Res Tech (2020) 9:3838–46. doi:10.1016/j.jmrt.2020.02.010

CrossRef Full Text | Google Scholar

43. Bilal S, Mahmood R, Majeed AH, Khan I, Nisar KS. Finite Element Method Visualization about Heat Transfer Analysis of Newtonian Material in Triangular Cavity with Square cylinder. J Mater Res Tech (2020) 9(3):4904–18. doi:10.1016/j.jmrt.2020.03.010

CrossRef Full Text | Google Scholar

44. Majeed AH, Mahmood R, Abbasi WS, Usman K. Numerical Computation of MHD Thermal Flow of Cross Model over an Elliptic Cylinder: Reduction of Forces via Thickness Ratio. Math Probl Eng (2021) 2021:1–13. doi:10.1155/2021/2550440

CrossRef Full Text | Google Scholar

45. Majeed AH, Jarad F, Mahmood R, Siddique I. Topological Characteristics of Obstacles and Nonlinear Rheological Fluid Flow in Presence of Insulated Fins: A Fluid Force Reduction Study. Egypt: Mathematical Problems in Engineering (2021).

Google Scholar

46. Turek S, Schafer M. Benchmark Computations of Laminar Flow Around a Cylinder. AIAA J (1996) 48:1.

CrossRef Full Text | Google Scholar