High Resolution Ex Vivo Diffusion Tensor Distribution MRI of Neural Tissue

Neural tissue microstructure plays a key role in developmental, physiological and pathophysiological processes. In the continuing quest to characterize it at ever finer length scales, we use a novel diffusion tensor distribution (DTD) paradigm to probe microstructural features much smaller than the nominal MRI voxel size. We first assume the DTD is a normal tensor variate distribution constrained to lie on the manifold of positive definite matrices, characterized by a mean and covariance tensor. We then estimate the DTD using Monte Carlo signal inversion combined with parsimonious model selection framework that exploits a hierarchy of symmetries of mean and covariance tensors. High resolution multiple pulsed field gradient (mPFG) MRI measurements were performed on a homogeneous isotropic diffusion phantom (PDMS) for control, and excised visual cortex and spinal cord of macaque monkey to investigate the capabilities of DTD MRI in revealing neural tissue microstructural features using strong gradients not typically available in clinical MRI scanners. DTD-derived stains and glyphs, which disentangle size, shape, and orientation heterogeneities of microscopic diffusion tensors, are presented for all samples along with the distribution of the mean diffusivity (MD) within each voxel. We also present a new glyph to visualize the symmetric (kurtosis) and asymmetric parts of the fourth-order covariance tensor. An isotropic mean diffusion tensor and zero covariance tensor was found for the isotropic PDMS phantom, as expected, while the covariance tensor (both symmetric and asymmetric parts) for neural tissue was non-zero indicating that the kurtosis tensor may not be sufficient to fully describe the microstructure. Cortical layers were clearly delineated in the higher moments of the MD spectrum consistent with histology, and microscopic anisotropy was detected in both gray and white matter of neural tissue. DTD MRI captures crossing and splaying white matter fibers penetrating into the cortex, and skewed fiber diameter distributions in the white matter tracts within the cortex and spinal cord. DTD MRI was also shown to subsume diffusion tensor imaging (DTI) while providing additional microstructural information about tissue heterogeneity and microscopic anisotropy within each voxel.

1 Introduction

Nervous tissue is rich and varied over multiple length scales in normal development and is affected in numerous pathological conditions [1, 2]. Diffusion tensor imaging (DTI) [3, 4] has been a key imaging method for revealing these features and their pathological changes. However, DTI assumes water diffusion within a MRI voxel can be described by a single mean diffusion tensor, which has some well-known limitations when applied to heterogeneous media, including neural tissue [5–7]. For example, a voxel composed of orientation-dispersed white matter fibers cannot be easily distinguished from one containing a spherical emulsion of neuronal soma such as in the gray matter as both motifs result in a similar isotropic diffusion tensor. A promising approach to probe heterogeneity within a MRI voxel was introduced by Jian et al. who described water diffusion using an ensemble of diffusion tensors drawn from a probability density function (pdf) in the space of diffusion tensors (i.e., diffusion tensor distribution, DTD) [8]. The MR signal is then expressed as the expected value of the Gaussian diffusion signal attenuation from the ensemble of micro-diffusion tensors sampled from the DTD. The goal of DTD MRI is to estimate the DTD from the measured MR signals in each voxel.

Determining a non-parametric DTD using the framework of Jian et al. is challenging due to the well known ill-posed nature of Laplace inversion [9]. The ill-posedness was partly overcome in several studies by reducing the dimension of DTD with or without regularization [10–13], using parametric DTDs [8, 12, 14], and using signal representations in terms of moments of DTD [15]. We previously proposed a normal tensor variate pdf that is constrained on the manifold of positive definite diffusion tensors (CNTVD) which is rich enough to describe a wide range of tissue heterogeneity and ensures monotonic signal decay with b-value unlike the cumulant signal representation which do not satisfy this constraint [16]. We also showed that the CNTVD is the maximum entropy distribution among all constrained pdfs with given first and second moments, which makes it the least biased distribution in the absence of any a priori information about the underlying tissue microstructure [17].

Using tensor algebra, we showed that rank-1 and rank-2 b-tensors generated in single and double-PFG experiments respectively are sufficient to accurately measure the first two moments of any DTD: the mean and covariance tensors [16]. However, implementing multiple-PFG (mPFG) MRI experiments [18, 19] can be challenging due to long echo time and coherence artifacts resulting from multiple RF pulses. Recently, q-trajectory imaging (QTI) methods introduced by Westin and coworkers overcame some of these challenges, however, with some attendant limitations, such as undefined diffusion gradient timing parameters that limit the physical interpretation of the MRI data, complex gradient waveforms that may be difficult to implement and sub-optimal gradient efficiency [15, 20, 21]. We had introduced a new pulse sequence which overcomes these drawbacks by sandwiching independent trapezoidal gradients on either side of the 180° RF pulse in a single spin echo (SE) sequence to generate arbitrary b-tensors of interest [22]. In addition to providing well defined diffusion gradient timing parameters and efficiency in terms of gradient utilization, our pulse sequence is also immune to concomitant gradient field artifacts which are known to affect DTD analysis [23].

Here, we apply our modeling framework with CNTVD and our novel pulse sequence to investigate the capabilities of DTD in resolving neural tissue microstructure using excised tissues at high k and q-space resolution. The small pulse widths and large gradient strengths feasible on microimaging scanners, combined with the low diffusivity of excised tissues allows us to probe length scales much smaller than that possible on an in vivo specimen on a typical clinical scanner. We first validate our method using an isotropic polydimethylsiloxane (PDMS) phantom and present results obtained in visual cortex and spinal cord specimen from perfusion-fixed macaque monkey. We also introduce new glyphs to help visualize the DTD covariance tensor which shows the variability in the diffusion tensors as a function of orientation. We show that our new method is capable of capturing the microscopic anisotropy and heterogeneity in both the brain and spinal cord specimen.

2 Materials and Methods

2.1 Theory

The MR signal from an ensemble of diffusion tensors distributed according to p (D_ij) is given by [8],

$S\left(b_{ij}\right)=S_0\left(\int e^{-b_{ij}{D}_{ij}}p\left(D_{ij}\right)d{D}_{ij}+\epsilon \right)(1)$

where S₀ is the signal without diffusion weighing, b_ij, D_ij are the second order symmetric diffusion tensor and diffusion weighting b-matrix or b-tensor, respectively [3] and ɛ is a scalar parameter to account for the non-zero signal that is known to persist at large b-values in neural tissue [24]. Assuming a CNTVD for p (D_ij), the signal equation is approximated using Monte Carlo (MC) integration with samples, D_ij, drawn from the CNTVD with a given mean and covariance tensor as shown below [16],

$S\left(b_{ij}\right)\approx S_0\left(\frac{{\sum }_{i=1}^n{e}^{-b_{ij}{D}_{ij}}\mathbf{1}\left(D_{ij}\in {\mathcal{M}}^{+}\right)}{{\sum }_{i=1}^n\mathbf{1}\left(D_{ij}\in {\mathcal{M}}^{+}\right)}+\epsilon \right)(2)$

where ${\mathcal{M}}^{+}$ is the space of positive definite second-order tensors, $\mathbf{1}(D_{ij}\in {\mathcal{M}}^{+})$ is the indicator function that is one when D_ij is positive definite and zero otherwise, and n is the number of MC samples (set to 200,000). For ease of sampling, the diffusion tensor is expressed as a 6D vector and covariance tensor as 6 × 6 symmetric positive definite matrix.

2.2 Pulse Sequence and Experimental Design

We used our new dPFG pulse sequence with an echo planar imaging (EPI) readout introduced in [22] to generate b-tensors of ranks 1 and 2 using trapezoidal gradients in a single spin echo. A compressed sensing type experimental design described in [16] was used to generate a set of rank-1 and rank-2 b-tensors. Briefly, eigenvectors of the b-tensor were randomly rotated to uniformly sample orientation while their two non-zero eigenvalues were constrained so that their sum and ratio follows an uniform distribution to uniformly sample the size and shape respectively. The physical diffusion gradient strengths in the new pulse sequence required to generate the desired b-tensors for a fixed δ and Δ are obtained by solving the equation, $b_{ij}=b_{ij}^{\prime }$, where $b_{ij}^{\prime }$ is the desired b-tensor and b_ij is the actual b-tensor numerically computed for a given diffusion weighted gradient set in the pulse sequence. The optimization was performed using a non-linear least squares fitting routine in MATLAB (Mathworks, Natick, MA) constrained by the current limits of the gradient hardware.

2.3 Specimen Preparation

Two adult rhesus macaque monkeys (Macaca mulatta) were perfused for the ex vivo MRI studies as described below. All procedures adhered to the Guide for the Care and Use of Laboratory Animals (National Research Council), and were carried out under a protocol approved by the Institutional Animal Care and Use Committee of the National Institute of Mental Health (NIMH) and National Institute of Health (NIH). First the animal was deeply anesthetized with sodium pentobarbital and perfused transcardially with 0.5 L of saline, followed by 4 L of 4% paraformaldehyde, both in 0.1 M phosphate buffer (pH 7.4). After the perfusion the brain was removed with intact spinal cord and post-fixed between 8 and 12 h in the same buffered paraformaldehyde solution and then transferred into 0.1 M phosphate buffered saline (PBS) with sodium azide. A portion of the tissue encompassing the primary (V₁) and secondary (V₂) area of the visual cortex and cervical spinal cord was dissected for MR imaging.

2.4 MRI Measurements and Image Pre-Processing

MRI data were acquired on a 7T vertical Bruker wide-bore Avance III MRI scanner (Bruker Biospin, Billerica, MA) equipped with a Micro2.5 microimaging probe and GREAT60 gradient amplifiers capable of generating up to 1.5 T/m gradient strength in all three axis. RF was transmitted and received using a 5 mm linear probe for polydimethylsiloxane (PDMS) and cortex, and 20 mm quadrature probe for the spinal cord. The DTD pulse sequence, gradient hardware, b-tensor calculations and model fitting were calibrated using 3.9 cSt cyclic PDMS in a 5-mm NMR tube at 17°C. Imaging was performed at 100 μm isotropic spatial resolution using 2-shot 3D EPI with the following parameters: Δ/δ = 20/5 ms, TR/TE = 1000/50 ms and 1 average. A total of 217 different b-tensors were sampled with b-values ranging from 0–12,000 s/mm².

Neural tissue (spinal cord and visual cortex) was immersed in perfluoro polyether (Fomblin, Solvay Specialty Polymers, Italy) for susceptibility matching and to achieve better image contrast. The imaging protocol was adjusted to suit the sample under study. The visual cortex specimen was imaged at 100 μm isotropic spatial resolution using 3-shot 3D EPI with the following parameters: TR/TE = 1000/38 ms and 4 averages. The spinal cord was imaged at 125 μm × 125 μm × 1 mm spatial resolution using 2-shot 3D EPI with the following parameters: TR/TE = 1000/60 ms and 4 averages. The b-tensors sampled and diffusion times used were identical to that acquired on PDMS.

The thermal noise in the images was filtered using a Marchenko-Pastur principal component analysis (PCA) algorithm [25] implemented in DIPY software [26], and the effect of eddy current induced image translation and shearing were reduced by registering the individual DWI volumes with b = 0 s/mm² acquisition using 3D affine transform [27, 28] implemented in FSL software [29] prior to DTD model fitting.

2.5 Parameter Estimation and Microstructural Imaging Stains

The second-order mean diffusion tensor and fourth-order covariance tensor characterizing the CNTVD were both estimated from the MR signal using methods outlined in [16]. Briefly, the different symmetries of the mean [30] and covariance tensors [31] were exploited to build a family of nested signal models, the most parsimonious of which was chosen using the Bayesian information criterion (BIC). For a given nested model, the MR signal is fit to Eq. 2 using a numerical optimization algorithm (COBYLA method [32] implemented in scipy’s optimize minimize subroutine in python) to estimate the unknown parameters.

The estimated CNTVD parameters are used to delineate several microstructural features within the voxel, which are also described in greater detail in [16]. Briefly, the micro-diffusion tensors in the voxel are simulated by drawing MC samples from the CNTVD with the estimated mean and covariance tensors. The macroscopic fractional anisotropy (FA) and orientation distribution function (ODF) are computed from the mean diffusion tensor, whereas the microscopic FA and ODF (i.e., μFA and μODF) are computed by averaging the ensemble of FAs and ODFs obtained in each of the micro diffusion tensors within the voxel. The size (V_size) and shape (V_shape) heterogeneity within a voxel are quantified by the median absolute deviation of average trace and FA-weighted eigenvalue skewness of the micro-diffusion tensors respectively, normalized by its value for the uniform distribution. The orientation heterogeneity within a voxel is quantified by extent of scatter about the mean eigenvector of the micro-diffusion tensors (V_orient) [16]. The spectrum or distribution of the mean diffusivity (MD) is obtained from plotting the histogram of average trace of micro-diffusion tensors from which moments such as the mean, standard deviation (σ_MD), and skewness are measured and mapped.

We previously showed that the kurtosis tensor is the fully symmetric part of the covariance tensor [16] and is thus subsumed by it, and can be visualized by taking projections of the covariance tensor along the unit vector [31]. In this work, we introduce a new glyph to visualize the asymmetric part of the covariance tensor, R_asymm(u), which becomes zero when the covariance tensor collapses to the fully symmetric kurtosis tensor as shown in Supplementary Section S1. In essence this glyph captures the additional information that is obtained with the dPFG measurements. The spherical functions describing these glyphs are as follows,

$R_{\text{sym}}\left(\mathbf{u}\right)={\mathsf{C}}_{\mathit{ijkl}}{u}_i{u}_j{u}_k{u}_l(3)$

$R_{\text{asymm}}\left(\mathbf{u}\right)=\sqrt{{⟨{\left({\mathsf{C}}_{\mathit{ijkl}}{u}_i{v}_j{u}_k{v}_l-{\mathsf{C}}_{\mathit{ijkl}}{u}_i{u}_j{v}_k{v}_l\right)}^2⟩}_{\mathbf{v}\perp \mathbf{u}}}(4)$

where $\mathsf{C}$ is the fourth order covariance tensor, u and v are orthogonal unit radius vectors, and angle brackets denotes averaging over all v for a given u. The analytic expression for orientation averaged terms above are derived in Supplementary Section S2.

3 Results

The DTD derived stains obtained in the PDMS phantom along with S₀ and offset parameter maps are shown in Figure 1. The stains obtained in PDMS were uniform across the sample with the offset accounting for approximately 2% of signal. The MD is approximately equal to 0.2 μm²/ms while all other stains were zero.

FIGURE 1

FIGURE 1. DTD derived stains obtained in PDMS phantom showing zero heterogeneity. This includes S₀ - non-diffusion weighted image, signal offset, ɛ, expressed as percent of S₀, MD—mean diffusivity, MD skewness— skewness of MD spectrum, FA—fractional anisotropy, μFA—microscopic fractional anisotropy, and V_size, V_shape, V_orient—size, shape and orientation heterogeneity respectively.

The stains obtained from a section of the visual cortex along with its overall location in the macaque brain is shown in Figure 2. The offset was approximately 5% in the cortex and 12% in the surrounding white matter. The cortical layers were delineated in MD standard deviation and skewness maps and to a lesser extent in V_size map similar to what was observed in histology. The cortex-white matter interface known to be injured in diseases such as traumatic brain injury (TBI) [33] was clearly identified as regions of high MD standard deviation. The white matter tract adjacent to the cortex, on either side of the inferior occipital sulcus (ios), despite having similar FA values were distinguished in the MD skewness map. Microscopic anisotropy was detected in the cortex with FA close to zero in many parts of the cortex $(\approx 0.2)$ while the μFA was elevated $(\approx 0.6)$. The high shape and orientation heterogeneity in the cortex reveals the source of this microscopic anisotropy maybe due to heterogeneously shaped neuronal soma and penetrating white matter tracts. The orientation heterogeneity stain exhibited higher values in regions of lower FA and vice-versa which is consistent with the picture that increased orientation heterogeneity of microscopic anisotropic structure tends to reduce the overall macroscopic anisotropy [5].

FIGURE 2

FIGURE 2. DTD derived stains obtained in a excised visual cortex of a macaque monkey showing microscopic anisotropy and heterogeneity. Approximate location in the macaque brain from which 10 mm ×5 mm × 5 mm piece was dissected for MR imaging shown using SMI-32 stained sections (highlights pyramidal neurons and their processes) in Saleem and Logothetis macaque brain atlas [50] in the left most column. The V₁ and V₂ areas of the visual cortex and inferior occipital sulcus (ios) are highlighted for reference. The DTD-derived stains shown include S₀—non-diffusion weighted image, signal offset, ɛ, expressed as percent of S₀, MD—mean diffusivity, MD skewness—skewness of MD spectrum, FA—fractional anisotropy, μFA—microscopic fractional anisotropy, and V_size, V_shape, V_orient - size, shape and orientation heterogeneity respectively.

Orientation dispersion in the visual cortex is shown by comparing macro and micro ODFs in two Gy-white matter interface regions highlighted in Figure 3 along with glyphs characterizing the covariance tensor of CNTVD. The asymmetric part of the covariance tensor was comparable to the symmetric part in many voxels in both the regions which show the additional information captured by the covariance tensor as compared to the kurtosis tensor alone. In interface 1, the macro ODFs in the gray and white matter show a single principal direction while the micro ODFs show the two fiber populations mixing. The symmetric part of the covariance tensor in the gray matter also show penetrating white matter fibers into the cortex. In interface 2, the macro ODFs are very similar while the micro ODFs show splaying of fibers.

FIGURE 3

FIGURE 3. Orientation dispersion observed in macaque visual cortex shown by comparing the macro and micro ODFs. The need for a DTD model and additional information obtained beyond the kurtosis tensor model is demonstrated by plotting the symmetric and asymmetric parts of the covariance tensor of the constrained normal tensor variate distribution. Two regions of interest (ROIs) at gray-white matter interface regions are highlighted in the direction-encoded color (DEC) map, showing the principal direction of the mean diffusion tensor, and S₀ map.

The stains obtained in cervical spinal cord are shown in Figure 4. The offset parameter in the spinal cord showed a similar contrast to that observed in the cortex, accounting for approximately 8% and 15% of the signal in gray and white matter respectively. DTD MRI identified sub-voxel features invisible with DTI. The intermediate zone (iz) in the gray matter and dorsal spinal nerve root (dsnr) exhibited highly skewed and broad MD distribution compared to other regions in the spinal cord. The intermediate zone also exhibited high size heterogeneity while zero shape and orientation heterogeneity thus indicating a spherical emulsion type DTD in this region. The spinal cord white matter appeared uniform in the size heterogeneity stain while the shape and orientation heterogeneity stains showed contrast with the peripheral tracts (e.g., gracile fasiculus, gf) exhibiting higher shape and orientation heterogeneity compared to the central white matter (e.g., lateral cortico-spinal tract, lcst). Microscopic anisotropy was detected in gray and peripheral white matter as shown by elevated μFA in this region with concomitant increase in shape and orientation heterogeneity.

FIGURE 4

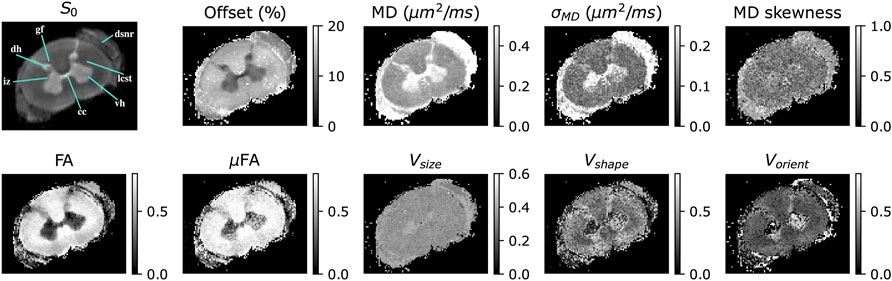
FIGURE 4. DTD derived stains obtained in a excised cervical spinal cord of macaque monkey showing microscopic anisotropy and heterogeneity. The following regions of interest in the spinal cord are highlighted in the non-diffusion weighted image (S₀): iz—intermediate zone, dh—dorsal horn, gf - gracile fasciculus, dsnr—dorsal spinal nerve root, lcst—lateral corticospinal tract, vh—ventral horn and cc—central canal. The DTD stains include the signal offset, ɛ, expressed as percent of S₀, MD—mean diffusivity, MD skewness—skewness of MD spectrum, FA—fractional anisotropy, μFA—microscopic fractional anisotropy, and V_size, V_shape, V_orient—size, shape and orientation heterogeneity respectively.

Orientation dispersion in representative white and gray-white matter interface regions in the spinal cord along with their covariance glyphs are shown in Figure 5. In white matter, macro and micro ODFs were uniform and indistinguishable showing a single principal fiber direction. The symmetric part of the covariance tensor was uniform, pointing along the principal fiber axis while the asymmetric part was close to zero. In the gray-white interface region, macro ODFs in the gray matter are planar while those in the white matter are linear. The micro ODFs show the fibers start splaying as they penetrate the gray matter with increased presence of orthogonal lateral fibers which was also visible in the symmetric part of the covariance tensor. The asymmetric part was close to zero in coherent white matter similar to what was observed in the cortex but non-zero in gray matter.

FIGURE 5

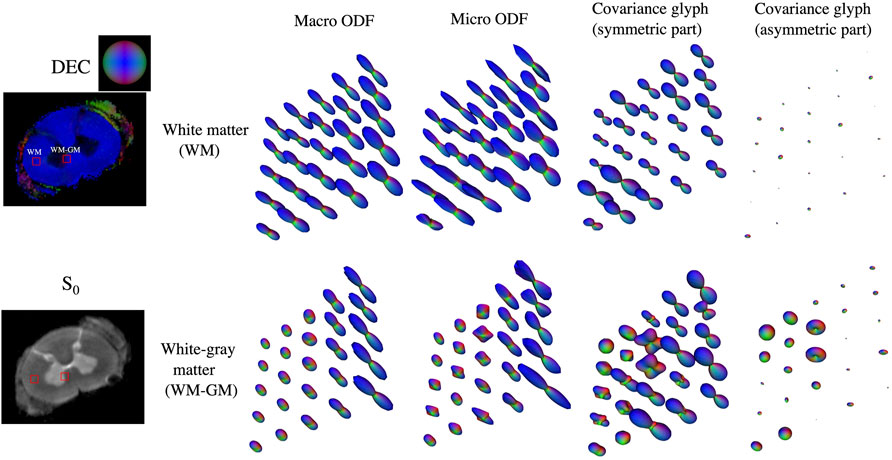
FIGURE 5. Orientation dispersion observed in macaque cervical spinal cord shown by comparing the macro and micro ODFs. The need for a DTD model and additional information obtained beyond the kurtosis tensor model is demonstrated by plotting the symmetric and asymmetric parts of the covariance tensor of the constrained normal tensor variate distribution. Two regions of interest (ROIs) one in white matter (WM) and gray-white matter (GM-WM) interface regions are highlighted in the direction encoded color (DEC) map, showing the principal direction of the mean diffusion tensor, and S₀ map.

4 Discussion

4.1 Validity of the Diffusion Tensor Distribution Method and its Measurement

At the length scales probed by DTD (discussed below), which still include a multitude of cells and processes, the Gaussian distribution of diffusion tensors provides a reasonable description for p(D). Gaussian diffusion within each micro-compartment, another assumption of the DTD methodology, is also reasonable given the likely absence of fully restricted compartments in the neural tissue due to the non-zero permeability of cell and organelle membranes to water mediated through lipid bilayer, aquaporins and transporters [34]. So, for instance, one would not expect to find significant microscopic restriction to water diffusion in live soft tissue as one would in some other porous media, such as sandstone and other rocks.

In the PDMS sample, the isotropic model was correctly selected for the mean tensor throughout the sample with mean diffusivity less than 5% from the actual value at ambient bore temperature set at 17°C and zero FA. The estimated covariance was zero as expected from the uniform DTD in the sample. The offset parameter which models noise in this case was less than 5% of the signal consistent with the DTI model fully explaining the MR signal. The so called “dot-compartment” thought to be present in neural tissue [24, 35] is also accounted for by the offset parameter in our model. Using spherical encoding, Tax et al. recently showed that the dot-compartment accounted for approximately 10% of the signal in the human brain which is close to what we observed in both the brain and spinal cord [36]. These results obtained using large b-values shows the accuracy of the b-tensor calculation and gradient pulses, and the pulse sequence free of artifacts.

4.2 Resolving Power of Diffusion Tensor Distribution MRI

The resolving power of DTD MRI is defined as the length of the smallest compartment, l, that can be distinguished in a DTD experiment. This length scale is limited by the pore saturation effect $\left(l\ge \sqrt{2D\delta }\right)$, extent of diffusion weighting $\left(l\ge \frac{\pi }{|{\mathbf{q}}_1+{\mathbf{q}}_2|}\right)$, and exchange rate $\left(k\le \frac{1}{\mathrm{\Delta }}\right)$. Given the diffusion gradient pulse width in our measurement and smallest measured MD, the diameter of the smallest resolvable compartment is approximately 4 μm which is approximately a factor of 4 smaller than that achieved on a typical clinical MRI scanner. At this length scale, individual axons in white matter and extra-cellular space are too small to be resolved by our measurement. However, heterogeneity in bundles of axons larger than 4 μm such as in kissing/crossing/splaying fibers should be detectable by our measurements. Setting the resolving power of the DTD experiment to the average axon diameter (i.e., 1 μm) and using the mean diffusivity of the brain tissue, the diffusion gradient strength and pulse duration required to probe axonal heterogeneity at this length scale are approximately 12 T/m (i.e., 1200 G/cm) and 1.5 ms, respectively. The former is an order of magnitude larger than what the gradient system used in this study can provide. In gray matter, DTD MRI can resolve cellular heterogeneity as shown by the delineation of cortical layers in MD spectra. This is in agreement with a recent electron microscopy study in human cerebral cortex which showed heterogeneity in cell sizes that vary across cortical layers [37].

4.3 Diffusion Tensor Distribution Derived Microstructural Information

The DTD measurement detected microscopic anisotropy and heterogeneity in gray and white matter of neural tissue consistent with previous findings [38, 39]. In the visual cortex, the higher moments of the MD spectrum showed unique features not visible in MD maps typically obtained via DTI [3]. The cortical layers visible in MD standard deviation and skewness maps matched well with the histology. The higher MD skewness in the adjacent whiter matter maybe reflective of the skewed distribution of axon fiber bundles in this region well known to exist in white matter regions. The shape and orientation heterogeneity in the cortex likely arose from a mixture of soma (spherical compartment) and splaying white matter fibers (prolate/oblate) known to enter the cortical region. DTD MRI clearly showed evidence of crossing and splaying of white matter fibers as they penetrate the cortex as shown by the μODF and covariance glyphs.

In the spinal cord, higher moments of MD in the intermediate zone is likely due to heterogeneous size of soma known to be present in this region. In white matter, the axon fiber diameters are known to be larger in nerve roots [40] and in peripheral regions of the cervical spinal cord [41, 42] compared to the central white matter which may have increased their conspicuity in DTD MRI. These regions are highlighted in the shape and orientation heterogeneity maps which has resulted in higher microscopic anisotropy. Non-zero orientation heterogeneity in gray matter could have arose from lateral white matter fibers that criss-cross this region [43]. This shows the ability of DTD-MRI to isolate white and gray matter heterogeneity within a voxel.

4.4 Covariance Tensor of Constrained Normal Tensor Variate Distribution vs. Kurtosis/Correlation Tensors and Previous Diffusion Tensor Distribution Implementations

The deviation of the diffusion weighted MR signal from the Gaussian decay has been represented using the kurtosis tensor based on q-vectors [44]. We showed mathematically that the kurtosis tensor is a fully symmetrized form of the more general covariance tensor based on the b-tensor [16] and may miss key features of tissue microstructure. In this study, we have experimentally verified that this is indeed the case for the neural tissue as the asymmetric part of the covariance tensor is non-vanishing. Recently, correlation tensor imaging [45, 46] was proposed to overcome some of the drawbacks of kurtosis tensor imaging by representing the dPFG signal using a collection of second and fourth order tensors to capture the asymmetric part in addition to the traditional mean diffusion and kurtosis tensors. However, this formalism may not be necessary as the covariance tensor formalism is more compact.

The covariance tensor measured in the QTI method is based on the cumulant expansion of the MR signal [15] with respect to the b-tensor, which is inaccurate as it leads to non-monotonic signal decay, thus limiting the range of b-values and the general applicability of that approach. This limitation is due to the inclusion of nonphysical negative definite micro-diffusion tensors as it can be observed that the signal expression is identical to that obtained by assuming a normal tensor variate distribution (NTVD) [47] in the DTD signal expression [8]. In this work, we have also overcome this drawback by constraining the micro-diffusion tensors to be positive definite which allows us to synthesize realistic micro-diffusion tensors from which salient statistical measures can be accurately measured and mapped. A limitation of our approach despite being general is the long computation time required for Monte-Carlo simulations since analytical signal model does not exist for CNTVD. However recent advances in computational hardware and software using graphics processing units (GPU) [48] should soon match the speed of direct signal inversion.

4.5 Prospective Applications

The proposed stains could inform normal and abnormal developmental and neurophysiology studies. The size heterogeneity stain may aid in detecting free water regions in the brain which have been implicated in diseases such as Parkinson’s [49]. The shape and orientation heterogeneity stains, and μODF glyphs may help detect subtle white matter changes implicated in several pathological conditions. Stronger Connectome-like gradients may enable improved cortical parcellation in live human subjects. As an addendum, while we have applied this approach to an isotropic phantom and fixed neural tissue in this work, this approach is readily applicable to imaging a broad range of tissues and tissue types outside the brain and spine in vivo, and various biological and non-biological materials and specimen suitable for MR analysis.

5 Conclusion

In this study, we present DTD measured in neural tissue. We demonstrate that our experimental design and signal inversion framework is able to capture heterogeneity in the brain and spinal cord. New heterogeneity stains may 1 day be useful in assessing disease, normal and abnormal developmental processes, degeneration and trauma in the brain and other soft tissues.

Data Availability Statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Ethics Statement

The animal study was reviewed and approved by Institutional Animal Care and Use Committee of the National Institute of Mental Health and National Institutes of Health.

Author Contributions

KM, DG and PB designed the research. MK wrote the pulse sequences and assisted with MRI measurements. KM performed the measurement, image analysis and drafted the manuscript. KS provided the specimen and helped interpret the results. All authors reviewed and edited the manuscript.

Funding

This work was supported by the Intramural Research Program (IRP) of the Eunice Kennedy Shriver National Institute of Child Health and Human Development, “Connectome 2.0: Developing the next generation human MRI scanner for bridging studies of the micro-, meso- and macro-connectome,” NIH BRAIN Initiative 1U01EB026996-01 and the CNRM Neuroradiology/Neuropathology Correlation/Integration Core, 309698-4.01-65310, (CNRM-89-9921).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Author Disclaimer

The opinions expressed herein are those of the authors and are not necessarily representative of those of the Uniformed Services University of the Health Sciences (USUHS), the Department of Defense (DOD), the NIH or any other US government agency, or the Henry M. Jackson Foundation for the Advancement of Military Medicine, Inc.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

This work utilized the computational resources of the NIH HPC Biowulf cluster (http://hpc.nih.gov). We would like to thank Dr. Wolfgang Resch for assisting with performing the computations in the NIH HPC cluster.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2022.807000/full#supplementary-material

References

1. Gilmore JH, Knickmeyer RC, Gao W. Imaging Structural and Functional Brain Development in Early Childhood. Nat Rev Neurosci (2018) 19(3):123–37. doi:10.1038/nrn.2018.1

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Moseley ME, Cohen Y, Mintorovitch J, Chileuitt L, Shimizu H, Kucharczyk J, et al. Early Detection of Regional Cerebral Ischemia in Cats: Comparison of Diffusion- and T2-Weighted MRI and Spectroscopy. Magn Reson Med (1990) 14(2):330–46. doi:10.1002/mrm.1910140218

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Basser PJ, Mattiello J, Lebihan D. Estimation of the Effective Self-Diffusion Tensor from the NMR Spin Echo. J Magn Reson Ser B. (1994) 103(3):247–54. doi:10.1006/jmrb.1994.1037

CrossRef Full Text | Google Scholar

4. Basser PJ, Mattiello J, LeBihan D. MR Diffusion Tensor Spectroscopy and Imaging. Biophysical J (1994) 66(1):259–67. doi:10.1016/s0006-3495(94)80775-1

CrossRef Full Text | Google Scholar

5. Pierpaoli C, Basser PJ. Toward a Quantitative Assessment of Diffusion Anisotropy. Magn Reson Med (1996) 36(6):893–906. doi:10.1002/mrm.1910360612

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Tuch DS, Reese TG, Wiegell MR, Wedeen VJ. Diffusion MRI of Complex Neural Architecture. Neuron (2003) 40(5):885–95. doi:10.1016/s0896-6273(03)00758-x

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Evren Ö, Mareci Thomas H. Generalized Diffusion Tensor Imaging and Analytical Relationships between Diffusion Tensor Imaging and High Angular Resolution Diffusion Imaging. Magn Reson Med (2003) 50(5):955–65. doi:10.1002/mrm.10596

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Jian B, Vemuri BC, Özarslan E, Carney PR, Mareci TH. A Novel Tensor Distribution Model for the Diffusion-Weighted MR Signal. NeuroImage (2007) 37(1):164–76. doi:10.1016/j.neuroimage.2007.03.074

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Callaghan Paul T. Translational Dynamics and Magnetic Resonance. Oxford University Press (2011).

Google Scholar

10. Avram Alexandru V, Sarlls Joelle E, Basser Peter J. Whole-Brain Imaging of Subvoxel T1-Diffusion Correlation Spectra in Human Subjects. Front Neurosci (2021) 15:682. doi:10.3389/fnins.2021.671465

CrossRef Full Text | Google Scholar

11. Avram AV, Sarlls JE, Basser PJ. Measuring Non-Parametric Distributions of Intravoxel Mean Diffusivities Using a Clinical MRI Scanner. NeuroImage (2019) 185:255–62. doi:10.1016/j.neuroimage.2018.10.030

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Topgaard D. Multidimensional Diffusion MRI. J Magn Reson (2017) 275:98–113. doi:10.1016/j.jmr.2016.12.007

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Yablonskiy DA, Bretthorst GL, Ackerman JJ. Statistical Model for Diffusion Attenuated MR Signal. Magn Reson Med (2003) 50(4):664–9. doi:10.1002/mrm.10578

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Alexis R. Matrix Moments of the Diffusion Tensor Distribution and Matrix-Variate Gamma Approximation. J Magn Reson Open (2021) 8:100016–9. doi:10.1016/j.jmro.2021.100016

CrossRef Full Text | Google Scholar

15. Westin CF, Knutsson H, Pasternak O, Szczepankiewicz F, Özarslan E, van Westen D, et al. Q-Space Trajectory Imaging for Multidimensional Diffusion MRI of the Human Brain. NeuroImage (2016) 135:345–62. doi:10.1016/j.neuroimage.2016.02.039

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Magdoom KN, Magdoom KN, Pajevic S, Dario G, Basser PJ. A New Framework for MR Diffusion Tensor Distribution. Sci Rep (2021) 11(1):2766. doi:10.1038/s41598-021-81264-x

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Jaynes ET. Information Theory and Statistical Mechanics. Phys Rev (1957) 106(4):620–30. doi:10.1103/physrev.106.620

CrossRef Full Text | Google Scholar

18. Mitra PP. Multiple Wave-Vector Extensions of the NMR Pulsed-Field-Gradient Spin-echo Diffusion Measurement. Phys Rev B (1995) 51(21):15074–8. doi:10.1103/physrevb.51.15074

CrossRef Full Text | Google Scholar

19. Jespersen SN, Lundell H, Sønderby CK, Dyrby TB. Orientationally Invariant Metrics of Apparent Compartment Eccentricity from Double Pulsed Field Gradient Diffusion Experiments. NMR Biomed (2013) 26(12):1647–62. doi:10.1002/nbm.2999

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Daniel T. Isotropic Diffusion Weighting in PGSE NMR: Numerical Optimization of the Q-MAS PGSE Sequence. Microporous Mesoporous Mater (2013) 178:60–3. doi:10.1016/j.micromeso.2013.03.009

CrossRef Full Text | Google Scholar

21. Jens S, Filip S, Markus N, Daniel T, Carl-Fredrik W, Hans K. Constrained Optimization of Gradient Waveforms for Generalized Diffusion Encoding. J Magn Reson (2015) 261:157–68. doi:10.1016/j.jmr.2015.10.012

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Magdoom KN, Komlosh Michal E, Dario G, Basser Peter J. Diffusion Tensor Distribution (DTD) MRI Reimagined. In: International Society for Magnetic Resonance in Medicine (2020).

Google Scholar

23. Szczepankiewicz F, Westin CF, Nilsson M. Maxwell-compensated Design of Asymmetric Gradient Waveforms for Tensor-Valued Diffusion Encoding. Magn Reson Med (2019) 82(4):1424–37. doi:10.1002/mrm.27828

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Bretthorst G. Larry. Characterizing Water Diffusion in Fixed Baboon Brain. In: AIP Conference Proceedings (2004).

Google Scholar

25. Veraart J, Novikov DS, Christiaens D, Ades-Aron B, Sijbers J, Fieremans E. Denoising of Diffusion MRI Using Random Matrix Theory. NeuroImage (2016) 142:394–406. doi:10.1016/j.neuroimage.2016.08.016

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Garyfallidis E, Brett M, Amirbekian B, Rokem A, van der Walt S, Descoteaux M, et al. Dipy, a Library for the Analysis of Diffusion MRI Data. Front Neuroinform (2014) 8(FEB):8. doi:10.3389/fninf.2014.00008

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Jenkinson M, Smith S. A Global Optimisation Method for Robust Affine Registration of Brain Images. Med image Anal (2001) 5(2):143–56. doi:10.1016/s1361-8415(01)00036-6

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Jenkinson M, Bannister P, Brady M, Smith S. Improved Optimization for the Robust and Accurate Linear Registration and Motion Correction of Brain Images. NeuroImage (2002) 17(2):825–41. doi:10.1016/s1053-8119(02)91132-8

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Smith SM, Jenkinson M, Woolrich MW, Beckmann CF, Behrens TE, Johansen-Berg H, et al. Advances in Functional and Structural MR Image Analysis and Implementation as FSL. NeuroImage (2004) 23(Suppl. 1):S208–S219. doi:10.1016/j.neuroimage.2004.07.051

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Freidlin RZ, Ozarslan E, Komlosh ME, Lin-Ching C, Jones DK, Basser PJ. Parsimonious Model Selection for Tissue Segmentation and Classification Applications: A Study Using Simulated and Experimental DTI Data. IEEE Trans Med Imaging (2007) 26(11):1576–84. doi:10.1109/tmi.2007.907294

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Basser PJ, Pajevic S. Spectral Decomposition of a 4th-Order Covariance Tensor: Applications to Diffusion Tensor MRI. Signal Process. (2007) 87(2):220–36. doi:10.1016/j.sigpro.2006.02.050

CrossRef Full Text | Google Scholar

32. Powell MJD. Direct Search Algorithms for Optimization Calculations. Acta Numerica (1998) 7:287–336. doi:10.1017/s0962492900002841

CrossRef Full Text | Google Scholar

33. Peerless SJ, Rewcastle NB. Shear Injuries of the Brain. Can Med Assoc J (1967) 96(10):577–82.

PubMed Abstract | Google Scholar

34. MacAulay N, Hamann S, Zeuthen T. Water Transport in the Brain: Role of Cotransporters. Neuroscience (2004) 129(4):1029–42. doi:10.1016/j.neuroscience.2004.06.045

CrossRef Full Text | Google Scholar

35. Stanisz GJ, Wright GA, Henkelman RM, Szafer A. An Analytical Model of Restricted Diffusion in Bovine Optic Nerve. Magn Reson Med (1997) 37(1):103–11. doi:10.1002/mrm.1910370115

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Tax CMW, Szczepankiewicz F, Nilsson M, Jones DK. The Dot-Compartment Revealed? Diffusion MRI with Ultra-strong Gradients and Spherical Tensor Encoding in the Living Human Brain. NeuroImage (2020) 210:116534. doi:10.1016/j.neuroimage.2020.116534

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Shapson-Coe A, Michał J, Berger Daniel R. A Connectomic Study of a Petascale Fragment of Human Cerebral Cortex. bioRxiv (2021). doi:10.1101/2021.05.29.446289

CrossRef Full Text | Google Scholar

38. Komlosh ME, Lizak MJ, Horkay F, Freidlin RZ, Basser PJ. Observation of Microscopic Diffusion Anisotropy in the Spinal Cord Using Double-Pulsed Gradient Spin echo MRI. Magn Reson Med (2008) 59(4):803–9. doi:10.1002/mrm.21528

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Lawrenz M, Finsterbusch J. Detection of Microscopic Diffusion Anisotropy in Human Cortical gray Matter In Vivo with Double Diffusion Encoding. Magn Reson Med (2019) 81(2):1296–306. doi:10.1002/mrm.27451

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Barth H. Group Conduction Velocities and Nerve Fibre Diameters of Alpha and Gamma-Motoneurons from Lower Sacral Nerve Roots of the Dog and Humans. Gen Physiol Biophys (1992) 11:85–99.

PubMed Abstract | Google Scholar

41. Zaimi A, Wabartha M, Herman V, Antonsanti PL, Perone CS, Cohen-Adad J. AxonDeepSeg: Automatic Axon and Myelin Segmentation from Microscopy Data Using Convolutional Neural Networks. Sci Rep (2018) 8(1):3816–1. doi:10.1038/s41598-018-22181-4

PubMed Abstract | CrossRef Full Text | Google Scholar

42. Duval T, Saliani A, Nami H, Nanci A, Stikov N, Leblond H, et al. Axons Morphometry in the Human Spinal Cord. NeuroImage (2019) 185:119–28. doi:10.1016/j.neuroimage.2018.10.033

PubMed Abstract | CrossRef Full Text | Google Scholar

43. Saliani A, Perraud B, Duval T, Stikov N, Rossignol S, Cohen-Adad J. Axon and Myelin Morphology in Animal and Human Spinal Cord. Front Neuroanat (2017) 11:129. doi:10.3389/fnana.2017.00129

PubMed Abstract | CrossRef Full Text | Google Scholar

44. Jensen JH, Helpern JA, Ramani A, Lu H, Kaczynski K. Diffusional Kurtosis Imaging: The Quantification of Non-gaussian Water Diffusion by Means of Magnetic Resonance Imaging. Magn Reson Med (2005) 53(6):1432–40. doi:10.1002/mrm.20508

PubMed Abstract | CrossRef Full Text | Google Scholar

45. Henriques RN, Jespersen SN, Shemesh N. Correlation Tensor Magnetic Resonance Imaging. NeuroImage (2020) 211:116605. doi:10.1016/j.neuroimage.2020.116605

PubMed Abstract | CrossRef Full Text | Google Scholar

46. Jespersen SN. Equivalence of Double and Single Wave Vector Diffusion Contrast at Low Diffusion Weighting. NMR Biomed (2012) 25(6):813–8. doi:10.1002/nbm.1808

PubMed Abstract | CrossRef Full Text | Google Scholar

47. Basser PJ, Pajevic S. A normal Distribution for Tensor-Valued Random Variables: Applications to Diffusion Tensor MRI. IEEE Trans Med Imaging (2003) 22(7):785–94. doi:10.1109/tmi.2003.815059

PubMed Abstract | CrossRef Full Text | Google Scholar

48. Przybylski A, Thiel B, Keller-Findeisen J, Stock B, Bates M. Gpufit: An Open-Source Toolkit for GPU-Accelerated Curve Fitting. Sci Rep (2017) 7(1):15722–9. doi:10.1038/s41598-017-15313-9

PubMed Abstract | CrossRef Full Text | Google Scholar

49. Ofori E, Pasternak O, Planetta PJ, Li H, Burciu RG, Snyder AF, et al. Longitudinal Changes in Free-Water within the Substantia Nigra of Parkinson's Disease. Brain (2015) 138(8):2322–31. doi:10.1093/brain/awv136

PubMed Abstract | CrossRef Full Text | Google Scholar

50. Saleem Kadharbatcha S, Logothetis Nikos K. A Combined MRI and Histology Atlas of the Rhesus Monkey Brain in Stereotaxic Coordinates. San Diego: Elsevier/Academic Press (2012).

Google Scholar