Introduction of the Hezar International Gravity Formula

The National Cartographic Center of Iran measured the differences in gravity between the Hezar summit and peak of Mount Damavand using a CG-5 gravity meter. The gravity recorded at the Hezar summit (4,499.416 m) was 213 mGal (0.00213 m/s²) lower than the reading recorded at the peak of Mount Damavand (5,605.730 m). Recently, the exact value of gravity at the Hezar summit and peak of Damavand mount have been measured. This study attempts to modify the conventional version of Hezar International Gravity Formula (HIGF) to calculate the experimental gravity in the Earth’s summits and land surfaces. Apart from describing the 213 mGal difference in gravity between Hezar summit and peak of Mount Damavand, HIGF is also in agreement with practical gravity with distance from sea level and latitude (93% confidence level). The results indicated that the experimental HIGF as g =978,031.85 (1 + 0.0053024 sin²θ−0.000032309786 sin²2θ)−0.27 h was in agreement with the practical gravity compared to the 1984 International Gravitational Formula (IGF84).

Introduction

The Earth is spheroidal and its surface is spheroid. In 1930, the International Gravity Formula (IGF) was adopted to calculate the theoretical value of gravity at any point on the spheroid. The 1930 IGF was based on Clairaut’s model, which was first developed in 1777. The 1930 IGF also incorporated the Potsdam datum. However, the 1930 IGF was further modified in 1967 by Geodetic Reference System (GRS 67), which was then refined and described by Woollard in 1979 using accurate satellite data by Jacobs in 1974. The GRS 67 was compatible with the International Gravity Standardisation Net 1971 datum. The differences between the 1930 IGF and GRS 67 were discussed by Lysonski [1]. The IGF does not explicitly depend on the Earth’s flattening because it is a theoretical gravity model [2]. Moreover, various systematic errors in computing the normal gravity were observed at the topographical surface on the Earth [3]. Hence, the new formulation of gravity required the computation of normal gravity at different points. The two Earth Gravitational Models (EGM) that are the best models to calculate gravity include EGM96 and EGM2008 [4], while the best-known IGFs are GRS30, GRS1967, GRS80 and WGS84 [5, 6]. Of which, the WGS84 equation was modified by several scholars [1, 6–8].

Almost all of the above mentioned models are theoretical models to estimate Earth’s gravity. Therefore, this study focuses on the formulation of an experimental model to estimate Earth’s gravity. The study revealed that the WGS84 model cannot explain the experimental gravity of the summits and the Earth’s surface, including the difference of −203 mGal in gravity between the peaks of the Hezar and Damavand mountains (4,499.416 m and 5,605.730 m, respectively) [9]. According to the physical geodetic survey performed at the National Cartographic Center of Iran (NCC), the gravity of summit Hezar is 203 mGa l lower than that of Mount Damavand’s peak. Therefore, the Hezar summit unexpectedly has a low gravity value throughout Iran. In the present study, we introduced a new four-coefficient gravimetric formula where the coefficients are calculated using experimental gravity data from four-point sets around the world. This experimental gravity equation was introduced in the form of the Hezar International Gravitational Formula (HIGF). The gravity at different elevations and latitudes can be measured using the HIGF and compared with the modified IGF84 (WGS84) [8]. The main novelty of this study is the formulation of four coefficients gravity formula based on the gravity measurement above sea level. In the following section, details of the HIGF equation are explained.

The Four Coefficients Gravity Formula

Since the Earth is spherical, the gravity is calculated using Eq. 1:

$g=G\frac{M}{r^2}(1)$

Where G is the gravitational constant, M is the mass of the Earth and r is the distance from the centre of the Earth.

The effects of non-spherical Earth, rotation of the Earth, distance of the elliptical Earth, free air correction [8] and the Bouguer phenomenon [10] on gravity were also investigated. The IGF with four coefficients was introduced as Eq. (2) [1, 5–7].

$g=A+B{\mathit{sin}}^2\theta +C{\mathit{sin}}^{2}2\theta -Dh(2)$

Where h and θ denote the height and latitude, respectively.

The changes in gravity due to the heights of the ellipsoidal Earth are introduced as 0.3086h [8]. The effect of Bouguer anomaly defined by the function of the density of the rock (ρ = 2.65 g.m³) and the height (h) is denoted as 0.04193ρh [8]. Therefore, accurate gravitational values can be obtained everywhere depending on the global Bouguer gravity anomaly illustrated in Figure 1 [11].

FIGURE 1

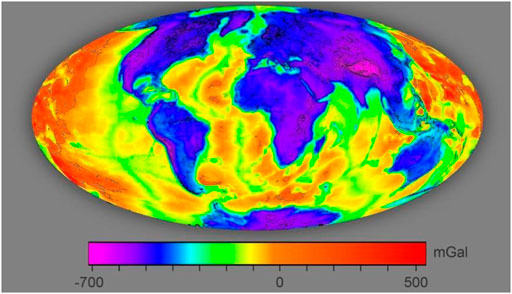
FIGURE 1. Bouguer gravity anomaly of the world [11].

The detail for Eq. (2) calculation is as below:

Earth is considered to be in three forms. In the first form, the Earth is ellipsoidal in uniformity with a radius, r, with r = R_e ( –F Sin²θ), where F is denoted in Eq. 3.

$\mathrm{F}=\frac{R_e- R_o}{R_e}(3)$

F is the asymmetry parameter of the spherical, R_e is the radius of the Earth at the equator and θ is the latitude. In the second form, the geoid is considered to be approximately +150 to −150 m above or below the elliptical Earth. The final form refers to the uneven distance on the surface of the Earth (h) from the elliptical Earth. According to the non-sphericity of the Earth and the changes in distance from the centre of the Earth, the interval change between each point on Earth and the centre of Earth is defined in Eq. (4):

$r=R_e\left(\mathit{1}-FSi{n}^2\theta \right)+h(4)$

$r=R_e\left(\mathit{1}-FSi{n}^2\theta +\frac{h}{R_e}\right)(5)$

$g=g_e\left(\mathit{1}-\mathit{2}\frac{h}{R_e}+\mathit{2}FSi{n}^2\theta +\mathit{3}{F}^{2}Si{n}^4\theta +\mathit{3}{\left(\frac{h}{R_e}\right)}^2-\mathit{6}Si{n}^2\theta \right)(6)$

According to the small amount of the last two terms, (Eq. 6) can be reiterated as Eq. 7.

$g=g_e\left(1+2FSi{n}^2\theta +3F^{2}Si{n}^4\theta \right)-2\frac{g_e}{R_e}h(7)$

The acceleration due to Earth’s rotation is represented by Eq. 8.

$a_R=R{\omega }^2=\left(r+h\right)Cos\theta {\omega }^2(8)$

The component of $a_R$ in the direction of r is presented as Eqs 9, 10.

$a_r=a_{R}Cos\theta (9)$

$a_r=\left(r+h\right)Co{s}^2\theta {\omega }^2(10)$

Using Eq. (5) and (Eq. 10) can also be modified into Eq. 11.

$a_r=R_e{\omega }^{2}Co{s}^2\theta -\frac{F R_e {\omega }^2}{4}Si{n}^{2}2\theta +h{\omega }^{2}Co{s}^2\theta (11)$

The effects of rotation on Earth’s gravity is obtained by substituting Eq. 7 and (11) with Eq. 12.

$g=g_e\left(1-\frac{R_e {\omega }^2}{g_e}+\left(2F+\frac{R_e {\omega }^2}{g_e}\right)Si{n}^2\theta +3F^{2}Si{n}^4\theta +\frac{2F R_e {\omega }^2}{4 g_e}Si{n}^{2}2\theta \right)-\left(2\frac{g_e}{R_e}+{\omega }^{2}Co{s}^2\theta \right)h(12)$

By ignoring ${\omega }^{2}Co{s}^2\theta$, because ω²<<1, Eq. (12) is expressed as Eq. 13.

$g=g_e\left(1-\frac{R_e {\omega }^2}{g_e}+\left(2F+\frac{R_e {\omega }^2}{g_e}\right)Si{n}^2\theta +3F^{2}Si{n}^4\theta +\frac{2F R_e {\omega }^2}{4 g_e}Si{n}^{2}2\theta \right)-\left(2\frac{g_e}{R_e}\right)h(13)$

The second part of Eq. (13) involving free-air correction presents the gravity changes due to the height of the ellipsoidal Earth, 0.3086 h [8]. Moreover, the effect of the Bouguer anomaly in Eq. (13) requires the formulation of the overall Bouguer effect as a function of the density of the rock (ρ = 2.65 g/cm³) and the height (h) denoted as 0.04193 ρh [8]. Therefore, accurate gravity can be measured everywhere depending on the global Bouguer gravity anomaly (Figure 1) [11].

By introducing $A=g_e\left(1-\frac{R_e {\omega }^2}{g_e}\right)$, $B=g_e\left(2F+\frac{R_e {\omega }^2}{g_e}\right)$, $C=\frac{F R_e {\omega }^2}{2}$, and $D=\left(2\frac{g_e}{R_e}\right)$, Eq. (13) can be rewritten as Eq. (2).

Coefficients A, B, C and D were calculated through the theoretical investigation of IGF84. In this study, coefficients A, B, C, and D were determined, and the HIGF formula was introduced using the experimental Earth gravitation data. The HIGF formula indicated high coincidence with the experimental data compared to the IGF84 formulation.

There are many gravitational formulas based on the format of Eq. (2), including FIG 1984 (WGS84) [5, 6], FIG 1987 (the modified version of WGS84) [1, 7] and the previous version of HIGF [9]. These formulas can be expressed as Eqs 14, 15 respectively.

$g_{84}=978032.68\left(1+0.0053024{\sin }^2\theta -0.0000058{\sin }^{2}2\theta \right)-0.3086h(14)$

$g_{84m}=978032.68\left(1+0.00193185138639{\sin }^2\theta \right){\left(1-0.00669437999013{\sin }^2\theta \right)}^{-0.5}-0.3086h(15)$

Where the behaviour of gravity variation versus elevation or free air effect (−0.3073 h) is close to Δg_h = -(0.3087691-0.0004398sin²θ) h+7.2125 × 10⁻⁸h² ≈ −0.3087 h [12]. The effect of the Bouguer anomaly is included in Eqs (2), (14) and (15) through the addition of the term 0.04193 ρh = 0.04193 × 2.65 h = 0.1111 h. Gravity at many points within Iran and across the world was calculated using Eqs (2), (14) without considering the Bouguer anomaly. However, when the Bouguer anomaly was included in the equations, the gravity formulas yielded the same offset values (0.1111 h). Meanwhile, the gravity of many points around the world was measured using the CG-5 gravimeters and other devices [13, 15, 16] (Table 1). Comparatively, the gravity calculated using Eqs (2), (14) revealed a slight difference to that of the experimental data. Hence, to estimate accurate gravity, a new gravity formula was proposed in this study using the Gauss-Jordan matrix elimination algorithm and practical gravitation data as the experimental HIGF.

TABLE 1

TABLE 1. The gravity of many locations in the world calculated using HIGF and IGF84 [13–15].

Introducing Hezar International Gravity Formula

According to Eq. (2), there is a polynomial equation for Earth’s gravity using four constant coefficients. These four constant coefficients can be determined with an accurate measurement of gravity at four different points with different coordinates and elevations. For instance, by choosing the poles, equator, summits of Damavand and Hezar as four points on Earth, the four equations of gravity for the four points on Earth are denoted in Eq. (16).

$\begin{array}{l}{g}_D=A+BSi{n}^2{\theta }_D+CSi{n}^{2}2{\theta }_D-D{h}_D\\ g_H=A+BSi{n}^2{\theta }_H+CSi{n}^{2}2{\theta }_H-D{h}_H\\ g_E=A+BSi{n}^2{\theta }_E+CSi{n}^{2}2{\theta }_E-D{h}_E\\ g_P=A+BSi{n}^2{\theta }_P+CSi{n}^{2}2{\theta }_P-D{h}_P\end{array}(16)$

Where g_P, g_E, g_D, g_H; θ_P, θ_E, θ_D, θ_H; and h_P, h_E, h_D, h_H refer to the gravity, latitude, and elevation of the Poles, Equator, the peaks of Mount Damavand and Hezar, respectively. These equations can also be represented in the form of matrix MX = Y as in Eq. (17).

$X=\left(\begin{array}{c}A\\ B\\ C\\ D\end{array}\right),Y=\left(\begin{array}{c}{g}_D\\ g_H\\ g_E\\ g_P\end{array}\right),M=\left(\begin{array}{cccc}1& Si{n}^2{\theta }_D& Si{n}^{2}2{\theta }_D& -h_D\\ 1& Si{n}^2{\theta }_H& Si{n}^{2}2{\theta }_H& -h_H\\ 1& Si{n}^2{\theta }_E& Si{n}^{2}2{\theta }_E& -h_E\\ 1& Si{n}^2{\theta }_P& Si{n}^{2}2{\theta }_P& -h_P\end{array}\right)(17)$

Using the matrix geometry and the definitions of (Eq. 16, 17) can be converted to X = MM⁻¹Y and by solving it, the matrix of coefficients (X) can be calculated.

The mean experimental coefficients A, B, C and D of the experimental HIGF were calculated by substituting the coordinate and gravitational data of the poles, equatorial vertices, Damavand and Hezar summits along with four other sets of different points presented in Table 1.

Results and Discussion

The coefficient of the associated matrix following the resolution was calculated and substituted into Eq. (1). Hence, the experimental HIGF is presented as Eq. 18.

$g=978031.85\left(1+0.0053024{\sin }^2\theta -0.000032309786{\sin }^{2}2\theta \right)-0.27h(18)$

The gravity of many points in the world was calculated using the HIGF (Eq. (18)). The differences between the HIGF and practical gravity of these points are presented in Table 1.

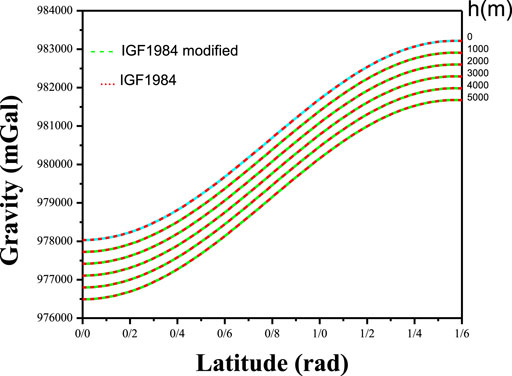
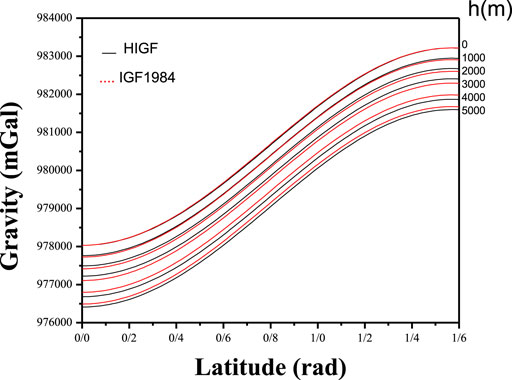
Figure 2 presents the behaviour of g_84m and g₈₄ by adding the free air effect or Δ_gh = −(0.3087691−0.0004398sin²θ)h + 7.2125 × 10⁻⁸ h² ≈-0.3086 h to Eqs (2), (14). Figure 2 also illustrates the differences between g_84m and g₈₄ at different heights and latitudes. According to Figure 2, no differences were observed between g_84m and g₈₄ formulations. Therefore, the g₈₄ or IGF84 with four coefficients was used to compare/analyse the differences between HIGF and IGF84 gravity formulations. Figure 3 depicts the differences between HIGF and IGF84 gravity formulations at different heights and latitudes. According to Figure 3, HIGF and IGF84 exhibited a good match near sea level and at different altitudes. Contrarily, HIGF’s behaviour is not similar to that of IGF84 above sea level because the HIGF formulation is based on experimental data and is a better formulation for the extraction of gravity above sea level compared to the formulation of IGF84. Table 1 summarises the gravity at many points calculated by HIGF and IGF84, their practical data [13–15] along with the differences between HIGF, IGF84, and practical gravity.

FIGURE 2

FIGURE 2. Behaviours of g84 m and g84 versus latitude at different heights.

FIGURE 3

FIGURE 3. Behaviours of the HIGF and IGF84 as a function of latitude at different heights.

Tables 1 and 2 also depict the chi-square {Sum [(Obs-Exp)²/Exp]} for HIGF and IGF84 as (Obs) and practical data as (Exp). According to Table 2, the chi-square values for Obs and Exp data were 0.291,008 and 0.787,851, respectively. Therefore, HIGF is more consistent with the experimental results compared to IGF84. Figure 4 illustrates the practical data at the heights of 0–100 m and latitudes of 0–90° in comparison with the HIGF and IGF84 formula. Based on the figure, HIGF and IGF84 are in good agreement with the experimental results (triangular mark) at lower altitudes. However, above sea level, HIGF performed similarly to the experimental data due to the low chi-square values at high altitudes. Therefore, the HIGF is more consistent with the experimental results compared to IGF84.

TABLE 2

TABLE 2. Chi-square of HIGF, IGF84 and practical data.

FIGURE 4

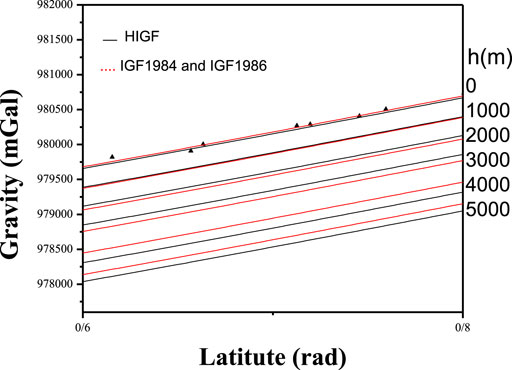
FIGURE 4. Practical data at an elevation range of 0–100 m and latitude of 0–90° with the HIGF and IGF84 profile.

The differences between the gravity of the peaks of Hezar and Mount Damavand using HIGF and IGF84 are as follows:

$\begin{array}{l}\left[\mathrm{g}\mathrm{H}\mathrm{e}\mathrm{z}\mathrm{a}\mathrm{r}-\mathrm{g}\mathrm{D}\mathrm{a}\mathrm{m}\mathrm{a}\mathrm{v}\mathrm{a}\mathrm{n}\mathrm{d}\right]\mathrm{H}\mathrm{I}\mathrm{G}\mathrm{F}=-214\mathrm{m}\mathrm{G}\mathrm{a}\mathrm{l}\\ \left[\mathrm{g}\mathrm{H}\mathrm{e}\mathrm{z}\mathrm{a}\mathrm{r}-\mathrm{g}\mathrm{D}\mathrm{a}\mathrm{m}\mathrm{a}\mathrm{v}\mathrm{a}\mathrm{n}\mathrm{d}\right]\mathrm{I}\mathrm{G}\mathrm{F}84=-187\mathrm{m}\mathrm{G}\mathrm{a}\mathrm{l}\end{array}(19)$

The experimental data indicated that the difference in the gravity of the peaks of Hezar and Mount Damavand was −203 mGal [9]. According to this data, the difference between HIGF, IGF84 and the experimental data were 11 and 16 mGal. Therefore, the HIGF is a better formula than IGF84. Based on the results in Table 1, HIGF can be introduced as an experimental Earth gravity formulation of every point in the sea and above sea level.

Conclusion

The rotating ellipsoidal Earth served as the basis for the International Gravity Formula adopted at the General Assembly of the International Union of Geodesy and Geophysics (IUGG). One particular ellipsoid of revolution is also called the normal Earth. The Geodetic Reference System 1967, Geodetic Reference System 1980 and World Geodetic System 1984 are all the “normal Earth” models. This paper is based on the theoretical normal Earth model formulation with 4 coefficients. These 4 coefficients in World Geodetic System 1984 were calculated using theoretical calculation. However, in this paper they were extracted by experimental calculation. Whereby, in this paper, an experimental gravity equation as Hezar International Gravity Formula (HIGF) was introduced using the experimental gravity of Earth data. In conclusion, HIGF provides accurate results as it is in better agreement with the practical data compared to IGF84.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding authors.

Author Contributions

MH, and SK, and MR, gave significant involvement to design, analysis, characterization, experimental, and application. MR, contributed to the conception and analytical approach of the article for important intellectual content. MRIF and MUK provided critical revision of the article.

Funding

This work was supported by the Research Universiti Grant, Universiti Kebangsaan Malaysia, Dana Impak Perdana (DIP), code: 2020-018.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Moritz H. Geodetic Reference System 1980. J Geodesy (2000) 74(1):128–33. doi:10.1007/s001900050278

CrossRef Full Text | Google Scholar

2. Abdel Zaher M, Elbarbary S, El-Shahat A, Mesbah H, Embaby A. Geothermal Resources in Egypt Integrated with GIS-Based Analysis. J Volcanology Geothermal Res (2018) 365:1–12. doi:10.1016/j.jvolgeores.2018.09.013

CrossRef Full Text | Google Scholar

3. Vajda P, Pánisová J. Practical Comparison of Formulae for Computing normal Gravity at the Observation point with Emphasis on the Territory of Slovakia. Contrib Geophys Geodesy (2005) 35(2):173–88.

Google Scholar

4. Claessens SJ, Featherstone WE, Anjasmara IM. Gravity, Geoid and Earth Observation. Berlin, Heidelberg: Springer (2010). p. 473–9. doi:10.1007/978-3-642-10634-7_63Is Australian Data Really Validating EGM2008, or Is EGM2008 Just In/validating Australian Data?

CrossRef Full Text | Google Scholar

5. Hackney R. Gravity, Data to Anomalies. Encyclopedia of Solid Earth Geophysics. Dordrecht: Springer (2020). p. 1–10.

CrossRef Full Text | Google Scholar

6. Chu PC. Ocean Dynamic Equations with the Real Gravity. Scientific Rep (2021) 11(1):1–10. doi:10.1038/s41598-021-82882-1

CrossRef Full Text | Google Scholar

7. Pail R, Goiginger H, Schuh WD, Höck E, Brockmann JM, Fecher T, et al. Combined Satellite Gravity Field Model GOCO01S Derived from GOCE and GRACE. Geophys Res Lett (2010) 37:1–5. doi:10.1029/2010gl044906

CrossRef Full Text | Google Scholar

8. Okocha FC. Gravitational Study of the Hastings Salt Dome and Associated Faults in Brazoria and Galveston Counties, Texas. Texas: Stephen F. Austin State University (2017). Doctoral dissertation. doi:10.1130/abs/2017sc-289183

CrossRef Full Text | Google Scholar

9. Rezaie MR, Hosseinzadeh P. Hezar International Gravity Formula. In: Proceeding of Annual Physics Conference of Iran 26th, 11-14 September 2010, Bu-Ali Sina University, Hamadan, Iran (2010). 1587-1590.

Google Scholar

10. Sabri LM, Sudarsono B, Jamal J, Mawardi S. Generating Bouguer Anomaly Map from Airborne Gravity Data (A Case Study in South East Sulawesi). Elipsoida: Jurnal Geodesi dan Geomatika (2020) 3.

Google Scholar

11.ESA. Bouguer Gravity Anomaly (2015). Available at: https://www.esa.int.

Google Scholar

12. Hinze WJ, Aiken C, Brozena J, Coakley B, Dater D, Flanagan G, et al. New Standards for Reducing Gravity Data: The North American Gravity Database. Geophysics (2005) 70(4):J25–J32. doi:10.1190/1.1988183

CrossRef Full Text | Google Scholar

13.TCL. NGCLI (2006). Available at: www.ncc.org.ir or http://gis.tavanir.org.ir/jeo86/sokan/y-hatam.pdf.

Google Scholar

14. Fukuda Y, Takiguchi H, Kazama T, Nishijima J, Gulyaev S, Natusch T, et al. New Absolute Gravity Measurements in New Zealand. In: International Symposium on Gravity, Geoid and Height Systems, 2016. Cham: Springer (2017). p. 95–101. doi:10.1007/1345_2017_18

CrossRef Full Text | Google Scholar

15. Fukuda Y, Higashi T, Takemoto S, Abe M, Dwipa S, Kusuma DS, et al. The First Absolute Gravity Measurements in Indonesia. J Geodynamics (2004) 38(3-5):489–501. doi:10.1016/j.jog.2004.07.009

CrossRef Full Text | Google Scholar

16. Robertson HW, Garrick RA. Gravity Measurements in New Zealand with the Cambridge Pendulum Apparatus. New Zealand J Geology Geophys (1960) 3(4):626–42. doi:10.1080/00288306.1960.10420150

CrossRef Full Text | Google Scholar