Relaxation, Percolation, and Non-Spontaneous Fluctuation of Linguistic Behavior in a Quasi-Isolated System

Linguistic behaviors arise from strongly interacting, non-equilibrium systems. There is a wide range of spatial and temporal scales that are relevant for the analysis of speech. This makes it challenging to study language from a physical perspective. This paper reports on a longitudinal experiment designed to address some of the challenges. Linguistic and social preference behavior were observed in an ad-hoc social network over time. Eight people participated in weekly sessions for 10 weeks, playing a total of 535 map-navigation games. Analyses of the degree of order in social and linguistic behaviors revealed a global relaxation toward more ordered states. Fluctuations in linguistic behavior were associated with social preferences and with individual interactions.

Introduction

The challenge in studying language as a complex system is that our knowledge of the component systems is limited. Even worse, the surroundings can interact strongly with those components. To make progress, one has to figure out how to usefully define systems and how to separate them from their surroundings. This includes constructing explicit state spaces, and attempting to reduce the influence of unobserved external forces. Efforts to accomplish these things are rarely pursued in linguistic research, and maybe with a good excuse: speech systems are profoundly complex. The modest aim of this paper is to show ways in which some of the issues associated with linguistic complexity can be addressed in an experimental context, by imposing constraints on behavior.

The analyses reported here are primarily concerned with how social and linguistic behavioral states of speakers evolve over time and over “space,” i.e. over a set of speakers. A 10-week longitudinal study was conducted in which 8 participants played 134 rounds (a total of 535 games) of a dyadic map-navigation task. Various design decisions were made to increase the degree of “isolation” of the observed system from its surroundings. There were two main findings. First, it was found that disorder in some of the behavioral systems exhibited an exponential decay-like pattern over the course of 10 weeks. This global relaxation may involve a series of transitions between steady states. Second, both temporally global and local evidence was found to support the hypothesis that language change results from a socially modulated accumulation of the effects of communicative interactions. Furthermore, linguistic behaviors are shown to percolate through the network of speakers.

The Complexity Problem in Speech

Studying linguistic behavior from a physical perspective is challenging for several reasons. First, the variables we observe in speech are generated by non-equilibrium, open systems: classical thermodynamic analyses are not applicable. Second, the range of relevant spatial and temporal scales is large, and speech systems may be strongly coupled to unobserved external systems across these scales. Third, analogous to the observer effect [1], linguistic systems are often disturbed in the act of observing them. Although these issues cannot be fully resolved, being aware of them can lead to methodological innovation. To better appreciate the challenges, consider the wide variety of information that is relevant for understanding the speech patterns of an individual speaker, illustrated in Figure 1. At any given time and place, our observations are contingent on the states of many interacting systems across a wide range of scales. Linguistic observations of speech often index states of speaker-/utterance-scale systems, defined in the phonological domain as sound patterns and in the syntactic domain as structures of words and phrases. However, these speaker-/utterance-scale patterns must emerge from the states of smaller scale systems, i.e., neural populations/circuits responsible for movement and perception.

FIGURE 1

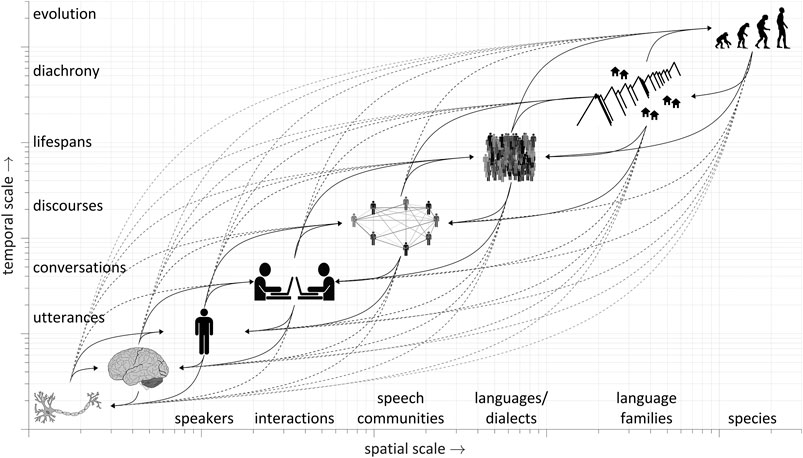
FIGURE 1. The multi-scale nature of speech and bidirectional causality. Horizontal and vertical axes are used to indicate the spatial and temporal scales that are commonly used for characterizing the dynamics of systems. Labels for spatial and temporal scales are included. Systems across all scales interact.

At the same time, individual speaker behavior is better understood when considering patterns on larger scales of interactions/conversations and speech communities/discourses, in which the conversational participants, goals, and other aspects of context are best defined [2, 3]. In turn, analyses of conversations and discourses are not inseparable from knowledge of larger scale organization associated with dialects and languages. Remarkably, the analysis of even a single speech sound is not independent of processes which have operated on evolutionary timescales [4–6].

The general problem can be stated in the following way: the language behaviors we observe on speaker/utterance scales are generated by strongly interacting, open, non-equilibrium systems; these systems experience forces which are hard to measure, because they are associated with a wide range of scales. A potential analogy to language change is the unanticipated avalanche in the sandpile model [7, 8]. An observer who is embedded in a system, yet has a spatially or temporally restricted view, is unable to anticipate sudden changes of state (avalanches) that may occur from even small perturbations of the system. The observer’s limited viewpoint did not allow them to infer that the system had organized to a critical state. This may be one reason why predicting language change is so difficult.

The current study is based on a speculative but possibly useful analogy drawn between a group of speakers and a non-equilibrium thermodynamic system. The experiments attempt to isolate the system of speakers as much as possible, by taking steps to diminish external influences. To flesh out this analogy, consider the “focused” system in Figure 2A. This system is a group of eight individuals, each of whom is a component subsystem. In Figure 2B, each component subsystem is characterized by a high dimensional state space. We examine just a few dimensions of this space by applying dimensionality reduction methods to our observations, which in this case are acoustic speech signals and social preference behaviors. Note that we assume that there are neural systems in the brain which are responsible for generating linguistic/social behaviors. The dimensions we construct from our observations can be viewed as tools to indirectly estimate the states of those neural systems.

FIGURE 2

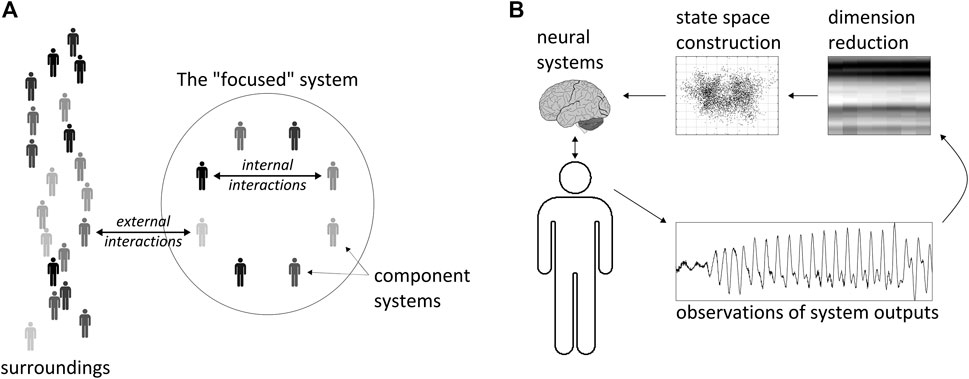
FIGURE 2. Schematic illustration of the physical system analogy. (A) the focused system is comprised of component systems which may interact with each other and the surroundings. (B) each component system is associated with a state space that we construct through dimensionality reduction methods.

In the analogy, interactions between speakers are viewed as redistributions of energy that create local order. In a physical analysis of communication, when a speaker speaks to a listener, it causes a series of entropy reductions in the environment and then in the nervous system of the listener. Specifically, the acoustic energy generated by the speaker is relatively ordered, and in turn creates ordered pressure waves in cochlear fluid which cause temporally predictable depolarization events in various types of neurons moving from peripheral to cortical areas of the brain. From this perspective, any conversational interaction can be viewed to transiently create ordered states in the nervous systems of conversational participants. Indeed, successful communication may rely on a sufficient degree of similarity between these states in the speaker and listener.

External forces on the focused system may influence system states, and yet those interactions cannot be observed (for logistical reasons). Thus we should attempt to isolate the system to diminish the influences of those forces. The current experiment was designed with this goal in mind: to reduce the influence of uncontrolled events in the daily lives of participants, on behaviors that are observed in the experiment. The quasi-isolation measures that were implemented are far from perfect, but they strengthen our ability to draw inferences about language change.

The Interaction Accumulation Hypothesis

How do large-scale patterns in language arise from smaller scale systems? It is known that language variation exists on a range of geographic scales, and that such variation is statistically associated with historical, contextual, and socioeconomic factors [9–12]. There is a wealth of research on these large-scale linguistic patterns, i.e. patterns that exist on the scale of geographic regions or the relatively smaller scale of speech communities. Such patterns are of interest not only to linguists, but also to physicists and biologists, who have applied various analogies such as surface tension [13], particle interactions and phase ordering [14–16], temperature [17], wave propagation and diffusion [18], random walks [19], network topology/graph spectra [20, 21], and replication and natural selection [22] to model various aspects of macroscale patterns of language variation (see also [23]). Some of these models show how large scale patterns may arise and evolve due to interactions of hypothetical individuals or agents.

Nearly all researchers appear to believe that at least some of the regional/community-level variation in language arises from the cumulative effects of communicative interactions between individuals. Specifically, by speaking and listening to each other, a people experience the linguistic behaviors of others. These experiences can lead to changes in their subsequent behavior, which is often referred to as accommodation or convergence [24, 25]. Over time small changes may be replicated and propagate through a community, giving rise to large-scale shifts. Many theories of language change assume some form of this idea (e.g. [9, 26–28]), with the main differences being the extent to which accommodation is automatic or conscious and how to conceptualize the role of social factors. For current purposes we refer to the general idea as the interaction accumulation hypothesis. Furthermore, it is commonly held that the effects of interactions may be weighted by social attitudes; we refer to this more specific idea as social modulation.

The interaction accumulation hypothesis makes intuitive sense, but it is quite difficult to test empirically. At a minimum, it requires frequent (if not complete) observation of interactions within a system of speakers over an extended period of time. Plenty of studies have found evidence for accommodation on short timescales, in the form of systematic changes over the course of conversational interactions [24, 25, 29, 30]. These patterns are classified as convergence when speaker behaviors become more similar, and as divergence when they become less similar; convergence and divergence have been associated with positive and negative attitudes, respectively [25, 31]. Studies have looked at speech both in spontaneous conversations, and in contexts which are experimentally controlled. An important example of the latter comes from [29], where a dyadic “map-task” [32] was used to elicit multiple repetitions of certain lexical items from participants. Perceptual similarity judgements showed that words produced by speakers during the task were more similar to their partner’s productions than words produced before the task. Laboratory studies have also extensively investigated the ability of listeners to remember talker-specific linguistic information [33–35], which is a prerequisite of the interaction aggregation hypothesis.

How can the interaction-aggregation hypothesis be investigated on temporal scales that are more relevant to language/dialect-related change? A number of corpus studies have conducted multi-annual longitudinal analyses of speech. Some examples include studies of phonetic patterns of U.S. Supreme Court justices [36], the Scottish parliament [37], or the Queen’s English [38]. An obvious issue in these cases is a high degree of non-isolation: the studies do not observe or control the system-internal or system-external interactions between speakers. Such studies can establish that language patterns change over time, but the inference that changes result from cumulative effects of interactions with other speakers is necessarily quite indirect.

The corpus study which has come closest to addressing the issue of non-isolation is a study of speech from the British version of the television show “Big Brother” [39, 40]. In the show a set of contestants are required to spend about 3 months in a house together, never leaving the house, and all the while being recorded on video. The study extracted several different phonetic variables from audio/video recordings of contestant “diaries”, and described how those variables evolved over time for a subset of participants. It is tempting to believe that this system (the set of contestants) is well-isolated. Yet contestants on the show frequently interact with producers and camerapersons, and the producers periodically force some contestants to leave the house and bring in new ones; this makes the composition of the system time-dependent. Most problematically, from the perspective of testing the interaction accumulation hypothesis, is the fact that for logistical reasons the analysis in [40] was restricted to “diary room” speech in which contestants speak to “Big Brother”, rather than interacting with each other. Any inferences about effects of interactions between contestants must necessarily be indirect, since the interactions themselves are neither observed nor quantified.

Rationale for Experiment Design and Analyses

The methodological innovations of the current study serve the goals of 1) diminishing unobserved/uncontrolled influences on behavioral systems, and 2) facilitating use of analysis methods commonly applied to physical systems. In other words, degree of isolation and statistical power are primary concerns. Many of the efforts to enhance statistical power derive from the task that participants performed. The experiment consisted of rounds in which pairs of people played a map-navigation game, often known as the “map task” [29, 32]. One person is the “giver” and has a map with a path on it. The other person is the “receiver” who has the same map but without the path. The goal is for the giver to communicate to the receiver how to draw the path. Here the maps were electronically generated and visible on laptop screens, and the receiver drew the path by clicking on the correct locations in the correct order. The map task allows the experimenter some control over which lexical items will be observed: givers will inevitably produce the names of locations which are labeled on the map.

The map task implemented here was augmented in the following ways. First, the paths used in the maps were always lines from one location to another, as opposed to going around locations. Thus at any given stage of a game, there is one specific location which the giver must communicate to the receiver. Second, in addition to being labeled with names, the map locations were shown with a small set of properties (three different colors and shapes, and two different sizes and textures). Thus givers commonly produce phrases that contain the properties which relate to the next location. Third, only a small set of location names were used; locations generally must be distinguished by both their names and properties. Fourth, speakers were not allowed to produce lexical items which were not immediately relevant to the game. The list of allowed items included the location names, properties, useful directional terms, and common discourse markers; extensive piloting was conducted to ensure that the list was adequate. These manipulations all served to increase the number of observations of certain linguistic behaviors that we analyze below.

A variety of efforts were made to increase the degree of isolation of social and linguistic systems. For one, a small set of novel, unfamiliar location names such as boc, dija, and shub were used in the maps. The systems associated with these lexical items are relatively more isolated than ones associated with familiar lexical items like green or up, because the unfamiliar forms are less likely to be produced or experienced outside of the experimental setting. Furthermore, participants were prohibited from interacting with each other during experimental sessions, except during gameplay. Of course, it is not possible to prevent people from interacting outside of the experimental sessions. However, all of participants selected for the experiment self-reported that they did not know each other prior to the experiment.

Finally, the two linguistic behaviors/system states which are analyzed here were selected on the basis of quasi-isolation and statistical power. One of these relates to the vowels which are produced in the novel location names. Vowel qualities (i.e. spectral distributions of acoustic energy) are known to vary considerably across speakers and dialects, and so these are good candidates for testing the interaction accumulation hypothesis. The other linguistic behavior relates to the syntactic organization of utterances in the game which communicate the next location on the map path; we call these utterances “instructions”. The information that is communicated in each instruction is stereotyped, yet there is ample variation. Developing ways to characterize the space of that variation is a novel contribution of this study. For convenience, we refer to the subsystems associated with these behaviors as “vowel systems” and “syntactic systems".

In addition to linguistic behaviors, a form of social preference behavior is analyzed. After each game, all players privately produced a teammate preference ranking—a ranked ordering of all other players—to indicate whom they want to play with in the next round. These rankings are used in analyses to quantify the states of the “social preference systems” that are associated with each participant. Of course, by eliciting teammate preference rankings, we (the observer) have perturbed the social system by drawing participants’ attention to this dimension of behavior. This perturbation seems unavoidable if one wants to investigate correlations between social and linguistic behaviors.

Methods

Experiment Design

A longitudinal study was conducted with an ad-hoc group of eight native English speakers (all college freshman/sophomores, four females/four males). The participants played a total of 134 rounds of a two-player cooperative map-navigation game over the course of 10 weeks, which amounted to 535 games in total. In the first 15 minutes of the experiment players were given instructions (see Supplementary Material: Game Instructions). Subsequently they repeatedly played the map game. Figure 3A shows part of a map (20% of map area, see Supplementary Material: Map Design) and provides an example of typical giver instructions for the first three path segments (twenty locations and thus nineteen total segments were present on each path). Players were allowed to say only location names (eight unfamiliar nonwords), location properties (three colors: red, green, blue; three shapes: circle, triangle, square; two sizes: big/large, small/little; two textures: filled, unfilled), and a small set of function words/discourse markers (up, down, left, right, and, okay, etc.—see Supplementary Material: Game Lexicon).

FIGURE 3

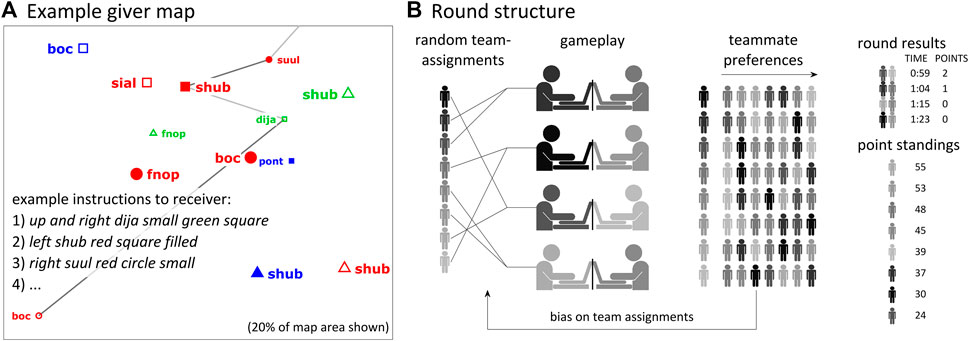
FIGURE 3. Example map and round structure. (A) Giver map with route from starting location. 20% of map area is shown. The receiver has an identical map, without the route. Example instructions to receiver for the first three path segments are shown. (B) Round structure: each round begins with random team assignments; after completing a game, participants produce confidential teammate preference rankings. Points are awarded to players on the two fastest teams in the round and cumulative point standings are displayed to all players. The teammate preference rankings are used to bias random team assignments in the next round.

The structure of each round is schematized in Figure 3B. Rounds began with a random assignment of the eight players to four teams. Two teams then played the game simultaneously in separate rooms, while the other two teams stayed in a waiting room until their turn to play. During gameplay, the giver instructs the receiver where to click on the map. The starting location is always the leftmost location, which was outlined on the maps. For the giver’s map shown in Figure 3A, the giver might begin by saying “up and right dija small green square”. Receivers then visually search for a nearby location with these properties, and typically say “okay” upon identifying the location. When the receiver clicks on the symbol of the correct location, the corresponding path segment is drawn on the receiver’s map. If the receiver clicks on an incorrect location, a message appears in the upper left of the screen warning them they that have received a 5 s penalty. With some practice, players were typically able to complete a full game in about 60–80 s.

Immediately after each game, players privately produced a teammate preference ranking. They did this using drop-down lists (Figure 4A) to order the other seven players according to whom they most/least wanted to be paired with in the next round. They also answered four survey questions (see Supplementary Materials: Surveys). The teammate preference rankings were used to bias the random team assignments in the next round. After all four games in a round had been completed, players were gathered in a lobby and the game completion times for each team were presented (Figure 3B, “round results”). Two/one points were awarded to players on the fastest/second fastest teams. Cumulative individual player point standings were displayed as well. Subsequently new teams were randomly generated with the preference ranking biases. The entire procedure was iterated for 90 min in each of the ten sessions. Additional minor details of the design are reported in [41] and in Supplementary Materials: Design.

FIGURE 4

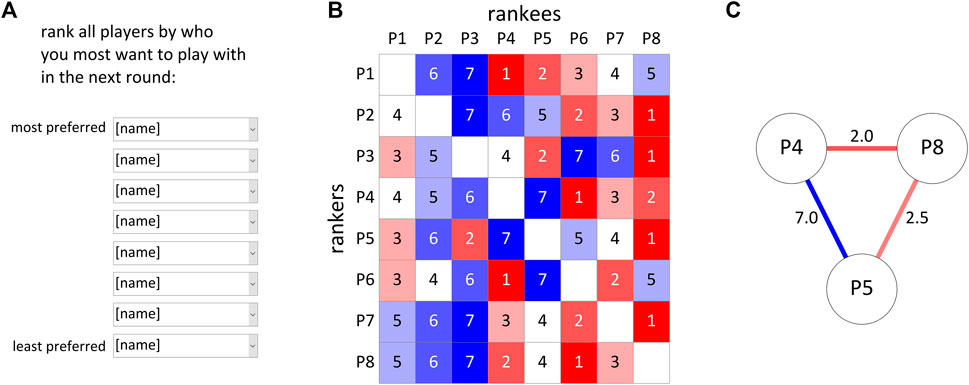
FIGURE 4. Example of social distance metric obtained from teammate preference rankings. (A) Players used drop-down lists to rank the other players. (B) Asymmetric ranking matrix, values represent teammate preference order. (C) Symmetrized social distances for the subnetwork of P4, P5, and P8, derived by averaging pairwise asymmetric rankings.

Quantification of Social System States

Teammate preference rankings were used to construct a social distance metric. The social system is conceptualized as a fully connected network (graph) of speakers, with bidirectional connections (pairs of directed edges). Each edge is associated with a scalar variable that represents a “social distance”; the collection of nodes and distances constitutes a state of the social network. As shown in Figure 4A, teammate preferences were solicited after each round with the instruction: “rank all players by who you most want to play with in the next round”. The rankings were produced by the selection of seven unique players (excluding the ranker) in drop-down lists, arranged vertically on the laptop screen. The initial ordering of player names in each list always corresponded to the player point standings (the player with the highest standing was listed first). Alphabetical ordering was used in the first round and when there were ties.

For each round an asymmetric ranking matrix is obtained from preference rankings, as in Figure 4B. Symmetrized versions of the rankings were calculated by averaging the asymmetric rankings for each player pair. An example is shown for a subset of players in Figure 4C. The distances are labeled on the connections between player-nodes. Note that social distance is not a metric space and that teammate preferences were strictly ordered; consequently total social distance is always conserved. It was deemed important to motivate players to care about the teammate preference rankings. Otherwise players might adopt the most expedient ranking strategy, which would be to rank players in the default list order. To prevent this, players were explicitly informed that their rankings would bias teammate assignments in the next round. The manipulation appears to have had the intended effect, as all players frequently produced teammate preference rankings which deviated from the most expedient rankings and which fluctuated substantially over time. These properties are evident in Figure 5, which shows the full time series of asymmetric rankings for each player-pair, with rows corresponding to rankers and columns to rankees. In each panel, the gray lines represent the current standing of the rankee (which would be the most expedient choice), and the black line represents the teammate preference ranking produced by the ranker. Red/blue areas correspond to rounds in which the ranker ranked the rankee more/less highly than their standing.

FIGURE 5

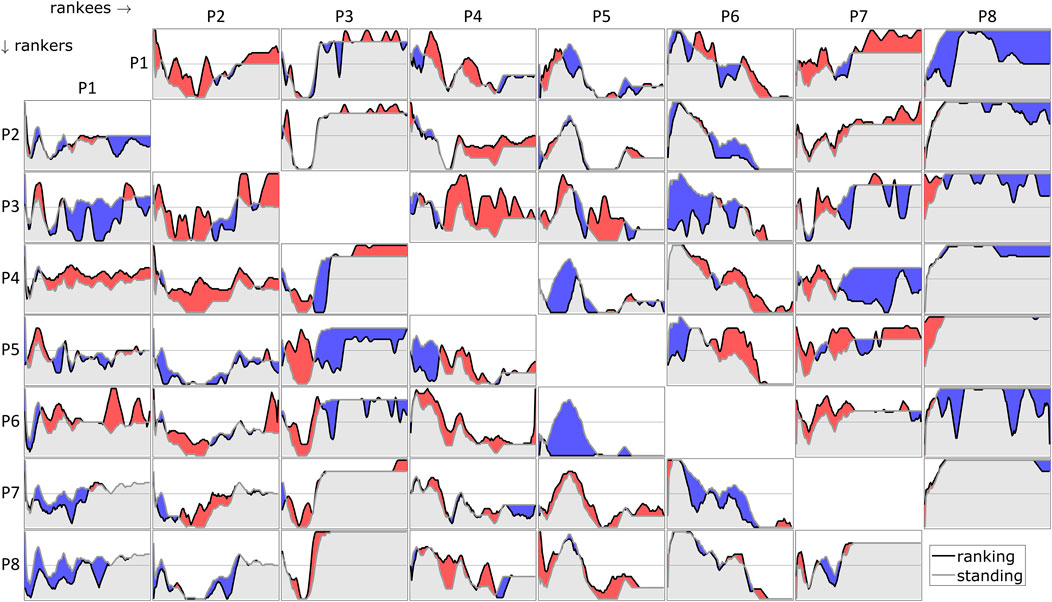
FIGURE 5. Ranking time series. Rows correspond to rankers, columns to rankees. Gray lines show standings (default ranking in drop-down lists), black lines show selected rankings; red/blue indicate positive/negative differences between ranking and standing.

Acoustic Data Processing and Analysis Procedures

Segmentation

Approximately 26.25 h (1,575 min) of audio were collected during the experiment. The HTK-HMM speech recognition toolkit [42] was used to generate word- and phone-level time-aligned transcripts for each game. The acoustic segmentation involves the following steps: receiver-giver channel alignment, manual labeling of training data, phone- and triphone-HMM training, recognition, and manual inspection/correction. Details of these procedures are provided in Supplementary Material: Acoustic Segmentation.

Vowel Quality States and Distance Measure

The spectral characteristics of a vowel produced by a given speaker at a given time can be interpreted as an index of the state of a neural system. This construct is justifiable on the grounds that spectral characteristics of waveforms associated with vowels are determined primarily by the geometry of the vocal tract [43], and current models of speech motor control agree that parameters must exist which define targets for the articulators that determine that geometry [44, 45]. Vowel quality analyses presented here are restricted to nine vowels from the nonword location names. To calculate distance between vowel qualities for each player-pair/vowel, the following procedures were used. First, each vowel waveform was transformed to an auditory spectrogram using a gammatone filterbank [46] with the following parameters: 64 e.r.b. filters in the range [70–10,000 Hz], 20 ms windows, 10 ms steps. Only the central 50% of the vowel waveform was used in order to diminish the influence of coarticulatory effects with flanking consonants. Second, auditory spectrograms were linearly time-warped to the median frame length in each vowel category. The median was calculated after excluding tokens with z-scored durations exceeding ±2.32 normalized units. Auditory feature vectors from just one frame (the midpoint) of boc are shown in Figure 6A for an example. Third, for each vowel category/player, feature vectors were excluded from subsequent analyses when their RMS deviation from the mean was greater than the 99th percentile. Fourth, auditory spectra were pooled across speakers and converted to principal components, as shown in Figure 6B.

FIGURE 6

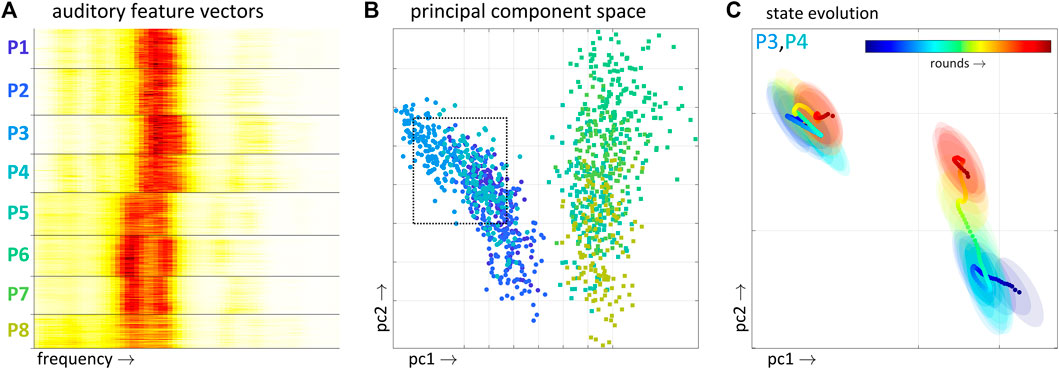
FIGURE 6. Example of vowel state estimation. (A) Vowel-midpoint auditory spectra for each token of boc. Actual feature vectors consist of a temporal series of such spectra, i.e., auditory spectrograms. (B) First two principal components of auditory spectrograms of boc. The first component encodes much of the gender-related variation. (C) Smoothed state-space trajectories over the experiment for players P3 and P4, exemplifying convergence; region shown corresponds to dashed box in panel (B).

Vowel quality distance was defined as the Euclidean distance between the average locations of the vowels in the first six dimensions of the principal component space. Only the first six dimensions were used because these accounted for 90–95% of the variance in each vowel category. The trajectories in Figure 6C show an example of convergent vowel state evolution, calculated with overlapping windows of 30 rounds. For analyses of vowel state variability, principal components were computed over all players/vowel categories. For analyses of mutual information between vowel distance and social distance, principal components were computed on data pooled separately for each pair of players.

Syntactic States and Distance Measure

Due to the repetitive, goal-oriented nature of discourse in the current study, along with constraints imposed on allowable words and their syntactic/semantic categories, there is a relatively high degree of regularity in the information that speakers communicate and in the syntactic organization of that information. This makes it possible to quantify variation in word selection and order. To do this we define an “instruction sequence” as the sequence of word categories that a giver uses when communicating information about each location on the map path. A total of 10,151 instruction sequences were identified by parsing the word sequences obtained from the word transcripts, using expected map path properties and receiver correct clicks to infer when each instruction sequence begins and ends. Sequences which contained low frequency words (e.g., no, not, or, repeat, sorry) were excluded from subsequent analyses (1.7%, 175 out of 10,151), as these tend to occur when the giver makes an error. Within each instruction, repetitions of one or two-word sequences were treated as a single instance, and hesitation words and silent pauses were ignored.

The quantification of syntactic state is based on the sequence of semantically defined word categories that occur in each instruction, as opposed to words themselves (i.e., lexical items). For example, an instruction that might be produced for one path segment (up and left big red dija filled) and an instruction with the same categories that might be produced for another path segment (down and right small green fnop unfilled) are treated as equivalent, because their sequences of word categories are identical (VERTICAL AND HORIZONAL SIZE COLOR LOCATION TEXTURE). Analysis at the level of word categories is preferrable because it is lower-dimensional and because lexical items vary randomly in response to characteristics of the map paths.

Syntactic states are expressed as a set of discrete probability distributions which together comprise a first-order Markov chain. Two examples are shown in matrix form in Figure 7. Each matrix row is a discrete probability distribution where the row header is the current state and the column header is the subsequent state. The word sequence for each instruction is assumed to have START and END states. Figure 7 also shows directed graph representations of the Markov chains, where each edge is labelled with a transition probability. There are several differences between the two examples, which are taken over five rounds beginning from the 105th round of the game. First, P7 used the conjunction and between the VERTICAL and HORIZONTAL words less frequently than P8. Second, P7 never used the directional preposition (to) before the location. Third, P7 more frequently used the location texture (filled or unfilled), which is evident from the fact that they transitioned from the SHAPE state to the TEXTURE state at a higher rate than P8 did.

FIGURE 7

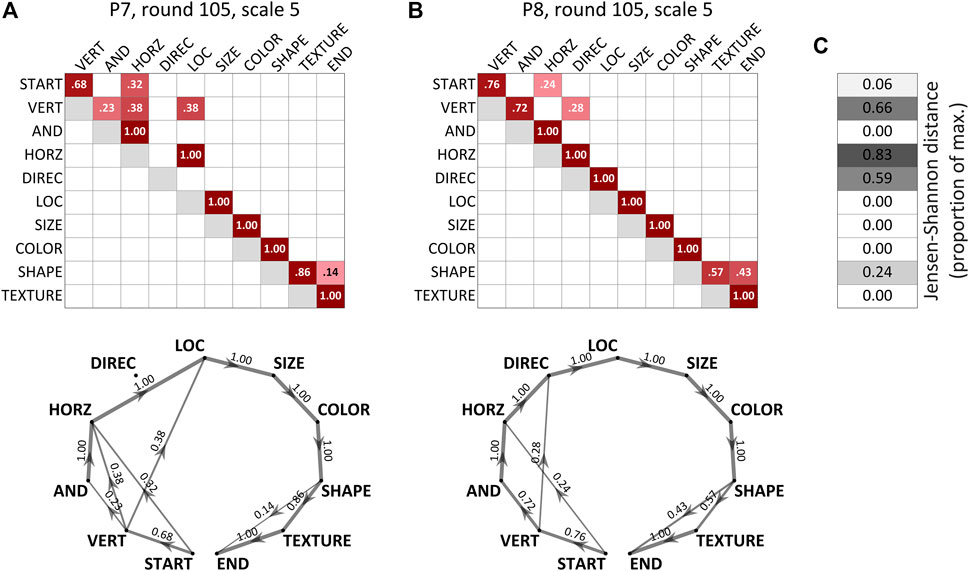
FIGURE 7. Examples of transition probability matrices and Jensen-Shannon distance. (A, B) Transition probability matrices and directed graph representations of Markov chains, calculated over five round windows beginning at round 105. (C) Jensen-Shannon distance (proportion of theoretical maximum) for each row.

To quantify syntactic states and distances, the following procedures were used. First, the instruction sequences were converted to forward word-category transition count matrices. For each player, first-order Markov chain transition probabilities were calculated from the counts, as shown in Figure 7. Next, Jensen-Shannon distance, which provides a metric measure of the similarity between two probability distributions, was calculated for each transition probability distribution between each player-pair at each time step. The Jensen-Shannon distance is the square root of the Jensen-Shannon divergence, which is defined as $\text{JSD}\left(\text{P}\left|\right|\text{Q}\right)=\left(\text{KL}\left(\text{P}\left|\right|\text{M}\right)+\text{KL}\left(\text{Q}\left|\right|\text{M}\right)\right)/2$. The terms $KL\left(P\left|\right|M\right)$ and $KL\left(Q\left|\right|M\right)$ are the Kullback-Leibler divergences of P and Q with respect to M, which is an equally weighted average of distributions P and Q. The JSD has the desirable property that it does not require absolute continuity between P and Q (see [47]). Cells with zero probability are ignored, which is motived by the fact that $\underset{x\to 0}{\lim }\text{p}\left(x\right)\log \left(p\left(x\right)\right)=0$ (see [48]). An example of the set of Jensen-Shannon distances for the two example states is shown on the right of Figure 7, where they are expressed as proportions of the maximum possible value. The syntactic distance between two Markov chains is defined as the average of the set of Jensen-Shannon distances.

Scale Variation Procedures

Each of the three distance metrics (social distance, vowel distance, and syntactic distance) was calculated pairwise between players on all available time-scales, from one round up to half of the experiment scale (134/2 = 67 rounds). However, not all vowel quality and syntactic states are observed from all players on the single-round timescale, because most observations are obtained from givers, and players may go one to several rounds without being the giver. The smallest timescale in which all relevant states are observed tends to be on the order of 3–5 rounds. For each integer time scale τ between 1 and 67 rounds, vowel states for each player/vowel category were defined as the average position in principal component space of all vowel tokens produced during an analysis window of size τ rounds. These state estimates were calculated for a sequence of windows that were offset by one round. Thus for scale τ there is a time series of 134 – (τ – 1) state estimates. Player-player vowel distance in each analysis window is simply the Euclidean distance between the average positions in principal component space. Similarly, distance estimates for syntactic states are calculated from Jensen-Shannon distances between forward transition probabilities obtained from word category transition counts in analysis windows of scale τ rounds. Distance estimates for social system states are the averages of the symmetric player-player teammate preference rankings in each analysis window.

In order to investigate whether interactions between players (i.e., single games) are associated with changes in behavioral states, a set of “interaction series” was identified. These are series of rounds that are well-suited for examining interaction effects because they provide maximally isolated estimates of behavioral states before and after an interaction. An interaction sequence is defined as a series of rounds in which a particular player (henceforth the “target” player) played as receiver exactly once, immediately after they played as giver one or more times (n_pre) and immediately before they played as giver one or more times (n_post). These giver (n_pre ≥ 1), receiver (n = 1), giver (n_post ≥ 1)) series are ideal for investigating the interaction scale because the target player experiences the behavioral states of the giver (G) in the interaction round, and the target player’s state can be estimated both before and after that interaction.

Mutual Information Estimation

Mutual information between vowel distance and social distance time series was calculated as follows. For each vowel and analysis scale, a two-dimensional joint distribution of samples of standardized vowel distance and standardized social distance was calculated over players and analysis windows. This was done by calculating a two-dimensional discrete Gaussian kernel density function, using a 30-point grid from −3.0 to 3.0, with optimal bandwidth of $n^{-\frac{1}{6}}$ (see [49] for motivation), where n is the number of observations. The density was then normalized to sum to unity. Similarly, one-dimensional independent distributions of vowel distances and social distances were estimated using the same grids and bandwidths. The mutual information was calculated as the sum of the entropy of the independent distributions minus the joint entropy. Because there are nine vowels and 28 unique player pairs, there are 252 measures of mutual information between vowel distance and social distance, for each analysis scale. In order to obtain expected distributions of mutual information in the absence of correlation between vowel distance and social distance, a Monte Carlo procedure was conducted in which the time-series of vowel distance for each player pair was randomly permuted before calculating the mutual information. The random permutation was repeated 200 times for each player-pair/vowel, on each analysis scale. Mutual information between syntactic distance and social distance was calculated with similar procedures, using the average of the Jensen-Shannon distances associated with each row of the syntactic category transition probability matrix.

Results

Below we examine how variability in behavioral states changed over the course of experiment, finding in some cases a relaxation-like pattern. We then report evidence supporting the interaction-accumulation hypothesis, using both relatively global and relatively local analyses.

Relaxation and Fluctuations in System States

Analyses of the time evolution of variability in system states shows relaxation-like decreases of disorder in some cases. Specifically, social and syntactic states—but not vowel states—showed exponential decay-like decreases in variability, which are suggestive of relaxation processes. Figure 8A shows the time evolution of variability measures of the three systems. For social preference states, the average standard deviation of teammate preference rankings is shown, calculated over windows of 20 rounds; the value is expressed relative to the mean social distance. For vowel states, the ratio of the average standard deviation to the mean distance is shown. For syntactic states, it is the ratio of entropy to mean Jensen-Shannon distance. By expressing all three variability measures relative to the mean player-player distances, it is easier to see that the reduction in variability of social and syntactic states was far more substantial than the reduction in variability of vowel states. The dotted lines are best-fitting negative exponential models; in the case of vowel state variability the model is a very poor fit. Figure 8B shows the time evolution of non-relativized average variability measures for timescales of 10, 20, 30, 40, and 50 rounds, and Figure 8C shows mean distances. The time evolution of mean social distance is not shown because it is constant.

FIGURE 8

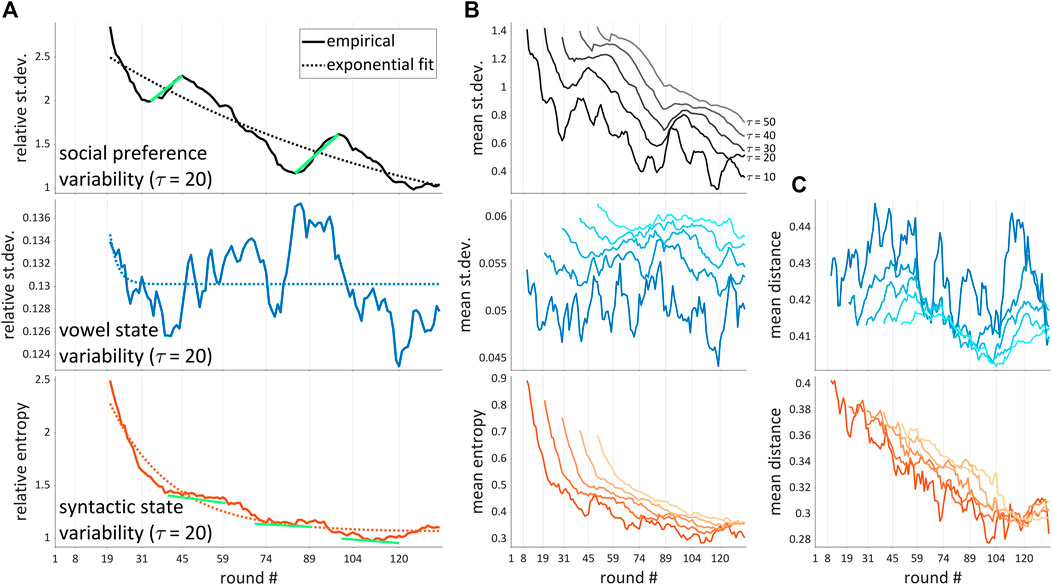
FIGURE 8. Temporal evolution of system states. (A): average measures of variability of social preference states (rankings), vowel states, and syntactic states calculated over 20 round windows; values are expressed relative to mean distances and are plotted at the end of the window. Green lines indicate potentially important departures from exponential decay. (B) time evolution of average variability measures calculated on a range of timescales. (C) time evolution of mean distances.

The exponential decay-like evolution of social and syntactic variability suggests that these systems undergo a relaxation-like process. Note however, that both the social and syntactic state variabilities show departures from exponential decay (green lines in Figure 8A). In the case of social preference states, there are two epochs (circa rounds 35–45 and rounds 80–95) in which variability increases. In the case of syntactic states, there are several epochs where the variability of states transiently flattens out. In the general discussion we consider how these departures from exponential decay bear upon our interpretation of the relaxation processes, as well as reasons why the relaxation pattern may be absent for vowel system states.

An important consideration in interpreting the time evolution of the systems is that the patterns may depend on the timescale used for estimating variability. Not surprisingly, smaller timescales reveal more complex dynamics. For example, the syntactic state variabilities (mean entropies) in Figure 8B suggest a smooth exponential decay on the relatively long timescale of τ = 50 rounds, but reveals transient fluctuations on the relatively short timescale of τ = 10 rounds.

Correlations Between Social and Linguistic Behavioral Distance

Are these fluctuations purely spontaneous or are they at least partly driven by influences of social forces? In other words, do speakers converge/diverge based upon their social preferences? To test this hypothesis, we first adopt a relatively global analysis to examine whether there exist correlations between the linguistic system state distances and social distances (see Sections 2.3 for definition of distance measures). Specifically, we use mutual information between social distance time series and linguistic behavioral distance (i.e., vowel distance or syntactic distance) time series as a measure of correlation, and compare the distribution of mutual information estimates to the distributions obtained when the time series are randomly permuted (see Section 2.3.5).

For vowel distances, there are nine vowels × 28 player-pairs = 252 estimates of mutual information. Figure 9A shows the empirical cumulative density of these estimates (red line) along with the cumulative density of estimates from randomly permuted time series (200 permutations for each vowel/player-pair). The random estimates represent the distribution of mutual information estimates that would be obtained from chance, if there were no correlation between distance measures over time. The cumulative density distributions show that there is a substantial excess of mutual information in the empirical estimates compared to the random one. Moreover, the excess mutual information is observed across analysis timescales. Figure 9B shows mean mutual information as a function of analysis timescale for both empirical (red line) and randomly permuted time-series (black line), along with the difference between means. The maximum difference occurs at τ = 16 rounds. This suggests that timescales in the neighborhood of 16 rounds are best-suited for capturing the correlation between vowel distances and social distance.

FIGURE 9

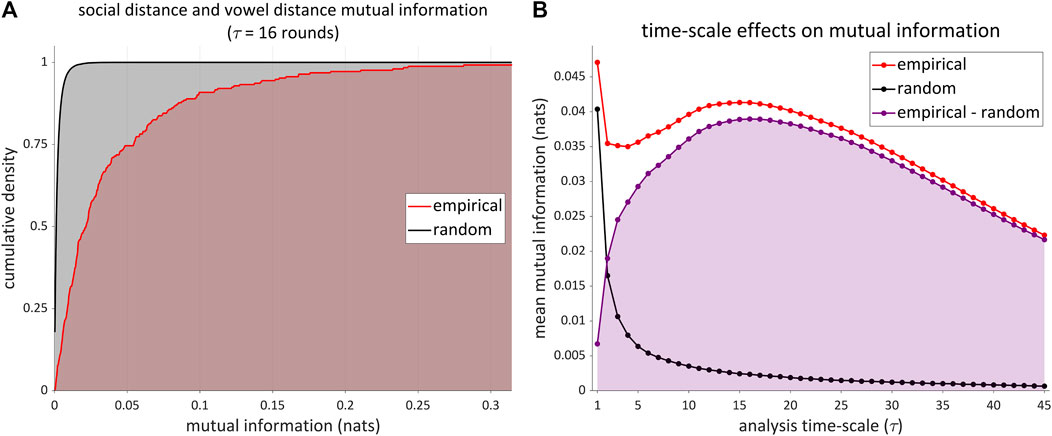
FIGURE 9. Mutual information between social distance and vowel distance time series. (A) Cumulative density of estimates of mutual information on a timescale of τ = 16 rounds (red line: empirical; black line: obtained from random permutation). (B) Mean mutual information as a function of analysis timescale, along with the difference between values associated with empirical and randomly permuted data (purple).

Excess mutual information is also observed between syntactic distance and social distance time series. Syntactic distance is defined as the average Jensen-Shannon distance of each row of the word category transition probability matrix (see Section 2.3.3). Hence there is one distance measure and mutual information estimate for each player-pair. Figure 10A shows the cumulative distribution of these estimates (red line) along with estimates obtained when the time series are randomly permuted 200 times (black line), both on the timescale of τ = 20 rounds. The density in the empirical distribution is shifted toward substantially higher values of mutual information than would be expected by chance. Figure 10B shows that this holds across analysis timescales; the maximum difference is obtained at τ = 20 rounds.

FIGURE 10

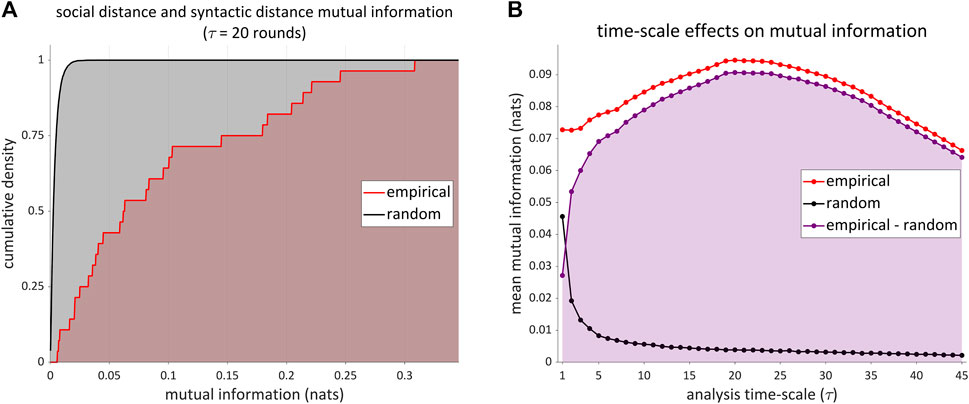
FIGURE 10. Mutual information between social distance and syntactic distance time series. (A) Cumulative density of estimates of mutual information on a timescale of τ = 20 rounds (red line); cumulative density of estimates obtained from randomly permuted time series (black line). (B) Mean mutual information as a function of analysis timescale, along with the difference (purple).

The above correlations between social distance and linguistic behavioral distances are consistent with the interaction accumulation hypothesis, as well as the more specific hypothesis of social modulation. However, because the correlation analysis is relatively global, we cannot rule out the possibility that unobserved external systems are responsible.

Interaction-Scale Analyses of Changes in Behavioral States

In order to draw stronger inferences regarding the interaction-accumulation hypothesis, we investigate whether changes in behavioral states are associated with individual interactions (i.e., single games). Specifically we examine behavioral state changes using the interaction series described in Section 2.3.4. Interaction series are series of rounds in which a target player participates as receiver exactly once, after participating as giver one or more times and before participating again as giver one or more times. Observations selected from these series provide estimates of the pre- and post-interaction behavioral states of the target player (S_pre and S_post), as well as the an estimate of the state that the target player experienced from the giver (G). If conversational interactions are partly responsible for mutual information between social distance and vowel distance, there should be relations between the G state estimate and the change in target player state. For vowel system states, which are represented as locations in a six-dimensional principal component space, these relations are quantified as angles between vectors. As schematized in two dimensions in Figure 11, the vector defined from S_pre to S_post is conceptualized as a “displacement vector”, and the vector defined from S_pre to G is conceptualized as a “force vector".

FIGURE 11

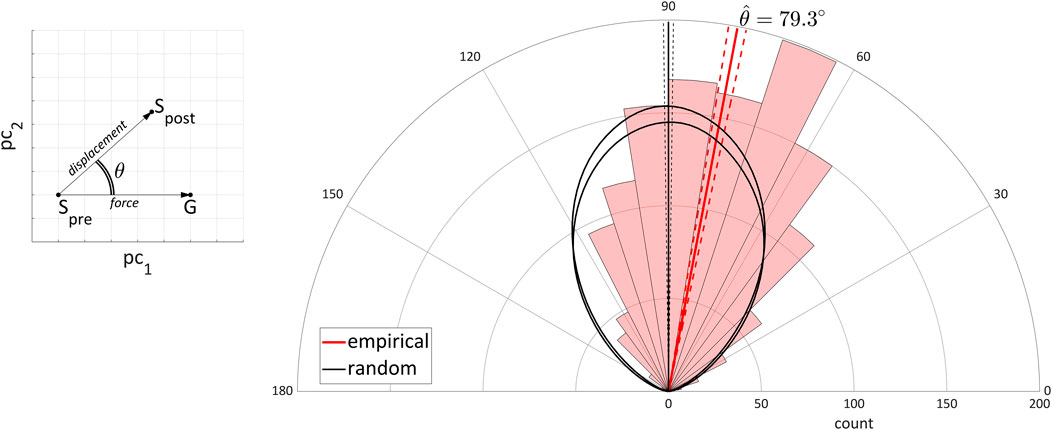
FIGURE 11. Distribution of angles between interaction force and displacement vectors. Left: schematic illustration of interaction force and displacement vectors in two dimensions. Right: polar histogram (empirical data) and density (random data) of angles calculated from first six principal components of vowel state space. Red lines: mean and ±2.0 s. e. of empirical angles. Black lines: ±2.0 s.d. of mean angle over 1,000 random permutations.

The semi-polar histogram (red boxes) in Figure 11 shows the distribution of angles over all interactions. The mean empirical value is θ = 79.3°, shown with a red line (dashed red lines show ±2.0 s. e.). For comparison, black lines show outlines of the ±2.0 s.d. of angles obtained from 1,000 displacement and force vectors selected randomly with replacement from all interactions. The random distribution shows that when the giver vowel state has no influence on receiver vowel state in an interaction, the mean angle between displacement and force vectors is approximately 90°. Comparison of the empirical distribution with the random one shows that the empirical angles are substantially biased away from 90° toward 0°. Not only does this indicate that individual interactions have an effect on vowel quality states, but it also shows that convergence is more common than divergence (which would be a bias toward 180°).

Percolation of Syntactic States

Another prediction of the interaction-accumulation hypothesis is that the spread of states through a group of speakers depends on the spatio-temporal pattern of interactions between those speakers. Here we refer to this sort of pattern as “percolation” by analogy to lattice-percolation models of physical systems, and we imagine that in each round the previous connections between nodes (the teamed pairs of players) are removed while new ones are created. The states analyzed here are associated with individual transitions in the Markov chain description of syntactic behavior. We treat these states as binary: a particular type of transition is or is not produced by a given player in a given round.

To illustrate, Figure 12 shows some examples of percolation of the VERTICAL→AND transition over time. Specifically, the behavior which spreads in this example is the use of the word and after a vertical term (up or down) in instruction sequences; we refer to this behavior as the target state. In each row of the figure, the numbered columns are rounds. For each round, pairs of givers (circles) and receivers (squares) who interacted in that round are connected by gray lines. Thus the “lattice” here is the set of player nodes in a given round, and node adjacency in each round is indicated by gray lines. When the target state is observed from a giver in a particular round, the corresponding circle is colored blue, as is the case for P3 in round 3. When the target state is observed in immediately consecutive rounds for a player as giver, a horizontal dark blue line indicates that the state has been retained. If the state is observed in consecutive rounds for a player as giver, with one or more intervening rounds in which the player was a receiver, the player is inferred to retain the state; the intervening receiver rounds and the horizontal transmission line are shaded light blue. An example of this inferred latent state is shown over the course of rounds 1-3 for P3.

FIGURE 12

FIGURE 12. Behavioral state transition analysis for VERTICAL→AND transition. Rounds increase from left to right and then top to bottom. Giver and reciever states are indicated by circles and squares respectively. Giver-receiver pairings are indicated by connections within rounds. Unfilled circles represent the absense of the use of a VERTICAL→AND transition (either overt or inferred). Dark blue: overt evidence for target state by giver; light blue: inferred latent state; orange: cessation of state; yellow: quasi-spontaneous emergence; green: possible percolation of state.

The percolation analysis is concerned with the relative frequency of two types of adoption events associated with Markov chain transitions (i.e., states) which were neither previously observed nor latent. First, there are putative “percolation” events (green lines/dots) in which a player, who did not exhibit the state in their most recent round as giver, adopts it immediately after a series of rounds as a receiver, during which they experienced at least one instance of the state from another player. For example, Figure 12 shows that in round 3, player P7 experienced the VERTICAL→AND transition from player P3, and in the next round in which P7 was a giver, round 5, they adopted this state. We conceptualize this pattern as a percolation of a state, made possible by a network link that was present in round 3. The second type of event is a “quasi-spontaneous” adoption (yellow dots). These correspond to cases in which the target state which is adopted is not associated with an experience of that state in immediately preceding rounds as receiver. An example of a quasi-spontaneous adoption is found in round 4 for player P8, who did not experience the transition in round 3 and did not use it as giver in round 2. A third type of event is the cessation of the use of a transition (orange dots): these are rounds in which a player as giver did not produce the transition despite having produced it in the most recent preceding round as giver.

Adoption events which are identified as percolation are not necessarily caused by interactions: they could simply be instances of quasi-spontaneous adoption which happen to occur when the criteria for percolation hold. To assess this, percolation and adoption rates were compared. Percolation rate is defined as the number of percolation occurrences per total number of interactions in which a percolation is possible. The adoption rate is defined as the sum of percolation and quasi-spontaneous emergence events per total number of interactions in which either of these is possible. Figure 13A shows the ratios of percolation rate to adoption rate for all Markov chain transitions for which there were at least twenty opportunities for a percolation event to occur. When this ratio is greater than one it indicates that percolative adoption occurred more frequently than would be expected if it was simply an instance of quasi-spontaneous adoption.

FIGURE 13

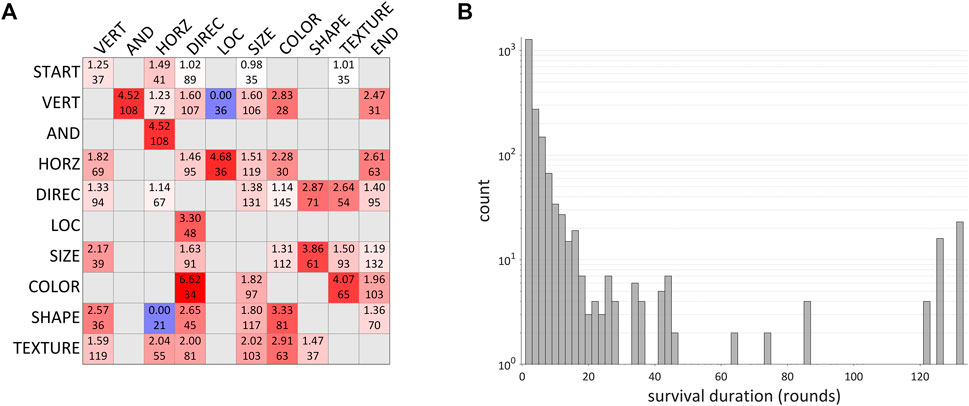
FIGURE 13. Analysis of interaction effects on Markov chain changes. (A) ratio of percolation rate to adoption rate for occurrences of particular transitions in instruction sequences; number of opportunities for percolation are shown as well. Gray cells are transitions which had fewer than 20 percolation opportunities. (B) histogram of survival durations of states, i.e., number of rounds that use of a transition persisted after being adopted; vertical axis is logarithmic.

The total percolation and adoption rates were 0.12 and 0.05 cases per opportunity, a ratio of 2.55: percolative adoptions were two-and-a-half times as likely to occur as adoptions in general. There were a total of 457 percolative adoptions out of 3,374 opportunities, and 1,616 spontaneous adoptions out of 110,165 opportunities. Pearson’s χ² test shows that overall frequencies of percolative and spontaneous adoptions were significantly different (χ² = 2,311.7, df = 1, p < 0.001) Furthermore, most of the transition-specific ratios in Figure 13A are greater than one, indicating that it is not just a handful of specific transitions that are driving the difference. Notice that the same ratios and numbers of opportunities were associated with VERTICAL→AND and AND→HORIZONTAL transitions; this follows from the fact that the word and, when used, always occurred between the VERTICAL and HORIZONTAL words. Because words often form larger phrasal units, the first-order Markov chain transitions which are analyzed here cannot be taken as fully independent. Nonetheless, the analysis supports the inference that interactions between speakers, and specifically the experience of a particular linguistic behavior during the interaction, cause changes that are analogous to percolation. Figure 13B shows a histogram of the distribution of survival durations for all of the Markov chain transitions which were analyzed; counts are plotted on a logarithmic scale because most of the durations are relatively short, on the order of 1–10 rounds. However, in a handful of cases, particular transitions persisted for much longer periods of time.

General Discussion and Conclusion

There are two main findings of the current experiment. First, some but not all behavioral systems exhibited a pattern of relaxation over time. This is important because it raises questions about the mechanisms which underly those relaxation processes and the nature of equilibria which may exist for the systems. Second, fluctuations in linguistic system states appear to be “non-spontaneous” both globally and locally, in the sense that they are correlated with social system states or associated with conversational interactions. These findings support the interaction accumulation hypothesis, which holds that language change results from the cumulative effects of interactions between language users. Below we discuss the findings in detail and speculate on various interpretations. However, it is worth noting that inferences that we wish to draw from the analyses are limited due to temporal and spatial bounds on the system. Nonetheless, by demonstrating the feasibility of implementing quasi-isolative experimental methods, we have shown that there is potential value in conducting larger scale studies.

Relaxation and Equilibria

Syntactic and social systems appear to have relaxed over time. This was seen in time series of measures of variability, which can be viewed as indices of the internal disorder of the systems. The variability measures showed exponential decay-like patterns over the 10 weeks of the study. Consider that exponential decay in physical contexts is often observed when a system is displaced from its equilibrium. Should we therefore infer that the syntactic and social systems of the experiment were initially displaced their equilibria? On one hand, the initial displacement interpretation makes a lot of sense. Regarding the social system, the players were unfamiliar with each other at the beginning of the experiment. Their teammate preference rankings early on were likely based mostly on scarce, non-verbal information. As more games were played, players had more opportunities to interact with each other, thereby acquiring more information. This plausibly led to stronger social preferences and more regularity in teammate preference rankings. Regarding initial conditions of the syntactic system, the task was unfamiliar to the players at the beginning of the experiment, and it is quite sensible to view the relaxation pattern as a consequence of learning: over time, players learned how to more effectively communicate the identity of the next location on the map path.

If the relaxation interpretation is viewed as generally useful, an important question is: what is the nature of the states toward which the syntactic and social systems evolve? Specifically: do end states of the experiment seem like stable equilibria which are global minima of disorder, or are they unstable, local minima? Perhaps an appropriate physical analogy here involves annealing vs. quenched cooling of glass materials. When cooled very slowly, glass will obtain a more regular, i.e. more ordered, crystalline structure, which may approach a minimum entropy, minimum energy state. However, when cooled more quickly, it will get stuck in local energy minima, and depending on the cooling rate, will transition through a series of local minima. The quenched cooling process seems more appropriate in this case. Consider that in the absence of any fluctuations, the global minimum of the syntactic system disorder would be zero (all players would use the same fixed word order). The empirically observed syntactic distance at the end of the experiment reflected only an approximately 25% decrease from the initial value, and it was still far from zero (Figure 8C).

A second reason that quenched cooling is more appropriate is that the relaxations that are observed are only very grossly exponential. From inspection of Figure 8 it is clear that social and syntactic systems exhibited substantial deviations from exponential decay; these deviations could be associated with transitions between a series of local minima. However, an alternative possibility is that the deviations result from the influence of unobserved social forces. A third case to be made for the quenching analogy is that, if the experiment were repeated many times (with initial conditions as similar as possible), it seems likely that syntactic behaviors observed at the end of the experiment would differ substantially. This would support the quenching interpretation, in which the final state depends on the stochastic path taken by the system. Of course, this is just a guess about what might happen, and it speaks to the need for such experiments to be conducted multiple times.

Indeed, a major shortcoming of the current study is that it is just one sample of system evolution, and its time horizon is fairly limited. Experimental studies of relaxation processes in physical systems with stochastic components would typically observe the process many times. Having just one sample severely limits our ability to draw inferences. Furthermore, physical experiments would typically be conducted long enough for a quasi-stationary state to be achieved. Let’s pretend that the experiment were continued for one hundred weeks, and consider several different hypothetical outcomes. One is that the variabilities of social and syntactic systems would in effect remain stationary, at the values which were observed near the end of the actual experiment. This is the least plausible outcome since we have almost no reason to assume that system states at the end of the 10 weeks were stationary. Another potential outcome is that the syntactic and social systems would sporadically exhibit transitions to more ordered states, and perhaps given long enough global minima would be achieved. This is a more plausible outcome given the arguments we have made above for the quenched glass-cooling analogy. A third potential outcome is that unobserved external forces will sporadically perturb the system, leading to a perpetual series of excitations and relaxations. The extent to which this outcome is plausible depends on how well we have isolated the systems which we observe.

Why did vowel systems evolve differently than social and syntactic ones? There are several aspects of the vowel-related behavior that might account for the absence of exponential decay. First, even though the location names were unfamiliar, novel word forms, the vowel categories themselves are highly familiar. For instance, the vowel of the orthographic form boc was interpreted as an /a/ (i.e. a low, central vowel), which belongs to the same category as the vowels in highly familiar words like rock or sock. Prior to participating in the experiment, players have heard many instances of this vowel. In exemplar theories of linguistic memory [28, 50, 51], each of these instances—which are called “exemplars”—has an influence on the way that vowel is subsequently perceived and produced. As speakers perceive more exemplars of a category, each new exemplar contributes less to subsequent behavior. Perhaps vowel systems did not exhibit relaxation because they are already near an equilibrium. Alternatively, the vowel systems might relax more slowly than other systems, in which case a longer observation period is required.

Another consideration is that the vowel system and syntactic system states are quite different when it comes to external physical/physiological constraints. These constraints are ultimately incommensurate. The vowel inventories of languages (i.e., sets of systematically related phonemic categories) are influenced strongly by nonlinearities in the mapping of articulatory configurations to acoustic spectral patterns [52, 53]. Hence there are articulatory constraints on the space of possible spectral patterns. In addition, there are perceptual constraints on how different two spectral patterns must be in order for them to be reliably perceived as members of distinct phonemic categories. Combinations of articulatory and perceptual constraints have been used to model the long-timescale (historical) evolution of vowel categories as objects which exert repulsive forces on each other in a bounded space [54].

In contrast to vowel system states, the syntactic system states observed in this study—probability distributions associated with first-order Markov chains—are constrained in very different ways. The order in which word categories occur is likely influenced by the salience and informativeness of the information that is relevant to identifying the next location on the path. This information includes the name of the location, its vertical and horizontal positions relative to the previous location, and properties of color, shape, size, and texture. Players did not just merely adopt one stereotyped template for ordering this information, even within a given game; rather, the categories that were included in any particular instruction appear to have been contingent on the extent to which those categories provided useful information. For example, if the vertical angle of the target location was less than ±5° from the previous one, givers were more likely to omit the vertical category than if the angle was ±50°. Of course, the absence of the category in a particular instruction is itself a form of information. Future analyses are planned to investigate these sorts of influences.

Ultimately, it is clear that the vowel systems are constrained in different ways than the syntactic ones: semantic information is highly relevant for the syntactic system states, while vowel system states are physiologically constrained in specific ways. These differences are likely a part of the reason why the two types of systems did not exhibit similar patterns of evolution over the experiment. Future analyses of other phonological/phonetic systems, such as the spectra of sibilants ( /s/ and /sh/ sounds), may shed some more light on these issues.

Support for the Interaction Accumulation Hypothesis

Several forms of support for the interaction accumulation hypothesis were observed. This hypothesis holds that language change arises from the cumulative effects of communicative interactions. A more specific hypothesis is that the effects of interactions are socially modulated. First, it was shown there exists more mutual information between linguistic behavioral distances and social distance than would be expected by chance. This was the case for all analysis timescales. In other words, by knowing the preferences that players have for their teammates, we can make better predictions about their vowel qualities and word order patterns. This global pattern of correlation is predicted by the social modulation hypothesis: the social valence of interactions modulates their influence on behavior.

However, the global analysis provides only a relatively indirect form of evidence for social modulation, because there could be unobserved external forces that are responsible for the correlations. Along these lines, it is curious that maximal excess mutual information was observed on timescales of 16/20 rounds for vowel/syntactic systems, respectively. It happens to be the case that, after the first three of the ten weekly sessions, the average number of rounds played per session was about 15. Is it a coincidence that excess mutual information peaks around the same analysis timescale that corresponds to the duration of most of the sessions? Consider that the temporal analyses, by using rounds as time indices, effectively ignore that fact that in real time, observations are intermittent—taken over just 1.5 h each week. We cannot rule out the possibility that the weekly structure of the experiment itself may be associated with unknown forces that give rise to the global correlations.

Another issue in interpreting the global correlation is that there is an interplay between the size of the system (number of players) and the rate at which players interact—these factors influence the expected times between interactions. This parameter of the system may have a strong influence on global analyses of correlation. For example, correlations might be weaker if the system were larger, because any two players would tend to interact less frequently. On the other hand, increasing the interaction scale (for example by allowing triadic games) or increasing the interaction rate (for example by having two sessions each week) might have the opposite effect. One confound worth mentioning here is that, because the teammate preference rankings were used to exert a bias on team generation, there is by design an association between social distance and interaction rate (see Supplementary Material: Team Generation). This means that players who had higher preferences for one another tended to interact more frequently. The downside of this is that the excess mutual information which was observed could be due simply to greater interaction rates. On the other hand, in real world social networks it is quite plausible that interaction rates are conditioned on social preferences, and so this aspect of the design makes the experimental system more natural.

Analyses conducted on the relatively local scale of interactions provide further support for the interaction accumulation hypothesis. With respect to vowel system states, this was found by calculating the angle between vectors defined in principal component space. Recall that S_pre is the state of a vowel system for a target player before an interaction, G is the state the player experiences during the interaction, and S_post is the state of the target player after the interaction. Taking S_pre as an origin, the vector from S_pre to S_post is viewed as a displacement in vowel state space. Likewise, the vector from S_pre to G defines a force that the interaction exerts on the vowel system. If this “force” did not have any effect on the vowel system, the angles between displacement and force vectors would be randomly distributed with a mean of 90°. To the contrary, the mean empirical angle was substantially less than that, indicating that player states tend to be “pulled” toward the states of other players who they interact with. Note that this attraction effect was found for principal component spaces of 2–6 dimensions.

The result also indicates that interaction effects were predominantly convergent. An angle of 0° between the force and displacement vectors corresponds to greater similarity of states and an angle of 180° to greater dissimilarity. Thus we can infer that interactions observed in this study tended to make vowel systems more similar. This is a more specific finding than what the global mutual information analysis tells us. However, it does not bear directly on the social modulation hypothesis because it does not account for social distance between players. Furthermore, we should not infer that all interactions are convergent, and it seems plausible that with a larger system or a different sample we might observe a dissimilatory mode (>90°) in the semipolar histogram.

One shortcoming of the interaction scale analysis of vowel system states is that it ignores quite a bit of the data. There were 182 interactions identified which met the pattern of a giver (n_pre≥1), receiver (n = 1), giver (n_post ≥1) sequence. These 182 interactions are just 17% of the total number of times that a player played a game (1,070 = 2 × 535 games). On the other hand, there are nine vowel systems states which are analyzed for each interaction. More importantly, the interactions constitute a subset of the data in which system states are more controlled than is otherwise the case, due to the restriction that the player plays exactly one round as receiver. This allows us to be a bit more confident that the effects of the interaction are associated with that interaction perse.

With respect to syntactic systems, support for the interaction accumulation hypothesis was found by adopting a percolation analogy for describing changes in syntactic states. Percolation rates for the occurrence of specific word category transitions were compared to generic adoption rates for those same transitions. Overall, percolation rates were higher than the generic adoption rates (0.12 vs. 0.05 adoptions per interaction), suggesting that syntactic system state changes were caused by interactions.

However, there are several qualifications to make regarding the percolation analysis. First, the analysis treated the occurrence of a word category transition as a binary variable and thus discards information about how frequent a category sequence is. Second, it does not account for cases in which more than two word categories interact (as in VERTICAL-AND-HORIZONTAL sequences), and thus may overcount some adoptions. Third, in all likelihood few cases of “quasi-spontaneous” adoption are truly spontaneous. Recall that these events were identified as cases in which a player begins to use a transition not having experienced it in immediately preceding rounds as receiver, nor having produced it in the most recent round as giver. This definition ignores the possibility the player experienced or produced the form in earlier rounds; in effect, it underestimates the memory that a player may have for previously heard forms. Note that this shortcoming suggests that we have underestimated percolative adoptions, and thus does not invalidate the inference that changes in syntactic states are associated with individual interactions. It is not far-fetched to imagine that players can remember the syntactic system states of other players, and that they adopt states not simply based on recent experience but taking into account past experience and their current teammate. This relates to yet another shortcoming of the analysis, which is that, like the interaction-scale analysis of vowel system states, the percolation analysis does not address the social modulation hypothesis; it simply tells us that communicative interactions are directly associated with linguistic change.

Conclusion and Future Directions

This experiment found that an exponential decay-like pattern was present in social and syntactic behavioral systems. These patterns were interpreted as the result of a relaxation process. Furthermore, fluctuations in linguistic behavior were partly non-spontaneous: they were associated with communicative interactions. This association appears to be modulated by social preferences, at least when viewed on a large scale. The findings are necessarily conditioned on the specific experimental context and constraints which were imposed, where the goal was to enhance isolation of the system. And yet, these constraints may be necessary to facilitate robust observation of behavioral systems. Hence there is a bit of paradox: in order study language as a complex system, we must impose constraints on that system. Otherwise, unobserved external interactions may compromise our ability to draw inferences. Even with the manipulations of the current experiment, there remains a fair bit of uncertainty in our inferences.

For an experiment that records acoustic signals of speech in a carefully controlled setting, the time horizon and system size of the current study are very large. Nonetheless, it is clear that even larger scales would be useful. There are three ways in which the experiment might be scaled up: 1) increasing the time period, 2) increasing the spatial size (more players), and 3) collecting multiple instances of the system (different participants). Expanding the time period would allow for better inferences regarding relaxation processes and the nature of equilibria which may or may not be obtained by systems. Expanding the spatial scale would allow for more interesting analyses of the spatial distribution of behavior in the system, but it also reduces the expected interaction rate, increasing the time it would take for behavioral states to spread throughout the system. Collecting multiple instances of the experiment, each with a different set of component subsystems (speakers) is highly desirable because it would allow for inferences regarding dependence on initial conditions.

Future experiments which aim to quasi-isolate systems may benefit from lessons learned by this one. Which methodological constraints were most influential, and might they be usefully revised or examined? One of the most important constraints was that all interactions were restricted to being dyadic—this greatly simplifies analyses but it also lowers the interaction rate. An altered version of the map task which allows for more than two-way interactions might be used to increase interaction rates. On that note, the map task itself is a highly asymmetric communicative interaction: the giver has all of the relevant information. The task could be made more symmetric by distributing different parts of the path to each player. Yet this would undoubtedly complicate interaction-scale analyses and necessitate analyses on the even smaller scale of conversational turns. Finally, it is unclear whether the vocabulary constraints are entirely necessary. Perhaps even in their absence, the goal-oriented nature of task is sufficient to ensure adequate sampling of behavior. The risk of an unconstrained vocabulary is that participants might develop radically different ways to perform the task which were unanticipated and which complicate analyses.

The teammate preference observation method is another important design feature, in part because it was intended not to do too much. It is tempting to seek information about other socially relevant dimensions of behavior, such as perceived attractiveness, likeability, and various aspects of social identity. The problem with eliciting such information is that it brings greater attention to those dimensions, thereby perturbing social system states in unknown ways. The teammate preferences are useful precisely because they avoid bringing participants’ attention to interpersonal social attitudes, and even more so because they cannot be readily interpreted in more familiar social terms (such whether a given player “liked” another). At most, the social distance metric should be viewed as a dimension-reducing projection of complex cognitive processes that underlie the teammate preference rankings. This neutral interpretation discourages us from pursuing ad hoc explanations for influences of social system states on linguistic behavior. One downside of the teammate preference sampling method is that, by forcing a strict ordering of preferences, the ordering may not index actual preferences very closely. This might be avoided by allowing for partial orderings, where two players may be ranked as equally preferred.

Language can be studied experimentally in the way that physical systems are studied. So doing, we may benefit from drawing analogies between physical systems and social/linguistic ones. However, this endeavor requires that we be explicit in constructing definitions of systems and state spaces, and that we pay attention to how our system interacts with its surroundings. An experimental approach is valuable because the “actual sample” of language that we obtain from history and from “speech in the wild” ultimately represents just one system state trajectory out of an enormous space of possible trajectories. To understand language as a complex system, we must work toward understanding the full space of trajectories and the likelihood that any particular trajectory might be observed. The first step in this endeavor is to construct quasi-isolated systems and repeatedly sample their evolution.

Data Availability Statement

The original contributions presented in the study are publicly available. All raw and processed data, including code for analyses and figures in this article, can be found here: https://osf.io/yp8fs.

Ethics Statement

The studies involving human participants were reviewed and approved by Cornell University Institutional Review Board. The patients/participants provided their written informed consent to participate in this study.

Author Contributions

The author confirms being the sole contributor of this work and has approved it for publication.

Conflict of Interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

The experiment described in this paper was a team effort. Bruce McKee, Chelsea Sanker, and Stacy Dickerman were instrumental in setting up and testing the game. Additional game testers were: Miloje Despic, John Hale, Amil Nikbin, Todd Snider. Testing was also done by graduate students in a Phonetics seminar: Dan Burgdorf, Amui Chong, Sarah D’Antonio, Naomi Enzinna, Andrea Hummel, Jixing Li, Yanyu Long, and Hao Yi, all of whom served as assistant experimenters and contributed to manual labeling of acoustic data. Undergraduate research assistants Nicole Bradbury, Christian Brickhouse, Matt Crescimanno, Melody Li, Hans Slechta, and Elisha Sword contributed to the segmentation procedures by manually labeling acoustic data and hand-correcting alignments.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2022.801740/full#supplementary-material

References

1. Dirac PAM. The Principles of Quantum Mechanics. Oxford, UK: Oxford University Press (1981).

Google Scholar

2. Eckert P. Language Variation as Social Practice: The Linguistic Construction of Identity in Belten High. Hoboken, NJ: Wiley-Blackwell (2000).

Google Scholar

3. Rickford JR, McNair-Knox F. Addressee-and Topic-Influenced Style Shift: A Quantitative Sociolinguistic Study. Sociolinguistic Perspect Regist (1994) 235–76.

Google Scholar

4. Ohala JJ. The Origin of Sound Patterns in Vocal Tract Constraints. In: The Production of Speech. Berlin: Springer (1983). p. 189–216. doi:10.1007/978-1-4613-8202-7_9

CrossRef Full Text | Google Scholar

5. Ohala JJ, Hinton L, Nichols J. Sound Symbolism. In: Proc 4th Seoul International Conference on Linguistics [SICOL] (1997). p. 98–103.

Google Scholar

6. Ohala JJ. Cross-language Use of Pitch: an Ethological View. Phonetica (1983) 40(1):1–18. doi:10.1159/000261678

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Bak P. How Nature Works: The Science of Self-Organized Criticality. Berlin: Springer Science & Business Media (2013).

Google Scholar

8. Bak P, Tang C, Wiesenfeld K. Self-organized Criticality. Phys Rev A (1988) 38(1):364–74. doi:10.1103/physreva.38.364

CrossRef Full Text | Google Scholar

9. Labov W. Principles of Linguistic Change, Volume 3: Cognitive and Cultural Factors, 36. Hoboken, NJ: John Wiley & Sons (2011).

Google Scholar

10. Labov W. The Social Motivation of a Sound Change. WORD (1963) 19(3):273–309. doi:10.1080/00437956.1963.11659799

CrossRef Full Text | Google Scholar

11. Trudgill P. Sociolinguistic Typology: Social Determinants of Linguistic Complexity. Oxford, UK: Oxford University Press (2011).

Google Scholar

12. Trudgill P. Sociolinguistics: An Introduction to Language and Society. London, UK: Penguin (2000).

Google Scholar

13. Smith ADM. Language Boundaries Driven by Surface Tension. Physics (2017) 10:80. doi:10.1103/physics.10.80

CrossRef Full Text | Google Scholar

14. Burridge J. Spatial Evolution of Human Dialects. Phys Rev X (2017) 7(3):031008. doi:10.1103/physrevx.7.031008

CrossRef Full Text | Google Scholar

15. Burridge J, Vaux B, Gnacik M, Grudeva Y. Statistical Physics of Language Maps in the USA. Phys Rev E (2019) 99(3):032305. doi:10.1103/PhysRevE.99.032305

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Lipowska D, Lipowski A. Evolution towards Linguistic Coherence in Naming Game with Migrating Agents. Entropy (2021) 23(3):299. doi:10.3390/e23030299

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Burridge J, Blaxter T, Vaux B. Evolutionary Paths of Language. Epl (2020) 128(2):28003. doi:10.1209/0295-5075/128/28003

CrossRef Full Text | Google Scholar

18. Burridge J. Unifying Models of Dialect Spread and Extinction Using Surface Tension Dynamics. R Soc Open Sci (2018) 5(1):171446. doi:10.1098/rsos.171446

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Feltgen Q. Statistical Physics of Language Evolution: The Grammaticalization Phenomenon. [PhD Thesis]. Paris (France): PSL research University (2017).

20. Loreto V, Baronchelli A, Mukherjee A, Puglisi A, Tria F. Statistical Physics of Language Dynamics. J Stat Mech (2011) 2011(04):P04006. doi:10.1088/1742-5468/2011/04/p04006

CrossRef Full Text | Google Scholar

21. Narayanan H, Niyogi P. Language Evolution, Coalescent Processes, and the Consensus Problem on a Social Network. J Math Psychol (2014) 61:19–24. doi:10.1016/j.jmp.2014.07.002

CrossRef Full Text | Google Scholar

22. Blythe RA, Croft WA. The Speech Community in Evolutionary Language Dynamics. Lang Learn (2009) 59:47–63. doi:10.1111/j.1467-9922.2009.00535.x

CrossRef Full Text | Google Scholar

23. Gong T, Shuai L, Zhang M. Modelling Language Evolution: Examples and Predictions. Phys Life Rev (2014) 11(2):280–302. doi:10.1016/j.plrev.2013.11.009

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Pardo JS. Measuring Phonetic Convergence in Speech Production. Front Psychol (2013) 4:559. doi:10.3389/fpsyg.2013.00559

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Babel M. Phonetic and Social Selectivity in Speech Accommodation. Berkeley: University of California (2009).

Google Scholar

26. Garrett A, Johnson K. Phonetic Bias in Sound Change. Origins of sound change: Approaches to phonologization (2013) 51–97. doi:10.1093/acprof:oso/9780199573745.003.0003

CrossRef Full Text | Google Scholar

27. Ohala JJ. The Phonetics of Sound Change. Hist linguistics: Probl Perspect (1993) 237–78.

Google Scholar

28. Pierrehumbert JB. Exemplar Dynamics: Word Frequency, Lenition and Contrast. Frequency emergence linguistic Struct (2001) 45:137. doi:10.1075/tsl.45.08pie

CrossRef Full Text | Google Scholar

29. Pardo JS. On Phonetic Convergence during Conversational Interaction. The J Acoust Soc America (2006) 119(4):2382–93. doi:10.1121/1.2178720

CrossRef Full Text | Google Scholar

30. Kim M, Horton WS, Bradlow AR. Phonetic Convergence in Spontaneous Conversations as a Function of Interlocutor Language Distance. Lab Phonol (2011) 2(1):125–56. doi:10.1515/labphon.2011.004

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Babel M. Evidence for Phonetic and Social Selectivity in Spontaneous Phonetic Imitation. J Phonetics (2012) 40(1):177–89. doi:10.1016/j.wocn.2011.09.001

CrossRef Full Text | Google Scholar

32. Anderson AH, Bader M, Bard EG, Boyle E, Doherty G, Garrod S, et al. The HCRC Map Task Corpus. Lang Speech (1991) 34(4):351–66. doi:10.1177/002383099103400404

CrossRef Full Text | Google Scholar

33. Goldinger SD. Words and Voices: Episodic Traces in Spoken Word Identification and Recognition Memory. J Exp Psychol Learn Mem Cogn (1996) 22(5):1166–83. doi:10.1037/0278-7393.22.5.1166

CrossRef Full Text | Google Scholar

34. Nygaard LC, Sommers MS, Pisoni DB. Speech Perception as a Talker-Contingent Process. Psychol Sci (1994) 5(1):42–6. doi:10.1111/j.1467-9280.1994.tb00612.x

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Nygaard LC, Pisoni DB. Talker-specific Learning in Speech Perception. Perception & Psychophysics (1998) 60(3):355–76. doi:10.3758/bf03206860

CrossRef Full Text | Google Scholar

36. Yu A, Abrego-Collier C, Phillips J, Pillion B, Chen D. Investigating Variation in English Vowel-To-Vowel Coarticulation in a Longitudinal Phonetic Corpus. In: ICPhS 2015; 2015 August 10-14; Glasgow, UK (2015).

Google Scholar

37. Hall-Lew L, Friskney R, Scobbie JM. Accommodation or Political Identity: Scottish Members of the UK Parliament. Lang Change (2017) 29(3):341–63. doi:10.1017/s0954394517000175

CrossRef Full Text | Google Scholar

38. Harrington J, Palethorpe S, Watson CI. Does the Queen Speak the Queen's English? Nature (2000) 408(6815):927–8. doi:10.1038/35050160

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Bane M, Graff P, Sonderegger M. Longitudinal Phonetic Variation in a Closed System. Proc CLS (2010) 46:43–58.

Google Scholar

40. Sonderegger M, Bane M, Graff P. The Medium-Term Dynamics of Accents on Reality Television. Language (2017) 93(3):598–640. doi:10.1353/lan.2017.0038

CrossRef Full Text | Google Scholar

41. Tilsen S. Speech and Social Network Dynamics in a Constrained Vocabulary Game: Design and Hypotheses. Cornell Working Pap Phonetics Phonology (2015).

Google Scholar

42. Young S, Evermann G, Kershaw D, Moore G, Odell J, Ollason D, et al. The HTK Book, 3. Trumpington St, Cambridge: Cambridge University Engineering Department (2002). p. 175.

Google Scholar

43. Ladefoged P. Vowels and Consonants: An Introduction to the Sounds of the World. Hoboken, NJ: Blackwell Publications (2001).

Google Scholar

44. Saltzman EL, Munhall KG. A Dynamical Approach to Gestural Patterning in Speech Production. Ecol Psychol (1989) 1(4):333–82. doi:10.1207/s15326969eco0104_2

CrossRef Full Text | Google Scholar

45. Tourville JA, Guenther FH. The DIVA Model: A Neural Theory of Speech Acquisition and Production. Lang Cogn Process (2011) 26(7):952–81. doi:10.1080/01690960903498424

PubMed Abstract | CrossRef Full Text | Google Scholar

46. Ellis D. Gammatone-like Spectrograms [Internet] (2009). Available from: http://www.ee.columbia.edu/∼dpwe/resources/matlab/gammatonegram/. Accessed 12 20, 2016.

Google Scholar

47. Lin J. Divergence Measures Based on the Shannon Entropy. IEEE Trans Inform Theor (1991) 37(1):145–51. doi:10.1109/18.61115

CrossRef Full Text | Google Scholar

48. MacKay DJ. Information Theory, Inference and Learning Algorithms. Oxford, UK: Cambridge University Press (2003).

Google Scholar

49. Silverman BW. Density Estimation for Statistics and Data Analysis, 26. Boca Raton: CRC Press (1986).

Google Scholar

50. Pierrehumbert J. Word-specific Phonetics. Lab phonology (2002) 7:101–39. doi:10.1515/9783110197105.101

CrossRef Full Text | Google Scholar

51. Johnson K. Decisions and Mechanisms in Exemplar-Based Phonology. Exp approaches phonology (2007) 25–40.

Google Scholar

52. Stevens KN. On the Quantal Nature of Speech. J phonetics (1989) 17(1–2):3–45. doi:10.1016/s0095-4470(19)31520-7

CrossRef Full Text | Google Scholar

53. Stevens KN, Keyser SJ. Quantal Theory, Enhancement and Overlap. J Phonetics (2010) 38(1):10–9. doi:10.1016/j.wocn.2008.10.004

CrossRef Full Text | Google Scholar

54. Liljencrants J, Lindblom B, Lindblom B. Numerical Simulation of Vowel Quality Systems: The Role of Perceptual Contrast. Language (1972) 48:839–62. doi:10.2307/411991

CrossRef Full Text | Google Scholar