Recent Advances of Optical Tweezers–Based Dynamic Force Spectroscopy and Mechanical Measurement Assays for Live-Cell Mechanobiology

Cells sense and respond to mechanical stimuli for activation, proliferation, migration, and differentiation. The associated mechanosensing and biomechanical properties of cells and tissues are significantly implicated in the context of cancer, fibrosis, dementia, and cardiovascular diseases. To gain more mechanobiology insights, dynamic force spectroscopies (DFSs), particularly optical tweezers (OT), have been further advanced to enable in situ force measurement and subcellular manipulation from the outer cell membrane to the organelles inside of a cell. In this review, we first explain the classic OT-DFS rationales and discuss their applications to protein biophysics, extracellular biomechanics, and receptor-mediated cell mechanosensing. As a non-invasive technique, optical tweezers’s unique advantages in probing cytoplasmic protein behaviors and manipulating organelles inside living cells have been increasingly explored in recent years. Hereby, we then introduce and highlight the emerging OT rationales for intracellular force measurement including refractive index matching, active–passive calibration, and change of light momentum. These new approaches enable intracellular OT-DFS and mechanical measurements with respect to intracellular motor stepping, cytosolic micro-rheology, and biomechanics of irregularly shaped nuclei and vesicles. Last but not least, we foresee future OT upgrades with respect to overcoming phototoxicity and system drifting for longer duration live-cell measurements; multimodal integration with advanced imaging and nanotechnology to obtain higher spatiotemporal resolution; and developing simultaneous, automated, and artificial intelligence–inspired multi-trap systems to achieve high throughput. These further developments will grant unprecedented accessibility of OT-DFS and force measurement nanotools to a wider biomedical research community, ultimately opening the floodgates for exciting live-cell mechanobiology and novel therapeutic discoveries.

Introduction

In the early 1970s, Arthur Ashkin demonstrated the capability of manipulating dielectric beads using radiation pressure from lasers [1]. The subsequent invention of optical tweezers (OT; also known as optical traps) was lauded with the 2018 Nobel Prize in Physics [2]. Over the past decades, OT have been configured by numerous groups, and the technical details have been comprehensively reviewed [3–5]. With the generic configuration illustrated in Figure 1, an OT system usually consists of trapping, imaging, and position detection light paths and associated optics. To trap a target bead or cell, an input laser beam (e.g., Nd:YAG 1064 nm) travels through a beam expander (L₁ and L₂). Then, the expanded beam is redirected by a dichroic mirror (DM₁, 850SP) to overfill the back aperture (e.g., diameter 5 mm) of a microscope objective (e.g., NA 1.2–1.4, oil or water immersion). Finally, the convergent beam traps a target bead or cell within the diffraction-limited focal spot at the sample stage. To detect the position, the air condenser (e.g., NA 0.25) projects the forward scattered light onto a second dichroic mirror (DM₂, 850SP) [6], which then reflects the light to a position detector (PD) like the quadrant photodetector (QPD) after filtering through a neutral density (ND) filter and converging through a plano-concave focusing lens (L₃) [3]. For the imaging path, the steering mirror deflects light from the objective toward a camera (e.g., CCD MTI IFG 300), where a tube lens (L₄) is required for image acquisition. An infrared (IR) filter is usually used to remove the trapping beam to prevent the camera from being damaged from overexposure [6].

FIGURE 1

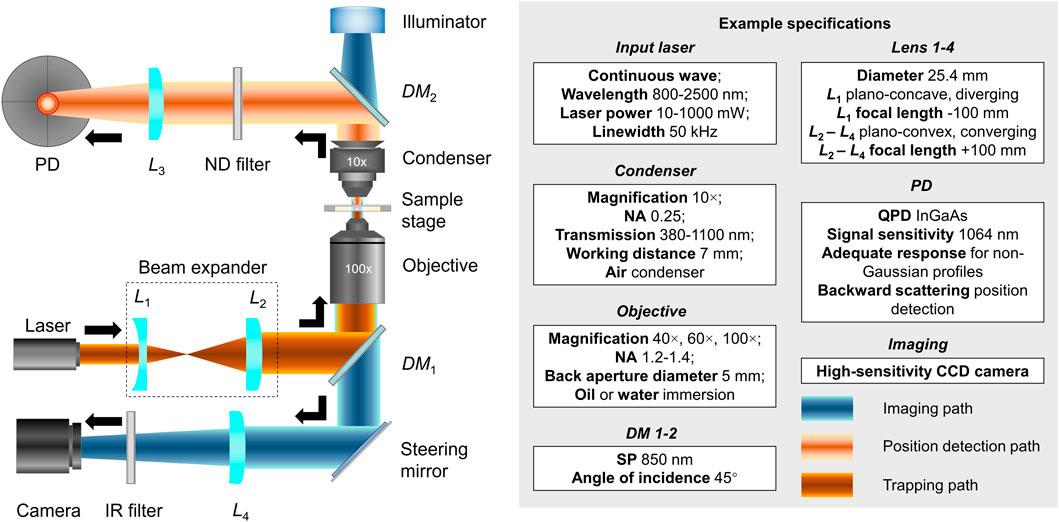
FIGURE 1. Generic configuration of an optical tweezer system. Left: Optical configurations of the trapping (dark orange), imaging (light orange), and position detection light paths and associated optics (blue). Right: Example specifications for the input laser, condenser, objective, DMs, lenses, PD, and imaging parts. Mentioned abbreviations: L_1-4, lens; PD, position detector; ND, neutral density; DM_1-2, dichroic mirrors; IR, infrared; NA, numerical aperture; SP, short pass; QPD, quadrant photodetector; CCD, charge-coupled device.

Thanks to their ultrafine and tunable trap stiffness (0.005–1 pN/nm), OT offer an impressive force range from 0.02 to 100 pN [7]. For the past 25 years, OT have been employed as a dynamic force spectroscopy (DFS) technique to investigate a broad range of extracellular mechanobiologies with delicate force control as well as high temporal (0.1 ms) and spatial (0.2 nm) resolutions in a single molecular scale [8]. These OT-DFS applications include but are not limited to receptor–ligand binding kinetics [9, 10], protein conformational changes [11–13], motor stepping in vitro [12, 13], and membrane tethering [14–18]. In classic OT-DFS experimental setups, most molecular constructs are either purified proteins [19] and nucleotides [20] or those reconstituted into liposomes [21] and expressed on the mammalian cell membrane [22]. Of note, in 1989, Ashkin and Dziedzic used OT to manipulate large intracellular organelles, such as chloroplasts and nuclei, and examined the viscoelastic properties of plastic flow, necking, and stress relaxation inside a living cell [23]. However, the classic trap stiffness calibration requires uniformly viscous media and spherical targets [6], while the cytosolic environment is viscoelastic [24] and organelles (e.g., nuclei) are irregularly shaped [25, 26]. The heterogeneity and complexity challenge accurate force measurements with cytoplasmic OT manipulation, thereafter preventing the application of OT-DFS from extracellular to intracellular space.

To this end, three new force measurement rationales emerged to enable OT force measurement assays on subcellular organelles and OT-DFS between molecules in the non-viscous cytoplasmic environment [27–29]. The first one matches the refractive index between the buffer media and the cytosol with a known refractive index [27]. Then, the trap stiffness is calibrated by suspending different sized lipid droplets in the index-matching buffer using the power spectrum method [30]. The second one relies on an internalized microbead (0.2–1 µm) inside the cell. It actively moves the trapped intracellular bead in an oscillatory manner to extract the viscoelasticity of the medium. The trap stiffness is then derived via observing the thermal fluctuation of the bead’s position [31]. The third one measures force via detection of the light momentum change without calibrating trap stiffness [32]. It usually requires a high NA (e.g., NA 1.4, oil immersion lens) condenser to collect a significant fraction of scattering light by the PD or a collecting lens [32, 33].

In this review, we first briefly introduce the classic versus emerging rationales of OT force measurements (Figure 2). We then summarize and discuss their exemplar applications in cell mechanobiology with respect to membrane tether pulling, motor stepping in vitro, receptor-mediated cell mechanosensing, intracellular motor stepping, cytosolic micro-rheology, and cell nucleus mechanics (Table 1). In the end, we share perspectives on future technical upgrades and integrations that would lead to breakthroughs in the cell mechanobiology field.

FIGURE 2

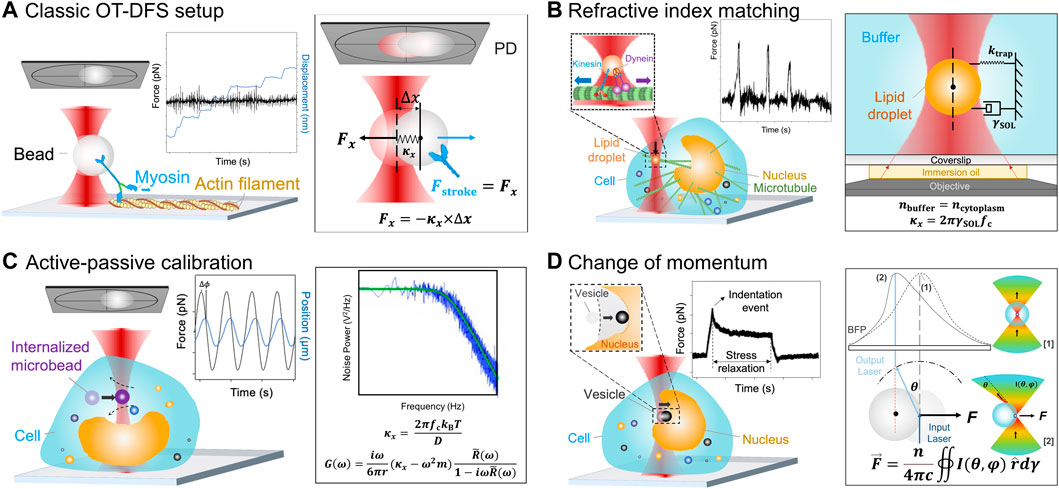
FIGURE 2. Schematics of the OT force measurement rationales. (A) Classic OT-DFS setup. Left: A representative motor stepping in vitro application is illustrated, where a myosin (blue) coupled handle bead (gray) is trapped and binds with tropomyosin on an actin filament (yellow); left inset: Myosin’s DFS displacement vs. time (blue line) and force vs. time (black line) characteristics are shown; right: Force measurement rationale. The trap stiffness κ_x is determined by the classic OT force calibration. The displacement of the handle bead Δx is detected by a QPD (gray) [59, 60]. (B) Refractive index matching rationale. Left: A representative intracellular motor stepping application is illustrated, where a lipid droplet (orange) is trapped and binds with the intracellular microtubule (green); left insets: The lipid droplet (orange) is coupled with kinesin (blue) and dynein (purple), where the kinesin is responsible for transportation from inside out and the dynein is responsible for transportation from outside in. Force vs. time (black line) DFS measurements of lipid droplets are shown; right: The force measurement rationale is also shown. Once the lipid droplets are suspended in a refractive index matching buffer, κ_x is determined by the corner frequency, f_c, and the hydrodynamic drag coefficient of the buffer, γ_SOL [61, 62]. (C) Active–passive calibration. Left: A representative cytosolic micro-rheology application is illustrated, where the sinusoidal frequency is applied to the intracellular trapped microbead (0.2–1 μm, purple, termed “internalized microbead”); left inset: DFS measurements of the internalized microbead’s position vs. time (blue line) and force vs. time (black line) are shown; right: The force measurement rationale is illustrated. Effective stiffness is determined by active–passive calibration which considers both ${\kappa }_x$ and the viscoelasticity of the medium G(ω) [31, 63]. (D) Change of momentum rationale. Left: A representative intracellular cell nucleus indentation application is illustrated, where a cytosolic vesicle (black) is trapped and manipulated to indent the nucleus (yellow); left inset: DFS measurements of vesicle’s force vs. time (black line) are shown; right: Force measurement rationale. With one-off calibration, force is measured based on the change in intensity profile [(1) initial, (2) off-center] [32].

TABLE 1

TABLE 1. Optical tweezers force spectroscopies and applications from extracellular to intracellular space.

Classic OT-DFS and Force Measurement Rationales

An optical trap is formed by tightly focusing a laser beam using an oil or water immersion objective of high numeric aperture (e.g., NA 1.2–1.4; Figure 1). The target object (e.g., a bead) near the focus of the laser will experience a force due to the incident photons, which keeps the target object “trapped” at the stable equilibrium position [51–54]. When the bead is displaced from its equilibrium position, the increased force experienced by the target will be approximately proportional to its displacement. Thus, the system can be described as a Hookean spring:

$F_x ={\kappa }_x\times \mathrm{\Delta }x ,(1)$

where F_x is the trapping force on the bead, κ_x is the trap stiffness, and Δx is the bead’s displacement from the center of the optical trap measured by the PD (Figure 2A).

With classic force measurement rationales, two categories of κ_x calibration methods are widely used: “Passive calibration” calibrates κ_x by analyzing the trapped bead’s Brownian trajectory. “Active calibration” analyzes the bead’s response toward a known force-triggered perturbation. For passive calibrations, the representative methods include potential analysis, equipartition method, mean squared displacement analysis, autocorrelation function analysis, power spectrum analysis, drift method, force reconstruction via maximum-likelihood-estimator, and Bayesian inference analysis. A detailed explanation of each method can be found in the review written by Gieseler et al. [6]. In short, to measure F_x that the target bead experiences, all methods mentioned above require ${\kappa }_x$ to be derived from the stochastic motion of the bead in the surrounding medium/buffer at thermal equilibrium.

For active calibration, where a constant [55] or a sinusoidal external force [56] is applied to the trapped target bead, the power spectrum P(f) of the moving bead is expressed as [6]

$P\left(f\right)=\underset{\begin{array}{c}\mathit{thermal\; \hspace{0.17em}contribution}\end{array}}{\underbrace{\frac{D}{{\pi }^2}\frac{1}{f^2+f_{\text{c}}^2}}} + \underset{\begin{array}{c}\mathit{mechanical\; \hspace{0.17em}contribution}\end{array}}{\underbrace{\frac{A^2}{2\left(1+\frac{f_{\text{c}}^2}{f_{\text{m}}^2}\right)}\delta \left(f-f_{\text{m}}\right)}},(2)$

where f is the Brownian motion frequency of the bead, A is the amplitude of the movement, f_m is the frequency of the movement of the media, and δ is the Dirac-delta function. After the power spectrum analysis, the result will then be used to compute the diffusion coefficient D and the corner frequency f_c. Thereby, ${\kappa }_x$ can be determined as

${\kappa }_x= \frac{2\pi f_c{k}_{\mathit{B}}T}{D}=2\pi f_c{\gamma }_{\mathit{SOL}},(3)$

where k_B is the Boltzmann constant, T is the absolute temperature, and γ_SOL is the hydrodynamic drag coefficient.

Of note, all classic rationales calibrate κ_x by assuming that the target is spherical and the medium is purely viscous [6]. Therefore, they are adapted to a simple homogenous experimental environment to perform force measurements exemplified by the following in vitro applications.

Membrane Tether Pulling

By pulling out a membrane tether, a lipid nanotube from the cell surface, the OT-DFS assay has been widely used to characterize the viscoelastic properties of the cell membrane and the underlying receptor–cytoskeleton linkages [57]. With applying a constant or increasing force on a molecular bond at the bead–cell interface, membrane tether formation would be signified by a non-linear transition in DFS [14] (Table 1, 1^st row), from which the tether force and membrane viscosity can be determined [58]. As an example, by pulling a tether from the membrane blebs of melanoma cells and renal epithelia cells, Dai and Sheetz revealed that membrane tension is a continuum property over the entire cell surface, and the tether force is determined by the membrane–cytoskeleton linkage [15]. Additionally, Raucher et al. used the same OT system and discovered that PIP2 acts as a second messenger to regulate the binding energy for membrane–cytoskeleton linkage in NIN-3T3 fibroblasts [18]. In these early studies, pulled tethers were considered to be pure lipid bilayers. A few years later, Pontes et al. further combined the OT system with epifluorescence imaging and for the first time found that actin exists in pulled membrane tethers from NIN-3T3 fibroblasts [17]. Moreover, Datar et al. performed membrane tether pulling on neuronal axons and identified two different mechanobiological phenotypes: 1) an F-actin–dependent cell-like behavior with highly dynamic sawtooth-like peaks in force vs. extension characteristics and 2) a free membrane-like behavior with a movable tether–membrane junction [16].

Motor Stepping In Vitro

OT have made it possible to characterize the stepping behaviors of highly dynamic motors in purified protein systems (Table 1, 2nd row). For the past two decades, they have been used to answer fundamental questions regarding 1) how motor proteins, such as myosin, kinesin, and dynein, progress along the actin filaments and microtubules; 2) how they transport cargos (molecules, droplets, and organelles) along cytoskeletal tracks over a long distance; and 3) how they produce the mechanical work needed to transport cargos through ATP hydrolysis [64]. To this end, numerous excellent review papers have comprehensively summarized the pivotal roles and contributions of OT in the progression of this field [51, 65, 66]. Hereby, we would like to highlight several key milestones of implicated OT-DFS technical advances. Specifically, in 1999, Veigel et al. used OT to detect the mechanical transitions made by a single myosin head attached to the actin, where they discovered that myosin-I produces a working stroke in two steps that potentially link to different biochemical states of the actomyosin cycle [13]. This landmark discovery was largely attributed to the improved time resolution of ∼1 ms by applying a 1 kHz oscillation to the OT-DFS. With the help of a 10 kHz sampling rate QPD and 200 nm beads, Uemura et al. further achieved a temporal resolution of 0.1 ms, which allowed them to successfully characterize the two mechanical states of a fast myosin-V motor [12]. Recently, Capitanio et al. developed a dual-trap force-clamp configuration that can record the sub-nanometer conformational change in the myosin with a temporal resolution of ∼10 µs [34]. Such high spatiotemporal resolution reveals that increasing the clamp force (1–10 pN) to the interaction between the myosin and actin leads to a more frequent premature unbinding (<5 ms), resulting in a working stroke that decreased with the load. In addition, Reinemann et al. used OT-DFS to study kinesin-14 HSET at single molecular level and for the first time uncovered its processive nature with a step size of 8 nm, which can be stalled by a 1.1 pN load [36]. These features would allow HSET to build up force on the scale of ∼100 nm. Although force can stall the motility of motors, Ariga et al. found that kinesin motors were accelerated in response to the fluctuating external forces applied via OT [35]. These results indicated that the mechanical fluctuation which is actively generated by the cytoskeleton network [67] is not noise; it actually improves the efficiency of molecular activities in a viscous and crowdy environment.

Receptor-Mediated Cell Mechanosensing

OT have also become a popular nanotool to examine how extracellular mechanical stimuli such as pressure, motion, and stretching are converted into intracellular biochemical signals via a number of mechanoreceptors on the cell membrane (Table 1, 3rd row) [68]. When combined with fluorescence imaging, OT-DFS directly correlates the force that acts on a mechanoreceptor, with the binding kinetics, and the subsequently triggered cell signals in one experiment [69]. For example, Kim et al. used the OT-DFS assay to generate forces to pull an αβ T-cell receptor (TCR) with controlled orientation while observing the triggered calcium mobilization [39]. The results indicated that αβTCR is an anisotropic mechanosensor, where its costimulatory activation is specific to an external tangential but not normal force (∼50 pN). Notably, Feng et al. further demonstrated that, in the absence of force, the initial TCR calcium triggering requires much higher pMHC ligand density—690 folds higher than physiologically observed [38]. Moreover, Das et al. performed OT-DFS to pull membrane tethers from Caenorhabditis elegans DAV neurons with the positive and the negative tension gradient [37]. They observed that the subsequential calcium mobilization upon increased membrane tension was associated with the activation of the TRP-4 channel and nompC (no mechanoreceptor potential C), which consequentially confines the neuronal activity for movement.

New Force Measurement Rationales Enable OT-DFS and Mechanical Measurements for Intracellular Applications

Although Ashkin and Dziedzic have demonstrated the intracellular OT manipulation in their early works [70] as mentioned above, the precision of intracellular force measurement is limited by the randomly distributed cell organelles and inherent viscoelasticity [29, 71]. To address this challenge, three new force measurement rationales have emerged:

1) The OT system calibrated by the refractive index matching rationale performs DFS measurements on in situ lipid droplets in a small cytosolic area with a known refractive index (Figure 2B) [27]. First, by adding beads into the buffer, the correlation between the apparent size and the actual size is calibrated to determine the real size of the lipid droplets in the buffer. Then, purified lipid droplets are dispersed into the buffer, so that the Brownian motion of the suspending lipid droplet can be analyzed. The trap stiffness ${\kappa }_x$ is calibrated by the power spectrum method given in Eq. 3 [27]. After calibration in the buffer, displacement of lipid droplets inside the cell will be analyzed, and the force experienced by the droplets can be calculated using Eq. 1.

2) The active–passive calibration method (Figure 2C) combines a) passive calibration by Berg-Sørensen and Flyvbjerg [30], which derives the power spectrum of the trapped bead P(ω), and b) active calibration by Mas et al. [31], Hendricks et al. [29], and Blehm et al. [42], which defines the relaxation spectrum R ̃(ω). The optical trap stiffness ${\kappa }_x$ can then be measured by the following equation:

${\kappa }_x-{\omega }^{2}m=2k_{B}T\frac{Re\left(\tilde{R}\left(\omega \right)\right)}{P\left(\omega \right)},(4)$

where ω is the driving frequency of the moving piezo stage, m is the mass of the trapped bead, Re(R ̃(ω)) is the real part of the relaxation spectrum, and r is the radius of the bead [31]. Then, ${\kappa }_x$ can be used to derive the viscoelastic modulus G(ω) of the medium, as follows:

$G\left(\omega \right)=\frac{i\omega }{6\pi r}\left({\kappa }_x-{\omega }^{2}m\right)\frac{\tilde{R}\left(\omega \right)}{1-i\omega \tilde{R}\left(\omega \right)}.(5)$

As the bead is manipulated inside the cell, both ${\kappa }_x$ and G(ω) contribute to the effective stiffness during manipulation [31]. Notably, this active–passive calibration method preserves the robustness in filtering periodic noise as the method is frequency-based.

Nevertheless, the refractive index matching still requires prior knowledge of the physical properties of the medium and beads to derive the ${\kappa }_x$ and the active–passive calibration method needs to derive the local power spectrum of the cytosolic environment every time to perform force measurements which inevitably makes the calibration tedious and not user-friendly.

3) The light momentum–based rationale is proposed to avoid the issues with the two rationales above. In this approach, the force is not derived by calibrating the trap stiffness but directly measured via detecting the momentum change of the scattered light (Figure 2D) [32]. Since the force acting on the target is induced by the exchange of momentum between the trapping laser light and the bead, if all the scattered light is captured via a PD and the momentum information is known in the form of angular intensity distribution I(θ, ϕ), the force on the target F can be derived by the following equation [32]:

$\overrightarrow{F}=\frac{n}{4\pi c}{\displaystyle ∯I(\theta , \varphi )\widehat{r}d\gamma },(6)$

where n is the refractive index of the suspension medium, c is the speed of light in vacuum, $\widehat{r}$ is the unit vector from the focus, γ is the solid angle, and the integration is performed on the surface of a spherical space with a larger radius than the target.

In this context, the change of momentum rationale only requires calibrating the OT instruments (e.g., the detector size, the light efficiency, and the total focal lens) once for all regardless of the applied experimental conditions (e.g., target’s shape and size, medium’s refractive index) [72, 73]. After this “one-off” calibration, the force on the target can be directly derived from the linear relation between the $\overrightarrow{F}$ and the voltage signal $\overrightarrow{V}$ from a PD (i.e., conversion constant α proposed by Farré et al. [73]) as shown in the following equation:

$\overrightarrow{F}=\alpha \overrightarrow{V}.(7)$

Furthermore, the momentum-based force measurement overcomes the restriction of spherical targets in classic OT force measurement applications [6]. Theoretically, its applicability extends to any irregularly shaped organelles and nuclei inside the cells. In the following sections, we will provide exemplar applications where the three new in situ force measurement rationales are used in OT-DFS experiments and mechanical measurements.

Intracellular Motor Stepping

OT with the refractive index matching rationale have been used to trap the endogenous liquid droplets and quantify the in situ interaction between motors dynein [27, 40, 41] and kinesin [41] with microtubules in the native and physiological environment (Table 1, 4th row). By combining OT with high-speed tracking, Sims and Xie were the first to observe the stepping behavior of dynein- and kinesin-driven lipid droplets under controlled force inside a living cell [41]. Leidal et al. used the same OT-DFS to precisely measure the stall force of dynein- and kinesin-driven lipid droplets in Drosophila embryos [27]. They found that distinct from the previous findings in vitro [74], intracellularly transported cargos exhibited a short-term memory in directionality, consequently explaining the reason that only one polarity of motors is active at any instant and why cargos need a regulatory event to switch the activity to the opposite polarity motor. In addition, both Leidal et al. [27] and Reddy et al. [40] found that dynein but not kinesin exhibited a force-strengthen bond (i.e., catch bond) with microtubules in OT experiments. Together, these OT-dependent intracellular studies demonstrated how dynein-mediated force adaption inside the cell improves the ability of motor-driven cargos to overcome potential subcellular obstacles. Furthermore, by applying the active–passive calibrated OT system, Blehm et al. observed that the inward stall force in situ (2–7 pN) is smaller than the results measured by beads coupled with purified kinesin (5–7 pN) [42]. These findings indicated the existence of an interaction between opposite polarity motors during inward transportation. Alternatively, Mas et al. performed a total number of 165 light momentum–based OT-DFS measurements on stall forces of motor-driven lipid droplets, showing that light momentum–based OT can perform DFS measurements without any local calibration (i.e., refractive index matching and active–passive calibration) [33].

Cytosolic Micro-Rheology

With injected microbeads (usually 0.2–1 μm in diameter) in the cytoplasm, OT demonstrate their superiority in non-invasive intracellular manipulation compared to other force measurement nanotools such as atomic force microscopy. By actively moving these microbeads, OT were implemented to characterize the viscoelasticity of the cell pertaining to its shape and intercellular interaction [75], as well as the direct motion of intracellular organelles [43, 75]. Mas et al. pioneered the active–passive calibration–based mechanical measurements (Figure 2D), by using which they successfully measured the viscoelastic moduli in the cytoplasm of yeast cells (Table 1, 5th row) [31]. Applying a similar approach, Almonacid et al. became the first to discover that the position of the nucleus is determined by the active intracellular diffusion process of vesicles, which is driven by myosin motors [43]. Recently, Bergeron-Sandoval applied the same force measurement rationale to characterize the viscoelasticity of protein condensates which are formed at clathrin-mediated endocytosis sites [46]. The results revealed that the binding between cytosol and condensate provides the energy to drive membrane invagination, thereby shaping and organizing cellular matters.

In an alternative approach proposed by Mas et al. [33], the light momentum–based force measurements can measure intracellular forces in a more efficient way since they only require a one-off calibration independent from the cytosolic environment. In this context, local cell elasticity and viscosity can also be measured, respectively, by obtaining the loss shear modulus and energy dissipation term. Recently, Hurst et al. used the same OT system to probe internalized microbeads and revealed the strong softening and fluidification of the cytoplasm during mitosis [45]. More excitingly, instead of manipulating internalized microbeads via OT, Colin et al. probed endogenous vesicles in the cytoplasm with sinusoidal forces and successfully measured the intracellular shear modules [44]. Their observation revealed that the actin mesh exerts a pressure-gradient–like force, which moves the nucleus from the periphery to the center in both Prophase I and Meiosis I.

Cell Nucleus Mechanics

OT were also implemented to indent the nucleus and other subcellular organelles, thereby interrogating their mechanosensing behaviors [76]. In an early example, OT were used to trap a naturally presenting granule in the cytoplasm of a fission yeast cell and observe the effect of its displacement during nuclear division [49]. The data showed that microtubules influence the position of the nucleus during the yeast cell fission and highlighted that the intersection between the division plane and the spindle axis is critical during this process. Similarly, Schreiner et al. combined wide-field deconvolution imaging with OT and revealed that the untethering chromatin from the inner nuclear membrane induces the deformation of nuclei [48]. Moreover, by manipulating a 1-µm microbead injected inside the embryo cell during its one-cell stage, light momentum–based mechanical measurement enables the exploration of nuclei behaviors in situ under indentation (Table 1, 5th row). In this context, Venturini et al. performed mechanical analysis upon indenting nuclei inside the zebrafish embryonic stem cells to measure the relaxation time of the nuclei when the cells were suspended or confined [47]. Since the relaxation time remains unchanged, the results revealed that the nucleus acts as a cellular strain gauge that enables the measurements of the cell shape deformation. Together with the concurrent fluorescence imaging obtained by a spinning disk confocal unit, study provided the key mechanobiology insights into how the nucleus sequentially senses the mechanical stimuli, adaptively activates calcium-dependent mechanotransduction pathways, and then regulates the contractility and migration plasticity of actomyosin.

Discussion

Optical tweezers have been demonstrated as a powerful DFS technique to study protein–protein interactions in vitro and subsequent cell mechanosensing. The emerging intracellular force measurement rationales revolutionized in in situ and intracellular biophysical studies by probing internalized beads or subcellular organelles such as lipid droplets [27], granules [31], and nuclei [47]. This breakthrough opens floodgates for live-cell mechanobiology studies with respect to subcellular organelle behaviors, cytosolic rheology, and nuclear biomechanics.

Nevertheless, challenges and limitations still exist in the applications of OT in live-cell studies. Firstly, the focused laser beam (Figure 1) produces photodamage to the cells, which restricts the duration of live-cell experiments to be less than 30 min [77]. Efforts have been made to improve the shaping of the beam and, therefore, minimize the phototoxicity of the lasers [78]. Secondly, the OT-DFS and mechanical measurement performance is more sensitive to the environmental drifting and Brownian motion of the trapped beads than to the refractive index of the medium. Environmental drifting can be reduced, but it normally requires expensive optical laboratory instrumentation, such as a heavy-duty anti-vibration table, ventilation control, and an additional detection laser. In contrast, the limitation raised by the Brownian motion cannot be easily overcome as it depends on the size of particles and the operating temperature in the system. Thirdly, when it comes to studies with multiple bead–cell pairs in use and cytosolic environments that are constantly changing [27, 28], the repetitive trap stiffness calibration process inevitably makes the OT experiments tedious and not user-friendly. In contrast, the one-off calibration process makes the momentum-based force measurement more suitable for live-cell mechanobiology studies which typically require a large sample size to draw a solid conclusion. The caveat of implementing such an OT system requires a specialized condenser with a high NA and an objective with a relatively smaller NA (e.g., NA 1.3) to collect all scattering light. This is technically challenging and high barriered to a wider biomedical community.

Technology-wise, we have observed a trend of improving OT’s temporal resolution to advance their applications [12, 13, 34]. Recently, an upgraded OT system was designed to promote ultrafast viscosity measurements with a temporal resolution of 20 µs, which is powerful enough to capture the fast dynamics of phase transitions to energy dissipation in the motor proteins’ power stroke [79]. Besides, multimodal integration becomes a second trend of OT advancement. For example, by combining holographic OT with a spinning disk confocal fluorescence microscope, Wolfson et al. enabled simultaneously manipulating on multiple objects while continuously characterizing their intracellular signaling events with high spatiotemporal resolution [80]. Meanwhile, Balaguer et al. used a similar system to be the first to visualize the direct interaction between ParB proteins and the parS loading site [81]. Additionally, the combination of OT with FRET-based molecular force microscopy also enables the concurrent quantification of force experienced by a cell and signal mechanotransduction within the cell [82].

Moreover, increasing efforts have been made to achieve high throughput in recent OT development [21, 80]. Horner et al. developed parallel optical traps to manipulate three targets simultaneously for robust data acquisition [21]. More recently, this multiple-trap OT system has been integrated with the change of light momentum measurements, where up to 10 individual particles’ forces are simultaneously measured [83]. Alternatively, the throughput can be improved by introducing automation and artificial intelligence to complete multiple tasks and minimize human input. Examples include bead detection, bead classification, and DFS measurement [84, 85]. Furthermore, neural networks could also be trained to address one of the remained obstacles, the quantification of the Brownian motion, by measuring the values of the trap stiffness and diffusion coefficient, thereby reducing OT system uncertainty [86]. The ultimate goals of these innovations are to relieve human labor, reduce time consumption, and automate the entire OT experimentation.

Last but not least, OT have also shown potential in assisting drug screening and therapeutic development. They can be applied in drug trapping, targeted delivery, and storage processes in the nanoscale [87, 88]. In this context, the behaviors of an actively moving object like a microswimmer in response to the force environment can reflect the effectiveness of drug delivery [89]. As the light momentum–based mechanical measurement can be performed on the target regardless of its shape, the stochastic forces generated by the microswimmer (Table 1, 6th row) were directly measured [50]. For the first time, the microswimmer’s complex force pattern and dynamic force were analyzed. Furthermore, live-cell OT systems can directly analyze intercellular interactions, cell–cell avidity, and cohesive force between cancer and immune cells as well as interrogating triggered mechanosensing signals and immunotherapeutic outcomes (Table 1, 7th row) [90]. Together, the OT-inspired live-cell mechanobiology promises excitingly new applications to drug delivery and screening strategies in the future [91].

Author Contributions

HW, YG, RZ, and LAJ conceived the study and wrote the manuscript. HH and YW co-wrote the manuscript. YW, FW, and LAJ provided critical comments, suggestions, and text. LAJ designed and supervised the study. All authors contributed to the article and approved the submitted version.

Funding

This work was supported by Australian Research Council (ARC) Discovery Project (DP200101970 - LAJ), the National Health and Medical Research Council (NHMRC) of Australia Ideas Grant (APP2003904 ‐ LAJ), NSW Cardiovascular Capacity Building Program (Early-Mid Career Researcher Grant - LAJ), Sydney Nano Grand Challenge funding (GC2022 - LAJ), NSW CVRN-VCCRI Research Innovation Grant and Ramaciotti Foundations Health Investment Grant (2020HIG76 - LAJ), USYD External Research Collaboration Seed Funding and NSW Government’s Boosting Business Innovation Program (BBIP - LAJ). LAJ is an ARC DECRA fellow (DE190100609) and National Heart Foundation Future Leader Level-2 (FLF2 105863).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

We acknowledge Yunduo Charles Zhao, Kiarash Kyanian, Yihao Wang, Albert Oskuee, and Rishabh Jain for helpful advice and discussion; Arnau Farré Flaquer and Oriol Nos Aguilà from IMPETUX OPTICS, SL, for constructive feedbacks on light momentum force measurement in optical tweezers; Simon Ringer and Gwenaelle Proust at the Sydney Manufacturing Hub for the support of lab startup; and Benjamin Eggleton and Stefano Palomba for NanoHealth network support on biophotonic research.

References

1. Ashkin A, Dziedzic JM, Bjorkholm JE, Chu S. Observation of a Single-Beam Gradient Force Optical Trap for Dielectric Particles. Opt Lett (1986) 11:288. doi:10.1364/ol.11.000288

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Essiambre RJ. Arthur Ashkin: Father of the Optical Tweezers. Proc Natl Acad Sci USA (2021) 118:e2026827118. doi:10.1073/pnas.2026827118

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Appleyard DC, Vandermeulen KY, Lee H, Lang MJ. Optical Trapping for Undergraduates. Am J Phys (2007) 75:5–14. doi:10.1119/1.2366734

CrossRef Full Text | Google Scholar

4. Bechhoefer J, Wilson S. Faster, Cheaper, Safer Optical Tweezers for the Undergraduate Laboratory. Am J Phys (2002) 70:393–400. doi:10.1119/1.1445403

CrossRef Full Text | Google Scholar

5. Smith SP, Bhalotra SR, Brody AL, Brown BL, Boyda EK, Prentiss M. Inexpensive Optical Tweezers for Undergraduate Laboratories. Am J Phys (1999) 67:26–35. doi:10.1119/1.19187

CrossRef Full Text | Google Scholar

6. Gieseler J, Gomez-Solano JR, Magazzù A, Pérez Castillo I, Pérez García L, Gironella-Torrent M, et al. Optical Tweezers - from Calibration to Applications: a Tutorial. Adv Opt Photon (2021) 13:74–241. doi:10.1364/aop.394888

CrossRef Full Text | Google Scholar

7. Neuman KC, Nagy A. Single-molecule Force Spectroscopy: Optical Tweezers, Magnetic Tweezers and Atomic Force Microscopy. Nat Methods (2008) 5:491–505. doi:10.1038/nmeth.1218

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Zhang X, Ma L, Zhang Y. High-resolution Optical Tweezers for Single-Molecule Manipulation. Yale J Biol Med (2013) 86:367–83.

Google Scholar

9. Hexnerová R, Křížková K, Fábry M, Sieglová I, Kedrová K, Collinsová M, et al. Probing Receptor Specificity by Sampling the Conformational Space of the Insulin-like Growth Factor II C-Domain. J Biol Chem (2016) 291:21234–45. doi:10.1074/jbc.M116.741041

CrossRef Full Text | Google Scholar

10. Riesenberg C, Iriarte-Valdez CA, Becker A, Dienerowitz M, Heisterkamp A, Ngezahayo A, et al. Probing Ligand-Receptor Interaction in Living Cells Using Force Measurements with Optical Tweezers. Front Bioeng Biotechnol (2020) 8:598459. doi:10.3389/fbioe.2020.598459

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Ayala YA, Pontes B, Ether DS, Pires LB, Araujo GR, Frases S, et al. Rheological Properties of Cells Measured by Optical Tweezers. BMC Biophys (2016) 9:5. doi:10.1186/s13628-016-0031-4

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Uemura S, Higuchi H, Olivares AO, De La Cruz EM, Ishiwata Si. Mechanochemical Coupling of Two Substeps in a Single Myosin V Motor. Nat Struct Mol Biol (2004) 11:877–83. doi:10.1038/nsmb806

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Veigel C, Coluccio LM, Jontes JD, Sparrow JC, Milligan RA, Molloy JE. The Motor Protein Myosin-I Produces its Working Stroke in Two Steps. Nature (1999) 398:530–3. doi:10.1038/19104

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Dai J, Sheetz MP. Mechanical Properties of Neuronal Growth Cone Membranes Studied by Tether Formation with Laser Optical Tweezers. Biophysical J (1995) 68:988–96. doi:10.1016/s0006-3495(95)80274-2

CrossRef Full Text | Google Scholar

15. Dai J, Sheetz MP. Membrane Tether Formation from Blebbing Cells. Biophysical J (1999) 77:3363–70. doi:10.1016/S0006-3495(99)77168-7

CrossRef Full Text | Google Scholar

16. Datar A, Bornschlögl T, Bassereau P, Prost J, Pullarkat PA. Dynamics of Membrane Tethers Reveal Novel Aspects of Cytoskeleton-Membrane Interactions in Axons. Biophysical J (2015) 108:489–97. doi:10.1016/j.bpj.2014.11.3480

CrossRef Full Text | Google Scholar

17. Pontes B, Viana NB, Salgado LT, Farina M, Neto VM, Nussenzveig HM. Cell Cytoskeleton and Tether Extraction. Biophysical J (2011) 101:43–52. doi:10.1016/j.bpj.2011.05.044

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Raucher D, Stauffer T, Chen W, Shen K, Guo S, York JD, et al. Phosphatidylinositol 4,5-Bisphosphate Functions as a Second Messenger that Regulates Cytoskeleton-Plasma Membrane Adhesion. Cell (2000) 100:221–8. doi:10.1016/s0092-8674(00)81560-3

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Arce NA, Cao W, Brown AK, Legan ER, Wilson MS, Xu E-R, et al. Activation of von Willebrand factor via mechanical unfolding of its discontinuous autoinhibitory module. Nat Commun (2021) 12:2360. doi:10.1038/s41467-021-22634-x

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Lang MJ, Fordyce PM, Engh AM, Neuman KC, Block SM. Simultaneous, Coincident Optical Trapping and Single-Molecule Fluorescence. Nat Methods (2004) 1:133–9. doi:10.1038/nmeth714

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Hörner F, Meissner R, Polali S, Pfeiffer J, Betz T, Denz C, et al. Holographic Optical Tweezers-Based In Vivo Manipulations in Zebrafish Embryos. J Biophotonics (2017) 10:1492–501. doi:10.1002/jbio.20160022610.1002/jbio.201600226

CrossRef Full Text | Google Scholar

22. Litvinov RI, Shuman H, Bennett JS, Weisel JW. Binding Strength and Activation State of Single Fibrinogen-Integrin Pairs on Living Cells. Proc Natl Acad Sci (2002) 99:7426–31. doi:10.1073/pnas.112194999

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Ashkin A, Dziedzic JM. Internal Cell Manipulation Using Infrared Laser Traps. Proc Natl Acad Sci (1989) 86:7914–8. doi:10.1073/pnas.86.20.7914

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Berret J-F. Local Viscoelasticity of Living Cells Measured by Rotational Magnetic Spectroscopy. Nat Commun (2016) 7:10134. doi:10.1038/ncomms10134

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Dorland YL, Cornelissen AS, Kuijk C, Tol S, Hoogenboezem M, van Buul JD, et al. Nuclear Shape, Protrusive Behaviour and In Vivo Retention of Human Bone Marrow Mesenchymal Stromal Cells Is Controlled by Lamin-A/C Expression. Sci Rep (2019) 9:14401. doi:10.1038/s41598-019-50955-x

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Voeltz GK, Prinz WA. Sheets, Ribbons and Tubules - How Organelles Get Their Shape. Nat Rev Mol Cel Biol (2007) 8:258–64. doi:10.1038/nrm2119

CrossRef Full Text | Google Scholar

27. Leidel C, Longoria RA, Gutierrez FM, Shubeita GT. Measuring Molecular Motor Forces In Vivo: Implications for Tug-Of-War Models of Bidirectional Transport. Biophysical J (2012) 103:492–500. doi:10.1016/j.bpj.2012.06.038

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Jun Y, Tripathy SK, Narayanareddy BRJ, Mattson-Hoss MK, Gross SP. Calibration of Optical Tweezers for In Vivo Force Measurements: How Do Different Approaches Compare. Biophysical J (2014) 107:1474–84. doi:10.1016/j.bpj.2014.07.033

CrossRef Full Text | Google Scholar

29. Hendricks AG, Holzbaur ELF, Goldman YE. Force Measurements on Cargoes in Living Cells Reveal Collective Dynamics of Microtubule Motors. Proc Natl Acad Sci (2012) 109:18447–52. doi:10.1073/pnas.1215462109

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Berg-Sørensen K, Flyvbjerg H. Power Spectrum Analysis for Optical Tweezers. Rev Scientific Instr (2004) 753:594–612.

Google Scholar

31. Mas J, Richardson AC, Reihani SNS, Oddershede LB, Berg-Sørensen K. Quantitative Determination of Optical Trapping Strength and Viscoelastic Moduli inside Living Cells. Phys Biol (2013) 10:046006. doi:10.1088/1478-3975/10/4/046006

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Smith SB, Cui Y, Bustamante C. Optical-Trap Force Transducer that Operates by Direct Measurement of Light Momentum. Methods Enzymol (2003) 361:134–62. doi:10.1016/S0076-6879(03)61009-8

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Mas J, Farré A, Sancho-Parramon J, Martín-Badosa E, Montes-Usategui M. Force Measurements with Optical Tweezers inside Living Cells. In: Optical Trapping and Optical Micromanipulation XI; San Diego, California, 91640U. United States: International Society for Optics and Photonics (2014).

CrossRef Full Text | Google Scholar

34. Capitanio M, Canepari M, Maffei M, Beneventi D, Monico C, Vanzi F, et al. Ultrafast Force-Clamp Spectroscopy of Single Molecules Reveals Load Dependence of Myosin Working Stroke. Nat Methods (2012) 9:1013–9. doi:10.1038/nmeth.2152

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Ariga T, Tateishi K, Tomishige M, Mizuno D. Noise-Induced Acceleration of Single Molecule Kinesin-1. Phys Rev Lett (2021) 127:178101. doi:10.1103/PhysRevLett.127.178101

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Reinemann DN, Norris SR, Ohi R, Lang MJ. Processive Kinesin-14 HSET Exhibits Directional Flexibility Depending on Motor Traffic. Curr Biol (2018) 28:2356–62. e5. doi:10.1016/j.cub.2018.06.055

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Das R, Lin L-C, Català-Castro F, Malaiwong N, Sanfeliu-Cerdán N, Porta-de-la-Riva M, et al. An Asymmetric Mechanical Code Ciphers Curvature-dependent Proprioceptor Activity. Sci Adv (2021) 7:eabg4617. doi:10.1126/sciadv.abg4617

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Feng Y, Brazin KN, Kobayashi E, Mallis RJ, Reinherz EL, Lang MJ. Mechanosensing Drives Acuity of αβ T-Cell Recognition. Proc Natl Acad Sci USA (2017) 114:E8204–E8213. doi:10.1073/pnas.1703559114

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Kim ST, Takeuchi K, Sun Z-YJ, Touma M, Castro CE, Fahmy A, et al. The αβ T Cell Receptor Is an Anisotropic Mechanosensor. J Biol Chem (2009) 284:31028–37. doi:10.1074/jbc.M109.052712

CrossRef Full Text | Google Scholar

40. Reddy BJN, Mattson M, Wynne CL, Vadpey O, Durra A, Chapman D, et al. Load-induced Enhancement of Dynein Force Production by LIS1-NudE In Vivo and In Vitro. Nat Commun (2016) 7:12259. doi:10.1038/ncomms12259

PubMed Abstract | CrossRef Full Text | Google Scholar

41. Sims PA, Xie XS. Probing Dynein and Kinesin Stepping with Mechanical Manipulation in a Living Cell. Chemphyschem (2009) 10:1511–6. doi:10.1002/cphc.200900113

PubMed Abstract | CrossRef Full Text | Google Scholar

42. Blehm BH, Schroer TA, Trybus KM, Chemla YR, Selvin PR. In Vivo optical Trapping Indicates Kinesin's Stall Force Is Reduced by Dynein during Intracellular Transport. Proc Natl Acad Sci USA (2013) 110:3381–6. doi:10.1073/pnas.1219961110

PubMed Abstract | CrossRef Full Text | Google Scholar

43. Almonacid M, Ahmed WW, Bussonnier M, Mailly P, Betz T, Voituriez R, et al. Active Diffusion Positions the Nucleus in Mouse Oocytes. Nat Cel Biol (2015) 17:470–9. doi:10.1038/ncb3131

CrossRef Full Text | Google Scholar

44. Colin A, Razin N, Almonacid M, Ahmed W, Betz T, Terret M-E, et al. Centering Based on Active Diffusion in Mouse Oocytes Is Non-specific. bioRxiv (2019) 219. 531657. doi:10.1101/531657

CrossRef Full Text | Google Scholar

45. Hurst S, Vos BE, Betz T. Intracellular Softening and Fluidification Reveals a Mechanical Switch of Cytoskeletal Material Contributions during Division. bioRxiv (2021). doi:10.1101/2021.01.07.425761

CrossRef Full Text | Google Scholar

46. Bergeron-Sandoval L-P, Heris HK, Hendricks AG, Ehrlicher AJ, François P, Pappu RV, et al. Endocytosis Caused by Liquid-Liquid Phase Separation of Proteins. BioRxiv (2017) 145664. doi:10.1101/145664

CrossRef Full Text | Google Scholar

47. Venturini V, Pezzano F, Català Castro F, Häkkinen H-M, Jiménez-Delgado S, Colomer-Rosell M, et al. The Nucleus Measures Shape Changes for Cellular Proprioception to Control Dynamic Cell Behavior. Science (2020) 370:3706514. doi:10.1126/science.aba2644

CrossRef Full Text | Google Scholar

48. Schreiner SM, Koo PK, Zhao Y, Mochrie SGJ, King MC. The Tethering of Chromatin to the Nuclear Envelope Supports Nuclear Mechanics. Nat Commun (2015) 6:7159. doi:10.1038/ncomms8159

PubMed Abstract | CrossRef Full Text | Google Scholar

49. Tolic´-Nørrelykke IM, Sacconi L, Stringari C, Raabe I, Pavone FS. Nuclear and Division-Plane Positioning Revealed by Optical Micromanipulation. Curr Biol (2005) 15:1212–6. doi:10.1016/j.cub.2005.05.052

PubMed Abstract | CrossRef Full Text | Google Scholar

50. Jones C, Gomez M, Muoio RM, Vidal A, McKnight RA, Brubaker ND, et al. Stochastic Force Dynamics of the Model Microswimmer Chlamydomonas Reinhardtii : Active Forces and Energetics. Phys Rev E (2021) 103:1033–1. doi:10.1103/PhysRevE.103.032403

CrossRef Full Text | Google Scholar

51. Moffitt JR, Chemla YR, Smith SB, Bustamante C. Recent Advances in Optical Tweezers. Annu Rev Biochem (2008) 77:205–28. doi:10.1146/annurev.biochem.77.043007.090225

PubMed Abstract | CrossRef Full Text | Google Scholar

52. Jones PH, Maragò OM, Volpe G. Optical Tweezers: Principles and Applications. United Kingdom: Cambridge University Press (2015).

Google Scholar

53. Neuman KC, Block SM. Optical Trapping. Rev scientific Instr (2004) 75:2787–809. doi:10.1063/1.1785844

CrossRef Full Text | Google Scholar

54. Gennerich A Optical Tweezers. Methods Mol Biol, 1486 (2017).555. doi:10.1007/978-1-4939-6421-5

CrossRef Full Text | Google Scholar

55. Simmons RM, Finer JT, Chu S, Spudich JA. Quantitative Measurements of Force and Displacement Using an Optical Trap. Biophysical J (1996) 70:1813–22. doi:10.1016/S0006-3495(96)79746-1

CrossRef Full Text | Google Scholar

56. Tolić-Nørrelykke SF, Schäffer E, Howard J, Pavone FS, Jülicher F, Flyvbjerg H. Calibration of Optical Tweezers with Positional Detection in the Back Focal Plane. Rev scientific Instr (2006) 7710:103101. doi:10.1063/1.2356852

CrossRef Full Text | Google Scholar

57. Baoukina S, Marrink SJ, Tieleman DP. Molecular Structure of Membrane Tethers. Biophysical J (2012) 102:1866–71. eng. doi:10.1016/j.bpj.2012.03.048

CrossRef Full Text | Google Scholar

58. Hochmuth FM, Shao JY, Dai J, Sheetz MP. Deformation and Flow of Membrane into Tethers Extracted from Neuronal Growth Cones. Biophysical J (1996) 70:358–69. doi:10.1016/S0006-3495(96)79577-2

CrossRef Full Text | Google Scholar

59. Ungai-Salánki R, Peter B, Gerecsei T, Orgovan N, Horvath R, Szabó B. A Practical Review on the Measurement Tools for Cellular Adhesion Force. Adv Colloid Interf Sci (2019) 269:309–33. doi:10.1016/j.cis.2019.05.005

CrossRef Full Text | Google Scholar

60. Reif M. Myosin-V Stepping Kinetics: A Molecular Model for Processivity. Proc Natl Acad Sci United States America (2000) 9717:9482–6. doi:10.1073/pnas.97.17.9482

CrossRef Full Text | Google Scholar

61. Vermeulen KC, Wuite GJL, Stienen GJM, Schmidt CF. Optical Trap Stiffness in the Presence and Absence of Spherical Aberrations. Appl Opt (2006) 45:1812–9. doi:10.1364/ao.45.001812

PubMed Abstract | CrossRef Full Text | Google Scholar

62. Yehoshua S, Pollari R, Milstein JN. Axial Optical Traps: A New Direction for Optical Tweezers. Biophysical J (2015) 108:2759–66. doi:10.1016/j.bpj.2015.05.014

PubMed Abstract | CrossRef Full Text | Google Scholar

63. Almendarez-Rangel P, Morales-Cruzado B, Sarmiento-Gómez E, Pérez-Gutiérrez FG. Finding Trap Stiffness of Optical Tweezers Using Digital Filters. Appl Opt (2018) 57:652–8. doi:10.1364/AO.57.000652

PubMed Abstract | CrossRef Full Text | Google Scholar

64. Sweeney HL, Holzbaur ELF. Motor Proteins. Cold Spring Harb Perspect Biol (2018) 10:a021931. doi:10.1101/cshperspect.a021931

PubMed Abstract | CrossRef Full Text | Google Scholar

65. Molloy JE, Padgett MJ. Lights, Action: Optical Tweezers. Contemp Phys (2002) 43:241–58. doi:10.1080/00107510110116051

CrossRef Full Text | Google Scholar

66. Choudhary D, Mossa A, Jadhav M, Cecconi C. Bio-Molecular Applications of Recent Developments in Optical Tweezers. Biomolecules (2019) 9:23. doi:10.3390/biom9010023

PubMed Abstract | CrossRef Full Text | Google Scholar

67. Mizuno D, Tardin C, Schmidt CF, Mackintosh FC. Nonequilibrium Mechanics of Active Cytoskeletal Networks. Science (2007) 315:370–3. doi:10.1126/science.1134404

PubMed Abstract | CrossRef Full Text | Google Scholar

68. Chen Y, Ju L, Rushdi M, Ge C, Zhu C. Receptor-mediated Cell Mechanosensing. MBoC (2017) 28:3134–55. doi:10.1091/mbc.E17-04-0228

PubMed Abstract | CrossRef Full Text | Google Scholar

69. Zhu C, Chen Y, Ju LA. Dynamic Bonds and Their Roles in Mechanosensing. Curr Opin Chem Biol (2019) 53:88–97. doi:10.1016/j.cbpa.2019.08.005

PubMed Abstract | CrossRef Full Text | Google Scholar

70. Ashkin A, Dziedzic JM. Internal Cell Manipulation Using Infrared Laser Traps. Proc Nation Acad Sci (1989) 8620:7914. doi:10.1073/pnas.86.20.7914

PubMed Abstract | CrossRef Full Text | Google Scholar

71. Fischer M, Berg-Sørensen K. Calibration of Trapping Force and Response Function of Optical Tweezers in Viscoelastic media. J Opt A: Pure Appl Opt (2007) 9:S239–S250. doi:10.1088/1464-4258/9/8/s18

CrossRef Full Text | Google Scholar

72. Farré A, Montes-Usategui M. A Force Detection Technique for Single-Beam Optical Traps Based on Direct Measurement of Light Momentum Changes. Opt Express (2010) 18:11955–68. doi:10.1364/OE.18.011955

PubMed Abstract | CrossRef Full Text | Google Scholar

73. Farré A, Marsà F, Montes-Usategui M. Optimized Back-Focal-Plane Interferometry Directly Measures Forces of Optically Trapped Particles. Opt Express (2012) 20:12270–91. doi:10.1364/OE.20.012270

PubMed Abstract | CrossRef Full Text | Google Scholar

74. Müller MJI, Klumpp S, Lipowsky R. Tug-of-war as a Cooperative Mechanism for Bidirectional Cargo Transport by Molecular Motors. Proc Natl Acad Sci (2008) 105:4609–14. doi:10.1073/pnas.0706825105

PubMed Abstract | CrossRef Full Text | Google Scholar

75. Guo M, Ehrlicher AJ, Jensen MH, Renz M, Moore JR, Goldman RD, et al. Probing the Stochastic, Motor-Driven Properties of the Cytoplasm Using Force Spectrum Microscopy. Cell (2014) 158:822–32. doi:10.1016/j.cell.2014.06.051

PubMed Abstract | CrossRef Full Text | Google Scholar

76. Newport JW, Forbes DJ. THE NUCLEUS: STRUCTURE, FUNCTION, AND DYNAMICS. Annu Rev Biochem (1987) 56:535–65. doi:10.1146/annurev.bi.56.070187.002535

PubMed Abstract | CrossRef Full Text | Google Scholar

77. Blázquez-Castro A. Optical Tweezers: Phototoxicity and Thermal Stress in Cells and Biomolecules. Micromachines (2019) 10:507. doi:10.3390/mi10080507

CrossRef Full Text | Google Scholar

78. Bunea AI, Glückstad J. Strategies for Optical Trapping in Biological Samples: Aiming at Microrobotic Surgeons. Laser Photon Rev (2019) 13:1800227. doi:10.1002/lpor.201800227

CrossRef Full Text | Google Scholar

79. Madsen LS, Waleed M, Casacio CA, Terrasson A, Stilgoe AB, Taylor MA, et al. Ultrafast Viscosity Measurement with Ballistic Optical Tweezers. Nat Photon (2021) 15:386–92. doi:10.1038/s41566-021-00798-8

CrossRef Full Text | Google Scholar

80. Wolfson D, Steck M, Persson M, McNerney G, Popovich A, Goksör M, et al. Rapid 3D Fluorescence Imaging of Individual Optically Trapped Living Immune Cells. J Biophoton (2015) 8:208–16. doi:10.1002/jbio.201300153

CrossRef Full Text | Google Scholar

81. Balaguer Fd. A, Aicart-Ramos C, Fisher GL, de Bragança S, Martin-Cuevas EM, Pastrana CL, et al. CTP Promotes Efficient ParB-dependent DNA Condensation by Facilitating One-Dimensional Diffusion from parS. Elife (2021) 10:10. doi:10.7554/eLife.67554

CrossRef Full Text | Google Scholar

82. Sergides M, Perego L, Galgani T, Arbore C, Pavone FS, Capitanio M. Probing Mechanotransduction in Living Cells by Optical Tweezers and FRET-Based Molecular Force Microscopy. Eur Phys J Plus (2021) 136:316. doi:10.1140/epjp/s13360-021-01273-7

CrossRef Full Text | Google Scholar

83. Strasser F, Moser S, Ritsch-Marte M, Thalhammer G. Direct Measurement of Individual Optical Forces in Ensembles of Trapped Particles. Optica (2021) 8:79–87. doi:10.1364/optica.410494

CrossRef Full Text | Google Scholar

84. Praeger M. Playing Optical Tweezers with Deep Reinforcement Learning: in Virtual, Physical and Augmented Environments. Machine Learn Sci Tech (2021) 2 3. doi:10.1088/2632-2153/abf0f6

CrossRef Full Text | Google Scholar

85. Lenton ICD. Machine Learning Reveals Complex Behaviours in Optically Trapped Particles. Machine Learn Sci Tech (2020) 1:4. doi:10.1088/2632-2153/abae76

CrossRef Full Text | Google Scholar

86. Dey R. Simultaneous Random Number Generation and Optical Tweezers Calibration Employing a Learning Algorithm Based on the Brownian Dynamics of a Trapped Colloidal Particle. Front Phys (2021) 8:629. doi:10.3389/fphy.2020.576948

CrossRef Full Text | Google Scholar

87. Aziz MS, Suwanpayak N, Jalil MA, Jomtarak R, Saktioto T, Ali J, et al. Gold Nanoparticle Trapping and Delivery for Therapeutic Applications. Int J Nanomedicine (2012) 7:11–7. doi:10.2147/IJN.S27417

CrossRef Full Text | Google Scholar

88. Liu X, Yuan J, Wu D, Zou X, Zheng Q, Zhang W, et al. All-optical Targeted Drug Delivery and Real-Time Detection of a Single Cancer Cell. Nanophotonics (2019) 9:611–22. doi:10.1515/nanoph-2019-0318

CrossRef Full Text | Google Scholar

89. Bunea A-I, Taboryski R. Recent Advances in Microswimmers for Biomedical Applications. Micromachines (2020) 11:1048. doi:10.3390/mi11121048

PubMed Abstract | CrossRef Full Text | Google Scholar

90. Bajpai A, Tong J, Qian W, Peng Y, Chen W. The Interplay between Cell-Cell and Cell-Matrix Forces Regulates Cell Migration Dynamics. Biophysical J (2019) 117:1795–804. doi:10.1016/j.bpj.2019.10.015

PubMed Abstract | CrossRef Full Text | Google Scholar

91. Johansen PL, Fenaroli F, Evensen L, Griffiths G, Koster G. Optical Micromanipulation of Nanoparticles and Cells inside Living Zebrafish. Nat Commun (2016) 7:10974. doi:10.1038/ncomms10974

PubMed Abstract | CrossRef Full Text | Google Scholar