From Thermodynamics to Information: Landauer’s Limit and Negentropy Principle Applied to Magnetic Skyrmions

Magnetic skyrmions are topological swirling spin textures objects that can be manipulated and employed as information carriers. This is accomplished based either on their ground-state properties or their thermodynamic properties. Landauer’s principle establishes an irreversible conversion from information to physics. The inverse mechanism, the inverse mechanism is proposed for magnetic topological defects forming in magnetic nanostructures that are regarded as closed thermodynamic systems confirming Szilard’s and Brillouin’s hypotheses. This mechanism consists of the creation of bits of information using a thermodynamic source having a form of negentropy. In this perspective article, the following are proved for magnetic skyrmions: 1) Landauer’s principle expressed in terms of negentropy and 2) the generalized second principle of thermodynamics based on Brillouin’s negentropy principle of information. The thermodynamic entropy is converted into information entropy at the expense of negentropy, “negative entropy” corresponding to the loss of thermodynamic entropy from the magnetic skyrmion itself. A recently proposed practical device enables the verification of points 1) and 2) and allows a full understanding of the interchange between thermodynamics and information and vice versa regarding skyrmions as information units and showing, in perspective, the considerable advantages offered by this type of storing and coding information.

Introduction

Magnetic skyrmions are axisymmetric topological solitons of vortex-like character hosted in ferromagnetic materials. Generally, they are stabilized by an exchange interaction of relativistic nature called Dzyaloshinskii–Moriya interaction (DMI) [1, 2]. Magnetic skyrmions are characterized by 1) a skyrmion number S (otherwise called the topological charge), an integer that indicates how many times magnetic moments within a skyrmion wrap a sphere; 2) helicity number, the phase appearing in the in-plane spin texture; and 3) a fixed rotation fashion called chirality χ. The skyrmion number is expressed as S = 1/(4π) ∫ d²ρ m·(∂m/∂x × ∂m/∂y) where m(ρ) = M(ρ)/M_s is the dimensionless magnetization vector with M representing the magnetization, ρ = (x, y) the in-plane coordinates, M_s representing the saturation magnetization, and ∂/∂x and ∂/∂y are first partial derivatives.

Recently, great efforts have been devoted to the manipulation of magnetic skyrmions forming in magnetic nanostructures based on their ground-state magnetic properties and giving rise to spintronic applications [1–4]. Very recently, magnetic skyrmions have been employed as qubits, a new class of quantum logic elements [5]. It has also been proposed the employment of magnetic skyrmions as information entropy carriers suggesting a data communication system based on the coding of information entropy [6]. This investigation stemmed from the theoretical and numerical exploration of the thermodynamic properties of magnetic skyrmions [7–10]. In this respect, the link between the physical and information entropies has been a subject matter of several studies [11–15]. On the other hand, the concept of negentropy was introduced first by Szilard who solved Maxwell’s demon paradox [16, 17], and then by Brillouin [18–23] who continued Szilard’s and Shannon’s investigations. After the discovery and formulation of Landauer’s principle [24–27], in recent decades, great efforts were made for the full understanding of information erasure and its relation with thermodynamics and logical computation from a philosophical, theoretical, and experimental viewpoints [28–47].

In this perspective article, this kind of investigation was applied to magnetic skyrmions. The aim of this study was threefold: 1) to show that Landauer’s limit is expressed in terms of variation of negentropy for a Néel skyrmion; 2) to show that the generalized second principle of thermodynamics based on Brillouin’s negentropy principle can be applied to a Néel skyrmion; and 3) to explain the interplay between information and negentropy and vice versa of a Néel skyrmion [6, 8]. This discussion could open the route in prospect for a new way of storing and coding information by using magnetic topological defects.

Negentropy and Landauer’s Limit for a Magnetic Skyrmion

A Néel skyrmion (or hedgehog skyrmion) forming in magnetic nanostructures as a result of the interfacial DMI is characterized by the magnetization texture $\mathbf{m}=\chi \sin \theta \widehat{\rho }+\cos \theta \widehat{z}$ in a cylindrical reference frame (ρ, φ, z) where χ = ±1 is the chirality (+1 outwardly magnetization, −1 inwardly magnetization), and θ is the polar angle with 0 ≤ θ ≤ π. Figure 1A shows an outwardly Néel skyrmion (χ = +1) with a negative polarity (θ = π) and skyrmion number S = −1 subjected to an external magnetic field H along the + z direction, while Figure 1B displays an inwardly Néel skyrmion (χ = −1) with a positive polarity (θ = 0) and skyrmion number S = +1 subjected to an external magnetic field H along the − z direction. In the following discussion, the Néel skyrmion texture shown in Figure 1A was taken into account to be consistent with the results of micromagnetic simulations carried out on a Néel skyrmion with χ = +1, negative polarity, and S = −1 [7]. However, note that this choice is purely arbitrary and the same conclusion would be drawn taking into account the Néel skyrmion with χ = −1, a positive polarity, and S = +1.

FIGURE 1

FIGURE 1. Pictorial representation of a Néel magnetic skyrmion in two magnetization textures. (A) Perpendicularly magnetized ferromagnet hosting an outwardly (chirality $\chi =+1$) Néel magnetic skyrmion with polarity p = −1. (B) Perpendicularly magnetized ferromagnet hosting an inwardly (chirality $\chi =-1$) Néel magnetic skyrmion with polarity p = +1. H lies along the z-axis [positive direction in (A) and negative direction in (B)].

The skyrmion energy was calculated from the microscopic micromagnetic Hamiltonian as a spatial integral of the skyrmion energy density within the thin-film limit including exchange, interfacial DMI, magnetostatic and perpendicular anisotropy contributions, and external magnetic field interaction [7–9]. Within this model, the exchange interaction among spins forming the magnetic skyrmion was rigorously taken into account. It was found that, in the vicinity of the absolute energy minimum at the equilibrium skyrmion diameter D_0sky, the skyrmion energy can be fitted by means of a parabolic curve for any temperature T and bias field amplitude H in the region of skyrmion metastability (0 ≤ T ≤ 300 K for μ₀ H > 5 mT and 0 ≤ T ≤ 200 K for μ₀H = 0 mT) [7]. Importantly, D_0sky strictly depends on the parameters of the microscopic Hamiltonian. In this respect, the determination of the skyrmion size for an isolated skyrmion by computing the skyrmion radius (both equilibrium and average) has recently been proved according to different analytical theories based on the minimization of the skyrmion energy with respect to the skyrmion radius [9, 48, 49]. In particular, it has been shown that both the average skyrmion size and the wall width separating the core from the outer domain of the skyrmion can be accurately computed [48]. This investigation has been generalized by studying the magnetic skyrmion’s size and spin profile in a condensed phase forming a skyrmion crystal at high skyrmion density [49]. In this latter case, it has been demonstrated that the dependence of skyrmion size on magnetic parameters is different compared to isolated skyrmions or to skyrmion stripes forming at low skyrmion density.

According to micromagnetic simulations, it was observed that the value of the Néel skyrmion diameters obeys a distribution analogous to Maxwell–Boltzmann (MB) of the molecules of an ideal gas at any T and for any H in the region of metastability [7]. Exploiting this physical analogy with ideal gases, an analytical MB distribution for a 3D skyrmion diameter population [7, 9] was proposed, and it was found an excellent agreement between the micromagnetic and the analytical results [7]. This analogy was also extended to the 2D skyrmion diameter distribution [8]. From the analogy with the 3D MB distribution of an ideal gas, the Gaussian distribution at the thermodynamic equilibrium at a given T and H for both 3D and 2D skyrmion diameter distribution can be written in the form

$f_0\left({\mathit{D}}_{\mathrm{sky}}\right)\mathit{=}{\mathit{C}}_{\mathrm{av}}{\mathit{e}}^{-\frac{\mathit{a}}{{\mathit{k}}_{\mathit{B}}\mathit{T}}{\left(\Delta \mathrm{\langle }{\mathit{D}}_{\text{sky}}\rangle \right)}^2},(1)$

where C_av is the normalization constant (in m^-2), k_B is the Boltzmann constant, a is a coefficient proportional to the skyrmion energy curvature, Δ<D_sky> = D_sky − < D_sky >, D_sky the skyrmion diameter, and <D_sky> the average skyrmion diameter with <D_sky> = <D_sky (T)>.

Owing to the mentioned analogy, it is useful to relate the diameter distribution depending on T and H to skyrmion’s thermodynamic entropy as occurs for the thermodynamic entropy of an ideal gas. Regarding this, it is important to note that the main source of entropy for domains forming in ferromagnets is represented by spin waves (or magnons). Recently, it has been found that the source of entropy and free energy for a domain and a domain wall (DW) in a magnetic nanowire is due to thermally activated magnons [50]. In this system, it has been demonstrated that the larger domain wall entropy is due to the increase in the magnon density of states at low energy, and the driving force allowing DW propagation under a temperature gradient towards the hotter region is the thermodynamic entropy itself. Under this condition, the system evolves toward a state that lowers its free energy by exploiting DW’s larger entropy [50]. The DW movement toward a hotter region driven by thermal gradients has also been proved in antiferromagnets and can be understood by means of the minimization of the free energy [51]. Also, the main source of the configurational entropy of a classical Néel magnetic skyrmion has been attributed to the thermal-breathing mode, a type of spin wave as observed in micromagnetic simulations [7].

The configurational entropy at thermodynamic equilibrium related to a classical Néel magnetic skyrmion diameter distribution was computed, at each T and H, as the Gibbs–Boltzmann’s statistical thermodynamic entropy, a quantity proportional to the statistical average H₀ = <lnf₀>, the Boltzmann order function at thermodynamic equilibrium, namely as S = −k_B H₀ with S = S(T) [7–9]. This entropy is the generalization of the Boltzmann entropy when the microstates of the statistical ensemble are not equiprobable. For a 2D skyrmion diameter population, after performing the statistical average H₀ within the continuous limit, it takes the form [8]

$S\mathit{=}-k_B\pi {\displaystyle \underset{\mathrm{0}}{\overset{\infty }{\int }}\mathit{d}{\mathit{D}}_{\mathrm{sky}}{\mathit{D}}_{\mathrm{sky}}{\mathit{f}}_{\mathrm{0}}\left({\mathit{D}}_{\mathrm{sky}}\right)\ln \left({\mathit{f}}_{01}\left({\mathit{D}}_{\mathrm{sky}}\right)\right).}(2)$

Here, f₀₁ (D_sky) = f₀<A_sky> with <A_sky> ≈1/4 π <D_sky>² the average skyrmion area and S > 0 (in J/K). The Gaussian distribution f₀ is the one that realizes the largest thermodynamic entropy according to the maximum entropy principle. In turn, <D_sky (T)> ≈ D_0sky [1+ k_B T/(2a D_0sky²)] with D_0sky = D_0sky(T) defined as the diameter at which the total skyrmion energy attains its absolute minimum. In turn, the value of D_0sky strictly depends on the magnetic parameters appearing as coefficients in the micromagnetic Hamiltonian such as the exchange stiffness constant A, the interfacial Dzyaloshinskii–Moriya parameter D, the uniaxial perpendicular anisotropy constant K_u, and on the external magnetic field amplitude H. The statistical thermodynamic entropy is also referred to as thermal entropy [52, 53] and is an increasing monotonic function of T.

The information entropy (expressed in terms of the number of bits) was calculated according to Jaynes’s information framework [11–15] and taking into account Eq. 2. The use of continuous variables was suggested by Jayne in [13, 14] and was applied to the definition of information entropy in the continuum case [15]. The information entropy (in bits) was determined as the 2D statistical average of the information content I (D_sky) = −log₂ (f₀₁ (D_sky)) (2 is the logarithm basis) [6] and can be rewritten in the form

$H_I=\pi {\displaystyle \underset{\mathrm{0}}{\overset{\infty }{\int }}d{D}_{\mathrm{sky}}{D}_{\mathrm{sky}}{\mathit{f}}_{\mathrm{0}}\left({\mathit{D}}_{\mathrm{sky}}\right)I\left({\mathit{D}}_{\mathrm{sky}}\right)},(3)$

with H_I > 0.

Landauer’s limit is derived starting from the configurational entropy and the corresponding information entropy. To create bits of information, S must decrease passing from an initial temperature T_i to a final temperature T_f with T_f < T_i. Starting from Eq. 1 and using some logarithm rules, the entropy variation ΔS = S (T = T_f) − S (T = T_i) with S (T = T_f) < S (T = T_i) such that ΔS < 0 can be written in a compact form as

$\Delta S=k_B\pi \left[{\displaystyle \underset{0}{\overset{\infty }{\int }}d{D}_{\text{sky}}{D}_{\text{sky}}\ln \left(\frac{f_{01}{\left(T=T_{\mathrm{i}}\right)}^{f_0\left(T=T_{\mathrm{i}}\right)}}{f_{01}{\left(T=T_{\mathrm{f}}\right)}^{f_0\left(T=T_{\mathrm{f}}\right)}}\right)}\right],(4)$

where the dependence of f₀₁ and f₀ on D_sky is omitted. Analogously, the variation of the information entropy coded by the magnetic skyrmion, ΔH_I = H_I (T = T_f) − H_I (T = T_i) with T_f > T_i (the temperature T_f appearing in H_I corresponds to the temperature T_i appearing in S and vice versa) and H_I (T = T_f) > H_I (T = T_i) such that ΔH_I >0 takes the form

$\Delta H_I=\pi \left[{\displaystyle \underset{0}{\overset{\infty }{\int }}d{D}_{\text{sky}}}{D}_{\text{sky}}{\log }_2\left(\frac{f_{01}{\left(T=T_{\mathrm{i}}\right)}^{f_0\left(T=T_{\mathrm{i}}\right)}}{f_{01}{\left(T=T_{\mathrm{f}}\right)}^{f_0\left(T=T_{\mathrm{f}}\right)}}\right)\right].(5)$

It is useful to introduce the corresponding thermodynamic variation of information entropy by defining S_I = k_B H_I. By comparing Eqs 4, 5 and taking into account that S_I = k_B H_I, Landauer’s limit can be derived. Indeed, substituting ln (f₀₁) = log₂ (f₀₁) ln2 in Eq. 2 and comparing Eq. 2 with Eq. 3, one gets, via ΔS_I = k_B ΔH_I, ΔS = −ΔS_I ln2. The creation of 1 bit of information leads to a variation ΔH_I = 1 bit and to an increment ΔS_I = k_B (units of 1 bit) yielding

$\Delta S=\mathit{-}{k}_B\ln 2.(6)$

Therefore, Landauer’s limit corresponds to the lower limit of the entropy lost in an observation as a result of the creation of 1 bit. In the present case, the thermodynamic entropy was lowered to create 1 bit of information and the minimum energy,

$\mathit{E}=\mathit{-}{k}_{B}T\ln 2,(7)$

was subtracted from the system. The amount of energy is the minimal work W = − k_B T ln 2 (W < 0) that must be extracted to create 1 bit of information, as established by Landauer’s principle. This is a different case with respect to that was considered by Landauer for which the logical irreversibility implies the thermodynamic irreversibility. The information coding by a magnetic skyrmion can be regarded as a thermodynamically reversible process. By introducing the negentropy, the entropic equivalent of degradation of energy [18], namely N = −S (N <0 and S >0) and ΔN = −ΔS >0 being ΔN = N (T = T_f) − N (T = T_i), N (T = T_f) < 0 and N (T = T_i) < 0 but N (T = T_f) > N (T = T_i) we get

$\Delta \mathit{N}=k_B\ln 2.(8)$

Therefore, Landauer’s limit can be regarded as the negentropy acquired by the system.

The Brillouin’s Negentropy Second Principle of Thermodynamics for a Magnetic Skyrmion

According to the second principle of thermodynamics, a magnetic system moves towards a state with a larger entropy or lower free energy [50]. The magnetic skyrmion’s Helmholtz free energy, viz. F = <E > − T S with <E > = <E (T)> the average skyrmion energy, in the absence of an external magnetic field, diminishes with increasing T and attains a minimum at the upper limit of the region of metastability at T = 300 K. With the magnetic parameters used (see the following section), F ≈ 5.5 10^–20 J at T = 150 K [9] corresponds to 1 bit of information.

Here, the generalized second principle of thermodynamics for a closed thermodynamic system such as a magnetic skyrmion in terms of Brillouin’s negentropy principle ΔS_tot = ΔS − ΔS_I ≥ 0 is discussed [18]. Therefore, the total entropy S_tot of a magnetic skyrmion does not decrease. In particular, ΔS_tot = S_{tot f} − S_{tot i} is the total entropy variation from the initial state i to the final state f, and ΔS = S_f −S_i >0 is the variation of the thermal entropy from the initial state to the final state (by the convention of an opposite sign with respect to that in Eq. 4), while ΔS_I = S_If −S_Ii > 0 is the increment of information entropy in thermodynamic units owing to the creation of bits of information. By introducing the negentropy variation ΔN = −ΔS < 0, the generalized second principle of thermodynamics is expressed in terms of Brillouin’s negentropy

$\Delta \left(N+S_I\right)\le 0.(9)$

Eq. 9 expresses thermodynamic reversibility when Δ(N + S_I) = 0, viz. ΔN = −ΔS_I but it does not state that physical reversibility necessarily implies logical reversibility.

New Perspectives in Information Theory: The Skyrmion Unit

In this section, new perspectives in information theory based on the use of the magnetic skyrmion as a unit of information entropy are outlined [6, 8].

The Role of the Sender and the Receiver in a Data Communication System

In a data communication system, it is crucial to understand how the information from the sender allows an amount of negentropy N to get converted into information entropy H_I. This occurs because the sender sends to the magnetic skyrmion a binary input of amplitude 2ⁿ where n is the number of bits of information entropy. This binary input might be regarded in a way similar to a light input interacting with matter (e.g., a laser source), and this interaction with the skyrmion allows rewriting its thermodynamic configuration and its corresponding entropy. For example, for n = 2 bits, there are g = 4 binary configurations [6] that refer to an average skyrmion diameter < D_sky> and to the average entropy S according, for instance, to the sampling: 00→ D_sky¹, 01 → D_sky², 10 → D_sky³, 11 → D_sky⁴ with D_sky^j (j = 1,2,3,4). This means that the jth binary configuration fixes the thermodynamic configuration corresponding to the jth entropy density $s\left(D_{\mathrm{sky}}^j\right)=-k_B{f}_0\left(D_{\mathrm{sky}}^j\right)\ln \left(f_{01}\left(D_{\mathrm{sky}}^j\right)\right)$. This is accomplished by viewing the sender involved in a “writing” operation linking the jth binary configuration to the jth entropy density $s\left({\mathit{D}}_{\mathrm{sky}}^j\right)$. The general effect of these subsequent reading operations is accounted in the calculation of a statistical average corresponding to S. The entropy cost of this operation is ΔN = − ΔS < 0 (dN = −dS), an entropy source employed as a reservoir for increasing the information entropy which causes a variation ΔS_I > 0 (dS_I > 0) that, in bit units, is ΔH_I > 0 (dH_I > 0) (see Figure 2A). If the process is reversible ΔN = −ΔS_I, while if it is irreversible ΔN < −ΔS_I (Eq. 9). Figure 2B shows the binary–thermodynamic correspondence in terms of signal sampling for a 2D MB population of magnetic skyrmion diameters of the form $\frac{dn}{d{D}_{\text{sky}}}=C_{\text{sky}}{D}_{\text{sky}}{e}^{-\frac{a}{k_{B}T}{\left(D_{\text{sky}}-D_{0\text{sky}}\right)}^2}$ at T = 300 K and μ₀H = 0 mT with dn/dD_sky, the number of diameters ranging between D_sky and D_sky + dD_sky, C_sky the normalization constant (in m⁻²). In the numerical calculations performed for ferromagnetic dot/heavy metal systems (e.g., Co/Pt), we employed the following geometric and magnetic parameters: dot radius R = 200 nm and Co thickness t = 0.8 nm, M_s (T = 0 K) = 6.0 × 10⁵ A/m, A (T = 0 K) = 2.0 × 10⁻¹¹ J/m, D (T = 0 K) = 3.0 × 10⁻⁶ J/m², and K_u (T = 0 K) = 0.6 × 10⁶ J/m³ [6–9, 54]. A, D, and K_u were scaled from their zero temperature values at non-zero temperature by using scaling laws [54]. For the parameters used, a = 0.71 × 10⁻⁵ J/m², D_0sky = 81.28 nm, and n ≈2. The coded information is read by the receiver as a sequence of 4 binary configurations (00, 01, 10, 11), the binary interpretation of the negentropy resulting from the information entropy. The receiver consists of a binary sensor made by binary inputs enabling to read the discrete signal corresponding to a sequence of binary configurations assigned to a given entropy density. This coding has the considerable advantage to potentially create more bits for an equal number of skyrmions. The employment of 4 magnetic skyrmions heated at room temperature could lead to the coding of 1 byte of information which represents a unit of computer information and g = 256 binary configurations.

FIGURE 2

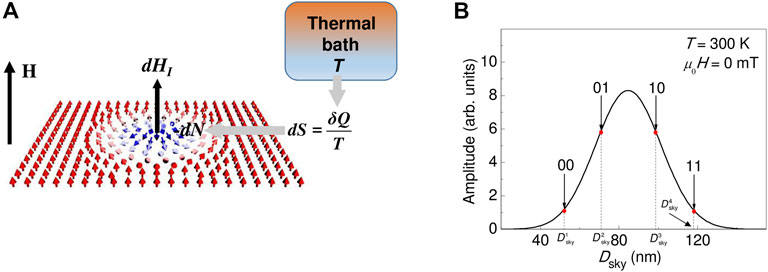
FIGURE 2. (A) Sketch of the ferromagnetic nanostructure (film) hosting a Néel magnetic skyrmion (outwardly magnetized and negative p = −1) regarded as a closed thermodynamic system. The infinitesimal reversible exchange of entropy dS ($\delta Q$ is the infinitesimal absorbed heat) between the thermal bath and the film at temperature T and between the film and the skyrmion is indicated. dN is the infinitesimal skyrmion negentropy, and dH_l is the infinitesimal information entropy. (B) The sampling of the skyrmions’ diameter distribution at T = 300 K and ${\mu }_{0}H=0\text{mT}$ via the assignment of the 4-bit configurations 00, 01, 10, and 11 to the skyrmion diameters, D_sky¹, D_sky², D_sky³, and D_sky⁴, respectively. For the parameters used [6], $H_{\mathit{l}}\approx 2$ bits and the number of bit configurations is 4.

Conclusion

In this study, the interplay between thermodynamics and information occurring in easily manipulated magnetic skyrmions forming in magnetic nanostructures was discussed. It has been proved that Landauer’s limit for a magnetic skyrmion can be expressed in terms of negentropy variation. It has been shown that the interchange between thermodynamic entropy and information entropy to create bits of information occurs by using a reservoir of negentropy that fulfills Brillouin’s negentropy second principle of thermodynamics. This type of coding information based on the information entropy could be employed in prospect for improving data transmission.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author Contributions

RZ conceived the theme, developed the physical ideas, and suggested the applications based on the relation between thermodynamics and information for magnetic skyrmions.

Conflict of Interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

The author acknowledges support from Gruppo Nazionale per la Fisica Matematica (GNFM) and Istituto Nazionale di Alta Matematica (INdAM) “F. Severi.”

References

1. Fert A, Cros V, Sampaio J. Skyrmions on the Track. Nat Nanotech (2013) 8:152–6. doi:10.1038/nnano.2013.29

CrossRef Full Text | Google Scholar

2. Fert A, Reyren N, Cros V. Magnetic Skyrmions: Advances in Physics and Potential Applications. Nat Rev Mater (2017) 2:17031. doi:10.1038/natrevmats.2017.31

CrossRef Full Text | Google Scholar

3. Müller J. Magnetic Skyrmions on a Two-Lane Racetrack. New J Phys (2017) 19:025002. doi:10.1088/1367-2630/aa5b55

CrossRef Full Text | Google Scholar

4. Zhang X, Zhou Y, Mee Song K, Park T-E, Xia J, Ezawa M, et al. Skyrmion-electronics: Writing, Deleting, reading and Processing Magnetic Skyrmions toward Spintronic Applications. J Phys Condens Matter (2020) 32:143001. doi:10.1088/1361-648X/ab5488

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Psaroudaki C, Panagopoulos C. Skyrmion Qubits: A New Class of Quantum Logic Elements Based on Nanoscale Magnetization. Phys Rev Lett (2021) 127:067201. doi:10.1103/PhysRevLett.127.0672010.1103/PhysRevLett.127.067201

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Zivieri R. Magnetic Skyrmions as Information Entropy Carriers. IEEE Trans Magn (2022) 58:1500105. doi:10.1109/TMAG.2021.3092693

CrossRef Full Text | Google Scholar

7. Zivieri R, Tomasello R, Chubykalo-Fesenko O, Tiberkevich V, Carpentieri M, Finocchio G. Configurational Entropy of Magnetic Skyrmions as an Ideal Gas. Phys Rev B (2019) 99:174440. doi:10.1103/PhysRevB.99.174440

CrossRef Full Text | Google Scholar

8. Zivieri R. Statistical Properties and Configurational Entropy of a Two-Dimensional Néel Magnetic Skyrmions Population. Appl Sci (2020) 10:352. doi:10.3390/app10010352

CrossRef Full Text | Google Scholar

9. Zivieri R. Statistical Thermodynamics of Chiral Skyrmions in a Ferromagnetic Material. Materials (2019) 12:3702. doi:10.3390/ma12223702

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Zivieri R, Chubykalo-Fesenko O. Static Properties of Magnetic Skyrmions, Chapt. 6. In: G Finocchio, and C Panagopoulus, editors. Magnetic Skyrmions and Their Applications. Sawston: Woodhead Publishing Series in Electronic and Optical Materials (2021). p. 181–231. doi:10.1016/b978-0-12-820815-1.00010-9

CrossRef Full Text | Google Scholar

11. Shannon CE. A Mathematical Theory of Communication. Bell Syst Tech J (1948) 27:379–423. doi:10.1002/j.1538-7305.1948.tb01338.x

CrossRef Full Text | Google Scholar

12. Shannon CE, Weaver W. The Mathematical Theory of Communication. Urbana, IL, USA: University of Illinois Press (1949).

Google Scholar

13. Jaynes ET. Information Theory and Statistical Mechanics. Phys Rev (1957) 106:620–30. doi:10.1103/PhysRev.106.620

CrossRef Full Text | Google Scholar

14. Jaynes ET. Information Theory and Statistical Mechanics. II. Phys Rev (1957) 108:171–90. doi:10.1103/physrev.108.171

CrossRef Full Text | Google Scholar

15. Jaynes ET. Prior Probabilities. IEEE Trans Syst Sci Cybern (1968) 4:227. doi:10.1109/TSSC.1968.300117

CrossRef Full Text | Google Scholar

16. Szilard L. über die Entropieverminderung in einem thermodynamischen System bei Eingriffen intelligenter Wesen. Z Physik (1929) 53:840–56. doi:10.1007/BF01341281

CrossRef Full Text | Google Scholar

17. Szilard L. On the Decrease of Entropy in a Thermodynamic System by the Intervention of Intelligent Beings. Syst Res (1964) 9:301–10. doi:10.1002/bs.3830090402

CrossRef Full Text | Google Scholar

18. Brillouin L. The Negentropy Principle of Information. J Appl Phys (1953) 24:1152–63. doi:10.1063/1.1721463

CrossRef Full Text | Google Scholar

19. Brillouin L. Maxwell's Demon Cannot Operate: Information and Entropy. IJournal Appl Phys (1951) 22:334–7. doi:10.1063/1.1699951

CrossRef Full Text | Google Scholar

20. Brillouin L. Physical Entropy and Information. II. J Appl Phys (1951) 22:338–43. doi:10.1063/1.1699952

CrossRef Full Text | Google Scholar

21. Brillouin L. Information Theory and Most Efficient Codings for Communication or Memory Devices. J Appl Phys (1951) 22:1108–11. doi:10.1063/1.1700116

CrossRef Full Text | Google Scholar

22. Brillouin L. Negentropy and Information in Telecommunications, Writing, and Reading. J Appl Phys (1954) 25:595–9. doi:10.1063/1.1721696

CrossRef Full Text | Google Scholar

23. Brillouin L. Science and Information Theory. Cambridge, USA: Academic Press (1956).

Google Scholar

24. Landauer R. Irreversibility and Heat Generation in the Computing Process. IBM J Res Dev (1961) 5:183–91. doi:10.1147/rd.53.0183

CrossRef Full Text | Google Scholar

25. Landauer R. Information Is Physical. Phys Today (1991) 44:23–9. doi:10.1063/1.881299

CrossRef Full Text | Google Scholar

26. Landauer R. Dissipation and Noise Immunity in Computation and Communication. Nature (1988) 335:779–84. doi:10.1038/335779a0

CrossRef Full Text | Google Scholar

27. Landauer R. The Physical Nature of Information. Phys Lett A (1996) 217:188–93. doi:10.1016/0375-9601(96)00453-7

CrossRef Full Text | Google Scholar

28. Bennett CH. Logical Reversibility of Computation. IBM J Res Dev (1973) 17:525–32. doi:10.1147/rd.176.0525

CrossRef Full Text | Google Scholar

29. Bennett CH. The Thermodynamics of Computation: a Review. Int J Theor Phys (1982) 21:905–40. doi:10.1007/BF02084158

CrossRef Full Text | Google Scholar

30. Shizume K. Heat Generation Required by Information Erasure. Phys Rev E (1995) 52:3495–9. doi:10.1103/PhysRevE.52.3495

CrossRef Full Text | Google Scholar

31. Earman J, Norton JD. EXORCIST XIV: The Wrath of Maxwell's Demon. Part II. From Szilard to Landauer and beyond. Stud Hist Philos Sci B: Stud Hist Philos Mod Phys (1999) 30:1–40. doi:10.1016/S1355-2198(98)00026-4

CrossRef Full Text | Google Scholar

32. Piechocinska B. Information Erasure. Phys Rev A (2000) 61:062314. doi:10.1103/PhysRevA.61.062314

CrossRef Full Text | Google Scholar

33. Frank MP. The Physical Limits of Computing. Comput Sci Eng (2002) 4:16–26. doi:10.1109/5992.998637

CrossRef Full Text | Google Scholar

34. Wang GM, Sevick EM, Mittag E, Searles DJ, Evans DJ. Experimental Demonstration of Violations of the Second Law of Thermodynamics for Small Systems and Short Time Scales. Phys Rev Lett (2002) 89:05060. doi:10.1103/PhysRevLett.89.050601

CrossRef Full Text | Google Scholar

35. Bennett CH. Notes on Landauer's Principle, Reversible Computation and Maxwell's Demon. Stud Hist Philos M P (2002) 34:501–10. doi:10.1016/S1355-2198(03)00039-X

CrossRef Full Text | Google Scholar

36. Maroney OJE. The (Absence of a) Relationship between Thermodynamic and Logical Reversibility. Stud Hist Philos Sci Part B: Stud Hist Philos Mod Phys (2005) 36:355–74. doi:10.1016/j.shpsb.2004.11.006

CrossRef Full Text | Google Scholar

37. Norton JD. Eaters of the lotus: Landauer's Principle and the Return of Maxwell's Demon. Stud Hist Philos Sci Part B: Stud Hist Philos Mod Phys (2005) 36:375–411. doi:10.1016/j.shpsb.2004.12.002

CrossRef Full Text | Google Scholar

38. Sagawa T, Ueda M. Minimal Energy Cost for Thermodynamic Information Processing: Measurement and Information Erasure. Phys Rev Lett (2009) 102:250602. doi:10.1103/PhysRevLett.102.250602

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Dillenschneider R, Lutz E. Memory Erasure in Small Systems. Phys Rev Lett (2009) 102:210601. doi:10.1103/PhysRevLett.102.210601

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Vaccaro JA, Barnett SM. Information Erasure without an Energy Cost. Proc R Soc A (2011) 467:1770–8. doi:10.1098/rspa.2010.0577

CrossRef Full Text | Google Scholar

41. Pop E. Energy Dissipation and Transport in Nanoscale Devices. Nano Res (2010) 3:147–69. doi:10.1007/s12274-010-1019-z

CrossRef Full Text | Google Scholar

42. Norton JD. Waiting for Landauer. Stud Hist Philos Sci Part B: Stud Hist Philos Mod Phys (2011) 42:184–98. doi:10.1016/J.SHPSB.2011.05.002

CrossRef Full Text | Google Scholar

43. Bérut A, Arakelyan A, Petrosyan A, Ciliberto S, Dillenschneider R, Lutz E, et al. Experimental Verification of Landauer's Principle Linking Information and Thermodynamics. Nature (2012) 483:187–9. doi:10.1038/nature10872

PubMed Abstract | CrossRef Full Text | Google Scholar

44. Sagawa T. Thermodynamic and Logical Reversibilities Revisited. J Stat Mech (2014) 2014:P03025. doi:10.1088/1742-5468/2014/03/P03025

CrossRef Full Text | Google Scholar

45. Jun Y, Gavrilov M, Bechhoefer J. High-Precision Test of Landauer's Principle in a Feedback Trap. Phys Rev Lett (2014) 113:190601. doi:10.1103/PhysRevLett.113.190601

PubMed Abstract | CrossRef Full Text | Google Scholar

46. Hong J, Lambson B, Dhuey S, Bokor J. Experimental Test of Landauer's Principle in Single-Bit Operations on Nanomagnetic Memory Bits. Sci Adv (2016) 2:e1501492. doi:10.1126/sciadv.1501492

PubMed Abstract | CrossRef Full Text | Google Scholar

47. Wolpert DH. The Stochastic Thermodynamics of Computation. J Phys A: Math Theor (2019) 52:193001. doi:10.1088/1751-8121/ab0850

CrossRef Full Text | Google Scholar

48. Wang XS, Yuan HY, Wang XR. A Theory on Skyrmion Size. Commun Phys (2018) 1:31. doi:10.1038/s42005-018-0029-0

CrossRef Full Text | Google Scholar

49. Wu H, Hu X, Jing K, Wang XR. Size and Profile of Skyrmions in Skyrmion Crystals. Commun Phys (2021) 4:210. doi:10.1038/s42005-021-00716-y

CrossRef Full Text | Google Scholar

50. Wang XS, Wang XR. Thermodynamic Theory for thermal-gradient-driven Domain-wall Motion. Phys Rev B (2014) 90:014414. doi:10.1103/PhysRevB.90.014414

CrossRef Full Text | Google Scholar

51. Selzer S, Atxitia U, Ritzmann U, Hinzke D, Nowak U. Inertia-Free Thermally Driven Domain-Wall Motion in Antiferromagnets. Phys Rev Lett (2016) 117:107201. doi:10.1103/PhysRevLett.117.107201

PubMed Abstract | CrossRef Full Text | Google Scholar

52. Simon F. On the Third Law of Thermodynamics. Physica (1937) 4:1089–96. doi:10.1016/s0031-8914(37)80205-0

CrossRef Full Text | Google Scholar

53. Feistel R. Distinguishing between Clausius, Boltzmann and Pauling Entropies of Frozen Non-equilibrium States. Entropy (2019) 21:799. doi:10.3390/e21080799

PubMed Abstract | CrossRef Full Text | Google Scholar

54. Tomasello R, Guslienko KY, Ricci M, Giordano A, Barker J, Carpentieri M, et al. Origin of Temperature and Field Dependence of Magnetic Skyrmion Size in Ultrathin Nanodots. Phys Rev B (2018) 97:060402. doi:10.1103/physrevb.97.060402

CrossRef Full Text | Google Scholar