Double-armed cone-shaped flexoelectric transducer

Compared with a single energy harvester, this tuning fork double-armed cone-shaped flexure transducer can fundamentally solve the problems of high resonance frequency, low output efficiency, and narrow bandwidth of the flexure transducer. Since the transducer limits the clamping losses of the cantilever beam, it provides sufficient stiffness-mass balance to lower the resonance frequency of the system and extend the bandwidth. The tapered structure provides sufficient strain gradient for the flexoelectric effect, improving the output efficiency of the whole system. The vibration frequency of the tuning fork structure and the derivation of the bandwidth formula are analyzed theoretically, and then the electrode width and thickness of the cone structure are studied through simulation to analyze the transducer output response, resonant frequency, bandwidth, and output impedance.

1 Introduction

It is well known that flexoelectricity and piezoelectricity work together in micro-nano composite materials [1]. In the design of flexoelectric structures, cantilever beam structures [2,3], wrinkled micro-dielectric films are often used [4,5], and nano-indentation designs use tips to induce non-uniform strains to improve flexoelectric effects [6]. Starting from a wide range of transducers, symmetrical dual-mode magneto-electromechanical coupled resonators are used to improve the output power of micro-energy harvesting based on magneto-electromechanical (MME) coupling [7]. When the tuning fork structure is designed as a vibrating capacitive surface potential measuring device, only when the vibration amplitude of the tuning fork is stable, the current output by the sensing electrode can be stable. And the current has a linear relationship with the measured potential V [8,9]. Quartz crystal tuning fork (QTF), as a mechanical resonator, is very attractive in the field of sense due to its small size, low cost, and high-quality factor [9].

The design of the transducer tries to identify areas with positive polarity (+1) and negative polarity (−1). The resulting design problem was addressed using a density-based topology optimization approach. Numerical examples confirm that piezoelectric modal transducers can be designed with simply connected electrode phases, providing efficient performance as well as improved manufacturabili [10]. It can also tuned by varying the stiffness using materials [11]. Flexible nanogenerators equipped with quadrant electrodes have also been reported as a simple, efficient, and general method for decoupling in-plane flexoelectricity from the total electromechanical output [12]. Some studies have established a self-powered system driven by a wireless nanogenerator (NG) [13] Studies have concluded on the flexoelectricity that giant bend-induced polarization can be obtained without an inherently large flexoelectricity, which will help to reconcile some of the current discrepancies regarding the true magnitude of the flexoelectricity [14] Among the factors affecting the transducer are residual surface stress [15], linear elastic substrate and magnetic field [16], ferroelectricity, microstructure and micro-inertia effects [17], which can further improve the performance of PZT energy harvesters. Futhermore, using ZnO can improve the flexoelectric effect [18].

The flexoelectric effect transducer is the same as other transducers, and bandwidth is one of the important indicators of the transducer. In the field of infrared spectroscopy, mQTF detectors are used instead of pyroelectric infrared detectors to collect infrared photoelectric new numbers, which have the Advantages of broadband optics [19]. When the thickness of the substrate layer is 400 nm, the maximum output voltage of the flexoelectric energy harvester is almost 5 times that of the piezoelectric energy harvester. The effects of parameters such as drag force, beam spacing, and needle tip mass on harvester performance were investigated. Experimental results show that, due to the collision of two beams, the operating bandwidth of the VEH is increased by nearly 4 times, at the same time, the output power density is enhanced in some cases [20].

2 Theoretical analysis

The flexoelectric effect is a kind of polarization caused by non-uniform deformation. It exists widely in most materials, while the piezoelectric effect exists only in non-centrosymmetric materials. In terms of the ability to convert mechanical stress into electrical voltage, piezoelectricity trumps flexoelectricity. However, with the advent of the realization that nanoscale strain gradients are much larger than macroscopic strain gradients, the importance of flexoelectricity has increased with miniaturization. It can improve energy conversion efficiency in smart structures and provide new methods for smart structure design.

The most widely used flexoelectric energy harvesting structure is the cantilever beam structure, but it has certain limitations. In the design, it is changed to a tuning fork double-arm structure as the driving component of the system, which can effectively control the flexoelectric energy conversion the stability of the device and the vibration frequency. During the vibration process of the tuning fork, the electrode and the flexoelectric layer move together, and there is no form of rotation around the center of the electrode, so the first-order or second-order model is used. By exciting the tuning fork to vibrate, when the frequency of the input signal is the same as the natural frequency of the tuning fork, the tuning fork resonates, which drive the flexoelectric layer on it converts mechanical energy into electrical energy. A flexoelectric layer fabricated with a tapered structure. When the stress load is applied, because of the different widths of the upper and lower surfaces, artificially created non-uniform deformation of the structure, uneven distribution of charges, great asymmetry in electric displacement and polarization, which makes the flexoelectric effect in ferroelectric materials more prominent. When the charge reaches the electrodes, the electric energy is taken out from the electrodes. Each electrode is connected in series, and an external resistor is connected for electrical performance testing.

In addition to the commonly used method of bending to create a strain gradient, the use of truncated corners and pyramids in the structure can also provide a certain strain gradient [21,22]. The normal strain in the pyramid structure changes continuously from the top to the bottom. This strain gradient induces charge flow between the top and bottom electrodes. The flexoelectric effect has a strong size dependence, so the use of micro-nanostructures can significantly improve its output effect. The electrical response (i.e., polarization or electric field) of a positive flexoelectric effect material to a mechanical stimulus (strain gradient) [23].

When the frequency of the applied pressure signal is consistent with the frequency of the transducer, resonance can be generated and the maximum amplitude can be obtained. For the structural analysis of the tuning fork structure, the double arm can be regarded as two cantilever beam structures, which can be regarded as two independent cantilever beams for structural vibration analysis, vibrating in the form of bending in the fluid medium, so the corresponding cantilever beam vibration Eq. 1 is [24]:

$\frac{EI}{l^4}\frac{{\partial }^{4}y\left(\eta ,t\right)}{\partial {\eta }^4}+f_1\frac{\partial y\left(\eta ,t\right)}{\partial t}+\left(\rho A+f_2\right)\frac{{\partial }^{2}y\left(\eta ,t\right)}{\partial t^2}=0(1)$

Among them: E is Young’s modulus, I is the moment of inertia, L is the length of the beam, ρ is the material density, A is the cross section of the cantilever beam, f₁ is the dissipative resistance parameter per unit length, f₂ is the inertial resistance parameter per unit length (the unit The additional quality of the length),η is the normalized length parameter.

By solving the vibration equation, the corresponding eigenfrequency solution can be obtained as Eq. 2:

${\omega }_n={\left[\frac{EI{k}_n^4}{\left(\rho A+f_2\right)l^4}-\frac{1}{4}{\left(\frac{f_1}{\rho A+f_2}\right)}^2\right]}^{\frac{1}{2}}(2)$

Among them: k_n is the parameter corresponding to the nth order mode, and it is much larger than the f₂ constant, and f₁ is small in air damping, so both of them can be ignored, then the (2) can be simplified to the corresponding resonance frequency expression for (3):

${\omega }_1=2\pi f_1=k_1^2\frac{d}{l^2}\sqrt{\frac{E}{12\rho }}(3)$

For the first-order vibration parameter k₁ of the cantilever beam is 1.875, d is the thickness of the cantilever beam, and l is the length of the corresponding cantilever beam, the corresponding first-order vibration frequency can be obtained from this formula, and the characteristic frequency of f (4) can be obtained by adjusting the order of Eq. 3:

$f=\frac{\pi d}{8\sqrt{12}{l}^2}\sqrt{\frac{E}{\rho }}{\mathrm{v}}_{\mathrm{n}}^2(4)$

Among them: v_n is a constant, n represents the corresponding number of overtones, only the fundamental frequency is considered in this design, and the corresponding fundamental frequency mode v₀ = 1.194. Therefore, it can be seen that the thickness and width of the tuning fork structure jointly affect the characteristic frequency of the system, and the Young’s modulus E and density ρ in the material jointly affect the change of the characteristic frequency.

The mechanical quality factor essentially reflects the output efficiency of the transducer. Considering the air damping factor in the air, the formula Q can be written as Eq. 5:

$Q=\frac{2\pi W_1}{W_d}=\frac{\pi l\left(\rho A+f_2\right){\omega }^2{\int }_0^1{\left(\frac{\partial y\left(\eta ,t\right)}{\partial t}\right)}^{2}d\eta }{I{f}_1{\omega }^2{\int }_0^1{\omega }^2\left(\eta \right){\int }_0^T{\left(\frac{\partial y\left(\eta ,t\right)}{\partial t}\right)}^{2}dtd\eta }(5)$

Among them: W₁ is the vibration storage energy, W_d is the energy consumed in each vibration cycle, so when the vibration storage energy is larger or the loss is smaller, the corresponding mechanical quality factor Q is larger, and the formula is simplified as:

$Q=\rho A\omega /f_1(6)$

Therefore, the mechanical quality factor Q is related to the density of the material and the cross-sectional area of the structure. When the material structure and shape are fixed, its corresponding mechanical quality factor remains unchanged. The relationship between mechanical quality factor and resonance frequency and bandwidth is as follows:

$\mathrm{\Delta }{\mathrm{f}}_{-3\mathrm{d}\mathrm{B}}=\frac{\mathrm{f}}{Q}(7)$

Therefore, when the resonant frequency is determined, the mechanical quality factor is inversely proportional to the −3 dB bandwidth.

3 Stablishment of the structural model of tuning fork double-armed cone

In COMSOL Multiphysics, the electrostatic module, solid mechanics module and circuit module are used to simulate the flexoelectric module. The material parameters of the tunning fork structure are shown in Table 1. The flexoelectric layer is made of PVDF material, and Ag is used as the electrode material. ZnO nanowires with strong flexoelectric properties have been reported to be used to construct self-powered systems [25] for enhanced flexoelectricity in non-ferroelectric high-permittivity composites [24].

TABLE 1

TABLE 1. Material parameter table.

In order to obtain a more accurate flexoelectric effect, the coefficient PVDF coefficient for setting the three directions of flexoelectricity horizontal, vertical and shear is added as follows:

Considering the fact that only one end of the commonly used cantilever beam structure is fixed, in the process of single-mode bending vibration, due to the unbalance of the fixture and the strong inertial force effect of the tip mass of the free end, the clamped end will inevitably have a considerable Mechanical energy loss (fixture loss) (Dong Lei, 2022b).

In order to overcome this dilemma, it is reasonable to design a pair of mechanically coupled resonators to limit the clamping loss, so it is thought of using a tuning fork structure to design to avoid this loss. The tuning fork structure can also solve the problem of excessive resonant frequency of the flexoelectric transducer. Figure 1A shows the overall design structure of the tuning fork double-arm cone transducer. The simplified model is the corresponding two-dimensional structure as shown in Figure 1B.

FIGURE 1

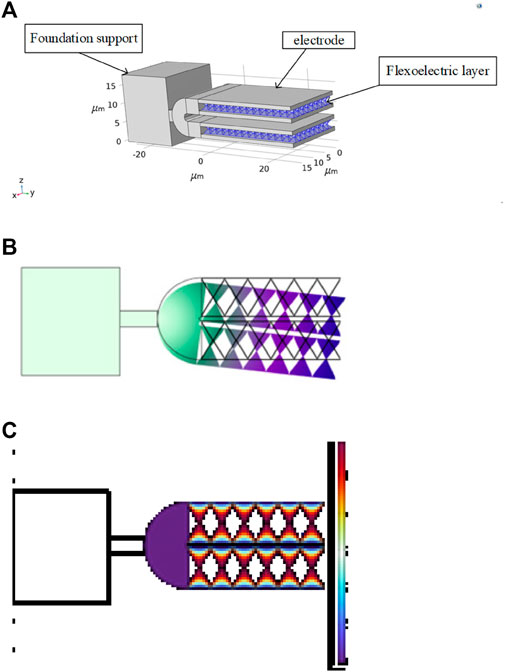
FIGURE 1. (A) The three-dimensional design diagram of the double-armed conical structure of the tuning fork; (B) The vibration diagram of the corresponding two-dimensional tuning fork structure; (C) The potential distribution diagram of the two-dimensional tuning fork double-arm vibration model.

In the previous research, a rectangular parallelepiped cone structure was designed, and its flexoelectric effect was analyzed nonlinearly. The sandwich electrode-conical flexoelectric layer-electrode structure has a certain effect on enhancing the flexoelectric effect. Therefore, in order to improve the output efficiency of the transducer at the micron scale, the most effective way is to further improve the output efficiency of the transducer from the output of the flexoelectric effect. The cone array structure can provide higher identical excitation, and it is easier to obtain greater output effect and bandwidth by adopting a series structure between the arrays than a parallel structure.

The time-domain voltage output comparison between the tuning fork double-arm transducer and its corresponding 1/4 single-arm transducer is carried out. Due to the high frequency of the structure, the time domain will cause a certain degree of distortion. Finally, when using the tuning fork double-arm structure its output voltage is 10 times higher than the peak-to-peak value of the output voltage of the common single-arm conical structure, while its resonance frequency is reduced from 689.9 kHz to 53.06 kHz, and the bandwidth has been significantly improved. Comparing the two, the time-domain analysis of the Fourier transform normalized bandwidth is shown in Figure 2.

FIGURE 2

FIGURE 2. Comparison of FFT frequency bands of double-arm and 1/4 single-arm vibration.

Different sign charges are induced on the upper and lower surfaces of the top and bottom. As can be seen in Figure 1C, the characteristic frequency domain analysis using these three cones as a unit shows that the potential distribution of the cones isn’t the same as the horizontal line on the upper surface of the pressure load, but the more it tends to the tip, the more the potential changes The slower, the maximum voltage output is reached near the electrodes. This may be due to the fact that the flexoelectric polarization distribution dependent on the strain gradient is manifested within a certain length and volume within the semiconductor [8]. The resonance frequency of the tuning fork structure is 48.16 kHz by sweeping the resonance frequency of the structural unit around 59.40 kHz. By scanning it, it can be seen that the resonance frequency of the tuning fork structure is reduced by 18.9%. It can be seen that the tuning fork structure can be provides some adjustment of The resonant frequency for the flexoelectric transducer. The material parameters of the tuning fork structure are shown in Tables 2, 3.

TABLE 2

TABLE 2. The flexoelectric coefficient of PVDF (polyvinylidene fluoride) can be roughly simplified into three parts.

TABLE 3

TABLE 3. Structural parameters.

The pyramidal structural unit of the flexoelectric layer was further studied, and a two-dimensional model of the pyramidal unit was established. Unlike the previous sandwich structure, the electrode was changed to a position more suitable for the flexoelectric layer, and the grid was divided Figure 3A. When a pressure load of 5 kPa is applied to the conical unit, the corresponding output potential distribution is obtained as shown in Figure 3B. The gradient of the color from cool blue to warm red represents the gradual increase of the electrode potential, so the conical electrode The voltage is maximum nearby, and the potential distribution gradually decreases in an arc shape from the tip of the cone to the bottom surface. This is the same as when the electrode is on the upper and lower surfaces, the electrode can contact more flexoelectric layers, collect more charges, and the corresponding potential is greater.

FIGURE 3

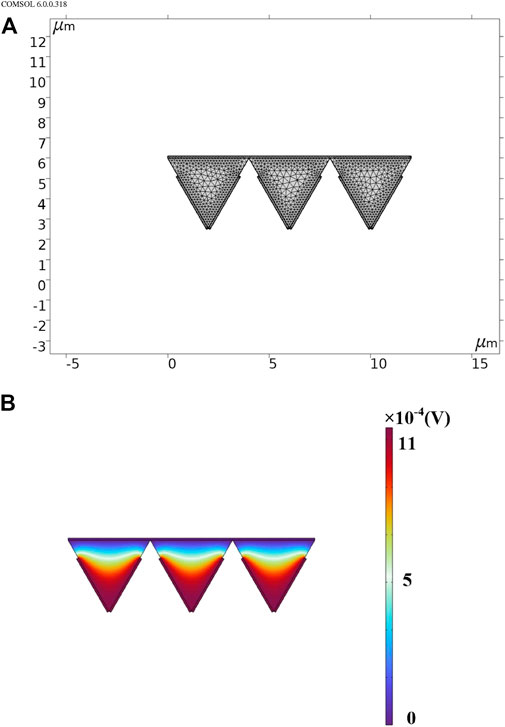
FIGURE 3. (A) This s the mesh division diagram of the conical structure (B) This s the potential distribution of the conical structure unit.

When the top is subjected to a bending moment, the conical structure makes it under pressure in a natural state, which will cause uneven distribution of charges. Both surfaces of the top are positively charged with the same potential and the bottom is negatively charged [17].

In addition to the study of the output efficiency of the flexoelectric layer, the electrode position was further studied. It can be seen that the output voltage when the electrodes are discrete is significantly higher than the voltage when connected, and almost all the charges caused by the flexoelectricity are neutralized.

4 Electrode position (affect on output)

Changing the width of the electrode attached to the surface of the tapered structure, the flexoelectric effect is more sensitive at the micro-nano scale, so the influence of the width, bandwidth and characteristic frequency of the electrode from 2.8 um to 3.8 um was studied. The corresponding resonance frequency change and its corresponding normalized bandwidth are as shown in Figure 4A. In the range of electrode width [2.8 um, 3.8 um], as the electrode width increases, the system stiffness decreases, However, the corresponding resonance frequency gradually decreases from 49 kHz, and the bandwidth increases first while then decreases with the increase of electrode length. The model reaches the maximum bandwidth value at 3.3 um.

FIGURE 4

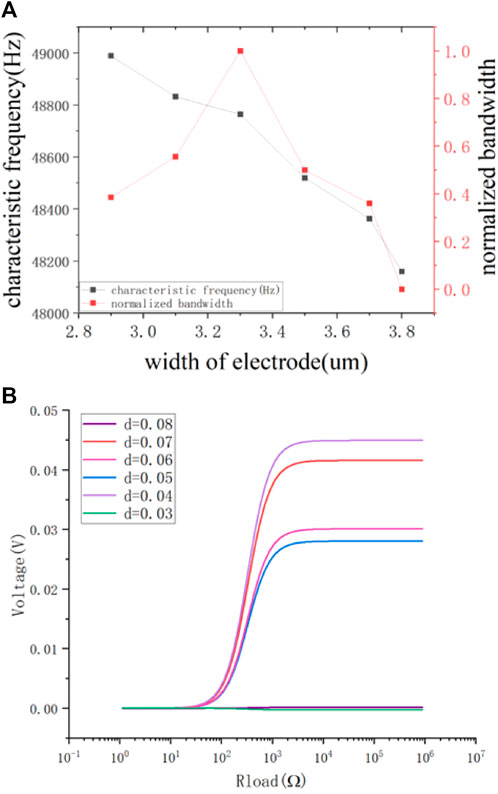
FIGURE 4. (A) The relationship diagram of electrode width and characteristic frequency and bandwidth; (B) The relationship diagram of electrode thickness, load resistance and voltage of tuning fork double-arm structure.

It should be noted here that the characteristic frequency of the flexoelectric effect at the micro-nano scale is about 10 times higher than the resonance frequency of the piezoelectric normal centimeter size, and its resonance frequency will increase as the size decreases. The characteristic frequency corresponding to the change of the width of the electrode also confirms this point.

Connect the electrode to a resistive load (R) to quantify the electrical power output as Figure 4B. After studying the width of the electrode, the thickness of the electrode on the hypotenuse of the conical flexoelectric layer was changed from (.03 um, .08 um). Different electrode thicknesses correspond to different resonant frequencies, and the resonant frequency of the structure corresponds to an optimal working load. Changing to test the resistive load of the output resistor from 10 Ω to 10⁸ Ω in steps of 10^0.15 Ω ohms, the energy loss caused by the resistance The resulting vibration attenuation is almost negligible. It is observed that as the overall situation increases with the resistance value, the output voltage first increases and then remains basically unchanged. The load resistance value is the performance of the output impedance of the transducer, which reflects the efficiency of the flexoelectric transducer to a certain extent, and the power is utilized to the greatest extent. When the electrode thickness is .04 um–.08 um, the corresponding output voltage increases with the increase of thickness. However, a sudden change occurs at .08 um and .03 um, both of which are in a small output efficiency, so the width and thickness of the electrode have a certain influence on the output voltage. The high efficiency of a transducer system is essentially the matching of the characteristic frequency of the transducer structure with the frequency of the external system. If the frequency is too high, the energy loss of the system is too large. Therefore, controlling the transducer within a certain range will result in more effective output.

5 Discussion

From the previous discussion, the ideal structure and parameter design of the transducer with the tuning fork structure at the micron scale can be obtained. Using the conical array structure in series can increase the output voltage of the transducer. In addition to reducing the mechanical energy loss of the system and adopting a more effective structural design with a high strain gradient to improve the output effect of the system, the size of the electrode also affects the output effects such as the resonant frequency, bandwidth, and output impedance of the flexoelectric transducer. The subsequent research can focus on the conical array Expand the connection mode to improve the flexoelectric output efficiency and bandwidth to a greater extent.

6 Conclusion

Based on theoretical analysis and simulation, a tuning fork double-arm conical flexoelectric transducer is designed. The vibration characteristic in the tuning fork structure is studied, and the resonant frequency equation of the tuning fork structure vibration and the relationship between the corresponding bandwidth and quality factor are derived. The problem that the characteristic frequency of the flexoelectric transducer is too high leads to excessive energy loss is improved, and the bandwidth of the flexoelectric system is widened to a certain extent. The method of increasing the strain gradient by using the pyramid array structure provides a certain idea for improving the output efficiency of flexoelectricity. It is proved that fixing the electrodes on the hypotenuse of the cone can better store the corresponding electric energy. The transducer output was studied for electrode thickness and width in the micron range. The results show that within a certain range, thinner electrode thickness and appropriate electrode length are beneficial to adjust the resonant frequency and bandwidth of the transducer. This research is helpful for the design of high-performance flexoelectric transducers.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

JZ and YC conceived the project. KL and HD carried out the research and analyzed the data. YC and ZL supervised the study. KL wrote the draft of the manuscript. All the authors edited the manuscript.

Funding

This research was funded by Postgraduate Research and Practice Innovation Program of Jiangsu Province, grant number SJCX22_1424.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. gyu Kim Y, Kim H, Lee G-J, Lee H-U, Lee SG, Baek C, et al. Flexoelectric-boosted piezoelectricity of batio3@srtio3 core-shell nanostructure determined by multiscale simulations for flexible energy harvesters. Nano Energy (2021) 89:106469. doi:10.1016/j.nanoen.2021.106469

CrossRef Full Text | Google Scholar

2. Lu T, Ikehara T, Maeda R, Mihara T. Energy dissipation mechanisms in lead zirconate titanate thin film transduced micro cantilevers. Jpn J Appl Phys (2006) 45:8795–800. doi:10.1143/jjap.45.8795

CrossRef Full Text | Google Scholar

3. Deng Q, Kammoun M, Erturk A, Sharma P. Nanoscale flexoelectric energy harvesting. Int J Sol Structures (2014) 51:3218–25. doi:10.1016/j.ijsolstr.2014.05.018

CrossRef Full Text | Google Scholar

4. Choi S-B, Kim G-W. Measurement of flexoelectric response in polyvinylidene fluoride films for piezoelectric vibration energy harvesters. J Phys D: Appl Phys (2017) 50:075502. doi:10.1088/1361-6463/50/7/075502

CrossRef Full Text | Google Scholar

5. Su S, Huang H, Zhu ZH. Flexoelectric energy harvesters utilizing controllably wrinkled micro-dielectric film. Energy (2021) 224:120056. doi:10.1016/j.energy.2021.120056

CrossRef Full Text | Google Scholar

6. Wang K, Wang B, Zeng S. Analysis of an array of flexoelectric layered nanobeams for vibration energy harvesting. Compos Structures (2018) 187:48–57. doi:10.1016/j.compstruct.2017.12.040

CrossRef Full Text | Google Scholar

7. Dong Lei SZe. a., Li S, Chu Z, Sun Z, Pourhosseini Asl MJ, Li F, et al. Significant output power enhancement in symmetric dual-mode magneto-mechano-electric coupled resonators. Adv Energ Mater (2022) 50:2202306. doi:10.1002/aenm.202202306

CrossRef Full Text | Google Scholar

8. Wang LSFX, Liu S, Feng X, Zhang C, Zhu L, Zhai J, et al. Flexoelectronics of centrosymmetric semiconductors. Nat Nanotechnol (2020) 15:661–7. doi:10.1038/s41565-020-0700-y

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Dong Lei SZ., Li S. Research progress of tuning fork quartz crystal oscillator for photoacoustic gas sensing. J Henan Normal Univ (2022) 50. doi:10.16366/j.cnki.1000—2367.2022.02.003

CrossRef Full Text | Google Scholar

10. Lou C, Liu X, Wang Y, Li R, Huang L, Liu X. Miniature quartz tuning fork-based broad spectral coverage and high detectivity infrared spectroscopy. Infrared Phys Technol (2022) 126:104322. doi:10.1016/j.infrared.2022.104322

CrossRef Full Text | Google Scholar

11. de Laat., , Pérez Garza. HH, Herder. JL, Ghatkesar MKM. A review on in situ stiffness adjustment methods in mems. J Micromechanics Microengineering (2016) 26:063001. doi:10.1088/0960-1317/26/6/063001

CrossRef Full Text | Google Scholar

12. Yan Y, Ma X, Nguyen TM, Ha S-H, Ahn H, Aben D, et al. Quadrant-electroded nanogenerators for decoupling piezoelectricity and flexoelectricity in the electromechanical outputs in flexible devices. Nano Energy (2022) 104:107909. doi:10.1016/j.nanoen.2022.107909

CrossRef Full Text | Google Scholar

13. Hu Y, Zhang Y, Xu C, Lin L, Snyder RL, Wang ZL. Self-powered system with wireless data transmission. Nano Lett (2011) 11:2572–7. doi:10.1021/nl201505c

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Narvaez J, Catalan G. Origin of the enhanced flexoelectricity of relaxor ferroelectrics. Appl Phys Lett (2014) 104:162903. doi:10.1063/1.4871686

CrossRef Full Text | Google Scholar

15. Yan Z. Modeling of a nanoscale flexoelectric energy harvester with surface effects. Physica E: Low-dimensional Syst Nanostructures (2017) 88:125–32. doi:10.1016/j.physe.2017.01.001

CrossRef Full Text | Google Scholar

16. Zhang Z, Zhou M. Bending and vibration analysis of flexoelectric beam structure on linear elastic substrates. Micromachines (Basel) (2022) 13:915. doi:10.3390/mi13060915

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Zhu J, Hu P, Chen Y, Chen S, Zhang C, Wang Y, et al. Waves propagating in nano-layered phononic crystals with flexoelectricity, microstructure, and micro-inertia effects. Nanomaterials (Basel) (2022) 12:1080. doi:10.3390/nano12071080

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Zheng Z, Huang P, Wang F. Shape memory effect based thermal cycling induced flexoelectricity for energy harvesting. Scripta Materialia (2021) 194:113701. doi:10.1016/j.scriptamat.2020.113701

CrossRef Full Text | Google Scholar

19. Xue J, Chen L, Chang L, Zhang W. A wideband flexoelectric energy harvester based on graphene substrate. Eng Structures (2021) 231:111779. doi:10.1016/j.engstruct.2020.111779

CrossRef Full Text | Google Scholar

20. Cross L. Flexoelectric effects: Charge separation in insulating solids subjected to elastic strain gradients. J Mater Sci (2006) 41:53–63. doi:10.1007/s10853-005-5916-6

CrossRef Full Text | Google Scholar

21. Deng Q (2017). size-dependent flexoelectric response of a truncated cone and the consequent ramifications for the experimental measurement of flexoelectric properties. J Appl Mech 84, doi:10.1115/1.4037552

CrossRef Full Text | Google Scholar

22. Deng S, Lv, , Tan K, Liang X, Shen S. The impact of flexoelectricity on materials, devices, and physics. J Appl Phys (2020) 128:080902. doi:10.1063/5.0015987

CrossRef Full Text | Google Scholar

23. Blom F. Dependence of the quality factor of micromachined silicon beam resonators on pressure and geometry. J Vacuum Sci &amp (1992) 10:19. doi:10.1116/1.586300

CrossRef Full Text | Google Scholar

24. Yong Li Y., Shu L, Wang H. Enhanced flexoelectric effect in a non-ferroelectric composite yong. J Vacuum Sci &amp (2013) 103. doi:10.1063/1.4824168

CrossRef Full Text | Google Scholar

25. Yu H., Wang Y. Design of capacitive surface potential measuring device by using tuning fork vibration. Spacecraft Environ Eng (2013) 39:169–74. doi:10.12126/see.2022.02.008

CrossRef Full Text | Google Scholar