
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Phys., 05 January 2023
Sec. Physical Acoustics and Ultrasonics
Volume 10 - 2022 | https://doi.org/10.3389/fphy.2022.1113330
This article is part of the Research TopicAdvances in Noise Reduction and Feature Extraction of Acoustic SignalView all 13 articles
Introduction: Parameter mismatch poses a challenge to source localization in cases involving environments with seabed uncertainties. By including environmental parameters in the search space, focalization can be used to estimate the location of the source using environmental information that is limited a priori. Methods: To reduce the number of parameters, a simplified seabed model is proposed here for such focalization. Only two geoacoustic parameters—the amplitude F and phase cF of reflection—are used to describe the seabed. Focalization is generally tested using genetic algorithms for the colored noise case (COLNOISE) benchmark problem. Results: The proposed simplified model can obtain the location of the source more easily than a layered model. Due to its advantage in terms of parameter sensitivity and inter-coupling, the simplified model can ensure the robustness of the results of inversion. The proposed method was tested on a broadband signal in the Asian Seas International Acoustics Experiment (ASIAEX2001), where both the location and the geoacoustic parameters were easily inverted. Discussion: The simplified model provides a sufficiently high acoustic resolution for focalization, and its reduction of the geoacoustic parameters helpes solve the problem of inversion.
Matched field processing (MFP) is a well-known technology for solving inversion problems by comparing acoustic data with solutions to wave equations [1]. Depending on the unknown quantity, MFP can be divided into source localization [2], tomography [3], and geoacoustic inversion [4, 5]. Owing to the temporal and spatial variations in environmental parameters in the ocean and difficulties of marine measurement, there is a mismatch between the ocean and its environmental model, which is a challenge for MFP. To overcome the mismatch and accurately estimate the location of the source with limited a priori environmental information, focalization has generally been used [6]. By including the environment in the parameter search space, focalization circumvents stringent requirements pertaining to accurate knowledge of the environment.
Because focalization involves more unknown parameters than traditional localization, it leads to a more complex optimization problem. In practical application, it becomes necessary to use a dimension reduction algorithm to parameterize the environment. The dimension reduction problem was solved by means of feature extraction [7–9]. A typical example is the empirical orthogonal function (EOF) [10, 11]. Using principal component extraction, the sound speed profile can be described by three to five parameters. However, environmental parameterization is often more complicated in case of the seabed. As the direct measurement of the bottom is difficult and expensive, it is more challenging to obtain parameters of the seabed than the sound speed profile. Actual structure of the bottom of the sea is generally too complex to mathematically represent. Therefore, it is usually described by an effect-equivalent description. The most common method in this vein involves describing a certain number of bottom layers using the sound speed, density, and attenuation. When the half-space model is used, the seabed is represented by three parameters. The number of geoacoustic parameters increases rapidly with the number of layers in the seabed, where this complicates focalization owing to sensitivity- and coupling-related problems. Qu and Hu proposed a single-parameter seabed model and designed a relevant method of geoacoustic inversion [12, 13]. As this single-parameter seabed model can calculate only an incoherent sound field, it is inapplicable to MFP. Shang developed a method called the rapid bottom characteristic using two parameters, P and Q, to analyze acoustic problems in shallow water [14, 15]. They were able to describe different types of regions of propagation, Green’s function, and the waveguide invariant [16–18]. Similarly, reflection loss was introduced by Harrison to explain reverberation [19]. The simplified seabed model with one or two parameters has been applied to geoacoustic inversion in several previous studies, but whether it can be used as an effective acoustic lens for source focalization remains to be studied.
This paper proposes a simplified seabed model with two parameters for the reflection of sound from the bottom, and examines focalization by using a small number of geoacoustic parameters. Section 2 discusses general aspects of the simplified geoacoustic model. In Section 3, focalization based on the simplified model is tested on the colored noise case (COLNOISE) benchmark problem. Compared with the layered model, some characteristics of the simplified model are discussed by using the objective function and marginal probability density. The linear relation between a new geoacoustic parameter and acoustic quantities is presented to help solve the inversion problem. In Section 4, the broadband focalization of data from the Asian Seas International Acoustics Experiment (ASISEX) in the East China Sea is analyzed, and the result shows that the search for the focalization parameter converges to the correct location of the source and the geoacoustic parameters. The conclusions and directions for future work are summarized in Section 5.
When sound interacts with the seabed, the result of acoustic reflection can be summarized in terms of amplitude and phase change. To simplify the geoacoustic model, the natural choice is to describe the seabed based on the amplitude and phase parameters of reflection. Past studies in the area have used parameters that are similar in physical significance, where some of them can be converted into one another under certain conditions. For compatibility with past work, this paper uses Jones’s mathematical expression F for the amplitude of reflection. The bottom loss BL can be expressed as [20]
Based on a large amount of historical data and theoretical derivation, it is well known that BL for a high-speed seabed whose sound speed is higher than the sound speed of sea water is always proportional to the grazing angle φ for a small value of the latter. Considering long-distance propagation, a large grazing angle yields is a large value of BL and a large number of reflections from the seabed. The resulting acoustic energy is almost completely consumed by reflection from the seabed. On the contrary, the value of BL for a small grazing angle is smaller, and there are fewer reflections off the seabed. The acoustic energy for a small grazing angle is still effective at long distances and becomes the dominant component in the far field. Therefore, the slope of the bottom loss F (dB/rad) can be used to describe the change in amplitude in the far field.
For representative phase calculations, which are necessary for MFP, the phase parameter must be given at the same time as the amplitude parameter. Based on the half-space model, the phase change θ can be calculated as
where n is the ratio of the sound speed in water to that on the seabed, and m is the ratio of the density of the seabed to that of water. For a small grazing angle,
Let
By substituting (4) into (2), the expression for the phase change θ in the limit of a small grazing angle is
Hence, the phase change increases approximately linearly with the grazing angle. The reflection phase varies from -π to 0 while the grazing angle increases from zero to the critical angle φc. We define a parameter of the reflection phase
where the critical angle of total reflection,
To get a sense of the relative merits of different schemes, the Naval Research Laboratory has provided a set of simulated data for MFP testing called the benchmark problem [21, 22]. According to the research objectives of this paper, the COLNOISE case was selected for a focalization test. The test environment is shown in Figure 1. The COLNOISE case is a range-independent waveguide with a depth of 100 m. The 250 Hz source depth sd is 66 m at a range r = 9.1 km. A vertical line array (VLA) of 20 hydrophones spanning the water column receives the signal, which is affected by color noise with a signal-to-noise ratio (SNR) of 40 dB. The color noise is design to describe the construction of a cross spectral density for noise due to breaking waves. The sound speed on the surface of the ocean is
A classic method of inversion based on the genetic algorithm has been used to test the geoacoustic model, as shown in Figure 2. The initial population was randomly generated according to the search space, and the copy field was calculated by the normal mode program KRAKENC (https://oalib-acoustics.org) to match with signals of the vertical array. An objective function was used to determine an individual’s fitness, and offspring replaced part of the population to approach the fittest population. Following this, a posteriori probability estimation was carried out on samples of the optimization process to obtain the complete results. The process is as shown below.
The first step of focalization is environmental parameterization, which helps set the search space for the geoacoustic and location-related parameters. In focalization according to the simplified model, four parameters were used: the source depth sd, range r, amplitude F, and phase
The genetic algorithm, which is based on an analogy with biological evolution, was used to find the global optimum without performing an exhaustive search [23]. According the results of environmental parameterization, an initial population was randomly generated. Then, based on the individual’s fitness of matching, the population moved to the fittest model vector through evolutionary steps consisting of selection, crossover, and mutation. Parameters of the optimization were set as follows: the population size was 100, reproduction rate was 0.5, crossover rate was 0.8 and mutation rate was 0.08. To collect samples to estimate the a posteriori probability distributions, 20 independent runs were executed in parallel.
To suppress ambiguous solutions, a high-resolution objective function is necessary for focalization. The Bartlett processor was used to match the “measured” sound field and the copy field. The objective function ψ(m) is
where Q is the “measured” pressure, P is the replica pressure, m is the vector in the search space, i is the number of hydrophones, and N is the total number of hydrophones. The fitness of each individual is evaluated by the objective function and the final result of the evolution approaches the optimum value of zero for a perfect match.
The complete solution to the focalization problem should involve a measure of uncertainty for the model parameters. The obtained samples of the search space can be used to estimate the a posteriori probabilities. Gerstoft offered a semi-empirical method based on the sampling procedure of the genetic algorithm. The probability σ of the k-th vector mk is given by [24].
where Nobs is the number of observed model vectors, and T is temperature, which is equal to the average value of objective function of the 50 best samples. The marginal probability distribution of the l-th parameter obtaining a particular value κ can be calculated by:
where δ is the Dirac function. Based on the marginal probability distribution of σ(ml), the robustness of the results can be analyzed. As theoretical solutions in the normal mode are efficient and appropriate for inversion problems, forward solutions of the acoustic equation were calculated by the normal mode model KRAKENC. By describing reflection off the seabed, parameters of the simplified model can also be entered into the KRAKENC programs to calculate the sound field.
In the benchmark problem test, all parallel runs converged to the same optimal vector. The depth of the source sd was 66 m, range r was 9.1 km, amplitude F was 1.9 dB/rad, and phase parameter
The most appealing characteristics of the simplified model when applied to focalization are intuitively illustrated in Figure 3. The process of evolution of the first 200 generations for the two environments is shown in the figure, and values of the objective function for all parameters of the randomly selected runs of focalization are given. Even though the evolution in different runs has random characteristics, a sense of how well each parameter has been estimated can be obtained from the scatter plot of the objective function for the two environments. The optimal value of the layered model (0.003) is significantly lower than that of the simplified model (0.963). This shows that more parameters can better describe the details of the seabed. However, the simplified model provides a sufficiently high acoustic resolution for focalization. In the parallel runs, almost all the inversion based on the simplified model converged to the global optimum earlier than that based on the layered model. At the same time, the optimal value of the geoacoustic parameters was obtained in the first 200 generations, whereas the geoacoustic parameters of the layered model could not be determined in the first few hundred generations. Because the two environments have the same conditions except for the geoacoustic model, it can be inferred that the simplified model can reduce the complexity of the inversion optimization.
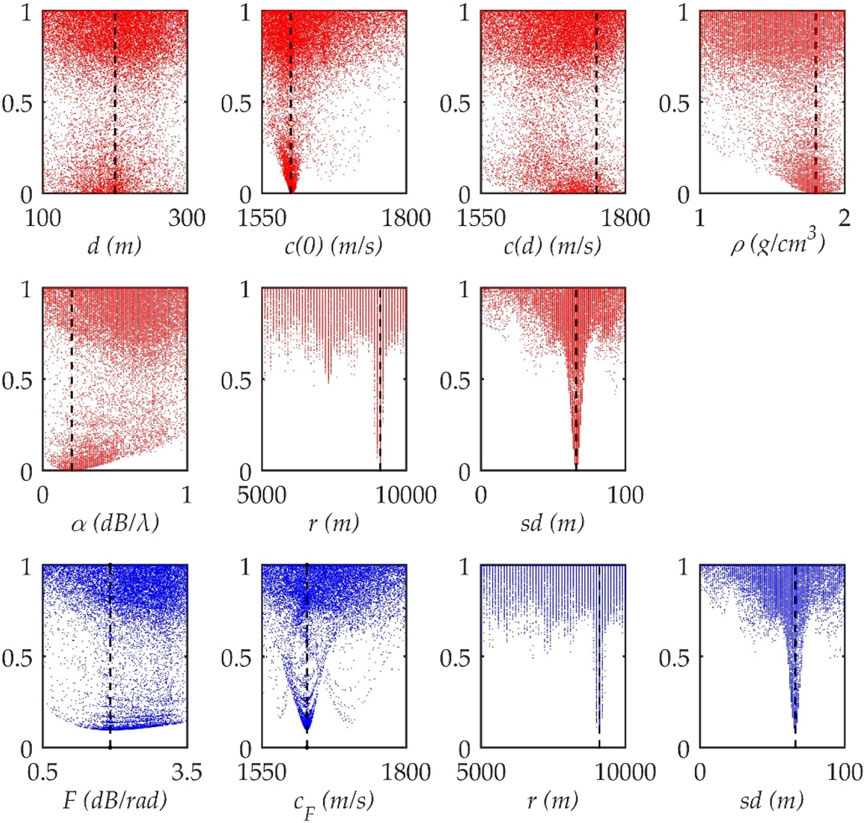
FIGURE 3. Values of the cost function obtained using optimization inversion. The dash lines represent the optimal values. Red represents the layered model. Blue represents the simplified model.
The scatter plots that appear as an arch (e.g.,
where I0 is the intensity at the source, H is the depth of water, λ is wavelength, and βl is the attenuation of the l-th normal mode, and can be expressed as
where V is the reflection coefficient and Sl the span of the l-th normal mode. The grazing angle of the l-th normal mode is
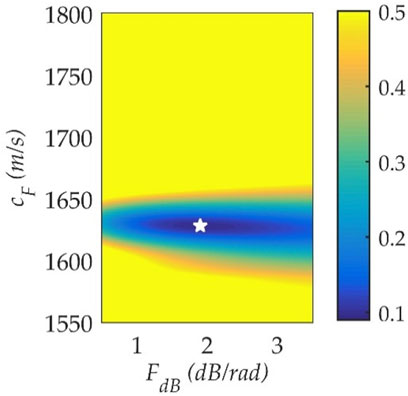
FIGURE 4. Ambiguous surface for geoacoustic parameters of the simplified model. The pentagram represents the optimal value.
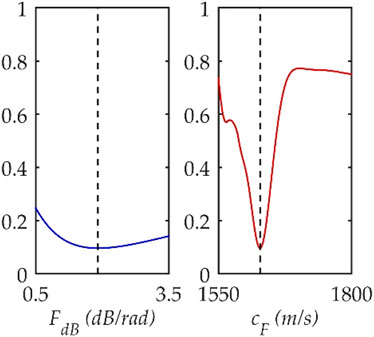
FIGURE 5. Values of the cost function for the geoacoustic parameter of the simplified model. The vertical lines represent the optimal value. Note also that the linear property of F is also an advantage for inversion. The change in F is linearly related to changes in the other quantities, which are derived from the measured pressure. Based on normal mode theory, the intensity I is given by.
The span of the l-th normal mode is
It is easy to find the relation between parameters of the amplitude V and F as
Combining the equations above, the intensity I over a range r can be rewritten as a function of F:
In application, the part in the parentheses is significantly smaller than one. Replacing the summation with the quadrature, the intensity is given by
The number of effective modes is N = 2H/λ. By including the Gaussian error function
For the far field, assuming
In addition to the intensity of sound, there is a linear relationship for the time domain quantity. The number of interactions of sound with the seabed in the l-th normal mode can be calculated by
The loss in intensity is
Based on the geometry of the reflection off the seabed, the time delay τ after direct arrival can be calculated by
where cw is the mean sound speed in seawater. The loss in intensity can then be rewritten as
Based on 18 and 22, F can be directly calculated from two acoustic measurement. The computationally fast linear relation ensures a change in the arch of the objective function that helps avoid the local optimum, which in turn helps reduce the complexity of numerical optimization [12, 13].
The complete solution of the inversion problem involves providing the estimated probability for a measure of the uncertainty of the result of inversion. The marginal probability density of the simplified model environment is shown in Figure 6. All parameters peak within the given bound, indicating that they are sensitive and well estimated. As all parameters converge to the global optimal value with the highest probability, the results of focalization are highly reliable.

FIGURE 6. Normalized marginal probability density for the simplified model environment. The vertical lines represent the optimal values.
The results of tests on the benchmark problem show that the simplified model is feasible and effective for focalization. As an environmental lens, it has sufficiently high acoustic resolution to focus on the correct positional parameters. With a decrease in the number of parameters to be solved, the amount of calculation needed for optimization is reduced. This also reduces the number of known conditions required, which simplifies marine measurement in applications. The relatively sensitive parameters and the lack of coupling between them are conducive to inversion.
The Asia Sea International Acoustic Experiment 2001 (ASIAEX2001) was conducted in the East China Sea. Owing to the good quality of data and thorough investigation of the environment, these data have been widely used to test various inversion problems. They were used to test the simplified model proposed here.
Two ships were used in the propagation experiment. The receiving ship anchored and hung a 32-elements vertical array for receiving signals, where the upper 16 elements were 2 m apart and the lower 16 were 4 m apart, and they covered a range of depth from 4.6 to 90.5 m. The launching ship moved away from the receiving ship in a straight line, throwing 38 g TNT wideband sources (WBS) at a fixed depth of 50 m. The depth of water can be roughly considered range independent at a depth of 105 m. Figure 7 shows the sound speed profile measured by the CTD in the experiment. In the MFP, the sound speed profile was used as known condition.
Focalization has been carried out using the same method as in the previous section, by using 35 frequency points in the 99–201 Hz frequency band. Two WBS at 10.2 km were selected for testing, and the results are shown in Table 2. The focalization of two sources yielded reliable location-related parameters, which verified the feasibility of the simplified model for broadband focalization. In the linear geoacoustic inversion [12], F is the single parameter to model the seabed. Due to reducing the number of parameters to one, F can be obtained using a least-squares fitting to transmission loss of different ranges. The critical angle is deduced from the variation of transmission loss, and then the equivalent speed cF can be calculated. In different inversion schemes, the inversion results of geoacoustic parameters of the simplified model are similar.
Note that the hierarchy of the parameters is the foundation of focalization. Because the sound field tended to be more sensitive to variation in the location-related parameters. In the benchmark problem, even if the layered model did not yield the correct value, the inversion still yielded the correct location-related parameters. However, the localization of the source is still influenced by the geoacoustic parameters. As shown in the focalization of the layered environment, the uncertainty in the geoacoustic parameters has a negative impact on the efficiency and accuracy of localization. Although obtaining the geoacoustic parameters is not the primary goal of focalization, it is important for it. Correct geoacoustic inversion not only improves our understanding of the ocean waveguide, but also helps obtain the location-related parameters more efficiently and accurately. A comparison between the measured transmission loss (TL) and the predicted TL based on the inverted geoacoustic parameters is shown in Figure 8. Even if errors have originated from the source depth, the TLs are in good agreement with each other. In the focalization, the simplified model also obtains accurate acoustic characteristics of the seabed while the complexity of inversion is reduced by reducing the number of parameters.
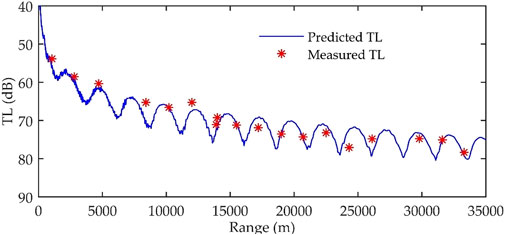
FIGURE 8. The predicted and the measured TL. The source depth is 50 m and the receiver depth is 60.5 m.
In this paper, a simplified model of the seabed that uses only two parameters has been applied for focalization. As the complexity of inversion increases with the number of parameters, it is valuable to reduce the dimensionality of the inversion problem.
Based on the genetic algorithm, focalization was tested on a benchmark problem using the simplified model and a layered model. In the COLNOISE case, the simplified model with only two parameters satisfied the requirements of MFP and obtained accurate results in terms of location. An analysis of the objective function led the amplitude F and phase cF to be more sensitive than some parameters of the layered model, and no clear coupling was noted between the parameters. This accelerated the convergence to the optimal solution and ensured the robustness of the results. In addition, some characteristic quantities of the sound field that can be used for matching in MFP are related linearly to F. These linear relations, manifests as an arched curve for changes to the objective function, render the optimization simple and reliable. When used on experimental data from ASIAEX on the East China Sea, the simplified model was found to be suitable for broadband focalization, and both the location-related and the geoacoustic parameters were obtained quickly and accurately.
In order to provide constraints to the dimensionality of inversion problem, the simplified model presents a very compact expression of the acoustic properties of seabed. It can accelerate the convergence to the optimal solution and ensure the robustness of the results. However, it also has limitations. For example, it can be used only in the far field. As the reduction in the number of parameters reduces the acoustic resolution, applications of the proposed model to low-SNR environments or single-hydrophone inversion need to be explored in future research.
The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.
ZO completed the literature research, analysis, and manuscript writing. KQ completed the Conceptualization, methodology and funding acquisition. LL completed the validation, visualization and project administration.
This research was funded by the Natural Science Foundation of Guangdong Province grant number [2022A1515011519].
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
1. Baggeroer AB, Kuperman WA, Mikhalevsky PN. An overview of matched field methods in ocean acoustics. IEEE J.Ocean.Eng. (1993) 18(4):401–24. doi:10.1109/48.262292
2. Zhang B, Hou X, Yang Y. Robust underwater direction-of-arrival tracking with uncertain environmental disturbances using a uniform circular hydrophone array. J.Acoust.Soc.Am. (2022) 151(6):4101–13. doi:10.1121/10.0011730
3. Zhao X, Wang D. Ocean acoustic tomography from different receiver geometries using the adjoint method. J.Acoust.Soc.Am. (2015) 138(6):3733–41. doi:10.1121/1.4938232
4. Zheng Z, Yang TC, Pan X. Geoacoustic inversion using an autonomous underwater vehicle in conjunction with distributed sensors. IEEE J.Ocean.Eng. (2020) 45(1):319–41. doi:10.1109/joe.2018.2869481
5. Chapman NR, Shang E. Review of geoacoustic inversion in underwater acoustics. J.Theor.Comput.Acous. (2021) 29(3):2021. doi:10.1142/s259172852130004x
6. Collins MD, Kuperman WA. Focalization: Environmental focusing and source localization. J.Acoust.Soc.Am. (1991) 98(3):1410–22. doi:10.1121/1.401933
7. Li Y, Geng B, Jiao S. Dispersion entropy-based lempel-ziv complexity: A new metric for signal analysis. Chaos.soliton.fract. (2022) 161:112400. doi:10.1016/j.chaos.2022.112400
8. Li Y, Gao P, Tang B, Yi Y, Zhang J. Double feature extraction method of ship-radiated noise signal based on slope entropy and permutation entropy. Entropy (2021) 24(1):22. doi:10.3390/e24010022
9. Li Y, Tang B, Yi Y. A novel complexity-based mode feature representation for feature extraction of ship-radiated noise using VMD and slope entropy. Appl.Acoust. (2022) 196:1088992022. doi:10.1016/j.apacoust.2022.108899
10. Bianco MJ, Gerstoft P. Dictionary learning of sound speed profiles. J.Acoust.Soc.Am. (2017) 141(3):1749–58. doi:10.1121/1.4977926
11. Cheng L, Zhao H, Li J, Xu W. Tensor-based basis function learning for three-dimensional sound speed fields. J.Acoust.Soc.Am. (2022) 151(1):269–85. doi:10.1121/10.0009280
12. Qu K, Zhao M, Hu C. Single parameter inversion using transmission loss in shallow water. Acta Acoust (2013) 38(4):472. doi:10.15949/j.cnki.0371-0025.2013.04.017
13. Qu K, Hu C, Zhao MChina Shanghai Acoustic Laboratory, Institute of Acoustics, Chinese Academy of Sciences, Shanghai 200032, China;University of Chinese Academy of Sciences, Beijing 100190, China. A rapid inversion scheme for seabed single parameter using time-domain impulse response. Acta Phys.Sin. (2013) 62(22):224303. doi:10.7498/aps.62.224303
14. Ge H, Zhao H, Gong X, Shang E. Bottom-reflection phase-shift estimation from ASIAEX data. IEEE J.Ocean.Eng. (2004) 29(4):1045–9. doi:10.1109/joe.2004.834180
15. Shang E, Gao T, Wu J. A shallow-water reverberation model based on perturbation theory. IEEE J.Ocean.Eng. (2008) 33(4):451–61. doi:10.1109/joe.2008.2001686
16. Shang E, Wu J, Zhao Z. Relating waveguide invariant and bottom reflection phase-shift parameter P in a Pekeris waveguide. J.Acoust.Soc.Am. (34512012) 131(4):3691–7. doi:10.1121/1.3699242
17. Zhao Z, Shang E, Rouseff D. The comparison of bottom parameter inversion in geoacoustic space and in (P, Q) space. J.Comput.Acoust. (2017) 25(2):1750011–23, Apr. doi:10.1142/s0218396x17500114
18. Zhang C, Wu J, Mo Y, Sun B, Ma L. The same reflective characteristics for different effective geoacoustic parameters in different models. IEEE J.Ocean.Eng. (2020) 1. doi:10.1109/JOE.2020.2984295
19. Harrison CH, Simons DG. Geoacoustic inversion of ambient noise: A simple method. J.Acoust.Soc.Am. (2002) 112(4):1377–89. doi:10.1121/1.1506365
20. Jones AD, Graham JD, Clarke PA. Single parameter description of seafloors for shallow oceans. J.Acoust.Soc.Am. (2008) 123(5):3214. doi:10.1121/1.2933399
21. Porter MB, Tolstoy A. The matched field processing benchmark problems. J.Comput.Acoust. (1994) 2(3):161–85. doi:10.1142/s0218396x94000129
22. Bonnel J, Pecknold SP, Hines PC, Chapman NR. An experimental benchmark for geoacoustic inversion methods. IEEE J.Ocean.Eng. (2020) 1558. doi:10.1109/JOE.2019.2960879
23. Gerstoft P, Rogers LT, Krolik JL, Hodgkiss WS. Inversion for refractivity parameters from radar sea clutter. Radio.sci. (80532003) 38(3). doi:10.1029/2002rs002640
24. Gerstoft P. Inversion of seismoacoustic data using genetic algorithms and a posteriori probability distributions. J.Acoust.Soc.Am. (1994) 95(2):770–82. doi:10.1121/1.408387
25. Chapman NR. A critical review of geoacoustic inversion: What does it really tell us about the ocean bottom. J.Acoust.Soc.Am. (30232016) 140(4):3023. doi:10.1121/1.4969376
Keywords: focalization, matched field processing, geoacoustic parameter, genetic algorithm, geoacoustic model
Citation: Qu K, Ou Z, Huang X and Liu L (2023) A simplified model for acoustic focalization in environments with seabed uncertainties. Front. Phys. 10:1113330. doi: 10.3389/fphy.2022.1113330
Received: 01 December 2022; Accepted: 19 December 2022;
Published: 05 January 2023.
Edited by:
Yuxing Li, Xi’an University of Technology, ChinaReviewed by:
Dan Liu, Institute of Acoustics (CAS), ChinaCopyright © 2023 Qu, Ou, Huang and Liu. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Xin Huang, c2hhb3NoYW5oeEAxMjYuY29t
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.