Dynamic analysis and optimal control of worm propagation model with saturated incidence rate

In order to prevent the propagation of computer worms effectively, based on the latent character of worms, the exposed compartments of computer and USB device are introduced respectively, and a series of computer worm propagation models with saturation incidence rate are proposed. The qualitative behavior of the proposed model is studied. Firstly, the threshold R₀ of the model is derived by using the next-generation matrix method, which completely characterized the stability of disease free equilibrium and endemic equilibrium. If R₀ < 1, the disease free equilibrium is asymptotically stable, implying that the worm dies out eventually and its attack remains under control; if R₀ > 1, the asymptotic stability of endemic equilibrium under certain conditions is proved, which means that the worm is always persistent and uncontrollable under such conditions. Secondly, the theoretical results are verified by numerical study, in which the relative importance of each parameter in worm prevalence is evaluated by sensitivity analysis. Finally, so as to minimize the number of computer and USB device carrying computer worms in short span of time, the worm propagation model is extended to incorporate three control strategies. The Pontryagin’s maximum principle is used to characterize the controls’ optimal levels. According to the control effect diagram, the combined strategy is effective in minimizing the transmission dynamics of worm virus in computer and USB devices populations respectively.

1 Introduction

As a storage medium, USB device is favored by many office workers because of its large storage capacity and portability. It is often used to copy data between different computers. In fact, the transmission of data via USB device may be accompanied by the spread of worms [1]. Computer worm is a common computer virus, which has the characteristics of wide spread and serious harm [2]. On 13 January 2021, the news of incaseformat worm flooded wechat circle of friends, and infection cases were found in many provinces, cities, and industries, with a trend of large-scale outbreak. After execution, the worm will automatically copy to the windows directory of the system disk and create a registry to start itself [3]. Once the user restarts the computer, this will cause the worm host to execute from the windows directory, and then the worm process will traverse all disks except the system disk and delete the files, causing irreparable losses to the user. Therefore, it has become an urgent problem in the field of network security to study the propagation rule of computer worm and effectively control its propagation.

A computer worm is a group of programmed code that can reproduce itself and affect the normal use of the computer [4]. A biological virus is a unique tiny living organism, which can make use of the nutrients of the host cell to copy its own essential constituent material DNA or RNA and proteins [5–7]. Computer worms and biological viruses are two concepts from different fields, but some of their properties have striking similarities [8]. Mainly in the following four aspects: firstly, computer worms and biological viruses are infectious. Computer worms can spread from an infected computer to an uninfected computer through network or other remavable devices. Biological viruses can also be transmitted by direct or indirect contact between living organisms. Then, computer worms and biological viruses are latent and generally not easy to find. Computer worms can integrate their own program fragments into the system programs, so that their most important code can be saved from the anti-virus software. Biological viruses can also integrate their genetic material into the host’s DNA or RNA, thereby escaping attack by the host’s immune system. In addition, computer worms and biological viruses will mutate in the process of spreading, making their species more and more diverse. Finally, both computer worms and biological viruses are destructive. Computer worms can damage the computer system and interfere with the normal operation of the computer. Biological viruses may damage the cells or organs of the host organism, which may pose a threat to the organism’s life. Because of the high similarity between computer worms and biological viruses, we used the method of studying the transmission of infectious diseases to explore the dynamic behavior of computer worms.

In epidemiology, dynamic model has been an important method in analysing the spread and control of infectious diseases qualitatively and quantitatively [9–11]. In 1991, Kephart and White first introduced the dynamic model of infectious disease into the study of the propagation of computer virus. Since then, the dynamic model has also become a vital tool for the study of various computer viruses [12–16]. The research on computer worms have experienced a rapid growth, and a large number of models have been established, mathematically analyzed, which provides some useful and valid references for the characteristics of computer worms transmission [17]. In 2011, Song et al. [18] studied removable device as an independent carrier for the first time. They hypothesized that computer worms spread via both web-based scanning and removable devices, established SIR model of computer population and SI model of removable devices population, studied their dynamic behavior, and gave corresponding control strategy. In 2012, Zhu et al. [19] proposed a new dynamic model to describe the spread of computer virus by using the same method as in Ref. [18]. In addition, by qualitative analysis, it is concluded that controlling R₀ below one is an effective means to extinguish virus, which provides a good start point for understanding the transmission of computer virus through such interactions. In 2015, Ma et al. [20] proposed SIBV model of fixed nodes and SI model of mobile nodes considering the influence of benign worms and mobile devices in the network environment, discussed the influences of removable devices on the interaction dynamics between malicious worms and benign worms. Through numerical analysis and simulation, it is proved that the anti-worm technology can effectively suppress the spread of malicious worms. In 2018, Zhu et al. [21] introduced two control strategies of disconnecting computers from removable devices and reorganizing computers on the basis of Ref. [19], and studied the optimal control of virus transmission between computers and removable devices. Different from previous studies, this paper does not use a fixed cost weight index in the objective function, but uses a state-based cost weight index. In 2020, Kim et al. [1] proposed and analyzed a scheme to control virus transmission through vaccination, that is, installing effective anti-virus software. The results showed that the higher the vaccination rate, the lower the number of infected computers.

Inspired by the models above, we establish a new worm transmission model. We adopt the saturation incidence rate [22, 23], which can present the inhibition effect of susceptible devices and the crowding effect of infectious devices and can also ensure the boundness of contact rate by choosing suitable parameters [24]. In addition, considering the latent character of computer worms, the exposed compartments of computer and USB are introduced [25–28]. The rest of the article is organized as follows: in Section 2, qualitative analysis of the dynamical system is carried out, and sufficient conditions for the existence of equilibria and asymptotic stability are given; numerical findings and discussion are conducted in Section 3; in Section 4, optimal control strategy is proposed; and conclusion is presented in Section 5.

2 Dynamical model

The main purpose of this paper is to explore the dynamic behavior of computer worms transmission in the process of using USB devices to transmit data, so as to formulate effective strategies to control the spread of worms. This model is an improved version of Kim et al. [1]. In this model, the computer acts as the host and the USB device acts as a vector. Among them, the total computer population is divided into the following four subclasses, which are S_c(t), E_c(t), I_c(t), and R_c(t), representing the numbers of susceptible computers, exposed computers, infectious computers and recovered computers at time t. And similarly for USB devices population, which is classified into three vector population subclasses, namely S_u(t), E_u(t), and I_u(t), represent the numbers of susceptible USB devices, exposed USB devices and infectious USB devices at time t, respectively. In addition, the following model assumptions are presented:

(H1) All newly launched computers and removable USB devices are susceptible.

(H2) At time t, the infectious force of infected USB devices to susceptible computers is given by $\frac{\left(1-\sigma \nu \right){\beta }_1{S}_c{I}_u}{1+{\alpha }_1{I}_{\text{u}}}$, while the infectibility of infected computers to susceptible USB devices is $\frac{\left(1-\sigma \nu \right){\beta }_1{S}_u{I}_c}{1+{\alpha }_2{I}_c}$.

(H3) Infected computers will gain temporary immunity after recovery due to anti-virus software installed, but after a period of time will join again susceptible class because of the variability of computer worms.

(H4) Computer dysfunction is not only related to natural death, but also to worm invasion.

The improved model as follow:

$\begin{array}{ccc}\hfill \frac{d{S}_c}{dt}& =\hfill & {\mathrm{\Lambda }}_1-\frac{\left(1-\sigma \nu \right){\beta }_1{S}_c{I}_u}{1+{\alpha }_1{I}_u}-\left(\sigma \nu +{\mu }_1\right)S_c+\tau R_c,\hfill \\ \hfill \frac{d{E}_c}{dt}& =\hfill & \frac{\left(1-\sigma \nu \right){\beta }_1{S}_c{I}_u}{1+{\alpha }_1{I}_u}-\left(\eta +ϵ+{\mu }_1\right)E_c,\hfill \\ \hfill \frac{d{I}_c}{dt}& =\hfill & \eta E_c-\left(\gamma +{\mu }_1+\theta \right)I_c,\hfill \\ \hfill \frac{d{R}_c}{dt}& =\hfill & \sigma \nu S_c+ϵE_c+\gamma I_c-\left(\tau +{\mu }_1\right)R_c,\hfill \\ \hfill \frac{d{S}_u}{dt}& =\hfill & {\mathrm{\Lambda }}_2-\frac{{\beta }_2{S}_u{I}_c}{1+{\alpha }_2{I}_c}-{\mu }_2{S}_u+\varphi E_u+p{I}_u,\hfill \\ \hfill \frac{d{E}_u}{dt}& =\hfill & \frac{{\beta }_2{S}_u{I}_c}{1+{\alpha }_2{I}_c}-\left(\xi +\varphi +{\mu }_2\right)E_u,\hfill \\ \hfill \frac{d{I}_u}{dt}& =\hfill & \xi E_u-\left(p+{\mu }_2\right)I_u.\hfill \end{array}(1)$

For the computer population in system (Eq. 1), Λ₁ is the recruitment rate of computer population; σ is the efficiency coefficient of the anti-virus software; ν is installation coverage rate coefficient of anti-virus software; β₁ is infection rate coefficient of susceptible computers by infectious USB devices; α₁ is the degree coefficient of protection measures taken for susceptible computers in case of worms outbreak; μ₁ is the natural elimination rate coefficient of computer population; θ is the elimination rate coefficient of computer population caused by worm invasion; τ, η, ϵ, γ are the transition rate coefficients among states in the computer population.

As for the USB population in system (Eq. 1), Λ₂ is the recruitment rate of USB population; β₂ is infection rate coefficient of susceptible USB devices by infectious computers; α₂ is the degree coefficient of protection measures taken for susceptible USB devices in case of worms outbreak; μ₂ is the natural elimination rate coefficient of USB population; ϕ, p, ξ are the transition rate coefficients among states in the USB population.

Suppose N_c and N_u are the total number of computer population and USB population at time t, respectively, satisfying N_c = S_c + E_c + I_c + R_c and N_u = S_u + E_u + I_u. Add the equations in system (Eq. 1) to get $\frac{d{N}_c}{dt}={\mathrm{\Lambda }}_1-{\mu }_1{N}_c-\theta I_c\le {\mathrm{\Lambda }}_1-{\mu }_1{N}_c$ and $\frac{d{N}_u}{dt}={\mathrm{\Lambda }}_2-{\mu }_2{N}_u$. The operable region for system (Eq. 1) is given below:

$\mathrm{\Delta }=\left\{\left(S_c,E_c,I_c,R_c,S_u,E_u,I_u\right)\in {\mathfrak{R}}_{+}^7|0\le N_c\le \frac{{\mathrm{\Lambda }}_1}{{\mu }_1},0\le N_u\le \frac{{\mathrm{\Lambda }}_2}{{\mu }_2}\right\}.(2)$

In this section, we firstly prove the existence of disease free equilibrium and endemic equilibrium of system (Eq. 1), and obtain the basic reproduction number R₀ through calculation which determines the propagation dynamics of system (Eq. 1). Secondly, we provide the local and global stability of disease free equilibrium and endemic equilibrium under certain conditions, which establishes the theoretical foundation for the control strategies of worm attack.

2.1 Existence of basic reproduction number and equilibria

Our aim is to study the characteristics of disease free equilibrium and endemic equilibrium. Let the right-hand side of system (Eq. 1) equals zero, and the disease free equilibrium can be obtained:

$P^0=\left(S_c^0,E_c^0,I_c^0,R_c^0,S_u^0,E_u^0,I_u^0\right)=\left(\frac{{\mathrm{\Lambda }}_1\left(\tau +{\mu }_1\right)}{{\mu }_1\left(\sigma \nu +\tau +{\mu }_1\right)},\mathrm{0,0},\frac{{\mathrm{\Lambda }}_1\sigma \nu }{{\mu }_1\left(\sigma \nu +\tau +{\mu }_1\right)},\frac{{\mathrm{\Lambda }}_2}{{\mu }_2},\mathrm{0,0}\right).(3)$

Next, we calculate the basic reproduction number R₀, which is essentially the number of secondary infectious cases produced in a susceptible class by a single infectious node in its overall infectious duration. This is a decisive threshold in epidemiological systems that can be used to predict whether computers will be continuously attacked by worms [29]. According to the next-generation matrix method in literature [30], we have the following:

$F=\left(\begin{array}{cccc}\hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \left(1-\sigma \nu \right){\beta }_1{S}_c^0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill {\beta }_2{S}_u^0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \end{array}\right),V=\left(\begin{array}{cccc}\hfill \eta +ϵ+{\mu }_1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill -\eta \hfill & \hfill \gamma +{\mu }_1+\theta \hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill \xi +\varphi +{\mu }_2\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill -\xi \hfill & \hfill p+{\mu }_2\hfill \end{array}\right).$

Thus, we obtain the basic reproduction number:

$\begin{array}{ccc}\hfill R_0& =\hfill & \sqrt{\frac{\left(1-\sigma \nu \right){\beta }_1{\beta }_2\eta \xi S_c^0{S}_u^0}{\left(\eta +ϵ+{\mu }_1\right)\left(\gamma +{\mu }_1+\theta \right)\left(\xi +\varphi +{\mu }_2\right)\left(p+{\mu }_2\right)}}\hfill \\ \hfill & =\hfill & \sqrt{\frac{\left(1-\sigma \nu \right){\beta }_1{\beta }_2\eta \xi \left(\tau +{\mu }_1\right){\mathrm{\Lambda }}_1{\mathrm{\Lambda }}_2}{\left(\eta +ϵ+{\mu }_1\right)\left(\gamma +{\mu }_1+\theta \right)\left(\xi +\varphi +{\mu }_2\right)\left(p+{\mu }_2\right)\left(\sigma \nu +\tau +{\mu }_1\right){\mu }_1{\mu }_2}}.\hfill \end{array}(4)$

Theorem 1 When R₀ > 1, system (Eq. 1) has a unique endemic equilibrium.

Proof: Make the right side of system (Eq. 1) equal to zero, and substitute the endemic equilibrium $P^{*}=(S_c^{*},E_c^{*},I_c^{*},R_c^{*},S_u^{*},E_u^{*},I_u^{*})$ into the equation:

$E_c^{\ast }=\frac{\gamma +{\mu }_1+\theta }{\eta }{I}_c^{\ast },R_c^{\mathrm{\ast }}=\frac{\sigma \nu S_c^{\ast }+ϵE_c^{\ast }+\gamma I_c^{\ast }}{\tau +{\mu }_1},E_u^{*}=\frac{p+{\mu }_2}{\xi }{I}_u^{*},$

$S_c^{\ast }=\frac{{\mathrm{\Lambda }}_1\left(\tau +{\mu }_1\right)+\tau \left(ϵE_c^{\ast }+\gamma I_c^{\ast }\right)}{{\mu }_1\left(\sigma \nu +\tau +{\mu }_1\right)+\frac{\left(1-\sigma \nu \right){\beta }_1{I}_u^{*}\left(\tau +{\mu }_1\right)}{1+{\alpha }_1{I}_u^{*}}},S_u^{*}=\frac{{\mathrm{\Lambda }}_2+p{I}_u^{*}}{{\mu }_2+\frac{\xi +{\mu }_2}{\xi +\varphi +{\mu }_2}\cdot \frac{{\beta }_2{I}_c^{\ast }}{1+{\alpha }_2{I}_c^{\ast }}},$

$I_u^{*}=\frac{\xi {\beta }_2{\mathrm{\Lambda }}_2{I}_c^{\ast }}{\left(\xi +\varphi +{\mu }_2\right)\left(p+{\mu }_2\right)\left(1+{\alpha }_2{I}_c^{\ast }\right){\mu }_2+{\mu }_2{\beta }_2\left(p+\xi +{\mu }_2\right)I_c^{\ast }}.$

We get the expression $G\left(I_c^{*}\right)=a{I}_c^{*}+b$ for $I_c^{*}$, where

$\begin{array}{ccc}\hfill a& =\hfill & {\alpha }_2{\mu }_2\left(\xi +\varphi +{\mu }_2\right)\left(p+{\mu }_2\right)+{\mu }_2{\beta }_2\left(p+\xi +{\mu }_2\right)\hfill \\ \hfill & \hfill & +\xi {\beta }_2{\mathrm{\Lambda }}_2{\alpha }_1{\mu }_1\left(\eta +ϵ+{\mu }_1\right)\left(\gamma +{\mu }_1+\theta \right)\left(\sigma \nu +\tau +{\mu }_1\right)\hfill \\ \hfill & \hfill & +\xi {\beta }_2{\mathrm{\Lambda }}_2\eta {\beta }_1\left({\mu }_1\gamma \left(1-\sigma \nu \right)+\left({\mu }_1+\theta \right)\left(1-\sigma \nu \right)\left(\tau +{\mu }_1\right)\right)\hfill \\ \hfill & \hfill & +\xi {\beta }_2{\mathrm{\Lambda }}_2{\beta }_1{\mu }_1\left(\gamma +{\mu }_1+\theta \right)\left(1-\sigma \nu \right)\left(\tau +{\mu }_1+ϵ\right)>0,\hfill \end{array}$

$b={\mu }_1{\mu }_2\left(\eta +ϵ+{\mu }_1\right)\left(\gamma +{\mu }_1+\theta \right)\left(\sigma \nu +\tau +{\mu }_1\right)\left(\xi +\varphi +{\mu }_2\right)\left(p+{\mu }_2\right)\left(1-R_0^2\right).$

When R₀ > 1, b < 0, so $I_c^{*}=-\frac{b}{a}>0$ and $G\left(I_c^{*}\right)=0$, that is, when R₀ > 1, there is a unique positive equilibrium P*.

2.2 Stability of disease free equilibrium

In this subsection, we analyze the asymptotical stability of disease free equilibrium P⁰.

Theorem 2 The disease free equilibrium P⁰ of system (Eq. 1) is locally asymptotically stable if R₀ < 1 and is unstable if R₀ > 1.

Proof: The Jacobian matrix of system (Eq. 1) at P⁰ is

$J^{\left|0\right|}=\left(\begin{array}{ccccccc}\hfill a_{11}\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \tau \hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill -\left(1-\sigma \nu \right){\beta }_1{S}_c^0\hfill \\ \hfill 0\hfill & \hfill a_{22}\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \left(1-\sigma \nu \right){\beta }_1{S}_c^0\hfill \\ \hfill 0\hfill & \hfill \eta \hfill & \hfill a_{33}\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill \sigma \nu \hfill & \hfill ϵ\hfill & \hfill \gamma \hfill & \hfill a_{44}\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill -{\beta }_2{S}_u^0\hfill & \hfill 0\hfill & \hfill -{\mu }_2\hfill & \hfill \varphi \hfill & \hfill p\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill {\beta }_2{S}_u^0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill a_{66}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \xi \hfill & \hfill a_{77}\hfill \end{array}\right),(5)$

where $a_{11}=-\left(\sigma \nu +{\mu }_1\right),a_{22}=-\left(\eta +ϵ+{\mu }_1\right),a_{33}=-\left(\gamma +{\mu }_1+\theta \right),a_{44}=-\left(\tau +{\mu }_1\right),a_{66}=-\left(\xi +\varphi +{\mu }_2\right),a_{77}=-\left(p+{\mu }_2\right)$. Obviously, one of the eigenvalues of J^|0| is λ₁ = −μ₂. In order to obtain the rest eigenvalues, the following simplified matrix is considered:

$J_1^{\left|0\right|}=\left(\begin{array}{cccccc}\hfill a_{11}\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \tau \hfill & \hfill 0\hfill & \hfill -\left(1-\sigma \nu \right){\beta }_1{S}_c^0\hfill \\ \hfill 0\hfill & \hfill a_{22}\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \left(1-\sigma \nu \right){\beta }_1{S}_c^0\hfill \\ \hfill 0\hfill & \hfill \eta \hfill & \hfill a_{33}\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill \sigma \nu \hfill & \hfill ϵ\hfill & \hfill \gamma \hfill & \hfill a_{44}\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill {\beta }_2{S}_u^0\hfill & \hfill 0\hfill & \hfill a_{66}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \xi \hfill & \hfill a_{77}\hfill \end{array}\right).(6)$

By elementary row operations, we get

$J_2^{\left|0\right|}=\left(\begin{array}{cccccc}\hfill a_{11}\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \tau \hfill & \hfill 0\hfill & \hfill -\left(1-\sigma \nu \right){\beta }_1{S}_c^0\hfill \\ \hfill 0\hfill & \hfill a_{22}\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \left(1-\sigma \nu \right){\beta }_1{S}_c^0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill b_{33}\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \left(1-\sigma \nu \right)\eta {\beta }_1{S}_c^0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill b_{44}\hfill & \hfill 0\hfill & \hfill b_{46}\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill b_{55}\hfill & \hfill \left(1-\sigma \nu \right)\eta {\beta }_1{\beta }_2{S}_c^0{S}_u^0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill b_{66}\hfill \end{array}\right),(7)$

where

$b_{33}=-\left(\eta +ϵ+{\mu }_1\right)\left(\gamma +{\mu }_1+\theta \right),$

$b_{44}=-{\mu }_1\left(\tau +\sigma \nu +{\mu }_1\right){\left(\eta +ϵ+{\mu }_1\right)}^2\left(\gamma +{\mu }_1+\theta \right),$

$b_{55}=-\left(\eta +ϵ+{\mu }_1\right)\left(\gamma +{\mu }_1+\theta \right)\left(\xi +\varphi +{\mu }_2\right),$

$b_{66}=\frac{\left(1-\sigma \nu \right)\xi \eta {\beta }_1{\beta }_2{S}_c^0{S}_u^0}{\left(\eta +ϵ+{\mu }_1\right)\left(\gamma +{\mu }_1+\theta \right)\left(\xi +\varphi +{\mu }_2\right)}-\left(p+{\mu }_2\right),$

$\begin{array}{ccc}\hfill b_{46}& =\hfill & \left(1-\sigma \nu \right)\eta {\beta }_1{S}_c^0\gamma \left(\sigma \nu +{\mu }_1\right)\left(\eta +ϵ+{\mu }_1\right)\hfill \\ \hfill & \hfill & +\left(ϵ{\mu }_1-\sigma \nu \left(\eta +{\mu }_1\right)\right)\left(1-\sigma \nu \right){\beta }_1{S}_c^0\left(\eta +ϵ+{\mu }_1\right)\left(\gamma +{\mu }_1+\theta \right).\hfill \end{array}$

When $\frac{(1-\sigma \nu )\xi \eta {\beta }_1{\beta }_2{S}_c^0{S}_u^0}{(\eta +ϵ+{\mu }_1)(\gamma +{\mu }_1+\theta )(\xi +\varphi +{\mu }_2)}<(p+{\mu }_2)$, that is, when R₀ < 1, the eigenvalues of $J_2^{|0|}$ are all negative, and therefore the eigenvalues of J^|0| are all negative. It shows that when R₀ < 1, the disease free equilibrium P⁰ of system (Eq. 1) is locally asymptotically stable in Δ, whereas P⁰ is unstable in Δ if R₀ > 1.

Theorem 3 The disease free equilibrium P⁰ of system (Eq. 1) is globally asymptotically stable in region Δ if R₀ < 1 and is unstable if R₀ > 1.

Proof: The Castillo-Chavez method in Refs. [31] is used to prove it. First, let χ₁ = (S_c, R_c, S_u), χ₂ = (E_c, I_c, E_u, I_u) and define $P^0=({\chi }_1^0,0)$, where

${\chi }_1^0=\left(\frac{{\mathrm{\Lambda }}_1\left(\tau +{\mu }_1\right)}{{\mu }_1\left(\sigma \nu +\tau +{\mu }_1\right)},\frac{{\mathrm{\Lambda }}_1\sigma \nu }{{\mu }_1\left(\sigma \nu +\tau +{\mu }_1\right)},\frac{{\mathrm{\Lambda }}_2}{{\mu }_2}\right).(8)$

We decompose system (Eq. 1) into two subsystems,

$\begin{array}{ccc}\hfill \frac{d{\chi }_1}{dt}& =\hfill & G\left({\chi }_1,{\chi }_2\right),\hfill \\ \hfill \frac{d{\chi }_2}{dt}& =\hfill & H\left({\chi }_1,{\chi }_2\right),\hfill \end{array}(9)$

where

$\begin{array}{c}G\left({\chi }_1,{\chi }_2\right)=\left(\begin{array}{c}\hfill {\mathrm{\Lambda }}_1-\frac{\left(1-\sigma \nu \right){\beta }_1{S}_c{I}_u}{1+{\alpha }_1{I}_u}-\left(\sigma \nu +{\mu }_1\right)S_c+\tau R_c\hfill \\ \hfill \sigma \nu S_c+E_c+\gamma I_c-\left(\tau +{\mu }_1\right)R_c\hfill \\ \hfill {\mathrm{\Lambda }}_2-\frac{{\beta }_2{S}_u{I}_c}{1+{\alpha }_2{I}_c}-{\mu }_2{S}_u+\varphi E_u+p{I}_u\hfill \end{array}\right),\hfill \\ H\left({\chi }_1,{\chi }_2\right)=\left(\begin{array}{c}\hfill \frac{\left(1-\sigma \nu \right){\beta }_1{S}_c{I}_u}{1+{\alpha }_1{I}_u}-\left(\eta ++{\mu }_1\right)E_c\hfill \\ \hfill \eta E_c-\left(\gamma +{\mu }_1+\theta \right)I_c\hfill \\ \hfill \frac{{\beta }_2{S}_u{I}_c}{1+{\alpha }_2{I}_c}-\left(\xi +\varphi +{\mu }_2\right)E_u\hfill \\ \hfill \xi E_u-\left(p+{\mu }_2\right)I_u\hfill \end{array}\right).\hfill \end{array}$

Because $S_c=S_c^0$, $R_c=R_c^0$, $S_u=S_u^0$, and $G\left({\chi }_1,0\right)=0$, we have

$G\left({\chi }_1,0\right)=\left(\begin{array}{c}\hfill {\mathrm{\Lambda }}_1-\left(\sigma \nu +{\mu }_1\right)S_c^0+\tau R_c^0\hfill \\ \hfill \sigma \nu S_c^0-\left(\tau +{\mu }_1\right)R_c^0\hfill \\ \hfill {\mathrm{\Lambda }}_2-{\mu }_2{S}_u^0\hfill \end{array}\right)=0.(10)$

According to (Eq. 10), when t → ∞, ${\chi }_1\to {\chi }_1^0$. Therefore, ${\chi }_1={\chi }_1^0$ is globally asymptotically stable.

Moreover, it is obvious that

$\begin{array}{ccc}\hfill H\left({\chi }_1,{\chi }_2\right)& =\hfill & B{\chi }_2-\bar{H}\left({\chi }_1,{\chi }_2\right)\hfill \\ \hfill & =\hfill & \left(\begin{array}{cccc}\hfill a_{22}\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \left(1-\sigma \nu \right){\beta }_1{S}_c^0\hfill \\ \hfill \eta \hfill & \hfill a_{33}\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill {\beta }_2{S}_u^0\hfill & \hfill a_{66}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill \xi \hfill & \hfill a_{77}\hfill \end{array}\right)\left(\begin{array}{c}\hfill E_c\hfill \\ \hfill I_c\hfill \\ \hfill E_u\hfill \\ \hfill I_u\hfill \end{array}\right)\hfill \\ \hfill & \hfill & -\left(\begin{array}{c}\hfill \left(1-\sigma \nu \right){\beta }_1{S}_c^0{I}_u-\frac{\left(1-\sigma \nu \right){\beta }_1{S}_c{I}_u}{1+{\alpha }_1{I}_u}\hfill \\ \hfill 0\hfill \\ \hfill {\beta }_2{S}_u^0{I}_c-\frac{{\beta }_2{S}_u{I}_c}{1+{\alpha }_2{I}_c}\hfill \\ \hfill 0\hfill \end{array}\right).\hfill \end{array}(11)$

The population limits of computer and USB device are $S_c^0,S_u^0$, that is, $S_c\le S_c^0,S_u\le S_u^0$, so $\left(1-\sigma \nu \right){\beta }_1{S}_c^0{I}_u\ge \frac{\left(1-\sigma \nu \right){\beta }_1{S}_c{I}_u}{1+{\alpha }_1{I}_u},{\beta }_2{S}_u^0{I}_c\ge \frac{{\beta }_2{S}_u{I}_c}{1+{\alpha }_2{I}_c}$, which means $\bar{H}\left({\chi }_1,{\chi }_2\right)\ge 0$. Also from (Eq. 11), B is an M-matrix. Thus condition 1 and 2 are satisfied in section 4.1 of Refs. [32]. Therefore, Theorem 3 is proved.

2.3 Stability of endemic equilibrium

In this subsection, we analyze the asymptotical stability of endemic equilibrium P*.

Theorem 4 The endemic equilibrium P* of system Eq. 1 is locally asymptotically stable if $\max \left\{ϵ,\gamma \right\}<\sigma \nu$ and $1<R_0<\frac{\left(1+{\alpha }_1{I}_u^{*}\right)\left(1+{\alpha }_2{I}_c^{*}\right)\sqrt{\left(\tau +{\mu }_1\right){\mathrm{\Lambda }}_1{\mathrm{\Lambda }}_2}}{\sqrt{\left(\sigma \nu +\tau +{\mu }_1\right){\mu }_1{\mu }_2{S}_c^{*}{S}_u^{*}}}$.

Proof: The Jacobian matrix of system (Eq. 1) at P* is given by

$J^{|*|}=\left(\begin{array}{ccccccc}\hfill c_{11}\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \tau \hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill -\frac{\left(1-\sigma \nu \right){\beta }_1{S}_c^{\star }}{{\left(1+{\alpha }_1{I}_u^{\ast }\right)}^2}\hfill \\ \hfill \frac{\left(1-\sigma \nu \right){\beta }_1{I}_u^{\ast }}{1+{\alpha }_1{I}_u^{\ast }}\hfill & \hfill a_{22}\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \frac{\left(1-\sigma \nu \right){\beta }_1{S}_c^{\ast }}{{\left(1+{\alpha }_1{I}_u^{\ast }\right)}^2}\hfill \\ \hfill 0\hfill & \hfill \eta \hfill & \hfill a_{33}\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill \sigma \nu \hfill & \hfill ϵ\hfill & \hfill \gamma \hfill & \hfill a_{44}\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill -\frac{{\beta }_2{S}_u^{\ast }}{{\left(1+{\alpha }_2{I}_c^{\ast }\right)}^2}\hfill & \hfill 0\hfill & \hfill c_{55}\hfill & \hfill \varphi \hfill & \hfill p\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill \frac{{\beta }_2{S}_u^{\ast }}{{\left(1+{\alpha }_2{I}_c^{\ast }\right)}^2}\hfill & \hfill 0\hfill & \hfill \frac{{\beta }_2{I}_c^{\ast }}{1+{\alpha }_2{I}_c^{\ast }}\hfill & \hfill a_{66}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \xi \hfill & \hfill a_{77}\hfill \end{array}\right),(12)$

where $c_{11}=-\left(\sigma \nu +{\mu }_1\right)-\frac{\left(1-\sigma \nu \right){\beta }_1{I}_u^{*}}{1+{\alpha }_1{I}_u^{*}},c_{55}=-{\mu }_2-\frac{{\beta }_2{I}_c^{*}}{1+{\alpha }_2{I}_c^{*}}$.

After simplification we get

$J_1^{\left|*\right|}=\left(\begin{array}{ccccccc}\hfill {\mathrm{c}}_{11}\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \tau \hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill -\frac{\left(1-\sigma \nu \right){\beta }_1{S}_c^{\ast }}{{\left(1+{\alpha }_1{I}_u^{\ast }\right)}^2}\hfill \\ \hfill 0\hfill & \hfill d_{22}\hfill & \hfill 0\hfill & \hfill \frac{\left(1-\sigma \nu \right){\beta }_1{I}_u^{\ast }\tau }{1+{\alpha }_1{I}_u^{\ast }}\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \frac{\left(1-\sigma \nu \right){\beta }_1{S}_c^{\ast }\left(\sigma \nu +{\mu }_1\right)}{{\left(1+{\alpha }_1{I}_u^{\ast }\right)}^2}\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill d_{33}\hfill & \hfill \frac{\left(1-\sigma \nu \right){\beta }_1{I}_u^{\ast }\eta \tau }{1+{\alpha }_1{I}_u^{\ast }}\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \frac{\left(1-\sigma \nu \right){\beta }_1{S}_c^{\ast }\eta \left(\sigma \nu +{\mu }_1\right)}{{\left(1+{\alpha }_1{I}_u^{\ast }\right)}^2}\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill d_{44}\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill d_{47}\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill -{\mu }_2\hfill & \hfill -\left(\xi +{\mu }_2\right)\hfill & \hfill p\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill d_{66}\hfill & \hfill d_{67}\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill d_{77}\hfill \end{array}\right),(13)$

where

$\begin{array}{c}{d}_{22}=-a_{22}{c}_{11},d_{33}=a_{22}{a}_{33}{c}_{11},\hfill \\ d_{44}={\mu }_1\left(\tau +\sigma \nu +{\mu }_1\right)a_{22}^2{a}_{33}{c}_{11}^2+\frac{{\mu }_1\left(1-\sigma \nu \right){\beta }_1{I}_u^{\ast }}{1+{\alpha }_1{I}_u^{\ast }}{a}_{22}^2{a}_{33}{c}_{11}^2+\left(\eta \left({\mu }_1+\theta \right)-{\mu }_1{a}_{33}\right)\frac{\tau \left(1-\sigma \nu \right){\beta }_1{I}_u^{\ast }}{1+{\alpha }_1{I}_u^{\ast }}{a}_{22}{c}_{11}^2,\hfill \\ d_{47}=\left(\sigma \nu \eta \theta +\left(ϵ-\sigma \nu \right){\mu }_1{a}_{33}-\eta {\mu }_1\left(\gamma -\sigma \nu \right)\right)\frac{\left(1-\sigma \nu \right){\beta }_1{S}_c^{\ast }}{{\left(1+{\alpha }_1{I}_u^{\ast }\right)}^2}{a}_{22}{c}_{11}^2,\hfill \\ d_{66}=\left(-\frac{{\beta }_2{I}_c^{\ast }}{1+{\alpha }_2{I}_c^{\ast }}\left(\xi +{\mu }_2\right)+{\mu }_2{a}_{66}\right)a_{22}{a}_{33}{c}_{11}{d}_{44},\hfill \\ d_{67}=\frac{{\beta }_2{I}_c^{\ast }p}{1+{\alpha }_2{I}_c^{\ast }}{a}_{22}{a}_{33}{c}_{11}{d}_{44}+{\mu }_1{\mu }_2\eta \left(\tau +\sigma \nu +{\mu }_1\right)\times \frac{\left(1-\sigma \nu \right){\beta }_1{S}_c^{\ast }}{{\left(1+{\alpha }_1{I}_u^{\ast }\right)}^2}\frac{{\beta }_2{S}_u^{\ast }}{{\left(1+{\alpha }_2{I}_c^{\ast }\right)}^2}{a}_{11}{a}_{22}^2{a}_{33}{c}_{11}^2\hfill \\ +\left({\mu }_1^2{\mu }_2\eta \tau a_{33}+{\mu }_1{\mu }_2\eta \tau ϵa_{33}+{\mu }_1{\mu }_2\eta a_{11}{a}_{22}{a}_{33}-{\mu }_1{\mu }_2{\eta }^2\tau \left({\mu }_1+\theta \right)-{\mu }_1{\mu }_2{\eta }^2\tau \gamma \right)\cdot \frac{\left(1-\sigma \nu \right){\beta }_1{I}_u^{\ast }}{1+{\alpha }_1{I}_u^{\ast }}\frac{{\beta }_2{S}_u^{\ast }}{{\left(1+{\alpha }_2{I}_c^{\ast }\right)}^2}\frac{\left(1-\sigma \nu \right){\beta }_1{S}_c^{\ast }}{{\left(1+{\alpha }_1{I}_u^{\ast }\right)}^2}{a}_{22}{c}_{11}^2,\hfill \\ d_{77}=-{\mu }_2\left(p+\xi +{\mu }_2\right)\frac{{\beta }_2{I}_c^{\ast }}{1+{\alpha }_2{I}_c^{\ast }}{a}_{22}{a}_{33}{c}_{11}{d}_{44}+\frac{\left(1-\sigma \nu \right){\beta }_1{I}_u^{\ast }}{1+{\alpha }_1{I}_u^{\ast }}{\mu }_2{a}_{22}{a}_{33}{a}_{66}{a}_{77}{d}_{44}+\xi {\mu }_2\eta \tau \left(\sigma \nu \eta \theta +\left(ϵ-\sigma \nu \right){\mu }_1{a}_{33}\right)\frac{\left(1-\sigma \nu \right){\beta }_1{I}_u^{\ast }}{1+{\alpha }_1{I}_u^{\ast }}\frac{{\beta }_2{S}_u^{\ast }}{{\left(1+{\alpha }_2{I}_c^{\ast }\right)}^2}\frac{\left(1-\sigma \nu \right){\beta }_1{S}_c^{\ast }}{{\left(1+{\alpha }_1{I}_u^{\ast }\right)}^2}{a}_{22}{c}_{11}^2\hfill \\ +\xi {\mu }_2\eta \tau \left(-\eta {\mu }_1\left(\gamma -\sigma \nu \right)\right)\frac{\left(1-\sigma \nu \right){\beta }_1{I}_u^{\ast }}{1+{\alpha }_1{I}_u^{\ast }}\frac{{\beta }_2{S}_u^{\ast }}{{\left(1+{\alpha }_2{I}_c^{\ast }\right)}^2}\frac{\left(1-\sigma \nu \right){\beta }_1{S}_c^{\ast }}{{\left(1+{\alpha }_1{I}_u^{\ast }\right)}^2}{a}_{22}{c}_{11}^2+\frac{a_{11}{a}_{44}{d}_{44}}{R_0^2}\frac{\left(1-\sigma \nu \right){\beta }_1{\beta }_2\eta \xi {\mathrm{\Lambda }}_1{\mathrm{\Lambda }}_2}{{\mu }_1\left(\sigma \nu +\tau +{\mu }_1\right)}\left(1-\frac{\left(\sigma \nu +\tau +{\mu }_1\right){\mu }_1{\mu }_2{S}_c^{\ast }{S}_u^{\ast }{R}_0^2}{\left(\tau +{\mu }_1\right){\mathrm{\Lambda }}_1{\mathrm{\Lambda }}_2{\left(1+{\alpha }_1{I}_u^{\ast }\right)}^2{\left(1+{\alpha }_2{I}_c^{\ast }\right)}^2}\right).\hfill \\ +\frac{a_{11}{a}_{44}{d}_{44}}{R_0^2}\frac{\left(1-\sigma \nu \right){\beta }_1{\beta }_2\eta \xi {\mathrm{\Lambda }}_1{\mathrm{\Lambda }}_2}{{\mu }_1\left(\sigma \nu +\tau +{\mu }_1\right)}\left(1-\frac{\left(\sigma \nu +\tau +{\mu }_1\right){\mu }_1{\mu }_2{S}_c^{\ast }{S}_u^{\ast }{R}_0^2}{\left(\tau +{\mu }_1\right){\mathrm{\Lambda }}_1{\mathrm{\Lambda }}_2{\left(1+{\alpha }_1{I}_u^{\ast }\right)}^2{\left(1+{\alpha }_2{I}_c^{\ast }\right)}^2}\right).\hfill \end{array}$

It is obvious that a₂₂, a₃₃, a₆₆, c₁₁, c₅₅ < 0, and then, d₂₂, d₃₃, d₄₄, d₆₆ < 0 can be obtained according to the above expressions. Besides, when $\max \left\{ϵ,\gamma \right\}<\sigma \nu$ and $1<R_0<\frac{\left(1+{\alpha }_1{I}_u^{\ast }\right)\left(1+{\alpha }_2{I}_c^{\ast }\right)\sqrt{\left(\tau +{\mu }_1\right){\mathrm{\Lambda }}_1{\mathrm{\Lambda }}_2}}{\sqrt{\left(\sigma \nu +\tau +{\mu }_1\right){\mu }_1{\mu }_2{S}_c^{\ast }{S}_u^{\ast }}}$, we get d₇₇ < 0. Just as we have shown that the real parts of all eigenvalues of $J^{\left|\ast \right|}$ are negative, so the endemic equilibrium $J^{\left|\ast \right|}$ is locally asymptotically stable under condition $\max \left\{ϵ,\gamma \right\}<\sigma \nu$ and $1<R_0<\frac{\left(1+{\alpha }_1{I}_u^{\ast }\right)\left(1+{\alpha }_2{I}_c^{\ast }\right)\sqrt{\left(\tau +{\mu }_1\right){\mathrm{\Lambda }}_1{\mathrm{\Lambda }}_2}}{\sqrt{\left(\sigma \nu +\tau +{\mu }_1\right){\mu }_1{\mu }_2{S}_c^{\ast }{S}_u^{\ast }}}$.

Next, the geometrical approach in Refs. [33] is used to determine the condition that system (Eq. 1) achieves global asymptotic stability at the endemic equilibrium.

Theorem 5 If $\max \left\{\frac{\varphi S_c^{\ast }}{E_c^{\ast }}-\frac{{\beta }_2{I}_c^{\ast }}{1+{\alpha }_2{I}_c^{\ast }},\frac{{\beta }_2{I}_c^{\ast }}{1+{\alpha }_2{I}_c^{\ast }}\cdot \frac{E_c^{\ast }}{S_c^{\ast }}\right\}<\frac{\left(1-\sigma \nu \right){\beta }_1{I}_u^{\ast }}{1+{\alpha }_1{I}_u^{\ast }}<\frac{{\beta }_2{I}_c^{\ast }}{1+{\alpha }_2{I}_c^{\ast }}\cdot \frac{S_u^{\ast }}{E_u^{\ast }}$ and R₀ > 1, then system (Eq. 1) is globally asymptotically stable at endemic equilibrium P∗ and unstable otherwise.

Proof: We prove the global stability of endemic equilibrium P∗ under the above conditions by using geometrical approach [32, 34, 35], which is the generalization of Lyapunov theory in essence, by using the third additive compound matrix. Consider the subsystems of system (Eq. 1)

$\begin{array}{ccc}\hfill \frac{d{S}_c}{dt}& =\hfill & {\mathrm{\Lambda }}_1-\frac{\left(1-\sigma \nu \right){\beta }_1{S}_c{I}_u}{1+{\alpha }_1{I}_u}-\left(\sigma \nu +{\mu }_1\right)S_c+\tau R_c,\hfill \\ \hfill \frac{d{E}_c}{dt}& =\hfill & \frac{\left(1-\sigma \nu \right){\beta }_1{S}_c{I}_u}{1+{\alpha }_1{I}_u}-\left(\eta +ϵ+{\mu }_1\right)E_c,\hfill \\ \hfill \frac{d{S}_u}{dt}& =\hfill & {\mathrm{\Lambda }}_2-\frac{{\beta }_2{S}_u{I}_c}{1+{\alpha }_2{I}_c}-{\mu }_2{S}_u+\varphi E_u+p{I}_u,\hfill \\ \hfill \frac{d{E}_u}{dt}& =\hfill & \frac{{\beta }_2{S}_u{I}_c}{1+{\alpha }_2{I}_c}-\left(\xi +\varphi +{\mu }_2\right)E_u.\hfill \end{array}(14)$

Let J be the Jacobian matrix of system (Eq. 14) given by

$J=\left(\begin{array}{cccc}\hfill -\left(\sigma \nu +{\mu }_1\right)-\frac{\left(1-\sigma \nu \right){\beta }_1{I}_u^{\ast }}{1+{\alpha }_1{I}_u^{\ast }}\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill \frac{\left(1-\sigma \nu \right){\beta }_1{I}_u^{\ast }}{1+{\alpha }_1{I}_u^{\ast }}\hfill & \hfill -\left(\eta +ϵ+{\mu }_1\right)\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill -{\mu }_2-\frac{{\beta }_2{I}_c^{\ast }}{1+{\alpha }_2{I}_c^{\ast }}\hfill & \hfill \varphi \hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill \frac{{\beta }_2{I}_c^{\ast }}{1+{\alpha }_2{I}_c^{\ast }}\hfill & \hfill -\left(\xi +\varphi +{\mu }_2\right)\hfill \end{array}\right).(15)$

Based on [35], the third additive compound matrix of J is denoted by

$J^{\left|3\right|}=\left(\begin{array}{cccc}\hfill A_{11}\hfill & \hfill \varphi \hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill \frac{{\beta }_2{I}_c^{\ast }}{1+{\alpha }_2{I}_c^{\ast }}\hfill & \hfill A_{22}\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill A_{33}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill \frac{\left(1-\sigma \nu \right){\beta }_1{I}_u^{\ast }}{1+{\alpha }_1{I}_u^{\ast }}\hfill & \hfill A_{44}\hfill \end{array}\right),(16)$

where

$\begin{array}{c}{A}_{11}=-\left(\sigma \nu +2{\mu }_1+{\mu }_2+\eta +ϵ\right)-\frac{\left(1-\sigma \nu \right){\beta }_1{I}_u^{\ast }}{1+{\alpha }_1{I}_u^{\ast }}-\frac{{\beta }_2{I}_c^{\ast }}{1+{\alpha }_2{I}_c^{\ast }},\hfill \\ A_{22}=-\left(\sigma \nu +2{\mu }_1+{\mu }_2+\eta +ϵ+\xi +\varphi \right)-\frac{\left(1-\sigma \nu \right){\beta }_1{I}_u^{\ast }}{1+{\alpha }_1{I}_u^{\ast }},\hfill \\ A_{33}=-\left(\sigma \nu +{\mu }_1+2{\mu }_2+\xi +\varphi \right)-\frac{\left(1-\sigma \nu \right){\beta }_1{I}_u^{\ast }}{1+{\alpha }_1{I}_u^{\ast }}-\frac{{\beta }_2{I}_c^{\ast }}{1+{\alpha }_2{I}_c^{\ast }},\hfill \\ A_{44}=-\left({\mu }_1+2{\mu }_2+\eta +ϵ+\xi +\varphi \right)-\frac{{\beta }_2{I}_c^{\ast }}{1+{\alpha }_2{I}_c^{\ast }}.\hfill \end{array}$

Now let us choose a function $P\left(\chi \right)=P\left(S_c,E_c,S_u,E_u\right)$ so that $P\left(\chi \right)=\mathit{diag}\left\{S_c,E_c,S_u,E_u\right\}$, and accordingly, $P^{-1}\left(\chi \right)=\mathit{diag}\left\{\frac{1}{S_c},\frac{1}{E_c},\frac{1}{S_u},\frac{1}{E_u}\right\}$. The time derivative of $P\left(\chi \right)$ yields that $P_f\left(\chi \right)=\mathit{diag}\left\{{\dot{S}}_c,{\dot{E}}_c,{\dot{S}}_u,{\dot{E}}_u\right\}$.

Therefore,

$P_f{P}^{-1}=\mathit{diag}\left\{\frac{{\dot{S}}_c}{S_c},\frac{{\dot{E}}_c}{E_c},\frac{{\dot{S}}_u}{S_u},\frac{{\dot{E}}_u}{E_u}\right\},(17)$

and

$P{J}^{\left|3\right|}{P}^{-1}=\left(\begin{array}{cccc}\hfill A_{11}\hfill & \hfill \frac{\varphi S_c^{\ast }}{E_c^{\ast }}\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill \frac{{\beta }_2{I}_c^{\ast }}{1+{\alpha }_2{I}_c^{\ast }}\cdot \frac{E_c^{\ast }}{S_c^{\ast }}\hfill & \hfill A_{22}\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill A_{33}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill \frac{\left(1-\sigma \nu \right){\beta }_1{I}_u^{\ast }}{1+{\alpha }_1{I}_u^{\ast }}\cdot \frac{E_u^{\ast }}{S_u^{\ast }}\hfill & \hfill A_{44}\hfill \end{array}\right).(18)$

So that $B=P_f{P}^{-1}+P{J}^{\left|3\right|}{P}^{-1}$,

$B=\left(\begin{array}{cccc}\hfill B_{11}\hfill & \hfill B_{12}\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill B_{21}\hfill & \hfill B_{22}\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill B_{33}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill B_{43}\hfill & \hfill B_{44}\hfill \end{array}\right),(19)$

where

$\begin{array}{c}{B}_{11}=\frac{{\dot{S}}_c}{S_c}-\left(\sigma \nu +2{\mu }_1+{\mu }_2+\eta +ϵ\right)-\frac{\left(1-\sigma \nu \right){\beta }_1{I}_u^{\ast }}{1+{\alpha }_1{I}_u^{\ast }}-\frac{{\beta }_2{I}_c^{\ast }}{1+{\alpha }_2{I}_c^{\ast }},B_{12}=\frac{\varphi S_c^{\ast }}{E_c^{\ast }},\hfill \\ B_{22}=\frac{{\dot{E}}_c}{E_c}-\left(\sigma \nu +2{\mu }_1+{\mu }_2+\eta +ϵ+\xi +\varphi \right)-\frac{\left(1-\sigma \nu \right){\beta }_1{I}_u^{\ast }}{1+{\alpha }_1{I}_u^{\ast }},B_{21}=\frac{{\beta }_2{I}_c^{\ast }}{1+{\alpha }_2{I}_c^{\ast }}\cdot \frac{E_c^{\ast }}{S_c^{\ast }},\hfill \\ B_{33}=\frac{{\dot{S}}_u}{S_u}-\left(\sigma \nu +{\mu }_1+2{\mu }_2+\xi +\varphi \right)-\frac{\left(1-\sigma \nu \right){\beta }_1{I}_u^{\ast }}{1+{\alpha }_1{I}_u^{\ast }}-\frac{{\beta }_2{I}_c^{\ast }}{1+{\alpha }_2{I}_c^{\ast }},\hfill \\ B_{44}=\frac{{\dot{E}}_u}{E_u}-\left({\mu }_1+2{\mu }_2+\eta +ϵ+\xi +\varphi \right)-\frac{{\beta }_2{I}_c^{\ast }}{1+{\alpha }_2{I}_c^{\ast }},B_{43}=\frac{\left(1-\sigma \nu \right){\beta }_1{I}_u^{\ast }}{1+{\alpha }_1{I}_u^{\ast }}\cdot \frac{E_u^{\ast }}{S_u^{\ast }}.\hfill \end{array}$

Consequently, if $\frac{\left(1-\sigma \nu \right){\beta }_1{I}_u^{\ast }}{1+{\alpha }_1{I}_u^{\ast }}+\frac{{\beta }_2{I}_c^{\ast }}{1+{\alpha }_2{I}_c^{\ast }}>\frac{\varphi S_c^{\ast }}{E_c^{\ast }}$, then

$\begin{array}{c}{h}_1\left(t\right)=B_{11}+\sum _{j=2}^4\left|B_{1j}\right|,\hfill \\ h_1\left(t\right)=\frac{{\dot{S}}_c}{S_c}-\left(\sigma \nu +2{\mu }_1+{\mu }_2+\eta +ϵ\right)\hfill \\ -\frac{\left(1-\sigma \nu \right){\beta }_1{I}_u^{\ast }}{1+{\alpha }_1{I}_u^{\ast }}-\frac{{\beta }_2{I}_c^{\ast }}{1+{\alpha }_2{I}_c^{\ast }}+\frac{\varphi S_c^{\ast }}{E_c^{\ast }}=\frac{{\dot{S}}_c}{S_c}-\left(\sigma \nu +2{\mu }_1+{\mu }_2+\eta +ϵ\right)-\left(\frac{\left(1-\sigma \nu \right){\beta }_1{I}_u^{\ast }}{1+{\alpha }_1{I}_u^{\ast }}+\frac{{\beta }_2{I}_c^{\ast }}{1+{\alpha }_2{I}_c^{\ast }}-\frac{\varphi S_c^{\ast }}{E_c^{\ast }}\right)\le \frac{{\dot{S}}_c}{S_c}-\left(\sigma \nu +2{\mu }_1+{\mu }_2+\eta +ϵ\right).\hfill \end{array}$

and if $\frac{\left(1-\sigma \nu \right){\beta }_1{I}_u^{\ast }}{1+{\alpha }_1{I}_u^{\ast }}>\frac{{\beta }_2{I}_c^{\ast }}{1+{\alpha }_2{I}_c^{\ast }}\cdot \frac{E_c^{\ast }}{S_c^{\ast }}$, then

$\begin{array}{ccc}\hfill h_2\left(t\right)& =\hfill & B_{22}+\sum _{\genfrac{}{}{0pt}{}{j=1}{j\ne 2}}^4\left|B_{2j}\right|,\hfill \\ \hfill h_2\left(t\right)& =\hfill & \frac{{\dot{E}}_c}{E_c}-\left(\sigma \nu +2{\mu }_1+{\mu }_2+\eta +ϵ+\xi +\varphi \right)-\frac{\left(1-\sigma \nu \right){\beta }_1{I}_u^{\ast }}{1+{\alpha }_1{I}_u^{\ast }}+\frac{{\beta }_2{I}_c^{\ast }}{1+{\alpha }_2{I}_c^{\ast }}\cdot \frac{E_c^{\ast }}{S_c^{\ast }}=\frac{{\dot{E}}_c}{E_c}-\left(\sigma \nu +2{\mu }_1+{\mu }_2+\eta +ϵ+\xi +\varphi \right)-\left(\frac{\left(1-\sigma \nu \right){\beta }_1{I}_u^{\ast }}{1+{\alpha }_1{I}_u^{\ast }}-\frac{{\beta }_2{I}_c^{\ast }}{1+{\alpha }_2{I}_c^{\ast }}\cdot \frac{E_c^{\ast }}{S_c^{\ast }}\right)\hfill \\ \hfill & \le \hfill & \frac{{\dot{E}}_c}{E_c}-\left(\sigma \nu +2{\mu }_1+{\mu }_2+\eta +ϵ+\xi +\varphi \right).\hfill \end{array}$

Similarly,

$\begin{array}{ccc}\hfill h_3\left(t\right)& =\hfill & B_{33}+\sum _{\genfrac{}{}{0pt}{}{j=1}{j\ne 3}}^4\left|B_{3j}\right|,\hfill \\ \hfill h_3\left(t\right)& =\hfill & \frac{{\dot{S}}_u}{S_u}-\left(\sigma \nu +{\mu }_1+2{\mu }_2+\xi +\varphi \right)-\frac{\left(1-\sigma \nu \right){\beta }_1{I}_u^{\ast }}{1+{\alpha }_1{I}_u^{\ast }}-\frac{{\beta }_2{I}_c^{\ast }}{1+{\alpha }_2{I}_c^{\ast }},\hfill \\ \hfill & \le \hfill & \frac{{\dot{S}}_u}{S_u}-\left(\sigma \nu +{\mu }_1+2{\mu }_2+\xi +\varphi \right).\hfill \end{array}$

and if $\frac{{\beta }_2{I}_c^{\ast }}{1+{\alpha }_2{I}_c^{\ast }}>\frac{\left(1-\sigma \nu \right){\beta }_1{I}_u^{\ast }}{1+{\alpha }_1{I}_u^{\ast }}\cdot \frac{E_u^{\ast }}{S_u^{\ast }}$, then

$\begin{array}{ccc}\hfill h_4\left(t\right)& =\hfill & B_{44}+\sum _{j=1}^3\left|B_{4j}\right|,\hfill \\ \hfill h_4\left(t\right)& =\hfill & \frac{{\dot{E}}_u}{E_u}-\left({\mu }_1+2{\mu }_2+\eta +ϵ+\xi +\varphi \right)-\frac{{\beta }_2{I}_c^{\ast }}{1+{\alpha }_2{I}_c^{\ast }}+\frac{\left(1-\sigma \nu \right){\beta }_1{I}_u^{\ast }}{1+{\alpha }_1{I}_u^{\ast }}\cdot \frac{E_u^{\ast }}{S_u^{\ast }}=\frac{{\dot{E}}_u}{E_u}-\left({\mu }_1+2{\mu }_2+\eta +ϵ+\xi +\varphi \right)-\left(\frac{{\beta }_2{I}_c^{\ast }}{1+{\alpha }_2{I}_c^{\ast }}-\frac{\left(1-\sigma \nu \right){\beta }_1{I}_u^{\ast }}{1+{\alpha }_1{I}_u^{\ast }}\cdot \frac{E_u^{\ast }}{S_u^{\ast }}\right)\hfill \\ \hfill & \hfill & \le \frac{{\dot{E}}_u}{E_u}-\left({\mu }_1+2{\mu }_2+\eta +ϵ+\xi +\varphi \right).\hfill \end{array}$

If $\left(h_1,h_2,h_3,h_4\right)\in R^4$ and we define the Lozinski measure $\mu \left(B\right)$ as $\mu \left(B\right)=h_i,i=\mathrm{1,2,3,4}$ then integration of $\mu \left(B\right)$ by taking limits as t → ∞ the following equations follow:

$\begin{array}{ccc}\hfill \underset{t\to \infty }{\lim }\sup \frac{1}{t}{\int }_0^t{h}_1\left(t\right)dt& \le \hfill & \frac{1}{t}\log \frac{S_c\left(t\right)}{S_c\left(0\right)}-\left(\sigma \nu +2{\mu }_1+{\mu }_2+\eta +ϵ\right)\hfill \\ \hfill & <\hfill & -\left(\sigma \nu +2{\mu }_1+{\mu }_2+\eta +ϵ\right),\hfill \\ \hfill \underset{t\to \infty }{\lim }\sup \frac{1}{t}{\int }_0^t{h}_2\left(t\right)dt& \le \hfill & \frac{1}{t}\log \frac{E_c\left(t\right)}{E_c\left(0\right)}-\left(\sigma \nu +2{\mu }_1+{\mu }_2+\eta +ϵ+\xi +\varphi \right)\hfill \\ \hfill & <\hfill & -\left(\sigma \nu +2{\mu }_1+{\mu }_2+\eta +ϵ+\xi +\varphi \right),\hfill \\ \hfill \underset{t\to \infty }{\lim }\sup \frac{1}{t}{\int }_0^t{h}_3\left(t\right)dt& \le \hfill & \frac{1}{t}\log \frac{S_u\left(t\right)}{S_u\left(0\right)}-\left(\sigma \nu +{\mu }_1+2{\mu }_2+\xi +\varphi \right)\hfill \\ \hfill & <\hfill & -\left(\sigma \nu +{\mu }_1+2{\mu }_2+\xi +\varphi \right),\hfill \\ \hfill \underset{t\to \infty }{\lim }\sup \frac{1}{t}{\int }_0^t{h}_4\left(t\right)dt& \le \hfill & \frac{1}{t}\log \frac{E_u\left(t\right)}{E_u\left(0\right)}-\left({\mu }_1+2{\mu }_2+\eta +ϵ+\xi +\varphi \right)\hfill \\ \hfill & <\hfill & -\left({\mu }_1+2{\mu }_2+\eta +ϵ+\xi +\varphi \right).\hfill \end{array}$

Thus, combining the above four inequalities, we get the following inequality:

$\bar{q}=\underset{t\to \infty }{\lim }\sup \frac{1}{t}{\int }_0^t\mu \left(B\right)dt<0.$

This shows that the subsystem of system (Eq. 1) containing four non-linear differential equations is globally asymptotically stable around the equilibrium $\left(S_c^{\ast },E_c^{\ast },S_u^{\ast },E_u^{\ast }\right)$. The solutions to the rest of the equations of system (Eq. 1) are $I_c\to I_c^{\ast },R_c\to R_c^{\ast },I_u\to I_u^{\ast }$ when t → ∞. Therefore, the endemic equilibrium P∗ is globally asymptotically stable.

3 Numerical simulation

In this section, we refer to the data of Refs. [36–38] to analyze the performance and dynamic behavior of the studied model through numerical simulation, and demonstrate the feasibility of the theoretical results obtained.

3.1 Stability of equilibria

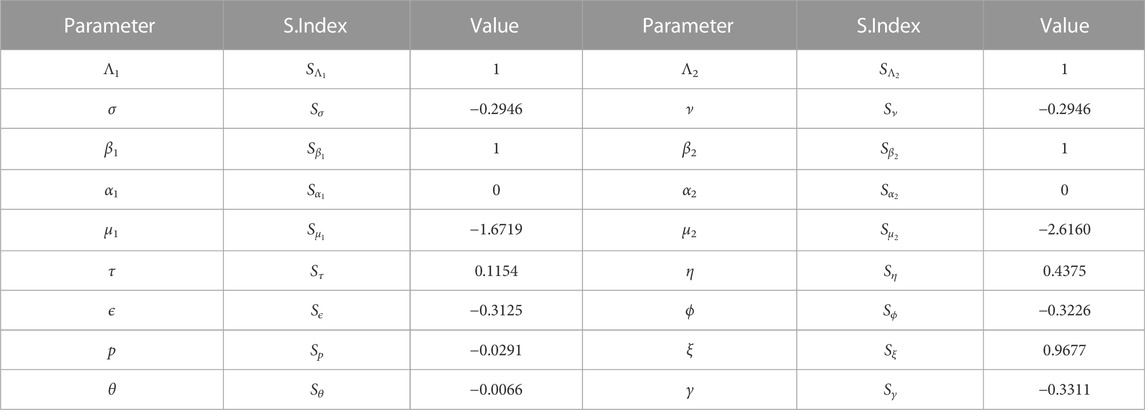
The stability of disease free equilibrium and endemic equilibrium of system (Eq. 1) is verified by numerical simulation. Figure 1 and Figure 2 show the stability simulation diagram of disease free equilibrium and endemic equilibrium. Initially the number of susceptible computers, exposed computers, infected computers, recovery computers, susceptible USB devices, exposed USB devices and infected USB devices are S_c(0) = 50,000, E_c (0) = 20,000, I_c(0) = 10,000, R_c (0) = 10,000, S_u(0) = 5,000, E_u (0) = 3,000, and I_u(0) = 1,000, separately. We take the parameters Λ₁ = 0.75, Λ₂ = 0.1, σ = 0.6, ν = 0.1, β₁ = 0.035, β₂ = 0.035, α₁ = 0.8, α₂ = 0.3, μ₁ = 0.1, μ₂ = 0.1, τ = 0.1, η = 0.45, ϵ = 0.25, ϕ = 0.05, p = 0.003, ξ = 0.005, θ = 0.001, γ = 0.05, at which time, R₀ ≈ 0.0039 < 1. It can be seen from Figure 1 that the number of exposed computers E_c, infected computers I_c, exposed USB devices E_u and infected USB devices I_u gradually approach zero, which shows the correctness of Theorem 2 and Theorem 3. When β₁ = 0.053, μ₁ = 0.01, ξ = 0.05, and other parameters remain unchanged, R₀ ≈ 1.0670 > 1. Compared with Figure 1, the number of exposed computers E_c, infected computers I_c, exposed USB devices E_u and infected USB devices I_u in Figure 2 are not zero and reach a stable value, which is also consistent with Theorems 4 and 5.

FIGURE 1

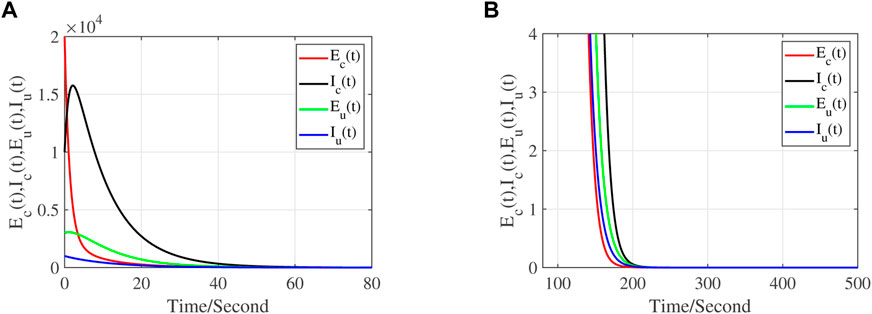
FIGURE 1. Time series plot of system (1) with Λ₁ = 0.75, Λ₂ = 0.1, σ = 0.6, ν = 0.1, β₁ = 0.035, β₂ = 0.035, α₁ = 0.8, α₂ = 0.3, μ₁ = 0.1, μ₂ = 0.1, τ = 0.1, η = 0.45, ϵ = 0.25, ϕ = 0.05, p = 0.003, ξ = 0.005, θ = 0.001, γ = 0.05. (A) the tendency of the worm propagation in a short period, (B) the tendency of the worm propagation in a later period.

FIGURE 2

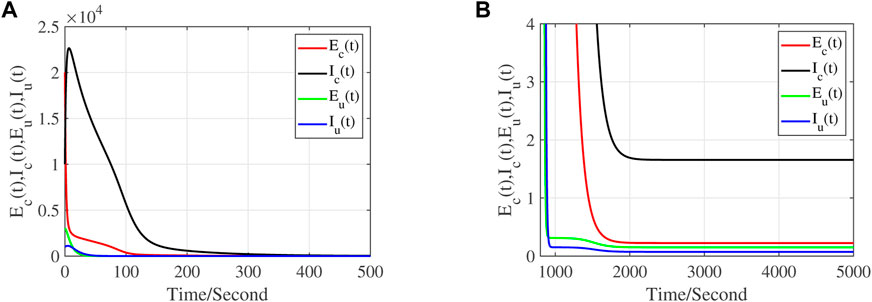
FIGURE 2. Time series plot of system (1) with Λ₁ = 0.75, Λ₂ = 0.1, σ = 0.6, ν = 0.1, β₁ = 0.053, β₂ = 0.035, α₁ = 0.8, α₂ = 0.3, μ₁ = 0.01, μ₂ = 0.1, τ = 0.1, η = 0.45, ϵ = 0.25, ϕ = 0.05, p = 0.003, ξ = 0.05, θ = 0.001, γ = 0.05. (A) the tendency of the worm propagation in a short period, (B) the tendency of the worm propagation in a later period.

3.2 Performance comparison of the SEIRSEI model with the SIRSI model

To evaluate the performance of the SEIRSEI model, numerical methods are used to compare it with the SIRSI model [1]. We simulate SEIRSEI and SIRSI models by Matlab. Both models share the same parameters as in Section 3.1. Figure 3 shows the number of infected computers and infected USB devices for both models. The results show that, compared with SIRSI model, the propagation speed of worms and the number of infected computers and USB devices in SEIRSEI model are significantly decreased. This implies that the SEIRSEI model takes much smaller time to combat the worm than the SIRSI model. Obviously, the results shown in Figure 3 verify that the proposed model is more effective in controlling computer worms attack than the previous model.

FIGURE 3

FIGURE 3. Performance comparison of the SEIRSEI model with the SIRSI model. (A) graph of infectious number of computers, (B) graph of infectious number of USB devices.

3.3 Sensitivity analysis

Sensitivity analysis is used to determine which parameters have a significant effect on decreasing the spread of disease. Forward sensitivity analysis is considered an important component of epidemic modeling, although it is tedious to calculate for complex biological models. The ecologist and epidemiologist paid a lot of attention to the sensitivity study of R₀.

Definition. The normalized forward sensitivity index of R₀ that depends differentiability on a parameter ω is defined as

$S_{\omega }=\frac{\omega }{R_0}\frac{\partial R_0}{\partial \omega }(20)$

The following three methods are normally used to calculate the sensitivity indices, (i) by direct differentiation, (ii) by a Latin hypercube sampling method, (iii) by linearizing system (Eq. 1), and then solving the obtain set of linear algebraic equations. We will apply the direct differentiation method as it gives analytical expressions for the indices. The indices not only shows us the influence of various aspects associated with the spreading of infectious disease but also gives us important information regarding the comparative change between R₀ and different parameters. Consequently, it helps in developing the control strategies.

Table 1 demonstrates that the parameters Λ₁, Λ₂, β₁, β₂, τ, η and ξ have a positive influence on the reproduction number R₀, which describe that the growth or decay of these parameters say by 10% will increase or decrease the reproduction number by 10%, 10%, 10%, 10%, 1.1%, 4.3% and 9.6% respectively. But on the other hand, the index for parameters σ, ν, μ₁, μ₂, ϵ, ϕ, p, θ and γ illustrates that increasing their values by 10% will decrease the values of reproduction number R₀ by 2.9%, 2.9%, 16.7%, 26.1%, 3.1%, 3.2%, 0.29%, 0.06%, and 3.3% respectively. α₁ and α₂ have no impact on the reproduction number R₀. Figures 4A–H are plotted to demonstrate the variations in the basic reproductive number R₀ with respect to the different model parameters.

TABLE 1

TABLE 1. Sensitivity indices of the basic reproduction number R₀ against mentioned parameters.

FIGURE 4

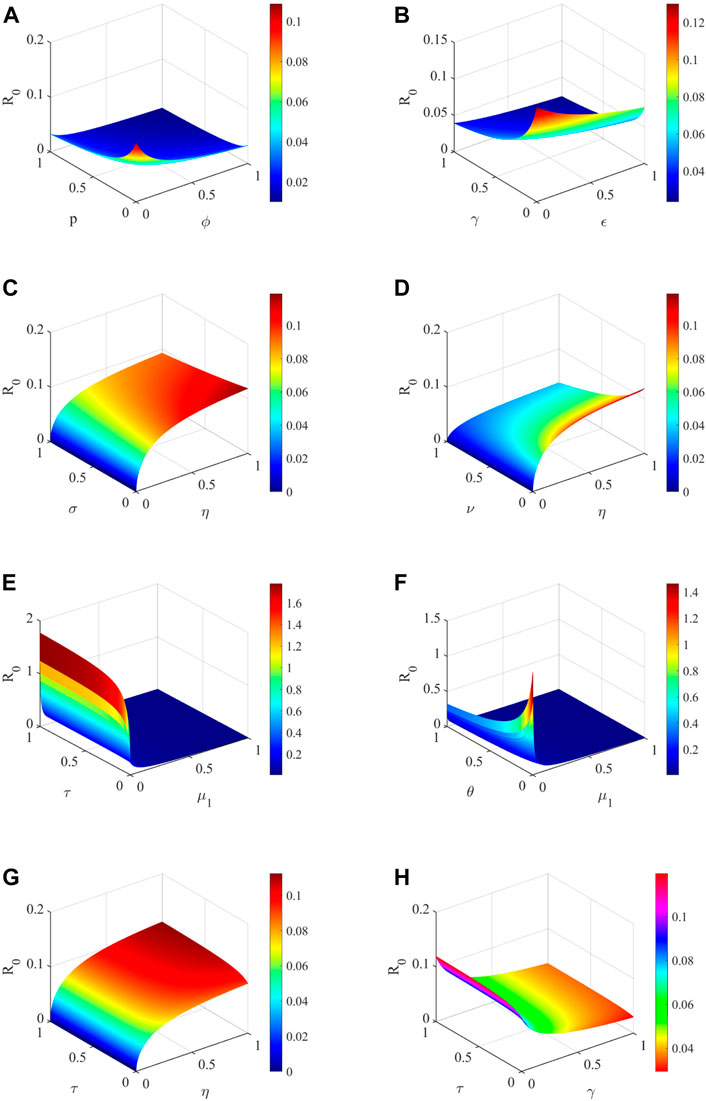
FIGURE 4. Sensitivity analysis of different parameters. (A) R₀ versus sensitive parameters p and ϕ, (B) R₀ versus sensitive parameters γ and ϵ, (C) R₀ versus sensitive parameters σ and η, (D) R₀ versus sensitive parameters ν and η, (E) R₀ versus sensitive parameters τ and μ₁, (F) R₀ versus sensitive parameters θ and μ₁, (G) R₀ versus sensitive parameters τ and η, (H) R₀ versus sensitive parameters τ and γ.

4 Optimal control strategy formulation

In order to explore how to effectively control the propagation of computer worms, system (Eq. 1) is improved in this section. Three control variables $u_i\left(t\right)\left(i=\mathrm{1,2,3}\right)$ are introduced into system (Eq. 1), which denote the effectiveness of the corresponding control strategy to inhibit worm propagation. $u_1\left(t\right)\left(0\le u_1\left(t\right)\le 1\right)$ represents the effectiveness of improving the installation coverage rate of anti-virus software, $u_2\left(t\right)\left(0\le u_2\left(t\right)\le 1\right)$ and $u_3\left(t\right)\left(0\le u_3\left(t\right)\le 1\right)$ represent the effectiveness of disinfecting computers and USB devices, respectively. Establish the optimal control system:

$\begin{array}{ccc}\hfill \frac{d{S}_c}{dt}& =\hfill & {\mathrm{\Lambda }}_1-\frac{\left(1-u_1\right){\beta }_1{S}_c{I}_u}{1+{\alpha }_1{I}_u}-\left(u_1+{\mu }_1\right)S_c+\tau R_c,\hfill \\ \hfill \frac{d{E}_c}{dt}& =\hfill & \frac{\left(1-u_1\right){\beta }_1{S}_c{I}_u}{1+{\alpha }_1{I}_u}-\left(\eta +u_2+{\mu }_1\right)E_c,\hfill \\ \hfill \frac{d{I}_c}{dt}& =\hfill & \eta E_c-\left(u_2+{\mu }_1+\theta \right)I_c,\hfill \\ \hfill \frac{d{R}_c}{dt}& =\hfill & u_1{S}_c+u_2{E}_c+u_2{I}_c-\left(\tau +{\mu }_1\right)R_c,\hfill \\ \hfill \frac{d{S}_u}{dt}& =\hfill & {\mathrm{\Lambda }}_2-\frac{{\beta }_2{S}_u{I}_c}{1+{\alpha }_2{I}_c}-{\mu }_2{S}_u+u_3{E}_u+u_3{I}_u,\hfill \\ \hfill \frac{d{E}_u}{dt}& =\hfill & \frac{{\beta }_2{S}_u{I}_c}{1+{\alpha }_2{I}_c}-\left(\xi +u_3+{\mu }_2\right)E_u,\hfill \\ \hfill \frac{d{I}_u}{dt}& =\hfill & \xi E_u-\left(u_3+{\mu }_2\right)I_u.\hfill \end{array}(21)$

Defining the objective function

$J\left(u_1,u_2,u_3\right)={\int }_0^T\left(A_1{E}_c+A_2{I}_c+A_3{E}_u+A_4{I}_u+\frac{1}{2}\left(B_1{u}_1^2+B_2{u}_2^2+B_3{u}_3^2\right)\right)\mathrm{d}t,(22)$

where A₁, A₂, A₃ and A₄ are positive weight constants of E_c, I_c, E_u and I_u respectively, and T is the final time to implement the control strategies.

The control set is defined as $U=\left\{\left(u_1\left(t\right),u_2\left(t\right),u_3\left(t\right)\right)\left|u_i\left(t\right)\left(i=\mathrm{1,2,3}\right)\right.\right\}$, which is a Lebesgue measurable control quantity satisfying $u_i\left(t\right)\in \left[\mathrm{0,1}\right]$ and $t\in \left[0,T\right]$. The purpose of this paper is to find the optimal control $\left(u_1^{\ast },u_2^{\ast },u_3^{\ast }\right)$ so that

$J\left(u_1^{\ast }\left(t\right),u_2^{\ast }\left(t\right),u_3^{\ast }\left(t\right)\right)=\min \left\{J\left(u_1\left(t\right),u_2\left(t\right),u_3\left(t\right)\right)\left|u_1\left(t\right),u_2\left(t\right),u_3\left(t\right)\in U\right.\right\}.$

Based on the boundedness of the right end of system (Eq. 21) and the convexity of the integrand of (Eq. 22), the existence of the optimal control $\left(u_1^{\ast },u_2^{\ast },u_3^{\ast }\right)$ can be obtained [39, 40].

To find the optimal solution of the optimal control problem (Eqs 21, 22), the Hamilton function is defined as follows

$\begin{array}{ccc}\hfill H& =\hfill & A_1{E}_c+A_2{I}_c+A_3{E}_u+A_4{I}_u+\frac{1}{2}\left(B_1{u}_1^2+B_2{u}_2^2+B_3{u}_3^2\right)\hfill \\ \hfill & \hfill & +{\lambda }_{S_c}\frac{d{S}_c}{dt}+{\lambda }_{E_c}\frac{d{E}_c}{dt}+{\lambda }_{I_c}\frac{d{I}_c}{dt}+{\lambda }_{R_c}\frac{d{R}_c}{dt}+{\lambda }_{S_u}\frac{d{S}_u}{dt}+{\lambda }_{E_u}\frac{d{E}_u}{dt}+{\lambda }_{I_u}\frac{d{I}_u}{dt},\hfill \end{array}(23)$

where ${\lambda }_{S_c},{\lambda }_{E_c},{\lambda }_{I_c},{\lambda }_{R_c},{\lambda }_{S_u},{\lambda }_{E_u},{\lambda }_{I_u}$ are the adjoint variables. According to Pontryagin’s maximum principle [41], the following theorem is obtained.

Theorem 6 Let $u_1^{\ast }\left(t\right),u_2^{\ast }\left(t\right),u_3^{\ast }\left(t\right)$ be optimal controls and $S_c^{\ast },E_c^{\ast },I_c^{\ast },R_c^{\ast },S_u^{\ast },E_u^{\ast },I_u^{\ast }$ be optimal state solutions of the optimal control problem (Eqs 21, 22), and then there exists adjoint variables ${\lambda }_{S_c},{\lambda }_{E_c},{\lambda }_{I_c},{\lambda }_{R_c},{\lambda }_{S_u}$, ${\lambda }_{E_u},{\lambda }_{I_u}$, satisfying,

$\frac{\mathrm{d}{\lambda }_i}{\mathrm{d}t}=-\frac{\partial H}{\partial i},(24)$

where i = S_c, E_c, I_c, R_c, S_u, E_u, I_u. In addition, the corresponding optimal control variables $u_1^{\ast }\left(t\right),u_2^{\ast }\left(t\right),u_3^{\ast }\left(t\right)$ are

$\begin{array}{ccc}\hfill u_1^{\ast }& =\hfill & \max \left\{0,\min \left\{\frac{\frac{{\beta }_1{S}_c{I}_u}{1+{\alpha }_1{I}_u}\left({\lambda }_{E_c}-{\lambda }_{S_c}\right)-S_c\left({\lambda }_{R_c}-{\lambda }_{S_c}\right)}{B_1},1\right\}\right\},\hfill \\ \hfill u_2^{\ast }& =\hfill & \max \left\{0,\min \left\{\frac{-E_c\left({\lambda }_{R_c}-{\lambda }_{E_c}\right)-I_c\left({\lambda }_{R_c}-{\lambda }_{I_c}\right)}{B_2},1\right\}\right\},\hfill \\ \hfill u_3^{\ast }& =\hfill & \max \left\{0,\min \left\{\frac{E_u\left({\lambda }_{E_u}-{\lambda }_{S_u}\right)-I_u\left({\lambda }_{I_u}-{\lambda }_{S_u}\right)}{B_3},1\right\}\right\}.\hfill \end{array}(25)$

Proof: To prove the theorem, the differential of (Eq. 23), namely the Hamiltonian function H, with respect to the state variables S_c, E_c, I_c, R_c, S_u, E_u, I_u are obtained, and the corresponding adjoint system is as follows:

$\begin{array}{ccc}\hfill \frac{\mathrm{d}{\lambda }_{S_c}}{\mathrm{d}t}& =\hfill & -\frac{\partial H}{\partial S_c}=-\frac{\left(1-u_1\right){\beta }_1{I}_u}{1+{\alpha }_1{I}_u}\left({\lambda }_{E_c}-{\lambda }_{S_c}\right)-u_1\left({\lambda }_{R_c}-{\lambda }_{S_c}\right)+{\mu }_1{\lambda }_{S_c},\hfill \\ \hfill \frac{\mathrm{d}{\lambda }_{E_c}}{\mathrm{d}t}& =\hfill & -\frac{\partial H}{\partial E_c}=-A_1-\eta \left({\lambda }_{I_c}-{\lambda }_{E_c}\right)-u_2\left({\lambda }_{R_c}-{\lambda }_{E_c}\right)+{\mu }_1{\lambda }_{E_c},\hfill \\ \hfill \frac{\mathrm{d}{\lambda }_{I_c}}{\mathrm{d}t}& =\hfill & -\frac{\partial H}{\partial I_c}=-A_2-\frac{{\beta }_2{S}_u}{{\left(1+{\alpha }_2{I}_c\right)}^2}\left({\lambda }_{E_u}-{\lambda }_{S_u}\right)-u_2\left({\lambda }_{R_c}-{\lambda }_{I_c}\right)+\left({\mu }_1+\theta \right){\lambda }_{I_c},\hfill \\ \hfill \frac{\mathrm{d}{\lambda }_{R_c}}{\mathrm{d}t}& =\hfill & -\frac{\partial H}{\partial R_c}=\tau \left({\lambda }_{R_c}-{\lambda }_{S_c}\right)+{\mu }_1{\lambda }_{R_c},\hfill \\ \hfill \frac{\mathrm{d}{\lambda }_{S_u}}{\mathrm{d}t}& =\hfill & -\frac{\partial H}{\partial S_u}=-\frac{{\beta }_2{I}_c}{1+{\alpha }_2{I}_c}\left({\lambda }_{E_u}-{\lambda }_{S_u}\right)+{\mu }_2{\lambda }_{S_u},\hfill \\ \hfill \frac{\mathrm{d}{\lambda }_{E_u}}{\mathrm{d}t}& =\hfill & -\frac{\partial H}{\partial E_u}=-A_3+u_3\left({\lambda }_{E_u}-{\lambda }_{S_u}\right)-\xi \left({\lambda }_{I_u}-{\lambda }_{E_u}\right)+{\mu }_2{\lambda }_{E_u},\hfill \\ \hfill \frac{\mathrm{d}{\lambda }_{I_u}}{\mathrm{d}t}& =\hfill & -\frac{\partial H}{\partial I_u}=-A_4-\frac{\left(1-u_1\right){\beta }_1{S}_c}{{\left(1+{\alpha }_1{I}_u\right)}^2}\left({\lambda }_{E_c}-{\lambda }_{S_c}\right)+u_3\left({\lambda }_{I_u}-{\lambda }_{E_u}\right)+{\mu }_2{\lambda }_{I_u},\hfill \end{array}(26)$

and with transversality conditions ${\lambda }_{S_c}\left(T\right)=0$, ${\lambda }_{E_c}\left(T\right)=0$, ${\lambda }_{I_c}\left(T\right)=0$, ${\lambda }_{R_c}\left(T\right)=0$, ${\lambda }_{S_u}\left(T\right)=0$, ${\lambda }_{E_u}\left(T\right)=0$, ${\lambda }_{I_u}\left(T\right)=0$. Also, the optimal controls $u_1^{\ast },u_2^{\ast }$ and $u_3^{\ast }$ satisfy $\frac{\partial H}{\partial u_i^{\ast }}=0$, i = 1, 2, 3. Therefore, the optimal controls are characterized by

$\begin{array}{c}{u}_1^{\ast }=\max \left\{0,\min \left\{\frac{\frac{{\beta }_1{S}_c{I}_u}{1+{\alpha }_1{I}_u}\left({\lambda }_{E_c}-{\lambda }_{S_c}\right)-S_c\left({\lambda }_{R_c}-{\lambda }_{S_c}\right)}{B_1},1\right\}\right\},\hfill \\ u_2^{\ast }=\max \left\{0,\min \left\{\frac{-E_c\left({\lambda }_{R_c}-{\lambda }_{E_c}\right)-I_c\left({\lambda }_{R_c}-{\lambda }_{I_c}\right)}{B_2},1\right\}\right\},\hfill \\ u_3^{\ast }=\max \left\{0,\min \left\{\frac{E_u\left({\lambda }_{E_u}-{\lambda }_{S_u}\right)-I_u\left({\lambda }_{I_u}-{\lambda }_{S_u}\right)}{B_3},1\right\}\right\}.\hfill \end{array}$

For sufficiently small final time T, the uniqueness of the optimal control of the system has been achieved owing to the boundedness of the state variables and adjoint variables together with the Lipschitz property of systems (Eq. 21) and (Eq. 26).

In order to show the rationality and effectiveness of the control strategy mentioned in Section 4, numerical simulation is carried out. Figure 5 shows a substantial decrease in the population of exposed computers, infected computers, exposed USB devices and infected USB devices respectively relative to the case of no control, when the combined strategy is implemented, including the installation coverage rate of anti-virus software and the disinfection of computer and USB device. Parameter Λ₁ = 0.75, Λ₂ = 0.1, σ = 0.6, ν = 0.1, β₁ = 0.035, β₂ = 0.035, α₁ = 0.8, α₂ = 0.3, μ₁ = 0.1, μ₂ = 0.1, τ = 0.1, η = 0.45, ϵ = 0.25, ϕ = 0.05, p = 0.003, ξ = 0.005, θ = 0.001, γ = 0.05. We draw the conclusion that the spread of worm virus can be effectively controlled by strengthening users’ computer security education, improving their understanding of anti-virus software, and calling on users to disinfect computers and USB devices regularly.

FIGURE 5

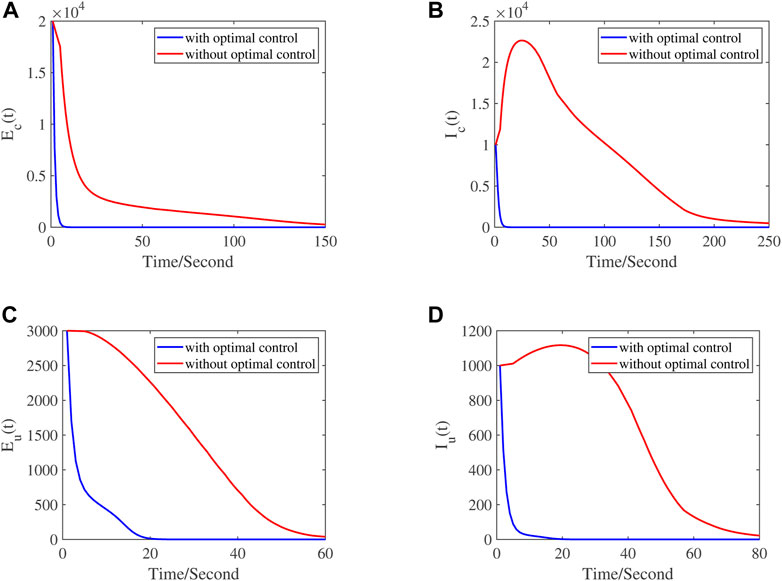
FIGURE 5. Plots of different classes showing the difference between with control and without control, respectively: (A) exposed computers, (B) infected computers, (C) exposed USB devices, (D) infected USB devices.

5 Conclusion and discussion

This paper mainly considers the dynamic behavior of computer worms in the process of using USB to transmit data. The novel ideas of our paper are as follows: (a) the exposed compartments of computer and USB are introduced because of the latent nature of worms; (b) infected computers will gain temporary immunity after recovery due to anti-virus software installed, but after a period of time will join again susceptible class because of the variability of computer worms; (c) the elimination rate of computers is not only related to natural mortality, but also to worm attacks; (d) the saturation incidence is used thanks to the inhibition effect of susceptible equipments and the crowding effect of infectious equipments.

Firstly, through theoretical analysis, the existence of disease free equilibrium and endemic equilibrium is studied, and the sufficient conditions for their asymptotic stability are given. The global stability of disease free equilibrium is carried out using the Castillo-Chavez method, whereas, the global stability of the unique endemic equilibrium is also investigated via using geometrical approach. It can be seen that when R₀ < 1, worm transmission is effectively controlled and verified by numerical simulation. Therefore, one effective means to extinguish worm is to keep R₀ below 1. Furthermore, the sensitivity analysis is complemented by numerical simulation to explore the influence of some parameter changes on the basic reproduction number R₀. It is seen that Λ₁, Λ₂, β₁, β₂, τ, η and ξ are positively correlated with R₀, while σ, ν, μ₁, μ₂, ϵ, ϕ, p, θ and γ are negatively correlated with R₀. Finally, we establish a optimal control system by taking the installation coverage rate of anti-virus software and the disinfection of computer and USB device as control variables. The numerical simulation results show that compared with the situation without control measures, the total number of computers and USB devices in the exposed state and infected state is significantly reduced after control measures are taken, that is to say, adding control could effectively reduce the spread of computer worms.

In this paper, the mathematical model is used to describe the propagation process of computer worms, which is helpful to analyze the propagation characteristics of worms, and then propose more effective defense measures and control strategies. In addition, the research of this subject is beneficial to predict the propagation trend of worms, test the effect of various defensive measures, and provide theoretical guidance for the defense and control of computer worms.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

RW, YX, and KX conceived the study. RW developed the mathematical model, computations, simulation coding, manuscript writing and data interpretation. YX contributed to supervision and validation. KX performed literature survey and computations. All authors contributed to the article and approved the submitted version.

Funding

This work was supported by the National Natural Science Foundation of China (grant number 11971278); the Shanxi Scholarship Council of China (grant number 2022-150) and Natural Science Foundation of Shanxi Province (grant number 202203021211086).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Kim KS, Ibrahim MM, Jung IH, Kim S. Mathematical analysis of the effectiveness of control strategies to prevent the autorun virus transmission propagation. Appl Maths Comput (2020) 371:124955. doi:10.1016/j.amc.2019.124955

CrossRef Full Text | Google Scholar

2. Deng Y, Pei Y, Li C. Parameter estimation of a susceptible–infected–recovered–dead computer worm model. SIMULATION (2022) 98:209–20. doi:10.1177/00375497211009576

CrossRef Full Text | Google Scholar

3. Piqueira JRC, Cabrera MA, Batistela CM. Malware propagation in clustered computer networks. Physica A: Stat Mech its Appl (2021) 573:125958. doi:10.1016/j.physa.2021.125958

CrossRef Full Text | Google Scholar

4. Xiao X, Fu P, Dou C, Li Q, Hu G, Xia S. Design and analysis of seiqr worm propagation model in mobile internet. Commun nonlinear Sci Numer simulation (2017) 43:341–50. doi:10.1016/j.cnsns.2016.07.012

CrossRef Full Text | Google Scholar

5. Zheng W, Wang T, Liu C, Yan Q, Zhan S, Li G, et al. Liver transcriptomics reveals microrna features of the host response in a mouse model of dengue virus infection. Comput Biol Med (2022) 106057:106057. doi:10.1016/j.compbiomed.2022.106057

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Carrillo M, Góngora PA, Rosenblueth DA. An overview of existing modeling tools making use of model checking in the analysis of biochemical networks. Front Plant Sci (2012) 3:155. doi:10.3389/fpls.2012.00155

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Yang G, Gómez Tejeda Zañudo J, Albert R. Target control in logical models using the domain of influence of nodes. Front Physiol (2018) 454:454. doi:10.3389/fphys.2018.00454

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Ren J, Xu Y. A compartmental model for computer virus propagation with kill signals. Physica A: Stat Mech its Appl (2017) 486:446–54. doi:10.1016/j.physa.2017.05.038

CrossRef Full Text | Google Scholar

9. Razzaq OA, Khan NA, Faizan M, Ara A, Ullah S. Behavioral response of population on transmissibility and saturation incidence of deadly pandemic through fractional order dynamical system. Results Phys (2021) 26:104438. doi:10.1016/j.rinp.2021.104438

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Paul AK, Kuddus MA. Mathematical analysis of a Covid-19 model with double dose vaccination in Bangladesh. Results Phys (2022) 35:105392. doi:10.1016/j.rinp.2022.105392

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Tiwari V, Deyal N, Bisht NS. Mathematical modeling based study and prediction of Covid-19 epidemic dissemination under the impact of lockdown in India. Front Phys (2020) 8:586899. doi:10.3389/fphy.2020.586899

CrossRef Full Text | Google Scholar

12. Toutonji O, Yoo S-M. Passive benign worm propagation modeling with dynamic quarantine defense. KSII Trans Internet Inf Syst (Tiis) (2009) 3:96–107. doi:10.3837/tiis.2009.01.005

CrossRef Full Text | Google Scholar

13. Wang F, Zhang Y, Wang C, Ma J, Moon S. Stability analysis of a seiqv epidemic model for rapid spreading worms. Comput Security (2010) 29:410–8. doi:10.1016/j.cose.2009.10.002

CrossRef Full Text | Google Scholar

14. Yao Y, Xie X-w., Guo H, Yu G, Gao F-X, Tong X-j. Hopf bifurcation in an internet worm propagation model with time delay in quarantine. Math Comput Model (2013) 57:2635–46. doi:10.1016/j.mcm.2011.06.044

CrossRef Full Text | Google Scholar

15. Zhou P, Gu X, Nepal S, Zhou J. Modeling social worm propagation for advanced persistent threats. Comput Security (2021) 108:102321. doi:10.1016/j.cose.2021.102321

CrossRef Full Text | Google Scholar

16. Yang L-X, Yang X. The impact of nonlinear infection rate on the spread of computer virus. Nonlinear Dyn (2015) 82:85–95. doi:10.1007/s11071-015-2140-z

CrossRef Full Text | Google Scholar

17. Zhang Z, Zou J, Upadhyay RK, ur Rahman G. An epidemic model with multiple delays for the propagation of worms in wireless sensor networks. Results Phys (2020) 19:103424. doi:10.1016/j.rinp.2020.103424

CrossRef Full Text | Google Scholar

18. Song L-P, Jin Z, Sun G-Q, Zhang J, Han X. Influence of removable devices on computer worms: Dynamic analysis and control strategies. Comput Maths Appl (2011) 61:1823–9. doi:10.1016/j.camwa.2011.02.010

CrossRef Full Text | Google Scholar

19. Zhu Q, Yang X, Ren J. Modeling and analysis of the spread of computer virus. Commun Nonlinear Sci Numer Simulation (2012) 17:5117–24. doi:10.1016/j.cnsns.2012.05.030

CrossRef Full Text | Google Scholar

20. Ma J, Chen Z, Wu W, Zheng R, Liu J. Influences of removable devices on the anti-threat model: Dynamic analysis and control strategies. Information (2015) 6:536–49. doi:10.3390/info6030536

CrossRef Full Text | Google Scholar

21. Zhu Q, Loke SW, Zhang Y. State-based switching for optimal control of computer virus propagation with external device blocking. Security and Communication Networks (2018). doi:10.1155/2018/4982523

CrossRef Full Text | Google Scholar

22. Upadhyay RK, Kumari S. Detecting malicious chaotic signals in wireless sensor network. Physica A: Stat Mech its Appl (2018) 492:1129–52. doi:10.1016/j.physa.2017.11.043

CrossRef Full Text | Google Scholar

23. Gao Q, Zhuang J. Stability analysis and control strategies for worm attack in mobile networks via a veiqs propagation model. Appl Maths Comput (2020) 368:124584. doi:10.1016/j.amc.2019.124584

CrossRef Full Text | Google Scholar

24. Hu R, Gao Q, Wang B. Dynamics and control of worm epidemic based on mobile networks by seiqr-type model with saturated incidence rate. Discrete Dyn Nat Soc (2021) 2021:1–22. doi:10.1155/2021/6637263

CrossRef Full Text | Google Scholar

25. Madhusudanan V, Srinivas M, Nwokoye CH, Murthy BN, Sridhar S. Hopf-bifurcation analysis of delayed computer virus model with holling type iii incidence function and treatment. Scientific Afr (2022) 15:e01125. doi:10.1016/j.sciaf.2022.e01125

CrossRef Full Text | Google Scholar

26. Mishra BK, Pandey SK. Dynamic model of worm propagation in computer network. Appl Math Model (2014) 38:2173–9. doi:10.1016/j.apm.2013.10.046

CrossRef Full Text | Google Scholar

27. Mishra BK, Pandey SK. Dynamic model of worms with vertical transmission in computer network. Appl Math Comput (2011) 217:8438–46. doi:10.1016/j.amc.2011.03.041

CrossRef Full Text | Google Scholar

28. Guillén JH, Del Rey AM, Encinas LH. Study of the stability of a seirs model for computer worm propagation. Physica A: Stat Mech its Appl (2017) 479:411–21. doi:10.1016/j.physa.2017.03.023

CrossRef Full Text | Google Scholar

29. Upadhyay RK, Singh P. Modeling and control of computer virus attack on a targeted network. Physica A: Stat Mech its Appl (2020) 538:122617. doi:10.1016/j.physa.2019.122617

CrossRef Full Text | Google Scholar

30. Van den Driessche P, Watmough J. Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math biosciences (2002) 180:29–48. doi:10.1016/S0025-5564(02)00108-6

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Castillo-Chavez C, Blower S, Van den Driessche P, Kirschner D, Yakubu A-A. Mathematical approaches for emerging and reemerging infectious diseases: Models, methods, and theory, 126. Springer Science & Business Media (2002).

Google Scholar

32. Khan A, Zarin R, Inc M, Zaman G, Almohsen B. Stability analysis of leishmania epidemic model with harmonic mean type incidence rate. The Eur Phys J Plus (2020) 135:528–0. doi:10.1140/epjp/s13360-020-00535-0

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Li MY, Muldowney JS. A geometric approach to global-stability problems. SIAM J Math Anal (1996) 27:1070–83. doi:10.1137/S0036141094266449

CrossRef Full Text | Google Scholar

34. Khan K, Zarin R, Khan A, Yusuf A, Al-Shomrani M, Ullah A. Stability analysis of five-grade leishmania epidemic model with harmonic mean-type incidence rate. Adv Difference Equations (2021) 2021:86–27. doi:10.1186/s13662-021-03249-4

CrossRef Full Text | Google Scholar

35. Khan A, Zarin R, Ahmed I, Yusuf A, Humphries UW. Numerical and theoretical analysis of rabies model under the harmonic mean type incidence rate. Results Phys (2021) 29:104652. doi:10.1016/j.rinp.2021.104652

CrossRef Full Text | Google Scholar

36. Yang F, Zhang Z, Zeb A. Hopf bifurcation of a veiqs worm propagation model in mobile networks with two delays. Alexandria Eng J (2021) 60:5105–14. doi:10.1016/j.aej.2021.03.055

CrossRef Full Text | Google Scholar

37. Haldar K, Mishra BK. A mathematical model for a distributed attack on targeted resources in a computer network. Commun Nonlinear Sci Numer Simulation (2014) 19:3149–60. doi:10.1016/j.cnsns.2014.01.028

CrossRef Full Text | Google Scholar

38. Khanh NH, Huy NB. Stability analysis of a computer virus propagation model with antidote in vulnerable system. Acta Mathematica Scientia (2016) 36:49–61. doi:10.1016/S0252-9602(15)30077-1

CrossRef Full Text | Google Scholar

39. Alexander ME, Moghadas SM, Röst G, Wu J. A delay differential model for pandemic influenza with antiviral treatment. Bull Math Biol (2008) 70:382–97. doi:10.1007/s11538-007-9257-2

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Lukes DL. Differential equations: Classical to controlled (1982).

Google Scholar

41. Pontryagin LS. Mathematical theory of optimal processes. New York, NY: CRC Press (1987).

Google Scholar