An unstable 0D model of ionization oscillations in Hall thruster plasmas

The breathing mode is an instability typical of Hall thrusters, which is characterized by oscillations of the discharge current with amplitude of the order of its mean value and frequency in the 5–30 kHz range. The strong link between this instability and the ionization processes is generally recognized. If, on one hand, 1D simulations have shown to be able to reproduce the breathing mode, on the other hand 0D models fell short in recovering self sustained oscillations, making it hard to identify the core physical mechanism governing their formation. In this work an original 0D model is presented and characterized by means of linear stability analysis and direct numerical integration. The electric field is allowed to vary in response to variations of the neutral density, acting on the ionization rate via the electron temperature and the ion dynamics. It is shown that the model is able to reproduce self-sustained oscillations with the typical characteristics of the breathing mode, even when fluctuations of the electron temperature are neglected. The stability of the model is strictly determined by the rigidity with which variations of neutral density reflect into variations of electron mobility.

1 Introduction

Hall thrusters are plasma-based electric propulsion devices for space applications featuring an E × B configuration that allows for the efficient ionization and acceleration of the gaseous propellant. For additional details on the design and operating principle of Hall thrusters refer to Ref. [1]. The strong coupling between the ionization and acceleration processes in these devices is associated with high amplitude, low frequency (5–30 kHz) oscillations of the discharge current and of the plasma properties, commonly referred to as breathing mode. Breathing mode is found ubiquitously in Hall thrusters, at least for some operating conditions, and appears to be a general feature of E × B discharges. Nevertheless, the specific characteristics of the oscillations vary greatly with the thruster design and operating condition [2, 3]. The presence of this oscillatory mode has detrimental effects on the thruster performance and can cause coupling issues with the driving electronics. Therefore, several experimental and theoretical efforts have been dedicated to the characterization of this oscillatory mode and to the determination of the feedback mechanism leading to its onset.

From the experimental perspective, intrusive and non-intrusive diagnostic systems have been employed to study the plasma dynamics in the thruster during oscillations [4–6]. The results show that breathing mode manifests as coherent longitudinal waves in the plasma, propagating in the channel and near plume without significant frequency dispersion. From the modeling point of view, breathing mode has been investigated with models of varying degree of complexity. Zero-dimensional formulations, originating from the work by Fife et al. [7], have demonstrated a similarity of breathing oscillations with predator-prey type instabilities, where the neutral population plays the role of prey while the electrons predate on them through ionization events. More complex formulations of the same system were proposed, including additional effects such as the neutral inflow density, the plasma-wall interaction, and the evolution of the electron temperature [8]. Nevertheless, the proposed 0D models could not reproduce self-sustained oscillations [9]. On the other hand, higher order formulations, such as multi-zone [10, 11] and 1D models (see, for instance [9, 12]), have demonstrated to be able to reproduce sustained oscillations with the typical features of the breathing mode. However, there is still no consensus about the stability criteria for its onset and growth.

In [13] a novel mechanism for the generation of breathing mode is identified by means of a three-species (neutrals, ions, electrons) 1D model of the plasma discharge in Hall thrusters. The model employs well established simulation techniques and is calibrated against a reference experimental configuration, as detailed in [12]. The analysis proposed in [13] focuses on both the linearized dynamics around the steady solution and on the non-linear behavior of the model. It is shown that the instability can be observed even if the electron mobility is linearized with respect to the neutral density, which implies fluctuations of the electric field in phase opposition with the oscillations of the neutral density. Two possible feedback mechanisms are proposed that may concur to the onset of breathing mode. The first one (E1), often considered in the literature, relies on the feedback produced by the oscillations of the electron temperature induced by the electric field, leading to variations in the ionization rate that sustain the instability. A second mechanism (E2) is also proposed, based on the observation that the oscillations of the electric field establish a positive feedback on the ionization rate also via the subsequent ion dynamics, through variations of the plasma density and regardless of the electron temperature. Indeed, the results of [13] show that fluctuations are observed also when the electron temperature is assumed to be stationary, indicating that the electron energy dynamics can influence the instability but is not necessary for its onset, at least in the investigated case.

In this work, a 0D model is proposed to further support the identification of the original feedback mechanism E2 highlighted above. The proposed 0D formulation is based on the 1D model and on the related results detailed in [13]. Unlike the one-dimensional case, in the 0D model the spatial gradients of the plasma properties are not resolved, and the focus is on the global behavior of the plasma in a control volume delimited by the anode and channel exit sections, and the lateral walls. We show here that it is indeed possible to formulate such a reduced-order model and that it can reproduce the main features of the breathing instability when the sole ingredients required for the identified feedback mechanism are included.

2 Methodology

The proposed 0D model is built on the basis of the 1D model detailed in [13]. The magnetic field is assumed to have a dominant radial component, which is representative of the magnetic field topology in conventional Hall thrusters. In order to formulate the algebraic form of the related 0D model, an integral form of the 1D equations reported in [13] is derived here. By integrating over a volume of length L enclosed between the anode (A) and channel exit (C), we obtain:

${\int }_V\frac{\partial n_n}{\partial t}dV+\frac{u_n}{L}\left(n_{nC}-n_{nA}\right)={-\int }_V{n}_{n}n{k}_{I}dV{+\int }_V{\dot{n}}_{w}dV,(1)$

${\int }_V\frac{\partial n}{\partial t}dV+\frac{\left(n_C{u}_{iC}-n_A{u}_{iA}\right)}{L}={\int }_V{n}_{n}n{k}_{I}dV{-\int }_V{\dot{n}}_{w}dV,(2)$

${\int }_V\frac{\partial n{u}_i}{\partial t}dV+\frac{\left(n_C{u}_{iC}^2-n_A{u}_{iA}^2\right)}{L}={\frac{e}{m_i}\int }_{V}nEdV{-\int }_V{u}_i{\dot{n}}_{w}dV,(3)$

$\begin{array}{c}\hfill {\int }_V\frac{\partial \frac{3}{2}n{k}_B{T}_e}{\partial t}dV+\frac{\left(\frac{5}{2}{n}_C{k}_B{T}_{eC}{u}_{eC}-\frac{5}{2}{n}_A{k}_B{T}_{eA}{u}_{eA}\right)}{L}\\ \hfill =\frac{\left(\frac{5}{2}\frac{{\mu }_C}{e}{n}_C{k}_B^2{T}_{eC}\frac{\partial T_e}{\partial z}{|}_C-\frac{5}{2}\frac{{\mu }_A}{e}{n}_A{k}_B^2{T}_{eA}\frac{\partial T_e}{\partial z}{|}_A\right)}{L}-{\frac{e}{m_i}\int }_{V}nE{u}_{e}dV{-\int }_V\left(n_{n}nK+nW\right)dV,\end{array}(4)$

where n_n and n are the neutral and plasma densities, u_n is the neutral velocity, which is considered constant and uniform, u_i is the ion velocity, u_e is the electron velocity, T_e is the electron temperature, E is the electric field, k_I is the ionization rate, ${\dot{n}}_w$ represent the neutral particles flowing in the domain from the lateral walls due to ion recombination, W is the electron power loss to the lateral walls, K is the collisional energy loss coefficient, e is the elementary charge and m_i is the mass of the neutral atoms. According to the results of [13], the feedback mechanism is not altered if the pressure term in the electric field is neglected, thus we consider the following closure for the electric field:

$E=-\frac{u_e}{\mu }.(5)$

The electron mobility μ is linearized as in [13], i.e.,

$\mu ={\mu }_b+\gamma \left(n_n-n_{nb}\right),(6)$

where the subscript b indicates the value taken at base state, which is the steady state upon which breathing may develop and which is identified as a steady solution of the model. γ in Eq. 6 plays the role of a rigidity coefficient for μ with respect to n_n. Both μ_b and γ in Eq. 6 are functions of the radial magnetic field intensity and the plasma properties (n_nb and T_eb) evaluated at the base state.

The following fundamental assumptions are made in passing from the original integral equations to the 0D model. Neutral and plasma densities, ionization rate, electron temperature and electron mobility are assumed uniform inside the control volume, while electron and ion velocities are assumed to vary linearly. We also assume that the current is carried only by electrons at the anode and only by ions at the channel exit section, thus, u_iA = u_eC = 0, $u_{eA}=u_{iC}=2\overline{u_i}$ and $\overline{u_e}=-\overline{u_i}$, where the overline indicates mean quantities in the considered control volume. Furthermore, the convective and heat flux terms have been neglected in the electron energy equation. The resulting model is the following:

$\frac{\mathrm{d}{\bar{n}}_n}{\mathrm{d}t}+\frac{u_n}{L}\left({\bar{n}}_n-n_{nA}\right)-2\alpha \frac{\bar{n}{\bar{u}}_B}{\mathrm{\Delta }R}=-{\bar{n}}_n\bar{n}{\bar{k}}_I(7)$

$\frac{\mathrm{d}\bar{n}}{\mathrm{d}t}+\frac{2\bar{n}{\bar{u}}_i}{L}+2\alpha \frac{\bar{n}{\bar{u}}_B}{\mathrm{\Delta }R}={\bar{n}}_n\bar{n}{\bar{k}}_I(8)$

$\frac{\mathrm{d}\bar{n}{\bar{u}}_i}{\mathrm{d}t}+\frac{4\bar{n}{\bar{u}}_i^2}{L}+2\alpha \frac{\bar{n}{\bar{u}}_B{\bar{u}}_i}{\mathrm{\Delta }R}=\frac{e}{m_i}\bar{n}\bar{E}(9)$

$\frac{\mathrm{d}\frac{3}{2}\bar{n}{k}_B{\bar{T}}_e}{\mathrm{d}t}=\frac{e}{m_i}\bar{n}\bar{E}{\bar{u}}_i-\bar{n}{\bar{n}}_n\bar{K}-\bar{n}\bar{W}(10)$

where

$\bar{E}=\frac{{\bar{u}}_i}{\bar{\mu }},(11)$

$n_{nA}=\frac{\dot{m}}{m_i{u}_n{A}_{ch}},(12)$

${\bar{u}}_B=\sqrt{\frac{k_B{\bar{T}}_e}{m_i}},(13)$

${\bar{k}}_I=k_I\left({\bar{T}}_e\right),(14)$

$\bar{K}=K\left({\bar{T}}_e\right),(15)$

$\bar{W}=\alpha \frac{{\bar{u}}_B}{1-\sigma }\left(2k_B{\bar{T}}_e+\left(1-\sigma \right)e{\bar{\varphi }}_w\right)\frac{2}{\mathrm{\Delta }R},(16)$

${\bar{\varphi }}_w=\frac{k_B{\bar{T}}_e}{e}\ln \left[\left(1-\sigma \right)\sqrt{\frac{m_i}{2\pi m_e}}\right],(17)$

$\bar{\mu }={\bar{\mu }}_b+\gamma \left({\bar{n}}_n-{\bar{n}}_{nb}\right).(18)$

In the previous equations, α is a coefficient modulating the plasma-wall interactions [12], ΔR is the channel width, A_ch is the channel area, $\dot{m}$ is the xenon mass flow rate injected into the channel, σ is the effective secondary electron emission yield and ϕ_w is the sheath potential drop at the lateral walls. We remind here that α does not have a direct physical meaning, but was introduced to account for the unresolved radial gradients in the plasma profiles and the uncertainties in the plasma–wall semi-empirical description. Coefficients k_I and K are computed as a function of the electron internal energy using the LXCat database [14] and the Bolsig+ [15] solver. Moreover, in the present analysis, both ${\bar{\mu }}_b$ and γ are considered independent parameters, in order to explore the stability of the model in a more general context.

Despite the strong assumptions, the resulting 0D model maintains all the core mechanisms believed to be involved in the onset of ionization oscillations in Hall thrusters, and is very similar to other models proposed in the literature [8, 9]. The main difference with existing literature is that, here, the electric field is allowed to oscillate in response to variations of neutral density through the relations 5 and 6. The strength of this response is strictly related to the parameter γ, which, as shown in the next section, plays a fundamental role in the onset of the instability, confirming the conclusions drawn in [13].

The capability of the model in reproducing self-sustained oscillations of breathing mode is appraised here both by linear stability analysis and by non-linear simulations. As concerns stability analysis, a linearized version of the code has been developed and coupled with an eigenvalue solver based on Krylov methods. For sake of simplicity, linearization of the solver has been carried out numerically as proposed in [16].

Based on the analysis of [13], temperature fluctuations are not necessary to trigger mechanism E2, which is alone sufficient for the onset of breathing. Thus, in the following we will explore the stability of the model both with and without the electron energy equation, and assuming isothermal electrons when the energy equation is not included.

3 Results

3.1 Constant electron temperature

We consider here only Eqs 7–9, thus, the electron temperature is constant in time, keeping strictly the sole ingredients allowing the E2 mechanism. In order to close the system, a number of free parameters, namely, $u_n,\dot{m},\alpha ,{\bar{T}}_e,{\bar{\mu }}_b$ and γ, must be assigned, as well as the geometry of the control volume. In the simulations, the channel geometry is that of SITAEL’s HT5k as in previous works (see, for instance, Ref. [12]) and the injected mass flow rate is 8 mg/s. Since a sensitivity analysis, not shown here for the sake of brevity, showed that varying α between .001 and 1 does not qualitatively affect the results, α is assigned to be equal to .115, which is the value resulting from the calibration process presented in our previous work [12]. This also suggests that wall interaction effects do not play a fundamental role on the onset of the instability. For the remaining quantities, a parametric study is presented in the following.

Results of the linear stability analysis applied to system (Eqs 7–9) are reported in Figure 1 for a reasonable range of ${\bar{\mu }}_b$ and γ. The other free parameters are u_n = 300 m/s and ${\bar{T}}_e=20$ eV, which are representative conditions of a real operative point [12]. The linear stability analysis yields a couple of complex conjugated eigenvalues, whose growth rate and frequency are reported in Figures 1A, B, respectively. As detailed in Figure 1A, there is a region on the (${\bar{\mu }}_b$-γ) plane where the growth rate is positive, i.e., the system is unstable. In particular, the growth rate increases with γ and decreases with ${\bar{\mu }}_b$; thus, the stability region in the parameters space expands as ${\bar{\mu }}_b$ is increased. We also note that for γ = 0, the system is always stable, in agreement with [13], indicating that fluctuations of electron mobility in response to variations of neutral density are fundamental for the onset of the unstable mode. The frequency of the unstable mode is in the range of 20–40 kHz (Figure 1B), close to the typical frequencies which are observed for breathing mode in Hall thrusters (see, for instance [6]). Moreover, both the growth rate and the frequency are definitely more sensitive to variations of γ rather than of ${\bar{\mu }}_b$. Figure 1C reports the stability curves for different values of u_n and ${\bar{T}}_e$, to explore a range of values which is typical for this specific configuration, as suggested by the calibrated simulations detailed in [12]. The unstable region in the ${\bar{\mu }}_b$-γ plane is larger for lower neutral injection velocities and lower electron temperatures. Figures 1D, E show the steady-state solution as a function of ${\bar{\mu }}_b$; the resulting plasma properties in the considered range of ${\bar{\mu }}_b$ are comparable to the mean values of the corresponding 1D steady solution inside the channel, which can be gathered from figures reported in Refs. [12, 13] (not shown here for brevity). Figure 1F shows the fluctuations around the steady state of neutral and plasma densities, ion velocity and electric field, at incipient instability. The relative phases of the various signals are in agreement with those observed in the 1D model [13], confirming that the instability observed in the two cases is indeed the same. In particular, neutral density is approximately in phase opposition with respect to ion velocity and electric field. Plasma density, instead, is approximately π/2 shifted, thus, when ${\bar{u}}_i-{\bar{u}}_{ib}>0$ we observe $\frac{\mathrm{d}\bar{n}}{\mathrm{d}t}<0$.

FIGURE 1

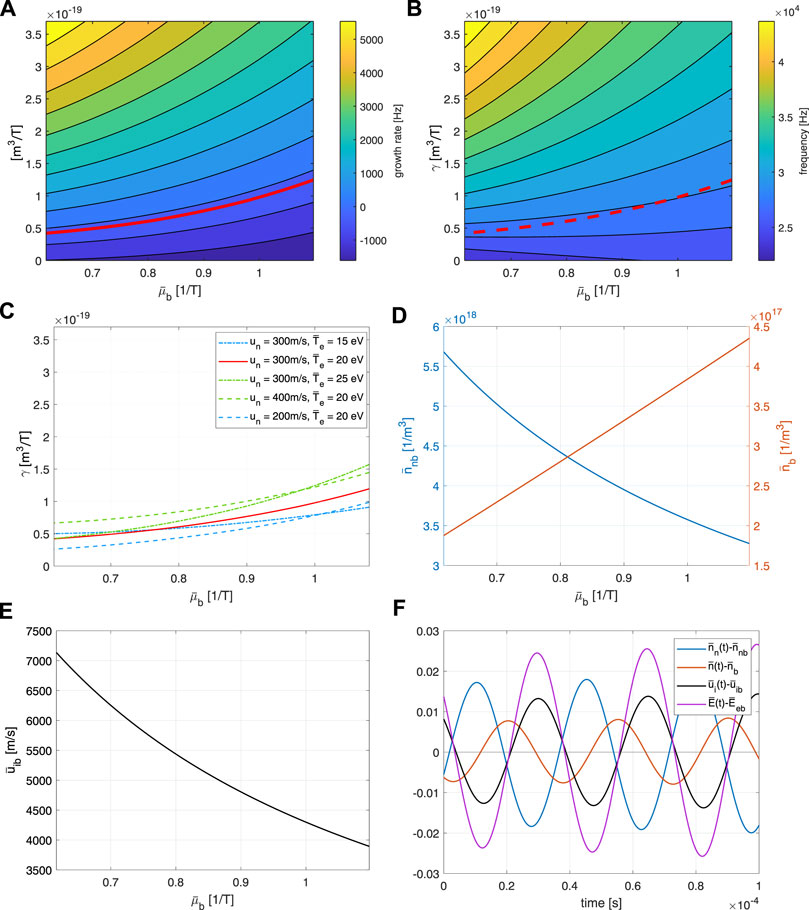
FIGURE 1. Result of linear stability analysis applied to system (Eqs 7–9) (isothermal electrons): growth rate (A) and frequency (B) of the unstable mode as a function of ${\bar{\mu }}_b$ and γ (the red line represents the marginal stability curve) for u_n = 300 m/s and ${\bar{T}}_e=20eV$; marginal stability curve for different combinations of u_n and ${\bar{T}}_e$ (C); neutral (blue) and plasma (orange) densities at steady state as a function of ${\bar{\mu }}_b$ (D); ion velocity at steady state as a function of ${\bar{\mu }}_b$ (E); oscillations of neutral density (blue), plasma density (orange), ion velocity (black) and electric field (purple) around the steady state at incipient instability (the quantities are normalized with n_ref = 10¹⁸ 1/m³, u_ref = 3,000 m/s, E_ref = 2,400 V/m) (F).

The above results fully support the conclusions reported in [13], i.e., mechanism E2 is sufficient, at least in certain conditions, to trigger breathing oscillations. Moreover, at least in the analyzed case, temperature fluctuations are not necessary for the onset of the unstable mode, and the parameter γ regulates the intensity of the destabilizing feedback involving the ion dynamics.

3.2 Full model

Even though electron temperature fluctuations are not necessary for the system to be unstable, they certainly play a role in the overall dynamics and can affect the results. Therefore, we consider now the full system (Eqs 7–10). Free parameters are set as in the previous section. As for the previous cases, results of the linear stability analysis around the base state are reported for u_n = 300 m/s in Figure 2.

FIGURE 2

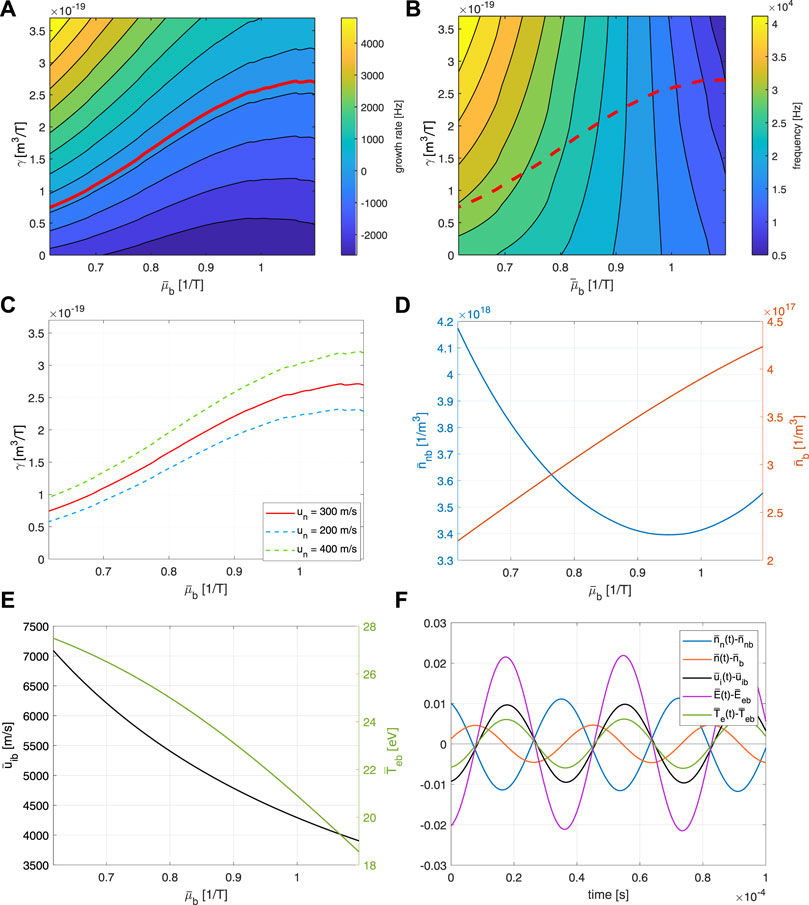
FIGURE 2. Result of linear stability analysis applied to system (Eqs 7–10): growth rate (A) and frequency (B) of the unstable mode as a function of ${\bar{\mu }}_b$ and γ (the red line represent the marginal stability curve) for u_n = 300 m/s; marginal stability curve for different values of u_n (C); neutral (blue) and plasma (orange) densities at steady state as a function of ${\bar{\mu }}_b$ (D); ion velocity (black) and electron temperature (green) at steady state as a function of ${\bar{\mu }}_b$ (E); oscillations of neutral density (blue), plasma density (orange), ion velocity (black), electron temperature (green), and electric field (purple) around the steady state at incipient instability (the quantities are normalized with n_ref = 10¹⁸ 1/m³, u_ref = 3,000 m/s, T_ref = 12 eV, E_ref = 2400 V/m) (F).

Concerning the growth rate, the results are qualitatively in line with the previous ones; for each ${\bar{\mu }}_b$, there is a threshold value of γ beyond which the system is unstable Figure 2A. The threshold value is higher with respect to the previous case, and grows more rapidly with ${\bar{\mu }}_b$. Moreover, the higher the neutral velocity is, the smaller the unstable region in the (${\bar{\mu }}_b$-γ) plane is, as shown in Figure 2C. The frequency of the unstable mode is in the range of 10–40 kHz, in line with the previous case and with typical breathing mode frequencies. However, in this case, the mode frequency mainly depends on ${\bar{\mu }}_b$, while it is only slightly sensitive to the value of γ (see Figure 2B). The values of resulting plasma properties at the steady state, which are reported in Figures 2D, E, are similar to the previous case and to other higher-order models and experiments (see, for instance [17]). Figure 2F shows the relative phases of the fluctuations around the steady state of the different plasma properties at incipient instability. Except for the presence of temperature oscillations, which are in phase with the electric field and, thus, in phase opposition with the neutral density, no qualitative difference is observable in the phase shifts with respect to the case with constant ${\bar{T}}_e$, confirming that, at least in the analyzed case, temperature fluctuations play a secondary role in the onset of the instability.

Finally, proposed models are appraised by means of non-linear simulations. In this regard, Figure 3 shows the discharge current signal $I=2e\bar{n}{\bar{u}}_i{A}_{ch}$ resulting from the direct integration of the system without (A) and with (B) the electron energy equation, when γ is arbitrarily chosen just under (red) and above (blue) the stability threshold. In both cases, the resulting dynamics resembles the behavior of the 1D model shown in [13]. Starting from the base state, the system starts oscillating with the frequency predicted by the linear stability analysis and, when unstable, the oscillations grow exponentially until they non-linearly saturate, settling on a periodic limit cycle. The frequency at limit cycle is approximately the same as at incipient instability. Also (not shown here), the growth rate and saturation amplitude of the oscillations, in both cases, are sensitive to the value of γ assigned, in agreement with [13]. This is another evidence that the observed instability has indeed the characteristics of the breathing mode and that, in the analyzed case, E2 is the dominant mechanism leading to its origin. More in detail, electron temperature fluctuations seem to play a fundamental role in the non-linear saturation phase, while they do not qualitatively affect the linear development of the instability.

FIGURE 3

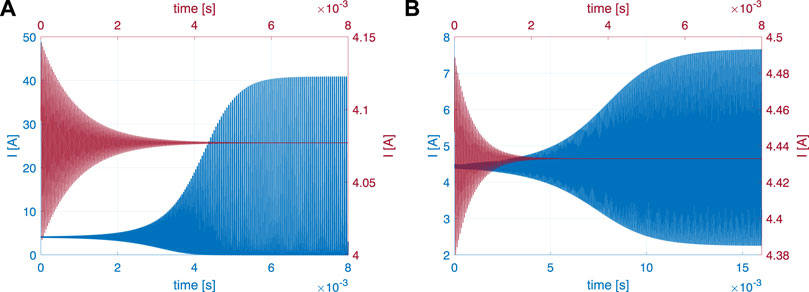
FIGURE 3. Numerical integration of the 0D model without (A) and with (B) the electron energy equation: discharge current signal. In the simulations shown, ${\bar{\mu }}_b=0.81/T$ while γ is selected just under (red line) and above (blue line) the marginal stability value. In particular, the selected values of γ are 5 × 10⁻²⁰ m³/T and 7 × 10⁻²⁰ m³/T for the constant temperature case, and 1.4 × 10⁻¹⁹ m³/T and 1.7 × 10⁻¹⁹ m³/T for the full system.

Concluding, we note that, in the present analysis, ${\bar{\mu }}_b$ and γ are treated as free parameters, while the correspondent quantities in the 1D formulation are both functions of the local magnetic field intensity and plasma properties. Introducing analogous functional relations in the presented 0D model would allow to link the stability of the model to the magnetic field intensity, and so to the operating condition of the thruster. Although we have verified that such a formulation can still provide unstable solutions, a more rigorous investigation in this direction is left for future works.

4 Conclusion

In this work we have presented a novel 0D model for the description of the breathing mode in Hall thrusters. The model is built on the basis of the 1D model detailed in [13], which was previously calibrated and validated against the experimental data available for SITAEL’s HT5K thruster [12]. The model is aimed at isolating the original feedback mechanism identified in Ref. [13] as the responsible one for the onset of breathing, and at further demonstrating the capability of such mechanism of triggering and sustaining low frequency ionization oscillations in Hall thrusters. The core of such mechanism, which we called E2, is represented by fluctuations of electron mobility in response to variations of neutral density. The resulting oscillations of the electric field act on the ionization rate through variations of the plasma density caused by the subsequent ion dynamics. We show that, by strictly keeping the only ingredients allowing E2 in the essential 0D formulation proposed here, the model is capable of reproducing unstable oscillations with the typical characteristics of the breathing mode. Moreover, the model further supports the conclusion that the electron energy equation is not necessary to induce instability in the considered configuration, and the stability of the model strictly depends on the magnitude of the rigidity coefficient relating variations of electron mobility and neutral density, in accordance to our previous study.

These results suggest that the breathing mode is not a spatially dependent phenomenon and confirm the conclusion according to which, at least in certain conditions, the mechanism E2 is responsible for the onset and sustenance of the breathing mode in Hall thrusters.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

Conceptualization, LL, SC, VG, and TA; methodology, LL, SC, VG, and TA; software, LL; analysis, LL, VG, SC, and TA; resources, SC and TA; writing—original draft preparation, LL, SC, and VG; writing—review and editing, LL, SC, VG, and TA. All authors have read and agreed to the published version of the manuscript.

Funding

The work described in this paper has been funded by the European Union under the H2020 Programme ASPIRE-GA 101004366.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Boeuf J-P. Tutorial: Physics and modeling of Hall thrusters. J Appl Phys (2017) 121:011101. doi:10.1063/1.4972269

CrossRef Full Text | Google Scholar

2. Sekerak MJ, Gallimore AD, Brown DL, Hofer RR, Polk JE. Mode transitions in Hall-effect thrusters induced by variable magnetic field strength. J Propulsion Power (2016) 32:903–17. doi:10.2514/1.B35709

CrossRef Full Text | Google Scholar

3. Giannetti V, Piragino A, Paissoni CA, Ferrato E, Estublier D, Andreussi T. Experimental scaling laws for the discharge oscillations and performance of Hall thrusters. J Appl Phys (2022) 131:013304. doi:10.1063/5.0070945

CrossRef Full Text | Google Scholar

4. Fabris AL, Young CV, Cappelli MA. Time-resolved laser-induced fluorescence measurement of ion and neutral dynamics in a Hall thruster during ionization oscillations. J Appl Phys (2015) 118:233301. doi:10.1063/1.4937272

CrossRef Full Text | Google Scholar

5. Lobbia R, Gallimore A. A method of measuring transient plume properties. In: In proceedings of the 44th AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit; 21 July 2008 - 23 July 2008; Hartford,CT (2008). doi:10.2514/6.2008-4650

CrossRef Full Text | Google Scholar

6. Giannetti V, Saravia MM, Andreussi T. Measurement of the breathing mode oscillations in Hall thruster plasmas with a fast-diving triple Langmuir probe. Phys Plasmas (2020) 27:123502. doi:10.1063/5.0022928

CrossRef Full Text | Google Scholar

7. Fife JM, Martinez-Sanchez M, Szabo J. A numerical study of low-frequency discharge oscillations in Hall thrusters. In: In proceedings of the 33rd Joint Propulsion Conference and Exhibit; 06-09 July 1997; Seattle, WA, USA (1997). (American Institute of Aeronautics and Astronautics Inc, AIAA). doi:10.2514/6.1997-3052

CrossRef Full Text | Google Scholar

8. Hara K, Sekerak MJ, Boyd ID, Gallimore AD. Perturbation analysis of ionization oscillations in Hall effect thrusters. Phys Plasmas (2014) 21:122103. doi:10.1063/1.4903843

CrossRef Full Text | Google Scholar

9. Lafleur T, Chabert P, Bourdon A. The origin of the breathing mode in Hall thrusters and its stabilization. J Appl Phys (2021) 130:053305. doi:10.1063/5.0057095

CrossRef Full Text | Google Scholar

10. Dale ET, Jorns BA. Two-zone Hall thruster breathing mode mechanism, part I: Theory. In: In proceedings of the 35th International Electric Propulsion Conference; October 8 – 12, 2017; USA (2019). IEPC-2019-354.

Google Scholar

11. Dale ET, Jorns BA. Two-zone Hall thruster breathing mode mechanism, part II: Experiment. In: In proceedings of the 35th International Electric Propulsion Conference; October 8 – 12, 2017; USA (2019). IEPC-2019-352.

Google Scholar

12. Giannetti V, Saravia MM, Leporini L, Camarri S, Andreussi T. Numerical and experimental investigation of longitudinal oscillations in Hall thrusters. Aerospace (2021) 8:148. doi:10.3390/aerospace8060148

CrossRef Full Text | Google Scholar

13. Leporini L, Giannetti V, Saravia MM, Califano F, Camarri S, Andreussi T. On the onset of breathing mode in Hall thrusters and the role of electron mobility fluctuations. Front Phys (2022) 10:951960. doi:10.3389/fphy.2022.951960

CrossRef Full Text | Google Scholar

14. Biagi S (2021). Biagi database. Available at: http://www.lxcat.net [Accessed on March 9, 2021].

Google Scholar

15. Hagelaar GJM, Pitchford LC. Solving the Boltzmann equation to obtain electron transport coefficients and rate coefficients for fluid models. Plasma Sourc Sci Tech (2005) 14:722–33. doi:10.1088/0963-0252/14/4/011

CrossRef Full Text | Google Scholar

16. Mettot C, Renac F, Sipp D. Computation of eigenvalue sensitivity to base flow modifications in a discrete framework: Application to open-loop control. J Comput Phys (2014) 269:234–58. doi:10.1016/j.jcp.2014.03.022

CrossRef Full Text | Google Scholar

17. Boeuf JP, Garrigues L. Low frequency oscillations in a stationary plasma thruster. J Appl Phys (1998) 84:3541–54. doi:10.1063/1.368529

CrossRef Full Text | Google Scholar