Nodal degeneracy of guided modes in uniaxial crystal slabs

We study the dispersions of the guided modes in the continuous uniaxial crystal slab waveguide and engineer their degeneracies through dielectric anisotropy. By switching the uniaxial positivity and negativity, we can obtain distinctive nodal types, point and line, for the lowest degeneracy in frequency. The mirror symmetry protections, ${\mathcal{M}}_x$ and ${\mathcal{M}}_y$, are pointed out, and the degeneracy properties are intuitively analyzed through comparing the approximate slopes of the guided modes. Our results reveal a link between the lowest nodal types and the positivity/negativity of the uniaxial crystal, and provide a new approach to regulate the topology of degeneracy in two-dimensional photonic bands.

Introduction

Recently, a research focus is concentrated on nodal degeneracy in band diagrams in periodical structures [1–5], such as quantum materials, photonic crystals, and phononic crystals, because new physics and novel applications are anticipated arising from peculiar band degeneracies including point degeneracy [6–16], line/loop degeneracy [17–28], nodal chain degeneracy [29–31], nodal surface degeneracy [32, 33] and so on.

Band degeneracy is generally enforced by symmetry in the physical system. It is well known that photonic guided waves in confined structures can be classified into transverse electric (TE) and transverse magnetic (TM) modes in terms of mirror symmetry [our meanings of “TE” and “TM” adapted to classical waveguide theory, see [34]. Taking an example of an isotropic dielectric slab waveguide, both modes evolve out from the light cone in free space, and their dispersion curves are rapidly asymptotic to the light cone in dielectrics as propagation constant increasing. Because of the asymptotic parallelism, the TE and TM dispersions cross rarely to form the degeneracy beyond the free space light cone, which is schematically depicted in Figure 1B. On the other hand, the slopes of the TE and TM modes in the dispersion diagram can be tailored in a polarization-distinguishable way through introducing the uniaxial anisotropy to the dielectric slab. The tailoring mechanism is rooted on the refractive index difference which is manifested likewise in the propagation of ordinary and extra-ordinary light in a uniaxial bulk crystal [35], seeing the index ellipsoid in Figure 1.

FIGURE 1

FIGURE 1. Schematics for the index ellipsoids (upper row) in a uniaxial bulk crystal where the optical axis $n_e$ is along the horizontal direction, and the guided modes (lower row) in the uniaxial crystal slab with the finite thickness along the x-direction as illustrated by the insets. The propagation of the guided modes is assumed along the optical axis, i.e., horizontal direction, labeled as z-axis in the insets. The dark red lines denote TE modes, the dark blue lines denote TM modes, and the dash lines denote the light line. $n_e$ or ${\epsilon }_z$ increases from left to right, as indicated by the arrow, and shows (A) negatively uniaxial, (B) isotropic, and (C) positively uniaxial cases.

In the study, we start with an isotropic dielectric slab, where TE and TM modes are not degenerate. By changing the dielectric constant into the uniaxial permittivity tensor and tuning the component of the tensor along the propagation direction, we show the slope of TM modes can either increase or decrease significantly while maintaining the slope of TE modes, which corresponds to the positively and negatively uniaxial anisotropy, respectively. Thus, the crossing between TE and TM modes can be engineered, as illustrated in Figure 1. Furthermore, the mirror symmetry along the out-of-slab direction imposes an extra enforcement on the degeneracy and leads to distinctive nodal types, Dirac point (DP) and Dirac line (DL), in the positive and negative uniaxial cases for the lowest degeneracy in frequency.

Guided mode in uniaxial crystal slabs

Here, we consider a two-dimensional (2D) infinite (along y- and z-directions), uniaxial crystal slab (finite thickness d = 2 mm in the x-direction) with non-magnetic permeability ($\mu /{\mu }_0=1$; ${\mu }_0$ being the permeability in vacuum). The slab is located in free space where the wave is assumed propagating along the z-direction, and the permittivity tensor has the diagonal form $diag\left[n_o^2,n_o^2,n_e^2\right]\cdot {\epsilon }_0$ with $n_o$ ($n_e$) being the refractive index of ordinary (extra-ordinary) light and ${\epsilon }_0$ being the permittivity in vacuum. The dielectric principal axis in the uniaxial crystal is spanned by $\left(n_o,n_o,n_e\right)$, shown in Figure 2A, where $\theta$ denotes the in-plane rotation of the optical axis. When $\theta =0$, the anisotropic permittivity tensor ${\epsilon }_1$ of the slab can be expressed in the $\left(x,y,z\right)$ coordinate system as:

$\begin{array}{c}{\epsilon }_1^{=}/{\epsilon }_0=\left[\begin{array}{ccc}{\epsilon }_x/{\epsilon }_0& 0& 0\\ 0& {\epsilon }_y/{\epsilon }_0& 0\\ 0& 0& {\epsilon }_z/{\epsilon }_0\end{array}\right]=\left[\begin{array}{ccc}{n}_o^2& 0& 0\\ 0& n_o^2& 0\\ 0& 0& n_e^2\end{array}\right]\end{array}(1)$

where ${\epsilon }_i$ is the permittivity along the $i\left(i=x/y/z\right)$ direction with relative value ${\epsilon }_{xr}={\epsilon }_x/{\epsilon }_0=n_o^2$, ${\epsilon }_{yr}={\epsilon }_y/{\epsilon }_0=n_o^2$, and ${\epsilon }_{zr}={\epsilon }_z/{\epsilon }_0=n_e^2$. The dielectric loss of the permittivity is neglected in the study. The time harmonic waves that propagate in the z-direction can be expressed as:

$\begin{array}{c}\exp \left[i\left(k_{x}x+k_{z}z-\omega t\right)\right]\end{array}(2)$

where $k_i$ represents the $i$ component of wave vector in the $i$ direction, $k_y=0$ has been assumed for homogeneity in the y-direction, and $\omega$ is angular frequency. Since the system shows the mirror symmetry ${\mathcal{M}}_y:\left(x,y,z\right)\to \left(x,-y,z\right)$, the guided wave is cataloged into two polarization modes, TE with non-zero electric field perpendicular to the mirror plane (any xz plane due to uniformity in the y-direction) and TM with non-zero electric field parallel to the mirror plane (any xz plane due to uniformity in the y-direction) [Ref. 34]. By expressing the field components and matching the boundary conditions on the two surfaces of the slab, we can get the characteristic equations for TE mode:

$\begin{array}{c}2\alpha k_x\cos k_{x}d+\left({\alpha }^2-k_x^2\right)\sin k_{x}d=0\end{array}(3)$

$\begin{array}{c}{k}_x^2+k_z^2={\epsilon }_{\mathrm{y}\mathrm{r}}{k}_0^2\end{array}(4)$

FIGURE 2

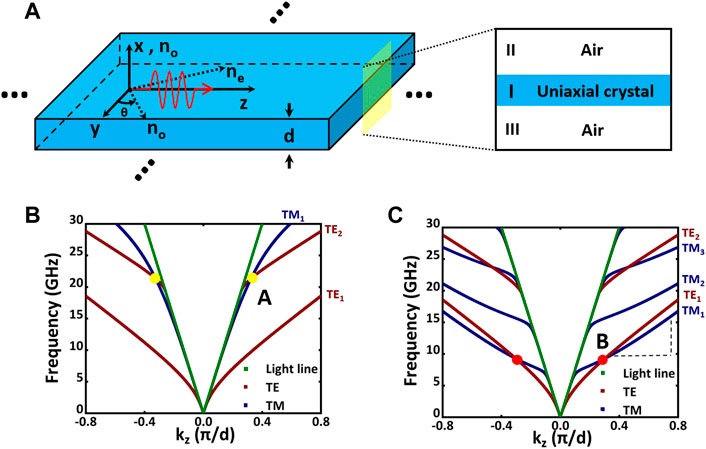
FIGURE 2. (A) The schematic picture of the anisotropic dielectric slab waveguide, where $\left(x,y,z\right)$ is the coordinate system for the slab; $\left(n_o,n_o,n_e\right)$ is the dielectric principal axes for the anisotropic permittivity. The red arrow represents the propagation direction of electromagnetic wave. The panel in the right shows the three layers structure in our system. The slab thickness d = 2 mm. (B) Dispersion diagram of TE and TM modes in the negatively uniaxial case when ${\epsilon }_z=4{\epsilon }_0$. The degenerate points are marked with yellow dots. (C) Dispersion diagram of TE and TM modes in the positively uniaxial case when ${\epsilon }_z=100{\epsilon }_0$. The degenerate points that we will investigate in details are marked with red dots. The velocity or effective index of the first-order modes (TM₁ and TE₁) near the point $B$ is approximated by the slope estimation $∆\omega /∆k_z$, as depicted by the right-angled dash lines.

and for TM mode:

$\begin{array}{c}\left({\alpha }^2-\frac{k_x^2}{{\epsilon }_{zr}^2}\right)\sin k_{x}d+\frac{2\alpha k_x}{{\epsilon }_{zr}}\cos k_{x}d=0\end{array}(5)$

$\begin{array}{c}\frac{k_x^2}{{\epsilon }_{zr}}+\frac{k_z^2}{{\epsilon }_{xr}}=k_0^2\end{array}(6)$

Above, Eqs 4, 6 are the dispersion relation in regime I, α is the imaginary part of perpendicular component of wave vector in theregime $\mathrm{I}\mathrm{I}$ and $\mathrm{I}\mathrm{I}\mathrm{I}$, and $k_0=\omega /c$ with the speed of light in vacuum $c=1/\sqrt{{\epsilon }_0{\mu }_0}$, which satisfies:

$\begin{array}{c}{k}_z^2-{\alpha }^2=k_0^2\end{array}(7)$

For concreteness, we choose ${\epsilon }_x={\epsilon }_y=16{\epsilon }_0$, and switch the value of ${\epsilon }_z$ for negatively uniaxial case (${\epsilon }_z=4{\epsilon }_0$) and positively uniaxial case (${\epsilon }_z=100{\epsilon }_0$). It is has known that 2D dielectric slabs have been extensively used as basic waveguides in microwave engineering and devices where a broad horizon of dielectric materials, e.g., high-k printed circuit board (PCB) and ceramics, may offer various permittivity including such values [36, 37]. The calculated results are shown in Figures 2B,C. Within a qualitative physical picture, we approximate the slope of TM modes beyond the light line to be roughly $\sim c/n_{eff}^{TM}$, and the effective index $n_{eff}^{TM}=\sqrt{{\epsilon }_{eff}^{TM}/{\epsilon }_0}\approx \sqrt{{avg(\epsilon }_x,{\epsilon }_z)/{\epsilon }_0}$, where the effective permittivity ${\epsilon }_{eff}^{TM}$ for TM mode can be regarded to some degree as special average of ${\epsilon }_x$; ${\epsilon }_z$ because the electric field is oriented along both x- and z-direction. In contrast, the slope, being roughly $\sim c/n_{eff}^{TE}$, of TE modes is related to $n_{eff}^{TE}=\sqrt{{\epsilon }_{eff}^{TE}/{\epsilon }_0}\approx \sqrt{{\epsilon }_y/{\epsilon }_0}$ in terms of the y-orientation of electric field. Therefore, given ${{\epsilon }_x=\epsilon }_y$ and when switching only ${\epsilon }_z$ from the negatively uniaxial case (${\epsilon }_z<{\epsilon }_y$) to positively uniaxial case (${\epsilon }_z>{\epsilon }_y$), we see that the slopes of the TE modes remain almost unchanged whereas the TM ones change expectedly in the dispersion diagram, as comparing Figure 2B with Figure 2C.

It is noted that the first-order TM mode (TM₁) crosses with the second-order TE mode (TE₂) for the negatively uniaxial case (${\epsilon }_z=4{\epsilon }_0$), as labeled by point $A$ in Figure 2B, and that it crosses with the first-order TE mode for positively uniaxial case (${\epsilon }_z=100{\epsilon }_0$), as labeled by point $B$ in Figure 2C, where TM curves are generally less steep than TE ones. For instance, the slope of TM₁ near the point $B$ is estimated as $\frac{∆\omega }{∆k_z}\sim \frac{2\pi \ast 7.48GHz}{0.5\pi /d}\sim c/5$ that corresponds to ${\epsilon }_{eff}^{TM1}/{\epsilon }_0$ ∼25, whereas the slope of TE₁ near the point $B$ is estimated as $\frac{∆\omega }{∆k_z}\sim \frac{2\pi \ast 9.34GHz}{0.5\pi /d}\sim c/4$ that corresponds to ${\epsilon }_{eff}^{TE1}/{\epsilon }_0$ ∼16. Therefore, the decrease in the slope of TM modes with ${\epsilon }_z$ leads to the switch of one of degenerating bands from TE₂ (point $A$) to TE₁ (point $B$). In addition, as increasing ${\epsilon }_z$, more TM modes appear in Figure 2C, and TM₃ is crossing with TE₂, which gives rise to more degeneracies at higher frequencies (see Section A in Supplementary Materials).

Type-II Dirac degeneracy in uniaxial crystal slabs

In order to exhibit the complete dispersion structure around the degenerate points, we need calculate the band diagram $\omega \left(k_y,k_z\right)$. In the calculation, we first rotate the in-plane dielectric principal axes around the $x$-direction with the angle $\theta$, as shown in Figure 2A. The non-diagonalized permittivity tensor ${\epsilon }_{\theta }$ after rotation can be written as

$\begin{array}{c}{\epsilon }_{\theta }^{=}=\left[\begin{array}{ccc}{\epsilon }_{xx}& 0& 0\\ 0& {\epsilon }_{yy}& {\epsilon }_{yz}\\ 0& {\epsilon }_{zy}& {\epsilon }_{zz}\end{array}\right]\end{array}(8)$

in which

${\epsilon }_{xx}={\epsilon }_x(9)$

${\epsilon }_{yy}={{\epsilon }_y\cos }^2\theta +{\epsilon }_z{\sin }^2\theta (10)$

${\epsilon }_{zz}={{\epsilon }_z\cos }^2\theta +{\epsilon }_y{\sin }^2\theta (11)$

${\epsilon }_{yz}={\epsilon }_{zy}=\left({\epsilon }_y-{\epsilon }_z\right)\sin \theta \cdot \cos \theta (12)$

Then, we assume that the waves still propagate along the z-direction and express the electric fields and magnetic fields in different regions. Because the mirror symmetry ${\mathcal{M}}_y$ is broken under the rotation, the guided modes are no longer pure TE or TM mode, but are their combination which we call hybrid mode. The characteristic equation for hybrid modes is solved by matching boundary conditions, which gives us the dispersion ${\omega }_{\theta }\left(k_z\right)$. Finally, the dispersion $\omega \left(k_y,k_z\right)$ is obtained through a standard map from polar coordinate to Cartesian coordinate. Although the calculation is based on the rotated dielectric principal axis, the results are the same as those of rotating the $\left(x,y,z\right)$ coordinate system while maintaining the dielectric principal axis, because both are the equivalent description of rotation.

We first analyze the degenerate point $A$ in negatively uniaxial case with ${\epsilon }_z=4{\epsilon }_0$, where it is the lowest degeneracy in frequency, as displayed in Figure 2B. We calculate the dispersion ${\omega }_{\theta }\left(k_z\right)$ when varying the angle $\theta$, and the degeneracy is seen to become gapped upon $\theta$ being nonzero, as shown in Figures 3A–C. Combining all $\theta$-cut plots, we can achieve the three-dimensional (3D) view of band diagram $\omega \left(k_y,k_z\right)$ in momentum space, as depicted in Figure 3D. The band structure around $A$ exhibits the characteristic of two over-tilted cones, and thus the degeneracy is just the type-II DP. The gapping reason is that the two modes display the like parity in the mirror symmetry ${\mathcal{M}}_x:\left(x,y,z\right)\to \left(-x,y,z\right)$ (the symmetry classifies all modes as even or odd parity with respect to the mirror plane x = 0, see Section B in Supplementary Materials) and simultaneously ${\mathcal{M}}_y$ is broken upon $\theta \ne 0$. Such 2D type-II DP has been observed in the artificially designed metasurfaces with periodic metallic patterns at microwave frequencies [38–40]. In contrast, our system is of no discrete translational symmetry, but continuous in space.

FIGURE 3

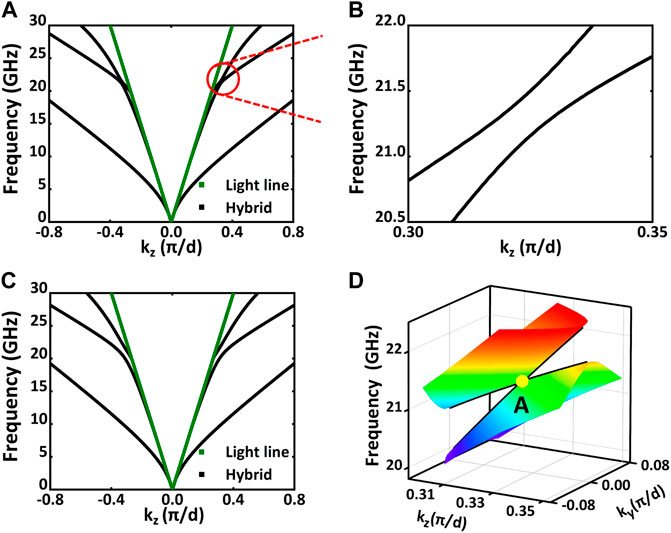
FIGURE 3. Type-II Dirac point in the dispersion diagram of the negatively uniaxial crystal slab when ${\epsilon }_z=4{\epsilon }_0$. (A) Shows the dispersion relation when $\theta$ is chosen as 2°. (B) Zoom-in view of the band gap in (A). (C) Shows the dispersion relation when $\theta$ = 10°. (D) 3D view around the degeneracy that gives rise to a type-II Dirac point in momentum space.

Next, let’s focus our attention on the degenerate point $B$ in positively uniaxial case with ${\epsilon }_z=100{\epsilon }_0$. Interestingly, in the cut plot with different $\theta$, the degeneracy persists, which forms a section of line in momentum space, as plotted in Figure 4. According to the slope of two crossing bands, such degeneracy is the Type-II DL. The degeneracy is protected by the mirror symmetry ${\mathcal{M}}_x$, in which the two bands display the opposite parity (see Section B in Supplementary Materials), and would be gapped if the uniaxial crystal slab lies in an asymmetric background, (see Section C in Supplementary Materials).

FIGURE 4

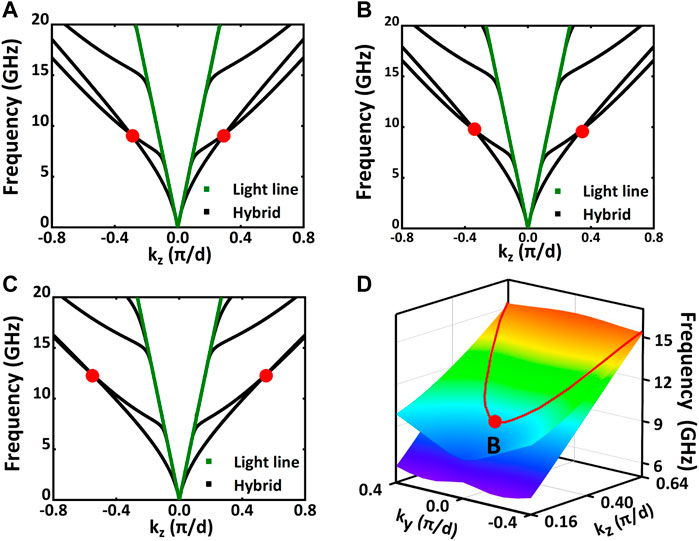
FIGURE 4. Type-II Dirac line in the dispersion diagram of the positively uniaxial crystal slab when ${\epsilon }_z=100{\epsilon }_0$. shows the dispersion relation when $\theta$ is chosen as 2°, 15° and 30°, where the red points label the linear cross of bands. 3D view around the (A-C) degeneracy B (red point), where all degenerated points give rise to the Type-II Dirac line in momentum space, which is (D) marked by red line.

It is also noted from Figure 4C that the two bands, responsible for the Dirac line, almost coincide with each other when $\theta$ comes to 30 $°$. If we increase the rotation angle further, the DL degeneracy will lift. The physical reason can be understood qualitatively from an effective permittivity point of view. Although being hybrid in nature upon $\theta \ne 0$, the two bands are dominated, respectively, by the TE₁ and TM₁ modes and can be considered as their descendants. As increasing the angle $\theta$, the slope of TE-like dispersion curve will decrease from $\sim c/\sqrt{{\epsilon }_y/{\epsilon }_0}$ at $\theta =0$ to $\sim c/\sqrt{{\epsilon }_{eff}^{TE-like}\left({\epsilon }_y,{\epsilon }_z,\theta \right)/{\epsilon }_0}$ at $\theta \ne 0$ where the effective permittivity ${\epsilon }_{eff}^{TE-like}$ is the $\theta$-mediated average between ${\epsilon }_y$ and ${\epsilon }_z$, and we make the approximation ${\epsilon }_{eff}^{TE-like}\left({\epsilon }_y,{\epsilon }_z,\theta \right)/{\epsilon }_0\approx n_{eff}^2\left(\theta \right)=n_o^2{n}_e^2/\left(n_o^2{\sin }^2\theta +n_e^2{\cos }^2\theta \right)$ (the relation expressed for extra-ordinary light in the bulk crystal [Ref. 35]). Consequently, the slope of TE-like dispersion may become comparable to that of TM-like dispersion upon some angle, and appear less than the latter beyond the angle, and such slope difference does not lead to the degeneracy any more. The threshold angle ${\theta }_c$ can be estimated through requiring the slope equality ${\epsilon }_{eff}^{TE-like}\left({\epsilon }_y,{\epsilon }_z,{\theta }_c\right)={\epsilon }_{eff}^{TM-like}\left({\epsilon }_x,{\epsilon }_z\right)$, where we assume ${\epsilon }_{eff}^{TM-like}\left({\epsilon }_x,{\epsilon }_z\right)\approx {\epsilon }_{eff}^{TM1}{\sim 25\epsilon }_0$ after noticing insignificant $\theta$-dependence of TM-like dispersions in Figure 4. Thus, the threshold angles are solved as ${\theta }_{c1}\sim {\pm 40}^{\mathrm{o}}$ and ${\theta }_{c2}\sim {\pm 140}^{\mathrm{o}}$, which are quite close to the numerical values ${\pm 35}^{\mathrm{o}}$ and ${\pm 145}^{\mathrm{o}}$ from COMSOL simulation and correspond to the $+k_z$ and $-k_z$ directions, respectively. Overall, this kind of nodal line is essentially different from the loop degeneracy [Ref. 40] because it cannot construct a closed loop in momentum space.

Discussions

When investigating the propagation of the guided modes along the direction perpendicular to the optical axis (e.g., the propagation along y-axis while the optical axis being z-axis, and the mirror symmetry ${\mathcal{M}}_z:\left(x,y,z\right)\to \left(x,y,-z\right)$ giving rise to the TE/TM modes), we find that the relative magnitude between the slopes of TM and TE modes will swap, because TE waves have the electric field polarized along the optical axis ${\epsilon }_z$ or $n_e$ and TM waves have the electric field components along both x- and y-directions. Thus, the DL degeneracy from the lowest two modes (even and odd parity) will occur to the negatively uniaxial case, and the DP degeneracy from the higher-order modes will appear in the positively uniaxial case (see Section D in Supplementary Materials).

In addition, we present a microwave metamaterial design which approximates at lower frequencies a positively uniaxial crystal with dispersive permittivity component, and the band degeneracy shows the similarity to and the difference from the case of the continuous crystal slab (see Section E in Supplementary Materials).

Conclusion

In conclusion, by controlling positivity/negativity of the refractive index ellipsoid, we can obtain the nodal point and nodal line degeneracies for the guided modes on the uniaxial crystal slab waveguide. Furthermore, the point and line characteristics and their connections with the refractive index ellipsoid can be swapped through switching the propagation direction. Our results link the band degeneracy with positivity/negativity of the uniaxial crystal, and provide a new approach to regulate the topology of degeneracy in 2D photonic bands.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

BH conceived and supervised the research; XP performed the research; HL, WD, XZ, KX, CH, and GW assisted in analyzing the data; and BH, XP, and HL wrote the manuscript.

Funding

This work was supported by the Natural Science Foundation of China (NSFC) (Grant No. 12074279), the Major Program of Natural Science Research of Jiangsu Higher Education Institutions (Grant No.18KJA140003), and the Priority Academic Program Development (PAPD) of Jiangsu Higher Education Institutions.

Conflict of interest

Chuandeng Hu was employed by Shenzhen Fantwave Tech Co., Ltd

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2022.1095669/full#supplementary-material

References

1. Armitage NP, Mele EJ, Vishwanath A. Weyl and Dirac semimetals in three-dimensional solids. Rev Mod Phys (2018) 90:015001. doi:10.1103/revmodphys.90.015001

CrossRef Full Text | Google Scholar

2. Li S, Yu Z-M, Yao Y, Yang SA. Type-II topological metals. Front Phys (2020) 15(4):43201. doi:10.1007/s11467-020-0963-7

CrossRef Full Text | Google Scholar

3. Lu L, Joannopoulos JD, Soljačić M. Topological photonics. Nat Photon (2014) 8:821–9. doi:10.1038/nphoton.2014.248

CrossRef Full Text | Google Scholar

4. Kim M, Jacob Z, Rho J. Recent advances in 2D, 3D and higher-order topological photonics. Light Sci Appl (2020) 9:130. doi:10.1038/s41377-020-0331-y

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Park HD, Gao W, Zhang X, Oh SS. Nodal lines in momentum space: Topological invariants and recent realizations in photonic and other systems. Nanophotonics (2022) 11(11):2779–801. doi:10.1515/nanoph-2021-0692

CrossRef Full Text | Google Scholar

6. Lu L, Wang Z-Y, Ye D-X, Ran L-X, Fu L, Joannopoulos JD, et al. Experimental observation of Weyl points. Science (2015) 349:622–4. doi:10.1126/science.aaa9273

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Gao W, Yang B, Lawrence M, Fang F, Béril B, Zhang S. Photonic Weyl degeneracies in magnetized plasma. Nat Commun (2016) 7:12435. doi:10.1038/ncomms12435

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Yang B, Guo Q, Tremain B, Barr LE, Gao W, Liu H, et al. Direct observation of topological surface-state arcs in photonic metamaterials. Nat Commun (2017) 8:97. doi:10.1038/s41467-017-00134-1

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Yang B, Guo Q, Tremain B, Liu R, Barr LE, Yan Q, et al. Ideal Weyl points and helicoid surface states in artificial photonic crystal structures. Science (2018) 359:1013–6. doi:10.1126/science.aaq1221

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Qiu P, Qiu W, Lin Z, Chen H, Ren J, Wang J-X, et al. Double Dirac point in a photonic graphene. J Phys D: Appl Phys (2017) 50:335101. doi:10.1088/1361-6463/aa7bc2

CrossRef Full Text | Google Scholar

11. Xiao M, Lin Q, Fan S. Hyperbolic Weyl point in reciprocal chiral metamaterials. Phys Rev Lett (2016) 117:057401. doi:10.1103/physrevlett.117.057401

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Yang Y, Gao Z, Feng X, Huang Y-X, Zhou P, Yang SA, et al. Ideal unconventional Weyl point in a chiral photonic metamaterial. Phys Rev Lett (2020) 125:143001. doi:10.1103/physrevlett.125.143001

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Liu G-G, Zhou P, Yang Y, Xue H, Ren X, Lin X, et al. Observation of an unpaired photonic Dirac point. Nat Commun (2020) 11:1873. doi:10.1038/s41467-020-15801-z

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Luo L, Deng W, Yang Y, Yan M, Lu J, Huang X, et al. Observation of quadruple Weyl point in hybrid-Weyl phononic crystals. Phys Rev B (2022) 106:134108. doi:10.1103/physrevb.106.134108

CrossRef Full Text | Google Scholar

15. Huang X, Lai Y, Hang ZH, Zheng H, Chan CT. Dirac cones induced by accidental degeneracy in photonic crystals and zero-refractive-index materials. Nat Mater (2011) 10:582–6. doi:10.1038/nmat3030

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Xu C, Ma G, Chen Z-G, Luo J, Shi J, Lai Y, et al. Three-dimensional acoustic double-zero-index medium with a fourfold degenerate Dirac-like point. Phys Rev Lett (2020) 124:074501. doi:10.1103/physrevlett.124.074501

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Lin JY, Hu NC, Chen YJ, Lee CH, Zhang X. Line nodes, Dirac points, and Lifshitz transition in two-dimensional nonsymmorphic photonic crystals. Phys Rev B (2017) 96:075438. doi:10.1103/physrevb.96.075438

CrossRef Full Text | Google Scholar

18. Yang S-Y, Yang H, Derunova E, Parkin SSP, Yan B, Ali MN. Symmetry demanded topological nodal-line materials. Adv Phys (2018) 3:1414631. doi:10.1080/23746149.2017.1414631

CrossRef Full Text | Google Scholar

19. Feng B, Fu B, Kasamatsu S, Ito S, Cheng P, Liu C-C, et al. Experimental realization of two-dimensional Dirac nodal line fermions in monolayer Cu₂Si. Nat Commun (2017) 8:1007. doi:10.1038/s41467-017-01108-z

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Feng B, Zhang R-W, Feng Y, Fu B, Wu S, Miyamoto K, et al. Discovery of Weyl nodal lines in a single-layer ferromagnet. Phys Rev Lett (2019) 123:116401. doi:10.1103/physrevlett.123.116401

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Wang S-S, Yu Z-M, Liu Y, Jiao Y, Guan S, Sheng X-L, et al. Two-dimensional nodal-loop half-metal in monolayer MnN. Phys Rev M (2019) 3:084201. doi:10.1103/physrevmaterials.3.084201

CrossRef Full Text | Google Scholar

22. You J-Y, Chen C, Zhang Z, Sheng X-L, Yang SA, Su G. Two-dimensional Weyl half-semimetal and tunable quantum anomalous Hall effect. Phys Rev B (2019) 100:064408. doi:10.1103/physrevb.100.064408

CrossRef Full Text | Google Scholar

23. Gao W, Yang B, Tremain B, Liu H, Guo Q, Xia L, et al. Experimental observation of photonic nodal line degeneracies in metacrystals. Nat Commun (2018) 9:950. doi:10.1038/s41467-018-03407-5

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Qiu H, Qiu C, Yu R, Xiao M, He H, Ye L, et al. Straight nodal lines and waterslide surface states observed in acoustic metacrystals. Phys Rev B (2019) 100:041303. doi:10.1103/physrevb.100.041303

CrossRef Full Text | Google Scholar

25. Deng W, Lu J, Li F, Huang X, Yan M, Ma J, et al. Nodal rings and drumhead surface states in phononic crystals. Nat Commun (2019) 10:1769. doi:10.1038/s41467-019-09820-8

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Xiong Z, Zhang R-Y, Yu R, Chan CT, Chen Y. Hidden symmetry enforced nexus points of nodal lines in layer-stacked dielectric photonic crystals. Light Sci Appl (2020) 9:176. doi:10.1038/s41377-020-00382-9

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Hu M, Zhang Y, Jiang X, Qiao T, Wang Q, Zhu S, et al. Double-bowl state in photonic Dirac nodal line semimetal. Light Sci Appl (2021) 10:170. doi:10.1038/s41377-021-00614-6

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Deng W-M, Chen Z-M, Li M-Y, Guo C-H, Tian Z-T, Sun K-X, et al. Ideal nodal rings of one-dimensional photonic crystals in the visible region. Light Sci Appl (2022) 11:134. doi:10.1038/s41377-022-00821-9

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Yan Q, Liu R, Yan Z, Liu B, Chen H, Wang Z, et al. Experimental discovery of nodal chains. Nat Phys (2018) 14(5):461–4. doi:10.1038/s41567-017-0041-4

CrossRef Full Text | Google Scholar

30. Wang Y, Zhou X, Li S, Zhang W, Hu C, Lu W, et al. Flatness and boundness of photonic drumhead surface state in a metallic lattice. Sci Rep (2021) 11:8684. doi:10.1038/s41598-021-88004-1

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Wu X, Fan H, Liu T, Gu Z, Zhang R-Y, Zhu J, et al. Topological phononics arising from fluid-solid interactions. Nat Commun (2022) 13:6120. doi:10.1038/s41467-022-33896-4

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Xiao M, Ye L, Qiu C, He H, Liu Z, Fan S. Experimental demonstration of acoustic semimetal with topologically charged nodal surface Sci. Adv. (2020) 6:eaav2360.

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Yang Y, Xia J-P, Sun H-X, Ge Y, Jia D, Yuan S-Q, et al. Observation of a topological nodal surface and its surface-state arcs in an artificial acoustic crystal. Nat Commun (2019) 10:5185. doi:10.1038/s41467-019-13258-3

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Joannopoulos JD, Meade RD, Johnson SG, Joshua N. Photonic crystals: Molding the flow of light. 2nd ed. Princeton, NJ: Princeton University Press (2011).

Google Scholar

35. Saleh BEA, Teich MC. Fundamentals of photonics. 2nd ed. New York, NY: John Wiley & Sons (2007).

Google Scholar

36. Pozer DM, Appendix G. Microwave engineering. 2nd ed. New York, NY: John Wiley & Sons (1998).

Google Scholar

37.ROGERSPCB MAIN (2020). Rogers laminates in stock. Available at: https://www.rogerspcb.com.cn/.

Google Scholar

38. Hu C, Li Z, Tong R, Wu X, Xia Z, Wang L, et al. Type-II Dirac photons at metasurfaces. Phys Rev Lett (2018) 121:024301. doi:10.1103/physrevlett.121.024301

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Li H, Hu C, Zhou X, Lu W, Hou B, Wen W. Conical diffraction from type-II Dirac point at metasurfaces. EPL (2020) 130:17007. doi:10.1209/0295-5075/130/17007

CrossRef Full Text | Google Scholar

40. Li H, Hu C, Jiang J-H, Wu J, Wen W, Hou B. Photonic type-III nodal loop and topological phase transitions at bilayer metasurfaces. Front Mater (2022) 9:909381. doi:10.3389/fmats.2022.909381

CrossRef Full Text | Google Scholar