Nonlinear Fourier analysis of matter-wave soliton interferometry

The bright solitons in quasi-1D atomic Bose-Einstein condensates are good candidates for constructing matter-wave interferometers with high sensitivity and long phase-accumulation times. Such interferometers at the mean-field level can be theoretically studied within the framework of quasi-1D Gross-Pitaevskii (GP) equation with narrow repulsive potential barriers. In this paper we present a basic proposal of using the nonlinear Fourier transform (NFT), also known as the inverse scattering transform, as an effective tool to analyze the soliton contents for those interferometers, which thanks to the nearly integrable nature of the GP equation when the normalized atom number fraction near the barrier is small. Based on typical cases, we show that the soliton components can be accurately detected from the output wave fields of the interferometers by computing the NFT spectra.

1 Introduction

Bright solitons are localized wavepackets that propagate without change on their profiles, due to the balance between dispersion and self-focusing nonlinearity. They have attracted significant interests in a wide range of nonlinear physical systems [1–3]. As a typical paradigm, the atomic Bose-Einstein condensates (BECs) with attractive interactions between atoms support bright matter-wave solitons, which have been experimentally created in the condensates of ⁷Li, ⁸⁵Rb, ³⁹K, and ¹³³Cs [4–8]. Furthermore the interactions between those solitons [9–11] and with potential barriers [12–26] have been explored both at the mean-field and at the quantum-mechanical level.

An important application of the bright solitons is to consider the soliton-barrier interaction for the design of matter-wave interferometers. Such interferometric proposals have been discussed in many theoretical works [18–26], and realized in several experiments [13, 14]. The basic elements of the interferometer include splitting and recombination of a bright soliton on a repulsive barrier [14, 18–23]. A fast soliton incident on a narrow barrier can split into transmitted and reflected solitons. Correspondingly, when two bright solitons interact at the location of the barrier, the redistribution of the norms (normalized atom numbers) of the outgoing waves depend on the relative phase of the incoming solitons [14, 18, 22]. This makes nearly total (perfect) recombination of the incident solitons possible. The soliton-based interferometers have their advantages such as high sensitivity and longer-time acquisition of phase shifts [14, 19].

The mean-field description of the atomic BEC solitons interacting with narrow potential barriers can be studied by the quasi-one-dimensional (1D) Gross-Pitaevskii (GP) equation [3], which presents the form of nonlinear Schrödinger (NLS) equation plus a localized potential term (we set the harmonic trapping potential vanished for convenience). The deviation between the quantum and GP approach becomes negligible for large number of atoms in the solitons. Depending on different forms of potential barriers, we can construct various schemes of soliton interferometers [23, 25–27]. In principle, the GP equation with general external potential is non-integrable. However, if the macroscopic wave function of the condensate sometime has negligible distribution of norms near the narrow (localized) repulsive barriers, the GP equation is close to integrable (nearly integrable). This would be the case that the incident solitons or outgoing waves (with most of the norms) are far enough away from the barrier.

On the other hand, the integrable NLS equation can be well studied by using the tool of nonlinear Fourier transform (NFT), also known as the inverse scattering transform [1, 28–30]. This technique decomposes the nonlinear waves into localized solitary eigenmodes and dispersive radiation components. The NFT may find its application in optical communications, where the nonlinear spectrum (mainly the solitonic part) was modulated to achieve the so-called “Eigenvalue communication” [31]. Recently, the NFT was also shown to be effective in analyzing some nearly integrable NLS models, where the perturbations such as dissipations, higher-order effects, or random noises are small [32–35]. For these systems, the slow variation of the nonlinear spectrum can be computed and traced as time evolves.

In this Brief Research Report, we use the NFT as a tool to “detect” the ingredients of the outgoing waves that emerge after the soliton collision with the narrow barrier for the soliton-based matter-wave interferometry. Through several typical cases, we show that those nonlinear contents (mainly the solitonic components) as well as their norm distribution can be accurately tested out by NFT, which is benefited from the nearly integrable nature of the systems outside the barrier-affected region. Therefore, we expect potential application of the nonlinear spectral analysis not only for the simulation results but also in detailed understanding of the experimental data such as those in [13, 14].

2 Methods

2.1 Quasi-1D GP equation

Considering a mean-field description, the dimensionless wave function ψ(x, t) of the condensate obeys the normalized quasi-1D GP equation with attractive interatomic interactions

$i\frac{\partial \psi \left(x,t\right)}{\partial t}=\left[-\frac{1}{2}\frac{{\partial }^2}{\partial x^2}-|\psi \left(x,t\right){|}^2+V\left(x\right)\right]\psi \left(x,t\right),(1)$

with the normalized temporal and spatial coordinates t and x, respectively measured in the units 1/ω_r and $a_r=\sqrt{\hslash /(m{\omega }_r)}$, where ω_r is the radial trap frequency and m is the atomic mass. See, e.g., [3, 18], for a more detailed discussion of the relevant units. Taking the realistic parameters in experiments [4, 5], where the bright BEC solitons have been created with ∼10^{3 7}Li atoms (ω_r = 2π × 700Hz), the 200 dimensionless time units correspond to ∼50 ms and 100 dimensionless length units correspond to ∼140 μm, which are under the current experimental capacity. The systematical derivation of Eq. 1 from the 3D GP equation can be found in [3, 20], and qualitative features of the 1D GP equation are fairly accurate for a wide range of atom numbers below the critical threshold.

The potential barrier V(x) may be modeled by some localized functions, such as the preferred Gaussian function generated by an off-resonant Gaussian light sheet [14, 18], or two Gaussian potentials forming the Fabry-Perot cavity [27]. This setup Eq. 1 can also include a nonlinear potential barrier that relates to the norm of the wave function [25]. Note that here we omit the harmonic trap along the x direction which can be approximately realized for a configuration of toroidal ring trap that introduces periodicity in x coordinate [18, 23].

2.2 Numerical simulations

We integrate Eq. 1 by using a fourth-order split-step method [36] in a box L = 128π with a uniform grid of N = 2¹³ nodes. The integration domain was chosen large enough to prevent boundary effects. The time step Δt = 0.0005 was employed which satisfies the requirement of numerical stability. We have double checked our results by increasing the box size, by fining the grid, as well as by using different integration schemes.

Our initial condition can take the form of a single incident soliton, or two oppositely moving bright solitons, even a bound state (soliton molecule) composed by two fundamental solitons. The general form of these nonlinear excitations at t = 0 can be written as

$\psi \left(x,t=0\right)=k_1\mathrm{s}\mathrm{e}\mathrm{c}\mathrm{h}\left[k_1\left(x+x_1\right)\right]e^{i{v}_{1}x}+k_2\mathrm{s}\mathrm{e}\mathrm{c}\mathrm{h}\left[k_2\left(x+x_2\right)\right]e^{i\left(v_{2}x+\mathrm{\Delta }\right)}.(2)$

Without loss of generality, setting k₂ = 0, we have a single soliton locating at x = −x₁, with the amplitude k₁ and moving velocity v₁; For sufficiently large values of |x₁| and |x₂| (x₁ > 0 and x₂ < 0), Eq. 2 approximately represents a pair of two bright solitons with oppositely velocities v₁ and v₂ (v₁ > 0 and v₂ < 0), and with a relative phase Δ; A bound state with zero phase difference (Δ = 0) can be constructed if |x₁−x₂| is relatively small by assuming v₁ = v₂.

On the other hand, the relative numerical norm (i.e., atom number fraction) that emerges on each side of (E_±), as well as near the narrow barrier (E₀) is computed by the following normalized integral quantities:

$\begin{array}{cc}\hfill E_{+}& =\frac{1}{\mathcal{N}}{\int }_{+d}^{+\infty }|\psi {|}^{2}dx,\hfill \\ \hfill E_{-}& =\frac{1}{\mathcal{N}}{\int }_{-\infty }^{-d}|\psi {|}^{2}dx,\hfill \\ \hfill E_0& =\frac{1}{\mathcal{N}}{\int }_{-d}^{+d}|\psi {|}^{2}dx,\hfill \end{array}(3)$

where the total norm $\mathcal{N}={\int }_{-\infty }^{+\infty }|\psi {|}^{2}dx$ representing the number of atoms is conserved, and d is the spatial position at which the effect of the localized potential vanishes V (±d) ≃ 0. Note that we have the conservation law E₊+E₋+E₀ = 1, and E₀ ≃ 0 insures the nearly integrable feature of the system [E₀ (t_f) < 1% is kept in all our simulations].

2.3 Nonlinear spectral analysis

To perform the NFT, we need to solve the Zakharov-Shabat spectral problem for a given wave function ψ(x, t)

$\frac{d\mathbf{Y}}{dx}=\left(\begin{array}{cc}\hfill -i\lambda \hfill & \hfill \psi \hfill \\ \hfill -{\psi }^{*}\hfill & \hfill i\lambda \hfill \end{array}\right)\mathbf{Y},(4)$

where Y(x, t; λ) is a vector and $\lambda =\xi +i\eta \in \mathbb{C}$ denotes the spectral eigenvalues, with ξ and η being the real and imaginary parts respectively. These eigenvalues are symmetrically distributed on the upper and lower complex planes. The discrete (solitonic) eigenvalues apparently away from the real and imaginary axes correspond to solitons, and their amplitudes are 2|η| while their velocities are associated with −2ξ. The eigenvalues appearing very near the real axis stand for small dispersive radiation waves.

Eq. 4 can be numerically solved by using the Fourier collocation method [36], which expands the Y(x, t; λ) components in the Fourier series and the spectral problem (4) is reformulated in the Fourier space. This method is convenient for computing the discrete solitonic eigenvalues. Our results are also double checked with the Boffetta-Osborne method [30]. Here solving the spectra we take the wave functions at the times long enough after the soliton-barrier interaction.

3 Results and discussions

3.1 Soliton splitting at a Gaussian barrier

We firstly show the example that the output after an incident soliton interacting with a finite-width Gaussian potential barrier can be well captured by the NFT. Here the linear potential V(x) = q exp (−x²/σ²) is used with its normalized strength and width q = 4.0 and σ = 0.14. The amplitude and initial position of the incident soliton were kept while its velocity varies, and the wave function at t_f = 2x₁/v₁ was chosen for computing the nonlinear spectrum [E₀ (t_f) is a very small quantity].

Figures 1A–C present the typical results for a low-, mediate-, high-speed incident soliton respectively. We see that the nonlinear spectra can clearly describe the features of the outgoing waves (the amplitudes and velocities of the reflected and transmitted solitons are accurately detected by the solitonic eigenvalues). In fact, there exist small-amplitude radiation waves that correspond to the eigenvalues very adjacent to the real axis. However, the solitonic eigenvalues take almost all the norms. Here, we define the following ratios $E_{-}^s=2{\eta }_s/k_1$ for ξ_s > 0 and $E_{+}^s=2{\eta }_s/k_1$ for ξ_s < 0, where λ_s = ξ_s + iη_s denote the discrete solitonic eigenvalues for solitons. This quantity $E_{\pm }^s$ refers to the percentage of the total norm that the transmitted or reflected solion takes since a soliton norm is proportional to its amplitude.

FIGURE 1

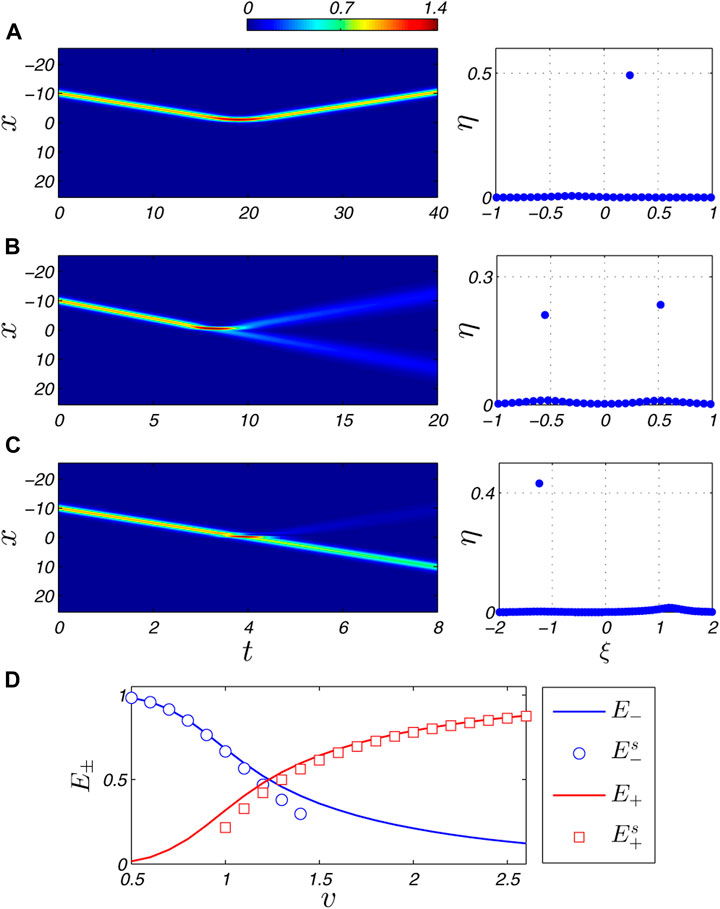
FIGURE 1. (Color online) Nonlinear spectral analysis of the soliton splitting at a repulsive Gaussian potential barrier. The incident soliton parameters include k₁ = 1, x₁ = 10, and (A) v₁ = 0.5; (B) v₁ = 1.2; (C) v₁ = 2.5. The left panels show the spatial-temporal intensities |ψ(x, t)|² (with the same colorbar as placed at the top), and the right panels correspondingly present the NFT eigenvalues calculated with ψ(x, t_f = 2x₁/v₁). Note that in (C) the eigenvalues near the real axis look more intensive since the window along ξ is twice of that as in (A) and (B). (D) Comparison of E_± with $E_{\pm }^s$ for the velocity of incident soliton varying from 0.5 to 2.6.

Figure 1D compares $E_{\pm }^s$ with E_± for a range of incident velocities. It suggests a good agreement for slow and fast incident solitons which is reasonable since the soliton tends to a complete reflection or transmission, such as those in Figures 1A, C. For the velocity near the 50:50 splitting, we found that $E_{\pm }^s$ is a bit smaller than E_±. This is due to the increased emission of radiation waves on both sides of the potential barrier [e.g., see in Figure 1B], which take a small fraction of the norms away from the solitons. Thus, the NFT may represent a suitable tool to explain the wave content in details, especially for the mediate-speed soliton splitting.

3.2 Soliton recombination at a Gaussian barrier

In this section we discuss the use of NFT after the collision of a soliton pair at the repulsive Gaussian barrier. We know that the asymmetries of two incident bright solitons scattered by the barrier may lead to the redistribution of the norms which is an effect depending on some parameters of the solitons, such as their relative phase, relative velocity, and even relative amplitude (inverse width) [18, 24]. Very slight deviation from the completely symmetric scenario can induce a nearly-perfect soliton recombination [24]. This parameter-sensitive phenomenon forms a base of the soliton interferometer.

Figures 2A–C show the cases that two oppositely moving solitons with only difference on their velocities collide at the barrier simultaneously, respectively generating the partial recombination, nearly total recombination, and symmetric outputs. The eigenvalues of the nonlinear spectra for these outputs are also presented. We see that the solitonic eigenvalues accurately capture the amplitudes and velocities of the outgoing solitons. A further comparison can be seen in Figure 2D, where variations of E₊ and $E_{+}^s$ with |v₂/v₁| are plotted [we concentrate on E₊ since the (partial) recombination occurs in the region x > 0 if |v₂/v₁| < 1]. We found a good agreement with very small deviation only for the regime of nearly-perfect recombination, which results from the emission of weak radiation waves. These examples further support the effectiveness of NFT in analyzing the outputs of two-soliton interactions at the narrow repulsive barrier.

FIGURE 2

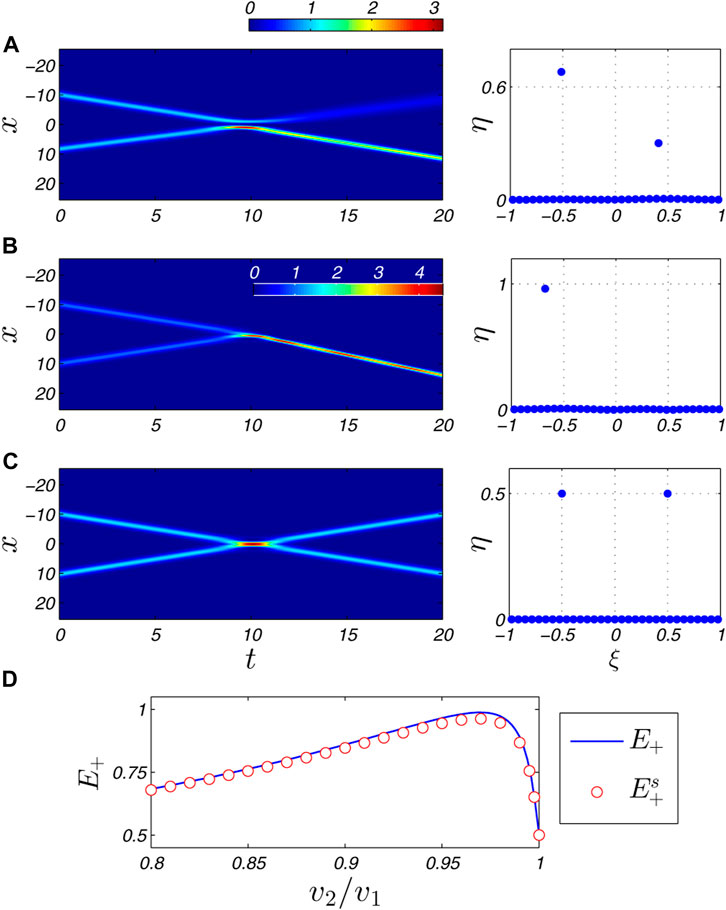
FIGURE 2. (Color online) Nonlinear spectral analysis of the soliton recombination at a repulsive Gaussian potential barrier. The parameters of the incident soliton pairs include k₁ = k₂ = 1, v₁ = 1, x₁ = 10, and (A) v₂ = −0.8; (B) v₂ = −0.97; (C) v₂ = −1. The relation x₁/v₁ = x₂/v₂ is required. The left panels show the spatial-temporal intensities |ψ(x, t)|² [(A) and (C) have the same colorbar as placed at the top, while (B) has its own insetted colorbar], and the right panels correspondingly present the NFT eigenvalues calculated with ψ(x, t_f = 2x₁/v₁). (D) Comparison of E₊ with $E_{+}^s$ for |v₂/v₁| varying from 0.8 to 1.

3.3 Scattering of soliton molecules at a Gaussian barrier

Two adjacent bright solitons with zero phase difference can form an oscillating bound state, also known as a type of soliton molecules [37–41]. This structure has a periodic internal interaction, which presents more colorful features when it is scatted by the potential barrier [15, 38]. Here we use Eq. 2 with short separation distance between solitons to construct a very good approximation of the two-soliton molecule, and launch this soliton molecule with different initial velocities.

Figure 3 shows the typical simulation results and the eigenvalues of the NFT spectra for the output wave fields. When the incident velocity is low, as seen in Figure 3A, the soliton molecule experiences a nearly-elastic reflection, with a very slight emission of radiation waves. The nonlinear spectrum detects this reflected soliton molecule very well. The two-point solitonic eigenvalues with the same real parts is the sign of a soliton molecule, and they are almost symmetric about the imaginary axis with the initial eigenvalues (not shown here). In Figure 3B, we simulate a mediate-speed soliton molecule scattered by the Gaussian barrier. The scattering process destructs the molecule, leading to the separation of a slow reflected soliton with large amplitude and a fast transmitted soliton with small amplitude. This result is exactly analyzed by the NFT spectrum, with two solitonic eigenvalues representing output of the reflected and transmitted solitons respectively. When a fast soliton molecule collide with the barrier, most of its norm can transmit the barrier with the molecule structure preserved. Figure 3C gives such an example, in which we also see a very small reflected soliton separating from the molecule. The eigenvalues of the outgoing waves also reveal this feature where the left two-point solitonic eigenvalues are for the transmitted molecule while the right individual eigenvalue corresponds to the small reflected soliton.

FIGURE 3

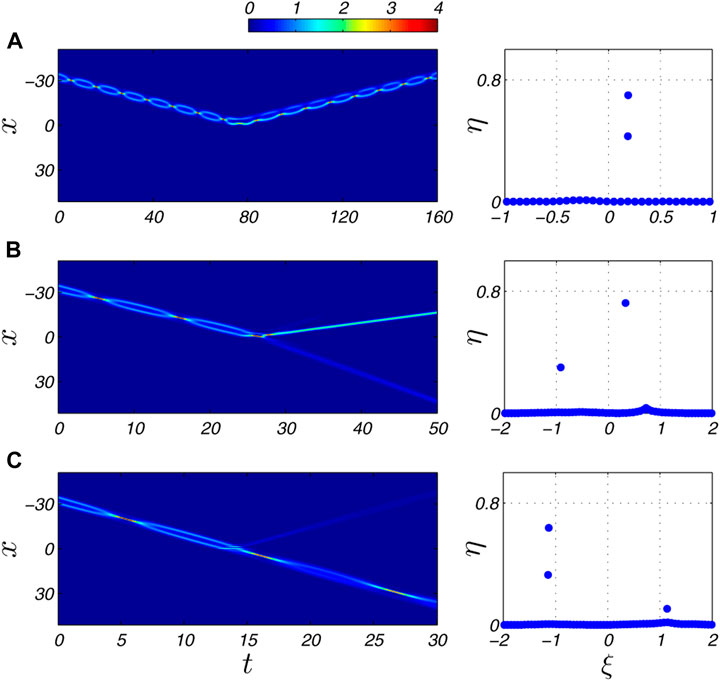
FIGURE 3. (Color online) Nonlinear spectral analysis of the soliton molecule scattered at a repulsive Gaussian potential barrier. The parameters of the soliton molecules include k₁ = k₂ = 1, x₁ = 30, x₂ = 34, and (A) v₁ = v₂ = 0.4; (B) v₁ = v₂ = 1.2; (C) v₁ = v₂ = 2.3. The left panels show the spatial-temporal intensities |ψ(x, t)|² (with the same colorbar as placed at the top), and the right panels correspondingly present the NFT eigenvalues calculated with ψ(x, t_f = 2x₁/v₁).

3.4 Soliton splitting and recombination at a nonlinear potential barrier

In the above sections, we have discussed the scattering of bright solitons at the linear (Gaussian shape) potential barrier, and shown the effectiveness of NFT in analyzing their output wave contents. Hereafter we offer the results for the setup with a nonlinear repulsive potential barrier. The simulations in [25] claim that the use of nonlinear splitter provides a higher sensitivity than its linear counterpart, and a nonlinear localized barrier may be realized by means of the localized Feshbach resonance, as well as in a nonlinear optical waveguide. We implement a nonlinear potential barrier of the form V(x) = q exp (−x²/σ²)|ψ|² with q = 4.0 and σ = 0.14. The similar simulations were performed considering a incident soliton splitting and two oppositely-moving solitons scattering at the nonlinear barrier.

Figure 4 presents our results. In Figure 4A, we compare E_± with $E_{\pm }^s$ for the nonlinear splitter, where with the velocity increasing the incident soliton gradually transmits the barrier, which is similar to the case of the linear splitter. The 50:50 splitting seems to occur at a slower incident velocity. This comparison suggests that the NFT can well detect the transmitted and reflected solitons that dominate the nonlinear wave field, with only slight deviations coming from the emission of radiation waves. In Figure 4B, we provide the data for two-soliton interaction at the nonlinear barrier. The trend from partial to nearly-perfect recombination next to symmetric scattering can also be found with |v₂/v₁| → 1. The difference between E₊ and $E_{+}^s$ is a bit larger than that of the linear splitter since the level of radiation waves is somewhat stronger for the nonlinear splitter, which is indicated by the NFT analysis.

FIGURE 4

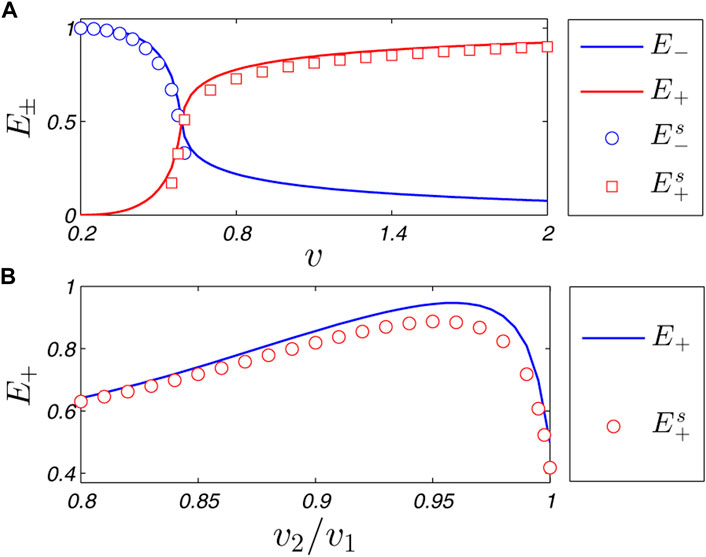
FIGURE 4. (Color online) (A) Comparison of E_± with $E_{\pm }^s$ for a soliton splitting at the nonlinear potential barrier, with its incident velocity varying from 0.2 to 2. Other soliton parameters are chosen the same as in Figure 1. (B) Comparison of E₊ with $E_{+}^s$ for two-soliton interaction at the nonlinear barrier, with the ratio |v₂/v₁| varying from 0.8 to 1. Other soliton parameters are the same as those in Figure 2.

4 Summaries

Our work introduced the basic idea of using NFT to analyze the nonlinear wave contents for the soliton-based matter-wave interferometry at the mean-field level. This idea is benefitting from the nearly integrable nature of the quasi-1D GP equation with a narrow potential barrier (when the normalized atom number fraction near the barrier is very small). We have studied typical cases including the soliton splitting and recombination at the linear and nonlinear Gaussian-shape repulsive barrier (see Figures 1, 2, 4), as well as scattering of the two-soliton molecules (see Figure 3). Our results show that the soliton ingredients can be accurately detected by the discrete solitonic eigenvalues of the nonlinear spectrum from the outputs of the interferometers. In addition, the magnitudes of the dispersive radiation waves separated from the soliton-barrier interactions might also be estimated. We therefore expect the NFT to be implemented as an effective tool in analyzing the simulation results and even the experimental data when applicable.

On the other hand, we envision related explorations such as applying the NFT to analyze the more complicated interferometry setups [23, 27], or considering the influence of random noise on the output data. Using the machine-learning networks for computing the eigenvalue spectra [42] would be another interesting prospect, while this type of technics has been successfully used in the quantum error correction and proved to be efficient to some extent [43, 44].

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

Y-JF, Z-YS, and XY contributed to conception and design of this study. Z-YS and XY performed the numerical simulations. Y-JF performed the spectral analysis. Y-JF wrote the first draft of the manuscript. All authors contributed to manuscript revision, read, and approved the submitted version.

Funding

This work was supported by the National Natural Science Foundation of China (Grant No.11902016), by the Fundamental Research Funds for the Central Universities, and by the Zhuoyue Talent Program of Beihang University. Y-JF wishes to acknowledge the support of R&D Program of Beijing Municipal Education Commission (KM202211417003).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Kivshar YS, Malomed BA. Dynamics of solitons in nearly integrable systems. Rev Mod Phys (1989) 61:763–915. doi:10.1103/revmodphys.61.763

CrossRef Full Text | Google Scholar

2. Kartashov YV, Malomed BA, Torner L. Solitons in nonlinear lattices. Rev Mod Phys (2011) 83:247–305. doi:10.1103/revmodphys.83.247

CrossRef Full Text | Google Scholar

3. Kevrekidis PG, Frantzeskakis DJ, Carretero-González R. Emergent nonlinear phenomena in Bose-Einstein condensates: Theory and experiment. In: Springer Series on Atomic, Optical, and Plasma Physics. Berlin: Springer (2008).

Google Scholar

4. Strecker KE, Partridge GB, Truscott AG, Hulet RG. Formation and propagation of matter-wave soliton trains. Nature (2002) 417:150–3. doi:10.1038/nature747

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Khaykovich L, Schreck F, Ferrari G, Bourdel T, Cubizolles J, Carr LD, et al. Formation of a matter-wave bright soliton. Science (2002) 296:1290–3. doi:10.1126/science.1071021

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Cornish SL, Thompson ST, Wieman CE. Formation of bright matter-wave solitons during the collapse of attractive Bose-Einstein condensates. Phys Rev Lett (2006) 96:170401. doi:10.1103/physrevlett.96.170401

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Lepoutre S, Fouché L, Boissé A, Berthet G, Salomon G, Aspect A, et al. Production of strongly bound ³⁹K bright solitons. Phys Rev A (2016) 94:053626. doi:10.1103/physreva.94.053626

CrossRef Full Text | Google Scholar

8. Mežnaršič T, Arh T, Brence J, Pišljar J, Gosar K, Gosar Ž, et al. Cesium bright matter-wave solitons and soliton trains. Phys Rev A (2019) 99:033625. doi:10.1103/physreva.99.033625

CrossRef Full Text | Google Scholar

9. Nguyen JH, Dyke P, Luo D, Malomed BA, Hulet RG. Collisions of matter-wave solitons. Nat Phys (2014) 10:918–22. doi:10.1038/nphys3135

CrossRef Full Text | Google Scholar

10. Parker NG, Martin AM, Cornish SL, Adams CS. Collisions of bright solitary matter waves. J Phys B (2008) 41:045303. doi:10.1088/0953-4075/41/4/045303

CrossRef Full Text | Google Scholar

11. Sun Z-Y, Gao Y-T, Yu X, Liu Y. Amplification of nonautonomous solitons in the Bose-Einstein condensates and nonlinear optics. EPL (2011) 93:40004. doi:10.1209/0295-5075/93/40004

CrossRef Full Text | Google Scholar

12. Marchant AL, Billam TP, Wiles TP, Yu MMH, Gardiner SA, Cornish SL. Controlled formation and reflection of a bright solitary matter-wave. Nat Commun (2013) 4:1865. doi:10.1038/ncomms2893

PubMed Abstract | CrossRef Full Text | Google Scholar

13. McDonald GD, Kuhn CCN, Hardman KS, Bennetts S, Everitt PJ, Altin P, et al. Bright solitonic matter-wave interferometer. Phys Rev Lett (2014) 113:013002. doi:10.1103/physrevlett.113.013002

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Wales OJ, Rakonjac A, Billam TP, Helm JL, Gardiner SA, Cornish SL. Splitting and recombination of bright-solitary-matter waves. Commun Phys (2020) 3:51. doi:10.1038/s42005-020-0320-8

CrossRef Full Text | Google Scholar

15. Al-Marzoug SM, Al-Amoudi SM, Al Khawaja U, Bahlouli H, Baizakov BB. Scattering of a matter-wave single soliton and a two-soliton molecule by an attractive potential. Phys Rev E (2011) 83:026603. doi:10.1103/physreve.83.026603

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Álvarez A, Cuevas J, Romero FR, Hamner C, Chang JJ, Engels P, et al. Scattering of atomic dark-bright solitons from narrow impurities. J Phys B (2013) 46:065302. doi:10.1088/0953-4075/46/6/065302

CrossRef Full Text | Google Scholar

17. Abdullaev FK, Brazhnyi VA. Solitons in dipolar Bose-Einstein condensates with a trap and barrier potential. J Phys B (2012) 45:085301. doi:10.1088/0953-4075/45/8/085301

CrossRef Full Text | Google Scholar

18. Helm JL, Billam TP, Gardiner SA. Bright matter-wave soliton collisions at narrow barriers. Phys Rev A (2012) 85:053621. doi:10.1103/physreva.85.053621

CrossRef Full Text | Google Scholar

19. Martin AD, Ruostekoski J. Quantum dynamics of atomic bright solitons under splitting and recollision, and implications for interferometry. New J Phys (2012) 14:043040. doi:10.1088/1367-2630/14/4/043040

CrossRef Full Text | Google Scholar

20. Cuevas J, Kevrekidis PG, Malomed BA, Dyke P, Hulet RG. Interactions of solitons with a Gaussian barrier: Splitting and recombination in quasi-one-dimensional and three-dimensional settings. New J Phys (2013) 15:063006. doi:10.1088/1367-2630/15/6/063006

CrossRef Full Text | Google Scholar

21. Polo J, Ahufinger V. Soliton-based matter-wave interferometer. Phys Rev A (2013) 88:053628. doi:10.1103/physreva.88.053628

CrossRef Full Text | Google Scholar

22. Helm JL, Rooney SJ, Weiss C, Gardiner SA. Splitting bright matter-wave solitons on narrow potential barriers: Quantum to classical transition and applications to interferometry. Phys Rev A (2014) 89:033610. doi:10.1103/physreva.89.033610

CrossRef Full Text | Google Scholar

23. Helm JL, Cornish SL, Gardiner SA. Sagnac interferometry using bright matter-wave solitons. Phys Rev Lett (2015) 114:134101. doi:10.1103/physrevlett.114.134101

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Sun Z-Y, Kevrekidis PG, Krüger P. Mean-field analog of the Hong-Ou-Mandel experiment with bright solitons. Phys Rev A (2014) 90:063612. doi:10.1103/physreva.90.063612

CrossRef Full Text | Google Scholar

25. Sakaguchi H, Malomed BA. Matter-wave soliton interferometer based on a nonlinear splitter. New J Phys (2016) 18:025020. doi:10.1088/1367-2630/18/2/025020

CrossRef Full Text | Google Scholar

26. Grimshaw CL, Billam TP, Gardiner SA. Soliton interferometry with very narrow barriers obtained from spatially dependent dressed states. Phys Rev Lett (2022) 129:040401. doi:10.1103/physrevlett.129.040401

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Manju P, Hardman KS, Wigley PB, Close JD, Robins NP, Szigeti SS. An atomic Fabry-Perot interferometer using a pulsed interacting Bose-Einstein condensate. Sci Rep (2020) 10:15052. doi:10.1038/s41598-020-71973-0

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Ablowitz MJ, Segur H. Solitons and the inverse scattering transform. Philadelphia: SIAM (1981).

Google Scholar

29. Osborne AR. Nonlinear Ocean waves and the inverse scattering transform. San Diego, CA: Academic (2010).

Google Scholar

30. Turitsyn SK, Prilepsky JE, Le ST, Wahls S, Frumin LL, Kamalian M, et al. Nonlinear Fourier transform for optical data processing and transmission: Advances and perspectives. Optica (2017) 4:307. doi:10.1364/optica.4.000307

CrossRef Full Text | Google Scholar

31. Hasegawa A, Nyu T. Eigenvalue communication. J Lightwave Tech (1993) 11:395–9. doi:10.1109/50.219570

CrossRef Full Text | Google Scholar

32. Chekhovskoy IS, Shtyrina OV, Fedoruk MP, Medvedev SB, Turitsyn SK. Nonlinear Fourier transform for analysis of coherent structures in dissipative systems. Phys Rev Lett (2019) 122:153901. doi:10.1103/physrevlett.122.153901

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Suret P, Tikan A, Bonnefoy F, Copie F, Ducrozet G, Gelash A, et al. Nonlinear spectral synthesis of soliton gas in deep-water surface gravity waves. Phys Rev Lett (2020) 125:264101. doi:10.1103/physrevlett.125.264101

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Sun Z-Y, Yu X. Nearly integrable turbulence and rogue waves in disordered nonlinear Schrödinger systems. Phys Rev E (2021) 103:062203. doi:10.1103/physreve.103.062203

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Sun Z-Y, Yu X. Nonlinear Schrödinger waves in a disordered potential: Branched flow, spectrum diffusion, and rogue waves. Chaos (2022) 32:023108. doi:10.1063/5.0077794

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Yang J. Nonlinear waves in integrable and nonintegrable systems. Philadelphia: SIAM (2010).

Google Scholar

37. Al Khawaja U, Stoof HTC. Formation of matter-wave soliton molecules. New J Phys (2011) 13:085003. doi:10.1088/1367-2630/13/8/085003

CrossRef Full Text | Google Scholar

38. Al Khawaja U. Stability and dynamics of two-soliton molecules. Phys Rev E (2010) 81:056603. doi:10.1103/physreve.81.056603

CrossRef Full Text | Google Scholar

39. Boudjemâa A, Al Khawaja U. Stability of N-soliton molecules in dispersion-managed optical fibers. Phys Rev A (2013) 88:045801. doi:10.1103/physreva.88.045801

CrossRef Full Text | Google Scholar

40. Sun Z-Y, Gao Y-T, Yu X, Liu W-J, Liu Y. Bound vector solitons and soliton complexes for the coupled nonlinear Schrödinger equations. Phys Rev E (2009) 80:066608. doi:10.1103/physreve.80.066608

PubMed Abstract | CrossRef Full Text | Google Scholar

41. Sun Z-Y, Gao Y-T, Yu X, Liu Y. Dynamics of the Manakov-typed bound vector solitons with random initial perturbations. Ann Phys (NY) (2012) 327:1744–60. doi:10.1016/j.aop.2012.03.003

CrossRef Full Text | Google Scholar

42. Sedov EV, Freire PJ, Seredin VV, Kolbasin VA, Kamalian-Kopae M, Chekhovskoy IS, et al. Neural networks for computing and denoising the continuous nonlinear Fourier spectrum in focusing nonlinear Schrödinger equation. Sci Rep (2021) 11:22857. doi:10.1038/s41598-021-02252-9

PubMed Abstract | CrossRef Full Text | Google Scholar

43. Wang H, Song Z, Wang Y, Tian Y, Ma H. Target-generating quantum error correction coding scheme based on generative confrontation network. Quan Inf. Process (2022) 21:280. doi:10.1007/s11128-022-03616-4

CrossRef Full Text | Google Scholar

44. Wang H, Xue Y, Ma Y, Hua N, Ma H. Determination of quantum toric error correction code threshold using convolutional neural network decoders. Chin Phys B (2022) 31:010303. doi:10.1088/1674-1056/ac11e3

CrossRef Full Text | Google Scholar