Versatile non-Hermitian piezoelectric metamaterial beam with tunable asymmetric reflections

Non-Hermitian systems have been widely utilized to achieve specific functions for manipulating abnormal wave motion, such as asymmetric mode switching, unidirectional zero reflection (UZR), and unidirectional perfect absorption (UPA). In this paper, a novel non-Hermitian piezoelectric metamaterial beam is proposed to realize the tunable UZR of flexural waves. The unit cell of this non-Hermitian metamaterial beam consists of a host beam and two pairs of piezoelectric patches shunting different resistor–inductor circuits. Based on the flexural wave theory, the transfer matrix method is introduced to analyze the influence of electrical boundary conditions on the UZR and further clarify the relationship between the UZR and the exceptional point. The exceptional point depends only on the dissipative circuit, and it has no need for the balanced gain and loss like parity–time symmetric metamaterial. Furthermore, the UZR for the desired frequency is realized by applying a genetic algorithm, and its effectivity is experimentally validated. In addition, the non-Hermitian metamaterial beam is designed to realize the UPA of flexural waves. Results indicate that the proposed metamaterial beam is versatile and can achieve tunable manipulations of asymmetric wave propagations and has widely promising applications in many fields, such as non-destructive testing, enhanced sensing, wave isolation and vibration attenuation.

1 Introduction

Controlling elastic wave propagation based on the metamaterial/metasurface has been explored to exhibit wide potential applications in wave isolation and vibration attenuation [1, 2], enhanced sensitivity in non-destructive testing [3], source illusion [4], wave travelling manipulation [5, 6], etc. Metamaterials have been widely investigated by artificially designing their microstructures for achieving highly unusual properties in elastic wave propagations, like broadening the passband [7] or bandgap [8], cloaking wave [9], negative refraction [10], and one-way wave transport [11]. Recently, non-Hermitian metamaterials with loss or/and gain, as open systems, have attracted a lot of attention because the viscosity loss is ubiquitous in natural materials, and more importantly, it has been forming non-Hermitian metamaterials to realize special wave phenomena, such as the skin effect [12], asymmetric mode switching [13], Bloch oscillations [14], and coherent perfect absorption using lasers [15]. The existence of the exceptional point (EP) in non-Hermitian systems is significant for realizing fascinating phenomena of wave propagation.

The EP is a branch point of singularity in a wave scattering matrix or a degeneracy point of non-Hermitian systems, and eigenvalues and eigenvectors simultaneously degenerate at this point [16]. Previously, a non-Hermitian system is usually constructed by a parity–time (PT) symmetric structure with balanced gain and loss, and the EP was first explored in optics [17] to realize the asymmetric reflection. Nowadays, the unusual unidirectional zero reflection (UZR) at the EP of PT-symmetric structure has been pursued to steer elastic waves, like longitudinal waves [18] or flexural waves [19]. However, the PT symmetric condition for balanced gain and loss is too hard to be satisfied in elastic metamaterials since the effective and stable gain is difficult to be provided. Therefore, the passive asymmetric metamaterials only involving the viscosity loss of materials were designed to achieve the UZR associated with the EP [20, 21], but the frequency of the EP or UZR is determined and unchangeable.

How to tune and broaden the working frequency of the UZR is an important issue for their extremely narrow band. Piezoelectric metamaterials are conveniently and accurately tunable because their shunted external circuits can be highly designable and controllable to change the effective mechanical parameters [22–24]. Based on piezoelectric metamaterials, Yi et al. [15] proposed reconfigurable metamaterials to design a coherent perfect absorber for longitudinal and flexural waves, Chen et al. [25] designed a metabeam to realize the tunable UZR of a flexural wave, and Katerina et al. [26] proposed a non-Hermitian metasurface for unidirectional focusing of flexural waves. However, these researches are only focused on numerical simulation, and there is still a lack of the corresponding experimental study for the tunable EP and UZR based on piezoelectric metamaterials. The EP not only can be used for the UZR but also can achieve the unidirectional perfect absorption (UPA), which provides convenience for designing dynamic control devices [27]. To obtain the UPA, Li et al. [28] constructed an asymmetrical metabeam with a pair of loss-induced asymmetrical resonators to find the EP and the critical coupling condition for extremely asymmetric flexural wave absorption based on the intrinsic viscosity loss. However, the EP and the UPA were determined and found to be not tunable for their fabricated asymmetrical metabeam. Therefore, how to accurately design the tunable EP at an arbitrarily desired frequency and simultaneously achieve the UZR or UPA is a challenging topic, but it has great potential applications in the fields of controlling wave travel and wave isolation.

In this paper, a non-Hermitian piezoelectric metamaterial beam is proposed to realize the tunable UZR and UPA of flexural waves by associating with the designable EP. The arrangement of the rest paper is as follows. In Section 2, we design a tunable non-Hermitian piezoelectric metamaterial beam with shunted electric circuits, and based on the flexural wave theory, the highly tunable EP and UZR are demonstrated through the transfer matrix method (TMM). In Section 3, enabled by genetic algorithm (GA), an optimization method is introduced to accurately design the UZR and UPA of flexural wave at the desired frequency in the non-Hermitian piezoelectric metamaterial beam. In addition, the experimental study is conducted to verify the effectivity of UZR. Finally, conclusions are provided in Section 4.

2 Tunable non-Hermitian piezoelectric metamaterial beam

2.1 Design of the non-Hermitian piezoelectric metamaterial beam

In order to extraordinarily achieve the abnormal flexural wave propagation, a non-Hermitian piezoelectric metamaterial beam is designed by a host beam with periodically attached pairs of PZT (lead zirconate titanate) patches, as shown in Figure 1A. There are two pairs of PZT patches bonded on both surfaces of the host beam to form the unit cell, as shown in Figure 1B, and the PZT patches are polarized along the z-axis, and both surfaces are covered with thin electrodes to shunt different resistor-–inductor (RL) circuits. In Figure 1B, the geometric parameters of the unit cell are illustrated as the width $b$, the thicknesses of the host beam and PZT patch, $h_b$ and $h_p$, and the lengths of the five segments, $l_1$, $l_2$, $l_3$, $l_4$, and $l_5$. In addition, the different pairs of PZT patches that shunted different RL circuits in Figure 1B are denoted by green and blue dashed rectangles for shunting $R_1{L}_1$ and $R_2{L}_2$ circuits, and they are simply marked as green and blue boxes in Figure 1A.

FIGURE 1

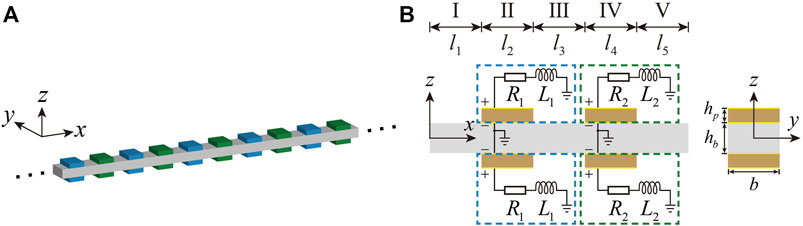
FIGURE 1. (A) Schematic representation of the non-Hermitian piezoelectric metamaterial beam. (B) Unit cell.

2.2 Transmission and reflection of the flexural wave

For the non-Hermitian piezoelectric metamaterial beam, based on the Euler–Bernoulli beam theory, its governing equation of the flexural wave can be written as follows:

$\frac{{\partial }^2}{\partial x^2}\left(D\left(x\right)\frac{{\partial }^2}{\partial x^2}w\left(x,t\right)\right)+\rho \left(x\right)\frac{{\partial }^2}{\partial t^2}w\left(x,t\right)=0,(1)$

where $w\left(x,t\right)$ is the deflection in the z-axis, and $D\left(x\right)$ and $\rho \left(x\right)$, respectively, denote the bending stiffness and density per length. The constitutive equations of the PZT patch can be expressed as follows [29, 30]:

$\left[\begin{array}{l}{S}_1\\ D_3\end{array}\right]=\left[\begin{array}{cc}{s}_{11}^E& d_{31}\\ d_{31}& {\epsilon }_{33}^T\end{array}\right]\left[\begin{array}{l}{T}_1\\ E_3\end{array}\right],(2)$

where subscripts 1, 2, and 3 correspond to x, y, and z axes, respectively; $S_1$ and $T_1$ are normal strain and normal stress along the x-axis; $D_3$ and $E_3$ are electric displacement and the electric field along the z-axis; $s_{11}^E$, $d_{31}$, and ${\epsilon }_{33}^T$ are the compliance coefficients of PZT under a constant electric field intensity, the piezoelectric constant, and dielectric constant of PZT under constant stress, respectively. For harmonic wave propagation, the equivalent elastic modulus of the PZT patch for the shunting $R_i{L}_i$ circuit can be obtained by the following equation [30]:

$E_p^i=\frac{h_p\left(1+\mathrm{j}\omega Z_i{C}_p^T\right)}{h_p{s}_{11}^E\left(1+\mathrm{j}\omega Z_i{C}_p\right)-\mathrm{j}\omega Z_i{d}_{31}^{2}A},\left(i=\mathrm{1,2}\right),(3)$

where $\mathrm{j}=\sqrt{-1}$ is the imaginary unit, $C_p^T={\epsilon }_{33}^{T}A/h_p$ is the electrical capacitance of PZT under constant stress, $Z_i=R_i+\mathrm{j}\omega L_i$ is the electrical impedance of the shunting $R_i{L}_i$ circuit, and A is the area of the electrode.

As shown in Figure 1B, in each unit cell, $D\left(x\right)$ and $\rho \left(x\right)$ in Eq. 1 can be separately determined by the following expression:

$D\left(x\right)=\left\{\begin{array}{cc}\frac{E_{b}b{h}_b^3}{12},& \mathrm{s}\mathrm{e}\mathrm{g}\mathrm{m}\mathrm{e}\mathrm{n}\mathrm{t}Ⅰ,Ⅲ,Ⅴ,\\ \frac{E_{b}b{h}_b^3+E_p^{i}b\left[{\left(h_b+2h_p\right)}^3-h_b^3\right]}{12},& \mathrm{s}\mathrm{e}\mathrm{g}\mathrm{m}\mathrm{e}\mathrm{n}\mathrm{t}Ⅱ,Ⅳ,\end{array}\right.(4)$

and

$\rho \left(x\right)=\left\{\begin{array}{cc}{\rho }_{b}b{h}_b,& \mathrm{s}\mathrm{e}\mathrm{g}\mathrm{m}\mathrm{e}\mathrm{n}\mathrm{t}Ⅰ,Ⅲ,Ⅴ,\\ {\rho }_{b}b{h}_b+2{\rho }_{p}b{h}_p,& \mathrm{s}\mathrm{e}\mathrm{g}\mathrm{m}\mathrm{e}\mathrm{n}\mathrm{t}Ⅱ,Ⅳ,\end{array}\right.(5)$

where $E_b$ is the elastic modulus of the host beam, and ${\rho }_b$ and ${\rho }_p$ are the densities of the host beam and PZT, respectively.

The plane wave solution for Eq. 1 can be written as follows:

$w\left(x,t\right)={\displaystyle \sum }_{n=1}^4{W_{n}e}^{{\xi }_{n}x-\mathrm{j}\omega t},(6)$

where $W_n$ is the wave amplitude, ${\xi }_{\mathrm{1,2}}$ and ${\xi }_{\mathrm{3,4}}$ separately represent the wave number of the propagating flexural wave and evanescent flexural wave, which can be obtained by substituting Eq. 6 into Eq. 1 and expressed as ${\xi }_{\mathrm{1,2}}=\pm \mathrm{j}\sqrt[4]{\frac{\rho {\omega }^2}{D}},{\xi }_{\mathrm{3,4}}=\pm \sqrt[4]{\frac{\rho {\omega }^2}{D}}.$

To analyze the transmission and reflection property of the flexural wave in the non-Hermitian piezoelectric metamaterial beam, TMM is introduced to solve the governing equation of the flexural wave in Eq. 1. For a unit cell, its state vector X is defined as the following equation:

$\mathbf{X}={\left[w,\frac{\partial w}{\partial x},M,T\right]}^{\mathrm{T}},(7)$

where M and T are the shear force and bending moment, respectively.

Since both M and T are the functions of $w$, the state vector X can be written as the following equation:

${\mathbf{X}}^k={\mathbf{A}}^k{\mathbf{W}}^k,\left(k=b\mathrm{o}\mathrm{r}p\right),(8)$

where the superscript b or p represents the segment without PZT or with PZT; the matrix A^k is expressed as follows:

${\mathbf{A}}^k=\left[\begin{array}{cccc}1& 1& 1& 1\\ {\xi }_1^k& {\xi }_2^k& {\xi }_3^k& {\xi }_4^k\\ D^k{\left({\xi }_1^k\right)}^2& D^k{\left({\xi }_2^k\right)}^2& D^k{\left({\xi }_3^k\right)}^2& D^k{\left({\xi }_4^k\right)}^2\\ D^k{\left({\xi }_1^k\right)}^3& D^k{\left({\xi }_2^k\right)}^3& D^k{\left({\xi }_3^k\right)}^3& D^k{\left({\xi }_4^k\right)}^3\end{array}\right](9)$

and

${\mathbf{W}}^k\left(x\right)={\left[W_1^k{e}^{\mathrm{j}{\xi }_1^{k}x},W_2^k{e}^{\mathrm{j}{\xi }_2^{k}x},W_3^k{e}^{\mathrm{j}{\xi }_3^{k}x},W_4^k{e}^{\mathrm{j}{\xi }_4^{k}x}\right]}^{\mathrm{T}}.(10)$

For simplicity, $x_m={\displaystyle \sum }_1^m{l}_m$ is defined to represent the positions of the interfaces between different segments. For segment Ⅰ, since there are no PZT patches attached on it, the state vectors between its two boundaries can be related through the transfer matrix T₁:

${\mathbf{X}}^b\left(x_1\right)={\mathbf{T}}_1{\mathbf{X}}^b\left(0\right).(11)$

Substituting Eq. 8 into Eq. 11, the transfer matrix can be derived as ${\mathbf{T}}_1={\mathbf{A}}^b{\mathbf{P}}_{l_1}^b{\left[{\mathbf{A}}^b\right]}^{-1}$, in which ${\mathbf{P}}_{l_1}^b$ is the propagating matrix. For the mth segment, the propagating matrix ${\mathbf{P}}_{l_m}^k$ is related to the wave amplitude vectors with the relationship ${\mathbf{W}}^k\left(x_m\right)={\mathbf{P}}_{l_m}^k{\mathbf{W}}^k\left(x_{m-1}\right)$, and its uniform expression can be expressed as follows:

${\mathbf{P}}_{l_m}^k=\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}\left\{e^{{\xi }_1^k{l}_m},e^{{\xi }_2^k{l}_m},e^{{\xi }_3^k{l}_m},e^{{\xi }_4^k{l}_m}\right\}.(12)$

Similarly, the transfer matrices for segment Ⅲ and segment Ⅴ can be expressed as follows:

$\begin{array}{l}{\mathbf{T}}_3={\mathbf{A}}^b{\mathbf{P}}_{l_3}^b{\left[{\mathbf{A}}^b\right]}^{-1},\\ {\mathbf{T}}_5={\mathbf{A}}^b{\mathbf{P}}_{l_5}^b{\left[{\mathbf{A}}^b\right]}^{-1}.\end{array}(13)$

For segment Ⅱ with PZT patches, considering the continuity conditions of the state vector X at positions $x_1$ and $x_2$, i.e.,

$\begin{array}{l}{\mathbf{X}}^b\left(x_1\right)={\mathbf{X}}^p\left(x_1\right),\\ {\mathbf{X}}^b\left(x_2\right)={\mathbf{X}}^p\left(x_2\right),\end{array}(14)$

the transfer matrix can be derived from Eq. 14 as follows:

${\mathbf{T}}_2={\mathbf{A}}^p\left(x_2\right){\mathbf{P}}_{l_2}^p{\left[{\mathbf{A}}^p\left(x_1\right)\right]}^{-1}.(15)$

Similarly, the transfer matrix for segment Ⅳ can be expressed as follows:

${\mathbf{T}}_4={\mathbf{A}}^p\left(x_4\right){\mathbf{P}}_{l_4}^p{\left[{\mathbf{A}}^p\left(x_3\right)\right]}^{-1}.(16)$

Finally, with the transfer matrix of the unit cell $\mathbf{T}={\mathbf{T}}_5{\mathbf{T}}_4{\mathbf{T}}_3{\mathbf{T}}_2{\mathbf{T}}_1$, the relationship of state vectors between both boundaries of the unit cell can be ${\mathbf{X}}^b\left(x_5\right)=\mathbf{T}{\mathbf{X}}^b\left(0\right)$ and the relationship of wave amplitude vectors is ${\mathbf{W}}^b\left(x_5\right)={\left({\mathbf{A}}^b\right)}^{-1}\mathbf{T}{\mathbf{A}}^b{\mathbf{W}}^b\left(0\right)=\mathbf{M}{\mathbf{W}}^b\left(0\right)$. When an incident flexural wave is with amplitude $W_1^b\left(0\right)$ from the left, the reflection coefficient $r_l$ and transmission coefficient $t_l$ can be defined separately by the reflected wave amplitude $W_2^b\left(0\right)$ and the transmitted wave amplitude $W_1^b\left(x_5\right)$ to be $r_l=W_2^b\left(0\right)/W_1^b\left(0\right)$ and $t_l=W_1^b\left(x_5\right)/W_1^b\left(0\right)$. Thus, the relationship of wave amplitude vectors can be written as follows:

$\left[\begin{array}{c}{t}_l\\ 0\\ t_l^{*}\\ 0\end{array}\right]=\left[\begin{array}{cccc}{M}_{11}& M_{12}& M_{13}& M_{14}\\ M_{21}& M_{22}& M_{23}& M_{24}\\ M_{31}& M_{32}& M_{33}& M_{34}\\ M_{41}& M_{42}& M_{43}& M_{44}\end{array}\right]\left[\begin{array}{c}1\\ r_l\\ 0\\ r_l^{*}\end{array}\right],(17)$

where the superscript ‘$*$’ represents the evanescent flexural wave. In terms of Eq. 17, the reflection coefficient $r_l$ for an incident flexural wave from the left can be derived as $r_l=\frac{-M_{44}{M}_{21}+M_{24}{M}_{41}}{M_{44}{M}_{22}-M_{42}{M}_{24}}$. Similarly, the reflection coefficient $r_r$ for an incident flexural wave from the right can be written as $r_r=\frac{M_{44}{M}_{12}-M_{42}{M}_{14}}{M_{44}{M}_{22}-M_{42}{M}_{24}}$. To characterize the asymmetry reflection of the metamaterial, a contrast ratio $\alpha$ is defined by the following expression:

$\alpha =\frac{r_r}{r_l}=\frac{M_{44}{M}_{12}-M_{42}{M}_{14}}{-M_{44}{M}_{21}+M_{24}{M}_{41}}.(18)$

The transmission coefficients of incident waves from the left and the right are the same, i.e., $t_l=t_r=t_{lr}$. Thus, the scattering matrix $\mathbf{S}$ of the unit cell is as follows:

$\mathbf{S}=\left[\begin{array}{cc}{t}_l& r_r\\ r_l& t_r\end{array}\right]=\left[\begin{array}{cc}{t}_{lr}& r_r\\ r_l& t_{lr}\end{array}\right].(19)$

2.3 EP and UZR

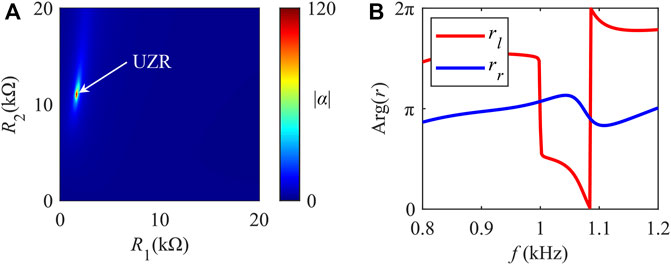
In order to demonstrate the realization of the EP and UZR, an aluminum (AL6061) beam is attached to the two pairs of PZT (PZT-5H) patches with shunted LR circuits to form the unit cell for studying the electromechanical coupling effect on wave motion. The geometric and material parameters of the metamaterial beam are listed in Table 1 and Table 2, respectively. Since there are four electrical parameters controlled by the external RL circuits, it is difficult to simultaneously study their effect on the asymmetric reflection of the metamaterial beam. To normalize the inductance of the shunt circuits, a resonant inductance $L_r$ is used, which is expressed as follows:

$L_r=\frac{1}{4{\pi }^2{f}^2{C}_p^T},(20)$

in which $f$ is the frequency of the incident flexural wave. If the frequency of the incident wave is set $f=1\mathrm{k}\mathrm{H}\mathrm{z}$, for the unit cell in Figure 1B, the resistances are changed at three cases: (1) $R_1=R_2=0$; (2) $R_1=R_2=100\mathrm{\Omega }$; and (3) $R_1=100\mathrm{\Omega },R_2=500\mathrm{\Omega }$. Then, the absolute values of the contrast ratio $\left|\alpha \right|$ for the unit cell can be calculated by the TMM with varying inductances, as shown in Figure 2. Without resistances in shunted circuits, as shown in Figure 2A, $\left|\alpha \right|$ remains constant and is equal to 1 for indicating $\left|r_l\right|=\left|r_r\right|$. For the two circuits with the same non-zero resistance, for example, $R_1=R_2=100\mathrm{\Omega }$, $\left|\alpha \right|$ is changed with varying inductances $L_1$ and $L_2$, as shown in Figure 2B. It means that the introduction of resistance as loss is essential for asymmetric reflection. Furthermore, if two resistances are set to $R_1\ne R_2$ and $R_1=100\mathrm{\Omega },R_2=500\mathrm{\Omega }$, the asymmetric reflection phenomenon can be achieved and illustrated by the highest value of $\left|\alpha \right|$ in Figure 2C. In addition, the maximum value of $\left|\alpha \right|$ is reached when the inductances $L_1$ and $L_2$ are slightly larger than the resonant inductance $L_r$.

TABLE 1

TABLE 1. Geometric parameters (mm).

TABLE 2

TABLE 2. Material parameters.

FIGURE 2

FIGURE 2. $\left|\alpha \right|$ varying with inductances $L_1$ and $L_2$ at (A) case 1: $R_1=R_2=0$, (B) case 2: $R_1=R_2=100\mathrm{\Omega }$, and (C) case 3: $R_1=100\mathrm{\Omega },R_2=500\mathrm{\Omega }$.

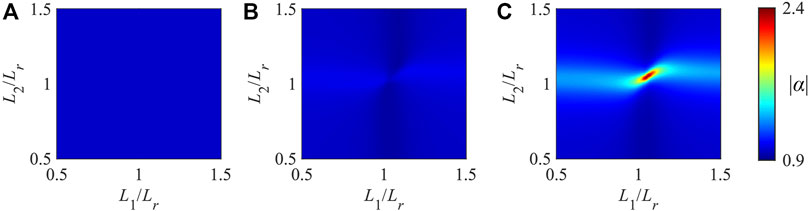
When the UZR appears, the contrast ratio $\left|\alpha \right|$ tends to be infinite or zero. To realize the UZR for the incident wave with frequency 1 kHz, setting two inductances $L_1$ and $L_2$ as $0.9L_r$ and $1.1L_r$ and altering resistances $R_1$ and $R_2$ in a range from 0 to 20 kΩ, the value of $\left|\alpha \right|$ is calculated by the TMM, as shown in Figure 3A, in which the UZR with extremely high $\left|\alpha \right|$ is clearly observed. To show the UZR is associated with the EP, by setting the inductance and resistance parameters to be such parameters corresponding to the observed UZR in Figure 3A but varying the incident wave frequency f, the reflection coefficients are calculated by the TMM, and their phases are shown in Figure 3B. In Figure 3B, there is an abrupt phase shift of π for $r_l$ at 1 kHz, which is a feature of the EP. To further confirm that the UZR corresponds to the EP, the eigenvalues of the scattering matrix $\mathbf{S}$ in Eq. 19 are calculated, as shown in Figure 4. It is obvious that there is a coalescence at 1 kHz, indicating the UZR is associated with the EP [25, 31].

FIGURE 3

FIGURE 3. (A) $\left|\alpha \right|$ varying with resistances $R_1$ and $R_2$. (B) Phases of reflection coefficients.

FIGURE 4

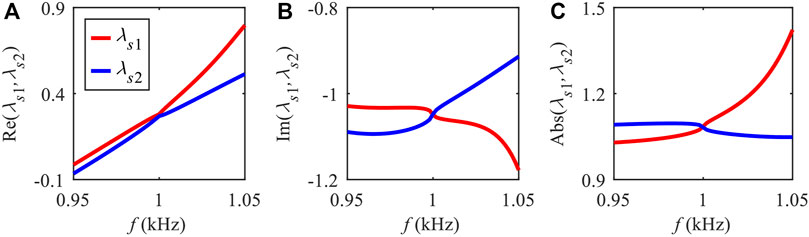
FIGURE 4. Eigenvalues of the scattering matrix: (A) real, (B) imaginary part, and (C) the absolute value.

3 Accurate designs for the UZR and UPA

3.1 Optimization algorithm for the UZR

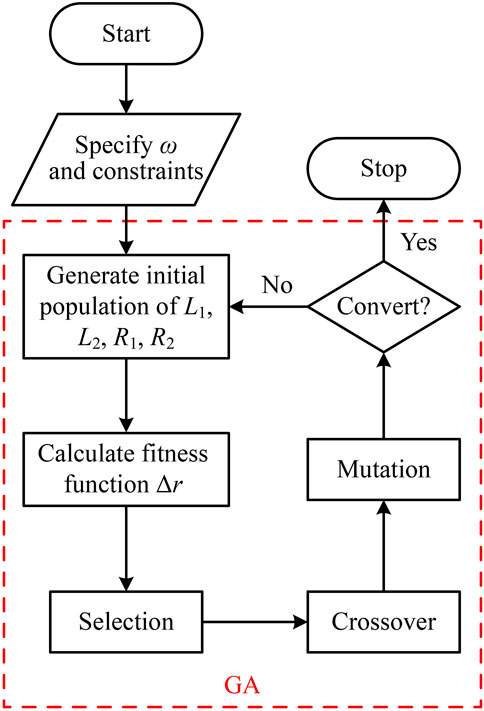
Since the frequency of the UZR is strongly dependent on the electrical parameters of the shunting RL circuits and is achieved by sweeping these parameters in large ranges, as illustrated in Figure 2 and Figure 3, the process of finding the UZR is very time-consuming and computationally expensive. It is necessary to introduce efficient algorithms to accelerate the design process [32, 33]. Therefore, we propose an optimization method to accurately design the UZR in the non-Hermitian piezoelectric metamaterial beam. The optimization problem for searching the proper parameters of shunting RL circuits can be expressed as follows:

$\begin{array}{c}\max \Delta r\left(L_1,L_2,R_1,R_2\right)=\left|r_r\left(L_1,L_2,R_1,R_2\right)\right|-\left|r_l\left(L_1,L_2,R_1,R_2\right)\right|\\ \begin{array}{cc}s.t.& \left|t\left(L_1,L_2,R_1,R_2\right)\right|>t_{\min },\end{array}\\ L_1,L_2\in \left[{\beta }_1{L}_r,{\beta }_2{L}_r\right],\\ R_1,R_2\in \left[R_{\min },R_{\max }\right],\end{array}(21)$

where $t_{\min }$ is defined as the minimum absolute value of the transmission coefficient, and ${\beta }_1{L}_r$, ${\beta }_2{L}_r$, $R_{\min }$, and $R_{\max }$ limit the selecting ranges of the corresponding electrical parameters, and GA is introduced to solve the optimization problem by MATLAB software. In addition, the TMM is not suitable to handle the structure with finite unit cells for numerical instability; thus, the finite element method (FEM) is used by the commercial software COMSOL to solve the problem of the flexural wave propagation in the non-Hermitian piezoelectric metamaterial beam. The flowchart of the optimization process for the aimed frequency $f_{\mathrm{a}\mathrm{i}\mathrm{m}}$ of the UZR is drawn in Figure 5. The interface between the FEM and GA is connected by COMSOL LiveLink to include the GA of MATLAB in the FEM calculation by COMSOL. Concretely, it can transfer the electrical parameters generated by GA codes to the COMSOL program, and then, it returns the reflection and transmission coefficients calculated by the FEM to GA codes. The detailed optimization process for the UZR is predicted in the red-dashed rectangle in Figure 5.

FIGURE 5

FIGURE 5. Flowchart of the optimization process.

For a five-cell metamaterial beam, if the aimed frequency of the UZR is determined as $f_{\mathrm{a}\mathrm{i}\mathrm{m}}=4\mathrm{k}\mathrm{H}\mathrm{z}$ and other parameters are set as $t_{\min }=0.5$, ${\beta }_1=0.8$, ${\beta }_2=1.2$, $R_{\min }=0$, and $R_{\max }=500\mathrm{\Omega }$, the optimization problem is to obtain the electric parameters of shunting RL circuits for realizing the UZR at the aimed frequency. For the GA optimization, the population size is 100, elite count is 5, and crossover fraction is 0.8. The optimization stops if the following possibilities occur: A) the average relative change in the best fitness function over 10 generations is less than or equal to $1\times {10}^{-4}$ or B) the generation is over 500. After the optimization process, the optimized electrical parameters for the UZR at $f_{\mathrm{a}\mathrm{i}\mathrm{m}}=4\mathrm{k}\mathrm{H}\mathrm{z}$ are $L_1=0.97L_r$, $L_2=0.83L_r$, $R_1=471\mathrm{\Omega }$, and $R_2=28\mathrm{\Omega }$. Based on these optimized parameters, the reflection coefficients from both sides of the metamaterial can be calculated by the FEM and are shown in Figure 6A. The results show that the left reflection coefficient $\left|r_l\right|$ and the right reflection coefficient $\left|r_r\right|$ are totally different when the frequency of incident waves is around $f_{\mathrm{a}\mathrm{i}\mathrm{m}}$. At $f_{\mathrm{a}\mathrm{i}\mathrm{m}}$, the values of $\left|r_l\right|$ and $\left|r_r\right|$ are 0.014 and 0.158, respectively, which means that the UZR appears since $\left|r_l\right|$ tends to become zero. Moreover, the wave fields are shown in Figure 6B by the squared absolute value ${\left|w\right|}^2$. The top panel in Figure 6B shows the incident harmonic wave with the frequency $f_{\mathrm{a}\mathrm{i}\mathrm{m}}$ from the left, and ${\left|w\right|}^2$ is almost constant at the left side of the metamaterial to indicate no reflected wave to interact with the incident wave. However, for the incident wave from the right, as shown in the bottom panel of Figure 6B, the interference pattern appears at the right side of the metamaterial to indicate the existence of the reflected wave.

FIGURE 6

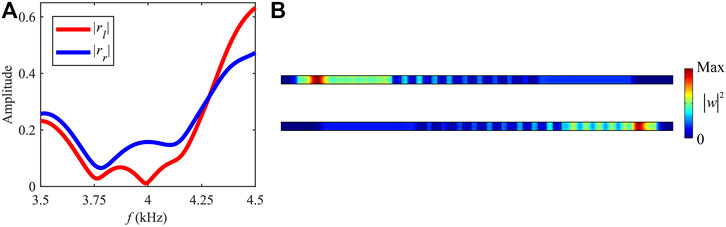
FIGURE 6. (A) Reflection coefficients of the metamaterial with optimized parameters. (B) Wave fields for the incident flexural waves with the frequency $f_{\mathrm{a}\mathrm{i}\mathrm{m}}$ from the left and right sides.

3.2 Optimized design for the UPA

For the non-Hermitian piezoelectric metamaterial beam, the transmission coefficients are the same no matter from which direction the wave is incident, the right or the left. It means the metamaterial beam is reciprocal. Therefore, the asymmetric absorption can be naturally realized when the contrast ratio $\alpha$ is not equal to 1. To quantitatively study the asymmetric absorption property, the absorptance is defined by the following expression:

$A_i=1-t_i^2-r_i^2,(22)$

where the subscripts $i=l$ and $r$ represent the incident directions. Thus, by elaborately designing the electrical parameters of the shunting RL circuits, if a perfect absorption $\left(A\ge 99\%\right)$ of the incident flexural wave can be obtained, the contrast ratio should be large enough to realize the UPA. Similarly, the electrical parameters of the shunting RL circuits for realizing the UPA at the aimed frequency can be optimized by the following expression:

$\begin{array}{c}\begin{array}{cc}\max & A_l=1-t_l^2-r_l^2.\end{array}\\ \begin{array}{cc}\mathrm{s}.\mathrm{t}.& A_l\ge 99\%,\end{array}\\ L_1,L_2\in \left[{\beta }_1{L}_r,{\beta }_2{L}_r\right],\\ R_1,R_2\in \left[R_{\min },R_{\max }\right].\end{array}(23)$

The optimization route for the UPA is consistent with that for the UZR, as shown in Figure 5, except for that the fitness function is replaced by $A_l$ and a new constraint for $A_l$ is added. For the same five-cell metamaterial beam, if the optimization problem is to realize the UPA at an aim frequency $f_{\mathrm{a}\mathrm{i}\mathrm{m}}=4\mathrm{k}\mathrm{H}\mathrm{z}$, the parameters of optimized ranges are set as ${\beta }_1=0.7$, ${\beta }_2=1.3$, $R_{\min }=0$, and $R_{\max }=500\mathrm{\Omega }$. After the optimized process, the electrical parameters for the UPA are obtained as $L_1=1.12L_r$, $L_2=1.21L_r$, $R_1=295\mathrm{\Omega }$, and $R_2=195\mathrm{\Omega }$, and the corresponding absorptance is $A_l=99.9\%$ for the left incident wave, but $A_r=56.4\%$ for the right incident wave to indicate that the UPA is achieved. The transmission and reflection coefficients for the left and right incident flexural waves are calculated by the FEM, and their absolute values are shown in Figure 7A, in which $\left|t\right|=\left|t_l\right|=\left|t_{lr}\right|$ because of the reciprocity. Far away from the UPA, i.e., 4 kHz, the absolute values of the reflection coefficients $\left|r_l\right|$ and $\left|r_r\right|$ are nearly the same. However, as the frequency is close to $4\mathrm{k}\mathrm{H}\mathrm{z}$, $\left|r_l\right|$ drops rapidly and reaches the minimum value, which tends to be zero, while $\left|r_r\right|$ remains large. In addition, the squared absolute value of the out-of-plane displacement ${\left|w\right|}^2$ at $f_{\mathrm{a}\mathrm{i}\mathrm{m}}$ is also plotted in Figure 7B to demonstrate the UPA. As shown in the top panel of Figure 7B, when the flexural wave is incident from the left, the value of ${\left|w\right|}^2$ is very small on the right side of the metamaterial and remains constant in the left side, and it indicates that the incident wave is almost totally absorbed. When the incident wave is from the right, as shown in the bottom panel of Figure 7B, in the right side of the metamaterial, ${\left|w\right|}^2$ is very large and the interference pattern can be observed, and it indicates that a large part of the incident wave is reflected.

FIGURE 7

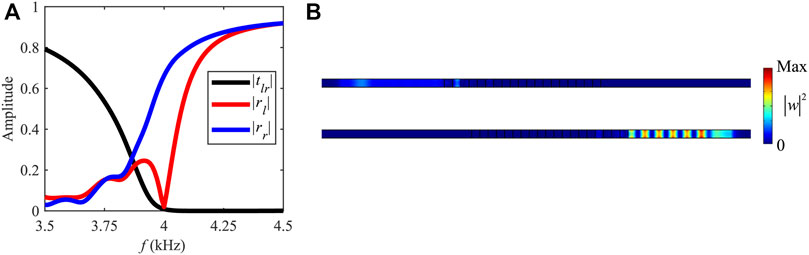
FIGURE 7. (A) Amplitudes of transmission and reflection coefficients. (B) Wave field ${\left|w\right|}^2$ for the incident flexural wave with the frequency $f_{\mathrm{a}\mathrm{i}\mathrm{m}}$ from the left and right sides.

3.3 Experiment verification

An experiment is carried out to verify the optimization method for the UZR. The experimental setup is shown in Figure 8A. The specimen with the same geometric and material parameters listed in Table 1 and Table 2 was fabricated and hung up to ensure a free boundary condition. Both ends of the specimen were attached to the blue tack to minimize reflected waves from boundaries. PZT patches are glued on the aluminum beam periodically, and each PZT patch is shunted with an independent RL circuit. The electric parameters are the same as the optimized results in Section 3.1. Antoniou’s circuit was applied to realize the adjustable inductor, as shown in Figures 8B,C. A DC power supply (JWY-30B) was used to supply constant voltage for the operational amplifiers. A 5.5-cycle tone burst with a central frequency of $4\mathrm{k}\mathrm{H}\mathrm{z}$ was generated using a signal generator (RIGOL, DG1022) and amplified using a power amplifier (Brüel & Kjær, 2718) to actuate a piezoelectric patch to generate a flexural wave. The out-of-plane velocity of the metamaterial beam was captured using a scanning laser Doppler vibrometer (Polytec, PSV-400).

FIGURE 8

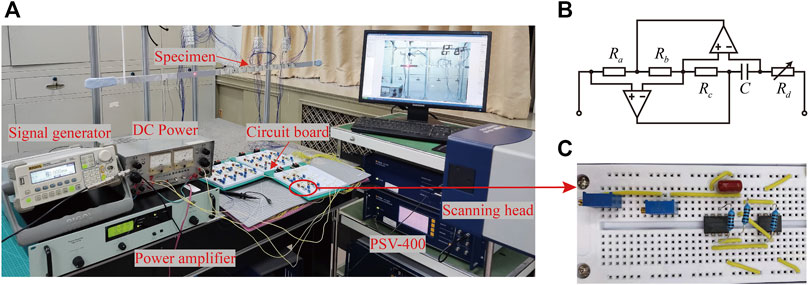
FIGURE 8. (A) Experimental setup. (B) Schematic representation of Antoniou’s circuit. (C) Realization of Antoniou’s circuit.

The incident and reflected waves are extracted from the measured data, and their frequency spectra are calculated by the fast Fourier transform (FFT), as shown in Figures 9A,B. In Figure 9A, it is clear that the incident wave has a narrow frequency range with the highest of $4\mathrm{k}\mathrm{H}\mathrm{z}$. In Figure 9B, the normalized frequency amplitude of the reflected wave by the right incident wave reaches a peak of $4\mathrm{k}\mathrm{H}\mathrm{z}$, whereas the amplitude of the reflected wave from the left at $4\mathrm{k}\mathrm{H}\mathrm{z}$ is much lower. For magnifying the difference, the frequency range is zoomed around $4\mathrm{k}\mathrm{H}\mathrm{z}$ and the reflection coefficients are shown in Figure 9C. Although the experimental results are a little different from the FEM results shown in Figure 6A, the tendency of the experimental results is in good agreement with the FEM for the UZR. Therefore, experimental results confirm the validation of the optimization method for designing the abnormal reflection of the non-Hermitian piezoelectric metamaterial beam.

FIGURE 9

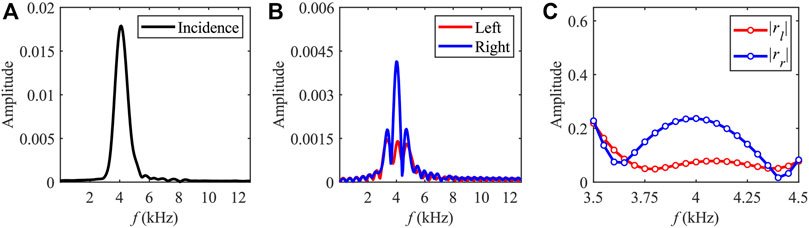
FIGURE 9. FFT coefficients of the (A) incident wave and (B) reflected waves. (C) Reflection coefficients for the left and right incident waves.

4 Conclusion

This paper has proposed a novel non-Hermitian piezoelectric metamaterial beam to realize the tunable UZR and UPA of flexural waves at the desired frequency. An optimization method based on the GA is developed to accurately design the electric parameters of shunting circuits for achieving the UZR or UPA at the aimed frequency, and its effectivity is verified by numerical simulation and an experimental test. With TMM analysis and FEM calculation, the UZR is associated with the EP. The properties of the metamaterial can be highly tuned by the shunting RL circuits to realize the accurate design of the UZR and UPA at the arbitrary frequency. In addition, results indicate that the resistance are important in manipulating the abnormal wave motion in the non-Hermitian system for altering the loss, and the extraordinary performance of PT system can be obtained by only involving the loss. These methods can be developed and applied in the control of other elastic waves, such as Lamb waves and Rayleigh waves. This study paves a way to design novel devices in signal processing, vibration control, and guided-wave based nondestructive testing.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary material; further inquiries can be directed to the corresponding author.

Author contributions

ZW: conceptualization, methodology, software, investigation, and writing—original draft. JY: writing—review and editing, investigation, and formal analysis. RX: writing—review and editing and data curation. JC: methodology, investigation, and resources. ZL: writing—review and editing, supervision, funding acquisition, and project administration.

Funding

This work was supported by the National Natural Science Foundation of China under Grant Nos. 12172008 and 11991033.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Huang Y, Li J, Chen W, Bao R. Tunable bandgaps in soft phononic plates with spring-mass-like resonators. Int J Mech Sci (2019) 151:300–13. doi:10.1016/j.ijmecsci.2018.11.029

CrossRef Full Text | Google Scholar

2. Li H, Hu Y, Chen J, Shou D, Li B. Lightweight meta-lattice sandwich panels for remarkable vibration mitigation: Analytical prediction, numerical analysis and experimental validations. Composites A: Appl Sci Manufacturing (2022) 163:107218. doi:10.1016/j.compositesa.2022.107218

CrossRef Full Text | Google Scholar

3. Rosa MIN, Mazzotti M, Ruzzene M. Exceptional points and enhanced sensitivity in PT-symmetric continuous elastic media. J Mech Phys Sol (2021) 149:104325. doi:10.1016/j.jmps.2021.104325

CrossRef Full Text | Google Scholar

4. Liu Y, Liang Z, Liu F, Diba O, Lamb A, Li J. Source illusion devices for flexural lamb waves using elastic metasurfaces. Phys Rev Lett (2017) 119:034301. doi:10.1103/PhysRevLett.119.034301

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Xia R, Yi J, Chen Z, Li Z. In situ steering of shear horizontal waves in a plate by a tunable electromechanical resonant elastic metasurface. J Phys D: Appl Phys (2020) 53:095302. doi:10.1088/1361-6463/ab5cbc

CrossRef Full Text | Google Scholar

6. Song L, Chen Z, Negahban M, Liang L, Li Z, Wu Z. Ultrathin coding metasurface for underwater wave focusing, branching and self-bending generation with one single actuator. Mod Phys Lett B (2022) 36:2250091. doi:10.1142/S0217984922500919

CrossRef Full Text | Google Scholar

7. Liu Y, Yi J, Li Z, Su X, Li W, Negahban M. Dissipative elastic metamaterial with a low-frequency passband. AIP Adv (2017) 7:065215. doi:10.1063/1.4991034

CrossRef Full Text | Google Scholar

8. Zhang X, Yu H, He Z, Huang G, Chen Y, Wang G. A metamaterial beam with inverse nonlinearity for broadband micro-vibration attenuation. Mech Syst Signal Process (2021) 159:107826. doi:10.1016/j.ymssp.2021.107826

CrossRef Full Text | Google Scholar

9. Ning L, Wang Y-Z, Wang Y-S. Active control cloak of the elastic wave metamaterial. Int J Sol Struct (2020) 202:126–35. doi:10.1016/j.ijsolstr.2020.06.009

CrossRef Full Text | Google Scholar

10. Zhu R, Liu XN, Hu GK, Sun CT, Huang GL. Negative refraction of elastic waves at the deep-subwavelength scale in a single-phase metamaterial. Nat Commun (2014) 5:5510. doi:10.1038/ncomms6510

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Miniaci M, Pal RK, Morvan B, Ruzzene M. Experimental observation of topologically protected helical edge modes in patterned elastic plates. Phys Rev X (2018) 8:031074. doi:10.1103/PhysRevX.8.031074

CrossRef Full Text | Google Scholar

12. Yao S, Wang Z. Edge states and topological invariants of non-Hermitian systems. Phys Rev Lett (2018) 121:086803. doi:10.1103/PhysRevLett.121.086803

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Doppler J, Mailybaev AA, Böhm J, Kuhl U, Girschik A, Libisch F, et al. Dynamically encircling an exceptional point for asymmetric mode switching. Nature (2016) 537:76–9. doi:10.1038/nature18605

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Longhi S. Bloch oscillations in complex crystals with PT symmetry. Phys Rev Lett (2009) 103:123601. doi:10.1103/PhysRevLett.103.123601

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Yi J, Ma Z, Xia R, Negahban M, Chen C, Li Z. Structural periodicity dependent scattering behavior in parity-time symmetric elastic metamaterials. Phys Rev B (2022) 106:014303. doi:10.1103/PhysRevB.106.014303

CrossRef Full Text | Google Scholar

16. Miri M-A, Alù A. Exceptional points in optics and photonics. Science (2019) 363:eaar7709. doi:10.1126/science.aar7709

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Lin Z, Ramezani H, Eichelkraut T, Kottos T, Cao H, Christodoulides DN. Unidirectional invisibility induced by PT-symmetric periodic structures. Phys Rev Lett (2011) 106:213901. doi:10.1103/PhysRevLett.106.213901

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Hou Z, Assouar B. Tunable elastic parity-time symmetric structure based on the shunted piezoelectric materials. J Appl Phys (2018) 123:085101. doi:10.1063/1.5009129

CrossRef Full Text | Google Scholar

19. Wu Q, Chen Y, Huang G. Asymmetric scattering of flexural waves in a parity-time symmetric metamaterial beam. J Acoust Soc Am (2019) 146:850–62. doi:10.1121/1.5116561

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Yi J, Li Z, Negahban M, Xia R, Zhu J. Asymmetric viscoelastic metamaterials for broad bandgap design and unidirectional zero reflection. Mech Syst Signal Process (2022) 162:108101. doi:10.1016/j.ymssp.2021.108101

CrossRef Full Text | Google Scholar

21. Liu Y, Liang Z, Zhu J, Xia L, Mondain-Monval O, Brunet T, et al. Willis metamaterial on a structured beam. Phys Rev X (2019) 9:011040. doi:10.1103/PhysRevX.9.011040

CrossRef Full Text | Google Scholar

22. Xia R, Shao S, Yi J, Zheng K, Negahban M, Li Z. Tunable asymmetric transmission of Lamb waves in piezoelectric bimorph plates by electric boundary design. Compos Struct (2022) 300:116111. doi:10.1016/j.compstruct.2022.116111

CrossRef Full Text | Google Scholar

23. Shao S, Xia R, Li Z. Tunable piezoelectric metasurface for manipulating multi-mode guided waves in plate. Eng Struct (2022) 270:114917. doi:10.1016/j.engstruct.2022.114917

CrossRef Full Text | Google Scholar

24. Xia R, Zhu J, Yi J, Shao S, Li Z. Guided wave propagation in multilayered periodic piezoelectric plate with a mirror plane. Int J Mech Sci (2021) 204:106539. doi:10.1016/j.ijmecsci.2021.106539

CrossRef Full Text | Google Scholar

25. Chen Z, Negahban M, Li Z, Zhu J. Tunable exceptional point and unidirectional zero reflection of a metabeam using shunted piezos. J Phys D: Appl Phys (2019) 53:095503. doi:10.1088/1361-6463/ab5f38

CrossRef Full Text | Google Scholar

26. Stojanoska K, Shen C. Non-Hermitian planar elastic metasurface for unidirectional focusing of flexural waves. Appl Phys Lett (2022) 120:241701. doi:10.1063/5.0097177

CrossRef Full Text | Google Scholar

27. Li X, Chen Y, Zhu R, Huang G. An active meta-layer for optimal flexural wave absorption and cloaking. Mech Syst Signal Process (2021) 149:107324. doi:10.1016/j.ymssp.2020.107324

CrossRef Full Text | Google Scholar

28. Li X, Yu Z, Iizuka H, Lee T. Experimental demonstration of extremely asymmetric flexural wave absorption at the exceptional point. Extreme Mech Lett (2022) 52:101649. doi:10.1016/j.eml.2022.101649

CrossRef Full Text | Google Scholar

29. Wang G, Chen S, Wen J. Low-frequency locally resonant band gaps induced by arrays of resonant shunts with Antoniou’s circuit: Experimental investigation on beams. Smart Mater Struct (2010) 20:015026. doi:10.1088/0964-1726/20/1/015026

CrossRef Full Text | Google Scholar

30. Airoldi L, Ruzzene M. Design of tunable acoustic metamaterials through periodic arrays of resonant shunted piezos. New J Phys (2011) 13:113010. doi:10.1088/1367-2630/13/11/113010

CrossRef Full Text | Google Scholar

31. Shen C, Li J, Peng X, Cummer SA. Synthetic exceptional points and unidirectional zero reflection in non-Hermitian acoustic systems. Phys Rev Mater (2018) 2:125203. doi:10.1103/PhysRevMaterials.2.125203

CrossRef Full Text | Google Scholar

32. Du Z, Chen H, Huang G. Optimal quantum valley Hall insulators by rationally engineering Berry curvature and band structure. J Mech Phys Sol (2020) 135:103784. doi:10.1016/j.jmps.2019.103784

CrossRef Full Text | Google Scholar

33. Luo J, Du Z, Liu C, Mei Y, Zhang W, Guo X. Moving morphable components-based inverse design formulation for quantum valley/spin Hall insulators. Extreme Mech Lett (2021) 45:101276. doi:10.1016/j.eml.2021.101276

CrossRef Full Text | Google Scholar