MSDenoiser: Muti-step adaptive denoising framework for super-resolution image from single molecule localization microscopy

Recent developments in single-molecule localization microscopy (SMLM) enable researchers to study macromolecular structures at the nanometer scale. However, due to the complexity of imaging process, there are a variety of complex heterogeneous noises in SMLM data. The conventional denoising methods in SMLM can only remove a single type of noise. And, most of these denoising algorithms require manual parameter setting, which is difficult and unfriendly for biological researchers. To solve these problems, we propose a multi-step adaptive denoising framework called MSDenoiser, which incorporates multiple noise reduction algorithms and can gradually remove heterogeneous mixed noises in SMLM. In addition, this framework can adaptively learn algorithm parameters based on the localization data without manually intervention. We demonstrate the effectiveness of the proposed denoising framework on both simulated data and experimental data with different types of structures (microtubules, nuclear pore complexes and mitochondria). Experimental results show that the proposed method has better denoising effect and universality.

1 Introduction

The spatial resolution of conventional optical microscopy techniques is limited to about half the wavelength of light. This is mainly due to the diffraction of light: when the light source passes through the optical imaging system, it will form a spot on the focal plane, which we call point spread function (PSF). PSF has normally a central peak of about 200–300 nm in width. Super-resolution microscopy overcomes the resolution limit, and achieves a spatial resolution on the order of 10–20 nm [1]. Among a variety of super-resolution imaging techniques, single-molecule localization microscopy (SMLM) with a straightforward principle and outstanding spatial resolution gains intensive attention from researchers [2]. SMLM is primarily based on the fact that the spatial coordinates of single fluorescent molecules can be established with high precision, if their PSFs do not overlap with each other. Currently, SMLM is able to image subcellular structures (such as nuclear pores complexes, viruses, chromatin complexes, and cytoskeletal filaments) with unprecedented details, and provides great opportunities for biomedical researchers in resolving biological structures at the nanoscale [3]. Unlike many other super-resolution microscopy strategies, such as Stimulated Emission Depletion (STED) [4] and Structured Illumination Microscopy (SIM) [5] that generate grayscale images directly, SMLM requires a series of complicated procedures to processes the raw images and finally reconstructs a final super-resolution image, as can be seen from the description below. Taking single color SMLM as an example, we label biological structures with a specific type of fluorescent molecules, and separate the spatially overlapping fluorescent emissions from these molecules into a series of sub images using the photophysical characteristics of the fluorescent molecules. In each diffraction-limited region, we control to excite only one or two fluorescent molecule. In this case, we can keep a low overlapping probability. After accumulating thousands of image frames of randomly distributed fluorescent molecule images, we apply a proper single molecule localization algorithm to the raw images to precisely find the center locations of each molecule. We combine all of the gathered localization points to create a localization table, which contains at least x, and y positions of individual emitters and sometimes complements by information on localization uncertainty, and emitter intensity, etc. Finally, we use the localization table to render a super-resolution image, which can present super-resolution topography information of the observed structures.

A typical SMLM image is usually suffered from a large amount of mixed and complex background noises, which are originated from autofluorescence, out-of-focus fluorescence, camera noises, as well as non-specific labelled fluorescent molecules. These background noises lead to the degradation of super-resolution image quality and affect the subsequent data analysis and processing [6, 7]. For example, in a cluster analysis task, background noises may cause excessive molecule counts, and this overcounting might lead to bias in cluster analysis and wrong interpretations of the biological findings [8]. Therefore, the localization table in SMLM should be cleaned before any further quantification, and background noise removal in SMLM data has an important engineering significance.

To remove background noises and improve the quality of super-resolution image, researchers have made many attempts. Usually, they first optimize the hardware in the imaging system to obtain high quality raw images. For example, illumination via Total Internal Reflection Fluorescence (TIRF) is introduced to improve the signal to noise ratio (SNR) of the raw image [9]. And, the selection of image sensors with high sensitivity, such as electron-multiplying charge-coupled device (EMCCD) and scientific complementary metal-oxide semiconductor (sCMOS) cameras, can further improve image SNR [10]. Due to the complexity of the imaging process, a large amount of noises are still introduced into the localization table, and thus should be processed before reconstructing a final super-resolution image. Although many image analysis strategies have been established for conventional fluorescence microscopy images [11, 12], these strategies cannot apply directly to localization-based super-resolution images, because a conventional fluorescence image is composed of pixels or voxels, while an SMLM image is composed of a series of 2D or 3D localization coordinates. The data form of the localization table makes many trivial operations on conventional images (such as thresholding and subtraction) to become challenging. One usual solution to these challenges is to transform the localization table into a grayscale image (that is, a reconstructed super-resolution image), and then perform denoising analysis on the grayscale image. However, this will inevitably lead to a loss of the precise localization information, and affects the analysis results in downstream tasks (such as clustering, co-location analysis) [13]. According to above discussions, it would be greatly beneficial to perform denoising directly from a localization table.

Most of the current denoising methods for localization table are based on clustering algorithms. Andronov et al adopt Voronoi Tessellation for clustering of protein complexes, where the clustered localization points have smaller Voronoi cell areas than the non-clustered points. The Voronoi Tessellation method uses this feature to achieve the purpose of denoising [14]. For another example, a background noise filter is included in the ThunderSTORM plug-in [15], which adopts Density-Based Spatial Clustering of Applications with Noise (DBSCAN) to filter out the localization point with poor localization. However, DBSCAN requires a careful parameter setting on radius and minimum number, which seriously affects the efficiency of denoising [6]. Machine learning-based clustering methods are also propose to denoise the localization data. For example, Williamson et al used neural networks to classify points from localization table as either clustered or non-clustered, based on a sequence of values derived from each point’s nearest-neighbor distances, and the non-clustered points are defined as noise [16]. However, these denoising algorithms can only remove a certain kind of noises, which are not sufficient for the remove of complex heterogeneous background noises. In addition, most of these methods need to determine manually the threshold or parameters, which is difficult and unfriendly for biological researchers.

Inspired by the fusion denoising algorithms and techniques in the field of image and point cloud processing [17–20], here we propose a multi-step adaptive denoising framework for super-resolution localization data, called MSDenoiser. This framework makes full use of the different characteristics of reported denoising algorithms (including Voronoi Tessellation [21], Local Outlier Factor (LOF) [22] and DBSCAN), and gradually removes the free non-polymer localization points, non-polymer localization points near the sample signal point area, and non-specific localization points. To solve the problem of manual parameter determination in the LOF and DBSCAN algorithms, our MSDenoiser framework uses the G-means algorithm to automatically generate a set of clusters with centers, and adaptively estimates the parameters in LOF and DBSCAN algorithms without manual intervention. At the same time, to evaluate the effect of the denoising framework on experimental microtubule datasets without groundtruth, we propose an evaluation index based on skeleton information. We proved that the evaluation index is consistent with the existing denoising evaluation index. We verified the performance of the proposed MSDenoiser framework in simulated and experimental datasets (microtubule, nuclear pore complexes, and mitochondrial protein). From experimental results, we found that the MSDenoiser framework can effectively eliminate the mixed noises, achieve less detail loss and higher image SNR. Compared with the commonly used denoising algorithm in SMLM, we showed that the proposed framework has better performance and convenience in processing localization data from different types of biological structures.

2 Materials and methods

2.1 The multi-step adaptive noise reduction framework for single-molecule localization microscopy image

The proposed MSDenoiser framework includes four steps (as shown in Figure 1). Firstly, a Voronoi Tessellation-based method is used to remove free non-polymer localization points (The green box in Figure 1). Secondly, G-means algorithm is used to generate a group of clusters with centers. Features of the clusters are counted, which are passed to the LOF and DBSCAN algorithms as parameters (The orange box in Figure 1). Thirdly, LOF is used to remove non-polymer localization points near the sample signal area (The purple box in Figure 1). Finally, DBSCAN is used to eliminate non-specific localization clusters (The blue box in Figure 1).

FIGURE 1

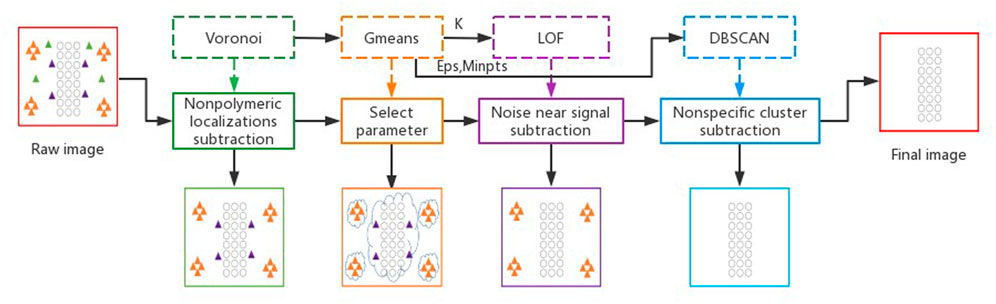
FIGURE 1. The multi-step adaptive noise reduction framework for SMLM image. The circles represent signal points, the triangles represent different type of noise points. Orange triangles represent nonspecific clusters, green triangles represent free non-polymer localization points, and purple triangles represent non-polymer localization points near the signal point.

2.1.1 Remove non-polymeric localizations using Voronoi Tessellation

Voronoi Tessellation has been applied in various fields from mathematics to natural sciences, and is usually used for clustering tasks in the field of super-resolution imaging [14, 23]. In Voronoi Tessellation, an image is divided into multiple polygonal regions centered on a set of points (seeds), with a single localization point at the center [24]. Voronoi cell represents the affected area of seed points, and the cell area provides an accurate measurement of local density of seed points. This property makes Voronoi Tessellations more suitable for describing the properties and neighborhoods of single molecules. Large Voronoi cells will be generated in low density area or randomly distributed points. Therefore, for a set of localization points with density of less than a given threshold, we can define it as noise.

2.1.2 Remove the noise near the structure point using local outlier factor

Local Outlier Factor (LOF) is an unsupervised outlier detection method [25]. LOF determines a point as an outlier by comparing the density of each point with its k neighborhood points, and considers the samples with densities much lower than those of its neighbors to be outliers. However, some boundary points may be excluded from the signal region, because their density is lower than that of the signal region. These characteristics enable LOF to be a good algorithm to deal with edge effect of point clouds, because LOF can remove non-polymer localization points near the signal point.

2.1.3 Remove nonspecific clusters using density-based spatial clustering of applications with noise

Density-Based Spatial Clustering of Applications with Noise (DBSCAN) is a typical density-based clustering method. DBSCAN divides the region with sufficient density into clusters, and can find clusters of arbitrary shapes in noisy spatial dataset. DBSCAN defines two parameters: neighborhood search radius (Eps), the minimum number of points within the search radius (MinPts) [6]. The algorithm starts from the point that has not been visited, and divides the data points into three types according to these two parameters: core points, boundary points, and noise points. DBSCAN has good noise recognition ability, and can filter the background noise. However, the setting of algorithm parameters is subjective, and it is difficult to determine appropriate parameters to ensure the quality of denoising.

2.1.4 Adaptive parameter selection using G-means algorithm

LOF and DBSCAN algorithms are used to identify high-density and low-density regions of point sets. The LOF algorithm eliminates as many non-clustered localization points as possible to minimize their interference to the DBSCAN algorithm in the next step. In this way, LOF effectively separates biologically relevant clusters from non-biologically relevant spurious clusters. But, the LOF algorithm requires an input parameter: k. The DBSCAN algorithm is able to distinguish noise points and signal points, from any shapes of clusters. However, two parameters are required for DBSCAN: Eps and MinPts.

To solve the problem of parameter selection in LOF and DBSCAN, we automatically generate a group of clusters with their centers by G-means algorithm, and count the features of the clusters to estimate the parameters of LOF and DBSCAN. Since the cluster centers generated by G-means can be affected by isolated noise and offset, which will further affect the parameters estimation, here we reprocess the data by Voronoi Tessellation to remove the isolated noise, so that the cluster center can better represent each cluster.

2.2 Simulated and experimental data

We simulated two representative kinds of biological structures (filament and ring) with different localization densities (1000 μm⁻²∼10,000 μm⁻²) to evaluate the feasibility of the proposed denoising framework, which can cover most experimental scenes.

Step 1: Generation of groundtruth dataset with no localization error or background noise. We firstly obtained a ring structure image with a radius of 150 nm and a structure diameter of 60 nm using Python language. Secondly, we downloaded the microtubules data from an open dataset website (https://srm.epfl.ch/Datasets). We used the QC-STORM plug-in to locate and render the microtubule data, and obtained the filament structure image [26]. Finally, we merged the images of the two structures and obtained the groundtruth dataset by ThunderSTORM plug-in.

Step 2: Generation of noise dataset. The noise dataset includes background clusters and random noise. To simulate false localization events due to background fluorescence, we generated 30 background clusters with the same localization density as the foreground. To better evaluate the effectiveness of the proposed denoising framework, we generated random noise with different noise level (from 5% to 50%), and the noise level was defined as a percentage of the number of foreground localization points.

Step 3: Generating simulated localization dataset with filament and ring structures. We combined the datasets in Step 1 and 2 to obtain a localization dataset with filament and ring structures.

To verify the effectiveness of the framework in the context of complex biological structures, we performed analysis on experimental dataset of microtubules, nuclear pore complexes and mitochondrial protein. Microtubules (alpha-tubulin) were obtained by indirect immunolabeling with AlexaFluor647 (DOL 1–4) in COS7 cell staining. Nuclear pore complexes data were obtained by staining the gp210 protein of the Xenopus nuclear pore complex with Alexa647. Mitochondrial protein data were obtained by labeling mitochondrial protein TOM22 with a secondary antibody immunolabeling strategy in COS7 cells. These experimental datasets include tube-like and amorphous structures, and thus are excellent reference structures to verify the denoising effect. These data are downloaded from ShareLoc.XY (https://shareloc.xyz/#/).

2.3 Evaluation criteria

We evaluated the performance of algorithm using two commonly used metrics in the simulated dataset with groundtruth: Recall and F1-score. The calculation process is formulated as follows:

$Recall=\frac{TP}{TP+FN}$

$F1-score=\frac{2 * Precision * Recall}{Precision+Recall}$

where Precision = TP/(TP + FP), and TP, FP, FN are true-positive (TP), false-positive (FP) and false-negative (FN), respectively. Recall represents the proportion of the total noise that is correctly removed. The larger of the value of recall, the more noise is removed. The F1-score metric balances the results of Precision and Recall. The value of F1-score ranges from 0 to 1, with 1 representing the best result of the algorithm and 0 representing the worst output result.

Because the experimental dataset lacks groundtruth, we try to extract skeleton from microtubule data as groundtruth, and use pixel accuracy (PA) as the evaluation metric of microtubule experimental data. The generation process of skeleton groundtruth is as follows:

Step1: Calculate the microtubule width. We select a relatively straight microtubule structure as our ROI, and then process the ROI vertically. We calculate the width of the horizontal cross section on each pixel of the ROI, and then fit it using a Gaussian function. The full width at half maxima (FWHM) is used to represent the microtubule width.

Step2: Extract the skeleton. We use the method mentioned in [27] to extract the skeleton information of microtubule data.

Step3: Expand the skeleton and get the groundtruth. The skeleton is expanded based on the calculated microtubule width. The expansion process is to add pixel values to the edge of the skeleton to expand the overall pixel value, and thus achieve the skeleton expansion. In this way, we obtain the groundtruth of microtubule data.

Based on skeleton groundtruth information, pixel accuracy (PA) can be defined as follows:

$PA=\frac{{\displaystyle \sum }_{i=0}^n{\sum }_{j=0}^m{Y}_{ij}}{{\displaystyle \sum }_{i=0}^n{\sum }_{j=0}^m{X}_{ij}}$

where m, n denote the number of vertical and horizontal pixel of the image, respectively, X denotes the noisy Groundtruth image, and Y denotes the noisy image calculated by the algorithm. PA indicates the proportion of correctly labeled noise pixel to the total noise pixel. Therefore, PA can be used to evaluate the denoising efficiency of the algorithm.

3 Results and discussion

3.1 Validation based on skeleton evaluation criteria

We simulated filament and ring data to verify the effectiveness of the proposed evaluation metric (PA) based on skeleton information. We selected the localization data with a localization density of 4000 μm⁻², and added random noise with a noise level of 50% and 30 localization background clusters. We used skeleton extraction algorithm in Section 2.3 to extract the skeleton of the rendered image (see in Figure 2B). We calculated the average microtubule width of the original image to be 45 nm. To eliminate the error caused by the uneven distribution of localization density of super-resolution image, we rounded up the calculated microtubule width and took 50 nm as the basis for the skeleton expansion. The expansion results were served as the groundtruth image of the structure signal point in our experiments, as shown in Figure 2C. We used the difference operation between the signal point groundtruth image and the original image to obtain the groundtruth image of noise data.

FIGURE 2

FIGURE 2. Comparison of the different evaluation metric. (A) Raw image. (B) The skeleton image. (C) The groundtruth image, which is the expanded skeleton image. (D) Three evaluation results with different noise reduction ratio.

We performed quantitative evaluation using three parameters (Recall, F1-score and PA) under different noise reduction ratio (from 10% to 90%), as shown in Figure 2D. We can see that the trends of all parameters (PA, Recall and F1-score) are generally consistent with each other. When the proportion of noise reduction is low, the correlation between the three parameters is strong and keeps rising rapidly. With the increase of the proportion of noise reduction, the rising of F1-score value is not as fast as those in Recall and PA. The reason is that, with the increase of proportion of noise reduction, some structure signal points may also be recognized as noise and thus removed, leading to the decrease of Precision and the affecting of the F1-score value. In addition, the evaluation metric based on skeleton has a disadvantage: it cannot evaluate the noise reduction in an area close to the structure signal points. This is also the reason for the difference in the value of Recall and PA, despite the strong correlation. From this analysis, we shown that the skeleton-based evaluation index PA is consistent with Recall and F1-score, and thus PA can quantitatively evaluate the denoising effect of experimental microtubule data.

3.2 Comparing the denoising performance using simulated data

To test the image denoising performance of MSDenoiser, we compared it with DBSCAN, Statistical Outlier Removal Filter (SORF) [28] and Radius Outlier Removal Filter (RORF) [29] using simulated data. DBSCAN is a commonly used denoising method in the field of super-resolution microscopy, while SORF and RORF are commonly used denoising methods in the field of point cloud. We adopted grid search strategy to select the optimal parameters of DBSCAN, RORF and SORF respectively in the following experiments, as shown in Figure 3. DBSCAN algorithm requires two parameters, Eps and MinPts. We set the input value of Eps to be 20–200 nm and the input value of MinPts to be 10–100, and used a total of 100 sets of parameters to find the best parameter combination. Similarly, the radius value of the RORF algorithm ranges from 20 nm to 200 nm, and the num_points value ranges from 10 to 100. The value of std_ratio for SORF ranges from 0.2 to 2, and the value of num_neighours ranges from 10 to 100. Note that RORF and SORF select the best combination from sets of parameters. Under different noise levels and localization densities, because the optimal parameters of the compared algorithms will be different, we select the optimal parameter combination for DBSCAN, RORF and SORF. For example, we show the heat map with optimal parameter selection under different localization densities in Figure 3. In contrast, our proposed MSDenoiser framework can automatically compute parameters without manual intervention.

FIGURE 3

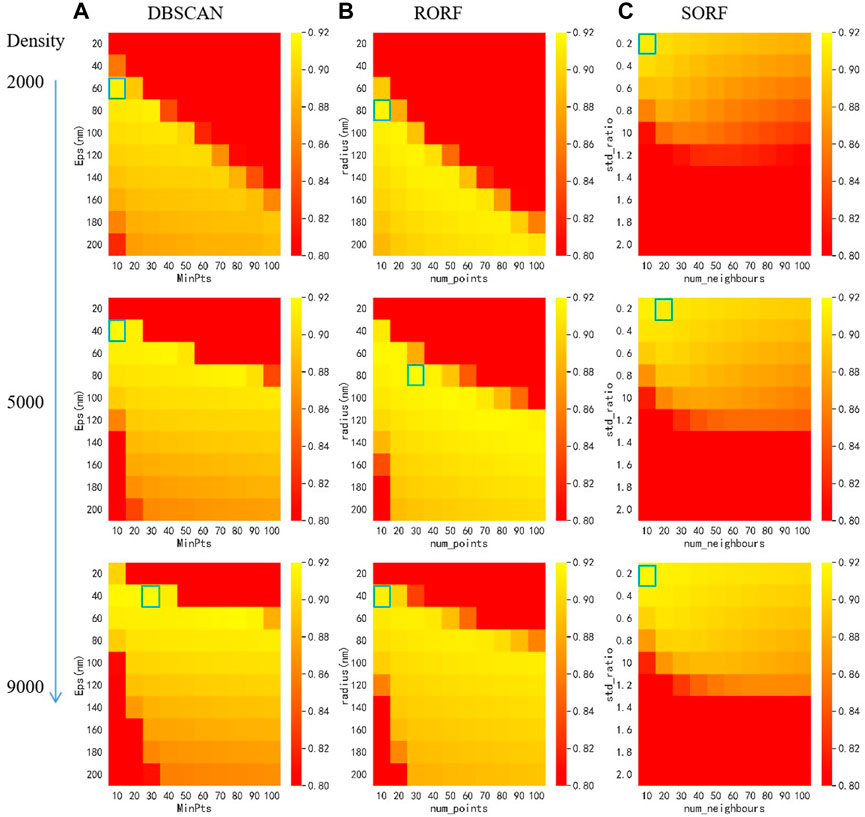
FIGURE 3. Heat map for parameter selection of different algorithms with different localization density using grid search. (A) Heat mat of DBSCAN. (B) Heat mat of RORF. (C) Heat map of SORF. The blue boxes indicate the optimal parameters.

Firstly, we compared the denoising performance of MSDenoiser and the three reported algorithms (DBSCAN, RORF and SORF) under the same localization density and different noise levels. The localization density of simulated data is 4000 μm⁻² and the noise level ranges from 5% to 50%. As shown in Figure 4, we find that all the four algorithms have small detail loss, but MSDenoiser achieves a balance of less detail loss and better SNR, and thus improves the quality of super-resolution images. However, although the results were similar at different noise levels, the value of Recall and F1-score changed. This is because the amount of non-specific clustering noise is unchanged. This finding also points out the bottleneck of the compared algorithms, that is, they cannot remove the non-specific clustering. At low noise level, the denoising performance of MSDenoiser is slightly worse than RORF, but it is still better than DBSCAN and SORF. The Recall value of MSDenoiser is not affected by the increase of noise, and reaches the maximum value of 0.86, when the noise level is 50%. The F1-score reaches the maximum value of 0.92. While the three reported algorithms benefit slightly from the careful selecting parameters, our proposed MSDenoiser can still achieve a good overall performance, without involving manual parameter search. Experiments with different noise levels demonstrate the robustness of our MSDenoiser method.

FIGURE 4

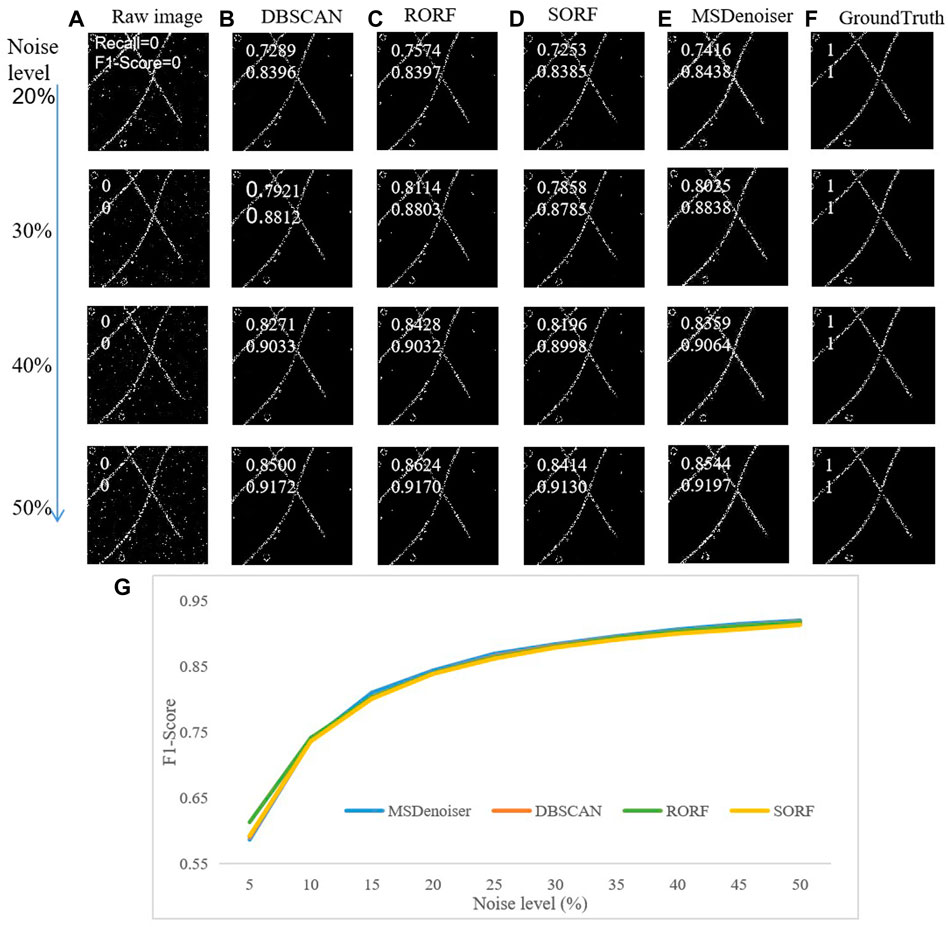
FIGURE 4. Comparison on the denoising performance in simulated microtubule data with different noise levels. (A) Raw rendered image. (B) Denoised image from DBSCAN. (C) Denoised image from RORF. (D) Denoised image from SORF. (E) Denoised image from MSDenoser. (F) Skeleton based groundtruth. (G) The dependence of F1-score on noise level.

Then, we compared the denoising performanceX of MSDenoiser and the other three compared algorithms under the same noise level and different localization densities. The noise level of simulated data is 50%, and the localization densities ranges from 1000 μm⁻² to 10,000 μm⁻². As shown in Figure 5, MSDenoiser performs slightly worse on simulated data with localization densities ranging from 1000 μm⁻² to 3000 μm⁻² (see in Figure 5G). When the localization density increases to larger than 4000 μm⁻², MSDenoiser achieves the best denoising performance. However, it is important to emphasize again, the MSDenoiser produces the best overall denoising results without the need of labor-intensive manual parameter setting.

FIGURE 5

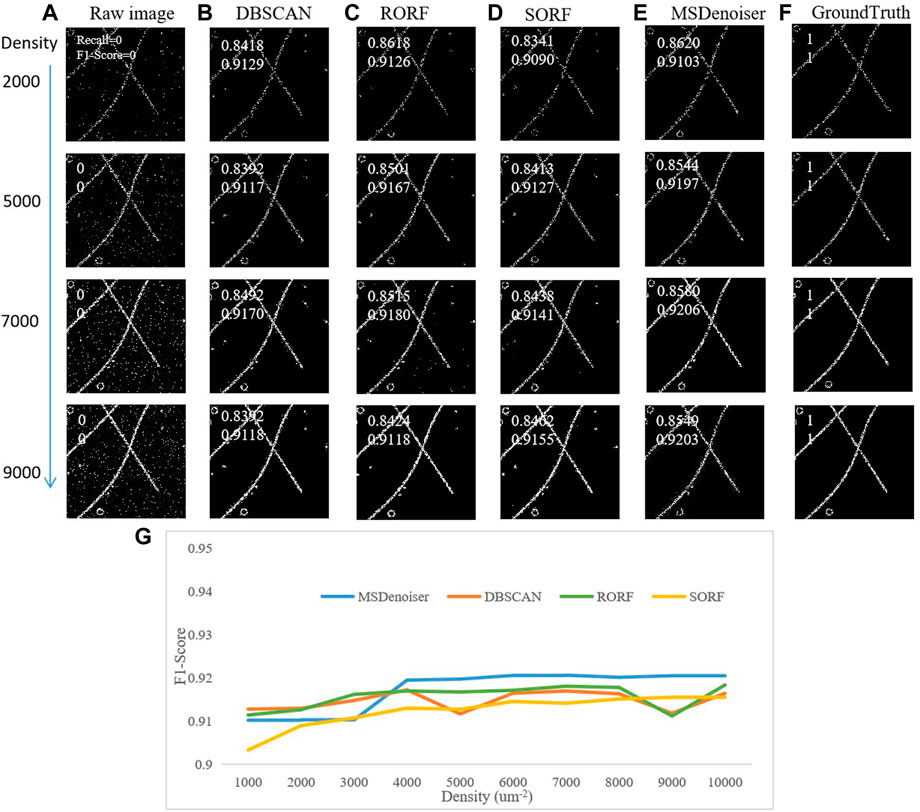
FIGURE 5. Comparison on the denoising performance in simulated patch microtubule data with different localization density by different methods. (A) Raw rendering image. (B) Denoised image from DBSCAN. (C) Denoised image from RORF. (D) Denoised image from SORF. (E) Denoised image from MSDenoiser. (F) Skeleton based groundtruth. (G) The dependence of F1-score on localization density.

Using the above discussions, we showed that MSDenoiser is capable to provide good denoising performance on simulated data with different localization densities and different noise levels. This new framework fully integrates the advantages of Voronoi Tessellation, LOF and DBSCAN, and selects parameters adaptively according to localization data, without reducing the effectiveness in removing mixed noise in SMLM data.

3.3 Comparing the denoising performance using experimental microtubule data

To verify the denoising ability of MSDenoiser in real dataset, we compared the performance among MSDenoiser, DBSCAN, RORF and SORF, using experimental microtubule data. Non-polymeric localizations and nonspecific clusters are distributed randomly within the field of view. We downloaded the experimental microtubule data from ShareLoc.XYZ, which includes 1231693 localization coordinates in the field-of-view of 300 μm², and the localization density is 4106 μm⁻². We showed in Figure 6E the raw image and its local enlarged details (rendered at 100 nm and 20 nm, respectively). We extracted the skeleton as the groundtruth of experimental microtubule data, and used them for quantitatively evaluating the denoising algorithms.

FIGURE 6

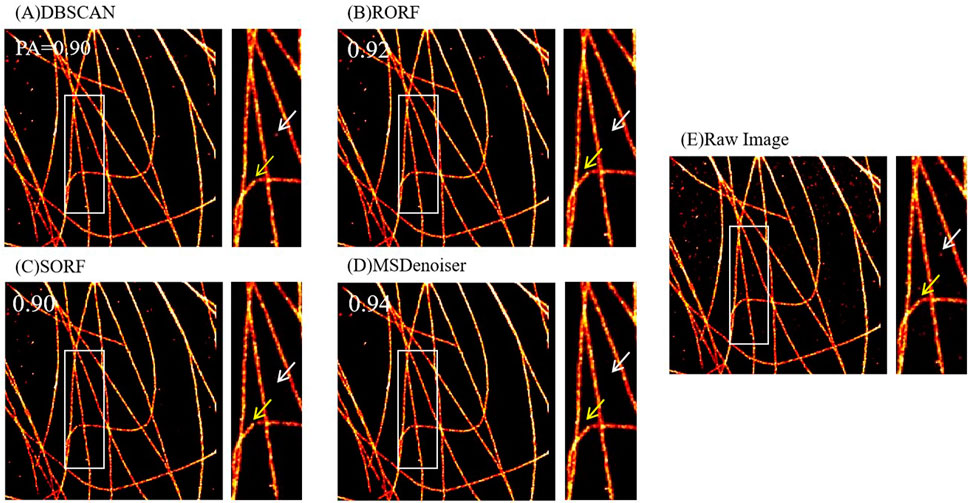
FIGURE 6. Comparison on the denoising performance of different methods using experimental microtubule data. (A) Denoised image from DBSCAN. (B) Denoised image from RORF. (C) Denoised image from SORF. (D) Denoised image from MSDenoiser. (E) Raw rendered image. The white arrows in (A–C) indicate noise, and the white arrow in (D) indicates the better denoising performance of MSDenoiser at the same location. The yellow arrows in (A–C) indicate broken microtubule structure, and the yellow arrow in (D) indicates the structure continuity from MSDenoiser at the same location.

Firstly, we discussed the parameter selection strategy for the four algorithms. The MSDenoiser can adaptively determine the parameters in the denoising framework. The parameters, Eps and MinPts, which are automatically calculated by MSDenoiser, can also be used by DBSCAN. In fact, for the experimental microtubule data, MSDenoiser sent the two parameters (Eps = 67 nm, MinPts = 215) to DBSCAN. The parameters in RORF and SORF were estimated by experience. The average localization density of experimental data was calculated to be 4106 μm⁻². The initial parameters were found according to the localization density in simulated data, and adjusted repeatedly according to the denoising effect. Therefore, the parameter are not required to be optimal at the beginning. The parameters in RORF are radius = 60 nm and num_points = 100, respectively. The parameters in SORF are std_ratio = 0.2 and num_neighbors = 80, respectively. Note that MSDenoiser framework does not require any manual intervention.

Then, we evaluated the denoising performance among these methods using PA value. We used experimental microtubule data as input data (as shown in Figure 6E, which were rendered from localization table data), and applied the four denoising methods to the localization table. We further analyzed the denoising performance from these methods. We found that MSDenoiser achieves the best denoising effect (that is, the highest PA value). Actually, as seen in Figures 6A–D, the PA value are 0.90 from DBSCAN, 0.92 from RORF, 0.90 from SORF, and 0.94 from MSDenoiser, respectively. From the local enlarged image, we observed that MSDenoiser removes nonspecific clusters, while DBSCAN does not remove this type of noise (see the white arrow in Figures 6A–D). Other methods removed these noises, along with the signal points of the microtubule structure, since we can see broken structures (see the yellow arrow in Figures 6A–D). MSDenoiser removed noise, but kept more signal points from microtubule structures.

3.4 Comparing the denoising performance using experimental amorphous structure data

In previous section, we demonstrated the applicability of MSDenoiser in relatively uniform and tube-like structures (microtubules). Here, we showed the denoising performance of MSDenoiser in datasets from nuclear pore complexes and mitochondrial protein (which contain amorphous features commonly seen in SMLM). We compared the denoising performance among MSDenoiser, DBSCAN, RORF, and SORF.

We downloaded experimental nuclear pore complexes and mitochondrial protein datasets from ShareLoc.XYZ. In the nuclear pore complexes dataset, a total number of 631214 fluorophores were identified from a field-of-view of 191 μm², and the localization density is 3305 μm⁻². In the mitochondrial protein dataset, a total number of 2270989 fluorophores were identified from a field-of-view of 2668 μm², and the localization density is 1002 μm⁻². Since there are no groundtruth for these experimental datasets, we only showed the results before and after denoising.

The parameter selection strategy in these two datasets is similar to that used in the experimental microtubule dataset. The parameters in DBSCAN were determined from the parameters automatically calculated by MSDenoiser. For the experimental nuclear pore complexes dataset, the parameters in DBSCAN are Eps = 42 nm and MinPts = 52, respectively. For the experimental mitochondrial protein dataset, the parameters in DBSCAN are Eps = 45 nm and MinPts = 58, respectively. According to the average localization density of experimental data (3305 μm⁻² for nuclear pore complexes, and 1002 μm⁻² for the mitochondria), we empirically selected the parameters in the RORF and SORF algorithms. For the experimental nuclear pore complexes dataset, the parameters in RORF are radius = 70 nm and num_points = 100, respectively, and the parameters in SORF are std_ratio = 0.2 and num_neighbor = 40, respectively. For the experimental mitochondrial protein data, the parameters in RORF are radius = 30 nm and num_points = 90, respectively, and the parameters in SORF are std_ratio = 0.2 and num_neighbor = 50, respetively. The MSDenoiser framework can adaptively determine parameters without manual intervention.

We then analyzed the denoising performance of the four algorithms qualitatively using experimental nuclear pore complexes and mitochondrial protein datasets. The results are shown in Figures 7, 8. The reported three algorithms only removed part of the nonpolymer localization points, and the noise in the ring structure of the nuclear pore complexes was not effectively removed (see the white arrows in Figures 7A–E). Similarly, the reported algorithms did not remove the nonspecific clustering from the mitochondrial protein data (see the white arrows in Figures 8A–E). However, these problems can be effectively solved by our new MSDenoiser algorithm, which is able to retain maximum details of biological structures and remove most of the noises. The experimental results on nuclear pore complexes and mitochondrial protein datasets show that our proposed algorithm also have good ability in removal of the mixed noises that are common on experimental data.

FIGURE 7

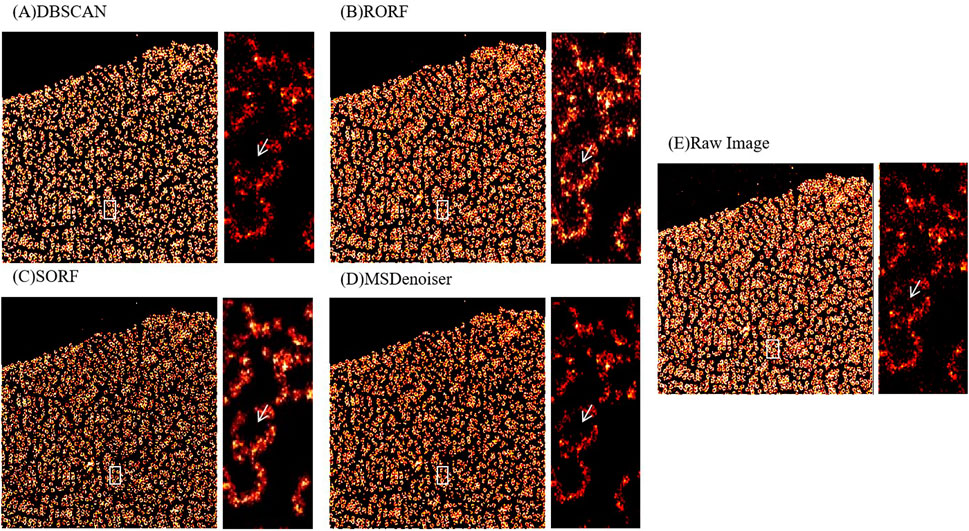
FIGURE 7. Comparison on the denoising performance of different methods using experimental nuclear pore complexes data. (A) Denoised image from DBSCAN. (B) Denoised image from RORF. (C) Denoised image from SORF. (D) Denoised image from MSDenoiser. (E) Raw rendered image. The white arrows in (A–E) indicate noise in ring structure, the white arrow in (D) indicates the better denoising effect of MSDenoiser at the same location.

FIGURE 8

FIGURE 8. Comparison on the denoising performance of different methods using experimental mitochondrial protein data. (A) Denoised image from DBSCAN. (B) Denoised image from RORF. (C) Denoised image from SORF. (D) Denoised image from MSDenoiser. (E) Raw rendered image. The white arrows in (A–E) indicate nonspecific clustering, the white arrow in (D) indicates the better denoising effect of MSDenoiser at the same location.

From the above results, we show that our proposed MSDenoiser framework can be applied to localization data from different biological structures. Using this new framework, we can not only obtain better denoising results, but also adaptively determine parameters without manually intervention.

4 Conclusion

We developed a new denoising framework, called MSDenoiser, for improving the image quality in SMLM. In this framework, we combine the advantages of different reported denoising algorithms (Voronoi Tessellation, LOF and DBSCAN) to remove the noise of different features, and adaptively estimate the parameters required by the new framework using the G-means algorithm. In this framework, we aim to remove heterogeneous noises (free non-polymer localization points, non-polymer localization points near the sample signal point area, and non-specific localization points). Using simulated and experimental datasets, we compared the denoising performance of MSDenoiser with DBSCAN (a commonly used denoising method in SMLM), RORF and SORF (commonly used denoising methods in point cloud). We found that MSDenoiser achieves better denoising effect than the three reported methods in the removal of mixed noises. Moreover, as compared with DBSCAN, RORF and SORF, the MSDenoiser can adaptively obtain parameters without manual intervention. We also verified the applicability of MSDenoiser in amorphous biological structures (nuclear pore complexes and mitochondrial protein), and proved that MSDenoiser has good robustness on different biological structures. Of course, there are still some limitations on our proposed MSDenoiser framework. The main limitation is the denoising speed, which needs to be improved for processing large SMLM localization table data. Because the MSDenoiser framework is composed of multiple algorithms, it takes a large amount of time on the automatic parameter selection process (G-means). When the field of view increases, the time spent in the parameter selection will increase significantly. In the future, we plan to develop a more efficient algorithm to take the place of G-means algorithm, so that we could shorten the processing time without reducing the denoising performance. Nevertheless, we believe this study points out a new strategy for solving the noise reduction challenge in SMLM.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

QF and ZW designed the study. QF generated simulated, analyzed the data, performed experiments, and drafted the manuscript. QS and MY generated simulated data, performed some experiments. ZH and ZW revised the manuscript. All the authors read and approved the final manuscript.

Funding

This work was partly supported by Key Research and Development Program of Hainan province (No. ZDYF2021GXJS017), National Natural Science Foundation of China (No. 82160345), the Major Science and technology plan of Hainan (ZDKJ2021016), Key science and technology plan project of Haikou (2021-016).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Betzig E, Patterson GH, Sougrat R, Lindwasser OW, Olenych S, Bonifacino JS, et al. Imaging intracellular fluorescent proteins at nanometer resolution. Science (2006) 313(5793):1642–5. doi:10.1126/science.1127344

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Schermelleh L, Ferrand A, Huser T, Eggeling C, Sauer M, Biehlmaier O, et al. Super-resolution microscopy demystified. Nat Cel Biol (2019) 21(1):72–84. doi:10.1038/s41556-018-0251-8

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Lelek M, Gyparaki MT, Beliu G, Schueder F, Griffié J, Manley S, et al. Single-molecule localization microscopy. Nat Rev Methods Primers (2021) 1(1):39. doi:10.1038/s43586-021-00038-x

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Vicidomini G, Bianchini P, Diaspro A. STED super-resolved microscopy. Nat Methods (2018) 15(3):173–82. doi:10.1038/nmeth.4593

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Wu YC, Shroff H. Faster, sharper, and deeper: Structured illumination microscopy for biological imaging. Nat Methods (2018) 15(12):1011–9. doi:10.1038/s41592-018-0211-z

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Mazouchi A, Milstein JN. Fast optimized cluster algorithm for localizations (FOCAL): A spatial cluster analysis for super-resolved microscopy. Bioinformatics (2016) 32(5):747–54. doi:10.1093/bioinformatics/btv630

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Whelan DR, Bell TDM. Image artifacts in single molecule localization microscopy: Why optimization of sample preparation protocols matters. Sci Rep (2015) 5:7924. doi:10.1038/srep07924

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Khater IM, Nabi IR, Hamarneh G. A review of super-resolution single-molecule localization microscopy cluster analysis and quantification methods. Patterns (New York, NY) (2020) 1(3):100038. doi:10.1016/j.patter.2020.100038

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Guo M, Chandris P, Giannini JP, Trexler AJ, Fischer R, Chen J, et al. Single-shot super-resolution total internal reflection fluorescence microscopy. Nat Methods (2018) 15(6):425–8. doi:10.1038/s41592-018-0004-4

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Herbert S, Soares H, Zimmer C, Henriques R. Single-molecule localization super-resolution microscopy: Deeper and faster. Microsc Microanal (2012) 18(6):1419–29. doi:10.1017/s1431927612013347

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Chen J, Sasaki H, Lai H, Su Y, Liu J, Wu Y, et al. Three-dimensional residual channel attention networks denoise and sharpen fluorescence microscopy image volumes. Nat Methods (2021) 18(6):678–87. doi:10.1038/s41592-021-01155-x

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Chan KG, Streichan SJ, Trinh LA, Liebling M. Simultaneous temporal superresolution and denoising for cardiac fluorescence microscopy. IEEE Trans Comput Imaging (2016) 2(3):348–58. doi:10.1109/tci.2016.2579606

CrossRef Full Text | Google Scholar

13. Schnitzbauer J, Wang Y, Zhao S, Bakalar M, Nuwal T, Chen B, et al. Correlation analysis framework for localization-based superresolution microscopy. Proc Natl Acad Sci U S A (2018) 115(13):3219–24. doi:10.1073/pnas.1711314115

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Andronov L, Orlov I, Lutz Y, Vonesch J-L, Klaholz BP. ClusterViSu, a method for clustering of protein complexes by Voronoi tessellation in super-resolution microscopy. Sci Rep (2016) 6:24084. doi:10.1038/srep24084

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Ovesny M, Krizek P, Borkovec J, Svindrych ZK, Hagen GM. ThunderSTORM: A comprehensive ImageJ plug-in for PALM and STORM data analysis and super-resolution imaging. Bioinformatics (2014) 30(16):2389–90. doi:10.1093/bioinformatics/btu202

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Williamson DJ, Burn GL, Simoncelli S, Griffie J, Peters R, Davis DM, et al. Machine learning for cluster analysis of localization microscopy data. Nat Commun (2020) 11(1):1493. doi:10.1038/s41467-020-15293-x

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Wang J, Zhang H, Gao J, Xiao D. Dust removal from 3D point cloud data in mine plane areas based on orthogonal total least squares fitting and GA-TELM. Comput Intelligence Neurosci (2021) 2021:1–8. doi:10.1155/2021/9927982

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Regaya Y, Fadli F, Amira A. Point-Denoise: Unsupervised outlier detection for 3D point clouds enhancement. Multimed Tools Appl (2021) 80(18):28161–77. doi:10.1007/s11042-021-10924-x

CrossRef Full Text | Google Scholar

19. Yang X, Xu Y, Quan Y, Ji H. Image denoising via sequential ensemble learning. IEEE Trans Image Process (2020) 29:5038–49. doi:10.1109/tip.2020.2978645

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Ma X, Ugurbil K, Wu X. Denoise magnitude diffusion magnetic resonance images via variance -stabilizing transformation and optimal singular -value manipulation. Neuroimage (2020) 215:116852. doi:10.1016/j.neuroimage.2020.116852

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Shivanasab P, Abbaspour RA. An incremental algorithm for simultaneous construction of 2D Voronoi diagram and Delaunay triangulation based on a face-based data structure. Adv Eng Softw (2022) 169:103129. doi:10.1016/j.advengsoft.2022.103129

CrossRef Full Text | Google Scholar

22. Duan L, Xu L, Liu Y, Lee J. Cluster-based outlier detection. Ann Oper Res (2009) 168(1):151–68. doi:10.1007/s10479-008-0371-9

CrossRef Full Text | Google Scholar

23. Levet F, Hosy E, Kechkar A, Butler C, Beghin A, Choquet D, et al. SR-tesseler: A method to segment and quantify localization-based super-resolution microscopy data. Nat Methods (2015) 12(11):1065–71. doi:10.1038/nmeth.3579

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Aurenhammer F. Voronoi diagrams—A survey of a fundamental geometric data structure. ACM Comput Surv (1991) 23(3):345–405. doi:10.1145/116873.116880

CrossRef Full Text | Google Scholar

25. Breunig MM, Kriegel H-P, Ng RT, Sander JLOF. Identifying density-based local outliers. In: Proceedings of the 2000 ACM SIGMOD international conference on Management of data. Dallas, Texas, USA: Association for Computing Machinery (2000). p. 93

CrossRef Full Text | Google Scholar

26. Sage D, Kirshner H, Pengo T, Stuurman N, Min J, Manley S, et al. Quantitative evaluation of software packages for single-molecule localization microscopy. Nat Methods (2015) 12(8):717–24. doi:10.1038/nmeth.3442

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Li M, Song Q, Xiao Y, Wu J, Kuang W, Zhang Y, et al. LuckyProfiler: An ImageJ plug-in capable of quantifying FWHM resolution easily and effectively for super-resolution images. Biomed Opt Express (2022) 13(8):4310–25. doi:10.1364/boe.462197

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Minh-Hai L, Cheng C-H, Liu D-G, Thanh-Tuan N. An adaptive group of density outlier removal filter: Snow particle removal from LiDAR data. Electronics (2022) 11(19):2993. doi:10.3390/electronics11192993

CrossRef Full Text | Google Scholar

29. Duan Y, Yang C, Li H. Low-complexity adaptive radius outlier removal filter based on PCA for lidar point cloud denoising. Appl Opt (2021) 60(20):E1–E7. doi:10.1364/ao.416341

PubMed Abstract | CrossRef Full Text | Google Scholar