- 1School of Electronics and Information Engineering, Sias University, Xinzheng, China
- 2Institute for Computational Materials Science, School of Physics and Electronics, Henan University, Kaifeng, China
- 3Patent Examination Cooperation (Henan) Center of the Patent Office, China National Intellectual Property Administration, Zhengzhou, China
- 4College of Physics Science and Technology, Yangzhou University, Yangzhou, China
Two-dimensional (2D) material is the promising for next-generation information technology. The recently discovered intrinsic magnetic crystals have simulated a renaissance in 2D spintronics, which provides an ideal platform for exploring novel physical phenomena. However, current experimental trial-and-error methods in discovering new spintronic material are still very expensive and challenging. In contrast, based on well-developed first-principles calculations, computationally designing the spintronic materials provides a more efficient way for exploring new ferromagnetic (FM) materials and understanding the nature of magnetic properties. Several predictions, such as CrI3 monolayer, CrGeTe3 bilayer, CrSBr monolayer, FeCl2 monolayer, and Fe3GeTe2 monolayer have been confirmed by experiments, showing the great performance of computational approaches. This minireview article attempts to give a brief of discovering intrinsic 2D spintronics from theoretical aspect, and in particular, we emphasize roles played by calculation based on first-principles methods in designing 2D FM materials and devices. The current challenges and proposals on future developments of 2D spintronics are also discussed.
1 Introduction
Due to non-volatility, lower energy consumption, and faster information operation compared to controlling a charge current, spintronic devices that use the spin of an electron for information processing have attracted worldwide interest [1–7]. Just as graphene, TMS2 (TM = Mo, W), and black P revolutionized condensed matter, the introduction of 2D van der Waals (vdW) magnetic materials promises to open new horizons in materials science and enable the potential development of spintrons [8–11]. In fact, 2D magnetism has been studied for decades but only recently they have been experimentally verified. The recent exciting 2D ferromagnetic breakthroughs, such as CrI3 monolayer, Fe3GeTe2 monolayer, CrGeTe3 bilayer, and CrSBr monolayer exfoliated from their vdW bulk, have promoted research into new magnetic properties and creative concepts [1,2,11–17].
Traditional trial and error experiments have no clear goals and guidelines, and face the fundamental challenges of long time and high cost. Computational simulations are an important first step in exploring possible applications of new materials. It not only can predict new 2D materials, but also suggest possible routes for their synthesis. Many interesting cases have been confirmed by experiment, such as the growth of borophene, ferroelectricity in SnTe. Compared to other computational methods, the first-principles approach, which is an effective method to study new materials, is the most widely used tool in designing new materials, requiring very few fundamental physical constants and atomic position coordinates. In fact, the rapid development of 2D FM materials benefits from theoretical simulation. From the theoretical point of view, magnetic anisotropy, which can improve the stability of magnetic information, can break the Mermin-Wagner theoryopening the door for 2D long-range FM materials. Firstly, ultra-thin VSe2 had been predicted to be intrinsic ferromagnetism theoretically in 2012, and has been confirmed by recent experiment [18–21]. The recent star ferromagnetic CrGeTe3 bilayer, CrI3 monolayer, CrSBr monolayer, FeCl2 monolayer, and Fe3GeTe2 monolayer were also first predicted theoretically [22–26], and they have recently been experimentally made [1,2,11,14,15], which show the strong power of first-principles calculations in designing these spintronics materials.
This minireview will summarize recent progress of 2D intrinsic FMSs in theoretical side and show the importance of first-principles calculations in designing new materials. Firstly, we give the reason why ferromagnetic order exists in 2D space theoretically. Then, we summarized the discovery processes and magnetic properties of recent landscape of several 2D ferromagnetic semiconductors, using 2D CrI3, CrSBr, and CrGeTe3 as the examples, respectively. Finally, we highlight the problems existing in the designed 2D FM materials and suggest possible directions for further development of computational simulations.
2 Results and discussion
2.1 Importance of MAE in low dimensional magnetic materials
Theoretically, spontaneous FM order takes place in three-dimensional (3D) system for isotropic Heisenberg model at finite temperatures, but is completely prohibited by the thermal fluctuations in 2D isotropic Heisenberg model according to the Mermin–Wagner (M-W) theorem. For 2D isotropic Heisenberg ferromagnet, due to the absence of a spin wave excitation gap, the diverging Bose-Einstein statistics at zero energy, and the abrupt onset of magnon density of states (DOS), there will be plenty of excitations of magnons at nonzero temperatures, which would cause the long-range spin ordering to collapse and giant magnon excitations (Figure 1A). However, the presence of uniaxial magnetocrystalline anisotropy (UMA) can open up the magnon excitation gap, which resists the thermal agitations (Figure 1B). This removes the M-W restriction by breaking the continuous rotational symmetry of the Hamiltonian and leads to the finite Curie temperature (TC) [6]. As the materials evolves from 2D to 3D, the density of states (DOS) spectrum of magnon has changed from a step function to a gradually increasing function with zero DOS at the threshold of excitation (Figures 1C,D). As a result, in 3D system, UMA is not the prerequisite for the existence of long-range FM order at finite temperature. As a result, MA is important in 2D magnets, which not only effects magnetic properties, but also is necessary to stabilize magnetic order in the 2D space limit.
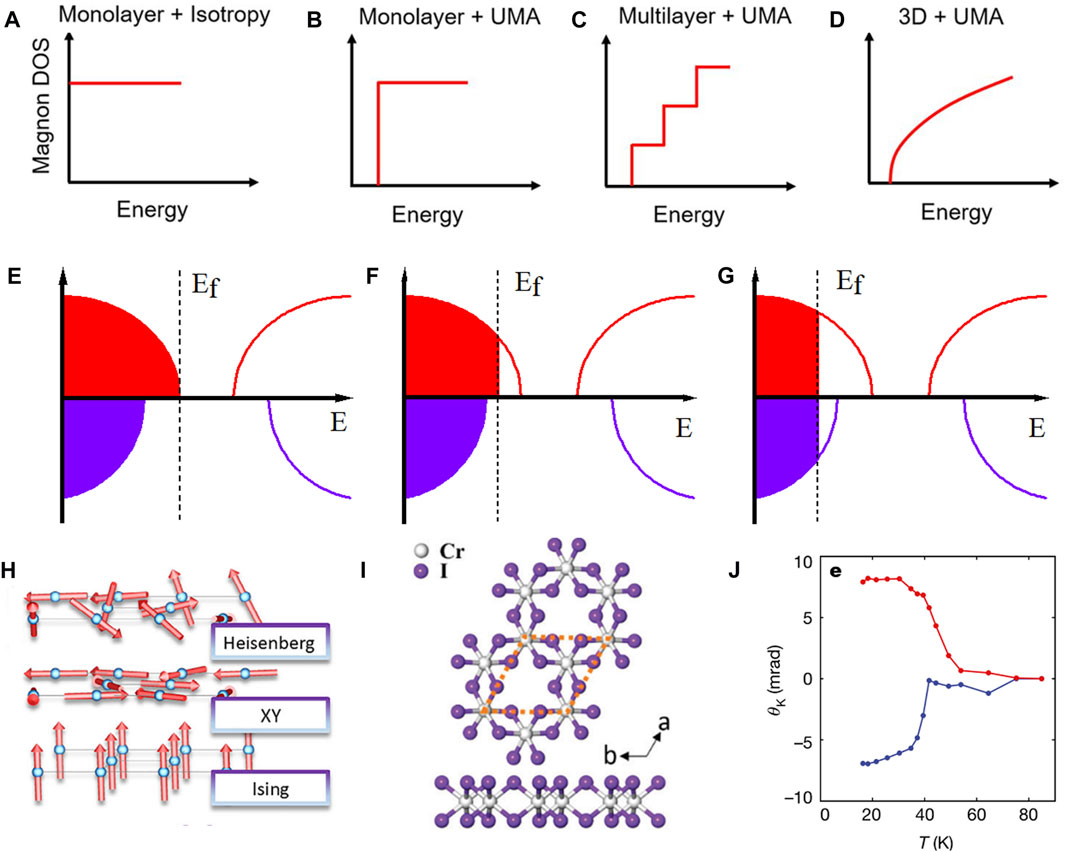
FIGURE 1. (A–D) Spin wave excitations in ferromagnets of different dimensionalities Reproduced with permission [6]. Copyright©2019 American Association for the Advancement of Science (AAAS). (E–G) Schematic DOS for three types of ferromagnetic semiconductor, half-metal, and metal materials. (H) Spin symmetries of MA for Heisenberg model, XY model, and Ising model, respectively. Reproduced with permission. Copyright©2020 John Wiley and Sons Australia. (I) The structure of CrI3 monolayer. (J) Polar MOKE signal for a CrI3 monolayer. Reproduced with permission [1]. Copyright©2017 Springer Nature.
The previous works show that the sizable MAE mainly arises from the strong SOC [27–30]. In addition to the SOC contribution, the shape anisotropy caused by the dipolar interaction also contributes to the MAE [24,31]. It is worth mentioning that the quantitative microscopic origin of MA is still an open question and the 2D magnetic materials usually possess small MAE (below meV), which is difficult to be measured directly. Therefore, it is in longing need of careful examination and more theoretical efforts will be spent to discover effective strategy to enhancing the MAE or searching new 2D FM materials with sizeable MAE.
2.2 Prediction of 2D magnetism
Magnetism usually originates from the spin of unpaired electrons in partially filled d or f orbitals. According to characteristics of electronic structures, the FM materials can be clearly classified into three types: ferromagnetic semiconductors (FMS), ferromagnetic metals (FMM) (Figure 1G), and ferromagnetic half-metals (FHM) (Figure 1F). Based on the easy magnetization directions, there are three forms of Heisenberg, XY, and Ising ferromagnet, respectively, as shown in Figure 1H. The Heisenberg ferromagnet has no MA; the XY ferromagnet possesses an easy magnetization plane, in which spin can rotate freely in the whole plane; and the Ising ferromagnet exhibits an out-of-plane easy axis.
FMS (Figure 1E), both spin-up and spin-down channels with semiconducting gaps, combines the advantages and properties of both semiconductors and magnets, which can be applied for spin injection, spin manipulation, and spin detection [32]. The history of the discovery of the typical 2D FMS, CrI3 monolayer (Figure 1I), illustrates the power of first-principles calculations, and shows the intimate interaction between experiment and theory, which greatly accelerates the discovery of new materials. The layered vdW bulk CrI3 possesses Ising ferromagnetism below the TC of 61 K with strong UMA [33]. Its monolayer was first predicted to be intrinsic FMS with TC of 95 K by using Monte Carlo (MC) simulations and large MAE (685 μeV/Cr), and could be easily exfoliated from the bulk crystals [34]. The other theoretical work showed the its TC was 107 K and can be further increased to 293 K by hole doping [22]. By lithium atom adsorption, the CrI3 monolayer can be switched from semiconducting to half-metallicity, which can further enhance the ferromagnetism of CrI3 sheets [35]. Excitingly, 2 years later, this CrI3 monolayer was exfoliated from its layered bulk successfully, and its intrinsic long-range ferromagnetic order was also confirmed by scanning magneto-optic Kerr microscopy with the TC of 45 K (Figure 1J) [1], which provides an ideal platform for the application of 2D spintronics. For CrI3 bilayer, the first-principles calculations show that it is interlayer antiferromagnetically coupled [36], and further theoretical study shows that the stacking order defines the antiferromagnetic (AFM) coupling, [37]. This result was confirmed by recent experiment [38], and the magnetic order of CrI3 bilayers can further transfer from AFM to FM order by electric fields [39] and pressure [40]. In addition, the isostructure vdW layered CrBr3 and CrCl3 also have FM ordering, and the previous predicted CrBr3 monolayer and CrCl3 bilayer has been confirmed by recent experiments (Figures 2A–C) [12,13,41], showing the accuracy and efficiency of computational predictions.
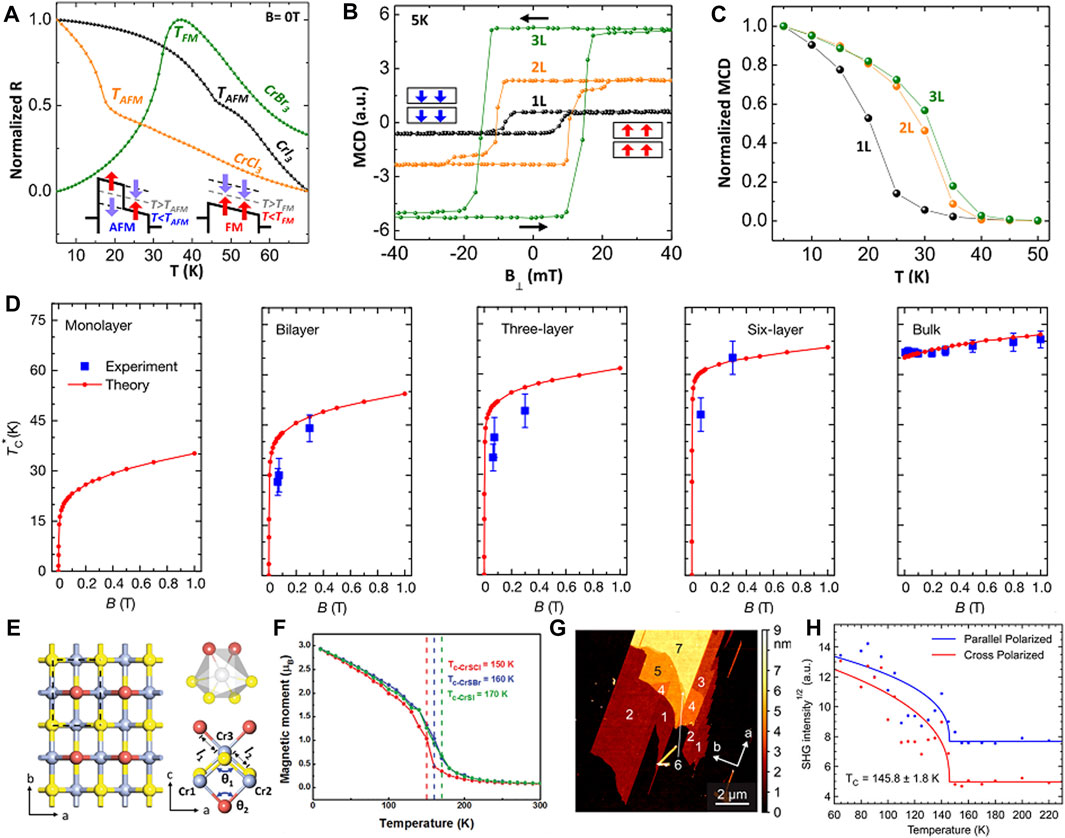
FIGURE 2. (A) Normalized temperature-dependent dc resistance of CrX3 (X = I, Br, and Cl) at constant current of 0.1 nA. Insets show schematics of the spin-dependent tunnel barrier for AFM and FM interlayer coupling. MCD measurements on CrBr3. (B) Low-temperature MCD vs B⊥ and (C) temperature-dependent normalized MCD at zero field (MCD↑(↓) (T) = MCD↑(↓),5K)for 1L, 2L, and 3L CrBr3. Reproduced with permission [41]. Copyright©2018 National Academy of Sciences. (D) Experimental (blue squares) and theoretical (red circles) field dependence of TC in samples of various thickness. Reproduced with permission [2]. Copyright©2017 Springer Nature. (E) The structure of CrSBr monolayer and (F) evolution of spin magnetic moment with respect to temperature of CrSX (X = Cr, S, and Br) monolayers. Reproduced with permission [25], Copyright©2018 Royal Society of Chemistry. (G) Atomic force microscopy image of an exfoliated flake of varying thicknesses from one to seven layers for CrSBr and (H) square roots of the average SHG intensities of monolayer CrSBr as a function of temperature. Reproduced with permission [11]. Copyright©2018 American Chemical Society.
Another typical 2D FMS is CrXY3 (X = Si, Ge, and Sn; Y = S, Se, and Te). In 2014, Yang’s group demonstrates the possibility of 2D intrinsic FMSs by exfoliating layered crystals of CrMTe3 (M = Si, Ge) through first-principles calculations, and the 2D FM order can persist up to 35.7 K (CrSiTe3) or 57.2 K (CrGeTe3) based on classical Heisenberg model in MC simulations [23]. Then, Sivadas et al. show that CrSiTe3 monolayer is an antiferromagnet (AFM) with a zigzag spin texture contrary to other studies, whereas CrGeTe3 is a FMS with a TC of 106 K based on Heisenberg model. Zhuang et al. have performed accurate hybrid density functional methods to predict that CrSnTe3 monolayer is a FMS and the calculated TC is about 170 K, which is higher than those of CrGeTe3 (130 K) and CrSiTe3 (90 K) monolayers based on Ising model [42, 43]. After that, Gong et al. confirmed the intrinsic long-range FM order in pristine 2D CrGeTe3 bilayer via scanning magneto-optic Kerr microscopy and the measured TC is about 30 K (Figure 2D) [2]. Although the value of calculated TC for CrGeTe3 is higher than that of experiment, the first-principles method is still an important tool to fuel the discovery of novel 2D FM materials and guide experimental understanding. Unfortunately, CrGeTe3 monolayer was not still confirmed, and the nature of magnetism in this monolayer needs more effort to be paid.
A class of 2D magnetic materials, CrMN (M = O, S, Se, and Te; N = Cl, Br, and I) will crystakize in the space group Pmmn, which has a vdW layered structure in the z-axis direction. As early as in 2018, our group shows that the FMS CrSX (X = Cl, Br, and I) monolayers possess high hole mobilities (103 cm2V−1s−1) and TC (150–170 K) (Figures 2E,F), which are competitive candidates for next-generation spintronics and electronics [25]. Then, Wang et al. have extensively explored the ferromagnetic properties of CrCX (C = S, Se, and Te; X = Cl, Br, and I) monolayers and found that they show extremely large anisotropy [26]. Recently, Millimeter-size CrSBr single crystals were grown by chemical vapor transport from Cr and S2Br2 [11] and was confirmed to be a layered vdW A-type AFM with a bulk Néel temperature (TN) of 132 K [25,26,44]. Interestingly, CrSBr monolayer was easily exfoliated from its bulk and the experiment value of TC is about 146 K (Figures 2G,H) [11], which is in good agreement with what we predicted. Besides, several other 2D Cr-based semiconductors such as CrOCl, CrOBr [45], CrOF [46], Cr2I3X3 (X = Br, and Cl) [47], Cr2O3 [48], were also predicted to possess robust FM order. Although the rapid development of theoretical work has generated a lot of very important results, the presently demonstrated 2D FMSs are still rare and more efforts should be paid to searching or designing interesting materials.
3 Conclusion and outlook
2D FM materials have received widespread attention and form the basis for next-generation nanoscale spintronics. Based on the first-principles simulations, plenty of theoretical efforts have been devoted to designing low-dimensional FM materials, and some of them have been confirmed later by experiment, which has promoted the rapid development of 2D magnetism field. Several interesting cases including 2D ferromagnetic semiconductors have been discussed in this minireview, showing the strong power of first-principles methods. The comparison between simulation and experiment proves the accuracy and efficiency of the calculation and prediction. As an important tool, first-principles calculations will remain a key component of designing materials, providing guidance for the development of spintronics. It should be emphasized that although great recent successes have been made, the study of 2D magnetism is still in its infancy, and searching for high 2D TC intrinsic ferromagnetism is still a current hotspot. Several key challenges are still needed to be overcome in the future as follow:
(1). Designing new members of 2D FM materials with high TC, large out-of-plane MAE, and easy experimental accessibility. On one hand, the types of 2D FM materials confirmed experimentally are rather limited, and should be enriched further. On the other hand, the present 2D FM materials suffer the problem of low TC and small MAE, greatly limit their application scope. One need to investigate the factors that affect Curie temperature (such as the exchange interaction and the magnetic anisotropy), and then find appropriate strategies to increase TC. Synthesizable 2D FM materials with high temperature TC and sizable MAE are still highly desirable.
(2). Improving the accuracy of theoretical prediction. Due to limitations of standard DFT theory, close cooperation between theory and experiment is needed to combine the advantages of both to accelerate the discovery and synthesis of 2D FM materials. For example, the predicted TC with the Ising model and mean field theory are usually overestimated compared with experiment values [49]. MC simulation based on Heisenberg model appears to be more reliable in the accurate prediction of TC, which is also very important to model new systems for practical applications.
(3). Making full use of rapid development of the 2D database. To take the advantage of the established database, high-throughput method [50–53] and machine learning [54–56] models need to be developed to reduce the number of required objective function evaluations (first-principles calculations) and avoid the amount of computational cost. These methods offer new tools for designing new 2D FM materials to overcome the challenges in the practical application of information technologies.
Author contributions
YT: Data curation, Investigation, Validation, Writing original draft; QL: Data curation, Investigation, Validation, Writing original draft; LH: Data curation, Investigation; PS: Conceptualization, Methodology; CJ: Methodology; JS: Data Curation; JZ: Formal analysis; XZ: Validation, Writing—Review and Editing, Supervision; Bing Wang: Writing—Review and Editing, Supervision, Funding acquisition.
Funding
This work was financially supported by the National Natural Science Foundation of China (Nos 12047517 and 12104130), and the China Postdoctoral Science Foundation (Nos 2020M682274 and 2020TQ0089). Innovative experimental training program for college students of Henan University (No. 20221011005), Open-ended research projects for undergraduates in the Scientific Research Laboratory (Platform) of Henan University.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Huang B, Clark G, Navarro-Moratalla E, Klein DR, Cheng R, Seyler KL, et al. Layer-dependent ferromagnetism in a van der Waals crystal down to the monolayer limit. Nature (2017) 546:270–3. doi:10.1038/nature22391
2. Gong C, Li L, Li Z, Ji H, Stern A, Xia Y, et al. Discovery of intrinsic ferromagnetism in two-dimensional van der Waals crystals. Nature (2017) 546:265–9. doi:10.1038/nature22060
3. Huang C, Feng J, Wu F, Ahmed D, Huang B, Xiang H, et al. Toward intrinsic room-temperature ferromagnetism in two-dimensional semiconductors. J Am Chem Soc (2018) 140:11519–25. doi:10.1021/jacs.8b07879
4. Burch KS. Electric switching of magnetism in 2D. Nat Nanotechnol (2018) 13:532. doi:10.1038/s41565-018-0165-4
5. Zhang Y, Chu J, Yin L, Shifa TA, Cheng Z, Cheng R, et al. Ultrathin magnetic 2D single-crystal CrSe. Adv Mater (2019) 31:e1900056. doi:10.1002/adma.201900056
6. Gong C, Zhang X. Two-dimensional magnetic crystals and emergent heterostructure devices. Science (2019) 363:eaav4450. doi:10.1126/science.aav4450
7. Wu Y, Sun W, Liu S, Wang B, Liu C, Yin H, et al. Ni(NCS)2 monolayer: A robust bipolar magnetic semiconductor. Nanoscale (2021) 13:16564–70. doi:10.1039/d1nr04816c
8. Mak KF, Lee C, Hone J, Shan J, Heinz TF. Atomically ThinMoS2: A new direct-gap semiconductor. Phys Rev Lett (2010) 105:136805. doi:10.1103/physrevlett.105.136805
9. Novoselov KS, Jiang D, Schedin F, Booth TJ, Khotkevich VV, Morozov SV, et al. Two-dimensional atomic crystals. Proc Natl Acad Sci U S A (2005) 102:10451–3. doi:10.1073/pnas.0502848102
10. Li L, Yu Y, Ye GJ, Ge Q, Ou X, Wu H, et al. Black phosphorus field-effect transistors. Nat Nanotechnol (2014) 9:372–7. doi:10.1038/nnano.2014.35
11. Lee K, Dismukes AH, Telford EJ, Wiscons RA, Wang J, Xu X, et al. Magnetic order and symmetry in the 2D semiconductor CrSBr. Nano Lett (2021) 21:3511–7. doi:10.1021/acs.nanolett.1c00219
12. Cai X, Song T, Wilson NP, Clark G, He M, Zhang X, et al. Atomically thin CrCl3: An in-plane layered antiferromagnetic insulator. Nano Lett (2019) 19:3993–8. doi:10.1021/acs.nanolett.9b01317
13. Zhang ZS, Jiang J, Rasmita C, Gao A, Yu WT. Direct photoluminescence probing of ferromagnetism in monolayer two-dimensional CrBr3. Nano Lett (2019) 19:3138–42. doi:10.1021/acs.nanolett.9b00553
14. Fei Z, Huang B, Malinowski P, Wang W, Song T, Sanchez J, et al. Two-dimensional itinerant ferromagnetism in atomically thin Fe3GeTe2. Nat Mater (2018) 17:778–82. doi:10.1038/s41563-018-0149-7
15. Deng Y, Yu Y, Song Y, Zhang J, Wang NZ, Sun Z, et al. Gate-tunable room-temperature ferromagnetism in two-dimensional Fe3GeTe2. Nature (2018) 563:94–9. doi:10.1038/s41586-018-0626-9
16. Guo S-D, Guo X-S, Zhu Y-T, Ang Y-SJAPL. Predicted ferromagnetic monolayer CrSCl with large vertical piezoelectric response: A first-principles study. Appl Phys Lett (2022) 121:062403. doi:10.1063/5.0109033
17. Hu J, Wang P, Zhao J, Wu R. Engineering magnetic anisotropy in two-dimensional magnetic materials. Adv Phys X (2018) 3:1432415. doi:10.1080/23746149.2018.1432415
18. Ma Y, Dai Y, Guo M, Niu C, Zhu Y, Huang B. Evidence of the existence of magnetism in pristine VX(2) monolayers (X = S, Se) and their strain-induced tunable magnetic properties. ACS Nano (2012) 6:1695–701. doi:10.1021/nn204667z
19. Zhuang HL, Hennig RG. Stability and magnetism of strongly correlated single-layerVS2. Phys Rev B (2016) 93:054429. doi:10.1103/physrevb.93.054429
20. Guo Y, Deng H, Sun X, Li X, Zhao J, Wu J, et al. Modulation of metal and insulator states in 2D ferromagnetic VS2 by van der Waals interaction engineering. Adv Mater (2017) 29:1700715. doi:10.1002/adma.201700715
21. Bonilla M, Kolekar S, Ma Y, Diaz HC, Kalappattil V, Das R, et al. Strong room-temperature ferromagnetism in VSe2 monolayers on van der Waals substrates. Nat Nanotechnol (2018) 13:289–93. doi:10.1038/s41565-018-0063-9
22. Liu J, Sun Q, Kawazoe Y, Jena P. Exfoliating biocompatible ferromagnetic Cr-trihalide monolayers. Phys Chem Chem Phys (2016) 18:8777–84. doi:10.1039/c5cp04835d
23. Li X, Yang J. CrXTe3 (X=Si, Ge) nanosheets: Two dimensional intrinsic ferromagnetic semiconductors. J Mater Chem C Mater (2014) 2:7071. doi:10.1039/c4tc01193g
24. Zhuang HL, Kent PRC, Hennig RG. Strong anisotropy and magnetostriction in the two-dimensional Stoner ferromagnetFe3GeTe2. Phys Rev B (2016) 93:134407. doi:10.1103/physrevb.93.134407
25. Guo Y, Zhang Y, Yuan S, Wang B, Wang J. Chromium sulfide halide monolayers: Intrinsic ferromagnetic semiconductors with large spin polarization and high carrier mobility. Nanoscale (2018) 10:18036–42. doi:10.1039/c8nr06368k
26. Wang C, Zhou X, Zhou L, Tong N-H, Lu Z-Y, Ji W. A family of high-temperature ferromagnetic monolayers with locked spin-dichroism-mobility anisotropy: MnNX and CrCX (X = Cl, Br, I; C = S, Se, Te). Sci Bull (Beijing) (2019) 64:293–300. doi:10.1016/j.scib.2019.02.011
27. Guo Y, Wang B, Zhang X, Yuan S, Ma L, Wang J. Magnetic two‐dimensional layered crystals meet with ferromagnetic semiconductors. InfoMat (2020) 2:639–55. doi:10.1002/inf2.12096
28. Mermin ND, Wagner H. Absence of ferromagnetism or antiferromagnetism in one- or two-dimensional isotropic Heisenberg models. Phys Rev Lett (1966) 17:1307–136. doi:10.1103/physrevlett.17.1307
29. Wang B, Zhang Y, Ma L, Wu Q, Guo Y, Zhang X, et al. MnX (X = P, as) monolayers: A new type of two-dimensional intrinsic room temperature ferromagnetic half-metallic material with large magnetic anisotropy. Nanoscale (2019) 11:4204–9. doi:10.1039/c8nr09734h
30. Wang X, Wu R, Wang D-S, Freeman AJ. Torque method for the theoretical determination of magnetocrystalline anisotropy. Phys Rev B (1966) 54:61–4. doi:10.1103/physrevb.54.61
31. Fang Y, Wu S, Zhu Z-Z, Guo G-Y. Large magneto-optical effects and magnetic anisotropy energy in two-dimensional Cr2Ge2Te6. Phys Rev B (2018) 98:125416. doi:10.1103/physrevb.98.125416
32. Li X, Yang J. First-principles design of spintronics materials. Natl Sci Rev (2016) 3:365–81. doi:10.1093/nsr/nww026
33. Mcguire MA, Dixit H, Cooper VR, Sales BC. Coupling of crystal structure and magnetism in the layered, ferromagnetic insulator CrI3. Chem Mater (2015) 27:612–20. doi:10.1021/cm504242t
34. Zhang W-B, Qu Q, Zhu P, Lam C-H. Robust intrinsic ferromagnetism and half semiconductivity in stable two-dimensional single-layer chromium trihalides. J Mater Chem C Mater (2015) 3:12457–68. doi:10.1039/c5tc02840j
35. Guo Y, Yuan S, Wang B, Shi L, Wang J. Half-metallicity and enhanced ferromagnetism in Li-adsorbed ultrathin chromium triiodide. J Mater Chem C Mater (2018) 6:5716–20. doi:10.1039/c8tc01302k
36. Sivadas N, Okamoto S, Xu X, Fennie CJ, Xiao D. Stacking-dependent magnetism in bilayer CrI3. Nano Lett (2018) 18:7658–64. doi:10.1021/acs.nanolett.8b03321
37. Jiang P, Wang C, Chen D, Zhong Z, Yuan Z, Lu Z-Y, et al. Stacking tunable interlayer magnetism in bilayer CrI3. Phys Rev B (2019) 99:144401. doi:10.1103/physrevb.99.144401
38. Huang B, Clark G, Klein DR, Macneill D, Navarro-Moratalla E, Seyler KL, et al. Electrical control of 2D magnetism in bilayer CrI 3. Nat Nanotechnol (2018) 13:544–8. doi:10.1038/s41565-018-0121-3
39. Jiang S, Shan J, Mak KF. Electric-field switching of two-dimensional van der Waals magnets. Nat Mater (2018) 17:406–10. doi:10.1038/s41563-018-0040-6
40. Song T, Fei Z, Yankowitz M, Lin Z, Jiang Q, Hwangbo K, et al. Switching 2D magnetic states via pressure tuning of layer stacking. Nat Mater (2019) 18:1298–302. doi:10.1038/s41563-019-0505-2
41. Kim HH, Yang B, Li S, Jiang S, Jin C, Tao Z, et al. Evolution of interlayer and intralayer magnetism in three atomically thin chromium trihalides. Proc Natl Acad Sci U S A (2019) 116:11131–6. doi:10.1073/pnas.1902100116
42. Sivadas N, Daniels MW, Swendsen RH, Okamoto S, Xiao D. Magnetic ground state of semiconducting transition-metal trichalcogenide monolayers. Phys Rev B (2015) 91:235425. doi:10.1103/physrevb.91.235425
43. Zhuang HL, Xie Y, Kent PRC, Ganesh P. Computational discovery of ferromagnetic semiconducting single-layerCrSnTe3. Phys Rev B (2015) 92:035407. doi:10.1103/physrevb.92.035407
44. Xu B, Li S, Jiang K, Yin J, Liu Z, Cheng Y, et al. Switching of the magnetic anisotropy via strain in two dimensional multiferroic materials: CrSX (X = Cl, Br, I). Appl Phys Lett (2020) 116:052403. doi:10.1063/1.5140644
45. Miao N, Xu B, Zhu L, Zhou J, Sun Z. 2D intrinsic ferromagnets from van der Waals antiferromagnets. J Am Chem Soc (2018) 140:2417–20. doi:10.1021/jacs.7b12976
46. Xiao T, Wang G, Liao Y. Theoretical prediction of two-dimensional CrOF sheet as a ferromagnetic semiconductor or a half-metal. Chem Phys (2018) 513:182–7. doi:10.1016/j.chemphys.2018.08.007
47. Zhang F, Mi W, Wang X. Spin‐dependent electronic structure and magnetic anisotropy of 2D ferromagnetic janus Cr2I3X3 (X = Br, Cl) monolayers. Adv Electron Mater (2019a1900778) 6:1900778. doi:10.1002/aelm.201900778
48. Chen JY, Li XX, Zhou WZ, Yang JL, Ouyang FP, Xiong X. Large‐spin‐gap nodal‐line half‐metal and high‐temperature ferromagnetic semiconductor in Cr2X3 (X=O, S, Se) monolayers. Adv Electron Mater (2020) 6:1900490. doi:10.1002/aelm.201900490
49. Sun Y, Zhuo Z, Wu X, Yang J. Room-temperature ferromagnetism in two-dimensional Fe2Si nanosheet with enhanced spin-polarization ratio. Nano Lett (2017) 17:2771–7. doi:10.1021/acs.nanolett.6b04884
50. Zhang X, Chen A, Zhou Z. High-throughput computational screening of layered and two-dimensional materials. WIREs Comput Mol Sci. (2018). p. e1385. doi:10.1002/wcms.1385
51. Mounet N, Gibertini M, Schwaller P, Campi D, Merkys A, Marrazzo A, et al. Two-dimensional materials from high-throughput computational exfoliation of experimentally known compounds. Nat Nanotechnol (2018) 13:246–52. doi:10.1038/s41565-017-0035-5
52. Ashton M, Paul J, Sinnott SB, Hennig RG. Topology-scaling identification of layered solids and stable exfoliated 2D materials. Phys Rev Lett (2017) 118:106101. doi:10.1103/physrevlett.118.106101
53. Paul JT, Singh AK, Dong Z, Zhuang H, Revard BC, Rijal B, et al. Computational methods for 2D materials: Discovery, property characterization, and application design. J Phys : Condens Matter (2017) 29:473001. doi:10.1088/1361-648x/aa9305
54. Correa-Baena J-P, Hippalgaonkar K, van Duren J, Jaffer S, Chandrasekhar VR, Stevanovic V, et al. Accelerating materials development via automation, machine learning, and high-performance computing. Joule (2018) 2:1410–20. doi:10.1016/j.joule.2018.05.009
55. Lu S, Zhou Q, Guo Y, Zhang Y, Wu Y, Wang J. Coupling a crystal graph multilayer descriptor to active learning for rapid discovery of 2D ferromagnetic semiconductors/half‐metals/metals. Adv Mater (2020) 32:2002658. doi:10.1002/adma.202002658
Keywords: two-dimensional, ferromaganetism, semiconductor, first-principal calculations, 2D spintronics
Citation: Tu Y, Liu Q, Hou L, Shi P, Jia C, Su J, Zhang J, Zhang X and Wang B (2022) Two-dimensional Cr-based ferromagnetic semiconductor: Theoretical simulations and design. Front. Phys. 10:1078202. doi: 10.3389/fphy.2022.1078202
Received: 24 October 2022; Accepted: 27 October 2022;
Published: 11 November 2022.
Edited by:
Guangzhao Wang, Yangtze Normal University, ChinaReviewed by:
Shan Guan, Institute of semiconductors, ChinaDongbao Luo, University at Buffalo, United States
Copyright © 2022 Tu, Liu, Hou, Shi, Jia, Su, Zhang, Zhang and Wang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Xiuyun Zhang, eHl6aGFuZ0B5enUuZWR1LmNu; Bing Wang, d2JAaGVudS5lZHUuY24=
†These authors have contributed equally to this work
 Yufei Tu
Yufei Tu Qingquan Liu3†
Qingquan Liu3† Bing Wang
Bing Wang