Kondo resonance effects in emergent flat band materials

Macroscopic degrees of freedom that are involved in the transport of carriers through mesoscopic electronic devices are susceptible to the effects of strong many-body correlations. The presence of magnetic impurities in dilute magnetic alloys typically allow for insights into Kondo effect from the scattering of free carriers by localized electron states of the magnetic impurities but this effect is not well understood when there are no d-band electron states. Herein, the signatures of Kondo resonance effect are elucidated in quantum dots derived from a carbon-nanoline embedded monolayer hexagonal boron nitride whose electron states host flat band ferromagnetism as distinct broken symmetry states. Quantum transport state of mesoscopic devices modelled as quantum dots tunnel coupled to metallic leads is computed by direct diagonalization of the Hamiltonian. The possibility of realizing quantum dots with highly tunable electron states in energy interconversion devices is discussed to show the importance of screening effects on single-electron energy levels. The quantum master equation is solved within different formalisms to determine the stationary-state particle and energy currents. Stability diagrams are calculated to show the dependence of the conductance on experimental control variables of the quantum dot device. The computed responses of the stationary-state transport signatures are used to characterize Kondo resonance effects from flat band states of embedded carbon nanoline-based quantum dots. It is found that the local network structure of the hexagonal ring carbon cluster-based quantum dot has a broken particle-hole symmetry in the transport state. This signals the formation of the quasiparticle states expected in second order scattering when the macroscopic “charge” pseudospin symmetry of the tunnelling electron state is broken dynamically due to charging. The results are discussed to show the implications of a vanishing particle-hole symmetry in the carrier transport state of quantum dots for energy conversion applications.

1 Introduction

Exotic phenomena such as d- and f-electron superconductivity, integer and half-integer quantum Hall states, quantum spin liquid state, and spontaneous formation of quasiparticles can emerge in quantum materials because of many-body correlations [1, 2]. It is also important to understand the non-equilibrium physics of the formation of broken symmetry states to understand how electron states couple to bosonic environments. A bosonic environment can be described by quasiparticles such as phonons, photons, anyons, polarons and excitons in an energy interconversion application [3]. Developing such understanding is important because the out of equilibrium behavior of quantum materials gives rise to intriguing electrodynamic properties, and unusual magnetic and topological phases which may be related to the ultrafast energy conversion processes [4, 5]. Quantum dots (QDs) offer an ideal platform for designing carrier transport devices under realistic conditions that allow the many-body correlation and strong quantum confinement effects that dominate mesoscopic transport to be probed at the single-electron level. The role of Coulombic interactions in exotic phenomena such as defect-induced d⁰-magnetism and single-electron tunneling is crucial in quantum dots. The QD is made from either a nanostructure or a single molecule coupled to metallic leads, and it can be integrated into energy harvesting systems for interconverting electromagnetic radiation into electric current [6].

The QD is a small-sized particle of a semiconducting material. In general, it is a nanocrystal with a diameter between 20–100 Å. It contains about 10–50 atoms and its electronic properties are unique because they often lie between the properties of a bulk semiconductor and a single molecule. The broad range of their properties arises because of its high surface-to-volume ratio. These unique range of properties lead to their intriguing applications in non-linear optics and energy application. For instance, in luminescence and fluorescence, QDs can be used to produce distinctive colors that are determined by the size of the particles. Due to its small size, electrons in a QD are confined in a small space known as the quantum box. When the radius of the nanocrystal is made smaller than the exciton Bohr radius (i.e., the average distance between the electron in the conduction band and the hole it leaves behind in the valence band), the energy levels become quantized according to Pauli’s exclusion principle. The discrete, quantized energy levels of the QD relates it more closely to atoms than to bulk materials and this has led to the QD being identified as the artificial atom [7, 8]. QDs host single-electron states just as vortices of bulk trivial superconductors, endpoints of 1D p-wave topological superconductor, and hybrid semiconductor-superconductor nanowires. The electron states manifest as a quantized zero-bias conductance peak (ZBCP) of height 2e²/h at 0 K and also above a critical magnetic field (B_c) that is determined by gating. Other metrics include symmetry breaking signatures in the tunnelling differential conductance spectra of electron-hole states. Since these signatures are also seen in superconductors and semiconductors due to a variety of other physical effects such as Andreev or Shiba bound states, Kondo resonances, etc, it is important to study them self-consistently.

The current drive towards the development of high-performance materials (HPMs) for use in the next-generation of technologies for a facile interconversion of energy has made it a fundamental scientific imperative to understand the nature of the underlying many-body correlation effects in quantum materials. Recent progress in energy materials shows that HPMs that have potential for being used as a flexible electronic “skin” are highly desirable for energy autonomy [9]. This desire for new HPMs has demanded the introduction of flexible and stretchable materials. In this respect, our previous studies had shown the graphene and monolayer hexagonal boron nitride are highly stretchable [10], making them equally suitable for development as HPMs for energy applications. The recent use of mixed caesium and formamidinium lead triiodide perovskite system (Cs_1−xFA_xPbI₃) promises a realistic pathway for achieving efficient photovoltaic and optoelectronic energy conversion using the QD architecture. The major drawback is the severe challenge of synthesizing multinary QDs with desirable properties for use in high-performance QD solar cells [11]. The present study therefore represents a crucial first step in developing such understanding from a multiscale multi-physics model of the electron states for understanding the role of HPMs in the facile interconversion of energy.

When a metal contains a magnetic impurity, conduction electrons of the metal scatter from the localized impurity spin and screens it to form a cloud of spin-polarized electrons [12]. Kondo effect arises from the interaction of conduction electrons with degenerate degrees of freedom of carriers in a material. When the Kondo effect is associated with dilute magnetic impurities in a non-magnetic host the phenomenon constitutes the traditional Kondo effect (TKE) [13]. In the TKE, the two degenerate states correspond to the two orientations (i.e., up, or down) of the impurity spin. Several variants of the TKE have been observed wherein the quantum impurity (QI) is coupled to a bath of conduction electrons. The Anderson’s model of the QI is a useful microscopic model for understanding the physics of the broken symmetry quantum state that forms in the TKE when localized impurity spins are dynamically screened by the conduction electrons [14]. Analogous broken symmetry states form as the underlying quasiparticle state that mediates the energy interconversion process whenever polarons, plasmons, excitons, charge- or spin-density waves form as a collective state for carrier transport. Kondo resonance effects in the carbon nanoline-embedded quantum dots are crucial for developing a rational understanding of the energy interconversion. This is because the Schrieffer-Wolff transformation is known under the Wilsonian renormalization group theory [15] to project out the high energy charge excitations in the Anderson QI model so that a low-energy effective Hamiltonian is obtained with only virtual charge fluctuations [16].

There are several alternative models of the TKE wherein the spin of the quantum dot is magnetically exchange-coupled to ferromagnetic leads [17], or with superconducting pair-breaking interactions [18], or with the surface state of topological insulators and to impurity states in Dirac and Weyl semimetals [19]. Although the QI model is mostly associated with spin [20, 21], orbital [22, 23] or structural [24, 25] degree of freedom of carriers in the TKE, these are not the models of the Kondo effect considered herein. There are other Kondo models that comprise of two degenerate degrees of freedom, which can also lead to the Kondo-like phenomena [24, 26]. For instance, consider that the “charge Kondo effect”, which corresponds to the dilute magnetic impurities with two degenerate charge states in the TKE, has been proposed for negative-U Anderson QI models [27]. As demonstrated experimentally by Matsushita, et al; [28], there are strong quantum valence fluctuations implicit in the charge Kondo effect (CKE) model to support the involvement of electrons pairs that tunnel on and off the impurity sites. Their experimental measurements also demonstrated that the electron pairing mechanism of the CKE model also provides the pairing mechanism for superconductivity, as well as the abrupt logarithmic increase in the low-temperature resistivity observed in superconducting Tl-doped PbTe. Also, the TKE is now known to arise from second-order scattering processes that involve virtual intermediate states or quasiparticles [29].

Herein, the effects of the screened charge pseudospin-½ state are discussed as signatures of Kondo resonance. The charge pseudospin of the tunnelling electronic state is the macroscopic degree of freedom that is screened by conduction electron cloud of the metallic leads when the QD is tunnel coupled. The charge Kondo effect is shown as the underlying mechanism that controls the interconversion of energy with quantum dots derived from carbon nanoline embedded in monolayer h-BN since energy interconversion process is limited by formation of the quasiparticle state. In the present analysis, quasiparticle states of an energy conversion process are considered to correspond to virtual intermediate states of a second-order scattering process, and both states saturate below the characteristic Kondo temperature in the unitary scattering limit [30]. This is illustrated by the dynamical formation of a broken particle-hole symmetry state due to Coulombic charging of the dots in the presence of pseudospin—an additional electronic degree of freedom inherent in graphene [31], which is also preserved in the embedded carbon nanoline. The CKE is implemented in gate controlled QD system [32, 33]. It uses either a metallic- or semiconducting-realization of the single-electron transistor via the tunnel coupling of the QD to metallic leads by charge-tuning of the quantum pseudospin degree of freedom. The charge pseudospin of the QD is construed as the macroscopic quantum variable that consists of two degenerate electronic states when the QD is coupled to metallic leads (i.e., treated here as a bath of many conduction electrons) [34]. Thus, the role of spin up (↑) or down (↓) in the TKE is played by the screened charge pseudospin.

Kondo resonance effects are demonstrated in the charge stability diagrams of QDs designed from an intrinsically non-metallic metamaterial. The platform consists of an embedded carbon nanoline conducting channel in the semiconducting matrix formed by the hexagonal boron nitride (hBN) monolayer. With its highly tunable carrier transport properties, it is argued herein that such drawbacks do not arise when graphene-nanoline based QDs are integrated into energy systems. Since quantum many-body interactions play a central role in the microscopic theory of a QD system [35], the electronic signatures of Kondo resonance are unraveled as a function of a tunable confinement potential and gate potential. It is shown that emergent flat band materials obtained from the highly flexible graphene and monolayer hexagonal boron nitride (hBN) are suitable HPMs for energy conversion when integrated in QD devices. This requires accurate characterization of the strength of the Coulombic interaction on carrier transport signatures in the absence of the d-band ferromagnetism expected from localized magnetic impurities in dilute magnetic ions (DMAs). Kondo effect is elucidated in carbon nanoline based QDs as an increase in the direct current conductance as temperature drops below the Kondo temperature of 10 K. Kondo resonance effects are shown to arise from an interplay between Coulombic and magnetic exchange interactions. The Kondo resonance effect of the screened charge pseudospin is traced to the presence of flat bands due to the broken structure-inversion and time reversal symmetries.

This paper is organized as follows. In Section 2, the theoretical framework employed here to calculate the ground state electronic structure of embedded carbon nanoline conducting channels in hBN monolayer is presented. Details are also provided for the protocols used to obtain mesoscopic transport signatures of quantum dot in exact diagonalization calculations. The latter includes electronic-level alignment strategies that describe a four-terminal transistor coupled to metallic leads by tunneling in the multilayer architecture. Results and discussion are presented in Section 3. The electronic band structure in different types of embedded hBN monolayers are presented. The quasiparticle band gaps, and magnetic properties are also analyzed. Results of the mesoscopic transport properties of the tunnelling current and their bias dependent conductance responses also analyzed in Section 3 with respect to simulated charge stability diagram parameters and the associated band topology. The results are discussed with special emphasis on the realization of tunable QDs for integration in devices for facile interconversion of energy. Finally, conclusions are drawn in Section 4.

2 Theoretical and computational details

2.1 Ground state electronic structure and self-consistent correction for the quasiparticle gap

First principles calculation of the ground state electronic structure was performed within density functional theory (DFT) using the grid-based projector augmented wave (GPAW) method [36, 37]. The calculations were first performed in the generalized gradient approximation (GGA) using the Perdew Burke and Ernzerhof (PBE) functional for the exchange correlation potential [38]. The Coulombic interaction between conduction electrons and ion cores were described using the projector-augmented wave (PAW) potentials [39, 40]. Electronic energy was converged to within 10⁻⁸ eV. A cutoff limit of 600 eV was used to expand the kinetic energy in the plane wave basis. For calculations of the primitive p (1 × 1) unit cell of the pristine hBN monolayer, a dense Monkhorst-Pack k-points mesh of size 10 × 10×1 was used to sample the Brillouin zone [41]. Electronic states were populated using the Fermi-Dirac distribution. A small smearing width of 01 eV was used to account for temperature dependence of the populated electron states to avoid intraband transitions. Spurious interactions between periodically repeating monolayers were avoided by inserting a vacuum region of 15 Å along the z-axis of the monolayer.

Nanoline conducting channels when embedded in an intrinsically non-magnetic monolayer hexagonal boron nitride (hBN) layer serves as a platform for gaining insights into defect-induced magnetic moments since there are no d-band contributions to electronic states. To embed a nanoline conducting channel in the semiconducting hexagonal boron nitride monolayer (hBN), a 5 × 5×1 supercell model was used. Six unique local geometries of the nanoline conducting channel were obtained when variable number of carbons replaces the B and N atoms along a contiguous line within the layer. Spin polarized ground state calculations were performed in each case using a reduced k-mesh of 2 × 2×1. Spin orbit interaction effects on the electronic bands were included non-self consistently as a correction of the ground state. This was sufficient to describe the band states induced within the semiconducting gap of the pristine layer when C replaces some of the B and N atoms of the layer along a contiguous line in the monolayer. Geometry optimization calculations were performed until the Hellman-Feynman forces on each atom converged to within 001 eV/Å.

It is well-known that native approximations to DFT such as the local density approximation (LDA) and generalized gradient approximation (GGA) give underestimated band gaps. As such, the GGA bandgaps obtained herein do not yield any insights on the effects of the broken symmetry states (i.e., quasiparticles such as polarons and excitons, etc.) that may be created in the HPMs. Corrected band gaps are calculated in this study to yield useful insights for understanding quasiparticle effects when a carbon nanoline based HPM is integrated in the QD device. The calculations are performed using the GLLB-SC functional [42]. The GLLB-SC functional uses the PBEsol exchange correlation potential to model the Kohn-Sham potential with the derivative discontinuity at integer particle numbers based on the self-consistent approximation introduced by Gritsenko et al. (GLLB) [43]. The fundamental quasiparticle gap was obtained from the GLLBSC functional as the sum of Kohn-Sham gap and the derivative discontinuity due to the response of the exchange-correlation hole to density variations.

2.2 Framework for the calculation of mesoscale transport

2.2.1 Unitary evolution of the density matrix

To describe the unitary evolution of the density matrix, consider that the dynamics of a closed quantum system is specified by the solutions of the time-dependent Schrödinger equation.

$\mathit{i}\hslash {\partial }_{\mathit{t}}\mathbf{\Psi }=\widehat{\mathbf{H}}\mathbf{\Psi },(1)$

where Ψ denotes the wave function, $\widehat{\mathbf{H}}$ denotes the Hamiltonian, and ℏ is Planck’s constant. The time-dependent Schrödinger equation is a first order partial differential equation where both Ψ and H are functions of space and time. For computational purposes, it is useful to expand Eq. 9 in a set of basis functions that span the Hilbert space of the Hamiltonian, and to write it in matrix and vector form $\mathit{i}\mathbf{\hslash }{\partial }_{\mathit{t}}\left|\mathbf{\Psi }\right.〉=\mathbf{H}\left|\mathbf{\Psi }\right.〉,$ where $\left|\mathbf{\Psi }\right.〉$ is the state vector and H is the matrix representation of the Hamiltonian. This matrix equation can, in principle, be solved by diagonalizing the Hamiltonian matrix H. In practice, however, it is difficult to perform this diagonalization unless the size of the Hilbert space (i.e., the dimension of the matrix H) is small.

While the evolution of the state vector in a closed quantum system is deterministic, open quantum systems are stochastic in nature. The effect of an environment on the system of interest is to induce stochastic transitions between energy levels, and to introduce uncertainty in the phase difference between states of the system. The state of an open quantum system is therefore described in terms of ensemble averaged states using the density matrix formalism. The density matrix ρ describes a probability distribution of quantum states $\left|{\mathbf{\Psi }}_{\mathit{n}}\right.〉$, in a matrix representation

$\mathit{\rho }={\displaystyle \sum }_{\mathit{n}}{\mathit{p}}_{\mathit{n}}\left|{\mathbf{\Psi }}_{\mathit{n}}\right.〉〈\left.{\mathbf{\Psi }}_{\mathit{n}}\right|,(2)$

where $p_n$ denotes the classical probability that the system is in the quantum state $\left|{\mathbf{\Psi }}_{\mathit{n}}\right.〉$. Calculation of the time evolution of the density matrix ${\dot{\mathit{\rho }}}_{\mathit{t}\mathit{o}\mathit{t}\mathit{a}\mathit{l}}$ of the tunnel-coupled quantum dot system is the objective of the mesoscopic transport calculation discussed herein. Thus, at the level of mesoscopic transport calculation, we are solving the time-evolution of the density matrix at different charging potentials of the quantum dot and applied magnetic field.

The quantum statistical mechanics approach for deriving equations of motion of an open quantum system that is interacting with its environment is to expand the scope of the system to include the environment [44, 45]. Since the combined quantum dot and metallic lead system is a closed quantum system, its evolution is governed by the von Neumann equation

${\dot{\mathit{\rho }}}_{\mathit{t}\mathit{o}\mathit{t}\mathit{a}\mathit{l}}={\partial }_{\mathit{t}}\left({\widehat{\mathit{\rho }}}_{\mathit{t}\mathit{o}\mathit{t}\mathit{a}\mathit{l}}\right)=-\mathit{i}{\hslash }^{-\mathbf{1}}\left[{\widehat{\mathit{H}}}_{\mathit{t}\mathit{o}\mathit{t}\mathit{a}\mathit{l}},{\widehat{\mathit{\rho }}}_{\mathit{t}\mathit{o}\mathit{t}\mathit{a}\mathit{l}}\right](3)$

Equation 11 is the equivalent Schrödinger equation expressed in density matrix formalism in Eq. 1. Here, the total Hamiltonian, H_total = H_sys + H_env + H_int, includes the original system Hamiltonian H_sys, the Hamiltonian for the environment H_env, and an additional term H_int that represents the interaction between the system and its environment. This corresponds to the systems Hamiltonian defined in Section 2.3. Since the interest is only in the dynamics of the system, it is possible to perform a partial trace over the environmental degrees of freedom in Eq. 3 to obtain a master equation for the motion of the original system density matrix.

The generalized form of the completely positive trace-preserving time evolution of the density matrix is the Lindblad master equation for the reduced density matrix ρ = Tr_env [ρ_total]. This is expressed in terms of the time-dependent Hamiltonian $\widehat{\mathit{H}}\left(\mathit{t}\right)$ and dissipation terms $\mathit{D}\left(\widehat{\mathit{\rho }}\right)$ as [46],

$\dot{\mathit{\rho }}\left(\mathit{t}\right)={\partial }_{\mathit{t}}\widehat{\mathit{\rho }}=-\mathit{i}{\hslash }^{-\mathbf{1}}\left[\widehat{\mathit{H}}\left(\mathit{t}\right),\widehat{\mathit{\rho }}\left(\mathit{t}\right)\right]+\mathit{D}\left(\widehat{\mathit{\rho }}\right),(4)$

where $\mathit{D}\left(\widehat{\mathit{\rho }}\right)=\sum \frac{\mathbf{1}}{\mathbf{2}}\left[\mathbf{2}{\mathit{C}}_{\mathit{n}}\mathit{\rho }\left(\mathit{t}\right){\mathit{C}}_{\mathit{n}}^{†}-{\mathit{\rho }\left(\mathit{t}\right)\mathit{C}}_{\mathit{n}}^{†}{\mathit{C}}_{\mathit{n}}-{\mathit{C}}_{\mathit{n}}^{†}{\mathit{C}}_{\mathit{n}}\mathit{\rho }\left(\mathit{t}\right)\right].$ The term ${\mathit{C}}_{\mathit{n}}={\gamma }_{\mathit{n}}\sqrt{{\mathit{A}}_{\mathit{n}}}$ denotes collapse operators (or the Lindbladian) while ${\mathit{A}}_{\mathit{n}}$ denotes the operators through which the environment couples to the system, and ${\gamma }_{\mathit{n}}$ are the corresponding collapse rates. Equation (4) is the primary equation that is solved in the transport model. The formal derivation of the Lindblad master equation is presented in several standard sources, including Refs [47–53], and will not be repeated here. Nonetheless, if one retains only the first term on the right-hand side of Eq. 4, then the Liouville-von Neumann equation results. The unitary evolution of the density operator of the QD is denoted by the Liouvillian. The second term on the right-hand side of Eq. 4 is the Lindbladian, which describes the non-unitary evolution of the density operator. It emerges only when one takes the partial trace of the interacting degrees of freedom between the electron in the QD and the bath of conduction electrons in the metallic leads. By adopting the interaction H_int of the form,

${\mathrm{H}}_{{}_{\mathrm{int}}=}\hslash \left[\mathit{\rho }\left(\mathit{t}\right){\mathit{C}}_{\mathit{n}}^{†}-\mathit{\rho }\left(\mathit{t}\right){\mathit{C}}_{\mathit{n}}^{†}{\mathit{C}}_{\mathit{n}}-{\mathit{C}}_{\mathit{n}}^{†}{\mathit{C}}_{\mathit{n}}\mathit{\rho }\left(\mathit{t}\right)\right],(5)$

the physical meaning of the Lindblad operators is understood as representation of the contribution of the QD charging energy to the interaction with conduction electrons. This is crucial since Eq. (4) is derived from the Liouville-von Neumann equation by tracing the degrees of freedom of the bath.

2.2.2 Numerical implementation

Analytically, it is a formidable task to calculate the dynamics of a QD system that has more than two states using the von Neumann equation (i.e., Eq. (3)). This becomes even more complicated when, in addition, one must consider dissipations due to the interaction of the QD with the surrounding environment using the Lindblad master equation (i.e., Eq. (4)). It is therefore necessary to resort to numerical approximations for these computational tasks to be performed in realistic situations. To this extent, the role of efficient and openly accessible computational tools, such as QuTip [54] and Kwant [55], in facilitating the numerical study of the dynamics of open quantum system calculations cannot be overstated. Herein, exact diagonalization calculations were performed to solve Eqs (3), (4) using different approximate master equations (i.e., Pauli, von Neumann, Redfield and Lindblad) as implemented in the Quantum master equation for Quantum (QmeQ) package [56]. QmeQ is an opensource PYTHON utility for simulating the stationary-state mesoscopic transport in QDs. The computational cost for solving the Lindblad equation numerically grows as additional complexity is introduced into the QD model. Hence, better numerical approximations are required for efficient numerical implementation of the solution. For derivation of the different approximate master equations that are implemented in the QmeQ package, and their pros and cons, see Appendices A–F in Ref; [56]. Key features of the approximate master equations used in the numerical simulations are listed below.

Second order von Neumann (2vN): This approach bridges the gap between rate equations and the transmission formalism which neglect level broadening and cotunneling which is essentially based on the single-particle picture thereby treating many-particle interactions on an approximate level. The 2vN is an approximation that is based on decoupling of the equations of motion for the density matrix. Only terms that involve up to two excitations n = 2 are retained in the Runge-Kutta algorithm for numerically solving the coupled ordinary differential equations. A Markov approximation is made to the two-excitation term. Electrons in the leads are assumed to be thermally distributed according to the Fermi-Dirac distribution, f. The 2vN resembles the resonant tunneling approximation, which is based on a suitable infinite re-summation of the perturbation series for the generalized master equation. (2vN) yields exact currents for non-interacting systems with H_Coulomb = 0. When interactions are introduced during charging (i.e., H_Coulomb ≠ 0) the results are only reliable at weak to moderate coupling strengths, wherein the Kondo temperature T_K is larger than (or equal to) the tunnelling rate Γ during the coupling. Also, the simulation temperature T must be larger than any Kondo temperature T_K in the system [54].

First order von Neumann (1vN): The 1vN approximation assumes that only the terms that involve one excitation n = 1 are retained in the Runge-Kutta algorithm for solving the coupled ordinary differential equations. A Markov approximation is made to the one-excitation term.

First-order Redfield: Retains all the assumptions, advantages, and disadvantages of the 1vN approximation. However, it implements an important exception wherein the Markov approximation to the one-excitation term is set to the steady-state solution of the Schrodinger equation, corresponding to Eq. 1, subject to the normalization condition. Thus, one can go to the Hamiltonian by transforming the first order Redfield master equation (also known as the second order in perturbation approximation) to the Lindblad master equation way.

Pauli master equation: Only the terms that involve one excitation n = 1 are retained, and all higher terms in the Runge-Kutta algorithm solving the coupled ordinary differential equations are discarded. The Markov approximation is made to the one-excitation term. The coherences of the reduced density matrix of the QD system are neglected. The Pauli master equation is obtainable from the 1vN or the Redfield approaches by neglecting the coherence.

Lindblad master equation: An approximate form of Eq. 4 is solved for the steady-state solution of the Schrodinger equation, corresponding to Eq. 1, subject to the normalization condition. This Lindblad approximation is the first order in rates and can describe the sequential tunneling in the presence of coherences. It preserves the positivity of the reduced density matrix as in the 2vN approach.

2.3 Relationships of mesoscale transport in QDs with DFT calculation of carbon nanolines

A system of coupled quantum dots is studied using a phenomenological model where carrier tunnelling is coupled to metallic leads. The Hamiltonian of the coupled QD/metallic lead system H_sys is obtained as a sum of terms,

$H_{sys}=H_{tunneling}+H_{leads}+H_{dot},(6)$

where H_leads, H_dot and H_tunneling denotes total energy contributions from the tunnelling between the QD and the leads, the metallic leads, and the QDs, respectively. The DFT calculations show two distinct possibilities wherein flat band electronic structure supports a ferromagnetic (or non-magnetic) ground state when number of carbons is odd (or even). Transport in the unpaired or paired electron spin system is modeled using the spinful single-orbital quantum dot (SSQD) model or spinless double quantum dot (SDQD) model in the regime where Coulombic interactions dominate. In this case, the energy level position of distinct local structure-derived flat band states is determined ab initio and fed as input into the stationary-state transport model calculation. Cronenwett, et al. [57] demonstrated over 2 decades ago that a QD can be designed to host a well-defined integral number of electrons. Thus, it is essential to allow a small tunnel coupling between the dot and nearby source and drain leads to probe electronic transport states. This magnitude of the coupling must be weak to prevent strong fluctuations in the number of confined electrons. A well-defined number of electrons also implies a definite amount of quantum mechanically confined charge, i.e., N times the elementary charge, e; Figure 1 shows the circuit diagram for simulating the coupling of a quantum dot to metallic leads that constitute the source (L) and drain (R) leads.

FIGURE 1

FIGURE 1. Schematic diagram of the tunnel coupling of quantum dot to the source and drain leads.

Carrier transport in the QD is described using the SSQD (or SDQD) model if the ground state magnetic moment of the nanoline-embedded QD is zero (or nonzero) using the approaches enumerated in Ref. [44]. In both cases, an on-site charging energy U due to an externally applied bias potential couples the quantum dot to the source (L) and drain (R) leads via tunnelling. The SSQD calculations are performed by parameterizing the energies of spin-polarized electrons for two single particle states $\left({ϵ}_{\uparrow },{ϵ}_{\downarrow }\right)$ as a function of a gate (or bias) potential V_g and a magnetic field B which are applied externally, where ${ϵ}_{\uparrow }=V_g+\frac{1}{2}B$ and ${ϵ}_{\downarrow }=V_g+\frac{1}{2}B.$ The total energy of the conduction electrons in the leads are described as non-interacting particles. This is expressed in the second quantization notation as

${\mathit{H}}_{\mathit{l}\mathit{e}\mathit{a}\mathit{d}\mathit{s}}={\displaystyle \sum }_{\mathit{\alpha }\mathit{k}}{\mathit{ϵ}}_{\mathit{\alpha }\mathit{k}}{\widehat{\mathit{c}}}_{\mathit{\alpha }\mathit{k}}^{†}{\widehat{\mathit{c}}}_{\mathit{\alpha }\mathit{k}},(7)$

where the ${\widehat{c}}_{\alpha k}^{†}\left({\widehat{c}}_{\alpha k}\right)$ operator creates (destroys) a spin-polarized electron at site $k$ in a lead channel $\alpha$. The site index k is a proper quantum number for the continuum energy. This allows the sum over k-space to be written using the density of states $g\left(E\right)$ as a thermalization mapping for the occupied states

${\displaystyle \sum }_{\mathit{k}}{\mathit{f}}_{\mathit{k}}\to \int \mathit{g}\left(\mathit{E}\right)\mathit{f}\left(\mathit{E}\right)\mathit{d}\mathit{E},(8)$

where $f\left(E\right)={\left[e^{\left(E-{\mu }_{\alpha }\right)/T_{\alpha }}+1\right]}^{-1}$ denotes the Fermi-Dirac distribution function with respective temperatures T_α and chemical potentials µ_α. The lead channel α describes a coupled system consisting of a source and drain lead label, and an electron spin depending on the physical setup of the QD.

The Hamiltonian of the QD (H_dot) is modelled as the sum of the DFT-derived single-particle Kohn-Sham states (H_KS) and the Coulomb interaction between the states,

$H_{dot}=H_{KS}+H_{Coilomb},(9)$

using the general form of the many-body Hamiltonian componnts

${\mathit{H}}_{\mathit{K}\mathit{S}}={\displaystyle \sum }_{\mathit{i}}{\mathit{ϵ}}_{\mathit{i}}{\widehat{\mathit{b}}}_{\mathit{i}}^{†}{\widehat{\mathit{b}}}_{\mathit{i}}+{\displaystyle \sum }_{\mathit{i}\ne \mathit{j}}{\mathbf{\Omega }}_{\mathit{i}\mathit{j}}{\widehat{\mathit{b}}}_{\mathit{i}}^{†}{\widehat{\mathit{b}}}_{\mathit{j}},(10)$

${\mathit{H}}_{\mathit{C}\mathit{o}\mathit{u}\mathit{l}\mathit{o}\mathit{m}\mathit{b}}={\displaystyle \sum }_{\mathit{m}\mathit{n}\mathit{k}\mathit{l}}{\mathit{U}}_{\mathit{m}\mathit{n}\mathit{k}\mathit{l}}{\widehat{\mathit{b}}}_{\mathit{m}}^{†}{\widehat{\mathit{b}}}_{\mathit{n}}^{†}{\widehat{\mathit{b}}}_{\mathit{k}}{\widehat{\mathit{b}}}_{\mathit{l}},\mathit{m}<\mathit{n}(11)$

where the operator ${\widehat{b}}_i^{†}\left({\widehat{b}}_i\right)$ creates (annihilates) a spin-polarized electron at site $i$ in a single-particle orbital of energy ${ϵ}_i$, ${\Omega }_{ij}$ denotes the strength of the hybridization between single particle orbitals. In the present calculations, the term ${\mathit{U}}_{\mathit{m}\mathit{n}\mathit{k}\mathit{l}}=〈\mathit{m}\mathit{n}\left|\mathit{U}\right|\mathit{k}\mathit{l}〉$ denotes the Coulomb matrix elements determined ab initio from DFT calculation of the ground state electronic structure. This is defined in the atomic ${\mathit{p}}_{\mathit{z}}$ basis ${\psi }_{\mathit{i}}\left(\mathbf{r}\right)$ of a given material as:

$〈\mathit{m}\mathit{n}\left|\mathit{U}\right|\mathit{k}\mathit{l}〉=\frac{e^2}{\mathbf{4}\mathit{\pi }{\mathit{\epsilon }}_{\mathit{r}}{\mathit{\epsilon }}_{\mathbf{0}}}\iint {d\mathbf{r}}_{\mathbf{1}}{d\mathbf{r}}_{\mathbf{2}}{\psi }_m^{*}{\left({\mathbf{r}}_{\mathbf{1}}\right)\psi }_n^{*}\left({\mathbf{r}}_{\mathbf{2}}\right){\psi }_k\left({\mathbf{r}}_{\mathbf{1}}\right){\psi }_l\left({\mathbf{r}}_{\mathbf{2}}\right),(12)$

for states where m < n. Finally, the tunnelling Hamiltonian is

${\mathit{H}}_{\mathit{T}\mathit{u}\mathit{n}\mathit{n}\mathit{e}\mathit{l}\mathit{l}\mathit{i}\mathit{n}\mathit{g}}={\displaystyle \sum }_{\mathit{\alpha }\mathit{k}\mathit{i}}{\mathit{t}}_{\mathit{\alpha }\mathit{k}\mathit{i}}{\widehat{\mathit{b}}}_{\mathit{i}}^{†}{\widehat{\mathit{c}}}_{\mathit{\alpha }\mathit{k}}+\mathbf{H}.\mathbf{c}.,(13)$

where H.c. represents the Hermitian conjugate of the first term and $t_{\alpha ki}$ denotes the tunneling amplitude between the leads and the QD. The above formulation introduces an important energy scale for these calculations through the tunneling rate such that

${\mathbf{Г}}_{\mathit{\alpha }\mathit{k}\mathit{i}}\left(\mathit{E}\right)=\mathbf{2}\mathit{\pi }{\displaystyle \sum }_{\mathit{k}}{\left|{\mathit{t}}_{\mathit{\alpha }\mathit{k}\mathit{i}}\right|}^{\mathbf{2}}\mathit{\delta }\left(\mathit{E}-{\mathit{ϵ}}_{\mathit{\alpha }\mathit{k}}\right).(14)$

The Hamiltonian of the SDQD model calculations is given by

${\mathit{H}}_{\mathit{t}\mathit{w}\mathit{o}}={\displaystyle \sum }_{\mathit{k};\mathit{l}=\mathit{L},\mathit{R}}{\mathit{ϵ}}_{\mathit{l}\mathit{k}}{\widehat{\mathit{c}}}_{\mathit{l}\mathit{k}}^{†}{\widehat{\mathit{c}}}_{\mathit{l}\mathit{k}}+{\displaystyle \sum }_{\mathit{k};\mathit{l}=\mathit{L},\mathit{R}}({\mathit{t}}_{\mathit{r}}{\widehat{\mathit{b}}}_{\mathit{r}}^{†}{\widehat{\mathit{c}}}_{\mathit{R}\mathit{k}}+{\mathit{t}}_{\mathit{l}}{\widehat{\mathit{b}}}_{\mathit{l}}^{†}{\widehat{\mathit{c}}}_{\mathit{L}\mathit{k}}+\mathbf{H}.\mathbf{c}.)+V_{\mathit{g}}\left({\widehat{\mathit{b}}}_{\mathit{r}}^{†}{\widehat{\mathit{b}}}_{\mathit{r}}+{\widehat{\mathit{b}}}_{\mathit{l}}^{†}{\widehat{\mathit{b}}}_{\mathit{l}}\right)+\left(\mathbf{\Omega }{\widehat{\mathit{b}}}_{\mathit{l}}^{†}{\widehat{\mathit{b}}}_{\mathit{r}}+\mathbf{H}.\mathbf{c}.\right)+\mathit{U}{\widehat{\mathit{b}}}_{\mathit{l}}^{†}{\widehat{\mathit{b}}}_{\mathit{r}}^{†}{\widehat{\mathit{b}}}_{\mathit{r}}{\widehat{\mathit{b}}}_{\mathit{l}}.(15)$

The SDQD model calculations are performed by parameterizing the energies of spin-polarized electrons for two single particle states $\left({ϵ}_{\uparrow },{ϵ}_{\downarrow }\right)$ as a function of a gate (or bias) potential V_g and a magnetic field B which are applied externally. The total energy of the conduction electrons in the leads are described as the internal energy of non-interacting particles. Consider that the experimental interpretation of carrier transport signatures in QDs is sometimes not straightforward-especially when the STM image maps of the QD are used in the characterization of the device. Theoretically modelled STM images may resolve conflicting possibilities and point to an underlying atomistic model. Although the DOS at ground state is derived from DFT only gives direct insight into the local electronic structure at 0 K, the calculated tunnelling DOS yields better insights into bias dependent transport state independent of the tunnelling rate, Γ. This is because at a given charging potential V, the current that tunnels through the QD to the leads is proportional to the thermalized population of carriers (see Eq. (8)), such that:

$\mathit{I}=\mathit{e}\mathit{V}{\displaystyle \sum }_{\mathit{k}}{\mathit{f}}_{\mathit{k}}\to {\int }_{{\mathit{\epsilon }}_{\mathit{F}}}^{{\mathit{\epsilon }}_{\mathit{F}}+\mathit{e}\mathit{V}}{\displaystyle \sum }_{\mathit{k}\mathit{n}}{\mathit{\omega }}_{\mathbf{k}}{\left|{\mathbf{\Psi }}_{\mathbf{k}\mathit{n}}\right|}^{\mathbf{2}}\mathit{\delta }\left(\mathit{\epsilon }-{\mathit{\epsilon }}_{\mathbf{k}\mathit{n}}\right)\mathit{d}\mathit{\epsilon },(16)$

where ${\mathit{\omega }}_{\mathbf{k}}$ is the k-point weight and ${\mathbf{\Psi }}_{\mathbf{k}\mathit{n}}$ is the wavefunction. The changes in current as a function of the applied bias or the tunnelling conductance (dI/dV) are also calculated. This is an experimentally observable physical quantity that correlate with the charge stability of the QD system.

When the bias dependent mesoscale carrier transport is treated perturbatively to lowest order in the tunneling couplings, QmeQ allows the use of different possible approaches to obtain the tunnelling current. These are Pauli (classical), first-order Redfield, and first order von Neumann master equations, and the Lindblad equation. When all the microscopic processes involving two-particle excitations in the leads are of interest, the 1vN approach can be applied. What is new in the master equation compared to the Schrödinger equation are processes that describe dissipation in the quantum system due to its interaction with an environment. These environmental interactions are defined by the operators through which the system couples to the environment, and rates that describe the strength of the processes. For instance, to describe the second-order scattering processes that involve virtual intermediate states or the broken-symmetry state of quasiparticles the 2vN is used to calculate the expected particle-hole asymmetry for comparison with predictions of the Pauli master equation. The Pauli approach and the 1vN approach, with three different values 0, 1, and 2 for the QmeQ Builder’s optional argument itype were used. The value of itype determines how the tunneling rate matrix Γ (see Eq. 14) is calculated. For itype = 2, the principal part integrals are neglected, for itype = 1 the principal part integrals are approximated using the digamma function [58]. This is equivalent to the logarithmic derivative of the gamma function. A full calculation is performed for itype = 0 using the SciPy implementation [59] of the DQAWC subroutine [60]. Results of the calculated tunnelling current are shown for solution to Eq. (3) using the methods from different master equations.

3 Results and discussion

3.1 Ground state properties

3.1.1 Local network structure

It is important to first characterize atomic network structure of the monolayer materials considered to appreciate their effects on electronic transport. Significant progress has been made in understanding the roles of defect in a covalently bonded solid. For instance, it is now well-known from our previous studies of tetrahedrally-bonded materials that the presence of an open-volume defect introduces localized electron states into the mid-gap region due to their dangling bonds [61, 62]. The density of the mid-gap defect states in the hydrogen-free amorphous silicon (a-Si) reduces significantly when it is passivated with hydrogen [63]. In this sense, the passivating hydrogen is an impurity in the disordered silicon network. In sp²-bonded crystalline materials, such as the hBN bilayer [64] and monolayer [65, 66], we also found that introduction of a point defect also introduces localized mid-gap electronic states. A single carbon substitutional defect introduced on the boron or nitrogen site creates s-resonant electronic states at the Fermi-level with finite magnetic moments. By contrast, the introduction of a few-carbon or on both boron and nitrogen sites either at near-neighbor positions or over an extended region of the monolayer also induces finite magnetic moments [67].

Although hydrogen-related point defects and vacancies are not considered in the QDs discussed in this work, it is demonstrated in the next section that an embedded carbon nanoline also introduces mid-gap defect states in the hBN monolayer leading to flat bands in the electronic structure. This leads to formation of the Fermi level resonant state when the number of embedded carbons is odd. By contrast, a significantly narrowed band gap is obtained when the number of embedded carbons is even. Such monolayer materials have been studied extensively for about 2 decades and graphene and monolayer boron nitride have both emerged as ideal Dirac material candidates for designing HPMs. More recently, our work has showcased different technology platforms that can utilize the ballistic transport capability of carriers in graphene, monolayer hBN or their derivatives in diverse technological applications like spintronics [68], skyrmionics [69], catalysis [70] and plasmonics [71]. Insights from these previous studies suggest that similar computational approaches can be used to gain unique insights into the efficacy of HPMs in energy conversion applications.

Figures 2A–F show the local atomic networks in the carbon nanoline-embedded hexagonal boron nitride monolayers. The short line of carbon (SLC), carbon dimer chain (CDC), hexagonal line of carbon (HLC), long line of carbon (LLC), and hexagonal ring carbon (HRC) represent unique nanoline geometries, respectively. The embedded SLC acts as a carrier conducting channel in the semiconducting layer. Its role in the hBN monolayer is analogous to the spin nanoroad observed in the spin-resolved charge density of the metal-insulator-metal heterostructure as a 1D conducting channel [71]. The nanoroad denotes the graphene conducting channels embedded within the hexagonal boron nitride layer [72]. As such, it is suggested that monolayer hBN QDs derived from carbon nanoline induced narrow bandgap semiconducting nanowires can serve as the building blocks for spin-based quantum information processing, and as HPMs for energy applications. QDs made with narrow bandgap semiconducting monolayers are advantageous because of their high electron mobility and small effective masses making it possible to manipulate the spin transport state.

FIGURE 2

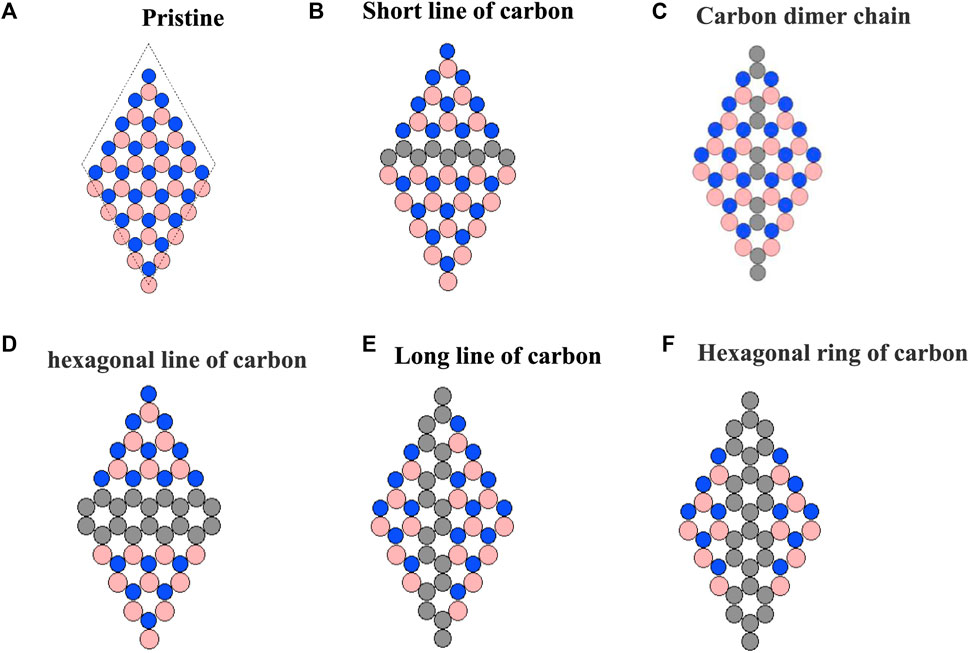
FIGURE 2. Different structures of the local atomic network geometry of the carbon nanoline-embedded hexagonal boron nitride monolayer showing the pristine monolayer structure (A) and the carbon nanoline conducting channel embedded within the semiconducting PML as a short line of carbon (B), a carbon dimer chain (C), a hexagonal line of carbon (D), a long line of carbon (E), and a hexagonal ring carbon (F).

3.1.2 Electronic band structure

Figure 3 shows the electronic band structure of nanoline-embedded monolayer hBN calculated with the GLLBSC functional. Firstly, the GLLBSC functional gives a significantly improved band gap of the pristine hBN monolayer relative to the experimental values. The band structure of the PML is characterized by a wide Kohn-Sham band gap of 5.827 eV. Figure 3A shows that the position of the highest occupied valence band state in the PML is localized at over 4 eV below the Fermi level. With a derivative discontinuity of 2.08 eV from the GLLBSC functional of the particle exchange-correlation hole, the fundamental quasiparticle band gap of 7.87 eV is obtained as expected. The calculations reveal that the electron states in the PML systems are time-reversal symmetric. Electrons from the two spin channels are not sensitive to spin polarization. As such, changes in direction of spin quantization does not affect the electron states. This causes the position of the corresponding highest occupied valence state to be localized at an energy level that is located at over 4 eV below the Fermi level. This leads to invariant direct interband transition from the valence to conduction states at Г-point of the Brillouin zone.

FIGURE 3

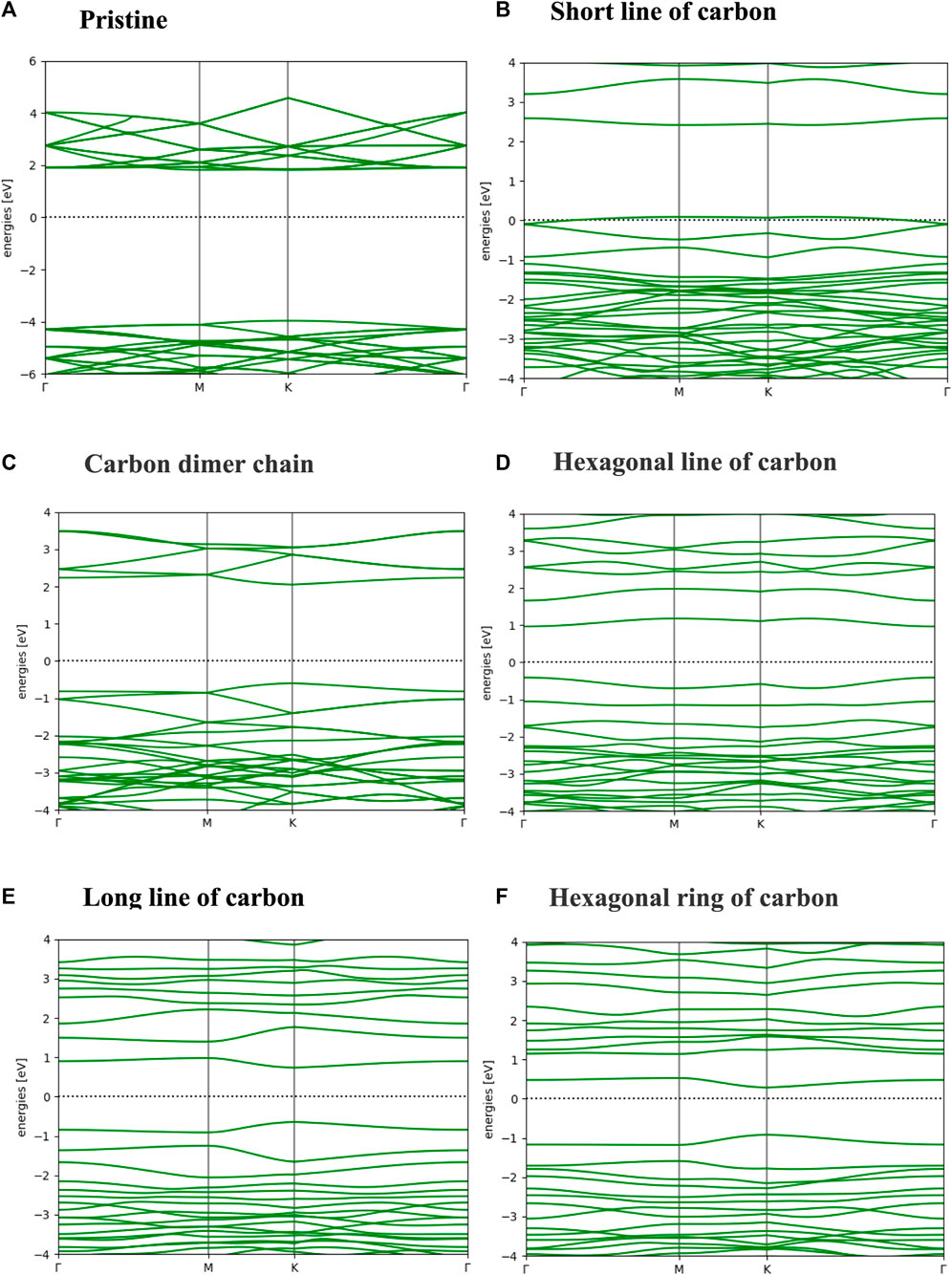
FIGURE 3. Electronic band structure of the nanoline embedded monolayer hexagonal boron nitride showing the pristine structure (A) and a short line of carbon (B), a carbon dimer chain (C), a hexagonal line of carbon (D), a long line of carbon (E), and a hexagonal ring carbon (F).

Using the nanoline geometry to embed carbon species in the monolayer introduces impurity band states in the gap region. Embedding the nanolines reduce the wide band gap in pristine hBN monolayer. Generally, Figure 3 shows that the carbon impurity states cause the position of the corresponding highest occupied valence band to shift towards the Fermi level. Except in the case of an embedded hexagonal line carbon, the lowest unoccupied conduction band states are shifted in energy to a position above 2 eV in the conduction band. These culminate in significant reductions in the size of the wide band gap obtained in the PML. As such, the band structure in each embedded system is only shown here in the energy interval of ±4 eV around the Fermi level (see Figures 3B–F). Figure 3B shows that the highest occupied valence band state lies directly at the Fermi level. This leads to metallic transport property in the SLC system. The other embedded systems yield a semiconducting band structure. Other embedded structures yield significantly reduced band gaps with a strong sensitivity to the local structure of the nanoline conducting channel.

There is a nearly flat band resonating with the Fermi level in Figure 3B. This band exists at the mid-gap region. It is due primarily from the carbon atoms at the zigzag edge nanoline of the SLC geometry. The behavior of this flat band state resembles a non-degenerate defect state in the pristine zigzag-edged graphene ribbon [70, 73]. Our previous studies [65–67] showed that the threshold for reconstruction of the local structure in the layer is sensitive to the presence of a substitutional carbon impurity. This implies that the layers are stable against puckering. The present study considers the embedded nanoline as a line defect and not as point defects. However, the origin of an associated magnetic moments behaves like the magnetic moments obtained with the substitutional carbon defects in the hBN monolayer. These are different from the magnetic moments obtained from d-electron states in dilute magnetic allots. As such, the associated Kondo resonance effects cannot be ascribed to a dispersive defect state. The Kondo effect associated with spin-dependent transport of carriers in a non-dispersive defect state is different to those in materials where magnetism arises from the d-band electron states. In the latter, d-electron states in transition metals lead to ferromagnetism but there are no d-band states in the monolayers considered herein.

Table 1 also shows the renormalized quasiparticle band gaps obtained in the GLLBSC approach. This description of electronic states in terms of the momentum space dispersion of energy leads to the non-magnetic ground state. Thus, the band structures shown in Figures 3C–F each has a finite gap, and the net magnetic moment is zero in each case. The ferromagnetism of the SLC-embedded system is due to the Fermi-level resonant state formed due to strong s-p hybridization. This gives rise to the dispersionless (or flat) band seen along the M-K direction of the Brillouin zone in Figure 3B. This flat band character is seen also along the Γ-M and the K-Γ directions. This is attributable to the combined effects of quantum confinement and the low dimensionality of the layer.

TABLE 1

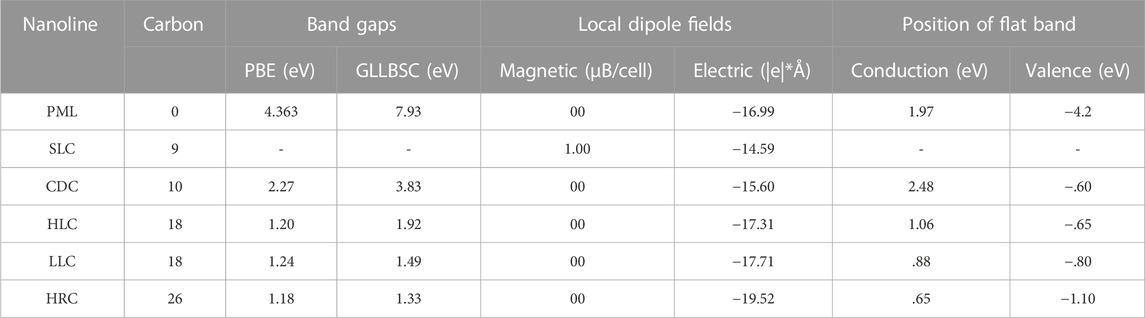
TABLE 1. Ground state properties of carbon nanoline embedded monolayer hBN showing the electronic, and magnetic properties as a function of the number of carbon atoms in embedded in the layers.

These have a strong influence on the interaction of electrons with local magnetic moments. The bandwidth of this flat band is ∼.05 eV. The magnitude of this band width is far smaller than the error of .2 eV expected from electronic energies obtained from DFT calculations with GPAW. This suggests that the SLC model of the flat bands will strongly contribute to the density of states (DOS) for occupied electrons and can be modelled within the SSQD approximation due to its unpaired electron spin. Presence of such a high DOS in the valence channel around the Fermi level position has crucial implications for carrier transport. This ferromagnetic moment give rise to interesting Kondo phenomena in QDs in ways that are different from the Kondo effect observed in DMAs in 3D materials.

3.1.3 Defect-induced local fields

Table 1 summarizes the defect induced local fields at ground state as the number of carbon changes. This shows the electric and magnetic dipole moments, changes in the GGA and GLLBSC band gaps for different nanolines, and derived position of the flat bands. This shows that the distribution of the energy level position of the most dominant flat band states in the nanoline embedded systems is sensitive to the number of carbons embedded in the layer. It is found that the position of the flat conduction band state decreases steadily towards the Fermi level while the flat valence band position is shifted deeper into the valence band as the number of carbons is increased in the layer. Similarly, the magnitude of the electric dipole moment also increases continuously with increasing number of carbons. The electronic structure of the SLC yields a distinctly metallic transport character while all the other embedded systems have a semiconducting character with reduced band gaps. It is important to also note that at the ground state of the SLC-embedded layer, the spin-split eigenvalues for up (↑) and down (↓) spin channel is −20.73912912029137 states/eV.cell and −20.477150085834335, respectively. This culminates in a total magnetic moment of 1.00 μB/cell. This is 3 orders of magnitude higher than the net magnetic moments in other embedded structure. The GLLBSC functional yields a total magnetic moment of 1.00 μB/cell for the SLC system. The energy-level positions of the flat bands are obtained in the vicinity of the Fermi level. In the SLC-embedded system, this was set to the Fermi level (i.e., 0 eV) since there is no band gap.

The positive net magnetic moment in the metallic system is suggestive of a ferromagnetically ordered local moment because the direction of spin quantization is along the z-axis of the monolayer. Thus, the GLLBSC band structure accurately describes the magnetic exchange interactions expected in the induced flat band ferromagnetism. This is important because when electronic spin in important in the tunnelling process making it convenient to view the spin tunneling as a magnetic exchange coupling. Several previous studies of the Hubbard model of ferromagnetism have shown that when the one-electron band structure contains flat bands [74–76], the magnitude of the repulsive electron–electron interaction will guarantee the emergence of a fully spin-polarized ground state whenever the flat band is half-filled. The above prediction of flat band ferromagnetism of the dominate carriers in the polarized spin-state was also confirmed in our previous calculations [69, 77]. This led to the conclusion that only small changes are expected in electron momentum due to deviations from perfect flat band dispersion in the free-standing monolayers compared to stacked multilayers [78]. This suggests that the signatures of Kondo physics in hBN are more likely to be easily delineated in the monolayer systems considered herein than in the multilayers.

The size of the narrowed band gaps of semiconducting sheets in Table 1 shows a strong sensitivity to the number of carbons in the embedded nanoline. With increasing number of carbons in the embedded layer, the overall electric dipole moment gets enhanced. However, the GLLBSC band gap decreases as number of carbons increases and gives rise to a progressively decreasing position of the flat bands for up and down spin channel. In the SLC, the odd number of carbons in the layer means there is an unpaired electron state in the system. This unpaired electron state forms an electronic resonance at the Fermi level leading to zero band gap—as would be expected. All the other embedded systems have a finite but reduced band gap. Only the SLC geometry is characterized by an odd number of carbons. Hence, the unpaired electron is the only physically plausible cause of the band (or itinerant) ferromagnetism observed in the carbon nanolines embedded monolayer. This is quite unlike the more localized Ising-type spins observed in DMAs due to the presence of localized d-band states in transition metal ions. Thus, our recent justification for using the Heisenberg exchange to model the interaction between localized spin moment in stacked monolayer systems is equally applicable in this case [79].

Figure 4 shows the effects of spin orbit coupling (SOC) on the electronic band structure of pristine monolayer hBN in the absence of carbon species. The color bar shows the evolution of the charge pseudospin degree of freedom under the effect of time reversal symmetry. It is crucial to emphasize that the presence of carbon in the hexagonal lattice of the hexagonal boron nitride (hBN) monolayer induces ferromagnetism. The phenomenon of carbon induced magnetism in monolayer hBN has been confirmed both experimentally [80–83] and theoretically [84–86]. Thus, consider too that the carbon-induced ferromagnetism and the intrinsically weak SOC of the nanoline-embedded monolayer enforces a broken time-reversal symmetry on the electron state of the hybrid monolayer. Since the presence of the carbon nanoline also breaks the local structural inversion symmetry of the material, it is the pseudospin ¹/₂ degree of freedom of the electron that gives rise to observable the Kondo effect. Irrespective of whether the QD has a magnetic or non-magnetic ground state, the pseudospin charge density contribution from each valley can be screened by being shifting spontaneously within the monolayer to reveal Kondo-like behavior because of Coulombic charging when the dot is tunnel-coupled to metallic leads.

FIGURE 4

FIGURE 4. Ground state electronic structure in the pristine monolayer hexagonal boron nitride under the effect of spin orbit coupling showing the band structure (top panels) and the corresponding electronic density of states (bottom panels) calculated from PBE (A, C) and GLLBSC (B, D) functionals in the absence of carbon species. The band structures show a reversal of the charge pseudospin degree of freedom at the time reversal symmetric K and K^’ points of the Brillouin zone because of the broken time reversal symmetry of the electron state.

To gain additional insights for understanding of the effect of the different flavors of the intrinsic broken structural inversion symmetry on the electron state caused by embedding of the carbon nanolines in hBN; Figure 4 shows the band structure of pristine hBN monolayer obtained from PBE (Figure 4A) and from GLLBSC (Figure 4B). The ground state electronic structure shows an intrinsically reversed magnitude of the “charge” pseudospin-½ degree of freedom at the K- and K’-points of the Brillouin zone. These denote the Brillouin zone points at which the electron state should remain invariant under time-reversal symmetry when the dynamics of the electron is observed in imaginary time under the effect of a symmetry-breaking field such as the SOC. The phenomenon of charge pseudospin reversal also occurs in pristine graphene—even though the two inequivalent sublattice sites are occupied by carbon species only quite unlike boron and nitrogen in monolayer hBN. The top panels of Figure 4 show the reversal of the charge pseudospin from +1.0 (at point K) to −1.0 (at point K’) in the absence of carbon. Hence, introduction of carbon nanoline in the QD influences the pseudospin as well as the valley degrees of freedom for carrier transport [87]. The calculated electronic DOS (bottom panels) in the absence of carbon species shows a consistently wide bang gap—as expected. These indicate that neither the spin nor charge is significant in the physics of the broken symmetry state expected in the Kondo phenomenon reported herein. It is instead the charge pseudospin in the carbon nanoline-embedded layers that needs to be screened by the cloud of valence electrons in the metallic leads of the dots that gives rise to the Kondo resonance effects. This is crucial because the pseudospin of carriers in Dirac-like materials is known to play the central role in determining the generic transport properties in both fully spin-polarized and channel-symmetric two-channel Kondo models [88].

From the experimental perspective, it is now common knowledge nanoelectronics that a new paradigm has emerged more recently wherein a large QD is coupled at quantum point contacts to source and drain leads to realize the charge-Kondo QDs. This perspective allows for realization of more complex QI models to be experimentally by controlling the microscopic interactions without any explicit reference to the localized ferromagnetic spin or spinless fermion. This is encapsulated by the fact that when the original two-channel charge-Kondo model [34] is combined with the pseudogap Kondo physics of graphene [89], one realizes a novel two-channel pseudogap charge-Kondo effect akin to the phenomenon investigated herein. As discussed in Refs. [34, 89, 90], it is the frustrated Kondo screening of the single “impurity-like” state that is caused by the two distinct channels of metallic conduction electrons that displays all the characteristic features of the Kondo physics. This single “impurity-like” state is akin to a screened charge-pseudospin-1/2 state in the QDs considered herein. Thus, even when a gated “spinless” dot is connected to two metallic leads, the frustrated screening of the QD charge pseudospin is the mechanism that realizes the Kondo physics.

The impurity-like state arises from the intrinsic pseudospin SU(4) symmetry of the honeycomb lattice. When there is a coupling of the dot charge pseudospin to two channels of conduction electrons (each with the characteristic linear pseudogap DOS of graphene), the pseudospin screening breaks the particle-hole symmetry in the spin and valley pseudospin degrees of freedom. This physics is investigated here using the SDQD model of the HRC cluster to unravel the Kondo resonance effects. Thus, the results of the first principles calculations shows that insertion of different local geometries of the carbon nanoline conducting channel in the semiconducting hBN monolayer leads to two distinct (i.e., magnetic, and non-magnetic) ground states at 0-K depending on whether the number of embedded carbons is odd or even. This interpretation is consistent with the two distinct ground states correspond to an electronic structure with either a “finite” or “zero” magnetic moment. Based on the obtained ground states, a quantum dot can be modelled with either a “finite” or “zero” magnetic moment. Quantum dots are designed within these two categories of ground states and described using either the spinful single-orbital quantum dot (SSQD) model or spinless double quantum dot (SDQD) model via a tunable coupling to metallic leads—depending on a tunable Coulomb interaction that is scaled by the ratio, V/U, and by using the gate voltage, V=V_g.

3.2 Mesoscale transport properties

Despite major advancements in current understanding of correlations effects in electronic structure theory, an accurate description of the effects of electron-electron interaction potential on the presence of quasiparticles is missing still. Such effects include electron-electron repulsion and Coulomb drag. These contribute to the Kondo phenomenon in layered magnetic materials elucidated in this section. Quasiparticle excitations in QDs, which are present due to strong effects of many-body correlations are accounted for by the renormalization of quasiparticle energies. Thus, the finite lifetimes of collective excitations are describable in the independent particle picture. The TKE in real metals originate from the coexistence of nearly degenerate electron states [11, 91]. More recently, Kleeorin and Meir [92] have showed that the dependence of Kondo effect on gate voltage is due to an interplay between the level occupation switching of nearly degenerate levels. Consider that the coherent exchange coupling of conduction electrons to local magnetic moments sets up the Kondo cloud that screens the impurity spin state in planar carbon materials [93]. Thus, despite the weak spin orbit coupling (SOC), the screened charge pseudospin of carriers in the carbon nanoline is responsible for the signatures of the Kondo physics observed herein.

Microscopic interactions in the system Hamiltonian described in the Hubbard-like model are carefully controlled by electrostatic charging to localize a single electrons state. This allows the many-body effects in the quantum transport of carriers to be determined from solution of different quantum master equations. This approach is justifiable since the macroscopic degrees of freedom that are involved in the transport of carriers through a mesoscopic electronic device are susceptible to the effects of strong many-body correlations and sensitive to the strength of the orbital hybridization and the gate voltage. The effects of many-correlation on carrier transport can be probed at single-particle level by controlling the external bias potential V and the gate voltage, V_g. In the following analyses, Kondo resonance effects are presented wherein collective degrees of freedom like currents and voltages behave quantum mechanically despite the small magnitude of spin orbit coupling in the monolayer hexagonal boron nitride layer.

3.2.1 Effects of temperature on dc conductance

Figures 5A,B shows the dependence of the magnitude of the tunneling current on gate voltage and strength of the orbital hybridization in the SDQD model at 0 K. The current is determined using the Pauli, Redfield, first-order von Neumann and Lindblad approaches using two different values of the itype variable in solution method implemented in QmeQ. The results are obtained using Γ= .5, U = 5, Ω = 2 as the simulation parameters. SDQD model data are obtained using energy position of 1.50 eV determined from the spin-split level of the two Fermi-level resonant flat bands at the Brillouin zone point K in the SLC nanoline model (see Figure 2B). Figure 4 shows the performance of different quantum master equation in the SDQD model for itype = 1. The colourmap denotes the distribution of the current at different charging potential. Note that setting itype = 0 yields a zero-tunnelling current irrespective of the simulation temperature. Hence, only the non-vanishing currents obtained with Pauli and Lindblad master equation for itype = 1 are displayed in Figures 4A,B.

FIGURE 5

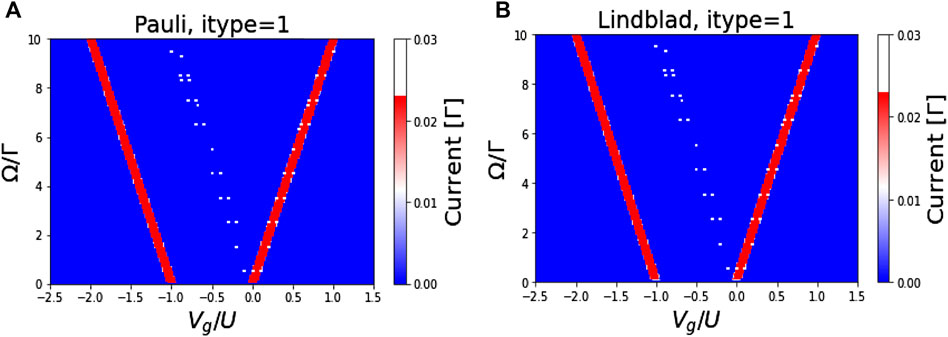
FIGURE 5. Tunnelling current obtained from different quantum master equations in the spinful single orbital quantum dot model showing the dependence of predicted Pauli (A) and Lindblad (B) tunnelling current on gate voltage and on strength of the orbital hybridization.

Nevertheless, it is also important to emphasize that the results presented here for the SDQD are not sensitive to values of the itype parameter. The Pauli and Lindblad master equations yield a similar non-vanishing current contour while the first order von Neumann (1vN) and Redfield master equations give rise to zero current. However, the Pauli method is known to accurately reproduce the current profile of the and Lindblad approaches only within the high-charging regime of the SDQD model. In Ref. [54] for instance, the current predicted with the Pauli master equation for the SDQD model is anomalously high in the limit of minimal (or low) charging of the QD wherein Ω/Г→ 0 irrespective of the value of the itype variable. The non-zero current obtained when Ω/Г < 0 suggests a finite current flow at negative charging. This trend is not seen obtainable with other master equations. Secondly, the tunnelling current behaves quantum quantum-mechanically. In this sense, changes in the current contour shows an asymptotic jump between maximal values and a minimal value in both Pauli and Lindblad methods. This is denoted by the sequential change in the color of the current contour from white at the dotted spots through the red line to the blue region at both values of 0 and 1 for the itype parameter. This characterizes the discrete quantal behavior of current flowing in the QD at 0 K. This shows that only a discrete number of electrons are transported across the quantum dot.

Figures 6A–D show contours of the current profile at 1 μK derived from the four quantum master equations. At extremely low but non-zero temperatures important differences are observed in each case. It is observed that the Redfield and first order von Neumann master equations only give a finite (i.e., nonzero) current at extremely low (but nonzero) temperatures, in each case. This shows that the Redfield and first order von Neumann currents match the Pauli and Lindblad currents exactly at the high values of ratio Ω/Г. When the Pauli and Lindblad currents are compared to the 0 K (see Figures 5A,B), it is observed that the linearly distributed white dots on blue the background has disappeared. This leaves only the localized white spots seen on the red contour line. When the strength of the electronic coupling between the flat band states is set to Ω/Г ≈ 1.5, two distinct localized regions of high tunnelling current are observed around the region where the Coulomb potential (denoted by V_g/U) is −1 and 5. These two regions are denoted by the two regions of smoothly graded white halos in Figures 6B,C. Otherwise, all the four forms of the quantum master equation yield the same Kondo current. The results show that the Kondo current survives up to 10 K before it disappears. The other signatures of the Kondo resonance are studied using the Lindblad formalism.

FIGURE 6

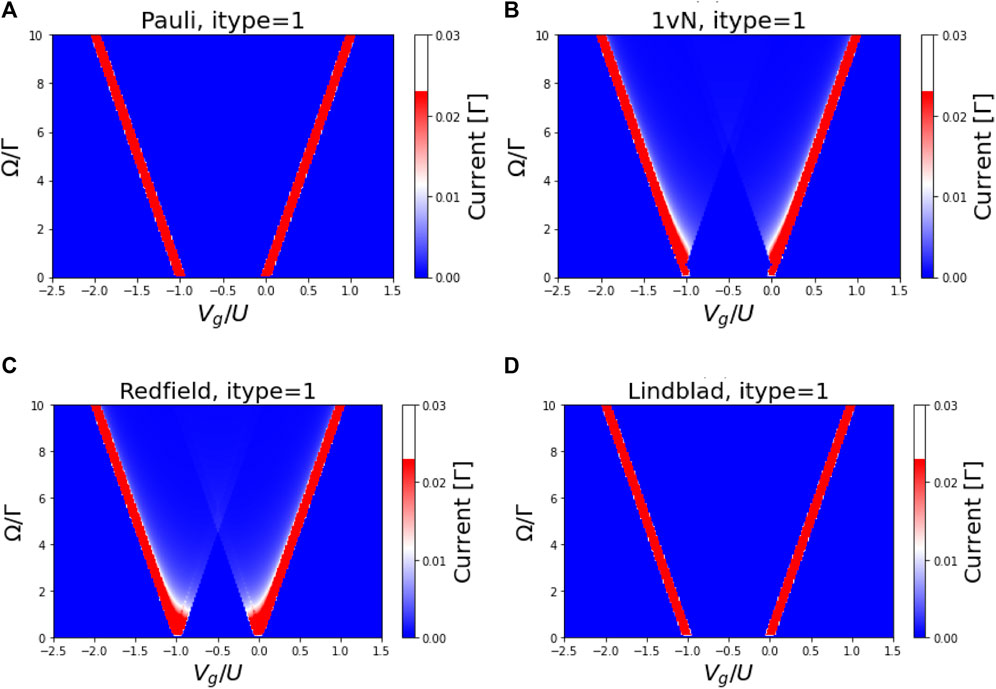
FIGURE 6. Performance of Pauli (A), first order von Neuman (B), Redfield (C) and Lindblad (D) quantum master equations in the spinful single orbital quantum dot model showing the dependence of the tunneling current on gate voltage and strength of the orbital hybridization.

It is well-known in the Kondo physics of a dilute magnetic alloy that at a characteristic temperature, which is also known as the Kondo temperature, the resistivity (or conductance) increases (or decreases) abruptly at a low temperature starting near the Kondo temperature. This phenomenon depends on the energy position of the impurity band state and on the nature of the metallic host in DMAs. However, it has recently been associated with the impurity-induced resonance peaks at the Hubbard band edges due to an isolated magnetic atom deposited onto monolayer 1T-TaSe₂ [94, 95]. Experimental measurements show that the observed Kondo resonance peaks disappear when the spatial overlap at the band edges is reduced or when the magnetic impurities are replaced with non-magnetic impurities. These effects are ascribed to the presence of spinons. A spinon is an exotic charge-neutral quasiparticle present only in the quantum spin liquid phase. As such, we have also studied the Kondo resonance effect associated with the effect of temperature on the conductance under zero and finite magnetic field. This includes the carrier stability diagram and the associated effects of temperature and magnetic field. Evidence of the tunneling transport of a well-defined number of electrons through the dot is obtainable from the charge stability diagram.

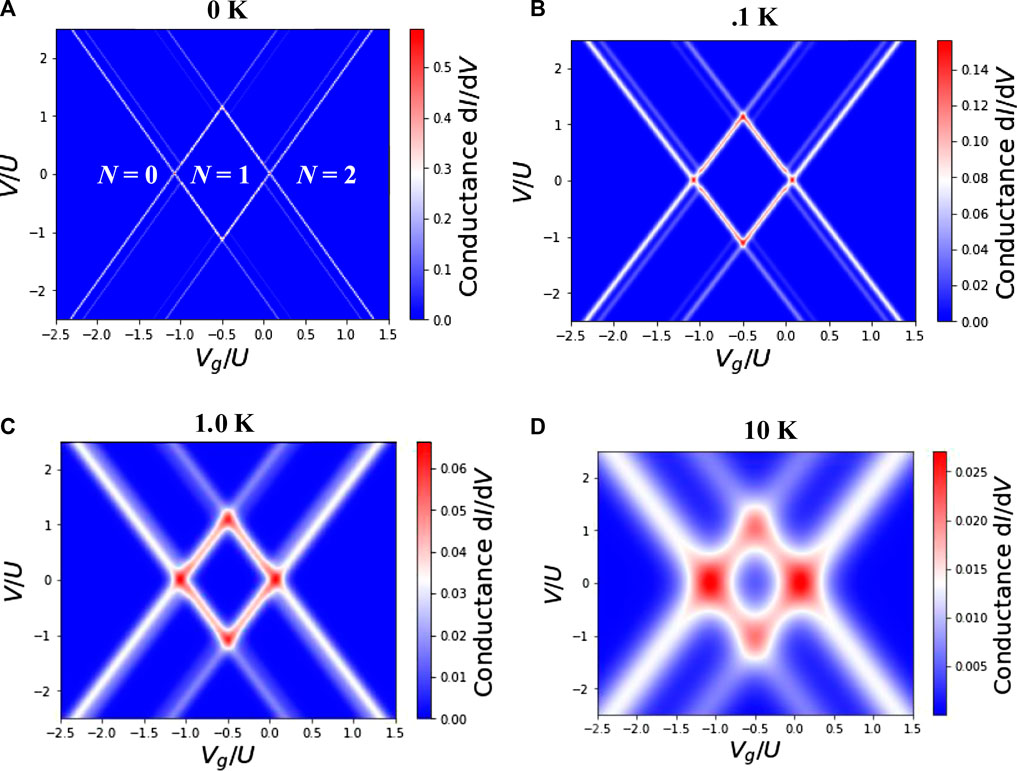
Figure 7 shows the charge stability diagram of a QD at four different but evenly separated low temperatures under zero magnetic field. Here, the Coulomb diamonds are labelled to show the quantized energy levels or microstates that are accessible to the electron. Firstly, there is considerable asymmetry in the size of the diamonds, i.e., the available energy levels. The size of the diamonds at N = 0 and N = 1 is not equal. This asymmetry is attributable to the two-fold degeneracy expected when the available energy levels in the HPM are filled with electrons at the valleys located at K and K’ in the Brillouin zone. Clearly, temperature has a non-trivial effect on the boundaries of the diamonds but not on their size. Secondly, negative charging yields an empty QD because the diamond labelled N = 0 does not close at all temperatures. At the center, the diamond closes at all temperatures with a relatively low energy penalty for adding the first electron. Secondly, excited states are visible outside the Coulomb diamonds. These appear near the diamonds as off-resonance conduction. This Kondo resonance effect is low at 0 K. However, the signature can be seen clearly up to .1 K (see Figure 7B). The edges of the Coulomb diamonds are no longer sharp at 1 K and the effects becomes more pronounced at 10 K. The smeared coulomb diamond edges are suggestive of the thermal broadening of accessible energy levels; Figures 6B–D illustrates the broadening of excited states in the interval between .1 and 10 K. The broadened off-resonance conduction characterizes the effect of temperature on quantized dc conductance at B = 0.

FIGURE 7

FIGURE 7. Direct current (dc) conductance at 0 K (A), .1 K (B) 1.0 K (C) 10 K (D) when B = 0.

The color bar in Figure 7 depicts the magnitude of the conductance. It is observed that the dc conductivity saturates at the peak value of 5 S/m at 0 K. As temperature increases to 1 K the conductance drops to 14 S/m and this decreases further to 025 S/m at 10 K. The results show that the dc conductance survives up to 10 K before it disappears. The above trend in the results agrees temperature dependence of the Kondo resonance effect of a Co atom observed experimentally by Otte, et al; [96]. Their experiments demonstrated that a single Co atom that is bound to the Cu₂N surface shows a sharp zero-voltage peak in its conductance spectrum. This peak was attributed to increased density of electronic states near the Fermi level. The expected high DOS around the Fermi level was ascribed to the effect of the Kondo screening of the Co impurity. In our case, the absence of a magnetic impurity means that the high DOS originated explicitly from the small bandwidth of the flat bands.

To gain experimentally useful insights into the transport calculations, it is important to recall that when the QD model (either SSQD or SDQD) is connected as shown in the measurement geometry of Figure 1, it will gain access to an effective electron base temperature (T_bas), which cannot be lower than the Kondo temperature, T_K. With experimental QD devices made from the GaAs/AlGaAs gated structure, a T_base of more than 45 mK was measured using a variable dc bias and/or an ac bias of 1 mV at 13.5 Hz for a lock-in detection [57]. This was experimentally measured from the widths of the conduction band peaks in the weak tunneling regime. The expected pseudospin coupling interactions that give rise to localized single electron states (shown in Figure 7A) are accessible experimentally even though the Kondo temperature T_K of the system is well-above 0 K. This is crucial because the effective tunnelling rate Г of the coupled QD system is a function of the Coulomb energies U, as well as the tunnelling rates of the right (${\mathrm{Г}}_{\mathit{R}}$) and left (${\mathrm{Г}}_{\mathit{L}}$) leads and these combine to determine the T_K using [97],

${\mathbf{T}}_{\mathbf{K}}=\sqrt{\mathit{U}\left(\frac{{\mathrm{Г}}_{\mathit{L}}{\mathrm{Г}}_{\mathit{R}}}{{\mathrm{Г}}_{\mathit{L}}{+\mathrm{Г}}_{\mathit{R}}}\right)}\mathbf{exp}\left(\frac{\left.{\mathbf{\pi }(\mathrm{Г}}_{\mathit{L}}{+\mathrm{Г}}_{\mathit{R}})(\mathbf{E}-{\mathbf{E}}_{\mathbf{F}}\right)}{\mathbf{2}{\mathrm{Г}}_{\mathit{L}}{\mathrm{Г}}_{\mathit{R}}}\right)(17)$

where the Coulomb energy U and the Fermi energy E_F are both determined from the DFT calculations. Thus, in the QD charging limit where interactions are introduced (i.e., H_Coulomb ≠ 0), parameters (${\mathrm{Г}}_{\mathit{R}}$) and left (${\mathrm{Г}}_{\mathit{L}}$) are tunable to the required weak to moderate coupling strengths when different materials are used as leads (${\mathrm{Г}}_{\mathit{R}}\ne {\mathrm{Г}}_{\mathit{L}}$) by setting the gate so that the conduction band peaks overlap. Alternatively, the same material can be used as leads (${\mathrm{Г}}_{\mathit{R}}={\mathrm{Г}}_{\mathit{L}}$) to access the same physics. For instance, these present calculations show that setting V_gate = −U/2 and B = .375U localizes a single electron state to the experimentally accessible particle-hole symmetric point. This is because during charge coupling, the pseudospin contribution is only significant when T_K is larger than (or equal to) the combined tunnelling rate, $\Gamma ={\mathrm{Г}}_{\mathit{L}}{\mathrm{Г}}_{\mathit{R}}/\left({\mathrm{Г}}_{\mathit{L}}{+\mathrm{Г}}_{\mathit{R}}\right).$ The predicted Kondo temperature of the two-quantum dot (i.e., SSQD and SDQD) models is 10 K and 50 K suggesting that T_K is structure tunable. These are consistent with the experimental T_K of ∼4 K evaluated from the width of zero-bias conductance peak of graphene QDs obtained by electron-beam lithography and reactive-ion etching [98], as well as the tunable T_K of up to ∼90 K in defective graphene QDs [99].

Figure 8A shows the summary of the changes in dc conductance with temperature when the magnetic field is set to B = .375U in comparison to B = 0. Figure 8B shows the magnetic field independent conductance of the quantum dot at 40 K. The applied magnetic field has minimal effects on the single electron conductance. However, as more electrons are added to the accessible energy levels, it is expected that magnetic field is capable of form Landau levels under strong magnetic fields. It is noted too that raising the temperature up to 40 K at a fixed value of B = .375 U only reduces the conductance to 009 S/m (see Figure 8B). The observed decrease in the dc conductance peak with increasing temperature is a systematic trendline. It does not depend on the applied magnetic field. This agrees with the arguments of thermally broadened Fano lineshape introduced to explain the temperature dependence of Kondo resonance effects of a single Kondo impurity [100].

FIGURE 8

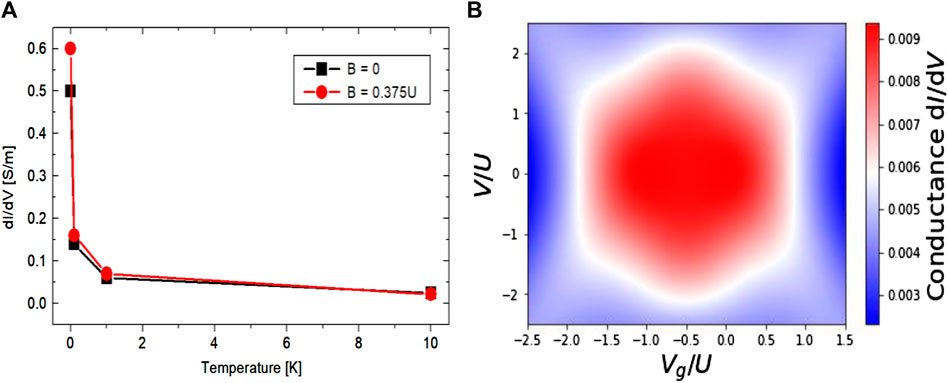
FIGURE 8. Summary of the changes in conductance with temperature with magnetic field (A). Zeeman spin-splitting magnetic-field independent conductance of the quantum dot at 40 K (B).

3.2.2 Implications of a bias-dependent particle-hole asymmetry

Recently, Lu, et al. [101] have reviewed the methods for transforming energy using QDs. The dependence of particle-hole symmetry on gate voltage has crucial implications in typical energy conversion applications. Consider that the Hamiltonian of the Hubbard model is symmetric under the exchange of particles and holes [102]. The Hamiltonian (see Eq. (1)) has a fascinating particle-hole symmetry (PHS) that allows to establish a direct relationship between its emergent physical properties at different values of the Hamiltonian tuning parameters. In this case, particle-hole symmetry denotes the anti-unitary operation which anti-commutes with the Hamiltonian. Since the local network structures of the QD systems considered herein preserve to the local symmetry of the Brillouin zone valleys at KK’, the symmetry property of the electronic structure enforces the constraint ε_k = ε_−k on the electronic structure as the necessary condition for particle-hole symmetry. Thus, electrons and holes feel the same Coulombic interactions in the material without changing their effective mass, conductivity, and response to bosonic fields. This only happens at the particle-hole symmetry point when carrier transport preserves time reversal symmetry.

Figure 9 shows the bias trace at the particle–hole symmetric point V_gate = −U/2 for B = .375 U for the SLC (Figure 9A) and HRC (Figure 9B) models. These parameters are chosen to simulate the response of the single electron that occupies the n = 1 C diamond in both QD models (Figure 7A). Results are also shown from calculation done with the Pauli and second order von Neumann (2vN) methods, in each case. In Figure 9A, the dc conductance rises exponentially. There is no peak conductance since does not saturate. This signature is characteristic of the absence of the global symmetry that would have been expected on time reversal. This can also be attributed to the presence of the broken symmetry states in the transport phase. By contrast; Figure 9B shows conductance peaks at V/U = ∼1.3, both Pauli and 2vN methods give a well-defined peak at the particle-hole symmetry point. This peak characterizes the global symmetry of the transport state wherein electrons and holes feel the same interactions without changing. Interpretation of these results overlaps with our recent proposal for the dynamic bosonization of the spin-½ transport state in interaction-driven lattices [103]. In this sense, artificial gauge field coupling to the transport state of carriers create quasiparticle states during the ultrafast process of energy interconversion. Although the proposal for dynamic bosonization has been implemented within cavity quantum electrodynamics, compelling evidence for the formation of quasiparticle-like transport state [i.e., the charge (or spin) density wave state] was reported recently in an electromagnetically driven Dirac materials-based metamaterial [73].

FIGURE 9

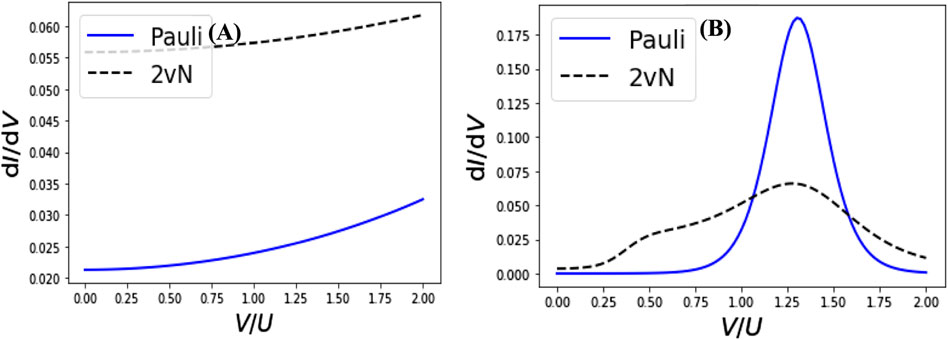
FIGURE 9. Bias trace at the particle–hole symmetric point at V_gate = −U/2 for B = .375U in the SLC (A) and HRC (B) models of the embedded nanoline quantum dot architecture.

Figure 8A shows the effect of Zeeman spin splitting magnetic field on the “broad-spectrum” of the tunneling conductance. By contrast, Figure 9B shows the effect of same Zeeman splitting magnetic field on the electronic structure of the localized electron state at the specific pair of points (K and K’) in the Brillouin zone of the HRC-model of the QD (see Figure 4) where particle-hole symmetry would have been expected to hold. The clear lack of particle-hole symmetry in Figure 8B means that the local structure of the QD model is capable of hosting quasiparticle states. Such states dominate the second-order scattering processes that mediate energy interconversion using quantum dots.

To understand the non-equilibrium physics of the energy interconversion process, consider that Hoffmann [104] has recently calculated the electromagnetic response of carriers in the half-filled Landau level. The calculations used the effective field theory proposed for composite fermion by Son [105]. The calculated electromagnetic response shows a cancellation or suppression of spurious interband transitions and collective modes that are present in the unmodified theory when the dipole terms from composite fermions is included in the calculation. It is crucial to note that cancelled (or suppressed) collective modes in the electromagnetic response are quasiparticles. The quasiparticles denote the bosonic field configurations of broken symmetry states in the Chern-Simons field theory [106, 107]. Within the framework for bosonization of the carrier transport state, the appearance of a collective transport state also applies to a QD when there is particle-hole asymmetry, i.e., εk ≠ ε−k. This is realizable in practice because gauge fields that preserve the U (1) gauge and translational symmetries of the lattice can be obtained by modifying the local atomic geometry of the HPM with a nanoline or by modulating the Bloch state of carriers by coupling them to bosonic fields.

Thus, to describe the fast processes of energy interconversion within the Hubbard model, an interaction term must be introduced in the Hamiltonian for coupling the carriers to artificial gauge fields in the QD. This reduces the Hubbard model to a many-body problem. Figure 8A suggests that the SLC-based QD system has comparably higher efficacy when integrated in energy applications. The above analyses allow for unique insights in to the non-equilibrium transport of electrons with a spin polarization in 2D materials. It is advantageous especially for understanding the effects of including the non-equilibrium magnetic moments in the energy transport mechanism. This is because the observed Kondo resonance effects are driven mainly by differences in chemical potentials of the QD model and by differences in temperature when a QD is tunnel coupled to metallic leads. Zirnbauer [108] has clarified the related particle-hole conjugation as an algebra automorphism that swaps single-fermion creation and annihilation operators. This was used to construct its invariant lift to the Fock space. This permits PHS to emerge as the concatenation of particle-hole conjugation with one (or another) involution that reverses the sign of the first quantized Hamiltonian.

The presence of broken PHS in the transport state is observed with the HRC-based QD model. This underscores the fact that it is experimentally feasible to form quasiparticles in the ultrafast energy conversion process using a suitably designed QD local structure. The above framework allows the PHS to be understood as a function of QD tunning parameters. Thus, the local network structure of the carbon nanoline based QD has a non-trivial effect on the particle–hole symmetric point. At DFT-level, the point is the time-reversal symmetric points of the Brillouin zone. The pseudospin state at points KK’ (see Figure 4) indicated that this is the point in which the macroscopic “charge” pseudospin ½ symmetry of the single electron state is broken dynamically due to the charging effect. The broken particle-hole symmetry state is observed in the bias trace of the HRC (Figure 9B). This therefore supports the expected formation of the quasiparticle states through second-order scattering processes expected when the QDs are used in devices to interconvert energy. Since the transported energy current is a sum of kinetic and mass (i.e., excitation) energy but not potential energy [109]. The above interpretation of the role of quasiparticle states is consistent with recent experimental evidence for a non-vanishing quasiparticle population during spin dependent transport of energy in a superconductor [110]. Thus, the presence of such broken symmetry state has crucial effects on energy interconversion with HPM-based QDs. This is because the energy current is obtainable as a sum of the Poynting vector, the kinetic energy flow and mass energy flow of the particles. It is physically plausible that the Coulombic many-body interactions in the QD renormalize the single electron state in the presence of quasiparticles leading to a dynamic bosonization of the single electron state.

Some experimental methods of energy interconversion with graphene quantum dots (GQDs) are derivable from their physical and chemical properties leading to broad prospects in energy storage and conversion. For instance, in addition to the excellent properties of graphene, GQDs also have quantum confinement effects and edge effects. The size of GQDs and types of their edges determine their properties [111]. Carbon-based QDs can generate electron-hole pairs, and well as act like an electron sink to suppress electron-holes pairs recombination. Due to their high carrier conductivity, the graphene-based QDs can effectively transport photo-generated electrons through its conductive networks in solar cells [112, 113]. Non-etheless, the main arguments advanced herein for the experimental realization of energy interconversion with QDs is from the perspective of light-matter interaction in cavity quantum electrodynamics [114]. When the quasiparticle (e.g., a photon field) couples coherently to the tunnelling ‘single’ electron from the QD (see Figure 7A), the electron will be confined within a single mode cavity. The reduced dimensionality of the QD enables the occurrence of few-level systems with strong non-linear features akin to those that occur in the process of energy conversion. This facile process can lead to the formation of polarons, excitons or plasmons, etc as the quasiparticles that play major roles in the energy conversion using a photovoltaic [115, 116], optoelectronic [117, 118], excitonic [119, 120] or photonic [121, 122] device. These analyses suggest that a suitable device can be designed to implement the weak or moderate couplings of the QD to specific bosonic (i.e., quasiparticle) modes, which is realizable in practice with the single photon coupling mode at minimized dissipation [103].

4 Conclusion

To summarize, a multiscale multi-physics study has been presented to unravel the Kondo resonance effects in carbon nanoline embedded hexagonal boron nitride quantum dots. The mesoscale transport calculations rely on solutions of the quantum master equation performed using flat band levels determined from accurate first principles calculation of the electronic structure. The GLLBSC functional was used in the calculations to determine quasiparticle gap to take into consideration the presence of broken symmetry states. Using an embedded short carbon line and hexagonal ring carbon nanoline as models of a high-performance monolayer hexagonal boron nitride material-based quantum dot coupling to metallic leads, computational solutions of the quantum master equations were obtained in a spinful orbital and spinless quantum dots. The electronic signatures of the Kondo resonance were obtained. The predicted Kondo temperature of the two quantum dot models are 10 K and 50 K. This suggests that the Kondo temperature is structure tunable. The lower bound of these results is consistent with the experimentally measured Kondo temperature of ∼4 K evaluated from the measured width of the zero-bias conductance peak of graphene quantum dots prepared by electron-beam lithography and reactive-ion etching. The upper bound of the estimated Kondo also agrees with the Kondo temperature of up to 90 K obtainable in defective-tunable graphene quantum dots. These show that the Kondo temperature is structure tunable. This work illustrates the insights that can be obtained when ab initio calculations of materials are combined with exact diagonalization calculations of mesoscopic transport properties. These calculations provide a useful framework for understanding the non-equilibrium dynamics that arises from the field coupling of itinerant electrons and local magnetic moments in typical energy application processes.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

AU initiated, designed, executed, and managed the research project. AU performed the data analyses, wrote the manuscript, and handled the peer review.

Funding

Funding for this research was provided by the National Research Foundation of South Africa under Grant No: 115056.

Acknowledgments

The author thanks the National Institute for Theoretical and Computational Sciences (NITheCS) for support under the Advanced Computational Modelling of Materials Research Program and the Center for High Performance Computing (CHPC) for computing time on the Lengau supercomputer under Research Program No. MATS0941.

Conflict of interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Giustino F, Lee JH, Trier F, Bibes M, Winter SM, Valentí R, et al. The 2021 quantum materials roadmap. J Phys Mater (2021) 3(4):042006. doi:10.1088/2515-7639/abb74e

CrossRef Full Text | Google Scholar

2. Keimer B, Moore JE. The physics of quantum materials. Nat Phys (2017) 13(11):1045–55. doi:10.1038/nphys4302

CrossRef Full Text | Google Scholar

3. Luo H, Yu P, Li G, Yan K. Topological quantum materials for energy conversion and storage. Nat Rev Phys (2022) 4(9):611–24. doi:10.1038/s42254-022-00477-9

CrossRef Full Text | Google Scholar

4. Mitrano M, Wang Y. Probing light-driven quantum materials with ultrafast resonant inelastic X-ray scattering. Commun Phys (2020) 3(1):184–9. doi:10.1038/s42005-020-00447-6

CrossRef Full Text | Google Scholar

5. Ravnik J, Diego M, Gerasimenko Y, Vaskivskyi Y, Vaskivskyi I, Mertelj T, et al. A time-domain phase diagram of metastable states in a charge ordered quantum material. Nat Commun (2021) 12(1):2323–8. doi:10.1038/s41467-021-22646-7

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Xu Q, Niu Y, Li J, Yang Z, Gao J, Ding L, et al. Recent progress of quantum dots for energy storage applications. Carbon Neutrality (2022) 1(1):13–8. doi:10.1007/s43979-022-00002-y

CrossRef Full Text | Google Scholar

7. Ashoori RC. Electrons in artificial atoms. Nature (1996) 379:559413–9. doi:10.1038/380559b0

CrossRef Full Text | Google Scholar

8. Kastner MA. The single electron transistor and artificial atoms. Annalen der Physik 512:11–894. doi:10.1002/1521-3889(200011)9:11/12<885::aid-andp885>3.0.co;2-8

CrossRef Full Text | Google Scholar

9. García Núñez C, Manjakkal L, Dahiya R. Energy autonomous electronic skin. npj Flexible Electron (2019) 3(1):1–24. doi:10.1038/s41528-018-0045-x

CrossRef Full Text | Google Scholar

10. Andrew RC, Mapasha RE, Ukpong AM, Chetty N. Mechanical properties of graphene and boronitrene. Phys Rev B (2012) 85(12):125428. doi:10.1103/physrevb.85.125428

CrossRef Full Text | Google Scholar

11. Hao M, Bai Y, Zeiske S, Ren L, Liu J, Yuan Y, et al. Ligand-assisted cation-exchange engineering for high-efficiency colloidal Cs1− xFAxPbI3 quantum dot solar cells with reduced phase segregation. Nat Energ (2020) 5(1):79–88. doi:10.1038/s41560-019-0535-7

CrossRef Full Text | Google Scholar

12. Borzenets IV, Shim J, Chen JCH, Ludwig A, Wieck AD, Tarucha S, et al. Observation of the Kondo screening cloud. Nature (2020) 579:7798210–3. doi:10.1038/s41586-020-2058-6

CrossRef Full Text | Google Scholar

13. Kondo J. Resistance minimum in dilute magnetic alloys. Prog Theor Phys (1964) 32:37–49. doi:10.1143/ptp.32.37

CrossRef Full Text | Google Scholar

14. Anderson PW. Localized magnetic states in metals. Phys Rev (1961) 124:41–53. doi:10.1103/physrev.124.41

CrossRef Full Text | Google Scholar

15. Wilson KG. The renormalization group: Critical phenomena and the Kondo problem. Rev Mod Phys (1975) 47:773–840. doi:10.1103/revmodphys.47.773

CrossRef Full Text | Google Scholar

16. Schrieffer JR, Wolff PA. Relation between the anderson and kondo Hamiltonians. Phys Rev (1966) 149:491–2. doi:10.1103/physrev.149.491

CrossRef Full Text | Google Scholar

17. Martinek J, Utsumi Y, Imamura H, Barnaś J, Maekawa S, König J, et al. Kondo effect in quantum dots coupled to ferromagnetic leads. Phys Rev Lett (2003) 91:127203. doi:10.1103/physrevlett.91.127203

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Franke K, Schulze G, Pascual J. Competition of superconducting phenomena and Kondo screening at the nanoscale. Science (2011) 332:940–4. doi:10.1126/science.1202204

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Mitchell AK, Schuricht D, Vojta M, Fritz L. Kondo effect on the surface of three-dimensional topological insulators: Signatures in scanning tunneling spectroscopy. Phys Rev B (2013) 87:075430. doi:10.1103/physrevb.87.075430

CrossRef Full Text | Google Scholar

20. Furusaki A, Matveev KA. Theory of strong inelastic cotunneling. Phys Rev B (1995) 52:16676–95. doi:10.1103/physrevb.52.16676

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Liang W, Shores MP, Bockrath M, Long JR, Park H. Kondo resonance in a single-molecule transistor. Nature (2002) 417:725–9. doi:10.1038/nature00790

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Sasaki S, Amaha S, Asakawa N, Eto M, Tarucha S. Enhanced Kondo effect via tuned orbital degeneracy in a spin1/2artificial atom. Phys Rev Lett (2004) 93:1017205. doi:10.1103/physrevlett.93.017205

CrossRef Full Text | Google Scholar

23. Jarillo-Herrero P, Kong J, van der Zant HS, Dekker C, Kouwenhoven LP, De Franceschi S. Orbital Kondo effect in carbon nanotubes. Nature (2005) 434:7032. doi:10.1038/nature03422

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Cox DL, Alfred Z. Exotic kondo effects in metals: Magnetic ions in a crystalline electric field and tunnelling centres. Adv Phys (1998) 47:599–942. doi:10.1080/000187398243500

CrossRef Full Text | Google Scholar

25. Ralph DC, Ludwig AWW, von Delft J, Buhrman RA. 2-channel Kondo scaling in conductance signals from 2 level tunneling systems. Phys Rev Lett (1994) 72:1064–7. doi:10.1103/physrevlett.72.1064

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Cox DL, Zawadowski A. Exotic Kondo effects in metals: Magnetic ions in a crystalline electric field and tunneling centers. Adv. Phys. (1998). 47: 599. doi:10.1080/000187398243500

CrossRef Full Text | Google Scholar

27. Taraphder A, Coleman P. Heavy-fermion behavior in a negative-U Anderson model. Phys Rev Lett (1991) 6621:2814–7. doi:10.1103/physrevlett.66.2814

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Matsushita Y, Bluhm H, Geballe TH, Fisher IR. Evidence for charge Kondo effect in superconducting Tl-doped PbTe. Phys Rev Lett (2005) 9415:157002. doi:10.1103/physrevlett.94.157002

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Hewson AC. The kondo problem to heavy fermions. In: Cambridge studies in magnetism. New York: Cambridge University Press (1997).

Google Scholar

30. Van der Wiel WG, Franceschi SD, Fujisawa T, Elzerman JM, Tarucha S, Kouwenhoven LP. The Kondo effect in the unitary limit. science (2000) 289:2105–8. doi:10.1126/science.289.5487.2105

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Song D, Paltoglou V, Liu S, Zhu Y, Gallardo D, Tang L, et al. Unveiling pseudospin and angular momentum in photonic graphene. Nat Commun (2015) 6:6272–7. doi:10.1038/ncomms7272

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Jing F-M, Zhang Z, Qin G, Luo G, Cao G, Li H, et al. Gate-controlled quantum dots based on 2D materials. Adv Quan Tech (2022) 5:2100162. doi:10.1002/qute.202100162

CrossRef Full Text | Google Scholar

33. Parafilo AV, Nguyen TKT, Kiselev MN. Thermoelectrics of a two-channel charge Kondo circuit: Role of electron-electron interactions in a quantum point contact. Phys Rev B (2022) 105:L121405. doi:10.1103/physrevb.105.l121405

CrossRef Full Text | Google Scholar

34. Iftikhar Z, Jezouin S, Anthore A, Gennser U, Parmentier FD, Cavanna A, et al. Two-channel Kondo effect and renormalization flow with macroscopic quantum charge states. Nature (2015) 526:7572233–6. doi:10.1038/nature15384

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Wang X, Yang S, Sarma SD. Quantum theory of the charge-stability diagram of semiconductor double-quantum-dot systems. Phys Rev B (2011) 84(11):115301. doi:10.1103/physrevb.84.115301

CrossRef Full Text | Google Scholar

36. Mortensen JJ, Hansen LB, Jacobsen KW. Real-space grid implementation of the projector augmented wave method. Phys Rev B (2005) 71(3):035109. doi:10.1103/physrevb.71.035109

CrossRef Full Text | Google Scholar

37. Enkovaara J, Rostgaard C, Mortensen JJ, Chen J, Dułak M, Ferrighi L, et al. Electronic structure calculations with GPAW: A real-space implementation of the projector augmented-wave method. J Phys Condensed matter (2010) 22(25):253202. doi:10.1088/0953-8984/22/25/253202

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Perdew JP, Burke K, Ernzerhof M. Generalized gradient approximation made simple. Phys Rev Lett (1996) 77(18):3865–8. doi:10.1103/physrevlett.77.3865

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Blöchl PE. Projector augmented-wave method. Phys Rev B (1994) 50(24):17953–79. doi:10.1103/physrevb.50.17953

CrossRef Full Text | Google Scholar

40. Kresse G, Joubert D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys Rev b (1999) 59(3):1758–75. doi:10.1103/physrevb.59.1758

CrossRef Full Text | Google Scholar

41. Monkhorst HJ, Pack JD. Special points for Brillouin-zone integrations. Phys Rev B (1976) 13(12):5188–92. doi:10.1103/physrevb.13.5188

CrossRef Full Text | Google Scholar

42. Kuisma M, Ojanen J, Enkovaara J, Rantala TT. Kohn-Sham potential with discontinuity for band gap materials. Phys Rev B (2010) 82(11):115106. doi:10.1103/physrevb.82.115106

CrossRef Full Text | Google Scholar

43. Gritsenko O, van Leeuwen R, van Lenthe E, Baerends EJ. Self-consistent approximation to the Kohn-Sham exchange potential. Phys Rev A (1995) 51(3):1944–54. doi:10.1103/physreva.51.1944

PubMed Abstract | CrossRef Full Text | Google Scholar

44. Bogolûbov NN, Bogolubov NN. Introduction to quantum statistical mechanics. World Scientific Publishing Company (2009).

Google Scholar

45. Kadanoff LP. Quantum statistical mechanics: Green’s function methods in equilibrium and nonequilibrium problems. Boca Raton, FL: CRC Press (2018).

Google Scholar

46. Lindblad G. On the generators of quantum dynamical semigroups. Commun Math Phys (1976) 48:119–30. doi:10.1007/bf01608499

CrossRef Full Text | Google Scholar

47. Ohlsson T, Zhou S. Density-matrix formalism for PT-symmetric non-Hermitian Hamiltonians with the Lindblad equation. Phys Rev A (2021) 103:022218. doi:10.1103/physreva.103.022218

CrossRef Full Text | Google Scholar

48. Gyamfi JA. Fundamentals of quantum mechanics in Liouville space. Eur J Phys (2020) 41:063002. doi:10.1088/1361-6404/ab9fdd

CrossRef Full Text | Google Scholar

49. Manzano D. A short introduction to the Lindblad master equation. AIP Adv (2020) 10:025106. doi:10.1063/1.5115323

CrossRef Full Text | Google Scholar

50. Nathan F, Rudner MS. Universal Lindblad equation for open quantum systems. Phys Rev B (2020) 102:115109. doi:10.1103/physrevb.102.115109

CrossRef Full Text | Google Scholar

51. Nolting W. Theoretical physics, 8. Cham, Switzerland: Springer International Publishing (2018).

Google Scholar

52. Brasil CA, Fanchini FF, Napolitano RDJ. A simple derivation of the Lindblad equation. Revista Brasileira de Ensino de Física (2013) 35:01–9. doi:10.1590/s1806-11172013000100003

CrossRef Full Text | Google Scholar

53. Pearle P. Simple derivation of the Lindblad equation. Eur J Phys (2012) 33:805–22. doi:10.1088/0143-0807/33/4/805

CrossRef Full Text | Google Scholar

54. Johansson JR, Nation PD, Nori F. QuTiP: An open-source Python framework for the dynamics of open quantum systems. Comput Phys Commun (2012) 183:1760–72. doi:10.1016/j.cpc.2012.02.021

CrossRef Full Text | Google Scholar

55. Groth CW, Wimmer M, Akhmerov AR, Waintal X. Kwant: A software package for quantum transport. New J Phys (2014) 16:063065. doi:10.1088/1367-2630/16/6/063065

CrossRef Full Text | Google Scholar

56. Kiršanskas G, Pedersen JN, Karlström O, Leijnse M, Wacker A. QmeQ 1.0: An open-source Python package for calculations of transport through quantum dot devices. Comput Phys Commun (2017) 221:317–42. doi:10.1016/j.cpc.2017.07.024

CrossRef Full Text | Google Scholar

57. Cronenwett SM, Oosterkamp TH, Kouwenhoven LP. A tunable Kondo effect in quantum dots. Science (1998) 281(5376):540–4. doi:10.1126/science.281.5376.540

PubMed Abstract | CrossRef Full Text | Google Scholar

58. Abramowitz M, Stegun IA. Handbook of mathematical functions with formulas, graphs, and mathematical tables. In: National bureau of standards applied mathematics series 55. Tenth Printing (1972).

Google Scholar

59. Virtanen P, Gommers R, Oliphant TE, Haberland M, Reddy T, Cournapeau D, et al. SciPy 1.0: Fundamental algorithms for scientific computing in Python. Nat Methods (2020) 17:261–72. doi:10.1038/s41592-019-0686-2

PubMed Abstract | CrossRef Full Text | Google Scholar

60.Netlib. quadpack (2022). https://netlib.org/quadpack/dqawc.f.

Google Scholar

61. Ukpong AM. Computational studies of the effect of hydrogen on the thermalized positron state in amorphous silicon. Mol Phys (2009) 107(16):1655–65. doi:10.1080/00268970903025659

CrossRef Full Text | Google Scholar

62. Ukpong AM. Modelling of defect states in covalent amorphous solids. [Cape Town (CT)]: University of Cape Town (2008). [dissertation/PhD thesis].

Google Scholar

63. Ukpong AM. Studies of the electronic and vibrational signatures of the unusual bonding geometries in melt-quenched amorphous silicon. Mol Phys (2009) 107(23-24):2521–30. doi:10.1080/00268970903386135

CrossRef Full Text | Google Scholar

64. Ukpong AM, Chetty N. Density functional studies of the defect-induced electronic structure modifications in bilayer boronitrene. Journal Phys Conf Ser (2012) 367:012004. No. 1.

CrossRef Full Text | Google Scholar

65. Ngwenya TB, Ukpong AM, Chetty N. Defect states of complexes involving a vacancy on the boron site in boronitrene. Phys Rev B (2011) 84(24):245425. doi:10.1103/physrevb.84.245425

CrossRef Full Text | Google Scholar

66. Ukpong AM, Chetty N. First principles molecular dynamics study of nitrogen vacancy complexes in boronitrene. J Phys Condensed Matter (2012) 24(26):265002. doi:10.1088/0953-8984/24/26/265002

PubMed Abstract | CrossRef Full Text | Google Scholar

67. Ukpong AM, Chetty N. Half-metallic ferromagnetism in substitutionally doped boronitrene. Phys Rev B (2012) 86(19):195409. doi:10.1103/physrevb.86.195409

CrossRef Full Text | Google Scholar

68. Ukpong AM. Tunable magnetotransport in Fe/hBN/graphene/hBN/Pt (Fe) epitaxial multilayers. J Phys D: Appl Phys (2018) 51(9):095302. doi:10.1088/1361-6463/aaa881

CrossRef Full Text | Google Scholar

69. Ukpong AM. Emergence of nontrivial spin textures in frustrated van der Waals ferromagnets. Nanomaterials (2021) 11(7):1770. doi:10.3390/nano11071770

PubMed Abstract | CrossRef Full Text | Google Scholar

70. Ukpong AM. Ab initio studies of propane dehydrogenation to propene with graphene. Mol Phys (2020) 118(24):e1798527. doi:10.1080/00268976.2020.1798527

CrossRef Full Text | Google Scholar

71. Hussien MA, Ukpong AM. Electrodynamics of topologically ordered quantum phases in Dirac materials. Nanomaterials (2021) 11(11):2914. doi:10.3390/nano11112914

PubMed Abstract | CrossRef Full Text | Google Scholar

72. Jung J, Qiao Z, Niu Q, MacDonald AH. Transport properties of graphene nanoroads in boron nitride sheets. Nano Lett (2012) 12(6):2936–40. doi:10.1021/nl300610w

PubMed Abstract | CrossRef Full Text | Google Scholar

73. Xu F, Yu Z, Gong Z, Jin H. First-principles study on the electronic and transport properties of periodically nitrogen-doped graphene and carbon nanotube superlattices. Front Phys (2017) 12(4):127306–8. doi:10.1007/s11467-017-0650-5

CrossRef Full Text | Google Scholar

74. Tasaki H. From Nagaoka's ferromagnetism to flat-band ferromagnetism and beyond: An introduction to ferromagnetism in the Hubbard model. Prog Theor Phys (1998) 99(4):489–548. doi:10.1143/ptp.99.489

CrossRef Full Text | Google Scholar

75. Mielke A, Tasaki H. Ferromagnetism in the Hubbard model. Commun Math Phys (1993) 158(2):341–71. doi:10.1007/bf02108079

CrossRef Full Text | Google Scholar

76. Lieb EH. Two theorems on the Hubbard model. Phys Rev Lett (1989) 62(10):1201–4. doi:10.1103/physrevlett.62.1201

PubMed Abstract | CrossRef Full Text | Google Scholar

77. Ukpong AM. Axial field induced spin response in Fe/hBN-based tunnel junctions. Phys Rev B (2019) 100(3):035424. doi:10.1103/physrevb.100.035424

CrossRef Full Text | Google Scholar

78. Ukpong AM. Ab initio studies of coherent spin transport in Fe-hBN/graphene van der Waals multilayers. J Phys Condensed Matter (2017) 29(28):285302. doi:10.1088/1361-648x/aa74a4

PubMed Abstract | CrossRef Full Text | Google Scholar

79. Hussien MA, Ukpong AM. Quantum phase transition in the spin transport properties of ferromagnetic metal-insulator-metal hybrid materials. Nanomaterials (2022) 12(11):1836. doi:10.3390/nano12111836

PubMed Abstract | CrossRef Full Text | Google Scholar

80. Zhao S, Chong , Wang H, Wei J, Wang W, Bai X, et al. Carbon-doped boron nitride nanosheets with ferromagnetism above room temperature. Adv Funct Mater (2014) 24:5985–92. doi:10.1002/adfm.201401149

CrossRef Full Text | Google Scholar

81. Si MS, Gao D, Yang D, Peng Y, Zhang ZY, Xue D, et al. Intrinsic ferromagnetism in hexagonal boron nitride nanosheets. J Chem Phys (2014) 140:20. doi:10.1063/1.4879055

PubMed Abstract | CrossRef Full Text | Google Scholar

82. Fan M, Wu J, Yuan J, Deng L, Zhong N, He L, et al. Doping nanoscale graphene domains improves magnetism in hexagonal boron nitride. Adv Mater (2019) 31:1805778. doi:10.1002/adma.201805778

CrossRef Full Text | Google Scholar

83. Ge Y, Chen L, Jiang C, Ji J, Tan Q, Pan D, et al. Edge magnetism of triangular graphene nanoflakes embedded in hexagonal boron nitride. Carbon (2022) 203:59–67. doi:10.1016/j.carbon.2022.11.034

CrossRef Full Text | Google Scholar

84. Maji R, Bhattacharjee J. Hybrid superlattices of graphene and hexagonal boron nitride: A ferromagnetic semiconductor at room temperature. Phys Rev B (2019) 99:125409. doi:10.1103/physrevb.99.125409

CrossRef Full Text | Google Scholar

85. Ramasubramaniam A, Naveh D. Carrier-induced antiferromagnet of graphene islands embedded in hexagonal boron nitride. Phys Rev B (2011) 84:075405. doi:10.1103/physrevb.84.075405

CrossRef Full Text | Google Scholar

86. Park H, Wadehra A, Wilkins JW, Castro Neto AH. Magnetic states and optical properties of single-layer carbon-doped hexagonal boron nitride. Appl Phys Lett (2012) 100:253115. doi:10.1063/1.4730392

CrossRef Full Text | Google Scholar

87. Rostamzadeh S, Sarisaman M. Charge–pseudospin coupled diffusion in semi-Dirac graphene: Pseudospin assisted valley transport. New J Phys (2022) 24:083026. doi:10.1088/1367-2630/ac86e8

CrossRef Full Text | Google Scholar

88. Pustilnik M, Borda L, Glazman LI, von Delft J. Quantum phase transition in a two-channel-Kondo quantum dot device. Phys Rev B (2004) 69:115316. doi:10.1103/physrevb.69.115316

CrossRef Full Text | Google Scholar

89. Fritz L, Vojta M. The physics of Kondo impurities in graphene. Rep Prog Phys (2013) 76:032501. doi:10.1088/0034-4885/76/3/032501

PubMed Abstract | CrossRef Full Text | Google Scholar

90. Affleck I, Ludwig AW. Critical theory of overscreened Kondo fixed points. Nucl Phys B (1991) 360:641–96. doi:10.1016/0550-3213(91)90419-x

CrossRef Full Text | Google Scholar

91. Nozieres P, Blandin A. Kondo effect in real metals. J de Physique (1980) 41(3):193–211. doi:10.1051/jphys:01980004103019300

CrossRef Full Text | Google Scholar

92. Kleeorin Y, Meir Y. Abrupt disappearance, and re-emergence of the SU (4) and SU (2) Kondo effects due to population inversion. Phys Rev B (2017) 96(4):045118. doi:10.1103/physrevb.96.045118

CrossRef Full Text | Google Scholar

93. Kurzmann A, Kleeorin Y, Tong C, Garreis R, Knothe A, Eich M, et al. Kondo effect and spin–orbit coupling in graphene quantum dots. Nat Commun (2021) 12(1):6004–6. doi:10.1038/s41467-021-26149-3

PubMed Abstract | CrossRef Full Text | Google Scholar

94. Chen Y, He WY, Ruan W, Hwang J, Tang S, Lee RL, et al. Evidence for a spinon Kondo effect in cobalt atoms on single-layer 1T-TaSe $ _2$. arXiv preprint arXiv:2202.07224. 2022 Feb 15.

95. Editorial: Exotic Kondo effect induced by spinons in a quantum spin liquid. Nat Phys (2022). doi:10.1038/s41567-022-01752-3

CrossRef Full Text | Google Scholar

96. Otte AF, Ternes M, Von Bergmann K, Loth S, Brune H, Lutz CP, et al. The role of magnetic anisotropy in the Kondo effect. Nat Phys (2008) 4(11):847–50. doi:10.1038/nphys1072

CrossRef Full Text | Google Scholar

97. Bickers NE. Review of techniques in the large-Nexpansion for dilute magnetic alloys. Rev Mod Phys (1987) 59:845–939. doi:10.1103/revmodphys.59.845

CrossRef Full Text | Google Scholar

98. Kanai Y. Detection Kondo effect in graphene quantum dots In: 2016 Compound Semiconductor Week (CSW)[Includes 28th International Conference on Indium Phosphide and Related Materials (IPRM) and 43rd International Symposium on Compound Semiconductors (ISCS) IEEE (2016).

CrossRef Full Text | Google Scholar

99. Chen J-H, Li L, Cullen WG, Williams ED, Fuhrer MS. Tunable Kondo effect in graphene with defects. Nat Phys (2011) 7:535–8. doi:10.1038/nphys1962

CrossRef Full Text | Google Scholar

100. Nagaoka K, Jamneala T, Grobis M, Crommie MF. Temperature dependence of a single Kondo impurity. Phys Rev Lett (2002) 88:077205. doi:10.1103/physrevlett.88.077205

PubMed Abstract | CrossRef Full Text | Google Scholar

101. Lu H, Huang Z, Martinez MS, Johnson JC, Luther JM, Beard MC. Transforming energy using quantum dots. Energ Environ Sci (2020) 13(5):1347–76. doi:10.1039/c9ee03930a

CrossRef Full Text | Google Scholar

102. Altland A, Simons BD. Condensed matter field theory. Cambridge, United Kingdom: Cambridge University Press (2010).

Google Scholar

103. Ukpong AM. Bosonization of the spin- 1/2 transport state in interaction driven lattices. In: AM Ukpong, KO Obodo, TPJ Kruger, editors. Theoretical physics of condensed matter: Quantum field theory on a lattice: Proceedings of the 1st international congress on advanced computational modelling of materials (CAMOM 2022) Pretoria: National Institute for Theoretical and Computational Sciences (NITheCS), Journal of Physics Conference Series (submitted).

Google Scholar

104. Hofmann J. Electromagnetic response of composite Dirac fermions in the half-filled Landau level. Phys Rev B (2021) 104(11):115401. doi:10.1103/physrevb.104.115401

CrossRef Full Text | Google Scholar

105. Son DT. Is the composite fermion a Dirac particle? Phys Rev X (2015) 5(3):031027. doi:10.1103/physrevx.5.031027

CrossRef Full Text | Google Scholar

106. Zee A. Quantum Hall fluids. In: Field theory, topology, and condensed matter physics. Heidelberg, Germany: Springer (1995). p. 99–153.

Google Scholar

107. Wen XG. Topological orders and edge excitations in fractional quantum Hall states. Adv. Phys. (1995) 44(5):405–473. doi:10.1080/00018739500101566

CrossRef Full Text | Google Scholar

108. Zirnbauer MR. Particle–hole symmetries in condensed matter. J Math Phys (2021) 62(2):021101. doi:10.1063/5.0035358

CrossRef Full Text | Google Scholar

109. Brueckner R. On the nature of the energy current in many-particle systems (2000). Orléans, France: arXiv e-printsphysics-0011057.

Google Scholar

110. Kuzmanović M, Wu BY, Weideneder M, Quay CH, Aprili M. Evidence for spin-dependent energy transport in a superconductor. Nat Commun (2020) 11(1):4336–7. doi:10.1038/s41467-020-18161-w

PubMed Abstract | CrossRef Full Text | Google Scholar

111. Liu Q, Sun J, Gao K, Chen N, Sun X, Ti D, et al. Graphene quantum dots for energy storage and conversion: From fabrication to applications. Mater Chem Front (2020) 4:421–36. doi:10.1039/c9qm00553f

CrossRef Full Text | Google Scholar

112. Molaei MJ. The optical properties and solar energy conversion applications of carbon quantum dots: A review. Solar Energy (2020) 196:549–66. doi:10.1016/j.solener.2019.12.036

CrossRef Full Text | Google Scholar

113. Fernando , Shiral KA, Liu Y, Lewis WK, Guliants EA, Jafariyan A, et al. Carbon quantum dots and applications in photocatalytic energy conversion. ACS Appl Mater Inter (2015) 7:8363–76. doi:10.1021/acsami.5b00448

PubMed Abstract | CrossRef Full Text | Google Scholar

114. Dutra SM. Cavity quantum electrodynamics: The strange theory of light in a box. Chichester, United Kingdom: John Wiley and Sons (2005).

Google Scholar

115. Wang H, Liu W, Jin S, Zhang X, Xie Y. Low-dimensional semiconductors in artificial photosynthesis: An outlook for the interactions between particles/quasiparticles. ACS Cent Sci (2020) 6:1058–69. doi:10.1021/acscentsci.0c00540

PubMed Abstract | CrossRef Full Text | Google Scholar

116. Zhong J, Xie J, Sheng W. Negative quasiparticle shifts in phosphorene quantum dots. Phys Rev B (2021) 103:235405. doi:10.1103/physrevb.103.235405

CrossRef Full Text | Google Scholar

117. Butler KT, McKechnie S, Azarhoosh P, Van Schilfgaarde M, Scanlon DO, Walsh A. Quasi-particle electronic band structure and alignment of the V-VI-VII semiconductors SbSI, SbSBr, and SbSeI for solar cells. Appl. Phys. Lett. (2016) 108(11):112103. doi:10.1063/1.4943973

CrossRef Full Text | Google Scholar

118. Bian A, Hao S, Fu Y, Zhang L, He J, et al. Dynamics of charge-transfer excitons in a transition metal dichalcogenide heterostructure. Nanoscale (2020) 12:8485–92. doi:10.1039/d0nr01924k

PubMed Abstract | CrossRef Full Text | Google Scholar

119. Sharma A, Zhu Y, Halbich R, Sun X, Zhang L, Wang B, et al. Engineering the dynamics and transport of excitons, trions, and biexcitons in monolayer WS2. ACS Appl Mater Inter (2022) 14:41165–77. doi:10.1021/acsami.2c08199

CrossRef Full Text | Google Scholar

120. Gartstein YN, Xiao L, Zhang. C. Exciton polaritons in transition-metal dichalcogenides and their direct excitation via energy transfer. Phys Rev B (2015) 92:075445. doi:10.1103/physrevb.92.075445

CrossRef Full Text | Google Scholar

121. Rivera N, Kaminer I. Light–matter interactions with photonic quasiparticles. Nat Rev Phys (2020) 2:538–61. doi:10.1038/s42254-020-0224-2

CrossRef Full Text | Google Scholar

122. Yang X, Zhao X, Vaswani C, Sundahl C, Song B, Yao Y, et al. Ultrafast nonthermal terahertz electrodynamics and possible quantum energy transfer in the Nb₃Sn superconductor. Phys Rev B (2019) 99:094504. doi:10.1103/physrevb.99.094504

CrossRef Full Text | Google Scholar