High-speed ghost imaging by an unpredictable optical phased array

Ghost imaging (GI) retrieves an image from the correlation between a sequence of illumination patterns on the object and their corresponding bucket detections. Traditionally, GI requires the precise information of the illumination patterns, which raises technology barriers on building a high-speed illumination source, limiting the scope of its application. In this study, we propose a high-speed GI system, which implements a self-correlation with a purely optical operation without determining illumination patterns. The light source is an optical phased array (OPA), built of a set of waveguide-type electro-optic phase modulators. The OPA is driven to randomly change the phases in every 200 ns, generating speckle patterns at a rate of 5 MHz. Although the speckle patterns are not predictable or post-determinable, with the help of the naked-eye GI scheme, the system in real time optically generates the images of the object at a frame rate of more than 1 kHz, which can be directly observed by eyes or using a camera. This method avoids acquiring the information of the illumination, thus providing a simple and easy way to realize high-speed GI. It also inspires a different way of applying OPAs to high-speed imaging.

1 Introduction

Ghost imaging (GI) exploits the second-order correlation of two photons to reconstruct an image [1,2], which is different from the conventional imaging methods that are based on the first-order interference and typically use lenses to construct images. Its imaging architecture possesses several advantages such as less sensitivity to optical turbulence [3,4], high detection sensitivity [5,6], lensless imaging capability [7], non-invasive imaging through strong scattering media [8], and being able to easily adapt to various scenarios [9–11]. During the past two decades, there is a growing body of research studies on GI, invoking a lot of potential applications in various fields ranging from optical imaging [12–15], X-ray imaging [16–18], atomic sensing [19,20], biological diagnostics [21], and feature extraction without image reconstruction [22,23] to physical encryption [24–26].

Recent research studies showed that GI has the ability of imaging under weak illumination [6,18], which suggested that GI has a great capability in high-speed imaging [6,27]. However, the traditional GI methods rely on the precise information of the illumination patterns on objects, which has become an obstacle to the realization of high-speed GI. It is because high technology is required for fabricating an illumination source to produce a sequence of preset or predictable patterns at a very high modulation rate. Meanwhile, the high speed raises the difficulty in synchronizing a sent-out pattern with its corresponding bucket detection. Although a GI technique with more than 1 MHz frame rate has been proposed, its resolution is limited [6], narrowing the scope in applications.

OPAs have been considered a promising technology for light detection and ranging (LiDAR) [28–31], where OPAs act as high-speed beam-steering components. OPAs are also key components for high-speed ghost imaging, since an OPA exploits the interference of a few antennas to generate complicated speckle patterns without sacrificing the modulation speed. Recently, OPA-based GI has been proposed [32]. Since 2017, on-chip OPAs has been used to experimentally implement ghost imaging [33–36]. OPA-based GI does not exploit beam steering. Instead, an OPA generates random speckle patterns in the far field. Compared with the beam-steering-based OPA method, OPA-based GI has several advantages: 1) the requirement of precise phase control is highly mitigated; 2) it does not limit the separation of the adjacent antennas, allowing high-power applications with large antennas’ separation; and 3) it does not need a repetitive phase-lock cycle via a specific algorithm throughout the measurement [37]. Instead, OPA-based GI only needs a simple calibration to record speckle patterns right before the measurement [34]. However, the calibration is indispensable since GI requires knowing the speckle patterns on an object, raising a challenge for a realistic application of OPA-based GI. First, due to phase drifts caused by thermal and acoustic noises, the calibration needs to be periodically performed to mitigate the dephasing. The calibration time is proportional to the pixel number of the imaging. Second, along with the increasing antennas’ separation, which is required for high power and high resolution, the phase drifts will become much more severe and the dephasing occurs much more frequently. How to predict or measure and compensate the phase drifts is one of the keys for OPA-based GI. Another way is to remove the requirement of knowing speckle patterns for GI.

Recently, Wang and Zheng proposed a scheme called naked-eye ghost imaging (NEGI) [38,39], which implements the correlation via an optical process in place of the traditional electronic process. During the whole process, the system neither needs to measure or predict the illumination patterns on the object nor requires the synchronization between the illumination patterns and their corresponding bucket detections. The optical correlation can directly display the image on human eyes or a camera. This paves a way to high-speed imaging for OPA-based GI. We built an optical phased array of 30 antennas, each of which is a waveguide-type electro-optic phase modulator (EOPM). The phases of the antennas were randomly modulated at a 5 MHz rate. The interference of the fields emitted from the EOPMs constructed random-like patterns on the object plane at the same rate. Since the thermal effect or vibration will cause an unpredictable phase drift on an EOM, the phases of the antennas are unpredictable, resulting in undeterminable illumination patterns. However, the proposed ghost-imaging system is able to directly display images at a frame rate of 1 kHz with the help of NEGI.

2 Experiment

The experimental setup is sketched in Figure 1. The laser is a 100 mW continuous wave fiber laser, whose wavelength is 1,064 nm with a line width of 100 kHz. The OPA consists of a light splitter (LS), 30 EOPMs, a controller, and a light combiner (LC). LS is a fiber splitter that splits the input laser beam into 30 sub-beams each of which is input into an EOPM. The intensity difference among the sub-beams is less than 2 dB. The input and output of each EOPM are single-mode fibers at 1,064 nm. The half-wave voltage of each EOPM is $\sim 2.4V$. Its maximum response bandwidth is more than 300 MHz. The voltage added on each EOPM is individually manipulated by the controller, which consists of a field-programmable gate array (FPGA) and 30 digital-to-analog converters (DACs). The controller can load a set of preset voltages onto the EOPMs which append corresponding phases to the 30 passing light fields. This process can run at a speed as high as 100 MHz. The other ends (fiber tips) of the EOPMs are randomly stacked in a 4 mm × 4 mm plane, constructing the OPA’s antenna array. Figure 2 shows the arrangement of the fiber tips (the antennas). The light fields emitting out from the fiber tips interfere together and construct a speckle-like pattern on the object plane, as shown in Figure 1.

FIGURE 1

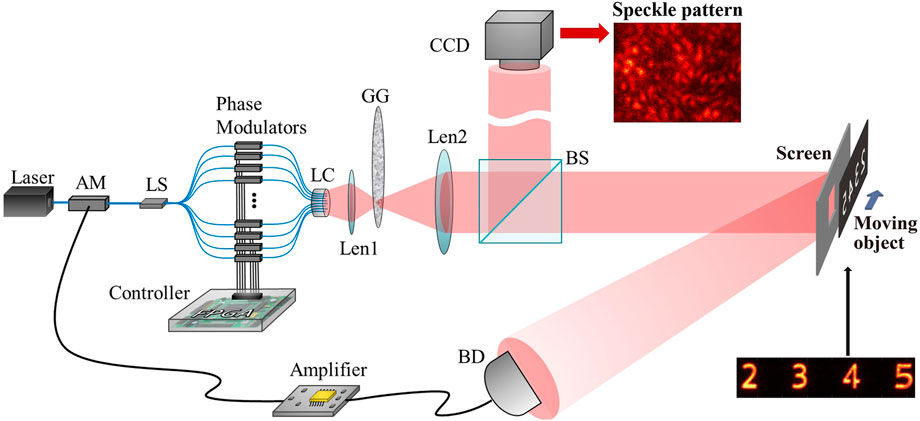
FIGURE 1. Schematic of the experiment. The intensity of a laser beam is modulated using an electro-optic amplitude modulator (AM) and then is split into 30 sub-beams with a light splitter (LS). Each sub-beam is input into an EOPM, which changes its phase at a very high rate. The other ends of the EOPMs are randomly stacked together, constructing a light combiner (LC). The light emitted from the OPA is focused onto a rotating ground glass (GG) with a lens (Len1). The scattered light from GG is collimated and projected toward the scene. The light reflected from a moving object is detected using a bucket detector (BD). The signal of BD is amplified with an amplifier and is then used to drive AM in real time. A beam splitter (BS) is placed right behind Len2 to copy the light patterns to a CCD camera that directly displays the image of the object after accumulating hundreds of time-varying patterns in a certain exposure time. A screen with an aperture is placed in front of a moving object. At the right-bottom is the profile of the object. The distance between Len2 and the object is 400 mm, so is the distance from Len2 to the camera. The focus length of Len1 is 25 mm. The focus length of Len2 is 300 mm. The distance between LC and Len1 is $\sim 80mm$. The distance between Len1 and GG is $\sim 36mm$. The distance between GG and Len2 is $\sim 300mm$.

FIGURE 2

FIGURE 2. Arrangement of the antennas.

Before the experiment, we generated 5000 sets of random numbers. Each set contains 30 random integer numbers ranging in [0, 15]. All these numbers were stored in the FPGA in advance. In the experiment, the controller took one set of random numbers (denoted as {d_j}), each of which was sent to its corresponding DAC. The jth DAC generates a voltage of {d_j*0.2V} to drive the jth EOPM, making the passing light field acquire a random phase. Such an operation was repeated every 200 ns. The interference of the light fields from the antennas constructed a time-varying random pattern at the rate of 5 MHz. The fields were incident onto an artifact removal system (which will be described in the following sections) and propagated toward the scene. Eventually, an object was illuminated by a random speckle pattern that changed every 200 ns.

The light reflected back from the object was received by a bucket detector, which was made of a high-speed avalanche photodiode detector (APD) and has a bandwidth of $\sim 150$MHz. The signal from the bucket detector was amplified using an amplifier. Figure 3 shows how the amplified bucket signal changed when the controller refreshed the speckle pattern. Each green pulse indicates when the controller refreshed the applied voltages on the EOPMs. The clock of the FPGA was 50 MHz, namely, that it finished the refreshing within 20 ns. The bucket signal correspondingly rushed to a new level within this time, as we can see the rising or falling curves within the green pulses in Figure 3. The amplified bucket signal was then used to drive an electro-optic amplitude modulator (AM), which linearly changed the input light intensity into the OPA. Therefore, each illumination pattern on the object has a total power proportional to the bucket detection called an “adaptive-power pattern.”A beam splitter (BS) is used to take a copy of those adaptive-power patterns and project them onto a camera (OSG030-815UM), which can run at a frame rate of 815@640*480, 1000@560*400, or 2000@280*200. The exposure time of the camera was set to 1 ms, during which the camera superposed 5000 adaptive-power patterns, directly yielding an image of the object. This process is equivalent to making a correlation between the illumination patterns and the bucket detections (see the following section for theoretical analysis). While the object (four numbers of “2 3 4 5” on a plate) was sliding by a screen, the camera captured a sequence of frames and stored each frame as a file. We picked frames every 10 ms and built a video at 100 fps (see the Supplementary Material S1). Figure 4 exhibits five of the frames. On the first row are the original captured images, while on the second row, there are the images after cutting off their backgrounds.

FIGURE 3

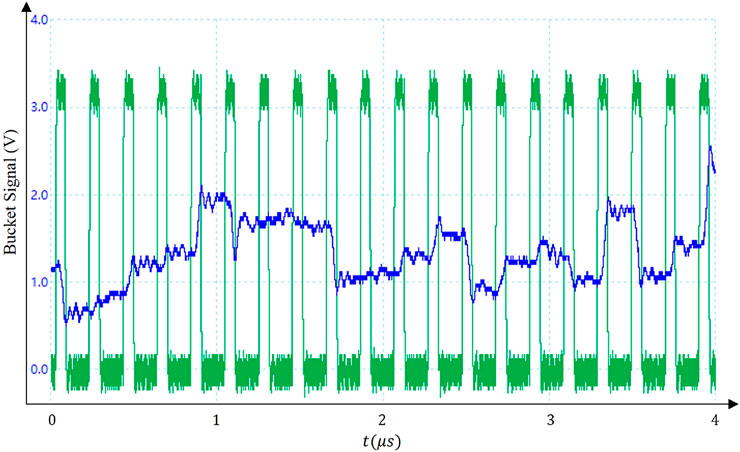
FIGURE 3. Signal of the amplified bucket detection. Each green pulse indicates when the controller triggered an operation of refreshing EOPMs’ phases. The separation of two adjacent pulses is 200 ns. The blue curve is the output from the amplifier that linearly amplified the signal from the bucket detector, whose value jumped once the controller generated a new random speckle pattern.

FIGURE 4

FIGURE 4. Images of a moving object. The first row exhibits five frames (the 50th, 150th, 250th, 350th, and 450th) of the video directly captured by the CCD at an exposure time of 1 ms. The second row are the images after applying simple background removal on the aforementioned images (refer Eq. 7).

Since the number of antennas is only 30, it is insufficient to sample the spatial frequencies of the object, causing repetitive visual artifacts in the reconstructed image [40,41]. To eliminate those artifacts, we employed a rotating ground glass to scramble the artifacts by focusing the emitted fields on GG with Len1 which was then collimated toward the scene with Len2. This caused the pattern of the artifact changing at a rate more than 40,000 Hz (the revolutions per minute of the GG was 40, and the focus spot was 45 mm off the axis). Therefore, within the exposure time of the camera, more than 40 different artifact patterns were averaged. The artifact was flattened out in a certain extend. Then, the image could be directly observed on the camera. On the other hand, the average of the artifact patterns causes a higher noisy background, as shown in the first row of Figure 4. By simply cutting out a certain background of each image, the contrast of the image is increased, as shown in the second row of Figures 4D–F. However, this process does not effectively flat out the artifact. They might be sufficiently eliminated using a neural network [41] or the “CLEAN” algorithm [40].

One drawback of GI is the trade-off between the resolution (the number of pixels) and the contrast. When an object occupies more pixels (a pixel size is an average size of a speckle), the signal-to-background ratio proportionally decreases, reducing the image contrast. In this system, the background is uneven. When the background rises up, the artifacts will become much obvious in the image, bringing much more difficulty in cutting the background without dramatically losing the information of the image. We therefore used a pinhole of 300 μm as an object to test the system. We used a CCD of Stingray F125BC and set a resolution of 1,024 × 768. It is important to note that the focus spot on GG was $\sim 1.5mm$, and the distance between GG and Len2 was $\sim 300mm$. Thus, a resolution cell of the speckle pattern has a size of λ*300mm/1.5 mm ≈ 200 μm. We manually moved the pinhole up and down with various moving speeds, while the CCD captured a video. For such a simple object, the background can be removed relatively thoroughly, and clean images were obtained as shown in Figure 5. The full video is given in Supplementary Material S2 “Pinhole.mp4.”

FIGURE 5

FIGURE 5. Images of a moving pinhole. These four frames are 1st, 60th, 150th, and 210th frames of the video captured by the CCD at an exposure time of 10 ms after applying simple background removal operation (refer Eq. 7).

3 Theory

3.1 Principle

Assume that the illumination pattern on the object at time t_j is P_j (x, y). After reflected from the object, the light is detected by BD which gives a bucket signal of B_j. The amplifier rectifies the signal to $\alpha \cdot (B_j-\bar{B})$ by using the AC coupling circuit, where α is the amplifying factor. $\bar{B}$ is the mean of the bucket signal. This rectified signal is used to drive AM, which changes the laser’s intensity from I₀ to $I_j=I_0\cdot [\alpha \cdot (B_j-\bar{B})+V_o]/V_{\pi }$. Here, V_π = 2.4V is the half-wave voltage of AM and V_o is the operating point of AM, which was intentionally adjusted to $V_o\approx \alpha (\bar{B}-B_{\min })$, where B_min is the minimum value of the bucket signal. Through this intensity modulation, the total power of the illumination pattern is adaptively changed according to the shape of the object, which is formulated as

$\begin{array}{ll}\hfill I_{OP}\left(x,y;t_j\right)& =I_j\cdot P_j\left(x,y\right)\hfill \\ \hfill & =I_0\cdot \left[\alpha \cdot \left(B_j-\bar{B}\right)+V_o\right]/V_{\pi }\cdot P_j\left(x,y\right).\hfill \end{array}(1)$

Recalling

$B_j=\int P_j\left(x,y\right)\cdot O\left(x,y\right)dxdy,(2)$

where O (x, y) is the profile function of the object. Substituting Eq. 2 into Eq. 1, we obtain

$I_{OP}\left(x,y;t_j\right)=\frac{\alpha I_0}{V_{\pi }}\cdot \left[\int P_j\left(x,y\right)\cdot P_j\left(x^{\prime },y^{\prime }\right)\cdot O\left(x^{\prime },y^{\prime }\right)d{x}^{\prime }d{y}^{\prime }+\left(V_o/\alpha -\bar{B}\right)\cdot P_j\left(x,y\right)\right].(3)$

After thousands of adaptive power patterns are superposed on the camera in an exposure time, the image M(x, y) on the camera is equivalently computed as

$M\left(x,y\right)=\sum _j{I}_{OP}\left(x,y;t_j\right)=\frac{\alpha I_0}{V_{\pi }}\cdot \left[\int \sum _j\left\{P_j\left(x,y\right)\cdot P_j\left(x^{\prime },y^{\prime }\right)\right\}\cdot O\left(x^{\prime },y^{\prime }\right)d{x}^{\prime }d{y}^{\prime }+\left(V_o/\alpha -\bar{B}\right)\cdot \sum _j{P}_j\left(x,y\right)\right].(4)$

If the pattern set {P_j (x, y)} covers the sufficient spatial frequencies, the second-order coherence function, which acts like a point-spread function (PSF) [40], is close to a peak-like function:

$S\left(x-x^{\prime },y-y^{\prime }\right)=\sum _j\left\{P_j\left(x,y\right)\cdot P_j\left(x^{\prime },y^{\prime }\right)\right\}={\delta }_D\left(x-x^{\prime },y-y^{\prime }\right)+{\mathcal{C}}_{DC},(5)$

where δ_D is a pulse function whose pulse width is the resolution. ${\mathcal{C}}_{DC}$ is the DC component of the summation. ${\sum }_j{P}_j(x,y)={\mathcal{C}}_P$ is also effectively a constant. Thus,

$\begin{array}{ll}\hfill M\left(x,y\right)& =\frac{\alpha I_0}{V_{\pi }}\cdot \left[\left[O⊛{\delta }_D\right]\left(x,y\right)+\mathrm{\Xi }\right]\hfill \\ \hfill \text{with}\mathrm{\Xi }& ={\mathcal{C}}_{DC}\int O\left(x^{\prime },y^{\prime }\right)d{x}^{\prime }d{y}^{\prime }+{\mathcal{C}}_P\cdot \left(V_o/\alpha -\bar{B}\right),\hfill \end{array}(6)$

where ⊛ is the convolution operator. M(x, y) reveals the image of the object.

3.2 The arrangement of the antennas

Due to the Fourier relationship between the source plane and object plane, a separation between any two antennas d_jk is related to a spatial frequency of λ*z/d_jk (here, we only consider one dimension for simplicity). The more the different separations of two antennas, the more the different spatial frequencies could be sampled in the object plane. Based on this idea, we arranged the 30 antennas in a way that it can maximally go through various separations of antennas. We therefore designed a random arrangement rather than a periodic grating structure, since the diffraction of a grating only contains spatial frequencies of λ*z/(j ⋅ d), where j = 1, 2, … , N_a, where N_a is the number of the antennas, and d is the separation of the two adjacent antennas. We investigate a periodic grating arrangement with numerical simulations as follows: let us consider 6 × 6 periodic antennas with d = 4/6 mm, as shown in Figure 6A. A speckle pattern constructed at a distance of z = 300 mm is shown in Figure 6B, which is obviously periodic. The period is L_p ≈ 2λ ⋅ z/= 0.94 mm. The second-order coherence function (acting as a PSF), S (x − x′, y − y′), exhibits periodic multiple peaks, as shown in Figure 6C. The average of 10,000 speckle patterns, ${\mathcal{C}}_P$, is also periodic, as shown in Figure 6D. The second-order correlation of 10,000 realizations displays a periodical repetitive image, as shown in Figure 6E. In addition to the repetitive problem, the distance of “2” and “4” in the recovered image is incorrect due to the multiple PSF peaks, as shown in Figures 6E and F.

FIGURE 6

FIGURE 6. Simulations for periodic antennas and the randomized antennas. The first row exhibits the properties of the periodic antennas: (A) antenna arrangement; (B) speckle pattern generated by the periodic antennas; (C) PSF; (D) ${\mathcal{C}}_P$; and (E) recovered image ΔG⁽²⁾. (F) Ground truth of the image. The last four sub-figures are of the randomized antennas described in Figure 2: (G) speckle pattern; (H) PSF; (I) ${\mathcal{C}}_P$; and (J) recovered image ΔG⁽²⁾.

In contrast, a speckle pattern of the randomized antennas looks quite random (Figure 6G). The second-order coherence function, S (x − x′, y − y′), is a single peak, as shown in Figure 6H, which will not cause an obviously repetitive image and incorrect distances among the sub-object in the scene. The background of the PSF, ${\mathcal{C}}_{DC}$, is not flat but fluctuates randomly. The average of speckle patterns, ${\mathcal{C}}_P$, also fluctuates randomly. These two terms contribute to the artifacts in the recovered images. One way to eliminate the uneven background is simply subtracting a constant, as described in the following equation:

$\mathrm{\Delta }{G}^{\left(2\right)}=M\left(x,y\right)-\overline{M\left(x,y\right)}-std\left\{M\left(x,y\right)\right\},(7)$

where $\overline{M(x,y)}$ is the mean value of the image and std{M(x, y)} calculates the standard deviation of M(x, y). The images in Figures 6E,J have been applied this background removal operation.

A sparse OPA largely reduces the cost. On the other hand, light patterns generated from a sparse OPA might not sufficiently sample the spatial frequencies of an object. As in this experiment and the simulations, ${\mathcal{C}}_{DC}$ and ${\mathcal{C}}_P$ are not constant, which produce an uneven background in the image. Meanwhile, δ_D is no longer a good peak function, which will have non-negligible side lobes, causing a repetitive artifact when being convolved with the object profile function [40,41]. In the experiment, we employed a rotating ground glass to scramble side lobes, which eliminated the artifact to a certain extent, enabling the image of the object directly observable on the camera. On the other hand, the background Ξ rises up as the imaging resolution increases. The contrast of the image can be increased by cutting a certain background (as shown in Eq. 7) from the captured image from the camera. These two processes can alleviate the bad imaging quality majorly caused by the artifact.

4 Conclusion

We demonstrated a high-speed ghost imaging with an optical phased array. The OPA generated time-varying speckle patterns at 5 MHz. We did not measure or predict the patterns. Based on the scheme of naked-eye ghost imaging, the image of a moving object is directly displayed on a CCD camera with the optical computation of the correlation simply with a beam splitter copying the light patterns on the object plane to the CCD plane. The image of the object is constructed on the CCD every $\sim 1ms$.

Wave-guide electro-optic modulators are not stable. When the field transmits through an EOPM, there is an additional phase drift appended to the field. This phase fluctuates at a rate around 0.1s ∼ 1s depending on the temperature fluctuation and vibration of the environment. If the environment is noisier, the phase fluctuates more quickly. Since the phase drift is unknown, it is hard to determine the interference pattern of the fields from the EOPMs. Typically, an OPA is designed for high-speed beam steering. In addition to trying to obtain the real-time steering angle, people have also been seeking a way to manipulate the beam shape in order to maintain a narrow main lobe but remove the side lobes. However, these are still the major problems due to the current state of the art. Although we used an OPA as a light source, we did not use it in a normal way. In this work, we used the OPA in an opposite way: we neither tried to manipulate the beam of the OPA nor did we measure or predict the beam shape; instead, the OPA randomly generated speckle patterns. Since ghost imaging can reconstruct images without knowing the illumination patterns with the help of optical computation of the correlation, the OPA brought us a high-speed ghost-image method. Here, we made use of the high-speed modulation feature of the OPA and its unpredictable phase change with time. In the experiment, we intentionally increased the environment noise by adding vibration in order to make the phase change more random. This method might be a candidate way of using OPAs.

On the other hand, this method uses a CCD to record a dynamic image. Although the frame rate of the system is merely determined by the CCD, the exposure time of a frame can be much shorter than the time interval of two adjacent frames, which, for example, can be less than 1 m. A short exposure time is suitable for a high-speed motion scenario. Second, GI has an advantage in imaging under low illumination [6,18], which is suitable not only for a biomedical scenario that requires weak light exposure but also for a long-distance imaging scenario. In contrast, the traditional imaging method (a CCD and lenses) hardly reaches such scenarios.

The experimental results still contain apparent artifacts. We have provided an analytical analysis and numerical simulations to investigate the causes. In addition to using a low-speed rotating ground glass to average the artifacts to a certain extent, for a better result, a suitable algorithm such as the SDDAN network [41] or the modified “CLEAN” algorithm [40] may be needed to give a clear image. Another way is increasing the number of antennas. Since this way raises the cost and highly adds to the manufacturing complexity, looking for an optimal number of antennas is the next key research objective. A comprehensive study needs to be carried out in the future on investigating the relationship between the number of antennas and the signal-to-noise ratio of images.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author contributions

HC and GW proposed the OPA ghost imaging method. XS and GW designed the experiment. XS, BQ, WX, and SL performed the experiment. BC prepared the OPA instruments. YY and YH were in charge of the data process and algorithms. HZ and ZX were in charge of the theory part and the selection of the electro-optic crystals.

Funding

This work is supported by the National Natural Science Foundation of China (Grant No. 61901353).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2022.1072482/full#supplementary-material

References

1. Pittman TB, Shih YH, Strekalov DV, Sergienko AV. Optical imaging by means of two-photon quantum entanglement. Phys Rev A (1995) 52:R3429–R3432. doi:10.1103/PhysRevA.52.R3429

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Valencia A, Scarcelli G, D'Angelo M, Shih Y. Two-photon imaging with thermal light. Phys Rev Lett (2005) 94:063601. doi:10.1103/PhysRevLett.94.063601

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Meyers RE, Deacon KS, Shih Y. Turbulence-free ghost imaging. Appl Phys Lett (2011) 98:111115. doi:10.1063/1.3567931

CrossRef Full Text | Google Scholar

4. Yang Z, Zhao L, Zhao X, Qin W, Li J. Lensless ghost imaging through the strongly scattering medium. Chin Phys. B (2016) 25:024202. doi:10.1088/1674-1056/25/2/024202

CrossRef Full Text | Google Scholar

5. Morris PA, Aspden RS, Bell JE, Boyd RW, Padgett MJ. Imaging with a small number of photons. Nat Commun (2015) 6:5913. doi:10.1038/ncomms6913

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Zhao W, Chen H, Yuan Y, Zheng H, Liu J, Xu Z, et al. Ultrahigh-speed color imaging with single-pixel detectors at low light level. Phys Rev Appl (2019) 12:034049. doi:10.1103/PhysRevApplied.12.034049

CrossRef Full Text | Google Scholar

7. Scarcelli G, Berardi V, Shih Y. Can two-photon correlation of chaotic light be considered as correlation of intensity fluctuations? Phys Rev Lett (2006) 96:063602. doi:10.1103/PhysRevLett.96.063602

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Yuan Y, Chen H. Unsighted ghost imaging for objects completely hidden inside turbid media. New J Phys (2022) 24:043034. doi:10.1088/1367-2630/ac62b3

CrossRef Full Text | Google Scholar

9. Peng H, Yang Z, Li D, Wu L. The application of ghost imaging in infrared imaging detection technology. In: Selected Papers of the Photoelectronic Technology Committee Conferences held June–July 2015. Bellingham, Washington, USA: International Society for Optics and Photonics (2015). p. 97952O. vol. 9795. doi:10.1117/12.2218294

CrossRef Full Text | Google Scholar

10. Liu H, Zhang S. Computational ghost imaging of hot objects in long-wave infrared range. Appl Phys Lett (2017) 111:031110. doi:10.1063/1.4994662

CrossRef Full Text | Google Scholar

11. Aspden RS, Gemmell NR, Morris PA, Tasca DS, Mertens L, Tanner MG, et al. Photon-sparse microscopy: Visible light imaging using infrared illumination. Optica (2015) 2:1049–52. doi:10.1364/optica.2.001049

CrossRef Full Text | Google Scholar

12. Shapiro JH. Computational ghost imaging. Phys Rev A (2008) 78:061802. doi:10.1103/physreva.78.061802

CrossRef Full Text | Google Scholar

13. Meyers R, Deacon KS, Shih Y. Ghost-imaging experiment by measuring reflected photons. Phys Rev A (2008) 77:41801. doi:10.1103/physreva.77.041801

CrossRef Full Text | Google Scholar

14. Ferri F, Magatti D, Lugiato LA, Gatti A. Differential ghost imaging. Phys Rev Lett (2010) 104:253603. doi:10.1103/physrevlett.104.253603

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Gong W, Zhao C, Yu H, Chen M, Xu W, Han S. Three-dimensional ghost imaging lidar via sparsity constraint. Sci Rep (2016) 6:26133. doi:10.1038/srep26133

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Pelliccia D, Rack A, Scheel M, Cantelli V, Paganin DM. Experimental x-ray ghost imaging. Phys Rev Lett (2016) 117:113902. doi:10.1103/PhysRevLett.117.113902

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Yu H, Lu R, Han S, Xie H, Du G, Xiao T, et al. Fourier-transform ghost imaging with hard x rays. Phys Rev Lett (2016) 117:113901. doi:10.1103/PhysRevLett.117.113901

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Zhang A, He Y, Wu L, Chen L, Wang B. Tabletop x-ray ghost imaging with ultra-low radiation. Optica (2018) 5:374–7. doi:10.1364/optica.5.000374

CrossRef Full Text | Google Scholar

19. Khakimov RI, Henson B, Shin D, Hodgman S, Dall R, Baldwin K, et al. Ghost imaging with atoms. Nature (2016) 540:100–3. doi:10.1038/nature20154

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Baldwin K, Khakimov R, Henson B, Shin D, Hodgman S, Dall R, et al. Ghost imaging with atoms and photons for remote sensing. In: Optics and Photonics for energy and the environment. Washington, DC, USA: Optical Society of America (2017). EM4B–1. doi:10.1364/ee.2017.em4b.1

CrossRef Full Text | Google Scholar

21. Ota S, Horisaki R, Kawamura Y, Ugawa M, Sato I, Hashimoto K, et al. Ghost cytometry. Science (2018) 360:1246–51. doi:10.1126/science.aan0096

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Jiao S, Feng J, Gao Y, Lei T, Xie Z, Yuan X. Optical machine learning with incoherent light and a single-pixel detector. Opt Lett (2019) 44:5186–9. doi:10.1364/OL.44.005186

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Liu H, Bian L, Zhang J. Image-free single-pixel segmentation. Opt Laser Technol (2023) 157:108600. doi:10.1016/j.optlastec.2022.108600

CrossRef Full Text | Google Scholar

24. Jiao S, Feng J, Gao Y, Lei T, Yuan X. Visual cryptography in single-pixel imaging. Opt Express (2020) 28(5):7301–13. doi:10.1364/oe.383240

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Zheng P, Li J, Li Z, Ge M, Zhang S, Zheng G, et al. Compressive imaging encryption with secret sharing metasurfaces. Adv Opt Mater (2022) 10:2200257. doi:10.1002/adom.202200257

CrossRef Full Text | Google Scholar

26. Xiao Y, Zhou L, Pan Z, Cao Y, Chen W. Physically-enhanced ghost encoding. Opt Lett (2022) 47:433–6. doi:10.1364/OL.447620

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Xu Z-H, Chen W, Penuelas J, Padgett M, Sun M-J. 1000 fps computational ghost imaging using led-based structured illumination. Opt Express (2018) 26:2427–34. doi:10.1364/OE.26.002427

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Meyer RA. Optical beam steering using a multichannel lithium tantalate crystal. Appl Opt (1972) 11:613–6. doi:10.1364/AO.11.000613

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Ninomiya Y. Ultrahigh resolving electrooptic prism array light deflectors. IEEE J Quan Electron. (1973) 9:791–5. doi:10.1109/JQE.1973.1077739

CrossRef Full Text | Google Scholar

30. McManamon P, Dorschner T, Corkum D, Friedman L, Hobbs D, Holz M, et al. Optical phased array technology. Proc IEEE (1996) 84:268–98. doi:10.1109/5.482231

CrossRef Full Text | Google Scholar

31. Hsu C-P, Li B, Solano-Rivas B, Gohil AR, Chan PH, Moore AD, et al. A review and perspective on optical phased array for automotive lidar. IEEE J Select Top Quan Electron. (2021) 27:1–16. doi:10.1109/JSTQE.2020.3022948

CrossRef Full Text | Google Scholar

32.[Dataset] Chen H, Xu Z. High-speed calculation correlated imaging system and method based on preset modulatable light source (2016). China Patent CN105807289A.

Google Scholar

33. Komatsu K, Ozeki Y, Nakano Y, Tanemura T. Ghost imaging using integrated optical phased array. In: Optical Fiber Communication Conference. Los Angeles, California, United States: Optica Publishing Group (2017). Th3H.4. doi:10.1364/OFC.2017.Th3H.4

CrossRef Full Text | Google Scholar

34. Li LJ, Chen W, Zhao XY, Sun MJ. Fast optical phased array calibration technique for random phase modulation lidar. IEEE Photon J (2018) 2018:1.

Google Scholar

35. Kohno Y, Komatsu K, Tang R, Ozeki Y, Nakano Y, Tanemura T. Ghost imaging using a large-scale silicon photonic phased array chip. Opt Express (2019) 27:3817. doi:10.1364/OE.27.003817

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Wang Z, Cao R, Sun Y, Liao J, Lu Y, Jin L, et al. Ghost imaging of moving target based on the periodic pseudo-thermal light field generated by a 2D silicon OPA. IEEE Photon J. (2022) 14:1–8. doi:10.1109/jphot.2022.3145000

CrossRef Full Text | Google Scholar

37. Vorontsov MA, Sivokon VP. Stochastic parallel-gradient-descent technique for high-resolution wave-front phase-distortion correction. J Opt Soc Am A (1998) 15:2745–58. doi:10.1364/JOSAA.15.002745

CrossRef Full Text | Google Scholar

38. Wang G, Zheng H, Tang Z, Zhou Y, Xu Z. All-optical naked-eye ghost imaging. Scientific Rep (2020) 10. doi:10.1038/s41598-020-59263-1

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Wang G, Zheng H, Tang Z, He Y, Zhou Y, Chen H, et al. Naked-eye ghost imaging via photoelectric feedback. 中国光学快报 (2020) 18:091101. doi:10.3788/col202018.091101

CrossRef Full Text | Google Scholar

40. Yang D, Wu G, Li J, Chang C, Luo B, Lin H, et al. Image recovery of ghost imaging with sparse spatial frequencies. Opt Lett (2020) 45:5356–9. doi:10.1364/OL.403288

PubMed Abstract | CrossRef Full Text | Google Scholar

41. He Y, Duan S, Li J, Chen H, Yuan Y, Zheng H, et al. Speckle-driving de-artifact nets ghost imaging. SSRN J (2022). doi:10.2139/ssrn.4139618

CrossRef Full Text | Google Scholar