- Faculty of Mathematical Physics, Nanjing Institute of Technology, Nanjing, China
In this study, the generalized Atangana’s fractional BBM–Burgers equation (GBBM-B) with the dissipative term is investigated by utilizing the modified sub-equation method and the new G'/(bG' + G + a)-expansion method; with the aid of symbolic computations, many types of new exact explicit solutions including solitary wave solutions, trigonometric function periodic solutions, and the rational function solutions are obtained. Some 3D and 2D plots of these solutions are simulated, which show the novelty and visibility of the propagation behavior and dynamical structure of the corresponding equation. Moreover, with the selection of different values on the parameters and orders, we can deduce many types of exact solutions in special cases. We also discussed the changes and characteristics of these solutions, which can help us further understand the inner structure of this equation. The obtained solutions indicate that the approach is easy and effective for nonlinear models with high-order dispersion terms.
1 Introduction
As is known, calculus was founded by Newton and Leibniz at the end of the 1660s, and fractional order calculus has gradually become one of the new special fields in natural sciences and mathematical physics since 1695 [1]. In recent years, due to the wide application of fractional order calculus in nonlinear partial differential equations (PDEs), especially fractional PDEs [2–4], many nonlinear phenomena come down to fractional models, such as ecological and economic systems [5], two-scale thermal science [6], mechanics [7], chaotic oscillations [8], atmospheric science [9], and optical fiber [10–12]. Searching for exact explicit solutions of these nonlinear fractional PDEs plays a significant role in the study of the dynamics of those phenomena. Until now, many powerful methods for this subject have been offered, such as the Darboux transformation [13], Bäcklund transformation method [14], and Hirota bilinear method [15], which can be used to find N-soliton solutions. The improved F-expansion method [16], projective Riccati equation method [17], sine-Gordon method [18], Jacobi elliptic function expansion method [19], G'/G-expansion method [20], (G'/G,1/G)-expansion method [21], improved (m + G'/G)-expansion method [22], improved G'/
Riemann–Liouville fractional derivative [35]:
Caputo fractional derivative [36]:
Jumarie’s fractional derivative [37]:
Ji-Huan He’s fractional derivative [38]:
Furthermore, the Atangana–Baleanu derivative [39], M-fractional derivative [40], conformable fractional derivative [41], and Atangana’s fractional derivative [42, 43] which will be utilized in this article, are built recently.
In this paper, we consider the generalized Atangana’s fractional BBM–Burgers equation with the dissipative term in the following form [44–47]:
where
Next, we review some basic definitions and properties of the Atangana fractional derivative which are used further in this paper [42, 43].
Definition: For a function
Also, we have the following important properties [42, 43]:
The rest of the paper is organized as follows. In Section 2, we introduce the modified sub-equation method [56–59] and the new G'/(bG'+G+a)-expansion method, while in Section 3, some exact solutions of the GBBM–Burgers equation are found and discussed by utilizing the proposed methods. Finally, the conclusion is presented in Section 4.
2 Description of the two methods
2.1 The modified sub-equation method
Consider the following Atangana’s fractional differential equation:
We use the following wave transformation [60]:
where the constant
Assume that Eq. 4 has the following solution:
where
Equation 6 gives the following solutions:
When
Substituting Eqs 6, 5 into Eq. 4, collecting the coefficients of
2.2 The G'/(bG' + G + a)-expansion method
With similar steps to technique Section 2.1, we give the main steps of this method.
Step 1. Assume that Eq. 4 has the following solution:
where
where
Case 1. When
Case 2. When
Step 2. Substituting Eqs 7, 9 into Eq. 4 and setting the coefficients of
3 Exact solutions to the GBBM–Burgers equation
3.1 Using the modified sub-equation method
Substituting Eq. 3 into Eq. 1 and integrating Eq. 1 once, we have
where
where
Solving the aforementioned AEs, we have the following cases:
Case 1.
Case 2.
We can obtain the following traveling wave solutions.
Family 1
Set 1
where
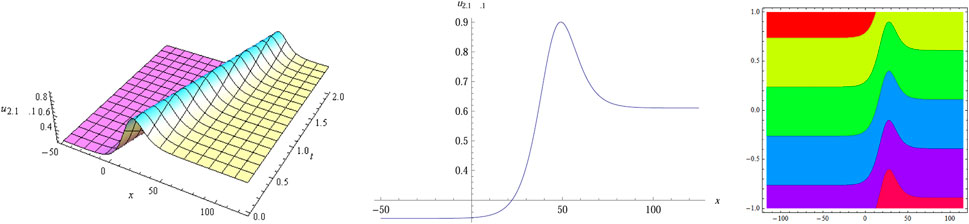
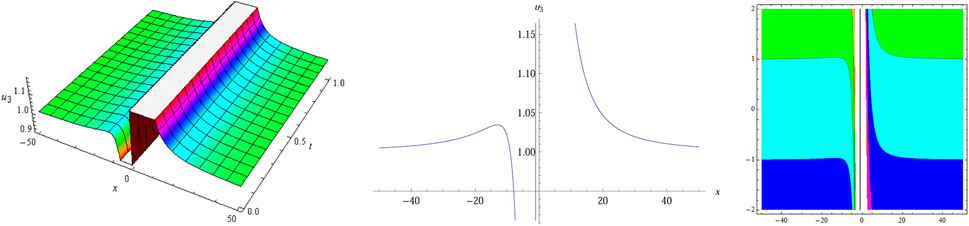
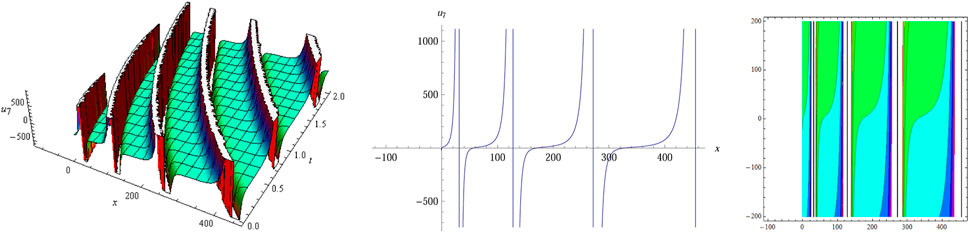
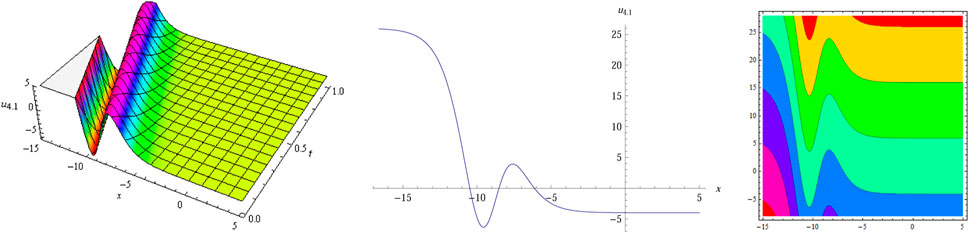
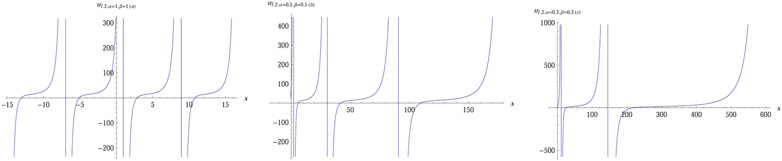
The numerical simulation of
Family 2
Set 2
where
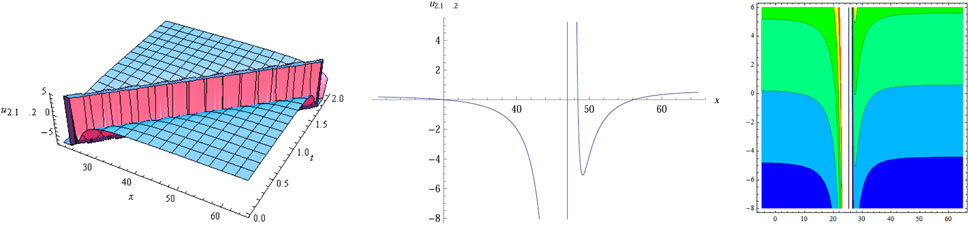
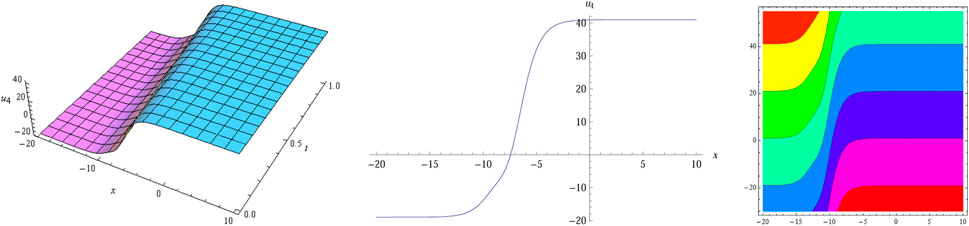
The numerical simulation of
Family 3
Set 3
If we select
3.2 Using the G'/(bG' + G + a)-expansion method
We assume that Eq. 10 has the following solutions:
where
We can deduce the following solutions with the aid of mathematical software.
Case 1.
Case 2.
Case 3.
Case 4.
We can determine the following solutions.
Family 4
For case 1, we have
Set 4
where
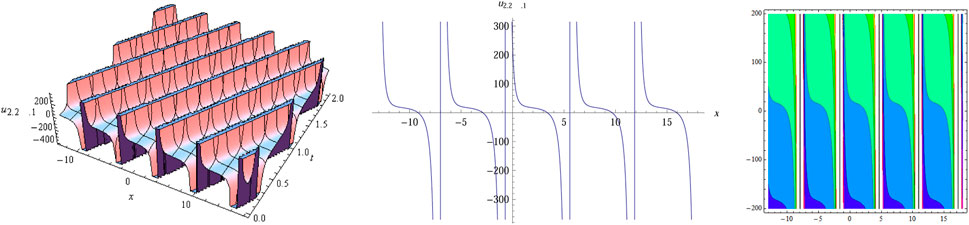
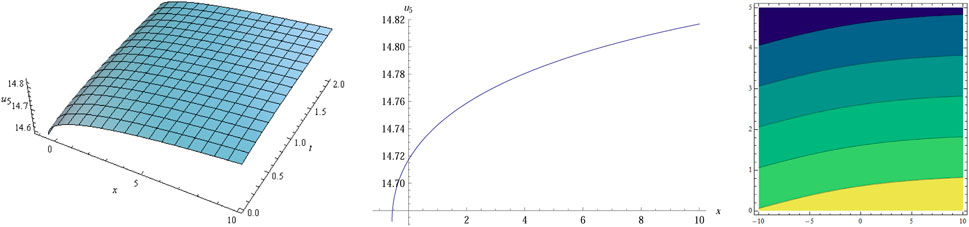
The numerical simulation of
For case 2, we have
Set 5
where
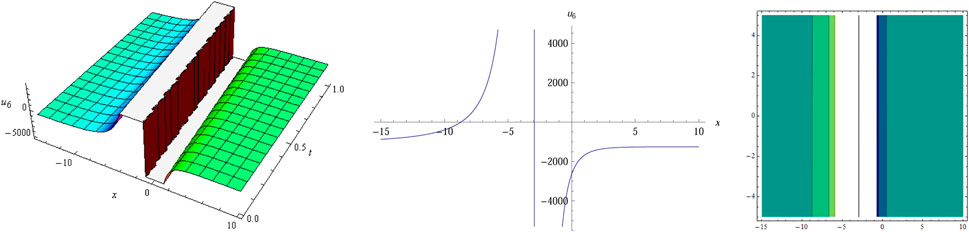
The numerical simulation of
For case 3, we have
Set 6
where
The numerical simulation of
Family 5
Set 7
where
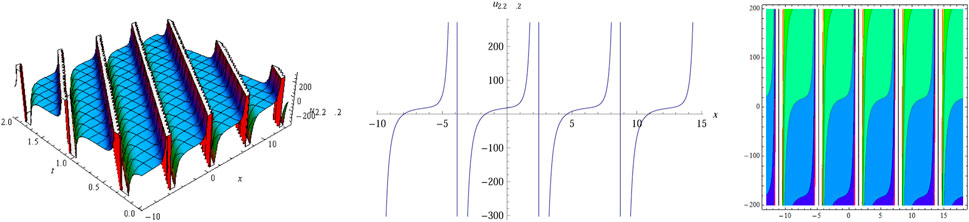
The numerical simulation of
Clearly, if we select the special value of
Thus, we obtain the following solutions:
If we select
Thus,
We have
The simulation of
3.3 Results and discussion
After utilizing the modified sub-equation method and the new G'/(bG'+G+a)-expansion method, we obtain many types of exact solutions of Eq. 1, and some structures of these solutions are simulated in Figures 1–10. Visualization can help us better understand the dynamic behavior and propagation property of these solutions. For example, the bell-shape-like solitary wave solution of Eq. 1 is shown in Figure 1, and we find that there are two asymptotes on either side of the peak for
4 Conclusion
In conclusion, many types of new exact solutions for the Atangana fractional GBBM–Burgers equation with the dissipative term have been found after utilizing the modified sub-equation method and the new G'/(bG' + G + a)-expansion method. Some propagation behavioral patterns of these solutions are discussed and simulated, the graphs of which show that these solitary wave solutions, trigonometric function periodic solutions, and rational function solutions are propagated through different patterns. The two efficient and significant methods can be used for many other nonlinear models such as the vmKdV equation, Ginzburg–Landau equation, and NLS-KDV equation. However, it is still worth researching whether the method can be used in a system with high dimensions and high order. Finally, all these solutions obtained in the present article have been checked by mathematical software.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.
Author contributions
BH: completed the study, carried out the tests, and drafted the manuscript.
Funding
This work is supported by the practical innovation training program projects for the university students of Jiangsu Province (Grant No. 202211276054Y), natural science research projects of Institutions in Jiangsu Province (Grant No. 18KJB110013), and the Nanjing Institute of Technology (Grant Nos. ZKJ201513 and YZKC2019086).
Conflict of interest
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
2. He JH, Jiao ML, He CH. Homotopy perturbation method for fractal Duffing oscillator with arbitrary conditions. Fractals (2022). doi:10.1142/S0218348X22501651
3. Khan RA, Li Y, Jarad F. Exact analytical solutions of fractional order telegraph equations via triple Laplace transform. Discrete & Continuous Dynamical Systems-S (2018) 14(7):2387–11. doi:10.3934/dcdss.2020427
4. Alshammari S, Iqba N, Yar M. Analytical investigation of nonlinear fractional Harry Dym and Rosenau-Hyman equation via a novel transform. J Funct Spaces (2022) 2022:1–12. doi:10.1155/2022/8736030
5. Almutairi A, El-Metwally H, Sohaly MA, Elbaz IM. Lyapunov stability analysis for nonlinear delay systems under random effects and stochastic perturbations with applications in finance and ecology. Adv Differ Equ (2021) 2021(1):186–32. doi:10.1186/s13662-021-03344-6
6. He JH. Seeing with a single scale is always unbelieving: From magic to two-scale fractal. Therm Sci (2021) 25(2B):1217–9. doi:10.2298/tsci2102217h
7. Zhang RF, Bilige S. Bilinear neural network method to obtain the exact analytical solutions of nonlinear partial differential equations and its application to p-gBKP equation. Nonlinear Dyn (2019) 95(4):3041–8. doi:10.1007/s11071-018-04739-z
8. Tavazoei MS, Haeri M, Jafari S, Bolouki S, Siami M. Some applications of fractional calculus in suppression of chaotic oscillations. IEEE Trans Ind Electron (2008) 55(11):4094–101. doi:10.1109/tie.2008.925774
9. Korn P. A Regularity-Aware algorithm for variational data assimilation of an idealized coupled Atmosphere-Ocean Model. J Sci Comput (2018) 79(2):748–86. doi:10.1007/s10915-018-0871-y
10. Yokus A, Baskonus HM. Dynamics of traveling wave solutions arising in fiber optic communication of some nonlinear models. Soft Comput (2022) 2022:1–10. doi:10.1007/s00500-022-07320-4
11. Abdelwahed HG, El-Shewy EK, Abdelrahman MAE, Alsarhana A. On the physical nonlinear (n+1)-dimensional Schrödinger equation applications. Results Phys (2021) 21:103798. doi:10.1016/j.rinp.2020.103798
12. Samei ME, Karimi L, Kaabar MKA. To investigate a class of multi-singular pointwise defined fractional $ q $–integro-differential equation with applications. AIMS Math (2022) 7(5):7781–816. doi:10.3934/math.2022437
13. Matveev VA, Salle MA. Darboux transformations and solitons. Berlin, Heidelberg: Springer-Verlag (1991).
14. Lu DC, Hong BJ. Bäcklund transformation and n-soliton-like solutions to the combined KdV-Burgers equation with variable coefficients. Int J Nonlinear Sci (2006) 1(2):3–10. http://www.worldacademicunion.com/journal/1749-3889-3897IJNS/IJNSVol2No1Paper1.pdf
15. Qi FH, Li S, Li ZH, Wang P. Multiple lump solutions of the (2+1)-dimensional sawada-kotera -like equation. Front Phys (2022) 10:1041100. doi:10.3389/fphy.2022.1041100
16. Bashar MH, Islam SMR. Exact solutions to the (2+1)-Dimensional Heisenberg ferromagnetic spin chain equation by using modified simple equation and improve F-expansion methods. Phys Open (2020) 5:100027. doi:10.1016/j.physo.2020.100027
17. Lu DC, Hong BJ, Tian LX. New explicit exact solutions for the generalized coupled Hirota-Satsuma KdV system. Comput Math Appl (2007) 53:1181–90. doi:10.1016/j.camwa.2006.08.047
18. Kundu RP, Fahim M, Islam ME, Akbar MA. The sine-Gordon expansion method for higher- dimensional NLEEs and parametric analysis. Heliyon (2021) 7(3):e06459. doi:10.1016/j.heliyon.2021.e06459
19. Hong BJ. New Jacobi elliptic functions solutions for the variable-coefficient mKdV equation. Appl Math Comput (2009) 215(8):2908–13. doi:10.1016/j.amc.2009.09.035
20. Mohanty SK, Kravchenko OV, Dev AN. Exact traveling wave solutions of the Schamel Burgers’ equation by using generalized-improved and generalized G′G expansion methods. Results Phys (2022) 33:105124. doi:10.1016/j.rinp.2021.105124
21. Siddique I, Jaradat MMM, Zafar A, Bukht Mehdi K, Osman M. Exact traveling wave solutions for two prolific conformable M-Fractional differential equations via three diverse approaches. Results Phys (2021) 33:104557. doi:10.1016/j.rinp.2021.104557
22. Ismael HF, Bulut H, Baskonus HM. Optical soliton solutions to the Fokas–Lenells equation via sine-Gordon expansion method and (m+(G'/G))-expansion method. Pramana (2020) 94(1):1–9. doi:10.1007/s12043-019-1897-x
23. Mohyud-Din ST, Bibi S. Exact solutions for nonlinear fractional differential equations using G′G2-expansion method-expansion method. Alexandria Eng J (2018) 57(2):1003–8. doi:10.1016/j.aej.2017.01.035
24. Fei J, Ma Z, Cao W. Soliton molecules of new (2+1)-dimensional Burgers-type equation. Eur Phys J Plus (2022) 137(1):104–11. doi:10.1140/epjp/s13360-021-02306-x
25. Fan EG. Two new applications of the homogeneous balance method. Phys Lett A (2000) 265:353–7. doi:10.1016/s0375-9601(00)00010-4
26. Ma WX, Osman MS, Arshed S, Raza N, Srivastava H. Practical analytical approaches for finding novel optical solitons in the single-mode fibers. Chin J Phys (2021) 72:475–86. doi:10.1016/j.cjph.2021.01.015
27. Ablowitz MJ, Solitons PAC. Nonlinear evolution equations and inverse scattering. New York: Cambridge University Press (1991).
28. Nass AM. Lie symmetry analysis and exact solutions of fractional ordinary differential equations with neutral delay. Appl Math Comput (2019) 347:370–80. doi:10.1016/j.amc.2018.11.002
29. Yue C, Lu DC, Khater MMA, Abdel-Aty AH, Alharbi W, Attia RAM. On explicit wave solutions of the fractional nonlinear DSW system via the modified Khater method. Fractals (2020) 28(8):2040034. doi:10.1142/s0218348x20400344
30. He JH, Elagan SK, Li ZB. Geometrical explanation of the fractional complex transform and derivative chain rule for fractional calculus. Phys Lett A (2012) 376(4):257–9. doi:10.1016/j.physleta.2011.11.030
31. He JH. Fractal calculus and its geometrical explanation. Results Phys (2018) 10:272–6. doi:10.1016/j.rinp.2018.06.011
32. Yu F, Yu Q, Chen H, Kong X, Mokbel AAM, Cai S, et al. Dynamic analysis and audio encryption application in IoT of a multi-scroll fractional-order memristive hopfield neural network. Fractal Fract (2022) 6(7):370. doi:10.3390/fractalfract6070370
33. Hong BJ, Lu DC, Chen W. Exact and approximate solutions for the fractional Schrödinger equation with variable coefficients. Adv Differ Equ (2019) 2019(370):370–10. doi:10.1186/s13662-019-2313-z
34. Biswas A. Conservation laws for optical solitons with anti-cubic and generalized anticubic nonlinearities. Optik (2019) 176:198–201. doi:10.1016/j.ijleo.2018.09.074
35. Haq A. Partial-approximate controllability of semi-linear systems involving two Riemann-Liouville fractional derivatives. Chaos Solitons Fractals (2022) 157:111923. doi:10.1016/j.chaos.2022.111923
36. Caputo M. Linear models of dissipation whose Q is almost frequency independent: Part II. Geophys J Int (1967) 13:529–39. doi:10.1111/j.1365-246x.1967.tb02303.x
37. Guner O, Atik H, Kayyrzhanovich AA. New exact solution for space-time fractional differential equations via (G'/G)-expansion method. Optik (2017) 130:696–701. doi:10.1016/j.ijleo.2016.10.116
38. He JH. A tutorial review on fractal spacetime and fractional calculus. Int J Theor Phys (Dordr) (2014) 53:3698–718. doi:10.1007/s10773-014-2123-8
39. Tajadodi H. A Numerical approach of fractional advection-diffusion equation with Atangana Baleanu derivative. Chaos Solitons Fractals (2020) 130:109527. doi:10.1016/j.chaos.2019.109527
40. Yao SW, Manzoor R, Zafar A, Inc M, Abbagari S, Houwe A. Exact soliton solutions to the Cahn-Allen equation and Predator-Prey model with truncated M-fractional derivative. Results Phys (2022) 37:105455. doi:10.1016/j.rinp.2022.105455
41. Khalil R, Al Horani M, Yousef A, Sababheh M. A new definition of fractional derivative. J Comput Appl Math (2014) 264:65–70. doi:10.1016/j.cam.2014.01.002
42. Atangana A, Baleanu D, Alsaedi A. Analysis of time-fractional hunter-saxton equation: A model of neumatic liquid crystal. Open Phys (2016) 14:145–9. doi:10.1515/phys-2016-0010
43. Yusuf A, Inc M, Aliyu AI, Baleanu D. Optical solitons possessing beta derivative of the chen-lee-liu equation in optical fibers. Front Phys (2019) 7:00034. doi:10.3389/fphy.2019.00034
44. Hong BJ, Lu DC. Homotopic approximate solutions for the general perturbed Burgers-BBM equation. J Inf Comput Sci (2014) 11(11):4003–11. doi:10.12733/jics20104244
45. Zhao HJ, Xuan BJ. Existence and convergence of solutions for the generalized BBM-Burgers equations with dissipative term. Nonlinear Anal Theor Methods Appl (1997) 28(11):1835–49. doi:10.1016/s0362-546x(95)00237-p
46. Chen SL, Hou WG. Explicit exact solutions of generalized B-BBM and B-BBM equations. Acta Physica Sinica (2001) 50(10):695–8. doi:10.7498/aps.50.1842
47. Mei M. Large-time behavior of solution for generalized Benjamin-Bona-Mahony-Burgers equations. Nonlinear Anal Theor Methods Appl (1998) 33:699–714. doi:10.1016/s0362-546x(97)00674-3
48. Benjamin TB, Bona JL, Mahony JJ. Model equations for long waves in nonlinear dispersive system. Philos Trans R Soc Lond Ser A: Math Phys Sci (1972) 272:47–78. doi:10.1098/rsta.1972.0032
49. Mathanaranjan T. Exact and explicit traveling wave solutions to the generalized Gardner and BBMB equations with dual high-order nonlinear terms. Partial Differential Equations Appl Math (2021) 4:100120. doi:10.1016/j.padiff.2021.100120
50. Kumar S, Kumar D. Fractional modelling for BBM-Burger equation by using new homotopy analysis transform method. J Assoc Arab Universities Basic Appl Sci (2014) 16:16–20. doi:10.1016/j.jaubas.2013.10.002
51. Alharthi MS, Ali HMS, Habib MA, Miah MM, Aljohani AF, Akbar MA, et al. Assorted soliton wave solutions of time-fractional BBM-Burger and Sharma-Tasso-Olver equations in nonlinear analysis. J Ocean Eng Sci (2022). doi:10.1016/j.joes.2022.06.022
52. Hossen MB, Roshid HO, Ali MZ. Dynamical structures of exact soliton solutions to Burgers’ equation via the bilinear approach. Partial Differential Equations Appl Math (2021) 3:100035. doi:10.1016/j.padiff.2021.100035
53. Li LL, Li DF. Exact solutions and numerical study of time fractional Burgers’ equations. Appl Math Lett (2020) 100:106011. doi:10.1016/j.aml.2019.106011
54. Fukuda I, Ikeda M. Large time behavior of solutions to the Cauchy problem for the BBM-Burgers equation. J Differential Equations (2022) 336:275–314. doi:10.1016/j.jde.2022.07.020
55. Oruç Ö. A new algorithm based on Lucas polynomials for approximate solution of 1D and 2D nonlinear generalized Benjamin-Bona-Mahony-Burgers equation. Comput Math Appl (2017) 74:3042–57. doi:10.1016/j.camwa.2017.07.046
56. Li C, Guo QL. On the solutions of the space-time fractional coupled Jaulent-Miodek equation associated with energy-dependent Schrödinger potential. Appl Math Lett (2021) 121:107517. doi:10.1016/j.aml.2021.107517
57. Gómez S CA, Salas AH, Frias BA. New periodic and soliton solutions for the Generalized BBM and Burgers-BBM equations. Appl Math Comput (2010) 217:1430–4. doi:10.1016/j.amc.2009.05.068
58. Kurt A, Rezazadeh H, Senol M, Neirameh A, Tasbozan O, Eslami M, et al. Two effective approaches for solving fractional generalized Hirota-Satsuma coupled KdV system arising in interaction of long waves. J Ocean Eng Sci (2019) 4:24–32. doi:10.1016/j.joes.2018.12.004
59. Akinyemi1 L, Şenol M, Akpan U, Oluwasegun K. The optical soliton solutions of generalized coupled nonlinear Schrödinger-Korteweg-de Vries equations. Opt Quan Electron (2021) 53:394. doi:10.1007/s11082-021-03030-7
Keywords: generalized BBM–Burgers equation, Atangana’s fractional derivative, dissipative term, modified sub-equation method, G'/(bG' + G + a)-expansion method, exact solutions
Citation: Hong B (2022) Assorted exact explicit solutions for the generalized Atangana’s fractional BBM–Burgers equation with the dissipative term. Front. Phys. 10:1071200. doi: 10.3389/fphy.2022.1071200
Received: 15 October 2022; Accepted: 26 October 2022;
Published: 25 November 2022.
Edited by:
Fei Yu, Changsha University of Science and Technology, ChinaReviewed by:
Ji-Huan He, Soochow University, ChinaKangsheng Zhao, Fudan University, China
Rongfei Xu, Nanjing Normal University, China
Copyright © 2022 Hong. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Baojian Hong, aGJqQG5qaXQuZWR1LmNu
 Baojian Hong
Baojian Hong