On universal butterfly and antisymmetric magnetoresistances

Butterfly magnetoresistance (BMR) and antisymmetric magnetoresistance (ASMR) are about a butterfly-cross curve and a curve with one peak and one valley when a magnetic field is swept up and down along a fixed direction. Other than the parallelogram-shaped magnetoresistance-curve (MR-curve) often observed in magnetic memory devices, BMR and ASMR are two ubiquitous types of MR-curves observed in diversified magnetic systems, including van der Waals materials, strongly correlated systems, and traditional magnets. Here, we reveal the general principles and the picture behind the BMR and the ASMR that do not depend on the detailed mechanisms of magnetoresistance: 1) The systems exhibit hysteresis loops, common for most magnetic materials with coercivities. 2) The magnetoresistance of the magnetic structures in a large positive magnetic field and in a large negative magnetic field is approximately the same. With the generalized Ohm’s law in magnetic materials, these principles explain why most BMR appears in the longitudinal resistance measurements and is very rare in the Hall resistance measurements. Simple toy models, in which the Landau-Lifshitz-Gilbert equation governs magnetization, are used to demonstrate the principles and explain the appearance and disappearance of BMR in various experiments. Our finding provides a simple picture to understand magnetoresistance-related experiments.

1 Introduction

Magnetoresistance (MR) is an important quantity that is often used to probe and to understand the electronic properties of a condensed matter [1]. Weak field MRs at a low temperature are a standard probe for extracting quantum coherence length and time of metals [2], and high field MRs are a powerful tool for measuring the Fermi surfaces of metals [1]. In magnetic materials with magnetic hysteresis, MR-curves can be classified into several types. One commonly-observed curve in magnetic memory devices is the parallelogram shape as shown in Figure 1. As an example, let us consider one type of memory devices shown in Figure 1B with a magnetic fixed layer, whose magnetization is pinned by either an exchange bias from another antiferromagnetic layer or by its bulky volume, a magnetic free layer, whose magnetization can be changed by an external force such as a magnetic field, and a spacer layer of either metal or insulator separating two magnetic layers. No matter what is the source of resistance and MR in particular, the device has a higher and a lower resistive states, respectively, when two magnetizations are antiparallel or parallel to each other [3–5]. Due to the coercivity of magnetic materials, when a magnetic field parallel to the magnetization of the fixed layer is swept up and down, a magnetic hysteresis loop is formed as the device moves between the two resistive states. This results in a parallelogram MR-curve. Other commonly-observed MR-curves are a butterfly-cross called butterfly magnetoresistance (BMR) of either upward (A) and downward (B) ones [6–9] as shown in Figures 2A,B, and an MR-curve with one peak and one valley, called antisymmetric magnetoresistance (ASMR), as shown in Figures 2C,D [10]. BMR was found in various magnetic materials, including van der Waals layered magnetic materials and strongly correlated materials, as well as many traditional magnetic materials [6–9, 11–35], at both high and low temperatures, in strong and weak magnetic fields, while people observed less common ASMR in topological Hall effect materials [36–39], antiferromagnetic topological insulators [40], magnetic multilayers [41, 42] and FeGeTe heterostructures [10]. The observation of BMR can date back to the 1950s [34, 35]. Although both BMR and ASMR were widely observed, the explanations in the literature, often involving detailed microscopic MR mechanisms, are different for different systems. For layered films such as metallic multilayers [Fe/Cr]_n [Co/Cu]_n, and van der Waals ClI₃ layers [27, 30–32], complicated strong or weak electron scatterings involved magnetizations of adjacent layers were used to explain all kinds of MR-curves. In magnetic nanowires [23], FeO film [11], Co/HfO₂/Pt sandwich structures [18], etc., BMR was attributed to the anisotropic MR effects that depend on the relative current and magnetization orientation. Electron-magnon scattering in systems like Fe₅GeTe van der Waal nanostructures [6], FePt films and nanowires [16, 19], and 2D layers of Ag₂CrO₂ antiferromagnetic films [7], where resistance depends not only on magnetization but also on the applied fields and the temperature, is associated with BMR observation. In traditional magnets like Fe₃O₄ films, the electron scattering, and tunnelling at the interfaces of nanograins [33] or scattering by the magnetization structures induced by fields and anti-phase boundaries [9] were claimed to be responsible to the observed BMR. In many 2D materials, BMR in ρ_xx is believed to be due to the quantum anomalous Hall effect (QAHE) [20, 21]. The transverse BMR is reported in some planar Hall effects [11, 24, 25]. In summary, both BMR and ASMR were attributed to very detailed microscopic interactions in the literature so far. The explanations lead to an impression that microscopic interactions are essential for these universal curves. People did relate the BMR to magnetization reversal and hysteresis. Magnetization reversal undoubtedly occurs in all magnetic materials, but BMR sometimes occurs, and other time does not. A simple universal route leading to their observation is lacking.

FIGURE 1

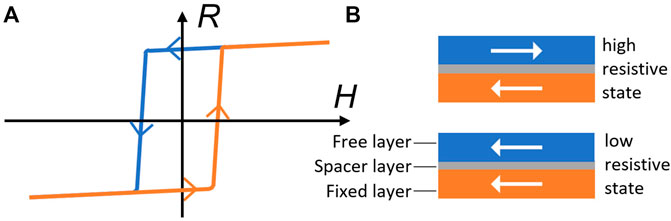
FIGURE 1. (A) Schematics of parallelogram MR-curves when a device moves between a higher resistive state and a lower one in a field sweeping-up and sweeping-down process. (B) Illustration of a memory device with two stable resistive states. The device is in a lower (higher) resistive state when the magnetization of the free-layer is parallel (antiparallel) with that of the fixed layer.

FIGURE 2

FIGURE 2. Illustration of butterfly magnetoresistance (BMR) and antisymmetric magnetoresistance (ASMR) curves. The orange and blue curves indicate resistance in the sweeping-up and sweeping-down processes, respectively. (A,B) Upward (A) and downward (B) butterfly MR-curves that display a butterfly cross. (C,D) Two possible ASMR-curves that have the feature of one peak and one valley.

Here we would like to ask whether the universal BMR and ASMR have a simple general route independent of the origins of MR. This is a sensible question because most MR-curves of all magnetic materials with magnetic hysteresis, if not all, can be grouped into one of the above three types or their variations: Parallelogram-shape, BMR, and ASMR. Since the parallelogram-shaped MR-curves have a simple picture mentioned above, there is no reason to believe that BMR and ASMR would be different.

2 The physics of BMR and ASMR

The resistance is a state function. For a magnetic system of a given magnetization distribution (magnetic/spin structure) and given external conditions such as the temperature, strains, external magnetic fields, etc., the resistance is fixed. Under a given magnetic field, a system may have one or more than one possible stable/metastable magnetic structure. If a system has only one stable magnetic structure, then the MR curve, no matter how complicated it might be, has no hysteresis. Otherwise, the MR curve has hysteresis when an external magnetic field is swept up and down in a fixed direction. Of course, hysteresis is a general feature of magnetic materials due to its coercivity.

An MR curve reflects the evolution path of the magnetic structure of a system. Whether an MR-curve is a parallelogram, a BMR, or an ASMR depends on whether the resistance of magnetic structures in a large positive magnetic field and in a large negative magnetic field are similar or different. When the resistances of large positive and negative magnetic fields are not too different, an MR-curve will be either a BMR or an ASMR, independent of the specific origin of the resistance. If the MR passes through two higher (lower) resistance states in sweeping-up and sweeping-down processes, the MR-curve displays two crossed peaks (valleys) and results in an upward (downward) BMR, as shown in Figures 2A,B. However, if the MR passes through one higher and one lower resistance state in sweeping-up and sweeping-down processes, respectively, the MR-curve displays one peak and one valley and becomes ASMR, as shown in Figures 2C,D. This simple picture is behind various magnetoresistance-related experiments on microscopic mechanisms although MR-curves can have different shapes from system to system. The coercivity field largely determines their locations of MR-loops while microscopic details modify their shapes, not their overall features.

Furthermore, with the generalized Ohm’s law in magnetic material, these principles can explain why most BMRs occur in longitudinal resistance measurements and are very rare in Hall resistance measurements. For a given magnetic material, its resistance, in general, depends on the magnetization when all other material parameters and their environment are fixed. Without losing any generality, let us define the current direction along the x-axis and transverse voltage measurement along the y-direction. The longitudinal and transverse resistance can be expressed as $R_{xx}=R_1+A_1{M}_x^2$ and R_xy = R₁M_z + A₁M_xM_y, respectively according to the generalized Ohm’s law in amorphous or polycrystalline magnetic materials [43–45]. R₁ and A₁ are material parameters whose values depends on microscopic interactions. They describe the anomalous Hall effect and the usual anisotropic MR (as well as the planar Hall effect), respectively. The above resistances are general for homogeneous systems and independent of electron scattering mechanisms that give rise to the resistance. For inhomogeneous systems, the generalized Ohm’s law should refer to the resistivity, and magnetization and coefficients in resistances formula above should be properly averaged. When a magnetic field H is swept up and down along a direction not exactly perpendicular to the magnetic easy-axis, the stable magnetic structures in a large positive magnetic field and a large negative magnetic field are two opposite magnetizations of (M_x0, M_y0, M_z0) and (−M_x0, − M_y0, − M_z0). The system transforms from one state into the other through different paths in sweeping-up and sweeping-down processes. Since R_xx is a function of $M_x^2$, no matter what M_x0 is, the resistances, $R_1+A_1{M}_{x0}^2$, in the two extreme states are the same. When M_x(H) moves between M_x0 and − M_x0, R_xx forms peaks and valleys and results in a BMR or an ASMR. Unlike R_xx which depends only on $M_x^2(H)$, R_xy depends on M_x(H)M_y(H) and M_z(H) at the same time. R_xy at the two extreme fields takes different values of 2R₁M_z0. This explains why most BMR appears in longitudinal resistance measurements but is rare in R_xy-measurements. However, when the magnetic field is in the xy-plane, i.e., the plane of applied current and voltage measurement. M_z0 is zero such that the two opposite stable magnetization states have approximately the same resistances. R_xy can have peak and valley, resulting in either a BMR or an ASMR. This is why these two phenomena can be observed in some planar Hall measurements [11, 24, 25].

3 Demonstration of principles with toy models

Whether a BMR or an ASMR appears depends only on whether the evolution of the magnetization has a hysteresis, and whether the resistances in two extreme states in large positive and negative magnetic fields are similar. In experiments, various factors can affect the appearance of BMRs, including anisotropy, thickness, temperature, etc. [6, 7, 9, 18, 27]. A BMR appears usually in a system with a strong anisotropy and at a low temperature. It appears sometimes in a thicker sample [9] and sometimes in a thinner one [6]. People knew that all these factors somehow affect the magnetization reversal through which system changes facilitate or prohibit the presence of a BMR, but a universal simple picture showing how and why a BMR occurs and does not occur in a specific system is lacking. Here, with the simple principles mentioned above, we use toy models to show these factors actually influence BMRs by changing the easy-axis and hysteresis, which are essential for BMRs and ASMRs.

Our toy model is for a ferromagnetic sample whose magnetic energy is

$\mathcal{E}={\int }_V\left\{A|\nabla \mathbf{m}{|}^2-K_{\text{u}}{m}_z^2-{\mu }_0{M}_{\text{s}}\left[\mathbf{H}+{\mathbf{H}}_{\text{d}}\right]\cdot \mathbf{m}\right\}\mathrm{d}{\mathbf{x}}^3,(1)$

where m, A, K_u, μ₀, M_s, H and H_d are the magnetization unit vector, the Heisenberg exchange stiffness, the perpendicular magneto-crystalline anisotropy, the vacuum permeability, the saturation magnetization, the external magnetic field, and the dipolar field, respectively. If not stated otherwise, the sample size is 100 × 20 × 2 nm³, and model parameters are A = 3 pJ/m, M_s = 0.86 MA/m, and K_u = 0.3 MJ/m³, around typical values of common magnetic materials. We also consider a weak disorder to mimic a realistic situation. Random granular sample of average 10 nm grains are generated in films by Voronoi tessellation. Anisotropies of grains vary randomly by 10% around its mean value. The non-linear Landau-Lifshitz-Gilbert (LLG) equation governs the spin dynamics of the model,

$\frac{\partial \mathbf{m}}{\partial t}=-\gamma \mathbf{m}\times {\mathbf{H}}_{\text{eff}}+\alpha \mathbf{m}\times \frac{\partial \mathbf{m}}{\partial t},(2)$

where γ, α and H_eff are respectively the gyromagnetic ratio, Gilbert damping constant, and the effective field. ${\mathbf{H}}_{\text{eff}}(\mathbf{x})=\frac{2A}{{\mu }_0{M}_{\text{s}}}{\nabla }^2\mathbf{m}(\mathbf{x})+\frac{2K_{\text{u}}}{{\mu }_0{M}_{\text{s}}}[\mathbf{m}(\mathbf{x})\cdot \mathbf{u}]\mathbf{u}+\mathbf{H}+{\mathbf{H}}_{\text{d}}$ includes the exchange field, the magneto-crystalline anisotropy field, the external magnetic field H, and the dipolar field H_d. Equation 2 is numerically solved by Mumax3 [46]. A large α = 1 is used to speed up the search for static solutions at given fields. The value of α shall not affect the principles of BMR and ASMR. The unit cell in the simulations is a cube of side 2 nm. The selection of the toy model is not exclusive. Other models could also be used to demonstrate the principles (see discussion). We use a dimensionless quantity ζ to mimic MR. ζ is a function of m_x, m_y, and m_z ($\zeta =m_x^2$ for example). Coefficients related to detail mechanisms are neglected in this simple model. The MR ratio is just its normalization of MR = (ζ_max − ζ)/ζ_max. ζ can well capture the shapes of BMR, ASMR, and parallelogram-shaped MR-curves. To consider the contributions from all local magnetization-dependent resistivity, we average ζ(m) over the whole sample,

$\zeta =\frac{1}{V}{\int }_V\zeta \left(\mathbf{m}\right)\mathrm{d}V.(3)$

where V is the total sample volume [23, 29, 47].

It is known that the magnetization dynamical path relies on the angle between the applied field and the easy-axis [48]. Hysteresis loops appear only when the field is not perpendicular to the easy-axis. Otherwise, the system has only one stable structure, and magnetization is reversible such that no BMRs and ASMRs are possible. Since a field was swept in all directions in all kinds of experiments and the easy-axis is sensitive to many factors such as thickness, temperature, etc., it is not surprising to see the appearance and disappearance of a BMR in similar measurements on similar samples, but with different details. To mimic the phenomenon, we consider a sample of K_u = 0 for simplicity. The demagnetization factors of $\widehat{x}$, $\widehat{y}$, and $\widehat{z}$ are N_x = 0.86, N_y = 0.12, and N_z = 0.02, and easy-axis aligns along $\widehat{x}$. We sweep the field in different directions in the xz-plane with an angle Θ_H to $\widehat{x}$. MH-curves for Θ_H = 0°, 60°, and 90° are shown in Figure 3A. For Θ_H not equal to 90°, an MH-curve displays hysteresis loops because of the easy x-axis. For Θ_H = 90°, or applied field perpendicular to its easy-axis, there is only one stable state at each given field such that the MH-curve is reversible and there is no hysteresis loop. The appearance of the BMR is closely related to that of hysteresis. We consider a resistance of $\zeta (\mathbf{m})=m_x^2$ for example, which can represent the anisotropic MR effect with a current along $\widehat{x}$. The obtained curves are shown in Figure 3D. When Θ_H ≠ 90°, this model satisfies the principle that has the same resistance states at both large positive and negative fields, and the MR-curve is BMR. As Θ_H approaches 90°, it degenerates from BMR to a simple curve. The vanish of the BMR is due to the disappearance of hysteresis, regardless of specific resistance mechanisms. This provides a new simple picture that can explain BMR’s appearance and disappearance when the magnetic field changes its direction in the experiments and simulations [11, 12, 23, 29].

FIGURE 3

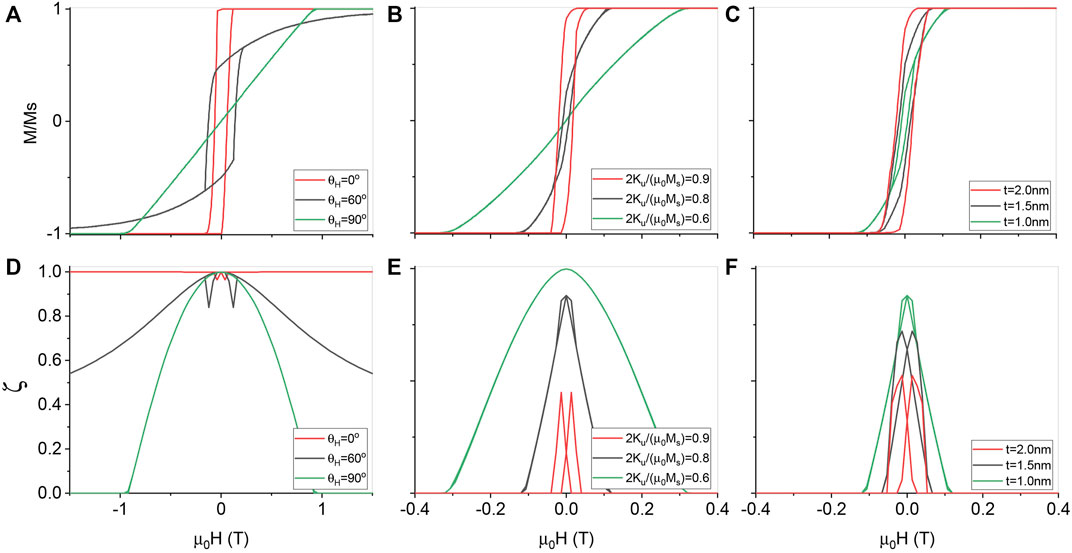
FIGURE 3. MH-curves and MR-curves for various field directions, crystalline anisotropy, and sample thickness. (A) mz vs. H along various directions. MH-curves display hysteresis when the field is not perpendicular to the easy-axis $(\widehat{x})$. (B) mz vs H along $\widehat{z}$ for various crystalline anisotropies. As Ku decreases, hysteresis disappears. (C) mz vs H along $\widehat{z}$ for various sample thicknesses and for a fixed crystalline anisotropy. Hysteresis becomes fatter as thickness grows. (D–F) Corresponding MR-curves of (A–C) with the resistance of $\zeta (\mathbf{m})=m_x^2$. A BMR appears only when a hysteresis exists.

Crystalline anisotropy varies from sample to sample and leads to the appearance and the disappearance of the BMR and the ASMR. Perpendicular magnetic anisotropy can both increase and decrease [49] with film thickness. For materials whose perpendicular anisotropy decreases or even vanishes as sample thickness increases, increase of thickness may result in vanishing BMR in the perpendicular field-sweeping. For thin films of perpendicular crystalline anisotropy that is insensitive to film thickness, the opposite behaviour can occur: Easy-axis changes from perpendicular to in-plane directions as sample thickness decreases. With the toy model, our theory can explain disappearance of a BMR when a sample thickness both increases [6, 27] or decreases. Figure 3B is the MH-curves for the field along the $\widehat{z}$ for K_u = 0.27 MJ/m³ $[2K_{\text{u}}/({\mu }_0{M}_{\text{s}}^2)=0.6]$, 0.36 MJ/m³ [$2K_{\text{u}}/({\mu }_0{M}_{\text{s}}^2)=0.8$], and 0.40 MJ/m³ $[2K_{\text{u}}/({\mu }_0{M}_{\text{s}}^2)=0.9]$ with other parameters unchanged. When K_u is significantly smaller than $1/2{\mu }_0{M}_s^2$, anisotropy is dominated by the demagnetization, and the easy-axis lies in the plane. There is no hysteresis since the field is perpendicular to the easy-axis. MR-curves, $\zeta (\mathbf{m})=m_x^2$ is shown in Figure 3E. The BMR and hysteresis disappear simultaneously. For another set of samples of 1nm, 1.5nm and 2 nm thick whose K_u = 0.36, MJ/m³ $[2K_{\text{u}}/({\mu }_0{M}_{\text{s}}^2)=0.8]$, MH-curves for field-sweeping along $\widehat{z}$ are shown in Figure 3C. Figure 3F is the MR-curves of $\zeta (\mathbf{m})=m_x^2$. With the increase of thickness, the hysteresis loop becomes fatter and the BMR is more pronounced because the perpendicular anisotropy is enhanced. The sharper BMR in a thicker film is previously attributed to the increase of anti-phase domain size [9], very different from our simple universal picture.

The change of crystalline anisotropy can come from other sources. For example, anisotropy K_u of some materials decreases with a power of M(T) [50], which is sensitive to the temperature near the Curie temperature. The change of K_u can be substantial. For example, the magnetic anisotropy of 1.2 nm CoFeB film could drop by 50% as the temperature increases from 300 K to 400 K [51]. As the temperature increases, perpendicular magnetic anisotropy gets smaller, and the easy-axis changes from out-of-plane to in-plane. Hysteresis, as well as BMR, thus no longer exists. In contrast to our universal picture of the BMR, the disappearance of the BMR at higher temperatures was attributed to the variation of electron scattering, which, in turn, was attributed to the vanish of partially disordered states [6, 7, 9, 18].

The resistance is a state function. BMR or ASMR curves are the manifestations of magnetic hysteresis. BMR and ASMR shapes and loop positions depend on resistance mechanisms and detailed magnetic properties such as coercivity fields. To further demonstrate this point, we use various configurations and resistance mechanisms to generate all kinds of BMR’s and ASMR’s with our toy models. First, we consider the in-plane fields. A smaller K_u = 0.3 MJ/m³ is used such that the easy-axis aligns with the $\widehat{x}$. We sweep fields along the direction 0.1° from the $\widehat{x}$ in the xz-plane. The system displays a hysteresis in its MH-curve as shown in Figure 4A with a coercivity field around 60 mT. If we apply a current along the x-direction and consider the resistance of $\zeta (\mathbf{m})=m_x^2$, the MR goes down and up. This results in a two-valley butterfly cross illustrated in Figure 4B. BMR valleys appear around coercivity fields. If we consider the resistance of ζ(m) = m_xm_y, the form of the planar Hall resistance. A transverse BMR can be obtained as shown in Figure 4C that qualitatively agrees with the in-plane sweeping experiment [11]. If we consider resistance in the form of ζ(m) = m_z, similar to the anomalous Hall effect, a transverse ASMR is obtained, as shown in Figure 4D. Although the curve shapes are different, peaks and valleys appear all around coercivity fields.

FIGURE 4

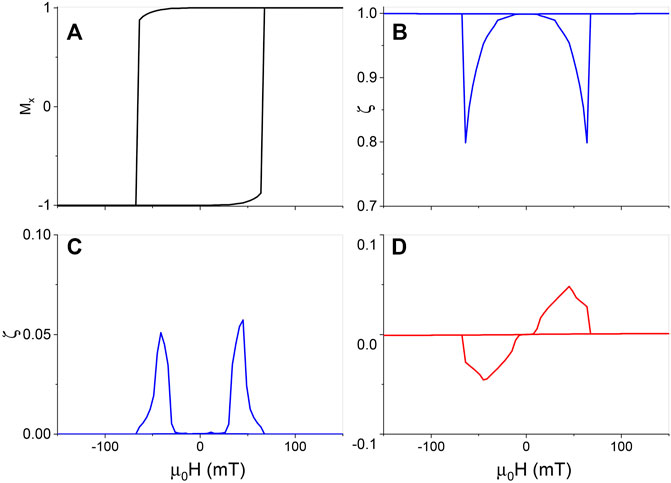
FIGURE 4. A BMR and an ASMR model for field-sweeping in the plane. The fields are swept along the direction that is 0.1° tilted from $\widehat{x}$ to $\widehat{z}$, and the current is along x-direction. (A) Mx as a function of (H) A hysteresis appears with a coercivity field around 60mT. (B) A downward BMR is obtained in the anisotropic magnetoresistance with two high resistance states at high fields. (C) An upward BMR is observed in the planar Hall resistance with two low resistance states at large positive and negative fields. (D) The ASMR curve is obtained for the quantum anomalous Hall systems due to Mz components with opposite signs in sweeping-up and sweeping-down processes, respectively. The resistance vanishes at large fields. Peaks and valleys are around the coercivity field.

To demonstrate the same BMR principles in the field sweeping along the perpendicular direction of a film, a larger K_u = 4.8 MJ/m³ is used in order to maintain $\widehat{z}$ as the easy-axis. We sweep fields along the direction that is 0.1° tilted from $\widehat{z}$ in the xz-plane. An MH-curve shows hysteresis in sweeping processes as shown in Figure 5A with a coercivity field around 130mT, which is sharper than Figure 4A. Let’s still consider the current aligning along x-direction and the anisotropic magnetoresistance of $\zeta (\mathbf{m})=m_x^2$. The resistance goes up and down, resulting in an upward BMR illustrated in Figure 5B. If the current is perpendicular to the film, the magnetoresistance becomes $\zeta (\mathbf{m})=m_z^2$ the MR goes down and up, resulting in two valleys in the MR-curves, i.e., a downward BMR shown in Figure 5C, which qualitatively agrees with experiments [18]. In this configuration, peaks and valleys appear at the coercivity fields, which differ from those of Figure 4. One can also reproduce BMR with other microscopic mechanisms, such as magnon-electron scattering, where the external fields tune the magnetization-dependent resistance [7, 16, 19]. If the resistance is linear in the field, i.e. ζ(m) = m_zμ₀H, a BMR curve similar to that in Ref. [16, 19] can be reproduced as shown in Figure 5D. If we consider the MR in the form of $\zeta (\mathbf{m})=-m_z\sqrt{\mathrm{\Delta }/(\mathrm{\Delta }+2)}$, where Δ ∝ H − H_a measures the difference between the applied field and the anisotropy field, a BMR of Figure 5E can be obtained, where we choose Δ = μ₀(H − H_a) as a demonstration. This result qualitatively agrees with experiments [7].

FIGURE 5

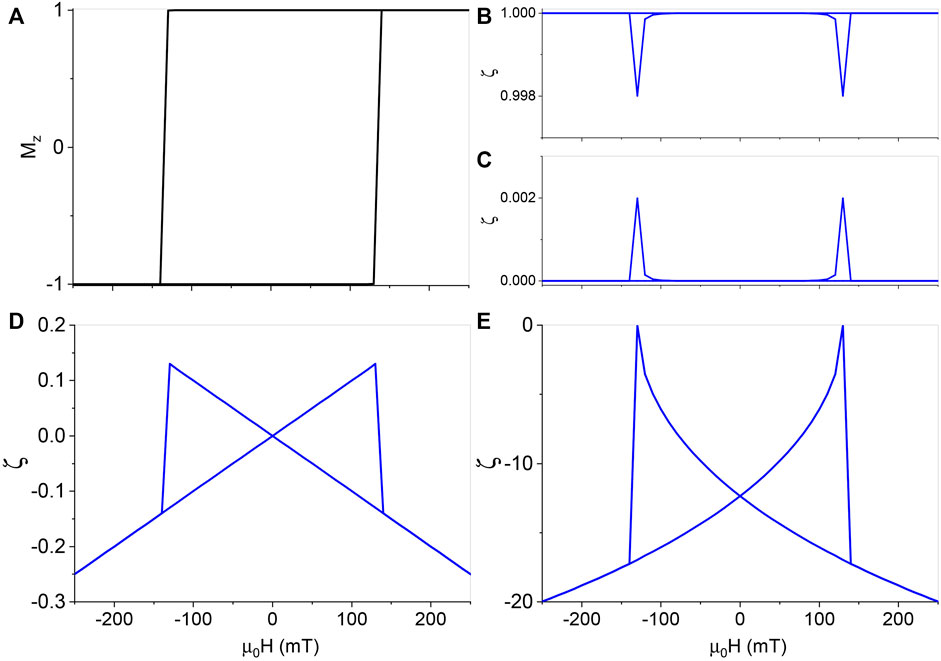
FIGURE 5. A BMR model for a field along 0.1° from $\widehat{z}$ in the xz−plane. (A) A square-like hysteresis loop in M_zH-curve with a coercivity field around 130mT. (B–C) Downward (B) and upward (C) BMR are obtained for the anisotropic magnetoresistance. The current is along the x and z direction, respectively. (D–E) The BMR from two different formulas for scatter-induced resistance discussed in the main text. They show minor differences in curvatures. Peaks and valleys are around the coercivity fields, which is different from that of Figure 4.

4 Discussions and conclusion

We used toy models governed by the LLG equation to demonstrate BMR and ASMR in various systems, because it is compatible with experiments involving incoherent magnetization reversal such as those in Refs. [16, 19, 23]. Other models could also be used in different scenarios. For example, BMR has also been observed in systems described by coherent-rotational models [52, 53], and other special reversal processes such as domain wall nucleation and motion described by the Kondorsky model [23]. Between two states at large positive and negative fields, there is a hysteresis in these systems, also consistent with the general picture here. If one uses the similar procedure as that in the third section, BMR or ASMR can also appear as long as the resistances is a function of magnetization, and the resistance of two states at high fields are not too different, see Supplementary Information for details.

The rules of BMR and ASMR revealed by the toy models are general. For example, in a sample of two free layers, in contrast to a memory cell where only one is free, as sketched in Figure 1B, the system has a lower resistive state of two magnetizations parallel to each other and a higher resistive state of two antiparallel magnetization. When the magnetic field is swept along the z-direction, the system moves between two stable low resistive states of magnetizations along $\widehat{z}$ and $-\widehat{z}$. The magnetization of two layers is no longer parallel to each other during the magnetization reversals, and the resistance forms two peaks and an upward BMR [27, 30–32] as shown in Figure 6. We also consider a system with the anomalous quantum Hall effect. Assume that the magnetic field is swept along z-direction, and the system switches between the ferromagnetic states of m_z = 1 and m_z = −1, both of which have R_xx equal to 0. However, in sweeping processes, the presence of magnetic structure leads to a finite R_xx, resulting in two peaks and an upward BMR [20, 21]. Fe₃O₄ films have the same resistance states at both high positive and high negative fields that decrease with a field strength in the same slope [9]. Consequently, it displays a BMR. In some chiral magnetic materials, the topological Hall resistance is related to the topological charge. The system reverses between the states of m_z = 1 and m_z = −1, which have zero topological charge and zero topological Hall resistances. In the sweeping-up and sweeping-down process, topological charges with opposite signs are generated in the system that produces one peak and one valley on the MR-curve manifesting an ASMR [36–38].

FIGURE 6

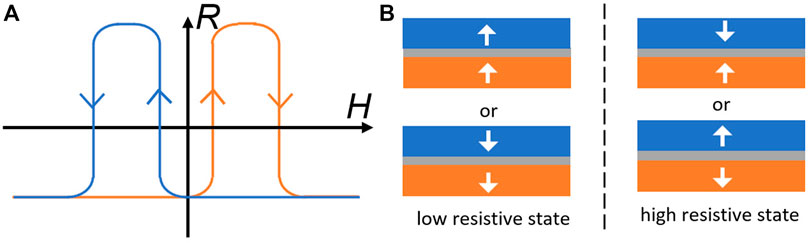
FIGURE 6. (A) Schematics of BMR in a bilayer. The system moves between two similar low resistive states by passing through a high resistive state during the field sweeping. (B) Illustration of resistive states. The device is in a higher (lower) resistive state when the magnetization of two layers are parallel (antiparallel) with each other.

It may be important to emphasize that the exact shapes and locations in a BMR and ASMR are not our concerns here. The hysteresis loop of BMR and ASMR could be very irregular in different systems. Their general features do not rely on any symmetries, as shown in the toy models of Figures 4, 5. When the resistance mechanism has inversion symmetry, the system is more likely to display ASMR as the toy model shown in Figure 4D. In general, any curve can always be decomposed into symmetric and antisymmetric components, as was usually done in experiments. Nevertheless, this kind of decomposition is not meaningful unless one can attribute each of them to a specific source. This is, of course, an interesting question but not the aim of this paper.

ASMR is less common than BMR in both R_xx and R_xy. In many experiments, the magnetic field is swept perpendicular to the currents. For the former, M_x(H) reverses between $\pm {\{M_x\}}_{\text{max}}$. These two opposite magnetizations have the largest R_xx, so in sweeping-up and sweeping-down processes, R_xx can only decrease first and then increase and form two valleys and a downward BMR. For the latter, M_x(H) changes from 0 to 0 through a path. The initial and final magnetizations have the lowest R_xx. So whether in the sweeping-up or sweeping-down process, R_xx can only rise and then fall, which is manifested as an upward BMR. For magnetic materials that obey the generalized Ohm’s law, ASMR that requires one peak and one valley is unlikely to occur in R_xx for either of the two common experimental settings.

In conclusion, similar to parallelogram MR, BMR and ASMR are universal MR behavior independent of the resistance origins. They appear as long as a system exhibits a hysteresis loop under sweeping-up and sweeping-down of a magnetic field, and its MR is approximately the same when the magnetization direction is reversed. From the generalized Ohm’s law in magnetic materials, BMR should be very common in longitudinal resistance and could also occur in transverse resistance when the magnetic field is in the plane of applied current and voltage measurement. The coercivity fields and microscopic details are encoded in the positions and shapes of a BMR and an ASMR. Although there is no inconsistency with the universal BMR/ASMR theory presented here, the explanations of many BMR and ASMR in literature [6, 7, 9–11, 18, 27, 29–32] are not the same as ours.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

XW planned the project. XW and HW wrote the manuscript. HW performed numerical simulations and prepared the figures. ZG and TM contributed to the result analysis and manuscript revision.

Funding

This work is supported by the Ministry of Science and Technology through grant 2020YFA0309600, the NSFC Grants (No. 12074301, 11974296), and Hong Kong RGC Grants (No. 16300522, 16302321, 16301518, and 16301619).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2022.1068605/full#supplementary-material

References

1. Grosso G, Parravicini GP. Solid state physics. Singapore): Elsevier Pte Ltd. (2000).

Google Scholar

2. Huckestein B. Scaling theory of the integer quantum hall effect. Rev Mod Phys (1995) 67:357–96. doi:10.1103/RevModPhys.67.357

CrossRef Full Text | Google Scholar

3. Kundt A. On the hall effect in ferromagnetic materials. Ann Phys (1893) 49:257–71. doi:10.1002/andp.18932850603

CrossRef Full Text | Google Scholar

4. Smith AW, Sears RW. The hall effect in permalloy. Phys Rev (1929) 34:1466–73. doi:10.1103/PhysRev.34.1466

CrossRef Full Text | Google Scholar

5. Pugh EM, Lippert TW. Hall e.m.f. and intensity of magnetization. Phys Rev (1932) 42:709–13. doi:10.1103/PhysRev.42.709

CrossRef Full Text | Google Scholar

6. Ohta T, Tokuda M, Iwakiri S, Sakai K, Driesen B, Okada Y, et al. Butterfly-shaped magnetoresistance in van der waals ferromagnet Fe₅GeTe₂. AIP Adv (2021) 11:025014. doi:10.1063/9.0000067

CrossRef Full Text | Google Scholar

7. Taniguchi H, Watanabe M, Tokuda M, Suzuki S, Imada E, Ibe T, et al. Butterfly-shaped magnetoresistance in triangular-lattice antiferromagnet ag2cro2. Sci Rep (2020) 10:2525. doi:10.1038/s41598-020-59578-z

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Mukherjee K, Das SD, Mohapatra N, Iyer KK, Sampathkumaran EV. Anomalous butterfly-shaped magnetoresistance loops in the alloy Tb₄LuSi₃. Phys Rev B (2010) 81:184434. doi:10.1103/PhysRevB.81.184434

CrossRef Full Text | Google Scholar

9. Li P, Zhang LT, Mi WB, Jiang EY, Bai HL. Origin of the butterfly-shaped magnetoresistance in reactive sputtered epitaxial fe3o4 films. J Appl Phys (2009) 106:033908. doi:10.1063/1.3187537

CrossRef Full Text | Google Scholar

10. Hu G, Zhu Y, Xiang J, Yang TY, Huang M, Wang Z, et al. Antisymmetric magnetoresistance in a van der waals antiferromagnetic/ferromagnetic layered MnPS₃/Fe₃GeTe₂ stacking heterostructure. ACS Nano (2020) 14:12037–44. doi:10.1021/acsnano.0c05252

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Stankiewicz J, Jiménez-Villacorta F, Prieto C. Magnetotransport properties of oxidized iron thin films. Phys Rev B (2006) 73:014429. doi:10.1103/PhysRevB.73.014429

CrossRef Full Text | Google Scholar

12. Zhou L, Song H, Liu K, Luan Z, Wang P, Sun L, et al. Observation of spin-orbit magnetoresistance in metallic thin films on magnetic insulators. Sci Adv (2018) 4:eaao3318. eaao3318. doi:10.1126/sciadv.aao3318

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Gilbert DA, Maranville BB, Balk AL, Kirby BJ, Fischer P, Pierce DT, et al. Realization of ground-state artificial skyrmion lattices at room temperature. Nat Commun (2015) 6:8462. doi:10.1038/ncomms9462

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Chen W, Qian L, Xiao G. Resistance of domain-wall states in half-metallic CrO₂. Phys Rev B (2018) 98:174402. doi:10.1103/PhysRevB.98.174402

CrossRef Full Text | Google Scholar

15. Ennen I, Kappe D, Rempel T, Glenske C, Hütten A. Giant magnetoresistance: Basic concepts, microstructure, magnetic interactions and applications. Sensors (2016) 16:904. doi:10.3390/s16060904

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Mihai AP, Attané JP, Marty A, Warin P, Samson Y. Electron-magnon diffusion and magnetization reversal detection inFePtthin films. Phys Rev B (2008) 77:060401. doi:10.1103/PhysRevB.77.060401

CrossRef Full Text | Google Scholar

17. Liu C, Wang Y, Yang M, Mao J, Li H, Li Y, et al. Magnetic-field-induced robust zero hall plateau state in MnBi₂Te₄ chern insulator. Nat Commun (2021) 12:4647. doi:10.1038/s41467-021-25002-x

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Li L, Liu Y, Teng J, Long S, Guo Q, Zhang M, et al. Anisotropic magnetoresistance of nano-conductive filament in co/hfo2/pt resistive switching memory. Nanoscale Res Lett (2017) 12:210. doi:10.1186/s11671-017-1983-2

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Nguyen VD, Vila L, Laczkowski P, Marty A, Faivre T, Attané JP. Detection of domain-wall position and magnetization reversal in nanostructures using the magnon contribution to the resistivity. Phys Rev Lett (2011) 107:136605. doi:10.1103/PhysRevLett.107.136605

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Deng Y, Yu Y, Shi MZ, Guo Z, Xu Z, Wang J, et al. Quantum anomalous hall effect in intrinsic magnetic topological insulator mnbi₂te₄ Science (2020) 367:895–900. doi:10.1126/science.aax8156

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Chang CZ, Zhang J, Feng X, Shen J, Zhang Z, Guo M, et al. Experimental observation of the quantum anomalous hall effect in a magnetic topological insulator. Science (2013) 340:167–70. doi:10.1126/science.1234414

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Huang B, McGuire MA, May AF, Xiao D, Jarillo-Herrero P, Xu X. Emergent phenomena and proximity effects in two-dimensional magnets and heterostructures. Nat Mater (2020) 19:1276–89. doi:10.1038/s41563-020-0791-8

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Lu J, Wang X. Magnetization reversal of single domain permalloy nanowires. J Magnetism Magn Mater (2009) 321:2916–9. doi:10.1016/j.jmmm.2009.04.057

CrossRef Full Text | Google Scholar

24. Li X, Collignon C, Xu L, Zuo H, Cavanna A, Gennser U, et al. Chiral domain walls of mn3sn and their memory. Nat Commun (2019) 10:3021. doi:10.1038/s41467-019-10815-8

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Tang HX, Kawakami RK, Awschalom DD, Roukes ML. Giant planar hall effect in epitaxial (Ga,Mn)As devices. Phys Rev Lett (2003) 90:107201. doi:10.1103/PhysRevLett.90.107201

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Miao YQ, Guo JJ, Luo ZY, Zhong MZ, Li B, Wang XG, et al. Anisotropic magnetoresistance effect of intercalated ferromagnet FeTa₃S₆. Front Phys (2022) 10. doi:10.3389/fphy.2022.847402

CrossRef Full Text | Google Scholar

27. Klein DR, MacNeill D, Lado JL, Soriano D, Navarro-Moratalla E, Watanabe K, et al. Probing magnetism in 2d van der waals crystalline insulators via electron tunneling. Science (2018) 360:1218–22. doi:10.1126/science.aar3617

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Zhang Z, Feng X, Guo M, Li K, Zhang J, Ou Y, et al. Electrically tuned magnetic order and magnetoresistance in a topological insulator. Nat Commun (2014) 5:4915. doi:10.1038/ncomms5915

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Wegrowe JE, Kelly D, Franck A, Gilbert SE, Ansermet JP. Magnetoresistance of ferromagnetic nanowires. Phys Rev Lett (1999) 82:3681–4. doi:10.1103/PhysRevLett.82.3681

CrossRef Full Text | Google Scholar

30. Bass J, Pratt W. Current-perpendicular (cpp) magnetoresistance in magnetic metallic multilayers. J Magnetism Magn Mater (1999) 200:274–89. doi:10.1016/S0304-8853(99)00316-9

CrossRef Full Text | Google Scholar

31. Miyazaki T, Tezuka N. Giant magnetic tunneling effect in Fe/Al₂O₃/Fe junction. J Magnetism Magn Mater (1995) 139:L231–4. doi:10.1016/0304-8853(95)90001-2

CrossRef Full Text | Google Scholar

32. Binasch G, Grünberg P, Saurenbach F, Zinn W. Enhanced magnetoresistance in layered magnetic structures with antiferromagnetic interlayer exchange. Phys Rev B (1989) 39:4828–30. doi:10.1103/PhysRevB.39.4828

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Lu ZL, Xu MX, Zou WQ, Wang S, Liu XC, Lin YB, et al. Large low field magnetoresistance in ultrathin nanocrystalline magnetite Fe₃O₄ films at room temperature. Appl Phys Lett (2007) 91:102508. doi:10.1063/1.2783191

CrossRef Full Text | Google Scholar

34. Hirsch A. Influence of a magnetic field on the electrical resistance of thin ferromagnetic layers at low temperatures. Physica (1959) 25:581–9. doi:10.1016/s0031-8914(59)96020-3

CrossRef Full Text | Google Scholar

35. Tatsumoto E, Kuwahara K, Goto M. Magnetoresistance effect in the magnetization reversal of permalloy films. J Phys Soc Jpn (1960) 15:1703. doi:10.1143/jpsj.15.1703

CrossRef Full Text | Google Scholar

36. Wang L, Feng Q, Kim Y, Kim R, Lee KH, Pollard SD, et al. Ferroelectrically tunable magnetic skyrmions in ultrathin oxide heterostructures. Nat Mater (2018) 17:1087–94. doi:10.1038/s41563-018-0204-4

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Zhang X, Ambhire SC, Lu Q, Niu W, Cook J, Jiang JS, et al. Giant topological hall effect in van der waals heterostructures of CrTe₂/Bi₂Te₃. ACS Nano (2021) 15:15710–9. doi:10.1021/acsnano.1c05519

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Qin Q, Liu L, Lin W, Shu X, Xie Q, Lim Z, et al. Emergence of topological hall effect in a srruo3 single layer. Adv Mater (2019) 31:1807008. doi:10.1002/adma.201807008

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Niu W, Cao Z, Wang Y, Wu Z, Zhang X, Han W, et al. Antisymmetric magnetoresistance in Fe3GeTe2 nanodevices of inhomogeneous thickness. Phys Rev B (2021) 104:125429. doi:10.1103/PhysRevB.104.125429

CrossRef Full Text | Google Scholar

40. He QL, Yin G, Yu L, Grutter AJ, Pan L, Chen CZ, et al. Topological transitions induced by antiferromagnetism in a thin-film topological insulator. Phys Rev Lett (2018) 121:096802. doi:10.1103/PhysRevLett.121.096802

PubMed Abstract | CrossRef Full Text | Google Scholar

41. Cheng XM, Urazhdin S, Tchernyshyov O, Chien CL, Nikitenko VI, Shapiro AJ, et al. Antisymmetric magnetoresistance in magnetic multilayers with perpendicular anisotropy. Phys Rev Lett (2005) 94:017203. doi:10.1103/PhysRevLett.94.017203

PubMed Abstract | CrossRef Full Text | Google Scholar

42. Lin W. Magnetization reversal, and generation and detection of pure spin-current. Nanjing, China: Ph.D. thesis (2007).

Google Scholar

43. Zhang Y, Wang XS, Yuan HY, Kang SS, Zhang HW, Wang XR. Dynamic magnetic susceptibility and electrical detection of ferromagnetic resonance. J Phys : Condens Matter (2017) 29:095806. doi:10.1088/1361-648x/aa547e

PubMed Abstract | CrossRef Full Text | Google Scholar

44. Zhang Y, Wang XR, Zhang HW. Extraordinary galvanomagnetic effects in polycrystalline magnetic films. Europhysics Lett (2016) 113:47003. doi:10.1209/0295-5075/113/47003

CrossRef Full Text | Google Scholar

45. Wang XR. A theory for anisotropic magnetoresistance in materials with two vector order parameters. Chin Phys Lett (2022) 39:027301. doi:10.1088/0256-307X/39/2/027301

CrossRef Full Text | Google Scholar

46. Vansteenkiste A, Leliaert J, Dvornik M, Helsen M, Garcia-Sanchez F, Van Waeyenberge B. The design and verification of Mumax3. AIP Adv (2014) 4:107133. doi:10.1063/1.4899186

CrossRef Full Text | Google Scholar

47. Chung TY, Hsu SY. Magnetization reversal in single domain permalloy wires probed by magnetotransport. J Appl Phys (2008) 103:07C506. doi:10.1063/1.2834709

CrossRef Full Text | Google Scholar

48. Sun ZZ, Wang XR. Fast magnetization switching of stoner particles: A nonlinear dynamics picture. Phys Rev B (2005) 71:174430. doi:10.1103/PhysRevB.71.174430

CrossRef Full Text | Google Scholar

49. Carcia PF, Meinhaldt AD, Suna A. Perpendicular magnetic anisotropy in Pd/Co thin film layered structures. Appl Phys Lett (1985) 47:178–80. doi:10.1063/1.96254

CrossRef Full Text | Google Scholar

50. Schlickeiser F, Ritzmann U, Hinzke D, Nowak U. Role of entropy in domain wall motion in thermal gradients. Phys Rev Lett (2014) 113:097201. doi:10.1103/PhysRevLett.113.097201

PubMed Abstract | CrossRef Full Text | Google Scholar

51. Lee KM, Choi JW, Sok J, Min BC. Temperature dependence of the interfacial magnetic anisotropy in W/CoFeB/MgO. AIP Adv (2017) 7:065107. doi:10.1063/1.4985720

CrossRef Full Text | Google Scholar

52. Zhao G, Wang X, Feng Y, Huang C. Coherent rotation and effective anisotropy. IEEE Trans Magn (2007) 43:2908–10. doi:10.1109/tmag.2007.893629

CrossRef Full Text | Google Scholar

53. Zhao GP, Zhao L, Shen LC, Zou J, Qiu L. Coercivity mechanisms in nanostructured permanent magnets. Chin Phys B (2019) 28:077505. doi:10.1088/1674-1056/28/7/077505

CrossRef Full Text | Google Scholar