Uncertainty quantification in electromagnetic observables of nuclei

We present strategies to quantify theoretical uncertainties in modern ab initio calculations of electromagnetic observables in light and medium-mass nuclei. We discuss how uncertainties build up from various sources, such as the approximations introduced by the few- or many-body solver and the truncation of the chiral effective field theory expansion. We review the recent progress encompassing a broad range of electromagnetic observables in stable and unstable nuclei.

1 Introduction

Uncertainty quantification is an emerging field in nuclear theory. It is nowadays expected for any theoretical calculation of nuclear observables to have a corresponding uncertainty bar, which is vital to make progress in our understanding of strongly interacting systems through the comparison of theoretical modeling with experimental data. While this is clearly the goal, the specific approach to uncertainty quantification and its sophistication level strongly depends on the used theoretical method and on the observables under investigation. In this review, we focus on electromagnetic reactions and on how they can be calculated with corresponding uncertainty in the so-called ab initio methods. It is fair to say that the sub-field of quantification of theoretical uncertainties is just now developing, and while there is still much to be done there has been recent significant progress. Here, we report on such progress, discuss its philosophy and identify areas where improvements can be expected in the future.

In the ab initio approach to nuclear theory [1–3] the goal is to explain nuclear phenomena, including electromagnetic processes, starting from protons and neutrons as degrees of freedom and to solve the related quantum-mechanical problem in a numerical way, either exactly or within controlled approximations. To achieve this, one typically solves the Schrödinger equation for a given Hamiltonian H and then computes transition matrix elements of the electromagnetic operator J^μ between the eigenstates of H. Hence, before discussing the approach devised to quantify uncertainties in electromagnetic observables, we define the dynamical ingredients (Hamiltonian and currents), as well as the specific observables we want to investigate.

1.1 Hamiltonians and currents

The starting point of an ab initio computation of a nucleus composed of A nucleons is the nuclear Hamiltonian,

$H=T_K+\sum _{i<j}^A{V}_{ij}+\sum _{i<j<k}^A{W}_{\mathit{ijk}},(1)$

where T_K is the intrinsic kinetic energy, V_ij is the two-body interaction and W_ijk is the three-body interaction. As opposed to a phenomenological derivation of nuclear forces, effective field theories (EFT) offer a more systematic approach [4]. In this paper, we will use effective Hamiltonians which are derived in chiral effective field theory (χEFT) [5–7]. In this framework, the Hamiltonian is expanded in powers of (Q/Λ), where Q is the typical low–momentum characterizing nuclear physics and Λ is the breakdown scale of the effective field theory. The various components relevant for V_ij and W_ijk are presented in terms of Feynman diagrams in Figure 1, where ν₀ is the first power entering in the counting. The unresolved short range physics is encoded in the values of the low energy constants (LECs), which are usually calibrated by fitting to experimental data. Different optimization and fitting strategies have been used to calibrate the LECs [8–11]. Here, we will use only a selected set of different Hamiltonians obtained from χEFT. Furthermore, interactions with explicit Δ degrees of freedom are becoming available [12–17] and should be explored. In the present work we will present results with both chiral Δ-full and Δ-less interactions.

FIGURE 1

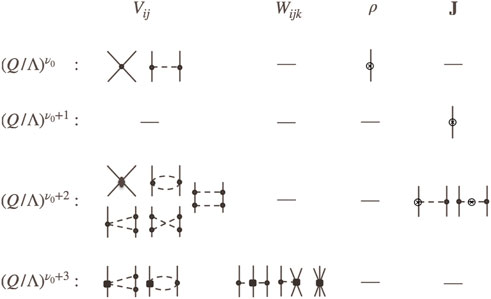
FIGURE 1. The χEFT expansion of the nuclear Hamiltonian and electromagnetic currents. The filled circles, squares and diamond denote strong-interaction vertices with chiral dimension 0,1 and 2, respectively. The ⊗ symbols denote the electromagnetic vertices. In the literature, ν₀ is usually taken as 0 for the potential and −3 for the currents.

The nuclear response to external probes is described by the interaction Hamiltonian, which depends on nuclear dynamics through the nuclear current operator. The χEFT expansion exists also for the electromagnetic four-vector current J^μ = (ρ, J), where the time-like component is the charge operator and the space-like component is the three-vector current operator. The first diagrams entering the χEFT expansion for (ρ, J) are shown in Figure 1, where we omit the diagrams that contribute to the elastic form factors. The reader can find more details on our implementation of the currents in Ref. [18]. While different authors adopt different power counting schemes for the currents [19–22], we follow the conventions of Ref. [22].

1.2 Electromagnetic observables

Electromagnetic probes are key tools to study nuclear structure because measured cross sections are easily related to the few-/many-body matrix elements of electromagnetic operators via perturbation theory. Here, we focus on electromagnetic observables that can be explained to high precision in first order perturbation theory, i.e., processes where one single photon is exchanged between the probe and the nucleus. This is the case for the photoabsorption process and the electron scattering process, see Figure 2. The exchanged photon can in general transfer energy ω and momentum q. In the photonuclear process, a real photon with ω = |q| = q is absorbed by the nucleus, while in electron scattering a virtual photon is exchanged, where one can vary ω and q independently.

FIGURE 2

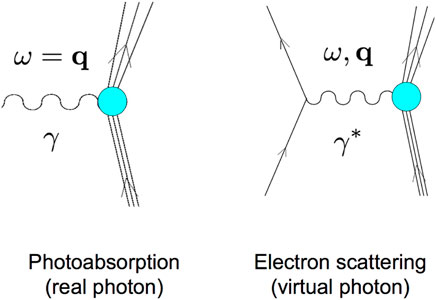
FIGURE 2. Feynman diagrams for the photoabsorption process (left), where a real photon γ is exchanged, and the electron scattering process, where a virtual photon γ* is exchanged between the probe and the nucleus (cyan blob).

In the cases of the photoabsorption and the electron-scattering process (see also Sections 3, 5), the cross section can be written in terms of a so-called response function, which, in the inclusive unpolarized case, is defined as

$R\left(\omega ,q\right)=\int \sum _{\bar{0}f}{\left|⟨{\mathrm{\Psi }}_f|\mathrm{\Theta }\left(q\right)|{\mathrm{\Psi }}_0⟩\right|}^2\delta \left(E_f-E_0-\omega \right).(2)$

Here, Θ(q) is the electromagnetic operator, which can be directly one of the operators (ρ, J) or can be just a multipole of them. |Ψ_0/f⟩ are the ground state and the excited states of the Hamiltonian H, respectively. The symbol ${\sum }_{\bar{0}}$ indicates an average on the initial angular momentum projection, while the symbol ∫∑_f corresponds to both a sum over discrete excited states and an integral over continuum eigenstates of the Hamiltonian. Indeed, |Ψ_f⟩ may include not only bound excited states, but also states in the continuum where the nucleus is broken up into fragments.

The calculation of continuum wave functions represents a challenging task especially in an inclusive process, where one needs information on all possible fragmentation channels of the nucleus at a given energy. To avoid the issue, one can use integral transforms, such as the Lorentz integral transform (LIT) technique [23, 24]. Originally used in few-body calculations, the LIT technique is based on the calculation of the following integral of the response function R (ω, q),

$L\left(\sigma ,\mathrm{\Gamma },q\right)=\frac{\mathrm{\Gamma }}{\pi }\int d\omega \frac{R\left(\omega ,q\right)}{{\left(\omega -\sigma \right)}^2+{\mathrm{\Gamma }}^2},(3)$

which can be shown to be the squared norm of the solution of a Schrödinger-like equation calculated using bound-state techniques. Once L (σ, Γ, q) is calculated, a numerical inversion procedure allows one to recover R (ω, q), see Ref. [24] for details.

1.3 Numerical solvers

In order to calculate electromagnetic observables, we first need a numerical solution of the Schrödinger equation. In the applications discussed in Sections 3, 4 and 5, we will use either few-body or many-body solvers depending on the mass range A of the addressed nuclei.

We obtain the bound-state and scattering-state wave functions for the A = 2 problem by solving the partial-wave Lippmann-Schwinger equations for the Hamiltonian. The response functions are then calculated by directly evaluating the matrix elements of the electromagnetic operator in coordinate space.

To calculate few-body problems with 2 < A < 8 we use hyperspherical harmonics expansions. In this framework, one expands the A-body intrinsic wave function in terms of hyperspherical harmonics ${\mathcal{H}}_K$ and hyperradial functions R_n as

$\mathrm{\Psi }=\sum _K^{K_{\mathit{max}}}\sum _n^{n_{\mathit{max}}}{\alpha }_{nK}{R}_n\left({\rho }_r\right){\mathcal{H}}_K\left(\mathrm{\Omega }\right),(4)$

where α_nK are the coefficients of the expansion and where for the sake of simplicity we omit spin and isospin degrees of freedom. Here, ρ_r is the hyperradius while Ω is a set of hyperangles, on which the hyperspherical harmonics ${\mathcal{H}}_K$ with grandangular momentum K depend. The expansion is performed up to a maximal value of hyperradial functions n_max and a maximal value of grandangular momentum K_max. Reaching convergence in n_max is typically not difficult. The expansion in hyperspherical harmonics is instead more delicate and one needs to ensure that the dependence of the calculated observables on this truncation is under control. To accelerate convergence, an effective interaction a la Lee-Suzuki can be introduced [25], obtaining the so-called effective interaction hyperspherical harmonics (EIHH) method, which allows to eventually achieve sub-percentage accuracy in the ⁴He calculations of binding energies and electromagentic observables [26]. Hyperspherical harmonics expansions can be conveniently used also to solve the Schrödinger-like equation obtained when applying the LIT method described above. The interested reader can consult, e.g., Refs. [2, 24–28] for more details.

For nuclei with A ≥ 8 we use coupled-cluster theory. In this framework, for a given Hamiltonian H one starts from a Slater determinant |Φ₀⟩ of single particle states and assumes an exponential ansatz to construct the correlated many-body wave function as

$|{\mathrm{\Psi }}_0\rangle =\exp \left(T\right)|{\mathrm{\Phi }}_{\mathrm{0}}\rangle .(5)$

The operator T is typically expanded in n-particle-n-hole excitations (or clusters) as T = T₁+T₂+⋯ + T_A. Coupled-cluster theory is exact when the expansion of the T operator is considered up to A particle—A hole excitations (Ap–Ah) within a model space determined by the number N_max of oscillator shells considered [29]. Even though truncations are typically introduced, they can lead to a result very close to the exact one due to the exponential ansatz Eq. 5). Because the computational cost of this method scales polynomially with increasing mass number A, it is a very convenient solver for medium mass and even heavy nuclei [30].

For closed (sub-) shell nuclei, coupled-cluster theory truncated at the 2p–2h level, in the so called coupled-cluster singles and doubles (CCSD) scheme, captures about 90% of the full correlation energy. When including triples excitation, even at the leading order in the so-called CCSDT-1 scheme [31], one can obtain almost 97% of the correlation energy [29, 32]. It has been shown that coupled-cluster theory can be also used in conjunction with the LIT method, where one can reduce the problem to the solution of a bound-state like equation of motion [33].

2 Uncertainty quantification

In each of our computations of electromagnetic observables, the final accuracy will be controlled on the one hand by the employed χEFT (determined by Hamiltonian and currents) and on the other hand by the accuracy to which one can solve the few–body or many–body problem for a given Hamiltonian and current operator. Hence, in the following we will divide the sources of uncertainties in two broad categories:

1) χEFT uncertainties;

2) Numerical uncertainties.

Among the uncertainties in 1), there are possible dependencies on the employed interaction or current model (including cutoff dependencies), as well as uncertainties introduced by the truncation to a given order ν of the employed χEFT, and uncertainties due to extracting the LECs from experimental data or from lattice calculations. If the LECs are well constrained by experimental data, the χEFT uncertainty is typically dominated by the truncation error of the χEFT expansion. Regarding the latter, if the leading non-vanishing contribution to a calculated observable $\mathcal{O}$ enters at order ν₀ and one is able to perform calculations that include all effects up to order ν₀+k, one can naively expect to incur a relative error of ${\delta }_{\mathcal{O}}^{\chi \mathrm{E}\mathrm{F}\mathrm{T}}/\mathcal{O}\approx {(Q/\mathrm{\Lambda })}^{k+1}$ from the neglected higher-order terms. A more rigorous estimate can be obtained by using the calculated order-by-order results ${\mathcal{O}}_{\nu }$ as “data” to inform the uncertainty analysis. For example, using the simple algorithm proposed by Ref. [34], the absolute truncation error can be estimated as

${\delta }_{\mathcal{O}}^{\chi \mathrm{E}\mathrm{F}\mathrm{T}}=\mathrm{m}\mathrm{a}\mathrm{x}\left\{{\left(\frac{Q}{\mathrm{\Lambda }}\right)}^{k+1}\left|{\mathcal{O}}_{{\nu }_0}\right|,{\left(\frac{Q}{\mathrm{\Lambda }}\right)}^k\left|{\mathcal{O}}_{{\nu }_0+1}-{\mathcal{O}}_{{\nu }_0}\right|,\dots ,\left(\frac{Q}{\mathrm{\Lambda }}\right)\left|{\mathcal{O}}_{{\nu }_0+k}-{\mathcal{O}}_{{\nu }_0+k-1}\right|\right\}.(6)$

More recently, Bayesian methods have been adopted for quantification of the χEFT truncation error [35–38]. These methods start from Bayesian priors that encode naturalness of the coefficients {c_ν} defined, using a suitable reference ${\mathcal{O}}_{\text{ref}}$, by

${\mathcal{O}}_{{\nu }_0+k}={\mathcal{O}}_{\text{ref}}\sum _{\nu =0}^k{c}_{\nu }{\left(\frac{Q}{\mathrm{\Lambda }}\right)}^{\nu }.(7)$

The priors are then updated using the calculated data to arrive at a Bayesian posterior for the truncation error ${\delta }_{\mathcal{O}}^{\chi \mathrm{E}\mathrm{F}\mathrm{T}}$. A key advantage of this approach is that the estimates have a statistical interpretation, which allows us to validate the assumptions made and to easily combine truncation errors with other sources of uncertainties such as fitting or random sampling of parameters. This opens a possible path for a complete and consistent accounting of theory uncertainty from all dynamical ingredients in the future.

Regarding the uncertainties in 2), the protocol to evaluate them will depend on the implemented numerical solver. On the one hand, when performing a few-body calculations with hyperspherical harmonics, one needs to carefully take the convergence in K_max into account. When using the LIT method, one also needs to consider the uncertainty of the inversion procedure. On the other hand, when using coupled-cluster theory, one needs to account for at least two different patterns of convergence. First, there is always a truncation on the model space controlled by the maximum number of harmonic oscillator (HO) shells N_max, which, in a sense, is analogous to the K_max in hyperspherical harmonics. If convergence in N_max is reached, the results should in principle be independent of the underlying HO frequency ℏΩ used for single particle states. However, in practice, one is always left with some residual ℏΩ dependence which should be explored. Second, in coupled-cluster theory one has a cluster expansion of the operator T. Here, the most frequently adopted approximation is CCSD. When possible, one should include higher order excitations, such as leading order triples corrections with CCSDT-1. Finally, when using the LIT method, one incurs the extra numerical uncertainty coming from the inversion procedure.

In general, we expect uncertainties of 2) to be sub–percentage or at most one percent in light nuclei up to mass number 4, while for medium–mass nuclei they may increase up to a few percent, depending on the specific observable. In particular, it is to note that binding energies, because of their eigenvalue nature, can usually be obtained with higher precision, while for example quadrupole transitions are notoriously difficult in methods such as coupled-cluster theory or in-medium similarity renormalization group [39]. Beyond the lightest nuclei, whether the uncertainties of 1) dominate over those of 2) may, in principle, depend on the specific system/observable considered. Experience has shown so far that uncertainties related to the χEFT 1) are typically the largest. We will compare the specific contributions in each example below.

3 Photoabsorption cross section

Photoabsorption cross sections have been extensively studied using ab initio techniques, especially in the sector of light nuclei, see Ref. [2] and references therein. The photoabsorption cross section is related to the response function by

${\sigma }_{\gamma }\left(\omega \right)=\frac{4{\pi }^2}{\omega }\alpha R_T\left(\omega ,\omega \right),(8)$

where R_T (ω, ω) is the response function of Eq. 2 where the Θ operator is the transverse (with respect to photon propagation) part of the electromagnetic current operator J and where ω = q. In the unretarded dipole approximation, the cross section can be obtained from

${\sigma }_{\gamma }\left(\omega \right)=4{\pi }^2\alpha \omega R_D\left(\omega \right),(9)$

where R_D(ω) is the response function of the electric dipole operator D (acting only on the Z protons) in the long wavelength approximation, defined as

$D=\sum _i^Z\left(z_i-Z_{cm}\right),(10)$

where z_i and Z_cm are the z-components of the ith particle and center-of-mass coordinates, respectively.

Below, we will discuss two examples. First, we will deal with the radiative capture reaction np → γd reaction, which is important for astrophysics and is related to the photoabsorption reaction γd → np by time-reversal. Next, we will discuss the inclusive photoabsorption of ⁴He, for which we will present new original results obtained with chiral forces at four different orders, including an analysis of its uncertainties.

3.1 The n p ↔ γd reaction

The primordial Deuterium abundance, which is very well constrained by astronomical [44] and cosmological [45] observations, can also be determined from nuclear physics by measuring or calculating the rates of the Deuterium production and burning reactions of the big-bang-nucleosynthesis network. While there is a reasonable agreement between these at the moment [46], a higher-precision comparison will search more rigorously for potential conflict which will be indicative of missing physics in one or the other and may even hint at new physics beyond the Standard Model. This elevates the importance of uncertainty quantification in the primordial Deuterium production reaction, np → γd.

In the relevant energy regime, M1 and E1 transitions are both important; we, therefore, evaluate the cross section using the full response function R_T (ω, ω) with the one- and two-body current operators shown in Figure 1. The uncertainties associated with the solution of the Schrödinger equation and other numerical approximations are negligible for this system. We therefore focus on χEFT uncertainties for this reaction. Working with fixed currents, we used the semi-local momentum-space-regularized chiral interactions of Ref. [47] to study the convergence properties of the χEFT expansion of the nuclear potential in Ref. [48]. We employed the Gaussian Process (GP) error model developed in Ref. [49] to perform a Bayesian analysis of the χEFT convergence for observables that have parametric dependence on a kinematic variable, which in this case is the np relative momentum. We performed detailed diagnostic checks to quantitatively assess the adequacy of the GP model and found that it described the observed convergence very well, which allowed us to extract reliable Bayesian posteriors for ${\delta }_{\mathcal{O}}^{\chi \mathrm{E}\mathrm{F}\mathrm{T}}$ at various orders.

In Figure 3, we show the 95% degree-of-belief bands for calculations at next-to-leading order (NLO), next-to-next-to-leading order (N2LO) and next-to-next-to-next-to-leading order (N3LO) obtained by using the leading order (LO) result as the reference ${\mathcal{O}}_{\text{ref}}$ (see Eq. 7). We note that the theory uncertainty from the truncation of χEFT at N2LO and N3LO are much smaller than experimental errors at the energy range of astrophysical relevance. The uncertainty from truncation of the current operator is a subject of future study.

FIGURE 3

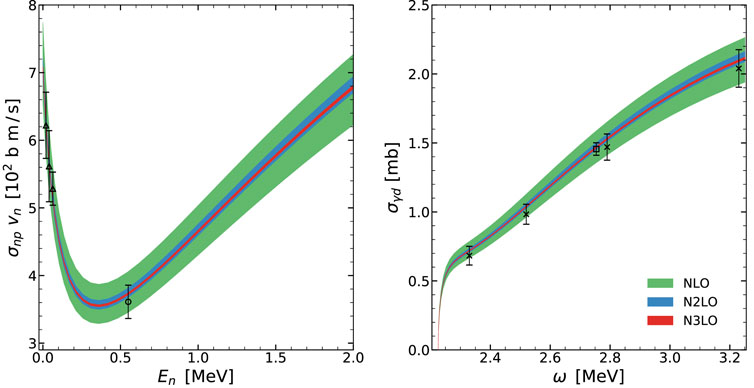
FIGURE 3. The product of p (n, γ)d cross section σ_np and the neutron speed v_n versus the neutron energy E_n (left panel); and the deuteron photodissociation cross section σ_γd as a function of the photon energy ω in the rest frame of the deuteron (right panel). The bands indicate 95% Bayesian degree-of-belief intervals at the various orders. Experimental data are from Ref. [40] (triangles) [41] (circle) [42] (crosses) and [43] (square). Experimental errors in beam-energy resolution are not shown.

3.2 The γ⁴He → X reaction

The photodisintegration cross section of ⁴He has been a focus of several past studies [50–55]. In this work, we provide new original results for this reaction obtained within the frameworks of χEFT using the EIHH [25, 56, 57] as a solver. We start from Eq. 9 and keep the dipole operator fixed, while changing the nuclear interaction in the Hamiltonian implementing different orders in the chiral expansion. We work up to N2LO with a maximally local version of the chiral interaction developed for the first time in Refs. [58–60], which we previously adapted to the EIHH method in Ref. [26]. In the same spirit of our work in the n p ↔ γd reaction, the uncertainty coming from the numerical solution of the Schrödinger equation is neglected here, since the EIHH method has been proven to be very precise for three- and four-body systems, with uncertainties that usually are below the percent level.

To bypass the explicit calculation of the continuum wave functions, the electric dipole response R_D(ω) of Eq. 9 is obtained by first computing its LIT and then performing the inversion. This introduces a numerical uncertainty of the order of 1%–2%, which can be seen in Figure 4 (left panel), where we present the calculation of σ_γ(ω) at LO, NLO, N2LO and N3LO in different colors. The width of the band is the uncertainty introduced by the inversion.

FIGURE 4

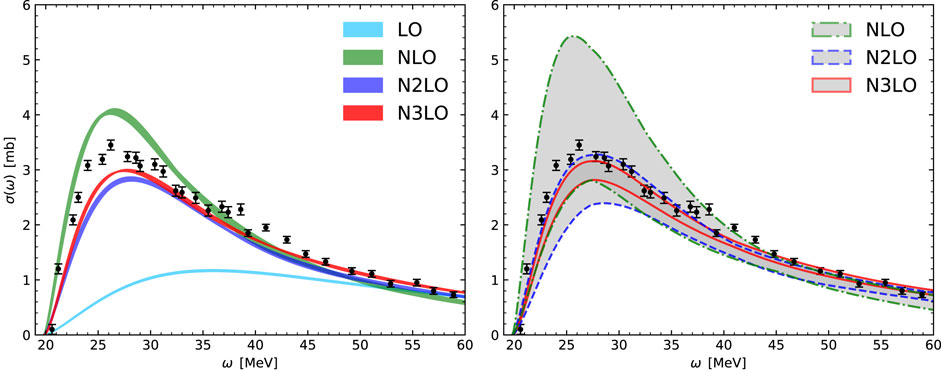
FIGURE 4. Inclusive ⁴He photoabsorption cross section calculated at different order in the chiral interaction. Left panel: bands display the numerical uncertainty in the inversion of the LIT. Right panel: bands display the χEFT truncation uncertainty, estimated using Eq. 6. The experimental data are taken from Ref. [61].

To assess uncertainty coming from the truncation of the chiral expansion, we start from the calculations of σ_γ(ω) at the various chiral orders and implement the algorithm in Eq. 6, which requires a choice for the expansion parameter Q/Λ. A reasonable choice for Q is obtained by a smooth max-function (see Eq. 46 of Ref. [49]) of m_π and $p_{\text{rel}}=\sqrt{2\mu \omega }$, where m_π is the pion-mass and μ is the reduced mass of the main photodisintegration channel, for which we take p−³H. For the breakdown scale Λ we conservatively take 500 MeV, which yields an expansion parameter for the χEFT consistent with Ref. [62]. When implementing Eq. 6, we go beyond our calculations with local chiral interactions which go all the way up to N2LO, and also consider the partial N3LO calculation from Ref. [54] and use it to estimate the uncertainty also at this order.

In Figure 4 (right panel), we show the cross section with corresponding χEFT uncertainty at the NLO, N2LO and N3LO orders. For every order the threshold energies are shifted to the experimental value. Clearly, the χEFT errors account for the largest portion of the overall uncertainty budget with respect to the numerical inversion uncertainty, which are therefore not even included in the right panel of Figure 4. The χEFT truncation errors are such that the calculated photoabsorption cross section at each order is consistent with the previous order within its uncertainties, as well as with the experimental data from Ref. [61]. At NLO we get an uncertainty at the cross section maximum of roughly 30% (half width), while at N2LO it is 15% (half width). Finally, the N3LO band, which is roughly 5% (half width), is located slightly below the shown experimental data. To facilitate comparison of theory with experiment, we have chosen to show only one representative set of data [61], which covers a wide range in energy. More data exist than are shown here, see, e.g., Ref. [2] and references therein.

4 Electromagnetic sum rules

Starting from the nuclear response function, one can compute electromagnetic sum rules, i.e., the moments of the response function of Eq. 2 interpreted as a distribution function. These quantities are defined as

$m_n\left(q\right)=\int d\omega {\omega }^{n}R\left(\omega ,q\right),(11)$

where n is an integer. Sum rules can be calculated directly from the LIT. Since for Γ → 0, the limit of a Lorentzian corresponds to a delta function, we get

$L\left(\sigma ,\mathrm{\Gamma }\to 0,q\right)=\int d\omega R\left(\omega ,q\right)\delta \left(\omega -\sigma \right)=R\left(q,\sigma \right).(12)$

This means that the moments of R(ω, q) can be obtained from the following expression

$m_n\left(q\right)=\int d\sigma {\sigma }^{n}L\left(\sigma ,\mathrm{\Gamma }\to 0,q\right).(13)$

As illustrated in Ref. [63], this procedure is equivalent to the computation and subsequent integration of the response. Moreover, this strategy does not require an inversion, which represents an additional source of uncertainty.

Among the sum rules, the electric dipole polarizability α_D is an interesting one, as it is correlated to parameters in the neutron-matter equation of state [64]. The electric dipole polarizability can be obtained starting from the inverse-energy weighted sum rule

${\alpha }_D=2\alpha \int d\omega \frac{R_D\left(\omega \right)}{\omega }=2\alpha m_{-1},(14)$

where m₋₁ is calculated using Eq. 11 and R_D(ω) is the response function of the dipole operator in the long wavelength approximation. From Eq. 14, it is clear that the polarizability is dominated by the low-energy part of the response function.

In a recent work [65], we performed coupled-cluster computations of dipole-excited state properties of the halo nucleus ⁸He, focusing on α_D and the energy-weighted sum rule m₁ using χEFT potentials derived at N2LO. Our calculations included an estimate of the theoretical uncertainty related to the model space convergence in N_max and to the truncation of the coupled-cluster expansion, according to the strategy illustrated in Ref. [66]. Regarding the first source of uncertainty, the maximum available model space is N_max = 14, so we consider the residual ℏΩ-dependence at this N_max as the uncertainty in the model space expansion. To assess the uncertainty in the coupled-cluster expansion, we take two different approximation schemes, the CCSD and the CCSDT-1, since we have no higher order coupled-cluster approximations available. The truncation uncertainty is then estimated taking half of the difference between the CCSD and CCSDT-1 results. The two contributions are then summed in quadrature.

To complement our previous analysis, we consider in this work the dependence on the order of the χEFT expansion in the case of the Δ-full interaction model, by providing a new calculation at a lower order (NLO). In Figure 5, we show the ℏΩ convergence pattern of α_D and m₁ for the ΔNLO_GO (450) and ΔN2LO_GO (450) potentials [17], indicating with bands the contribution of the coupled-cluster truncation uncertainty. In the case of the dipole polarizability, the theoretical error receives substantial contributions from both the many-body method and the residual dependence on the coupled-cluster convergence parameters. The polarizability is sensitive to the outer part of the nuclear wave function, and this makes the convergence slower for a loosely-bound system like ⁸He. ΔNLO_GO (450) predicts a slightly larger polarizability with respect to ΔN2LO_GO (450). Taking into account the uncertainty budget coming from the many-body solver (around 7% of the central value), the two results come out to agree within errobars.

FIGURE 5

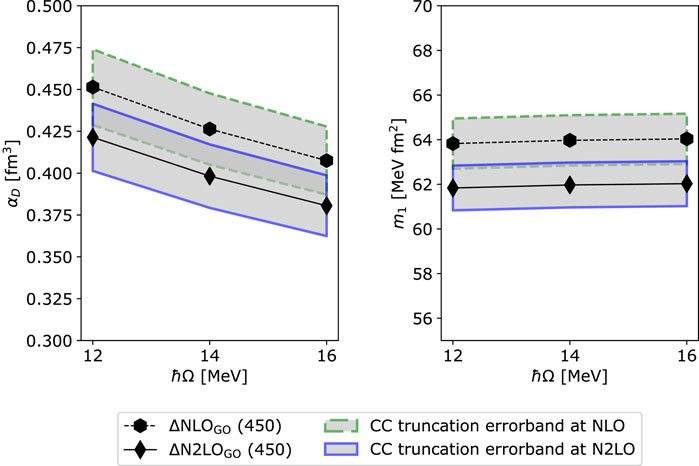
FIGURE 5. The ℏΩ-convergence pattern of α_D and m₁ for ⁸He calculated with ΔNLO_GO (450) and ΔN2LO_GO (450) at fixed N_max =14. The green and blue bands indicate the CC truncation uncertainty. The black points are the results obtained including 3p-3h excitations in both the ground- and excited-state computations.

The situation changes when turning to the energy-weighted sum rule. Here the overall uncertainty is dominated by the coupled-cluster truncation and it is estimated to be below 2%. Also in this case ΔNLO_GO (450) leads to a larger value for m₁. However, due to the smooth convergence of this observable, the difference between the two chiral orders, amounting to 3%, can be better appreciated than in the case of the polarizability. At the moment it is possible only to compute two orders in the χEFT expansion, namely the NLO and N2LO, therefore we refrain from using the algorithm of Eq. 6 in this case. Clearly, the uncertainty analysis is then less sophisticated than for the A = 2, 4 nuclei, but it is reassuring to see that the NLO and N2LO error bands overlap.

5 Electron scattering cross section

Electron scattering has proven to be a powerful tool to investigate the nuclear structure and dynamics at various energy scales and for different systems. Very recently we started investigating the region of the quasielastic peak which becomes a dominating mechanism for the momentum transfer of the order of hundreds of MeV, below the pion production threshold. The inclusive electron-nucleus cross section can be expressed as

$\frac{d^2\sigma }{d\mathrm{\Omega }d\omega }={\sigma }_{\text{Mott}}\left(\frac{{\mathbf{q}}^2-{\omega }^2}{{\mathbf{q}}^2}{R}_L\left(\omega ,q\right)+\left(\frac{{\mathbf{q}}^2-{\omega }^2}{2{\mathbf{q}}^2}+{\tan }^2\frac{\theta }{2}\right)R_T\left(\omega ,q\right)\right)(15)$

with the longitudinal and transverse response functions R_L/T and the scattering angle θ. The response functions can be disentangled experimentally via the Rosenbluth separation technique. From the theoretical point of view, it is convenient to investigate first the longitudinal component, which is the response function of Eq. 2 where the operator Θ(q) is the charge operator

$\rho \left(q\right)=\sum _{i=1}^Z{e}^{iq\left(z_i-Z_{cm}\right)}.(16)$

Typically, then nucleon form factors are folded in (see e.g. Ref. [68]). The operator structure of ρ is simpler than that of the electromagnetic current J and two-body contributions appear at a high order in the chiral expansion (see Figure 1), so that it can be neglected if performing studies up to N2LO. While the ab initio calculations of R_L in light systems were performed in several theoretical frameworks, we recently extended these studies to the region of medium-mass nuclei [69]. We focused on ⁴⁰Ca, for which Rosenbluth separated response functions are available, using two different N2LO potentials [9, 17]. Here, we complement our uncertainty analysis by performing a new calculation with an NLO potential.

Similarly to the photoabsorption considered in Section 3.2, the calculation of R_L requires computing the LITs which afterwards have to be inverted, introducing an additional source of uncertainty with respect to the sum-rule calculation. We obtain the LITs using coupled-cluster theory within the CCSD approximation. The role played by 3p−3h excitations will be a topic of the future investigation. We calculate R_L using a single model space of N_max = 14 and harmonic oscillator frequency ℏΩ = 16 MeV. In our previous work [69] we varied the frequency of the underlying harmonic oscillator basis and its size and we found that the LITs are already well converged. In this situation, the numerical uncertainty is driven by the inversion procedure which is represented by the band shown in Figure 6.

FIGURE 6

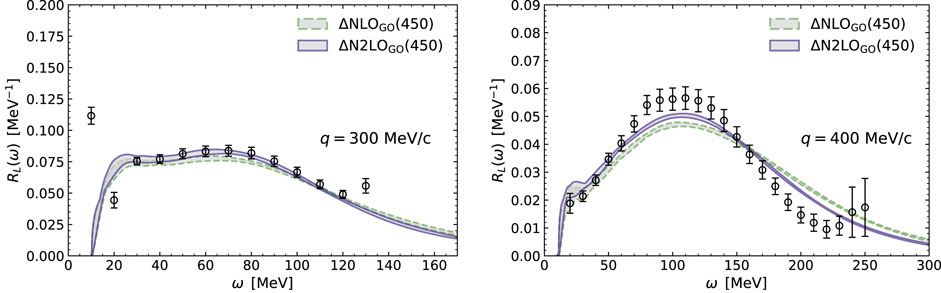
FIGURE 6. Longitudinal response functions of ⁴⁰Ca for the momentum transfer q =300 MeV/c (left panel) and q =400 MeV/c (right panel). Two orders of the chiral expansion of the nuclear Hamiltonian are shown. The uncertainty band originates from the inversion procedure of the LITs. The experimental data are taken from Ref. [67].

To assess the uncertainty coming from the χEFT expansion we look at the dependence on the order of expansion of the Δ-full potential [17] at NLO and N2LO. In Figure 6 we present R_L for q = 300 MeV/c (left panel) and q = 400 MeV/c (right panel). At q = 300 MeV/c the predictions of ΔNLO_GO (450) and ΔN2LO_GO (450) agree to great extent within the uncertainty bands and with the data. In contrast, at q = 400 MeV, the uncertainty bands of ΔNLO_GO (450) and ΔN2LO_GO (450) overlap less and the agreement with data slightly deteriorates. When comparing the two interactions, we see that the ΔN2LO_GO (450) leads to a slightly higher and narrower quasielastic peak with respect to the ΔNLO_GO (450) (the difference of around 8% in the peak for q = 400 MeV/c), bringing the results closer to the data as the chiral order increases. Because a quantitative analysis would require more than two orders of the χEFT Hamiltonian, we refrain here from applying Eq. 6, which would only contain one term.

At the qualitative level, we observe that the size of the uncertainties of kind 1) and 2) are comparable, and those of kind 1) seem to depend on the momentum transfer and grow at larger q value. This is, after all, not surprising, because χEFT is expected to work better at low momenta than at higher momenta.

6 Conclusion

In this paper, we review the recent progress made in uncertainty quantification for ab initio calculations of electromagnetic observables focusing on the one hand on our recent results and on the other hand providing also new original results to complement the uncertainty analysis. We show several examples where nuclei of different masses are scrutinized.

We first showcase the recent computations of the n p ↔ γd reaction, where an uncertainty analysis of the χEFT truncation with Bayesian tools was implemented. Then, we show new results for the photoabsoprtion cross section of ⁴He computed with χEFT potentials at LO, NLO and N2LO. The uncertainty quantification we present is based on the use of Eq. 6 and pushed to N3LO using the results from Ref. [54]. For both these examples in the sector of light nuclei, we find that numerical uncertainties are negligible and the bulk of the error stems from the truncation of the χEFT expansion. Next, we discuss sum rules in the exotic ⁸He nucleus, where we confront the existing calculation at N2LO with a new computation at NLO in the χEFT expansion using Δ degrees of freedom. Here, we see that numerical uncertainties and χEFT truncation errors are comparable in size. Finally, we show results for the longitudinal response function of ⁴⁰Ca using the same interactions we used for ⁸He. Also in this case, the uncertainty stemming from the χEFT truncation seems comparable to that coming from the numerical solver. It is important to note here that we are not yet able to fully account for the numerical uncertainties, because we have not yet included 3p–3h excitations. Furthermore, we only have two orders in the χEFT so a quantitative uncertainty cannot yet be reliably estimated. Interestingly, we qualitatively observe a momentum-transfer dependence in the difference between the calculation at NLO and N2LO, which is not unexpected given that χEFT is a low-momentum expansion. A precise quantitative description of the dependence of the χEFT expansion on the momentum transfer, which is obscured by the fact that we use phenomenological form factors to represent photon-nucleon vertices, is a subject of future study.

Clearly, the level of sophistication of our uncertainty quantification is higher for lighter nuclei and decreases as the mass grows. The most rigorous analysis was performed for A = 2, where we were able to express the truncation errors as Bayesian degree-of-belief intervals. For the range of A ≃ 4 one can expect that a Bayesian analysis will be implemented in the future. A quantitative analysis of nuclei with A ≥ 8 will need more effort. We expect LO calculations to be far from experimental data for these nuclei, but if one wants to go beyond N2LO in the χEFT expansion, one would need consistent potentials that are soft enough for many-body calculations to converge. Moreover, to fully assess uncertainties in electromagnetic observables, one must also consider the χEFT expansion in the current and in the interaction simultaneously. Examples of how one can vary the χEFT expansion in the current operators can be found in the literature for example in Refs. [2, 70] and reference therein. Another consideration to take into account in a full uncertainty quantification is the variation between different χEFTs, i.e., different regularization schemes [38] or different degrees of freedom [15]. Here, we have explored only a few options and obviously more work in this direction needs to be done by the whole community. Finally, in the future statistical approaches for the variation of the LECs such as those shown in Ref. [30] should be applied broadly to the study of electroweak dynamical observables, such as response functions and cross sections.

Author contributions

All authors contributed in equal parts to this paper. BA led in the deuteron calculations, SSL the ⁴He calculations, FB the ⁸He calculations, and JES together with BA performed the ⁴⁰Ca calculations. While SB took the main responsibility for the drafting of the paper, all authors contributed to the writing of the manuscript.

Funding

This work was supported by the Deutsche Forschungsgemeinschaft (DFG) through Project-ID 279384907 - SFB 1245 and through the Cluster of Excellence “Precision Physics, Fundamental Interactions, and Structure of Matter” (PRISMA⁺ EXC 2118/1) funded by the DFG within the German Excellence Strategy (Project ID 39083149). BA’s work at ORNL is supported by the Neutrino Theory Network Fellowship Program (Grant No. DE-AC02-07CH11359). JES acknowledges the support of the Humboldt Foundation through a Humboldt Research Fellowship for Postdoctoral Researchers and funding from the European Union’s Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement No. 101026014. Computer time was provided by the Innovative and Novel Computational Impact on Theory and Experiment (INCITE) program and by the supercomputer Mogon at Johannes Gutenberg Universität Mainz. This research used resources of the Oak Ridge Leadership Computing Facility located at ORNL, which is supported by the Office of Science of the Department of Energy under Contract No. DE-AC05-00OR22725.

Acknowledgments

We would like to acknowledge Weiguang Jiang for sharing the matrix elements for the ΔNLO_GO(450) potential with us. We would like to thank Nir Barnea and Gaute Hagen for access to the hyperspherical harmonics and coupled-cluster codes, respectively. Finally, we would like to thank Thomas R. Richardson for a critical reading of the manuscript.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Leidemann W, Orlandini G. Modern ab initio approaches and applications in few-nucleon physics with A ≥ 4. Prog Part Nucl Phys (2013) 68:158–214. doi:10.1016/j.ppnp.2012.09.001

CrossRef Full Text | Google Scholar

2. Bacca S, Pastore S. Electromagnetic reactions on light nuclei. J Phys G: Nucl Part Phys (2014) 41:123002. doi:10.1088/0954-3899/41/12/123002

CrossRef Full Text | Google Scholar

3. Hebeler K, Holt JD, Menéndez J, Schwenk A. Nuclear forces and their impact on neutron-rich nuclei and neutron-rich matter. Ann Rev Nucl Part Sci (2015) 65:457–84. doi:10.1146/annurev-nucl-102313-025446

CrossRef Full Text | Google Scholar

4. Hammer HW, Furnstahl R. Effective field theory for dilute fermi systems. Nucl Phys A (2000) 678:277–94. doi:10.1016/S0375-9474(00)00325-0

CrossRef Full Text | Google Scholar

5. Weinberg S. Nuclear forces from chiral Lagrangians. Phys Lett B (1990) 251:288–92. doi:10.1016/0370-2693(90)90938-3

CrossRef Full Text | Google Scholar

6. Epelbaum E, Hammer HW, Meißner UG. Modern theory of nuclear forces. Rev Mod Phys (2009) 81:1773–825. doi:10.1103/RevModPhys.81.1773

CrossRef Full Text | Google Scholar

7. Machleidt R, Entem D. Chiral effective field theory and nuclear forces. Phys Rep (2011) 503:1–75. doi:10.1016/j.physrep.2011.02.001

CrossRef Full Text | Google Scholar

8. Ekström A, Baardsen G, Forssén C, Hagen G, Hjorth-Jensen M, Jansen GR, et al. Optimized chiral nucleon-nucleon interaction at next-to-next-to-leading order. Phys Rev Lett (2013) 110:192502. doi:10.1103/PhysRevLett.110.192502

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Ekström A, Jansen GR, Wendt KA, Hagen G, Papenbrock T, Carlsson BD, et al. Accurate nuclear radii and binding energies from a chiral interaction. Phys Rev C (2015) 91:051301. doi:10.1103/PhysRevC.91.051301

CrossRef Full Text | Google Scholar

10. Navarro Pérez R, Amaro JE, Ruiz Arriola E. Statistical error analysis for phenomenological nucleon-nucleon potentials. Phys Rev C (2014) 89:064006. doi:10.1103/PhysRevC.89.064006

CrossRef Full Text | Google Scholar

11. Piarulli M, Girlanda L, Schiavilla R, Pérez RN, Amaro JE, Arriola ER. Minimally nonlocal nucleon-nucleon potentials with chiral two-pion exchange including Δ resonances. Phys Rev C (2015) 91:024003. doi:10.1103/PhysRevC.91.024003

CrossRef Full Text | Google Scholar

12. Kaiser N, Gerstendörfer S, Weise W. Peripheral nn-scattering: Role of delta-excitation, correlated two-pion and vector meson exchange. Nucl Phys A (1998) 637:395–420. doi:10.1016/S0375-9474(98)00234-6

CrossRef Full Text | Google Scholar

13. Krebs H, Epelbaum E, Meißner UG. Nuclear forces with Δ excitations up to next-to-next-to-leading order, part i: Peripheral nucleon-nucleon waves. Eur Phys J A (2007) 32:127–37. doi:10.1140/epja/i2007-10372-y

CrossRef Full Text | Google Scholar

14. Epelbaum E, Krebs H, Meißner UG. Δ-excitations and the three-nucleon force. Nucl Phys A (2008) 806:65–78. doi:10.1016/j.nuclphysa.2008.02.305

CrossRef Full Text | Google Scholar

15. Piarulli M, Girlanda L, Schiavilla R, Kievsky A, Lovato A, Marcucci LE, et al. Local chiral potentials with Δ-intermediate states and the structure of light nuclei. Phys Rev C (2016) 94:054007. doi:10.1103/PhysRevC.94.054007

CrossRef Full Text | Google Scholar

16. Ekström A, Hagen G, Morris TD, Papenbrock T, Schwartz PD. Δ isobars and nuclear saturation. Phys Rev C (2018) 97:024332. doi:10.1103/PhysRevC.97.024332

CrossRef Full Text | Google Scholar

17. Jiang WG, Ekström A, Forssén C, Hagen G, Jansen GR, Papenbrock T. Accurate bulk properties of nuclei from a = 2 to ∞ from potentials with Δ isobars. Phys Rev C (2020) 102:054301. doi:10.1103/PhysRevC.102.054301

CrossRef Full Text | Google Scholar

18. Acharya B, Bacca S. Neutrino-deuteron scattering: Uncertainty quantification and new L_{1, A} constraints. Phys Rev C (2020) 101:015505. doi:10.1103/PhysRevC.101.015505

CrossRef Full Text | Google Scholar

19. Pastore S, Schiavilla R, Goity JL. Electromagnetic two-body currents of one- and two-pion range. Phys Rev (2008) C78:064002. doi:10.1103/PhysRevC.78.064002

CrossRef Full Text | Google Scholar

20. Pastore S, Girlanda L, Schiavilla R, Viviani M, Wiringa RB. Electromagnetic currents and magnetic moments in chiral effective field theory (χeft). Phys Rev C (2009) 80:034004. doi:10.1103/PhysRevC.80.034004

CrossRef Full Text | Google Scholar

21. Kölling S, Epelbaum E, Krebs H, Meißner UG. Two-pion exchange electromagnetic current in chiral effective field theory using the method of unitary transformation. Phys Rev C (2009) 80:045502. doi:10.1103/PhysRevC.80.045502

CrossRef Full Text | Google Scholar

22. Phillips DR. Electromagnetic structure of two- and three-nucleon systems: An effective field theory description. Annu Rev Nucl Part Sci (2016) 66:421–47. doi:10.1146/annurev-nucl-102014-022321

CrossRef Full Text | Google Scholar

23. Efros VD, Leidemann W, Orlandini G. Response functions from integral transforms with a lorentz kernel. Phys Lett B (1994) 338:130–3. doi:10.1016/0370-2693(94)91355-2

CrossRef Full Text | Google Scholar

24. Efros VD, Leidemann W, Orlandini G, Barnea N. The lorentz integral transform (lit) method and its applications to perturbation-induced reactions. J Phys G: Nucl Part Phys (2007) 34:R459–528. doi:10.1088/0954-3899/34/12/r02

CrossRef Full Text | Google Scholar

25. Barnea N, Leidemann W, Orlandini G. State dependent effective interaction for the hyperspherical formalism. Phys Rev C (2000) 61:054001. doi:10.1103/PhysRevC.61.054001

CrossRef Full Text | Google Scholar

26. Li Muli SS, Bacca S, Barnea N. Implementation of local chiral interactions in the hyperspherical harmonics formalism. Front Phys (2021) 9. doi:10.3389/fphy.2021.671869

CrossRef Full Text | Google Scholar

27. Barnea N, Novoselsky A. Hyperspherical wave functions with orthogonal and permutational symmetry. Phys Rev A (1998) 57:48–58. doi:10.1103/PhysRevA.57.48

CrossRef Full Text | Google Scholar

28. Ji C, Bacca S, Barnea N, Hernandez OJ, Dinur NN. Ab initio calculation of nuclear-structure corrections in muonic atoms. J Phys G: Nucl Part Phys (2018) 45:093002. doi:10.1088/1361-6471/aad3eb

CrossRef Full Text | Google Scholar

29. Hagen G, Papenbrock T, Dean DJ, Hjorth-Jensen M, Asokan BV. Ab initio computation of neutron-rich oxygen isotopes. Phys Rev C (2009) 80:021306. doi:10.1103/PhysRevC.80.021306

CrossRef Full Text | Google Scholar

30. Hu B, Jiang W, Miyagi T, Sun Z, Ekström A, Forssén C, et al. Ab initio predictions link the neutron skin of ²⁰⁸Pb to nuclear forces Nature Phys (2022) 18(10):1196–1200. doi:10.1038/s41567-022-01715-8

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Watts JD, Gauss J, Bartlett RJ. Coupled-cluster methods with noniterative triple excitations for restricted open-shell Hartree–Fock and other general single determinant reference functions. energies and analytical gradients. J Chem Phys (1993) 98:8718–33. doi:10.1063/1.464480

CrossRef Full Text | Google Scholar

32. Bartlett RJ, Musiał M. Coupled-cluster theory in quantum chemistry. Rev Mod Phys (2007) 79:291–352. doi:10.1103/RevModPhys.79.291

CrossRef Full Text | Google Scholar

33. Bacca S, Barnea N, Hagen G, Orlandini G, Papenbrock T. First principles description of the giant dipole resonance in ¹⁶O. Phys Rev Lett (2013) 111:122502. doi:10.1103/PhysRevLett.111.122502

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Epelbaum E, Krebs H, Meißner UG. Precision nucleon-nucleon potential at fifth order in the chiral expansion. Phys Rev Lett (2015) 115:122301. doi:10.1103/PhysRevLett.115.122301

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Schindler M, Phillips D. Bayesian methods for parameter estimation in effective field theories. Ann Phys (2009) 324:682–708. doi:10.1016/j.aop.2008.09.003

CrossRef Full Text | Google Scholar

36. Furnstahl RJ, Phillips DR, Wesolowski S. A recipe for EFT uncertainty quantification in nuclear physics. J Phys G: Nucl Part Phys (2015) 42:034028. doi:10.1088/0954-3899/42/3/034028

CrossRef Full Text | Google Scholar

37. Ekström A. Analyzing the nuclear interaction: Challenges and new ideas. Front Phys (2020) 8. doi:10.3389/fphy.2020.00029

CrossRef Full Text | Google Scholar

38. Epelbaum E, Krebs H, Reinert P. High-precision nuclear forces from chiral eft: State-of-the-art, challenges, and outlook. Front Phys (2020) 8. doi:10.3389/fphy.2020.00098

CrossRef Full Text | Google Scholar

39. Stroberg SR, Henderson J, Hackman G, Ruotsalainen P, Hagen G, Holt JD. Systematics of e2 strength in the sd shell with the valence-space in-medium similarity renormalization group. Phys Rev C (2022) 105:034333. doi:10.1103/PhysRevC.105.034333

CrossRef Full Text | Google Scholar

40. Suzuki T, Nagai Y, Shima T, Kikuchi T, Sato H, Kii T, et al. First measurement of a p(n, γ)d reaction cross section between 10 and 80 kev. Astrophysical J (1995) 439:L59. doi:10.1086/187744

CrossRef Full Text | Google Scholar

41. Nagai Y, Suzuki TS, Kikuchi T, Shima T, Kii T, Sato H, et al. Measurement of ¹H(n, γ)²H reaction cross section at a comparable M1/E1 strength. Phys Rev C (1997) 56:3173–9. doi:10.1103/PhysRevC.56.3173

CrossRef Full Text | Google Scholar

42. Hara KY, Utsunomiya H, Goko S, Akimune H, Yamagata T, Ohta M, et al. Photodisintegration of deuterium and big bang nucleosynthesis. Phys Rev D (2003) 68:072001. doi:10.1103/PhysRevD.68.072001

CrossRef Full Text | Google Scholar

43. Moreh R, Kennett TJ, Prestwich WV. ²H(γ, n) absolute cross section at 2754 kev. Phys Rev C (1989) 39:1247–50. doi:10.1103/PhysRevC.39.1247

PubMed Abstract | CrossRef Full Text | Google Scholar

44. Cooke RJ, Pettini M, Steidel CC. One percent determination of the primordial deuterium abundance. Astrophys J (2018) 855:102. doi:10.3847/1538-4357/aaab53

CrossRef Full Text | Google Scholar

45. Aghanim N, Akrami Y, Ashdown M, Aumont J, Baccigalupi C, Ballardini M, et al. Planck 2018 results. VI. Cosmological parameters. Astron Astrophys (2020) 641:A6. [Erratum: Astron.Astrophys. 652, C4 (2021)]. doi:10.1051/0004-6361/201833910

CrossRef Full Text | Google Scholar

46. Pisanti O, Mangano G, Miele G, Mazzella P. Primordial deuterium after LUNA: Concordances and error budget. JCAP (2021) 04:020. doi:10.1088/1475-7516/2021/04/020

CrossRef Full Text | Google Scholar

47. Reinert P, Krebs H, Epelbaum E. Semilocal momentum-space regularized chiral two-nucleon potentials up to fifth order. Eur Phys J A (2018) 54:86. doi:10.1140/epja/i2018-12516-4

CrossRef Full Text | Google Scholar

48. Acharya B, Bacca S. Gaussian process error modeling for chiral effective-field-theory calculations of np ↔ dγ at low energies. Phys Lett B (2022) 827:137011. doi:10.1016/j.physletb.2022.137011

CrossRef Full Text | Google Scholar

49. Melendez JA, Furnstahl RJ, Phillips DR, Pratola MT, Wesolowski S. Quantifying correlated truncation errors in effective field theory. Phys Rev C (2019) 100:044001. doi:10.1103/PhysRevC.100.044001

CrossRef Full Text | Google Scholar

50. Ellerkmann G, Sandhas W, Sofianos SA, Fiedeldey H. Integral equation calculations for the photodisintegration process ⁴He(γ, n)³He. Phys Rev C (1996) 53:2638–44. doi:10.1103/PhysRevC.53.2638

PubMed Abstract | CrossRef Full Text | Google Scholar

51. Efros VD, Leidemann W, Orlandini G. Is there a pronounced giant dipole resonance in ⁴he? Phys Rev Lett (1997) 78:4015–8. doi:10.1103/PhysRevLett.78.4015

CrossRef Full Text | Google Scholar

52. Barnea N, Efros VD, Leidemann W, Orlandini G. Total ⁴He photoabsorption cross section reexamined: Correlated versus effective interaction hyperspherical harmonics. Phys Rev C (2001) 63:057002. doi:10.1103/PhysRevC.63.057002

CrossRef Full Text | Google Scholar

53. Quaglioni S, Leidemann W, Orlandini G, Barnea N, Efros VD. Two-body photodisintegration of ⁴He with full final state interaction. Phys Rev C (2004) 69:044002. doi:10.1103/PhysRevC.69.044002

CrossRef Full Text | Google Scholar

54. Quaglioni S, Navrátil P. The 4he total photo-absorption cross section with two-plus three-nucleon interactions from chiral effective field theory. Phys Lett B (2007) 652:370–5. doi:10.1016/j.physletb.2007.06.082

CrossRef Full Text | Google Scholar

55. Gazit D, Bacca S, Barnea N, Leidemann W, Orlandini G. Photoabsorption on ⁴He with a realistic nuclear force. Phys Rev Lett (2006) 96:112301. doi:10.1103/PhysRevLett.96.112301

PubMed Abstract | CrossRef Full Text | Google Scholar

56. Barnea N, Efros VD, Leidemann W, Orlandini G. Incorporation of three-nucleon force in the effective-interaction hyperspherical-harmonic approach. Few-Body Syst (2004) 35:155–67. doi:10.1007/s00601-004-0066-y

CrossRef Full Text | Google Scholar

57. Barnea N, Leidemann W, Orlandini G. Improved effective interaction for the hyperspherical formalism. Phys Rev C (2003) 67:054003. doi:10.1103/PhysRevC.67.054003

CrossRef Full Text | Google Scholar

58. Gezerlis A, Tews I, Epelbaum E, Freunek M, Gandolfi S, Hebeler K, et al. Local chiral effective field theory interactions and quantum Monte Carlo applications. Phys Rev C (2014) 90:054323. doi:10.1103/PhysRevC.90.054323

CrossRef Full Text | Google Scholar

59. Lynn J, Tews I, Carlson J, Gandolfi S, Gezerlis A, Schmidt K, et al. Chiral three-nucleon interactions in light nuclei, neutron-α scattering and neutron matter. Phys Rev Lett (2016) 116:062501. doi:10.1103/PhysRevLett.116.062501

PubMed Abstract | CrossRef Full Text | Google Scholar

60. Lynn J, Tews I, Carlson J, Gandolfi S, Gezerlis A, Schmidt KE, et al. Quantum Monte Carlo calculations of light nuclei with local chiral two- and three-nucleon interactions. Phys Rev C (2017) 96:054007. doi:10.1103/PhysRevC.96.054007

CrossRef Full Text | Google Scholar

61. Arkatov YM, Vatset P. I., Voloshuchuk V. I., Zolenko V. I., Prokhorets I. M., Chimil V. I. Sov J Nucl Phys (1974) 19:598.

62. Wesolowski S, Svensson I, Ekström A, Forssén C, Furnstahl RJ, Melendez JA, et al. Rigorous constraints on three-nucleon forces in chiral effective field theory from fast and accurate calculations of few-body observables. Phys Rev C (2021) 104:064001. doi:10.1103/PhysRevC.104.064001

CrossRef Full Text | Google Scholar

63. Miorelli M, Bacca S, Barnea N, Hagen G, Jansen GR, Orlandini G, et al. Electric dipole polarizability from first principles calculations. Phys Rev C (2016) 94:034317. doi:10.1103/PhysRevC.94.034317

CrossRef Full Text | Google Scholar

64. Roca-Maza X, Brenna M, Colò G, Centelles M, Viñas X, Agrawal BK, et al. Electric dipole polarizability in208Pb: Insights from the droplet model. Phys Rev C (2013) 88:024316. doi:10.1103/PhysRevC.88.024316

CrossRef Full Text | Google Scholar

65. Bonaiti F, Bacca S, Hagen G. Ab initio coupled-cluster calculations of ground and dipole excited states in ⁸He. Phys Rev C (2022) 105:034313. doi:10.1103/PhysRevC.105.034313

CrossRef Full Text | Google Scholar

66. Simonis J, Bacca S, Hagen G. First principles electromagnetic responses in medium-mass nuclei - recent progress from coupled-cluster theory. Eur Phys J A (2019) 55:241. doi:10.1140/epja/i2019-12825-0

CrossRef Full Text | Google Scholar

67. Williamson CF, Yates TC, Schmitt WM, Osborn M, Deady M, Zimmerman PD, et al. Quasielastic electron scattering from40Ca. Phys Rev C (1997) 56:3152–72. doi:10.1103/PhysRevC.56.3152

CrossRef Full Text | Google Scholar

68. Bacca S, Arenhövel H, Barnea N, Leidemann W, Orlandini G. Inclusive electron scattering off ⁴He. Phys Rev C (2007) 76:014003. doi:10.1103/PhysRevC.76.014003

CrossRef Full Text | Google Scholar

69. Sobczyk JE, Acharya B, Bacca S, Hagen G. Ab initio computation of the longitudinal response function in ⁴⁰Ca. Phys Rev Lett (2021) 127:072501. doi:10.1103/PhysRevLett.127.072501

PubMed Abstract | CrossRef Full Text | Google Scholar

70. Krebs H. Nuclear currents in chiral effective field theory. Eur Phys J A Eur (2020) 56:234. doi:10.1140/epja/s10050-020-00230-9

CrossRef Full Text | Google Scholar

71. Richardson TR, Schindler MR. Large-N_c analysis of magnetic and axial two-nucleon currents in pionless effective field theory. Phys Rev C (2020) 101:055505. doi:10.1103/PhysRevC.101.055505

CrossRef Full Text | Google Scholar