Exploring the implications of the uncertainty relationships in quantum mechanics

Heisenberg guessed, after he established the matrix quantum mechanics, that the non-commutativity of the matrices of position and momentum implied that the position and momentum of a particle could not be precisely simultaneously determined. He consequently conjectured that time and energy should also have a similar relationship. Soon after, Robertson derived an inequality concerning the space coordinate and momentum, which was thought to be the mathematical expression of the uncertainty relation guessed by Heisenberg. Since then, people have tried various devices to prove the correctness of these two relations. However, no one conducted a careful analysis of Heisenberg’s primary paper. In this work, we point out some serious problems in Heisenberg’s paper and the literature talking about the uncertainty relationships: the physical concepts involved in the uncertainty relations are not clear; one physical concept had more than one explanation, i.e., switching concepts; there has never been measurement experiment to support the relations. The conclusions are that the so-called coordinate–momentum uncertainty relation has never been related to actual measurement and there does not exist a time–energy uncertainty relation.

1 Introduction

As soon as Heisenberg founded quantum mechanics (QM) in matrix form [1–3], he acutely perceived that the matrices of the position and momentum of a particle were non-commutative. He thought that this non-commutativity should have some physical meaning. In a later paper [4], he guessed that the physical meaning of the non-commutativity was that the position and momentum of a microscopic particle could not be precisely simultaneously determined by experimental measurement. He was unable to provide an explicit expression for that, but merely presented qualitative discussion, including the gedanken experiments. He inferred consequently that there was a similar relationship between time and energy.

Soon after that, Robertson [5] derived an inequality, which was believed the mathematical expression of the uncertainty relation guessed by Heisenberg. Thus, the guess of the uncertainty relationship proposed by Heisenberg was generally accepted by people, and this was set in stone. Almost all QM textbooks introduce the coordinate–momentum relation and time–energy relation [6–30]. The uncertainty relations are thought of as fundamental ones in QM. They have been frequently mentioned by researchers and were even promoted as a principle—uncertainty principle [6–12].

When the present author carefully read the introductions and explanations of the uncertainty relations in Heisenberg’s primary paper [4] and the literature, questions emerged. A striking problem is that the uncertainty relations ought to be related to actual measurement, but it seems not to be so. Even in [4], Heisenberg merely talked about idealized experiments. The narrations connecting the uncertainty relations and the experiments are farfetched and specious. Confusions between different conceptions appear frequently. As a matter of fact, someone has been aware that there exist wrong explanations in the literature [31, 32]. We think that it is desirable to analyze in detail all the aspects involved in the uncertainty relations.

In the 1920s, Heisenberg, Schrödinger, Dirac et al. performed pioneering work in founding QM, which was a completely new field in physics. A series of new concepts merged. Some new concepts were formed. Among the new concepts, some were not very clear to people; they were not very clear even to these pioneers themselves, which should not be surprising. Hence, no one could guarantee that their works were flawless.

For example, when Schrödinger proposed his wave equation of QM, he unknowingly put down the negative kinetic energy (NKE) Schrödinger equation (33). However, this NKE Schrödinger equation was never realized by himself and others and was abandoned since then. We found that the NKE Schrödinger equation could be obtained by taking low-momentum approximation from relativistic quantum mechanics equations (RQMEs), and it was of explicit physical meanings [34, 35]. Dirac explained the NKE solutions of his RQME as representing antiparticles. Although people know that this explanation implied contradictions, no one could propose the right scenario to resolve the contradictions. We have given a correct explanation of the NKE solutions [35, 36].

There are two reasons that make people not aware of these pioneers’ mistakes in some aspects. One is that due to their genius achievements, people think that what they said was right. The other is that the related mistakes have not brought perceivable affection up till now. For instance, if there is no so-called uncertainty relationship, the evaluations and measurements in QM are not affected. The new theories raised after the uncertainty relations had been established, such as RQMEs, quantum electrodynamics (QED), quantum field theory (QFT), and quantum information, did not resort to the uncertainty relations. The computation of the band structures in solid-state materials and of nuclear physics does not need uncertainty relations. Physical experiments have never been arranged under the guidance of uncertainty relations, in spite of that, they are called principles. The uncertainty relations are usually employed to provide explanatory notes to some known phenomena and results.

After almost one hundred years, as later generations, we have grasped knowledge much more and wider than the pioneers did. People nowadays ought to have more sophisticated and rigorous reasoning. We should be able to recognize what the problems left by these pioneers are and how to resolve them. With clearer distinguishing and understanding of physical concepts, we are able to solve some difficulties left in QM [34–42].

The study of physics obeys physical laws. The physical laws are represented by fundamental equations and statements. The conclusions in physics need to be verified by experiments, which means that quantitative results are necessary. Theoretically, quantitative results are obtained by mathematical derivation starting from the fundamental equations. Theoretical discussions observe rigorous logical reasoning. We believe that in order to avoid the flaws in physical discussions as far as possible, some principles related to the physical contents discussed should be obeyed besides the mathematical derivation. The principles are presently called the basic viewpoints of the author.

The basic viewpoints depended on the concrete contents under discussion. The author’s previous papers [34–42] concerned some basic problems in QM. When we discussed one of these problems, certain viewpoints were based on [35, 42].

The uncertainty relationship is believed to be a fundamental topic in QM. In the present work, we are going to investigate this topic based on certain points of view. In the author’s following work, more topics will be touched on, and corresponding basic viewpoints will be stemmed on.

All the basic viewpoints we have been aware of are listed in Supplementary Appendix SA. We think that only when these viewpoints are abided by can one guarantee logical rigorousness and validity of the conclusions in discussing physical problems. Or, conception confusion may occur, and subsequently, the problem may not be solved correctly.

Here we mention one of the basic points of view. In QM, we always deal with wave functions. Every wave function satisfies a fundamental QM equation. Explicitly, the fundamental QM equation is in the form of

$\mathrm{i}\mathit{\hslash }\frac{\partial }{\partial t}\psi \left(t\right)=H\psi \left(t\right).$(1.1)

Here, the coordinate variables are not explicitly shown. In this paper, we always assume that (Eq. 1.1) is Schrödinger equation. If the Hamiltonian H is time-independent, the dependence of the wave function on time can be written as

$\psi \left(t\right)={\mathrm{e}}^{-\mathrm{i}Et/\mathit{\hslash }}\phi .$(1.2)

Thus, the function $\phi$ meets the stationary equation

$H\phi =E\phi .$(1.3)

Every wave function is necessarily the solution of Eq. 1.1. The wave functions of stationary states observe Eq. 1.3. In other words, when one discusses a wave function, he must be able to put down the corresponding Hamiltonian H. This is important. In textbooks, some functions are treated as wave functions because of their seemingly good behaviors. However, they are not the solutions of Eq. 1.1, i.e., there is no corresponding Hamiltonian. In Section 2, we will see two examples: the wave packet and wave train with the finite length for moving particles.

In Sections 2 and 3, we discuss coordinate–momentum and time–energy uncertainty relations, respectively. We will point out that physical conceptions are confused in the literature in discussing the two uncertainty relations. In [4], Heisenberg proposed the possible relations between the uncertainties of position and momentum, directed against single particles. Naturally, the similar relation between time and energy that he guessed was also for single particles. We stress this because in the literature, the problems of single-particles are confused with those of many-body systems. Section 4 is further discussion, and Section 5 contains the conclusions. Supplementary Appendix SA lists our basic viewpoints. Supplementary Appendix SB introduces the derivation of the so-called coordinate–momentum uncertainty relation.

2 Coordinate–momentum uncertainty relation

There are confusions of concepts when the coordinate–momentum uncertainty relation is discussed. The inequality derived by Robertson [5] was irrespective of experiments and Heisenberg’s primary paper [4]. This section presents a detailed analysis.

In this paper, we always consider the case of one dimension.

2.1 Heisenberg’s primary discussion

The paper [4] was the first one to talk about possible uncertainty relationships. The whole article did only qualitative discussion with no rigorous mathematical derivation. Heisenberg, based on his established QM in matrix form, found that the commutator of the two matrices q and p had the following result:

$pq-qp=\mathrm{i}\hslash .$(2.1)

The nonzero result meant that the two matrices could not exchange the order in their product. From this, he guessed that when a particle’s position and momentum were measured, both had some uncertainties.

“Let $q_1$ be the precision with which the value q is known ($q_1$ is, say, the mean error of q); therefore, here, it is the wavelength of the light. Let $p_1$ be the precision with which the value p is determinable; that is, here, it is the discontinuous change of p in the Compton effect. Then, according to the elementary laws of the Compton effect, $p_1$ and $q_1$ stand in the relation

$q_1{p}_1\sim \hslash .”\left[4\right].$(2.2)

Here, the definition of the uncertainty of q was obvious: “$q_1$ be the precision with which the value q is known ($q_1$ is, say, the mean error of q)”. $q_1$ is also the measurement precision of q. Then, its value must rely on the measurement equipment and measurement process. For instance, he mentioned a special case where photons were used to impinge a particle. Then, the uncertainty of the particle’s position was the photon’s wave length. This example showed that the measurement precision was indeed closely related to the measurement instrument chosen.

According to the basic viewpoint I.1 in Supplementary Appendix SA, every physical concept should have an explicit mathematical expression, or people would not clearly understand the conception.

First, in QM, a particle is described by its wave function. The wave function is the function of the spatial coordinate q, that is to say, q is an argument in a function, e.g., Eqs. 3, 12–(14) in [4]. In Heisenberg’s words, “Let $q_1$ be the precision with which the value q is known”. What is the meaning of the q in this sentence was not clear. In Eq. 2.1, q and p are matrices. It seems that Heisenberg unknowingly regarded them as numbers.

Next, we discuss the contents in the QM field. Following the viewpoint II.2, a wave function must be the solution of a fundamental QM equation. Heisenberg put down functions for discussion, but some of them were not the solutions of the Schrödinger equation for the system under consideration.

“If, for any definite state variable $\eta$, we determine the position q of the electron as $q^{\prime }$ with an uncertainty $q_1$, then we can express this fact by a probability amplitude $S\left(\eta ,q\right)$, which differs appreciably from zero only in a region of spread $q_1$ near $q^{\prime }$. For example, one can write

$S\left(\eta ,q\right)\propto \exp \left[-{\left(q-q^{\prime }\right)}^2/2q_1^2-\mathrm{i}{p}^{\prime }\left(q-q^{\prime }\right)/\hslash \right]”.\left[4\right].$(2.3)

This should be a wave function in QM. Such a function was called a Gaussian wave packet and used in the literature [6, 13–16]. It is time independent. Only the stationary eigenfunctions of a harmonic oscillator are of the form of $\psi \left(x\right)\propto {\mathrm{e}}^{-\alpha x^2}$, and the possible parameter is the location of the center of the oscillator. Otherwise, we do not know what the Hamiltonian of the wave function Eq. (2.3) is, while describing a moving particle we are talking about. When the Hamiltonian of a free particle is acted on this function,

$-\frac{{\hslash }^2}{2m}\frac{{\partial }^2}{\partial q^2}\psi \left(q\right)=\frac{{\hslash }^2}{2m}\left[\frac{1}{2q_1^2}-{\left(\frac{q}{2q_1^2}+\frac{\mathrm{i}{p}^{\prime }}{\hslash }\right)}^2\right]\psi \left(q\right).$(2.4)

It is seen that the function (Eq. 2.3) is not a free particle. We do not know what a potential $V\left(q\right)$ enables us to put down the stationary equation for the wave function (2.3).

$\left[-\frac{{\hslash }^2}{2m}\frac{{\partial }^2}{\partial q^2}+V\left(q\right)\right]\psi \left(q\right)=E\psi \left(q\right).$(2.5)

We are unable to write down a $V\left(q\right)$ other than the oscillator potential, and neither the expression of the corresponding Hamiltonian H.

In Eq. 2.3, q is the spatial coordinate of the wave function, but not the position of the electron. Heisenberg confused the concepts.

Eq. 18 in [4] was

$S\left(t,p\right)={\mathrm{e}}^{-\alpha t}\psi \left(E_2,p\right){\mathrm{e}}^{-\mathrm{i}{E}_{2}t/\hslash }+{\left(1-{\mathrm{e}}^{-2\alpha t}\right)}^{1/2}\psi \left(E_1,p\right){\mathrm{e}}^{-\mathrm{i}{E}_{1}t/\hslash }.$(2.6)

This was a time-dependent function. When it is substituted into the left-hand side of Eq. 1.1, the result is

$\begin{array}{l}\mathrm{i}\hslash \frac{\partial }{\partial t}S\left(t,p\right)=\left(-\alpha -\mathrm{i}{E}_{2}t/\hslash \right){\mathrm{e}}^{-\alpha t}\psi \left(E_2,p\right){\mathrm{e}}^{-\mathrm{i}{E}_{2}t/\hslash }\\ +\left(\frac{\alpha {\mathrm{e}}^{-2\alpha t}}{1-{\mathrm{e}}^{-2\alpha t}}-\mathrm{i}{E}_1/\hslash \right){\left(1-{\mathrm{e}}^{-2\alpha t}\right)}^{1/2}\psi \left(E_1,p\right){\mathrm{e}}^{-\mathrm{i}{E}_{1}t/\hslash }.\end{array}$(2.7)

We are unable to find a time-dependent Hamiltonian $H\left(t\right)$ such that the function Eq. 2.6 satisfies Schrödinger Eq. 1.1:

$\mathrm{i}\hslash \frac{\partial }{\partial t}S\left(t,p\right)=H\left(t\right)S\left(t,p\right).$(2.8)

Therefore Eq. 2.6 is not a wave function in QM.

For the wave function (22) in [4], one was unable to write a corresponding Hamiltonian as well, and so it was not a wave function in QM.

When writing down a function, one should first prove that it is the solution of a fundamental QM equation or has its corresponding Hamiltonian. Otherwise, it cannot be treated as a wave function in QM.

Third, Heisenberg did not present explicit expressions or rigorous mathematical derivations when he mentioned some physical conceptions.

For example, he mentioned “statistical error” more than once, but we do not know what he meant by it.

In Eq. 2.6, a concept of “radiation damping” was used. However, Heisenberg did not provide the mathematical derivation for the form in Eq. 2.6. In QM, a single particle does not have the concept of “radiation damping.” This concept must belong to a many-body system.

In [4], the argument below Eq. 8 was questionable. A beam of electrons was arranged to run through two fields successively in two different manners. In the second manner, no derivation was presented. Therefore, one could not know how the result $Z_{nl}={\displaystyle \sum }_m{c}_{nm}{\overline{c}}_{nm}{d}_{ml}{\overline{d}}_{ml}$ was reached.

Fourth, according to viewpoint I.3, when a gedanken experiment leads to a positive conclusion, it cannot explain anything. Such a conclusion could neither be proved nor be disproved.

In short, Heisenberg’s primary paper [4] lacked rigorous mathematics, was not quantitatively related to real experiments, and was not very clear in some physical concepts.

Heisenberg’s paper [4] just considered the measurement precisions of the position and the momentum of a single particle.

2.2 The analysis of the coordinate–momentum uncertainty relation

In 1929, Robertson [5] derived the famous mathematical inequality, see Supplementary Appendix SB. The conclusion was that the mean square errors of coordinate and momentum obeyed the following inequality:

$\Delta x\Delta p\ge \hslash /2.$(2.9)

This inequality was believed to be the mathematical expression of the uncertainties of coordinate and momentum that Heisenberg guessed. So, (2.9) was called the Heisenberg uncertainty relation.

Here, we distinguish the concepts of the position of a particle and coordinate. Heisenberg discussed the uncertainties of the measured position and momentum of a particle, so that his assumed relation was called the position–momentum uncertainty relation. However, in QM, a particle at a state is described by a wave function, which is a function of coordinates. The $\Delta x$ in (2.9) does not involve the meaning of a particle’s position. Hereafter, (2.9) is called the coordinate–momentum uncertainty relation.

According to the current understanding, the $\Delta x$ and $\Delta p$ in (2.9) are two quantities related to measurement. We point out in Supplementary Appendix SB that (2.9) is irrespective to both measurement and the content in Ref. [4].

Now, we explain that it is not right to understand the $\Delta x$ and $\Delta p$ in (2.9) as measurement uncertainties of coordinate and momentum, and as a matter of fact, it is impossible to implement measurement in the way of (2.9).

Usually, the recognition of (2.9) is that if one measures the position x and momentum p of a particle, they cannot be precisely simultaneously measured, and the smaller the measuring deviation of one quantity is, the greater the other. This recognition is incorrect.

Since (2.9) is regarded as the relation between the ncertainties of position and momentum, it ought to be related to the statistics of measured quantities. This prompts us to explain the implication of the inequality and the way of statistics of measured quantities.

2.2.1 The implication of the coordinate–momentum uncertainty relation

The coordinate is expressed by x, and the momentum operator is $p=-\mathrm{i}\hslash \frac{\partial }{\partial x}$. Suppose a microscopic system’s Hamiltonian H is known, and its wave function ψ is solved from (1.1).

The inner product of any two functions ψ and φ is defined by

$\left(\psi ,\phi \right)=\int \mathrm{d}x{\psi }^{*}\phi ={\left(\phi ,\psi \right)}^{*}.$(2.10)

We perform the following calculations:

$\overline{x}=\left(\psi ,x\psi \right),$(2.11)

$\Delta x={\left({\psi ,\left(x-\overline{x}\right)}^2\psi \right)}^{1/2}.$(2.12)

$\overline{p}=\left(\psi ,-\mathrm{i}\hslash \frac{\partial }{\partial x}\psi \right).$(2.13)

$\Delta p={\left({\psi ,\left(-\mathrm{i}\hslash \frac{\partial }{\partial x}-\overline{p}\right)}^2\psi \right)}^{1/2}.$(2.14)

The four calculated quantities meet (2.9).

Because the forms of 2.11–2.14 seem the same as that of the definition of mean square error, people mistakenly believe that 2.11–2.14 are of the meanings of the mean square error in the sense of measurement.

When talking about 2.9, people usually think that the smaller the one of $\Delta x$ and $\Delta p$, the larger the other. However, it is seen from 2.11–2.14 that $\Delta x$ and $\Delta p$ are uniquely determined by the given wave function, and their product necessarily meet (2.9). As a matter of fact, neither of $\Delta x$ and $\Delta p$ is variable.

For a one-dimensional harmonic oscillator, the nth stationary state wave function is denoted by ${\psi }_n$. It is evaluated [3, 7, 17] that in ${\psi }_n$, $\Delta x=\sqrt{n+1/2}\frac{1}{\alpha }$ and $\Delta p=\sqrt{n+1/2}\mathit{\hslash }\alpha$, so that $\Delta x\Delta p=\left(n+\frac{1}{2}\right)\mathit{\hslash }$. Both $\Delta x$ and $\Delta p$ increase with the index n. For the wave functions of hydrogen, we have $\Delta x=\frac{a_0}{2\sqrt{3}}\sqrt{7n^2+5}$, which increases with energy level, and $\Delta p=\frac{\hslash }{\sqrt{3}{a}_0}$, remaining unchanged for all the energy levels [3].

We turn to look at the comparison between the ground states of different systems. A hydrogen atom and an atomic nucleus have different dimensions. Compared with the hydrogen atom, the dimension of the nucleus is smaller, and so, the uncertainty $\Delta q$ seems smaller and that of momentum $\Delta p$ seems larger. This is often used as an example showing that if one of $\Delta q$ and $\Delta p$ is smaller, the other is necessarily larger. However, such a comparison is incorrect. It is meaningless to compare the quantities in two different systems. Furthermore, in the comparison, one confuses the two conceptions: the dimension of a particle and the uncertainty of the particle’s position, which will be made clear in Section 2.3.1 below.

Personally, Eq. 2.9 has only one usage: it can be used to judge if the wave function solved from (1.1) has some error. If the $\Delta x$ and $\Delta p$ calculated through (2.11–2.14) do not meet (2.9), then it is assured that the wave function is not a correct one in QM. What if (2.9) is satisfied? Nothing is explained because (2.9) is originally an inequality that every normalized function ought to satisfy.

2.2.2 There is no way to implement measurement according to the uncertainty relation

People usually say that (2.9) concerns measurement, and it shows that the position and momentum of a particle cannot be precisely simultaneously measured. We recall how the statistics of the measured results are made.

Suppose that there is a sample, Y. We measure its value. The ith measured value is denoted as y_i. After N times of the measurement, this sample’s averaged value and mean square deviation are evaluated by

$\overline{y}=\frac{1}{N}{\displaystyle \sum }_{i=1}^N{y}_i$(2.15)

and

$\Delta y={\left[\frac{1}{N}{\displaystyle \sum }_{i=1}^N{\left(y_i-\overline{y}\right)}^2\right]}^{1/2}.$(2.16)

Now, we have a QM system, and a mechanical quantity F is to be measured. Suppose that an appropriate device is designed, and the value of F can be measured experimentally.

According to QM, the average of the mechanical quantity F in a state ψ is

$\overline{F}=\left(\psi ,F\psi \right).$(2.17)

The inner product is defined by (2.10). In order to evaluate the average (2.17), in principle, at any spatial coordinate x, the value of F should be measured. Actually, one has to check, if possible, the measurement at discrete x points. Hence, the integration is replaced with the form of summation

$\overline{F}={\displaystyle \sum }_{i=1}^N{b}_{i}F\left(x_i\right).$(2.18)

The coefficients $b_i$s are related to the square of the absolute value of the wave function at point $x_i$, ${\left|\psi \left(x_i\right)\right|}^2$. If this can be done, one further measures the values of $F^2\left(x_i\right)$ at point $x_i$s. After these manipulations, one calculates $\overline{F^2}$ by

$\overline{F^2}=\left(\psi ,F^2\psi \right)={\displaystyle \sum }_{i=1}^N{b}_i{F}^2\left(x_i\right).$(2.19)

In this way, the mean square deviation $\Delta F={\left(\overline{F^2}-{\overline{F}}^2\right)}^{1/2}$ can be obtained.

However, what is the meaning of $F\left(x_i\right)$ in (2.18)—measuring the value of a physical quantity at individual coordinates? How can this quantity be measured? The same questions also rise for $F^2\left(x_i\right)$ in (2.19).

In QM, the state of a particle is represented by its wave function. The wave function distributes in space at any time. One cannot say that the wave function is at a point at one instant and another point at the next instant. The physical quantity F belongs to the whole QM system and is not fixed to discrete spatial points.

We do not know how to experimentally measure $\overline{x}$, $\overline{x^2}$, $\overline{p}$, and $\overline{p^2}$ in the way of (2.18, 2.19). In short, Eq. 2.9 cannot correspond to practical measurement. As a matter of fact, people never apply (2.11–2.14) to perform measurements.

Furthermore, from Eq. 2.9 itself, we are unable to see the concepts of “position uncertainty” and “momentum uncertainty”, since it is irrespective to measurement. That is to say, the uncertainty relation (2.9) itself does not contain the concepts of “position uncertainty” and “momentum uncertainty”, since it does not contain the information related to measurement.

The relation (2.9) is sometimes called a principle. However, no one designs an experiment based on this so-called principle.

The conclusion is that Eq. 2.9 is irrespective to measurement.

2.3 The discussions of the uncertainty relation in the literature

We have pointed out above that in [4], there was no rigorous argument and mathematical derivation, and some concepts were confused. However, people a priori believed that the content in this paper was right and the mathematical expression was what Robertson [5] provided. Some textbooks presented (2.9) without explanation [8, 17, 18]. Some others tried various devices in order to explain that this uncertainty relation was correct.

Because the narration in [4] was not clear, when later people talked about the uncertainty relation, they did not have fixed rules, but depended on their own imaginative development. Different people had different explanations. Each explanation was unable to overturn others. Therefore, according to the basic viewpoint I.2, none of the explanations were right. The so-called examples, that were believed to support the uncertainty relation, were just farfetched ex-post explanations.

There are three typical examples giving farfetched explanations: finite-length wave train or a piece of truncated plane wave, single-slit diffraction, and the ground state of hydrogen atom. Before analyzing these examples, we distinguish between two concepts: a particle’s dimension and the uncertainty of its position.

2.3.1 Distinguishing a particle’s dimension and the uncertainty of its position

A particle’s dimension and the uncertainty of its position are two different conceptions.

In QM, a particle at a state is described by a wave function. For each wave function, we are able to roughly define a range in space, outside which the wave function can be regarded as zero. This range is defined as the dimension of this particle at this state. For instance, in an infinitely deep square potential with width a, the dimension of a particle is just the potential width a. For a one-dimensional harmonic oscillator, the ground state wave function is ${\psi }_0\propto {\mathrm{e}}^{-{\alpha }^2{x}^2/2}$. We define the length of the interval $\left[-\frac{\sqrt{2}}{\alpha },\frac{\sqrt{2}}{\alpha }\right]$ as the dimension of this particle in the ground state. In the case that Eq. 2.3 represents the wave packet of a particle, then the dimension of this particle is the length of the interval $\left[-\sqrt{2}{q}_1,\sqrt{2}{q}_1\right]$. As soon as a state is known, the dimension is definitely determined by its wave function.

The De Broglie relation tells us that as long as a particle’s momentum is known, its dimension can be roughly estimated by

$\lambda =h/p.$(2.20)

Here, we regard De Broglie wave length as the particle’s dimension. The De Broglie relation tells us that the larger the momentum of a particle, the less its dimension. It is seen that Eq. 2.2 guessed by Heisenberg was more like the De Broglie relation.

The uncertainty of a particle’s position can be roughly defined as the precision, or error range, of the measured position of the particle.

We stress that a particle’s dimension and the uncertainty of a particle’s position are two different concepts. The former is uniquely determined by the wave function, independent of measurement, whereas the latter depends on the measurement devices and measurement process.

For example, Heisenberg mentioned [4] that when a photon was employed to collide with a particle, “the highest attainable accuracy in the measurement of position is governed by the wavelength of the light.” Thus, roughly speaking, when the light wavelength is λ, the measuring precision of the particle’s position is λ; when the light wavelength is 2λ, the precision will be 2λ.

In literature, the two concepts were confused frequently.

In [4], Heisenberg put down a wave packet, Eq. 2.3, and said that the wave function “differs appreciably from zero only in a region of spread $q_1$ near $q^{\prime }$.” That is to say, $2q_1$ was the dimension of the wave packet. Then, he thought that the relation $p_1{q}_1=\hslash$ limited the precision of the wave packet, where $q_1$ is the precision of measuring the position of the wave packet. So, he equated the dimension and uncertainty. On one hand, the uncertainty $q_1$ ought to be given after measurement and might vary depending on the measurement. On the other hand, $q_1$ was the half dimension of the wave packet and was contained in the function already. In this case, the two concepts were confused.

The confusion of the two concepts, or concept stealing, also occurred later [14, 19].

2.3.2 Wave train with finite length

Figures 1A,B are often used to represent the two states of a moving particle. This picture is utilized to explain the coordinate–momentum uncertainty relation [9]. An intuitive understanding is that the shorter the particle’s dimension or its position uncertainty, the greater its momentum uncertainty. Comparison of Figures 1A,B prompted such a recognition: “we can see very clearly that the better the position is defined, the more poorly is the momentum defined” [9].

FIGURE 1

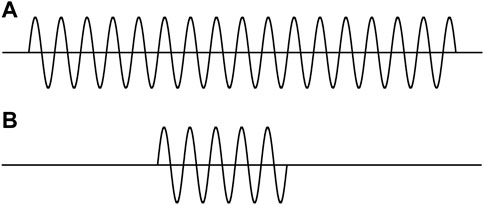
FIGURE 1. Two wave trains (interrupted sine waves) with finite lengths. (A) Longer length. (B) Shorter length.

Here, we are considering a particle with a mass. Figure 1 represents the wave functions of the particle. Following basic viewpoint II.2, the wave functions should be the solutions of Eq. 1.1.

The two pictures in Figure 1 are actually the stationary wave functions in two one-dimensional infinitely deep square potential wells with different widths. Because the widths are different, the two wells are of different Hamiltonians. The two wave functions are in different systems. Comparing the positions and momenta of the particles in the different systems is meaningless. Furthermore, the average of momentum in each state is exactly zero. In this case, discussing the momentum uncertainty is meaningless.

It can be certain that a particle which is marching is not represented by the functions in Figure 1. Thus, the two pictures in Figure 1 are not wave functions in QM for describing a moving particle.

Now, suppose that ${\psi }_a$ and ${\psi }_b$ are two real wave functions in QM, instead of those in Figure 1. Assume that the dimension of ${\psi }_a$ is longer than that of ${\psi }_b$. In this situation, we make following discussion.

First, we should not say that the uncertainty of ${\psi }_a$ is greater than that of ${\psi }_b$, because we have not arranged the measurement. The discussion of the uncertainties of the functions in Figure 1 actually confuses dimension and uncertainty, which is known as concept stealing.

Next, since ${\psi }_a$ and ${\psi }_b$ are two different wave functions, they may either belong to different Hamiltonians, i.e., different systems, or belong to one Hamiltonian but two different states. In either case, comparing the uncertainties of two different states is meaningless.

Another analysis commonly used is to write a function’s Fourier transformation and inverse Fourier transformation [9].

$\psi \left(x\right)={{\displaystyle \int }}_{-\infty }^{\infty }\mathrm{d}p{\mathrm{e}}^{\mathrm{i}px}A\left(p\right).$(2.21)

$A\left(p\right)={{\displaystyle \int }}_{-\infty }^{\infty }\mathrm{d}x{\mathrm{e}}^{-\mathrm{i}px}\psi \left(x\right).$(2.22)

It was analyzed that the more localized the $\psi \left(x\right)$ in space, the more extended the $A\left(p\right)$ in momentum space. An illustration of it was Figure 4 in [13].

Equations 2.21 and 2.22 are Fourier transformation and its inverse of each other. This is a general mathematic property, not a unique property in QM. Furthermore, the localization and extension of the $\psi \left(x\right)$ refer to the dimension, not uncertainty. In the Fourier components, the ranges of momenta and the uncertainties of momenta are confused. Since the explicit form of 2.21 is not given, one does not know if it is a wave function in QM. If it is, the corresponding Hamiltonian should be given. This pair of functions should not be used to explain the uncertainty relation.

2.3.3 Single-slit diffraction

Single-slit experiment is often used to explain the uncertainty relation of a particle [9, 13, 14].

Let the width of a slit be d and the wavelength of particles be λ. The particles go through the slit and diffraction occurs as $\lambda >d$. At the moment when a particle just reaches the position of the slit, its wave function is confined within the slit. Then, the slit width d is regarded as the uncertainty $\Delta x$ in (2.9).

$\Delta x=d.$(2.23)

This is not correct. When a particle is within the slit, its wave function is zero outside of the slit. At this moment, the width d is the dimension of the particle, which is independent of measurement. However, $\Delta x$ must be evaluated by the wave function following 2.12, not simply written in terms of the geometric dimension of the system. Eq 2.23 is again an example that a particle’s dimension is confused with its position’s uncertainty. This confusion also reflects that people subconsciously do not think of the $\Delta x$ in 2.9 as a quantity related to measurement.

If the measurement precisions of the position and momentum of a particle obey the uncertainty relation, these precisions ought to be obtained in experimental measurements. In single-slit diffraction experiment, neither a single particle’s position nor its momentum is measured. The energy of the incident particle is already known. Since the slit width d is known, the diffraction pattern, the distribution of the outgoing particles with diffraction angle, is determined, which can be evaluated by means of the diffraction law before the experiment. The diffraction pattern obtained experimentally is in agreement with the theoretical calculation, and is stable. The single-slit diffraction experiment just lets particles go through a slit, and all the information is known before the experiment. According to viewpoint I.3, this experiment is not a measurement.

The single-slit experiment is just an observation of a phenomenon, not a measuring manipulation. Every wave, when going through a region, the room of which is less than the wave length, yields diffraction. Water waves are the same, and no one would explain the water diffraction by uncertainty relation. The behavior of water waves is explained by the Huygens–Fresnel principle. The wavelength of radio waves can be as long as kilometers, so that they can diffract in a larger room. The distribution of the electromagnetic field can be evaluated by Maxwell equations under specific boundary conditions. These diffractions are irrespective to uncertainty relation.

Suppose that there are two slits, with widths $d_1$ and $d_2$, respectively, and $d_1>d_2$. People may say that the first order diffraction minimum from $d_1$ slit is less than that from $d_2$ slit, which seems to embody the uncertainty relation. Please note that the two slits with widths $d_1$ and $d_2$ are two different systems, because their Hamiltonians are different. Comparing the quantities in two different systems is meaningless. To verify the uncertainty relation, one should measure a particle’s position and momentum simultaneously in one system, which implies that the slit width d remains unchanged,

In [4], Heisenberg considered using photons to probe electrons, a measurement of single particle. In the single-slit experiment, no physical quantity of a single particle is measured. The single-slit diffraction shows the angular distribution of a large number of particles after going through the slit. The distribution is stable, and there is no concept of uncertainty.

Single-slit diffraction is a collective effect of many particles. Trying to explain the uncertainty relation by the single-slit diffraction is a confusion of the single-particle system and many-particle system.

Figure 2.8 in [19] actually showed the distribution of a large number of particles, and not the uncertainty of a particle’s position.

2.3.4 The ground state of hydrogen atom

There is a way of estimating the energy of the ground state of a hydrogen atom [6, 9, 20, 21], which is thought of as an application of the uncertainty relation. The energy of a hydrogen atom reads

$E=\frac{p^2}{2m}-\frac{e^2}{r}.$(2.24)

The dimension of this system is very small, i.e., the r is very small and $\Delta r$ is of the same order of magnitude as r. So, r is replaced by $\Delta r$. Because $\Delta p$ is the same order of magnitude as p, p is replaced by $\Delta p$. Then, the relation

$\Delta r\Delta p\sim \hslash$(2.25)

is used to express $\Delta p$ by $\Delta r$. These replacements recast (2.24) to become

$E\sim \frac{{\hslash }^2}{2m{\left(\Delta r\right)}^2}-\frac{e^2}{\Delta r}.$(2.26)

By taking the derivative of $\Delta r$, the energy minimum is estimated:

$E_{\min }=-\frac{m{e}^4}{2{\hslash }^2}.$(2.27)

In this course, it seems that the uncertainty relation (2.25) is employed. This method is also employed to estimate the ground state energy of a nucleus.

First, this example is irrespective to measurement. It is just an estimation of the energy minimum. Second, the above procedure can be simplified. Using $rp\sim \hslash$, which is actually the De Broglie relation, Eq. 2.24 can be recast to become $E\sim \frac{{\hslash }^2}{2m{r}^2}-\frac{e^2}{r}$. Then, taking the derivative of r leads to the same energy minimum. There is no need for replacing r by $\Delta r$ and replacing p by $\Delta p$. That is to say, the so-called uncertainty relation (2.25) is actually not touched. Third, the r here is actually the dimension of the hydrogen atom. Replacing r by $\Delta r$ is substantially again the confusion of a particle’s dimension and its position uncertainty. Fourth, taking derivative with respect to $\Delta r$ is ridiculous, because $\Delta r$ is, in the sense of either (2.12) or the position uncertainty, not a variable. In the course of derivation, the uncertainty relation (2.25) is used, but a definite result is obtained. This is not a correct mathematical derivation because wrong logic is involved.

We stress once more that a particle’s dimension is a definite quantity, whereas its position’s uncertainty relies on measurement.

2.4 Real measurement experiments

Until now, when discussing the uncertainty relation, often idealized experiments have been concerned, which are irrelative to the experiment of measurement.

Actually, there is no such experiment in which the position and momentum of a particle are measured simultaneously, and their uncertainties are estimated from the measured information, so as to meet Eq. 2.9.

To gain the uncertainty of a particle’s position, one first has to measure its position. Nevertheless, in QM, a particle is described by a wave function, and has a dimension as having been defined in Section 2.3.1. In QM, the concept of a particle’s position is not clearly defined. Because of this fact, in experiments, no measurement of the so-called position of a particle is carried out.

People did measure a particle’s momentum, and estimate the uncertainty from the information of the experiment. However, they did not measure the particle’s position in the same experiment simultaneously. There are two examples [14].

One is that the momentum of a charged particle is measured by deflection in a constant magnetic field, the strength of which is denoted by B. An electron with a charge e enters the magnet after passing through a diaphragm with width $d_1$, and leaves it through another diaphragm with width $d_2$ after having suffered a 180-degree deflection. The trajectory of the electron in the magnet is a semicircle, the radius R of which is equal to half of the distance between the two diaphragms. When the momentum of the electron is measured to be p, the precision is estimated to be

$\Delta p=\frac{p}{R}\left(d_1+d_2\right).$(2.28)

At the instant at which the electron enters the magnet through the first diaphragm, it moves along the y axis. The uncertainty is estimated as

$\Delta y\approx \frac{4\mathrm{\pi }\hslash }{eB{d}_1}.$(2.29)

Thus, it seems that $\Delta y\Delta p\approx 4\pi \hslash \left(1+\frac{d_2}{d_1}\right)$, satisfying the coordinate–momentum uncertainty relation.

However, the right-hand side of Eq. 2.29 has been already known before the measurement. In the experiment, the position of the electron is not detected, and consequently, one is unable to estimate the precision of the position of the electron from measurement. This experiment does not need the knowledge of QM.

Another experiment measuring a particle’s momentum is to let a photon collide with the particle. Before the collision, the photon’s frequency $\nu$ is precisely known and the momentum of the particle is p. Let us suppose that before and after the collision, the photon and the particle move along a line, set as y axis. After the collision, the measured momentum and frequency are $p^{\prime }$ and ${\nu }^{\prime }$, respectively. The precision $\Delta p^{\prime }$ of the $p^{\prime }$ relies on the $\Delta {\nu }^{\prime }$ of ${\nu }^{\prime }$:

$\Delta p^{\prime }\approx mc\frac{\Delta {\nu }^{\prime }}{{\nu }^{\prime }+\nu }.$(2.30)

Assuming that the uncertainty at the time of the collision is $\Delta t$,

$\Delta {\nu }^{\prime }\Delta t\ge 1.$(2.31)

Within the time, the particle can go a distance of

$\Delta y=\frac{\left|p-p^{\prime }\right|}{m}\Delta t.$(2.32)

Substitution of (2.31) into (2.32) leads to the uncertainty of the position of the particle.

$\Delta y\ge \frac{\left|p-p^{\prime }\right|}{m\Delta {\nu }^{\prime }}=\frac{2\mathrm{\pi }\hslash }{mc}\frac{\nu +{\nu }^{\prime }}{\Delta {\nu }^{\prime }}.$(2.33)

It seems that $\Delta y\Delta p^{\prime }\ge \hslash$, meeting the uncertainty relation.

This explanation is problematic. The relation 2.31 has neither rigorous mathematical derivation nor experimental verification. Eq. 2.32 assumes that within the time uncertainty $\Delta t$, the particle goes with the velocity of about $p/m$. Unfortunately, $\Delta t$ is a part of the time period within which the collision occurs. In this period, the particle’s momentum changes drastically, such that the particle’s velocity cannot be estimated in the way of 2.32. This experiment does not involve the particle’s wave function in QM, i.e., the particle is treated as a classical one.

The common features of these two examples are as follows: the measurement of a particle’s position is out of question; the measured particles are actually treated as classical ones. Though the momentum is measured, the estimated $\Delta p$ based on the measurements has nothing to do with Eq. 2.14. In conclusion, these two experiments do not embody the uncertainty relation.

3 Time–energy uncertainty relation

3.1 There is no way to derive the time–energy uncertainty relation

In Ref. [4], having discussed the possible uncertainty relation between the position and momentum, Heisenberg noticed that the product of the coordinate and momentum was of the dimension of angular momentum, and the result was proportional to the Planck constant. He associated the commutator of time and energy, and thus postulated the following commutator:

$\left[t,E\right]=\mathrm{i}\hslash .$(3.1)

Then, imitating the discussion of position and momentum, he thought that the uncertainties of time and energy obeyed, similarly to (2.2), the relation

$tE\sim \hslash .$(3.2)

Later, people accepted his postulation. Furthermore, imitating $\Delta x\Delta p\ge \hslash /2$, people guessed that there was a similar inequality,

$\Delta t\Delta E\ge \hslash /2.$(3.3)

Since $\Delta t$ and $\Delta E$ in 3.3 are uncertainties, they should be quantities related to measurement.

Eq. 3.3 is the so-called time–energy uncertainty, but it is even worse than the coordinate–momentum uncertainty relation.

Heisenberg put forth Eq. 3.1 without any derivation and proof. He did not even present the concrete form of the operator E. Hilgevoord [32] thought that “a relation like” (3.1) “does not occur in quantum mechanics”. His reason was that “there is no Poisson bracket defined between t and H. Consequently, in quantum mechanics, one does not have a relation like” Eq. 3.3. “Accordingly, there is no natural analog for energy and time of the ‘canonical’ uncertainty relations” Eq. 2.9.

At the time when QM was established, Heisenberg himself did not know explicitly what the relation between time and energy was. The mathematical theory of QM had not been accomplished yet. In Heisenberg’s paper [4], there was neither rigorous derivation nor an association with real experiments.

Thus, Heisenberg did not give a convincing conclusion, but people deemed that what he said was right. Later, many people tried to show that there was indeed the inequality (3.3). Everyone raised his own version, without rigorous derivation and experimental correspondence.

Until 1961, “there has been an erroneous interpretation of uncertainty relations of energy and time.” [31] Until 1990, “no general agreement has been reached. One finds physicists claiming that ‘there is no energy–time uncertainty relation at all,’ while others stress, for instance, that the relation is applied quite effectively to the analysis of individual short-lived elementary particles (resonances). Even among those who accept the validity of the relation, there is appreciable disagreement as to meanings of the relation.” [43] Until 1996, “It is generally thought desirable that quantum theory entail an uncertainty relation for time and energy similar to the one for position and momentum. Nevertheless, the existence of such a relation has still remained problematic” [32].

As a matter of fact, up to now, there has been no final verdict with respect to the time–energy uncertainty relation.

It should also be noted that Heisenberg discussed the measurement of individual particles, which can be inferred from his examples about the uncertainty relation (2.9). Subsequently, the discussion of time–energy uncertainty should be for individual particles. However, later, people often discuss many-particle systems.

Now we start to carefully analyze the so-called time–energy uncertainty relation.

First, let the two operators in Eq. (B1) be time and energy, respectively, $F=t$ and $G=H$. Nevertheless, the commutator

$\left[t,H\right]$(3.4)

does not have a definite result. When the Hamiltonian H is independent of time, the result is zero.

$\left[t,H\right]=0,\mathrm{w}\mathrm{h}\mathrm{e}\mathrm{n}H\mathrm{i}\mathrm{s}\mathrm{i}\mathrm{n}\mathrm{d}\mathrm{e}\mathrm{p}\mathrm{e}\mathrm{n}\mathrm{d}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{o}\mathrm{f}\mathrm{t}\mathrm{i}\mathrm{m}\mathrm{e}.$(3.5)

The key is that the coordinate and momentum operators on the left-hand side of (2.1) have explicit forms, no matter what function they act on. By contrast, the form of Hamiltonian H depends on the system under investigation. Hilgevoord noticed that “for a system of particles, one should not demand a communication relation between t and H as a complement to the ones between q and p, nor could there be such a commutation relation.” [32].

Time t is not an operator. According to Pauli, “the introduction of an operator t is basically forbidden, and the time t must necessarily be considered as an ordinary number (‘c-number’).” [12] The average of t in any normalized state is still the time itself, $\overline{t}=\left(\psi ,t\psi \right)=t\left(\psi ,\psi \right)=t$, which makes the average meaningless.

Therefore, there is no way to derive a time–energy uncertainty relation starting from (3.4) in the way in Supplementary Appendix SB.

People may think that although the Hamiltonian H in (3.4) depends on systems, the operator $\mathrm{i}\mathit{\hslash }\frac{\partial }{\partial t}$ on the left-hand side of (1.1) corresponds to Hamiltonian and is independent of systems. There is a definite commutator

$\left[t,\mathrm{i}\hslash \frac{\partial }{\partial t}\right]=\mathrm{i}\hslash .$(3.6)

It seems, then, that imitating the procedure of deriving (2.9) can lead to (3.3). It is not so. Obviously, the averages of time t and its square $t^2$ in any normalized function are still t and $t^2$, so that $\Delta t=0$. It is easily verified that ${\left(\psi ,\mathrm{i}\hslash \frac{\partial }{\partial t}\psi \right)}^2={(\psi ,(\mathrm{i}\hslash \frac{\partial }{\partial t})}^2\psi )$. Therefore, along this routine, one is unable to reach Eq. 3.3.

The conclusion is that there is no way to acquire (3.3) through the procedure in Supplementary Appendix SB. In [44], Eq. 3.3 was just a hypothesis.

3.2 The operator of taking a derivative with respect to time

Here we intend to clarify the implication of the operator $\mathrm{i}\hslash \frac{\partial }{\partial t}$. Someone thought it to be an energy operator and denoted it by [22]

$\widehat{E}=\mathrm{i}\hslash \frac{\partial }{\partial t}.$(3.7)

Following this definition, (3.1) could be understood as (3.5), but this problematic.

When we put down $\frac{\partial }{\partial t}$, it is just an operator taking a derivative with respect to time, without any other physical information. When we put down $\mathrm{i}\hslash \frac{\partial }{\partial t}$, we just let the dimension of the operator become that of energy and make it a Hermitian one, and no physical information is added yet.

An operator should have its eigenvalues and corresponding eigenfunctions under appropriate boundary conditions, such as a momentum operator. The operator $\mathrm{i}\hslash \frac{\partial }{\partial t}$ is not of this property. In [19], an attempt was made to define a time operator, but no eigenvalue and eigenfunction could be given. One may define an operator in some way, but it is meaningless if the operator does not have eigenvalues and eigenfunctions.

Then, why do people think of $\mathrm{i}\hslash \frac{\partial }{\partial t}$ as an energy operator? The reason is based on the fundamental QM equation. In Eq. 1.1, $\mathrm{i}\hslash \frac{\partial }{\partial t}$ is directly connected to Hamiltonian H. When, and only when, in this equation, the operator $\mathrm{i}\hslash \frac{\partial }{\partial t}$ represents the Hamiltonian on the right-hand side of this equation.

It is stressed that $\mathrm{i}\hslash \frac{\partial }{\partial t}$ should not be regarded as a Hamiltonian operator or energy operator carelessly except in the case of (1.1). The following two points are important: (i) according to Eq. (1.1), the operator $\mathrm{i}\hslash \frac{\partial }{\partial t}$ must be related to a specific Hamiltonian of the system under investigation; (ii) only when the operator $\mathrm{i}\hslash \frac{\partial }{\partial t}$ acts on the wave function $\psi$ satisfying (1.1), can it show the meaning of energy, because this action is just that of this specific Hamiltonian on this wave function $\psi$.

When these two points are met, the result calculated through

$\left(\psi ,\mathrm{i}\hslash \frac{\partial }{\partial t}\psi \right)=\left(\psi ,H\psi \right)=\overline{E}$(3.8)

is of the meaning of the energy average in this state.

For any function of $\phi$ not satisfying (1.1), $\left(\phi ,\mathrm{i}\hslash \frac{\partial }{\partial t}\phi \right)$ is not of the meaning of energy.

Since the implication of the operator $\mathrm{i}\hslash \frac{\partial }{\partial t}$ is clarified, we are able to figure out the Pauli difficulty, which is as follows [12, 19].

Let Hamiltonian H be independent of time and its eigenfunction be denoted as ${\psi }_E$.

$H{\psi }_E=E{\psi }_E.$(3.9)

We construct a wave function ${\mathrm{e}}^{-\mathrm{i}\alpha t/\hslash }{\psi }_E$, where α can be any real number. Let the Hamiltonian act on this function $H{\mathrm{e}}^{-\mathrm{i}\alpha t/\hslash }{\psi }_E$, and make the Taylor expansion of the factor ${\mathrm{e}}^{-\mathrm{i}\alpha t/\hslash }$. It follows that

$H{\mathrm{e}}^{-\mathrm{i}\alpha t/\hslash }{\psi }_E=\left(E-\alpha \right){\mathrm{e}}^{-\mathrm{i}\alpha t/\hslash }{\psi }_E.$(3.10)

This result shows that for any $\alpha$, $E-\alpha$ is an eigenvalue of the H. That is to say, the eigenvalues of the H compose a continuous spectrum covering the whole real axis. However, the energy spectrum of the Schrödinger equation (1.1) must have a lower limit. This contradiction is the Pauli difficulty.

We explain how this difficulty is yielded. When taking the Taylor expansion of the factor ${\mathrm{e}}^{-\mathrm{i}\alpha t/\hslash }$ on the left-hand side of (3.10), the commutator $\left[t,H\right]=\mathrm{i}\hslash$ is employed [19], which results on the right-hand side of (3.10). The reason of the Pauli difficulty is the employment of the relation $\left[t,H\right]=\mathrm{i}\hslash$. We have pointed out above that there is no such relation. Eq. 3.8 is one for stationary states, i.e., H is independent of time. So, Eq. 3.5 has to be employed. Starting from the left-hand side of (3.10), one obtains

$H{\mathrm{e}}^{-\mathrm{i}\alpha t/\hslash }{\psi }_E=E{\mathrm{e}}^{-\mathrm{i}\alpha t/\hslash }{\psi }_E,$(3.11)

instead of the right-hand side of (3.10). If

$\psi ={\mathrm{e}}^{-\mathrm{i}\alpha t/\hslash }{\psi }_E$(3.12)

is still an eigenfunction of the H, it must meet (1.1).

$\mathrm{i}\hslash \frac{\partial }{\partial t}{\mathrm{e}}^{-\mathrm{i}\alpha t/\hslash }{\psi }_E=H{\mathrm{e}}^{-\mathrm{i}\alpha t/\hslash }{\psi }_E.$(3.13)

Since ${\psi }_E$ is independent of time,

$\mathrm{i}\hslash \frac{\partial }{\partial t}{\mathrm{e}}^{-\mathrm{i}\alpha t/\hslash }{\psi }_E=\alpha {\mathrm{e}}^{-\mathrm{i}\alpha t/\hslash }{\psi }_E.$(3.14)

The right-hand side of (3.11) and (3.14) should be equal. It is seen that $\alpha =E$; i.e., α must be an eigenvalue of the H, not an arbitrary number.

3.3 The derivations and explanations of the so-called time– energy uncertainty relation in the literature

In [4], the relation (3.3) between the uncertainties of time and energy was guessed without derivation, and the discussion was vague. People believed that what Heisenberg said was right. Some first assumed (3.3), resembling (3.3), and then, tried to derive it by supposing various scenarios. Different persons present the derivation based on their own understanding of the uncertainties of time and energy. Among different derivations, none of them could overturn the others. Therefore, according to viewpoint I.2, none was correct. In fact, every derivation was apparently right but actually wrong. Although it was noticed [31, 32] that some of the derivations were wrong, a thorough analysis is desired.

In the following, we list several derivations and present our comments. In each case, we extract the concepts of $\Delta t$ and $\Delta E$, demonstrating that the concepts differ from person to person. The common features are that almost every proof has concept stealing and that no one made the measurements that could match the formulas.

Before the introduction, we emphasize that in inequality (B14),

$\Delta A\Delta E\ge \frac{1}{2}\left|\langle \left[H,A\right]\rangle \right|,$(3.15)

and $\Delta A$ is defined by

$\Delta A=\sqrt{\overline{A^2}-{\overline{A}}^2}={\left[\left(\psi ,A^2\psi \right)-{\left(\psi ,A\psi \right)}^2\right]}^{1/2}.$(3.16)

It is a definite quantity determined by the known wave function but not a variable. One more point should be stressed that $\Delta A$ is finite, meaning that it is neither infinitely small nor infinitely large.

1) Using the concept of wave packet [14, 15, 19]:

This is for a single particle. Suppose that the particle is a wave packet with width $\Delta x$, moving along the x axis with speed v. The time it passes one point in the x axis is not definitely determined, but has an uncertainty

$\Delta t\approx \frac{\Delta x}{v}.$(3.17)

On the other hand, the wave packet has some extension in momentum space, so that the particle’s energy has an uncertainty $\Delta E$.

$\Delta E\approx \frac{\partial E}{\partial p}\Delta p=v\Delta p.$(3.18)

The product of these two equations yields

$\Delta t\cdot \Delta E\approx \Delta x\cdot \Delta p.$(3.19)

Then Eq. 2.9 is used to result in (3.3), “which limits the product of the spread $\Delta E$ of the energy spectrum of the wave packet and the accuracy $\Delta t$ of the prediction of the time of passage at a given point” [19].

Comment:

Since the right-hand side of (3.19) is just (2.9), the $\Delta x$ and $\Delta p$ ought to be evaluated in the way of (3.16). However, the $\Delta x$ from (3.17) is the dimension of the wave packet and the $\Delta p$ from (3.18) is the increment of the momentum, both not being the meanings of uncertainties. The concept stealing is obvious.

The use of (3.19) means that Eqs. (2.9) and (3.3) ought to be compatible. However, the two relations were thought to express two different and incompatible viewpoints in [19].

Here, $\Delta t$ is the time a wave packet needs to pass through a distance. The $\Delta E$ is the increment of energy irrespective to measurement.

2) Making use of the formulas in Supplementary Appendix SB [3, 14, 19, 21, 23]:

When a quantity A varies, the time it needs to change $\Delta A$ is

$\Delta t=\frac{\Delta A}{\left|\mathrm{d}\langle A\rangle /\mathrm{d}t\right|}.$(3.20)

We make use of the formula

$\frac{\mathrm{d}\langle A\rangle }{\mathrm{d}t}=\frac{1}{\mathit{\hslash }}\left|\langle \left[H,A\right]\rangle \right|.$(3.21)

Then, by (3.15)

$\Delta A\Delta E\ge \frac{1}{2}\left|\langle \left[H,A\right]\rangle \right|=\frac{\mathit{\hslash }}{2}\frac{\mathrm{d}\langle A\rangle }{\mathrm{d}t}.$(3.22)

The combination of these three equations results in

$\Delta t\Delta E\ge \frac{\mathit{\hslash }}{2}.$(3.23)

Comment:

We point out that Eq. 3.20 is strange. In the denominate and following equations, A is regarded as an operator, and the numerator should be written as $\Delta \langle A\rangle$. It is not clear from which fundamental formula (3.20) was derived.

In Eq. 3.20, the $\Delta t$ is variable and is the time increment when A has an increment $\Delta A$. In (3.22), both the $\Delta A$ and $\Delta E$ should be calculated by (3.16), and are not variable. The $\Delta A$ in (3.20) is different form that in (3.22). The concept confusion happens from (3.20) to (3.22). Furthermore, both the $\Delta t$ and $\Delta E$ do not have the meanings of uncertainty.

The authors of [45] recast (3.22) to be the form $\Delta t\Delta E\ge \frac{\hslash }{2}\frac{\mathrm{d}\langle A\rangle }{\mathrm{d}A}$ by replacement of the $\Delta A$ by $\mathrm{d}A$ and of the $\mathrm{d}t$ by $\Delta t$, which seemed to be a smart way to obtain (3.23), but this was wrong. The $\mathrm{d}A$ was a variable and could be taken as infinitesimal, but the $\Delta A$ on the left-hand side of (3.22) is calculated by (3.16), so it is finite and not a variable. This distinction stands also for the $\mathrm{d}t$ and $\Delta t$. Therefore, the replacements were illegal. The authors of [45] addressed that the quantity A in (3.20) could be arbitrary: “its physical meaning depending thus on the choice of this quantity.” However, the A could not be t.

Here, the $\Delta t$ is a time increment when a quantity A changes $\Delta A$, and the $\Delta E$ is calculated by (3.16), both being irrespective to measurement.

3) Making use of the difference of two energy levels [3, 14]:

Suppose that a particle had two energy levels, $E_1$ and $E_2$. Their difference is

$\Delta E=\left|E_1-E_2\right|.$(3.24)

When the two states superpose, the particle oscillates between the two states and the oscillation period is

$\tau =\frac{\hslash }{\Delta E}.$(3.25)

Then, $\Delta E$ is explained as the uncertainty of the energy level, and τ is explained as the time one needs to observe the system’s variation. Eq. 3.25 is recast to be

$\tau \Delta E\approx \hslash ,$(3.26)

which is explained as the time–energy uncertainty relation.

Comment:

Here, the τ is the oscillation period between two energies of the system, and the $\Delta E$ is the difference of the two energies, both being not of the meaning of uncertainty.

Eq. 3.26 is simply the copy of (3.25), but the concepts are endowed different connotations, i.e., concept stealing. In Eq. 3.26, the $\Delta E$ and τ are respectively said to be the uncertainties of energy and time, which are created out of nothing.

4) Using the concept of “time packet” [6]:

It was assumed that a particle’s behavior was a pulse or ‘time packet’.

“We consider the case such that $\psi \left(t\right)$ is a pulse or ‘time packet’, which is negligible except in a time interval $\Delta t$.” This time packet can be expressed as a superposition of monochromatic waves of angular frequency $\omega$ by the Fourier integral

$\psi \left(t\right)={\int }_{-\infty }^{\infty }\mathrm{d}\omega G\left(\omega \right){\mathrm{e}}^{-\mathrm{i}\omega t},$(3.27)

where the function $G\left(\omega \right)$ is given by

$G\left(\omega \right)=\frac{1}{\sqrt{2\pi }}{{\displaystyle \int }}_{-\infty }^{\infty }\mathrm{d}t\psi \left(t\right){\mathrm{e}}^{\mathrm{i}\omega t}.$(3.28)

As the $\psi \left(t\right)$ takes only significant values for a duration $\Delta t$, it follows from the general properties of Fourier transformations that $G\left(\omega \right)$ is only significant for a range of angular frequencies such that

$\Delta \omega \Delta t\ge 1.$(3.29)

Since

$E=\hslash \omega ,$(3.30)

the width of the distribution in energy, $\Delta E$, satisfies the time–energy uncertainty relation

$\Delta E\Delta t\ge \hslash .”\left[6\right].$(3.31)

In this way, it seems that the uncertainty relation can be proved.

Comment:

Here, the $\Delta t$ is the time the particle exists—from its appearance to its vanishing, and the $\Delta E$ is the width of the distribution of the particle’s energy. Both the concepts are strange, because we cannot image what the system is and how its Hamiltonian is written.

It is well known that a light pulse can be produced experimentally. But what about a massive particle? This imagined pulse or ‘time packet’ of a massive particle is not possible. No one is able to find a Hamiltonian H such that the solution $\psi \left(t\right)$ of Eq. 1.1 is a ‘time packet’. If someone knew such a Hamiltonian, he would have put it down.

5) Making use of the interaction between the measured system and measuring device [10, 24, 46]:

The measured system and measuring device are combined to become a larger system. In other words, the whole system is divided into two parts, measured system and measuring devices, the energies of which are E and ε, respectively. “We suppose that it is known that at some instant these parts have definite values of the energy, which we denote by E and ε, respectively.” “The energies E, ε, on the other hand, can be measured to any degree of accuracy at any instant” [10].

Because of the interaction between the two parts, each time the measurement would cause the energy E to change, say, to be $E^{\prime }$. It was treated as the transition between the energies E and $E^{\prime }$. The transition probability for a system subject to a periodic perturbation was given by the formula (43.2) in [10]. By taking $\omega =0$ in this formula, the transition probability was

$\frac{{\sin }^2\left[\left(E^{\prime }-E\right)t/2\hslash \right]}{{\left(E^{\prime }-E\right)}^2}.$(3.32)

According to this formula, “The most probable value of $E^{\prime }-E$ is of the order of the magnitude of $\hslash /t$.” [10]. Subsequently, it was believed that

$\left|E+\epsilon -E^{\prime }-{\epsilon }^{\prime }\right|\Delta t\sim \hslash .$(3.33)

This was called the “uncertainty relation for energy.”

Comment:

According to this result, the energy conservation in QM was understood in an alternative way. “It shows that, in quantum mechanics, the law of conservation of energy can be verified by the means of two measurements only to an accuracy of the order of $\hslash /\Delta t$, where $\Delta t$ is the time interval between the measurements.” “The quantity $\left(E+\epsilon \right)-\left(E^{\prime }+{\epsilon }^{\prime }\right)$ in (44.1) is the difference between two exactly measured values of the energy $E+\epsilon$ at two different instants, and not the uncertainty in the value of the energy at a given instant” [10]. However, “the statement that the conservation law of energy may be violated by an amount $\delta E$ during a time $\delta t\cong \hslash /\delta E$…… confuses the energy of the actual system with the energy of the unperturbed system” [32].

It was believed that the relation $\Delta t\Delta E>\mathit{\hslash }$ “does not signify that the energy cannot be known exactly at a given time (for in that case the concept of energy would have no meaning), nor does it means that the energy cannot be measured with arbitrary accuracy within a short time” [10].

This scenario is totally different from the above ones. Here the energy of a system can be measured in any accuracy, which contradicts the uncertainty of energy.

According to [10, 46], because the measured system is interacted by the measuring device, its energy shifts after the measurement. The amount of the shift and the time interval between adjacent measurements form the time–energy uncertainty relation: “the smaller the time interval $\Delta t$, the greater the energy change that is observed” [10]. This brings a question that why the shorter the time interval, the greater the energy shift.

In the transition probability formula, the difference of two energy levels is used, which is not the energy uncertainty. Furthermore, in [10], Eq. (42.3) was valid under a condition of (42.1) which required that the frequency ω should not be zero. It is hard to understand the transition expressed by (3.32) without releasing or absorbing photons.

Equations (3.32) and (3.33) contradict each other. Eq. 3.32 means that there were two energy levels $E$ and $E^{\prime }$ in the system. The existence of the two energy levels was determined by the Hamiltonian of the system, independent of whether the transition happened or not. What is more, it was thought that $\Delta \left(E-E^{\prime }\right)>\hslash /\Delta t$ [46], which meant both $E$ and $E^{\prime }$ had some uncertainties. However, Eq. 3.33 reflected that there was only one energy level E, which, after the measurement, shifted to $E^{\prime }$. That is to say, before the measurement, there was no energy level $E^{\prime }$, and after the measurement, there was no energy level E.

Here, the $\Delta t$ is the lifetime of an energy level. The $\Delta E$ is the energy shift caused by the measurement, and meanwhile, it is the difference of two energy levels.

This scenario was criticized in [31].

In [10, 46], following the above content, momentum variation was discussed by collision as an example. Nevertheless, Eq. 3.32 was obtained by perturbation theory, while collision could not be treated by the perturbation theory.

The last part of Section 44 in [10] related the difference $E-E^{\prime }$ to the lifetime of energy level. This recognition, also seen in other textbooks [6, 7], is going to be expounded in next subsection.

All in all, it is seen from the entries 1) – 5) that people presumed the relation (3.3) and then designed certain ideas to scrape it together. None of the above scenarios were connected to a real measurement. All of them are incorrect.

Different people had different explanations of the $\Delta t$ and $\Delta E$ in (3.3). In one textbook, more than one explanation arose [3, 10, 14, 18]. This fully revealed the serious confusion regarding these concepts. Some other narrations are as follows.

In [13], the relation (3.3) was given without derivation. The explanation was that “an energy determination that has an accuracy $\Delta E$ must occupy at least a time interval $\Delta t\sim \hslash /\Delta E$; thus if a system maintains a particular state of motion not longer than a time $\Delta t$, the energy of the system in that state is uncertain by at least the amount $\Delta E\sim \hslash /\Delta t$, since $\Delta t$ is the longest time interval available for the energy determination.” Here the $\Delta t$ had the implication of the lifetime of the state of the system.

In [14], the $\Delta E$ was regarded as the uncertainty of the measured energy or the change of the energy of the system, but meanwhile, the $\Delta E$ is the difference of two energy levels, which could be both measured precisely.

In [19], there were contradictory statements. One was that “the energy of a system can be determined with arbitrary precision at any time.” The other was that Eq. 3.3, written as $\tau \Delta E\sim \hslash$, “is the lifetime–width relation for unstable systems, i.e., systems which are not stationary and do not correspond to a well-defined value of the energy but rather to an energy spectrum with a certain spread $\Delta E$, called the level width. The mean lifetime τ of the stable (or metastable) state here plays the role of the characteristic time considered above”. “In this case, the accuracy $\Delta E$ of the energy measurement is connected with the time $\Delta t$ required for the measurement itself.”

In [24], the $\Delta t$ and $\Delta E$ were replaced by $\delta t$ and $\delta E$, respectively. “The time–energy uncertainty relation relates the rate at which the state of a system changes to the uncertainty $\delta E$ of its energy. If the state of the system changes appreciably during a time interval $\delta t$, then the time–energy uncertainty relation states that $\delta t\delta E\ge \hslash$. I have written $\delta t$ and $\delta E$, rather than $\Delta t$ and $\Delta E$, to emphasize that these are not standard deviations.” Here, the time interval $\delta t$ was regarded as the lifetime of the system.

3.4 The concept of the lifetime of an energy level

One explanation of the $\Delta t$ in (3.3) was the lifetime of an energy level [16, 31, 32], and correspondingly, one of explanations of the $\Delta E$ was the width of the energy level [14, 19, 31, 32]. It is necessary to clarify the concept of the lifetime of an energy level [47, 48].

In Eq. 3.3, the $\Delta E$, as mentioned in Section 3.3, at least has three explanations: the energy shift, energy width, and difference of two energy levels. All the explanations concern the real part of the energy. Unfortunately, the lifetime of a state is irrelative to the real part of the energy of the state. Let us recall the definition of the lifetime of a state.

In a wave function, there is a factor containing energy E and time t, ${\mathrm{e}}^{-\mathrm{i}Et}$. If the energy is a complex number,

$E=\epsilon -\mathrm{i}\gamma ,$(3.34)

then

${\mathrm{e}}^{-\mathrm{i}Et/\hslash }={\mathrm{e}}^{-\mathrm{i}\epsilon t/\hslash }{\mathrm{e}}^{-\gamma t/\hslash }.$(3.35)

The wave function decays with time exponentially. After a time period of about

$\tau \sim \hslash /\gamma ,$(3.36)

the wave function almost disappears. Due to this fact, we say that the lifetime of this state is about $\mathit{\hslash }/\gamma$.

Here, we emphasize the following points: (1) The lifetime τ of a state is determined by the imaginary part, not the real part, of the state’s energy. (2) The lifetime is defined by (3.36). It is not the case that we have first the two quantities $\Delta E$ and τ, which then meet Eq. 3.3. (3) The lifetime of the state is determined by the state itself, irrespective of the measurement process. (4) The lifetime reflects the decay of the state wave function, but is not related to the shift of the energy. From the lifetime, one is unable to gain the information of energy shift. (5) The lifetime does not involve energy level broadening, which is a property of the real part of the energy. From the lifetime, one is unable to gain the information of the energy level broadening. (6) The energy (3.34) has an imaginary part. This fact shows that this is a many-particle system.

In a many-particle system, there are interactions between particles, such as electron–phonon interaction, collision, and so on. Due to the interactions, elementary excitations are formed, and they are of finite lifetimes. An elementary excitation’s lifetime is determined by the imaginary part of its energy [47, 48].

A detailed analysis was given in [25]. The interactions inside a system result in transitions between energy levels. The transitions in turn cause an energy shift and broadening. Now we introduce the analysis.

Suppose that in a system there are two states denoted by a and b, respectively. When there is no interaction, both are stationary states, and their energies are $E_a$ and $E_b$, respectively. When there are interactions, the transition between them can occur. Suppose that a and b are, respectively, the initial and final states of the transition. In the course of the transition, the initial state a will vary. The state after the change is denoted by ${\mathrm{a}}^{\prime }$ with energy $E_a^{\prime }-\mathrm{i}\Gamma$, i.e., energy changes,

$E_a\to E_a^{\prime }-\mathrm{i}\mathrm{\Gamma }.$(3.37)

The change yields not only a shift of the energy but also an imaginary part of the energy, the latter being determined by transition probability. This imaginary part determines the lifetime of the state ${\mathrm{a}}^{\prime }$. This is because the amplitude of the state ${\mathrm{a}}^{\prime }$ contains a factor

${\mathrm{e}}^{-\mathrm{i}\left(E_a^{\prime }-\mathrm{i}\Gamma \right)t/\hslash }={\mathrm{e}}^{-\mathrm{i}{E}_a^{\prime }t/\hslash }{\mathrm{e}}^{-\mathrm{\Gamma }t/\hslash }.$(3.38)

It is seen that in about time $\Delta t_a$, where

$\mathrm{\Gamma }\Delta t_a\sim \hslash ,$(3.39)

the state ${\mathrm{a}}^{\prime }$ will almost vanish. Therefore, $\Delta t_a\sim \hslash /\Gamma$ is the lifetime of the state ${\mathrm{a}}^{\prime }$.

Meanwhile, the energy of the final state b has a broadening with a Lorentz line shape, the half height width of which happens to be Γ, too. We denote this half height width by $\Delta E_b$.

$\Delta E_b=\mathrm{\Gamma }.$(3.40)

Then,

$\Delta E_b\Delta t_a\sim \hslash .$(3.41)

Equations (3.39) and (3.41) seem to be the form of the time–energy uncertainty relation, but they are not. The former is the definition of the $\Delta t_a$, the lifetime of state ${\mathrm{a}}^{\prime }$. The latter relates the lifetime of state ${\mathrm{a}}^{\prime }$ and the half height width of the energy of state b. Among these quantities, none has the physical meaning of uncertainty, and none is to be determined by measurement.

4 Discussion

People subjectively thought that what Heisenberg said in his paper [4] were certainly right, and the inequality that Robertson derived [5] was just what Heisenberg wanted to express. Under these presumptions, people tried their best to present explanations to the coordinate–momentum uncertainty relation, and to derive the so-called time–energy uncertainty relation. There is no uniform and standard explanation. Several scenarios were proposed. From the source, the discussions in Heisenberg’s primary paper [4] were ambiguous. The explanations and derivations are of the following defects.

One mathematical symbol has different explanations, that is, concept stealing. In the coordinate–momentum uncertainty relation, the $\Delta x$ should be the uncertainty of measuring a particle’s position, but is often replaced by the dimension of that particle, the range that the particle’s wave function is not zero; the $\Delta p$ should be the uncertainty of measuring a particle’s momentum, but is often replaced by the width of the momentum range of the Fourier component of a wave packet. In the so-called time–energy uncertainty relation, the $\Delta t$ is explained as either the time that a wave packet goes through a space point, or the time needed for measuring an energy level, or the lifetime of an energy level; the $\Delta E$ is explained as energy shift, or the difference of two energies, or energy width.

A truncated plane wave with finite length for a moving particle is not the wave functions in QM.

All the derivations of the so-called time–energy uncertainty relation are not rigorous, but simply patchwork. The last words in [31], “energy can be measured reproducibly in an arbitrarily short time”, utterly negated the so-called time–energy uncertainty relation.

No real measurement was touched. Gedanken experiments were assumed, which could not verify the uncertainty relations. The application of the coordinate–momentum uncertainty relation was just to make some ex-post explanations to well-known phenomena such as single-slit diffraction. Even in these explanations there were confusions of the concepts.

In discussion of the time–energy uncertainty relation, the problems in one-particle and many-particle systems were confused.

There is more than one explanation for an uncertainty relation. This fact itself illustrates that none of the explanations is right. If one explanation was right, the other would be no longer displayed.

We have mentioned in Introduction the reasons that people do not realize the problem of the uncertainty relations. The uncertainty relations have never been related to real measurements, and solving problems and establishing new theories in QM do not resort to the uncertainty relations.

Up to now, the quantum measurement problem, that what precisely happens when a quantum measurement is performed, is still in dispute [49, 50], but the so-called uncertainty principle for quantum measurement was proposed long before. That is strange!

5 Conclusion

Heisenberg’s primary paper did not explicitly present an uncertainty relation.

Robertson derived the coordinate–momentum uncertainty relation $\Delta x\Delta p\ge \hslash /2$. In this relation, $\Delta x$ and $\Delta p$ are uniquely determined by the wave function, and are not variable. In this relation, there is no quantity that needs to be gained by measurement. This relation does not need any knowledge of Heisenberg’s primary paper and of measurement. The conclusion is that the coordinate–momentum uncertainty relation is irrespective to measurement.

There is no definite result for the commutation of time and Hamiltonian $\left[t,H\right]$. This is because Hamiltonian depends on systems. The operator $\mathrm{i}\hslash \frac{\partial }{\partial t}$ can represent a concrete Hamiltonian H only when the $\mathrm{i}\hslash \frac{\partial }{\partial t}$ and H are connected in one quantum mechanics equation. The discussions of the time–energy uncertainty relation in the literature are incorrect. The conclusion is that there is no so-called time–energy relation.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author contributions

H-YW carried out the whole work of this article.

Funding

This work was supported by the National Natural Science Foundation of China (Grant no. 12234013).

Conflict of interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2022.1059968/full#supplementary-material

References

1. Heisenberg W. Quantum-theoretical Re-interpretation of kinetic and mechanical relations. Z Phys (1925) 333: 879-893. In: Van Waerden BL, editor. Source of quantum mechanics, New York: Dover Publications Inc. (1968). p. 261–276.

Google Scholar

2 Aitchison I. J. R., MacManus D. A., Snyder T. M. Understanding Heisenberg’s “magical” paper of july 1925: A new look at the calculational details. Am J Phys (2004) 72:1370–9. doi:10.1119/1.1775243

CrossRef Full Text | Google Scholar

3 Razavy M. Heisenberg’s quantum mechanics. London, UK: World Scientific Publishing Co. Pte. Ltd. (2011).

Google Scholar

4 Heisenberg W. Uber den anschaulichen Inhalt der quantentheoretischen Kinematik und Mechanik. Zeitschrift fur Physik (1927) 43: 172-198. “The Physical Content of Quantum Kinetics and Mechanics”. In: Wheeler JA, Zurek WH, Editor. Quantum Theory and Measurement. Princeton: Princeton University Press (1983). 62-84.

CrossRef Full Text | Google Scholar

5 Robertson H. P. The uncertainty principle. Phys Rev (1929) 34:163–4. doi:10.1103/PhysRev.34.163

CrossRef Full Text | Google Scholar

6 Bransden B. H., Joachain C. J. Quantum mechanics. 2nd ed. London, UK: Pearson Education Limited (2000).

Google Scholar

7 Bes D. R. Quantum mechanics A modern and concise introductory course. Berlin, Germany: Spinger-Verlag (2004).

Google Scholar

8 Hameka H. F. Quantum mechanics. New York, NY, USA: John Wiley & Sons (1981). p. 55–6.

Google Scholar

9 Wichmann E. H. Quantum Physics Berkeley Physics Course, 4. New York: McGraw-Hill (1971).

Google Scholar

10 Landau L. D., Lifshitz F. M. Quantum Mechanics, Oxford, UK: Pergamon Press (1977). p. 2, 47, 157.

Google Scholar

11 Weinberg S. Lectures on quantum mechanics. 2nd ed. Cambridge, UK: Cambridge University Press (2015).

Google Scholar

12 Pauli W. General principles of quantum mechanics. Berlin, Germany: Springer-Verlag (1980). p. 63.

Google Scholar

13 Schiff L. I. Quantum mechanics. New York, NY, USA: McGraw-Hill Book Company Inc. (1949).

Google Scholar

14 Messiah A. Quantum mechanics Vol. I. Amsterdam: North-Holland Pub. Co. (1961).

Google Scholar

15 Blinder S. M. Foundations of quantum mechanics. London, UK: Academic Press (1974).

Google Scholar

16 Band Y. B., Avishai Y. Quantum Mechanics with Application to Nanotechnology and Information Science. Amsterdam: Elsivier Ltd (2013). p. 68, 297.

Google Scholar

17 Bohm A. Quantum mechanics: Foundations and applications. 3rd ed. New York, NY, USA: Springer-Verlag (1993).

Google Scholar

18 Zettili N. Quantum mechanics: Concepts and applications. New York, NY, USA: John Wiley & Sons (2001). p. 28.

Google Scholar

19 Auletta G., Fortunato M., Parisi G. Quantum Mechanics. Cambridge, UK: Cambridge University Press (2009). p. 82–89, 130–40.

Google Scholar

20 Scheck F. Quantum physics. 2nd ed. Berlin, Heidelberg: Springer-Verlag (2013). Chap. 1.

Google Scholar

21 Ballentine L. E. Quantum Mechanics A Modern Development. 2nd ed., Singapore: World Scientific Publishing Co. Pte. Ltd. (2015). p. 223-227, 271, 345.

Google Scholar

22 Liboff R. L. Introductory quantum mechanics. San Fransisco: Holden-Day, Inc. (1980).

Google Scholar

23 Kroemer H. Quantum mechanics for engineering, materials science, and applied physics. Englewood Cliffs, NJ, USA: Prentice-Hall (1994). p. 249–50.

Google Scholar

24 Mandl F. Quantum mechanics. New York, NY, USA: John Wiley & Sons (1992). p. 82–6.

Google Scholar

25 Abers E. S. Quantum mechanics. Upper Saddle River, NJ, USA: Pearson Education, Inc. (2004).

Google Scholar

26 Beck M. Quantum mechanics theory and experiment. New York, NY, USA: Oxford University Press (2012).

Google Scholar

27 Manoukian E. B. Quantum theory A wide spectrum. The netherland. Dordrecht: Springer (2006).

Google Scholar

28 Peres A. Quantum theory: Concepts and methods. New York, NY, USA: Kluwer Academic Publishers (2002).

Google Scholar

29 Cohen-Tannoudji G., Diu B., Laloë F. Quantum Mechanics, 1. New York, NY, USA: John Wiley & Sons (1977). p. 250.

Google Scholar

30 Hecht K. T. Quantum mechanics. New York, NY, USA: Springer-Verlag (2000). p. 24.

Google Scholar

31 Ahronov Y., Bohm D. Time in the quantum theory and the uncertainty relation for time and energy. Phys Rev (1961) 122:1649–58. doi:10.1103/PhysRev.122.1649

CrossRef Full Text | Google Scholar

32 Hilgevoord J. The uncertainty principle for energy and time. Am J Phys (1996) 64:1451–6. doi:10.1119/1.18410

CrossRef Full Text | Google Scholar

33 Schrödinger E. Ann Phys (1926). 386 (18): 109–139.; Quantisation as a problem of proper values (Part IV). In: Collected papers on wave mechanics. London and Glasgow: Blackie & son Limited (1926). p. 102–123.

Google Scholar

34 Wang H. Y. New results by low momentum approximation from relativistic quantum mechanics equations and suggestion of experiments. J Phys Commun (2020) 4:125004. doi:10.1088/2399-6528/abd00b

CrossRef Full Text | Google Scholar

35 Wang H. Y. The modified fundamental equations of quantum mechanics. Phys Essays (2022) 35(2):152–64. doi:10.4006/0836-1398-35.2.152

CrossRef Full Text | Google Scholar

36 Wang H. Y. Fundamental formalism of statistical mechanics and thermodynamics of negative kinetic energy systems. J Phys Commun (2021) 5:055012. doi:10.1088/2399-6528/abfe71

CrossRef Full Text | Google Scholar

37 Wang H. Y. Solving Klein’s paradox. J Phys Commun (2020) 4:125010. doi:10.1088/2399-6528/abd340

CrossRef Full Text | Google Scholar

38 Wang H. Y. Macromechanics and two-body problems. J Phys Commun (2021) 5:055018. doi:10.1088/2399-6528/ac016b

CrossRef Full Text | Google Scholar

39 Wang H. Y., Virial theorem and its symmetry. J. North China Inst Sci Technology (2021) 18(4):1–10. (in Chinese).

Google Scholar

40 Wang H. Y. Resolving problems of one-dimensional potential barriers based on Dirac equation. J North China Inst Sci Technology (2022) 19(1):97–107. (in Chinese) doi:10.19956/j.cnki.ncist.2022.01.016

CrossRef Full Text | Google Scholar

41 Wang H. Y. Evaluation of cross section of elastic scattering for non-relativistic and relativistic particles by means of fundamental scattering formulas. astp (2022) 16(3):131–63. doi:10.12988/astp.2022.91866

CrossRef Full Text | Google Scholar

42 Wang H. Y. There is no vacuum zero-point energy in our universe for massive particles within the scope of relativistic quantum mechanics. Phys Essays (2022) 35(3):270–5. doi:10.4006/0836-1398-35.3.270

CrossRef Full Text | Google Scholar

43 Busch P. On the energy-time uncertainty relation, Part I: Dynamical time and time indeterminacy. Found Phys (1990) 20(1):1–32. doi:10.1007/BF00732932

CrossRef Full Text | Google Scholar

44 Busch P. On the energy-time uncertainty relation. Part II: Pragmatic time versus energy indeterminacy. Found Phys (1990) 20(1):33–43. doi:10.1007/BF00732933

CrossRef Full Text | Google Scholar

45 Mandelstam L., Tamm I. The uncertainty relation between energy and time in nonrelativistic quantum mechanics. J Phys (Ussr) (1945) 9:249–54.

Google Scholar

46 Landau L., Peierls R. Erweiterung des Unbestimmtheisprinzips fur die relativistische Quantentheorie. Z Phys (1931) 69: 56; translated into English: Lev Davidovich Landau and Rudolf Peierls, Extension of the uncertainty principle to relativistic quantum theory in Quantum Theory and Measurement. edited by John Archibald Wheeler and Wojciech Hubert Zurek. Princeton: Princeton University Press (1983). 465-472.

Google Scholar

47 Mahan G. D. Many-particle physics. 2nd ed. New York, NY, USA: Plenum Press (1990).

Google Scholar

48 Wang H. Y. Green’s function in condensed matter physics. Beijing: Alpha Science International ltd. and Science Press (2012).

Google Scholar

49 Mermin N. D. There is no quantum measurement problem. Phys Today (2022) 76(6):62–3. doi:10.1063/PT.3.5027

CrossRef Full Text | Google Scholar

50 Carroll S. M. Addressing the quantum measurement problem. Phys Today (2022) 75(7):62–3. doi:10.1063/PT.3.5046

CrossRef Full Text | Google Scholar