
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Phys. , 05 January 2023
Sec. Nuclear Physics
Volume 10 - 2022 | https://doi.org/10.3389/fphy.2022.1057603
This article is part of the Research Topic Using High Energy Density Plasmas for Nuclear Experiments Relevant to Nuclear Astrophysics View all 10 articles
 Daniel T. Casey1*
Daniel T. Casey1* Chris R. Weber1
Chris R. Weber1 Alex B. Zylstra1
Alex B. Zylstra1 Charlie J. Cerjan1
Charlie J. Cerjan1 Ed Hartouni1
Ed Hartouni1 Matthias Hohenberger1
Matthias Hohenberger1 Laurent Divol1
Laurent Divol1 David S. Dearborn1
David S. Dearborn1 Neel Kabadi2
Neel Kabadi2 Brandon Lahmann3
Brandon Lahmann3 Maria Gatu Johnson3
Maria Gatu Johnson3 Johan A. Frenje3
Johan A. Frenje3The enhancement of fusion reaction rates in a thermonuclear plasma by electron screening of the Coulomb barrier is an important plasma-nuclear effect that is present in stellar models but has not been experimentally observed. Experiments using inertial confinement fusion (ICF) implosions may provide a unique opportunity to observe this important plasma-nuclear effect. Herein, we show that experiments at the National Ignition Facility (NIF) have reached the relevant physical regime, with respect to the density and temperature conditions, but the estimated impacts of plasma screening on nuclear reaction rates are currently too small and need to be increased to lower the expected measurement uncertainty. Detailed radiation hydrodynamics simulations show that practical target changes, like adding readily available high-Z gases, and significantly slowing the inflight implosion velocity, while maintaining inflight kinetic energy, might be able to push these conditions to those where plasma screening effects may be measurable. We also perform synthetic data exercises to help understand where the anticipated experimental uncertainties will become important. But challenges remain, such as the detectability of the reaction products, non-thermal plasma effects, species separation, and impacts of spatial and temporal gradients. This work lays the foundation for future efforts to develop an important platform capable of the first plasma electron screening observation.
For decades, numerous research groups have identified plasma-electron screening as an important physical process worth pursuing in high-energy-density (HED) experiments. For example, the National Research Council [1] describes a “raging debate” surrounding questions related to plasma screening models and that HED experiments may be well suited to help. In fact, ideas emerge periodically from the literature challenging the established models [2–7], but the debate is hampered by the complete lack of experimental data. This situation is exacerbated by the “electron screening puzzle” caused by discrepancies observed in terrestrial laboratory target experiments [8–15] when compared to screening theory [5, 6]. This makes measurements made directly in the plasma environments of stellar interiors particularly important so that stellar plasma screening models can be tested against data.
The screening process becomes important when nuclei undergo a fusion reaction as their kinetic energy overcomes the repulsive Coulomb force and exploits favorable binding energy. In many HED environments where these reactions are occurring, such as in stellar cores or inertial confinement fusion implosions, the nuclei are embedded in a plasma. The background electrons in this plasma can lower the Coulomb barrier, enhancing the fusion reactivity.
Plasma screening of nuclear reactions occurs when ions within the plasma interact with a Coulomb potential energy of
where
A similar screening effect occurs in accelerators that study nuclear reactions. In accelerator experiments, the bound electrons of the target screen the target nuclei and enhance the reaction rate. In this bound-electron screening scenario, the targets are not sufficiently hot to fully ionize the target nuclei. This effect, differing from plasma screening, must be removed to compute the bare nuclear cross section. This effect is significant for low center-of-mass energy cross-sections and has in some cases been observed to be ∼1.7–1.8 times larger than expected [10, 11, 17].
Despite widespread interest, the realization of a nuclear plasma screening experiment has been elusive because of several daunting challenges. First, extreme density and temperature conditions must be produced and diagnosed. Second, precise nuclear cross-section measurements must be made where these conditions are produced, implying the presence of strong density and temperature gradients. Finally, as the effect on fusion rates is often weak in the regimes that can be reproduced in the laboratory, care must be exercised to develop a test where the magnitude of the measurement is expected to exceed the experimental uncertainties. Significant progress has recently made resolving the first two of these challenges by using gas-filled indirect-drive experiments at the NIF [18]. Likewise, the 3He + T gamma-branch cross-section was obtained [19] and the emitted 3He + T and 3He+3He reaction product spectra have been recovered from ICF experiments at OMEGA [20]. This demonstrates that nuclear physics and cross-section experiments can be conducted in the complex environments of ICF implosions, while also carefully diagnosing the plasma using nuclear diagnostic and neutron and x-ray imaging. Here, we seek to partly address the third challenge by assessing whether these ICF implosions can produce conditions where this screening effect is expected to be large enough to be measured.
This paper is organized as follows, Section 1 introduces the problem, Section 2 discusses the approach to measuring plasma screening, Section 3 overviews detailed design considerations and offers a potential experimental design solution, and Section IV concludes and summarizes.
The generation of thermonuclear plasmas at the National Ignition Facility (NIF) may enable an observation of plasma screening of nuclear reactions. Inertial Confinement Fusion (ICF) experiments at NIF use 192 laser beams, with a maximum 1.9 MJ of energy delivered, to irradiate the inside of a gold or uranium cylindrical enclosure (“hohlraum”). This creates an x-ray environment that ablatively implodes a spherical capsule. When the capsule compresses radially by a factor of 20–40, the central hot-spot typically reaches temperatures of 2–6 keV and densities of 1–100 g/cm3.
Figure 1A shows the stellar-core density and temperature trajectories of relevant stars with metallicity of Z = 0.02 and with 1, 4, 10, and 40 solar mass (where 1 solar mass or Msun = 1 corresponds to the Sun’s mass) calculated with a 1D stellar evolution code [21]. These stars spend the majority of their time in the main hydrogen burning phase of their lifetime, as indicated by the largest jump in the corresponding color scale that illustrates the age of the star in years. As the stars begin to extinguish the hydrogen in their core, they contract and heat to the point where helium can begin to burn. Likewise, as the star evolves, hydrogen in regions outside the depleted core (shell regions) can achieve the conditions that can sustain burn.
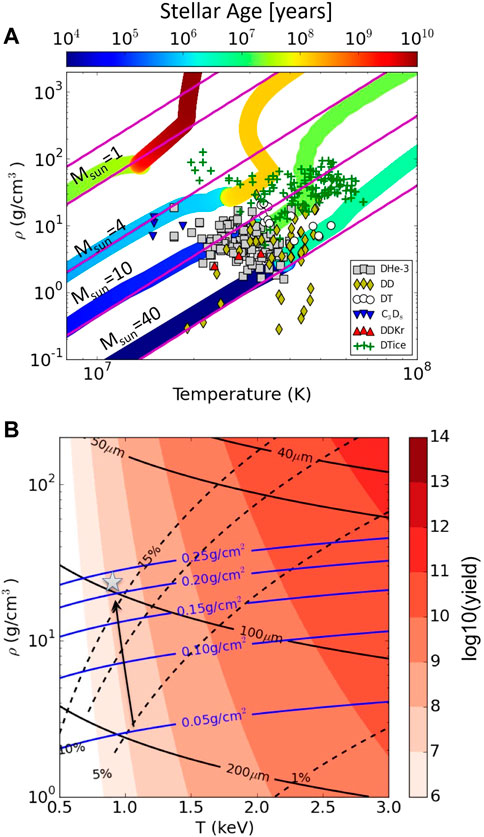
FIGURE 1. (A) Stellar conditions computed for the evolution of stars with 1, 4, 10, and 40 solar mass compared with NIF experiments. (B) Design space considering various requirements of a potential screening experiment. The arrow illustrates how current experiments need to be modified to reach an optimum in design space (the star) that balances various design constraints.
Figure 1A also compares these stellar conditions to ICF implosions by plotting inferences of density and temperature from a wide range of NIF experiments. The experimental data from the NIF (points) are plotted in terms of the burn-averaged temperature, as observed from the width of the neutron spectrum in time-of-flight measurements [22–24], and the burn-averaged density, as inferred from the yield, hot-spot size, and burn-width [25]. Each NIF experiment features a gas (on the order of 10 mg/cm3 fill density) or an ice-layer filled capsule (on the order of ∼100 μm thick) made of high-density carbon, plastic, or beryllium. The green “+” symbols show implosions that have a cryogenically frozen DT ice layer inside the shell. The cryogenic layer allows the implosion to achieve higher compression and larger densities. We are more interested in the other points which are gas-filled capsules (symcaps) as they provide more flexibility in the gas composition and because the ratio method requires multiple reactants that is enabled by mixed species. Mixed species are especially challenging to field in solid layers because of differences in species freezing temperatures. Each solid symbol represents a different gas-fill class (squares utilize D3He gas, diamonds pure D gas, circles DT gas, downward triangles deuterated propane, and upward triangles Kr doped D). The comparison between the NIF data and the stellar calculations shows that implosion conditions on NIF are very similar to that of stars during most of the stellar lifetime.
The 3He + D mixture has some promising features, including two branches, a gamma (3He + D→5Li+γ) and proton (3He + D→ 4He + p) branch and the presence of deuterium enables the observation of neutrons from the D + D→3He + n (note we expect the proton branch is not be measurable because of high-plasma densities) reaction within the same experiment. These features will be considered in greater detail later in the manuscript. In following sections, we will detail the feasibility of fielding D-3He filled capsules, but a couple of other interesting cases stand out here. The red points show the effect of the addition of krypton gas (0.01–0.03 atomic percent), which cools the implosion temperature and increases the effective Z of the background plasma. A similar effect is seen in the C3D8 (deuterated propane) implosions, which have cooler temperatures than the other cases. This effect pushes the screening enhancement up to 3%.
A successful plasma screening experiment requires the following: 1) the expected screening enhancement is larger than fusion product yield (proton, neutron, or gamma) measurement uncertainties, 2) the total yield (proton, neutron, or gamma) is at a measurable level, and 3) if measuring protons, the areal density must be low enough that they will escape and reach the proton detector. At the NIF, wedge-range-filter proton detectors are routinely employed to detect protons between the energies of ∼6–15 MeV [26, 27]. A modified step-range filter detector [28] is also being developed to extend the measurement to lower energies (∼1 MeV), and thus enabling higher ρR measurements.
To find conditions in density-temperature space where a plausible screening measurement could occur, consider an inertially confined sphere of plasma with a density
A. Observation Using the Ratio Method
To observe the impact of screening, we propose to observe the relative ratio of fusion products from D3He (protons or gammas) and DD (neutrons) reactions emitted in the same ICF implosion. Then, following the same procedure developed in [18, 29, 30], we plan to use this to infer the relative reactivities (R is the D3He/DD reactivity ratio
And that
where
If the S-factor is non-resonant within the region of the reacting nuclei, the term
B. Estimating the Impact of Gradients on the Ratio Method
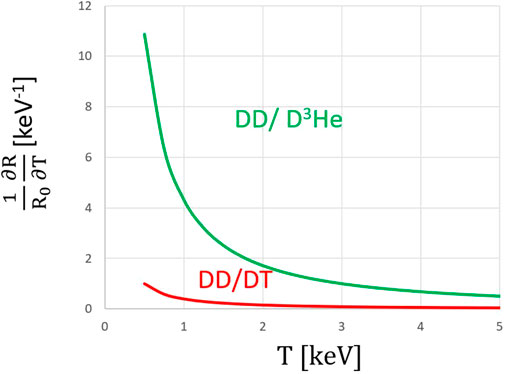
FIGURE 2. Plot of the temperature dependance of the relative reactant reactivities (
To evaluate how spatial and temporal profiles impact burn weighted quantities like yield and temperature, a simple hotspot model developed by Betti [32] can be used. Figure 3 shows the results of reactant distributions in space at peak compression (a and c) and evolutions in time (b and d) for two example implosions. One example is representative of the conditions required for a screening measurement (Figures 3A, B) with burn averaged temperatures of
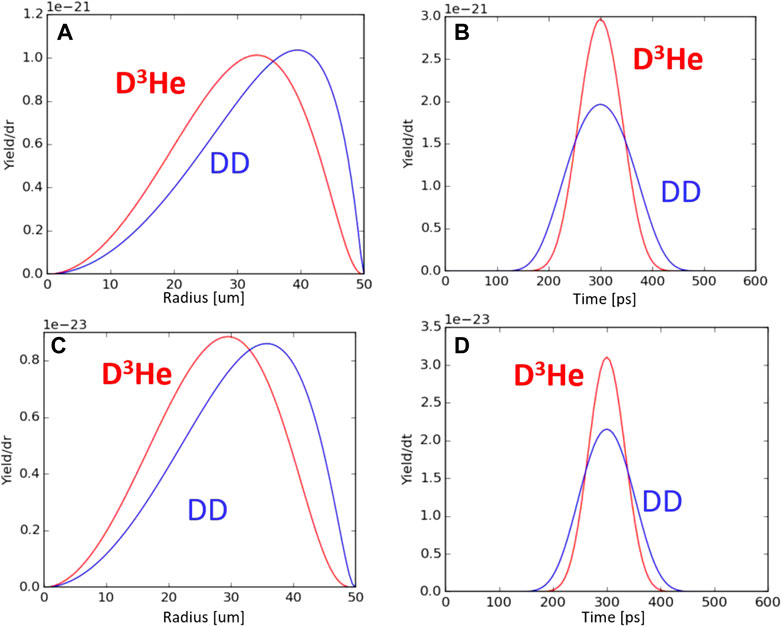
FIGURE 3. DD and D3He reactant distribution in space (A,C) and time (B,D) using a numeric hotspot model to estimate the impact of temporal and spatial gradients on burn-weighted quantities for two different example implosions.
Figure 4A shows the results of comparing the analytic equation for
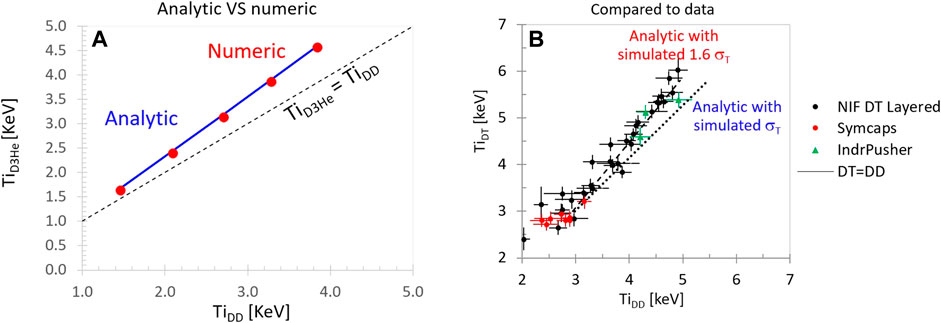
FIGURE 4. (A) Comparison of
As a check on how the formula for extracting the reactivity ratio will work with these predicted gradients, the ENDF evaluated cross sections were input [40] with a 1D Betti [32] hotspot profile from which the yields and temperatures were calculated and used to recover the reactivity input in the calculation. The results are shown in Figure 5 and indicate that in the presence of this level of temperature variation, the extracted reactivity ratio is recovered.
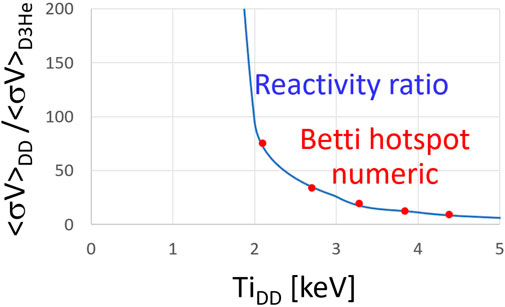
FIGURE 5. Comparison of the reaction ratio for DD and D3He vs. the extracted reactivity ratio using a synthetic data set calculated using a Betti 1D hotspot profile [32].
To help understand the design space for a screening experiment, Figure 6 shows the results of an ensemble of 1D HYDRA simulations. These start with existing experimental design features and then perturb in directions to increase the calculated enhancement of the reaction rate from plasma screening, which is shown as the background color scale. The size of each individual point is proportional to the simulated D3He yield. Markers with solid outlines represent yield and ρR combinations that are promising for a screening experiment. The star points are the experimental results from gas-filled implosions, shown previously in Figure 1A.
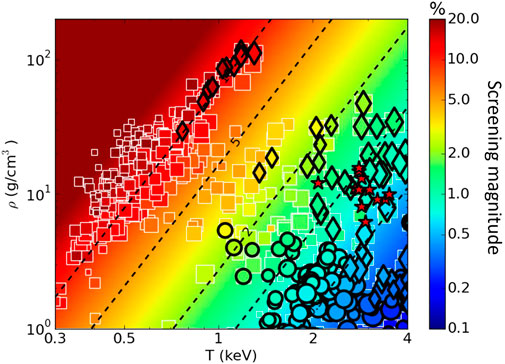
FIGURE 6. Large collection of HYDRA simulations of capsule implosions. The size of each marker is proportional to the simulated D3He yield. Several designs show significant screening and the most promising are outlined in black.
To observe screening in an ICF experiment, two principal design paths are being actively explored. The first would use D3He protons as the primary measurement that would require the total areal density to not exceed the ∼15 MeV proton range (∼0.25 g/cm2) to be detectable with WRF or step range filters [27, 28] placed near the implosion. Existing data in gas filled implosions was examined to assess the ability to measure D3He protons from implosions with moderately high compression (or areal density) and then determine the reactivity <σv> D3He in density and temperature conditions where screening is expected to be weak. This work initially encountered significant detector analysis challenges with low energy protons (∼7 MeV) and work is ongoing to attempt to resolve those issues [41]. The points with dark outlined circles are implosions that have proton yields high enough for a WRF measurement (>105) and ρRs low enough for the protons to be detectable (<0.2 g/cm2).
An alternative design path would be to maximize the yield at high hotspot density for measurements of the D3He gamma ray (branching ratio ∼ 1e-4) [42], since gammas and neutrons can escape high areal density implosions but carry with it increased uncertainty due to uncertainties in the gamma branching ratio [42] and reduced absolute signal levels. Therefore, this measurement would require a high solid angle Cherenkov detector [43, 44]. Since these detectors have high systematic uncertainties, we would measure the D3He/DD yield ratio at both screening-relevant conditions and in a low-density plasma (exploding pusher) to eliminate systematics. HYDRA simulations explored the potential parameter space and have found several interesting designs that look promising in each of these design directions. In Figure 6, the diamonds with dark outlines represent designs with D3He yields that are potentially high enough (>109) for a gamma branch measurement.
The results in Figure 6 show that estimated screening corrections greater than 10% can be achieved, but most of these simulated designs would be significantly challenging to measure because of high ρR. Of these, some designs show potential (marked as black-outlined points). In the next section, we delve into one of the most promising black-outlined diamond points, to understand what features make this an interesting potential design to observe plasma screening.
A. The “Slow-Cooker” Radiative Cooling Design Proposal
One especially interesting HYDRA simulation in Figure 6 is explored in more detail in Figure 7. This design uses a large 1400 μm inner radius capsule that is 200 μm thick, and initially filled with a D3He mixture with added Kr. The large capsule ensures that high areal density will remain to produce a prominent compression phase. Figure 7B shows that after the shock flash, the Kr mixed in with the gas cools the hot spot and so it reaches an iso-thermal state near 1 keV, lasting for almost 1 ns For perspective, typical NIF implosions are confined for about a 10th of a nanosecond. This interesting set of implosion dynamics is established as the temperature and density conditions are in a radiation dominated energy loss regime, rather than the more typical thermal conduction dominated regimes of most hotspot ICF designs. This design is called the “slow-cooker,” because the conditions are advantageous for increasing the burn by maximizing the plasma confinement, while also favoring the conditions for finite screening of reacting nuclei. Furthermore, the radiation cooling dominated regime may also result in reduced spatial temperature gradients because the hotspot becomes nearly iso-thermal. This radiation dominated isothermal system is interesting enough to warrant study just to understand this radiation dominated physics regime for its own sake, but also to produce conditions where screening becomes non-negligible, as shown in the subplot of the reaction rate and time dependent screening magnitude Figure 7.
B. Estimating the Uncertainty of the Yield and Ti at Low Yield
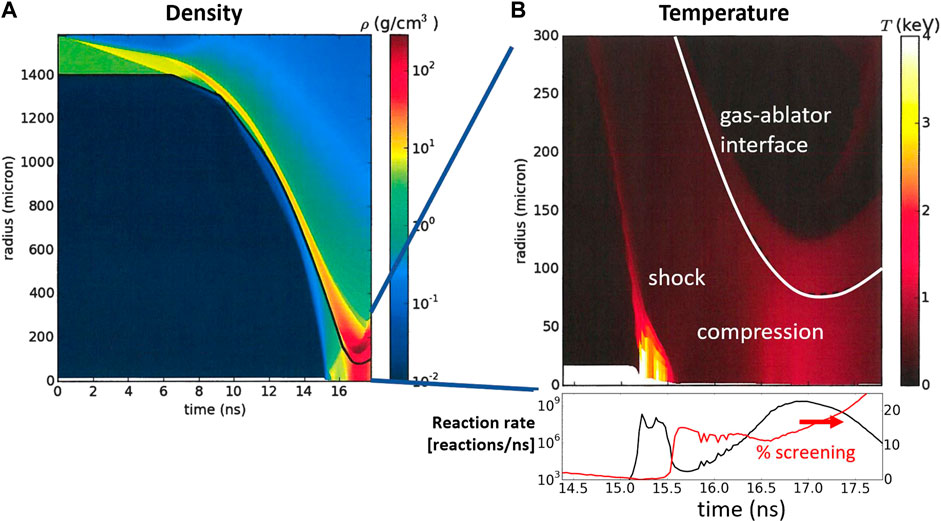
FIGURE 7. (A) HYDRA simulation of radius vs. time for an example screening experiment design candidate. The hotspot density reaches high conditions ∼100 g/cm3 (B) Zoom in temperature dynamics showing a brief shock flash and extended compression phase. Also shown are the reaction rate and screening magnitude of this design.
The design space of interest for observing screening is expected to produce neutron yields from DD fusion of order 107 to 108 neutrons. This low yield also presents a challenge to the neutron time-of-flight spectrometry that will be used to measure the yield and ion temperature of the implosions. To help enable measurements at these challenging yields, the current analysis process [22] was modified to include neutron elastic scattering from both the D3He and the ablator shell, to account for scattering effects on the low-energy tail. This modified analysis was then performed on the higher yield shot data from shot N160410-001-999 [note that NIF experiments have the following naming convention N (Year) (Month) (day)-(Shot index of that day)-999, where-999 indicates a full system shot], and on the simulated HYDRA post-shot neutron spectrum. The post-shot spectrum was transformed into a synthetic neutron time-of-flight including the various features of the neutron transport, detection, and digitization. This time-of-flight data was then analyzed and compared to the shot data. Figure 8 shows the results of this process. This analysis will allow additional simulation generated neutron spectra to be generated and analyzed to investigate the statistical significance of both yield and ion temperature.
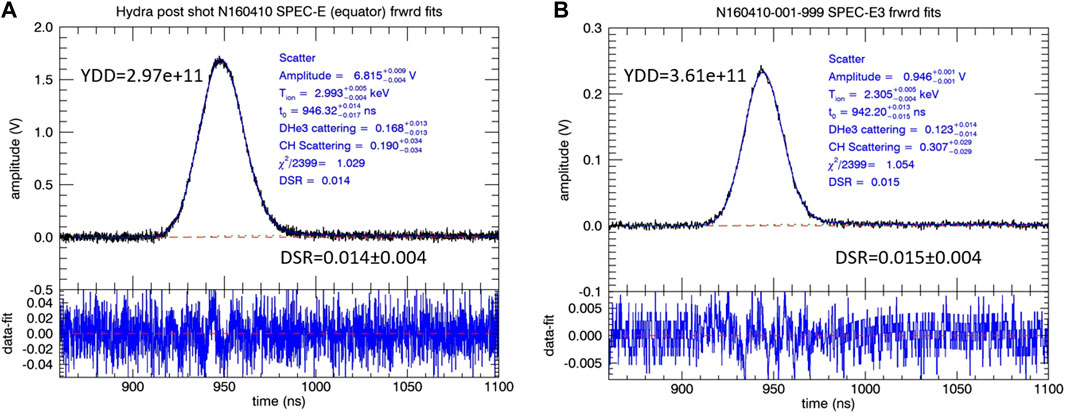
FIGURE 8. The result of a forward fit model to, (A) the data from shot N160410–001 and (B) of the synthetic neutron time-of-flight spectrum generated in post-shot Hydra simulation. Included in the forward fit model are the effects of neutron scattering from the CH ablator shell and the compressed D3He fuel. The “down scatter ratio,” DSR, is fraction of yield for neutrons of energy 1.9–2.2 MeV divided by the yield from 2.2 to 2.7 MeV.
Plasma electron screening is an important fundamental process in the thermonuclear burn of astrophysical objects, like stars, but observing it in laboratory plasma experiments is a significant challenge. In this work, we show that ICF implosions have already reached the relevant conditions for stellar burn but that the magnitude of the plasma screening effect was too weak to directly measure in those experiments. However, there are clear design directions to increase the magnitude of the plasma screening effect by utilizing higher-Z reactions, higher-Z plasmas, reducing the plasma ion temperature, and increasing the plasma density. The ratio method is a powerful approach to infer the thermonuclear S-fact in the presence of strong temperature and density gradients. We show a simple treatment that includes a correction to the ratio method for these gradients that is needed at the very low temperatures for a screening measurement. Furthermore, to develop a credible experimental design, an ensemble of HYDRA simulations was run to increase the calculated level of plasma electron screening to levels >10%. A promising resultant design, called the “slow-cooker,” features a very large (1400 μm inner diameter) and thick ablator (200 μm) filled with a mixture of Kr/D/3He. The slow-cooker enters the radiation dominated implosion regime, resulting in a relatively cold (1 keV) and dense (100 g/cm3) Kr/D/3He plasma that is confined for nearly 1 ns. These conditions are all favorable for plasma electron screening and are predicted to increase the D+3He reaction rate relative to D + D to levels that may be measurable on the NIF.
The present work assessed the issues with respect to a plasma screening measurement and identifies some credible solutions to long standing challenges. The next step is to test the null hypothesis of implosions where screening is expected to be negligible, an effort that is currently underway in the NIF discovery science program [45]. The physics of the radiation dominated “slow-cooker” implosion should also be explored and tested to see if the required conditions are achieved and assess whether the reaction products will be measurable. While substantial challenges remain, we have shown that experiments on NIF show promise and may enable the first observation of plasma screening of nuclear reactions, addressing one of the fundamental questions of high-energy-density physics. This work is performed under the auspices of the U.S. Department of Energy by LLNS, LLC, under contract no. DE-AC52-07NA27344.
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
DC lead author and screening project PI. CW capsule design and HYDRA simulations. AZ experiment analysis and screening DS project PI. CC capsule design expert. EH nuclear and time-of-flight detector analysis. MH experiment and analysis. LD HYDRA simulations. DD stellar system simulations. NK experiment and particle detector analysis. BL particle detector analysis. MGJ nuclear and particle detector analysis. JF nuclear and particle detector analysis.
This work is performed under the auspices of the U.S. Department of Energy by LLNS, LLC, under contract no. DE-AC52-07NA27344.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
1.National Research Council. Frontiers in high energy density physics: The X-games of contemporary science. Washington, D.C: The National Academies Press (2003).
2. Bahcall JN, Brown LS, Gruzinov A, Sawyer RF. The Salpeter plasma correction for solar fusion reactions. A. A (2002) 383:291–5. doi:10.1051/0004-6361:20011715
3. Shaviv NJ, Shaviv G. Obtaining the electrostatic screening from first principles. Nucl Phys A (2003) 719:C43–C51. doi:10.1016/S0375-9474(03)00956-4
4. Däppen W, Mussack K. Dynamic screening in solar and stellar nuclear reactions. Contrib Plasma Phys (2012) 52:149–52. doi:10.1002/ctpp.201100099
5. Spitaleri C, Bertulani CA, Fortunato L, Vitturi A. The electron screening puzzle and nuclear clustering. Phys Lett B (2016) 755:275–8. doi:10.1016/j.physletb.2016.02.019
6. Bertulani CA, Spitaleri C. Nuclear clustering and the electron screening puzzle. EPJ Web Conf (2017) 165:02002. doi:10.1051/epjconf/201716502002
7. Dzitko H, Turck-Chieze S, Delbourgo-Salvador P, Lagrange C. The screened nuclear reaction rates and the solar neutrino puzzle. ApJ (1995) 447:428. doi:10.1086/175887
8. Adelberger EG, Austin SM, Bahcall JN, Balantekin AB, Bogaert G, Brown LS, et al. Solar fusion cross sections. Rev Mod Phys (1998) 70:1265–91. doi:10.1103/revmodphys.70.1265
9. Adelberger EG, Balantekin AB, Bemmerer D, Bertulani CA, Chen JW, Costantini H, et al. (2010). Solar fusion cross sections II: The pp chain and CNO cycles.
10. Aliotta M, Raiola F, Gyurky G, Formicola A, Bonetti R, Broggini C, et al. Electron screening effect in the reactions 3He(d, p)4He and d(3He, p)4He. Nucl Phys A (2001) 690:790–800. doi:10.1016/s0375-9474(01)00366-9
11. Aliotta M, Langanke K. Screening effects in stars and in the laboratory. Front Phys (2022) 10. doi:10.3389/fphy.2022.942726
12. Raiola F, Migliardi P, Gang L, Bonomo C, Gyurky G, Bonetti R, et al. Electron screening in d(d, p)t for deuterated metals and the periodic tablep)t for deuterated metals and the periodic table. Phys Lett B (2002) 547:193–9. doi:10.1016/S0370-2693(02)02774-0
13. Cognata ML, Spitaleri C, Tumino S, Typel S, Cherubini S, Lamia L Bare-nucleus astrophysical factor of the (3)He(d, p)(4)He reaction via the ``Trojan horse'' method. Phys Rev C (2005) 72(6):065802. doi:10.1103/PhysRevC.72.065802
14. Czerski K, Huke A, Biller A, Heide P, Hoeft M, Ruprecht G. Enhancement of the electron screening effect for d + d fusion reactions in metallic environments. Europhys Lett (2001) 54:449–55. doi:10.1209/epl/i2001-00265-7
15. Kasagi J, Yuki H, Baba T, Noda T, Ohtsuki T, G. Lipson A. Strongly enhanced DD fusion reaction in metals observed for keV D+ bombardment. J Phys Soc Jpn (2002) 71:2881–5. doi:10.1143/JPSJ.71.2881
16. Salpeter E. Electron screening and thermonuclear reactions. Aust J Phys (1954) 7:373–88. doi:10.1071/PH540373
17. Schröder U, Engstler S, Krauss A, Neldner K, Rolfs C, Somorjai E, et al. Search for electron screening of nuclear reactions at sub-coulomb energies. Nucl Instr Methods Phys Res Section B: Beam Interactions Mater Atoms (1989) 40-41:466–9. doi:10.1016/0168-583x(89)91022-7
18. Casey DT, Sayre DB, Brune CR, Smalyuk VA, Weber CR, Tipton RE, et al. Thermonuclear reactions probed at stellar-core conditions with laser-based inertial-confinement fusion. Nat Phys (2017) 13:1227–31. doi:10.1038/nphys4220
19. Zylstra AB, Herrman HW, Johnson MG, Kim YH, Frenje JA, Hale G, et al. Using inertial fusion implosions to measure the $\mathrm{T}+^{3}\mathrm{He}$ fusion cross section at nucleosynthesis-relevant energies. Phys Rev Lett (2016) 117(3):035002.
20. Zylstra AB, Frenje JA, Gatu Johnson M, Hale GM, Brune CR, Bacher A, et al. Proton spectra from 3He+T and 3He+3He fusion at low center-of-mass energy, with potential implications for solar fusion cross sections. Phys Rev Lett (2017) 119(22):222701. doi:10.1103/PhysRevLett.119.222701
21. Dearborn DSP, Lattanzio JC, Eggleton PP. Three-dimensional numerical experimentation on the core helium flash of low-mass red giants. ApJ (2006) 639:405–15. doi:10.1086/499263
22. Hatarik R, Sayre DB, Caggiano JA, Phillips T, Eckart MJ, Bond EJ, et al. Analysis of the neutron time-of-flight spectra from inertial confinement fusion experiments. J Appl Phys (2015) 118:184502. doi:10.1063/1.4935455
23. Moore AS, Schlossberg DJ, Hartouni EP, Sayre D, Eckart MJ, Hatarik R, et al. A fused silica Cherenkov radiator for high precision time-of-flight measurement of DT γ and neutron spectra (invited). Rev Scientific Instr (2018) 89:10I120. doi:10.1063/1.5039322
24. Glebov VY, Sangster TC, Stoeckl C, Knauer JP, Theobald W, Marshall KL, et al. The National Ignition Facility neutron time-of-flight system and its initial performance (invited). Rev Scientific Instr (2010) 81:10D325–326. doi:10.1063/1.3492351
25. Cerjan C, Springer PT, Sepke SM. Integrated diagnostic analysis of inertial confinement fusion capsule performance. Phys Plasmas (1994-present) (2013) 20:056319. doi:10.1063/1.4802196
26. Zylstra AB, Frenje JA, Seguin FH, Rosenberg MJ, Rinderknecht HG, Johnson MG, et al. Charged-particle spectroscopy for diagnosing shock rho R and strength in NIF implosions. Rev Scientific Instr (2012) 83:10D901. doi:10.1063/1.4729672
27. Seguin FH, Frenje JA, Li CK, Hicks DG, Kurebayashi S, Rygg JR, et al. Spectrometry of charged particles from inertial-confinement-fusion plasmas. Rev Scientific Instr (2003) 74:975–95. doi:10.1063/1.1518141
28. Lahmann B, Johnson MG, Frenje JA, Birkel AJ, Adrian PJ, Kabadi N, et al. Extension of charged-particle spectrometer capabilities for diagnosing implosions on OMEGA, Z, and the NIF. Rev Scientific Instr (2021) 92:083506. doi:10.1063/5.0062584
29. Kabadi NV, Adrian PJ, Bose A, Casey DT, Frenje JA, Gatu Johnson M, et al. A second order yield-temperature relation for accurate inference of burn-averaged quantities in multi-species plasmas. Phys Plasmas (2021) 28:022701. doi:10.1063/5.0032139
30. Zylstra AB, Herrmann HW, Kim YH, McEvoy A, Frenje JA, Johnson MG, 2H(p,γ)3He cross section measurement using high-energy-density plasmas. Phys Rev C (2020) 101(4):042802. doi:10.1103/PhysRevC.101.042802
31. Munro DH. Interpreting inertial fusion neutron spectra. Nucl Fusion (2016) 56:036001. doi:10.1088/0029-5515/56/3/036001
32. Betti R, Umansky M, Lobatchev V, Goncharov VN, McCrory RL. Hot-spot dynamics and deceleration-phase Rayleigh? Taylor instability of imploding inertial confinement fusion capsules. Phys Plasmas (2001) 8:5257–67. AIP. doi:10.1063/1.1412006
33. Casey DT, Smalyuk VA, Tipton RE, Pino JE, Grim GP, Remington BA, et al. Development of the CD Symcap platform to study gas-shell mix in implosions at the National Ignition Facility. Phys Plasmas (2014) 21:092705. doi:10.1063/1.4894215
34. Khan SF, MacLaren SA, Salmonson JD, Ma T, Kyrala GA, Pino JE, et al. Symmetry tuning of a near one-dimensional 2-shock platform for code validation at the National Ignition Facility. Phys Plasmas (2016) 23:042708. doi:10.1063/1.4947223
35. Le Pape S, Divol L, Berzak Hopkins L, Mackinnon A, Meezan N, Casey D, et al. Observation of a reflected shock in an indirectly driven spherical implosion at the national ignition facility. Phys Rev Lett (2014) 112:225002. doi:10.1103/physrevlett.112.225002
36. Gatu Johnson M, Knauer JP, Cerjan CJ, Eckart MJ, Grim GP, Hartouni EP, et al. Indications of flow near maximum compression in layered deuterium-tritium implosions at the National Ignition Facility. Phys Rev E (2016) 94:021202. doi:10.1103/physreve.94.021202
37. Edwards MJ, Lindl JD, Spears BK, Weber SV, Atherton LJ, Bleuel DL, et al. The experimental plan for cryogenic layered target implosions on the National Ignition Facility?The inertial confinement approach to fusion. Phys Plasmas (2011) 18(5):051003.
38. Marinak MM, Kerbel GD, Gentile NA, Jones O, Munro D, Pollaine S, et al. Three-dimensional HYDRA simulations of national ignition facility targets. Phys Plasmas (2001) 8:2275–80. doi:10.1063/1.1356740
39. Schlossberg DJ, Grim G, Casey D, Moore A, Nora R, Bachmann B, et al. Observation of hydrodynamic flows in imploding fusion plasmas on the national ignition facility. Phys Rev Lett (2021) 127:125001. doi:10.1103/PhysRevLett.127.125001
40. Chadwick MB, Oblozinsky P, Herman M, Greene N, McKnight R, Smith D, et al. ENDF/B-VII.0: Next generation evaluated nuclear data library for nuclear science and technology. Nucl Data Sheets (2006) 107:2931–3060. doi:10.1016/j.nds.2006.11.001
42. Kim Y, Mack JM, Herrmann HW, Young CS, Hale GM, Caldwell S, et al. D-T gamma-to-neutron branching ratio determined from inertial confinement fusion plasmas. Phys Plasmas (2012) 19:056313. doi:10.1063/1.4718291
43. McEvoy AM, Herrmann HW, Kim Y, Zylstra AB, Young CS, Fatherley VE, et al. Gamma ray measurements at OMEGA with the newest gas Cherenkov detector “GCD-3”. J Phys : Conf Ser (2016) 717:012109. doi:10.1088/1742-6596/717/1/012109
Keywords: astrophysics, nuclear physics, plasma physcis, high-energy density astrophysics, inertial confinement fusion (ICF)
Citation: Casey DT, Weber CR, Zylstra AB, Cerjan CJ, Hartouni E, Hohenberger M, Divol L, Dearborn DS, Kabadi N, Lahmann B, Gatu Johnson M and Frenje JA (2023) Towards the first plasma-electron screening experiment. Front. Phys. 10:1057603. doi: 10.3389/fphy.2022.1057603
Received: 29 September 2022; Accepted: 05 December 2022;
Published: 05 January 2023.
Edited by:
Giuseppe Verde, Universities and Research, ItalyReviewed by:
Marco La Cognata, Laboratori Nazionali del Sud (INFN), ItalyCopyright © 2023 Casey, Weber, Zylstra, Cerjan, Hartouni, Hohenberger, Divol, Dearborn, Kabadi, Lahmann, Gatu Johnson and Frenje. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Daniel T. Casey, Y2FzZXkyMUBsbG5sLmdvdg==
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.