- 1Los Alamos National Laboratory, Los Alamos, NM, United States
- 2LP2I Bordeaux, UMR5797, Université de Bordeaux, CNRS, Gradignan, France
- 3Lawrence Livermore National Laboratory, Livermore, CA, United States
- 4CEA, DAM, DIF, Arpajon, France
- 5CEA, Laboratoire Matière en Conditions Extrêmes, Université Paris-Saclay, Bruyères-le-Châtel, France
In the last decade, there has been a renaissance of fission research resulting in new high-precision experiments and advanced fission modeling. For instance, the Chi-Nu and CEA teams supplied, for the first time, the 239Pu prompt fission neutron spectrum (PFNS) for broad ranges of incident and outgoing neutron energies. The CEA team also measured 239Pu average prompt neutron multiplicities,
1 Introduction
The process of prompt emission after fission has been investigated experimentally and theoretically since the 1940s [1], but open questions remain. For instance, the average number of prompt fission neutrons emitted,
An accurate description of fission is key to performing reliable simulations of applications in reactor physics and nuclear criticality safety, for instance. Simulations are performed with neutron transport codes. These rely on nuclear data to compute the probability of particle interactions with matter. Nuclear data incorporate information from differential experiments and theory. Combinations of nuclear data of several observables are jointly validated with respect to integral experiments [19]. These experiments represent an application of interest. For instance, the effective neutron multiplication factor, keff, of ICSBEP critical assemblies [20], describes the number of neutrons lost versus produced in a critical assembly from one generation to the next in a chain reaction. Its simulation relies on nuclear data such as scattering and the fission source term [PFNS,
Here, we implement new high-precision measurements and consistent fission modeling, which are described in Section 2, into evaluations of PFNS,
2 Evaluation input and methodology
2.1 New high-precision prompt fission neutron spectrum measurements
The Chi-Nu experiment was built over the last ∼15 years to produce high-precision PFNS for major actinides, with a well-documented experimental setup and detailed covariance analysis. Incident neutrons for these experiments are produced via proton spallation reactions on a tungsten target at the Weapons Neutron Research (WNR) facility at the Los Alamos Neutron Science Center (LANSCE). The resulting incident neutron spectrum available for Chi-Nu is Einc = ≈0.7–700 MeV, with neutrons up to 20 MeV utilized for this measurement. The flight path located 15° to the left of the incident proton beam direction was used for Chi-Nu measurements; it has a “get-lost basement” (2 m of empty space beneath an Al floor) to significantly reduce environmental neutron scattering. Neutron-induced fission events are measured using a parallel-plate avalanche counter (PPAC) target [33]. Neutrons are detected with two detector arrays in two separate experiments: a twenty-two detector Li-glass array to measure PFNS neutrons from ∼0.01–1.5 MeV and the other a fifty-four detector liquid scintillator array for neutrons from ∼0.8–10.0 MeV. Data from both neutron detection arrays are combined to form a single PFNS shape result for outgoing neutron energies Eout = 0.01–10.0 MeV, at twenty contiguous Einc ranges from 1.0 to 20.0 MeV. Covariances for each PFNS are calculated including statistical and all systematic uncertainties from, e.g., input nuclear data for MCNP simulations, fission detection efficiency, and more [22] for PFNS across all Eout and Einc. Results from various target isotopes (e.g., 239Pu [22, 34], 235U [35], 238U, etc.) are correlated as well, allowing for accurate results for PFNS ratios to be calculated [36], of which there were only two measurements of the 239Pu/235U PFNS ratio at or near 1.5 MeV incident neutron energy prior to Chi-Nu results.
Also at WNR, another experimental campaign to measure the PFNS has taken place over recent years led by the French Atomic and Alternative Energy Commission (CEA)/DAM [23]. The differences and similarities between the Chi-Nu and CEA PFNS experimental approaches and 239Pu PFNS results are reviewed in detail in Ref. [24]. Briefly, both measurements share the same fifty-four liquid scintillator array, experimental flight path, and incident neutron flux shape. While Chi-Nu uses the Li-glass array for measurements of lower PFNS energies, CEA measurements utilize only the liquid scintillator array with a lower PFNS energy limit (200 keV) from this array compared with Chi-Nu. The other most notable difference between these experiments is the use of a CEA-made fission chamber [37] as opposed to a PPAC. The third most notable difference is that, while Kelly et al. simulated the neutron detector efficiency, the CEA team measured it with respect to a 252Cf source. Despite these differences, results from these two experiments for 239Pu are in overall agreement across the overlapping Einc of 1.0–20.0 MeV within uncertainties for nearly all data points. Lastly, while there appear to be some systematic shape differences between these two data sets, comparisons of results from each experiment shown as ratios to data at the lowest Einc (thereby canceling or reducing many systematic effects in the analysis) show near perfect agreement between the two results for all Einc and Eout. Previously, high-precision experimental 239Pu PFNS existed for Einc ≤ 2 MeV, whereas CEA and Chi-Nu measurements have now decisively mapped out the 239Pu PFNS across broad Einc and Eout ranges.
2.2 New high-precision
An accurate and precise measurement of 239Pu(n,f)
2.3 New high-precision (n,f) cross section measurement with a time projection chamber
New measurements of the shape of the 239Pu(n,f)/235U(n,f) cross section ratio were performed by the NIFFTE TPC (Neutron Induced Fission Fragment Tracking Experiment Time Projection Chamber) collaboration to address concerns regarding the spread in the previous data relative to the Neutron Data Standard evaluation uncertainty [25]. The bulk of past measurements were undertaken using fission chambers which could be subject to several potential sources of systematic uncertainty [10, 11, 45]. The similar design of previous measurements also means they are often highly correlated with one another. The NIFFTE TPC tackled that by using a new type of detector, the fission Time Projection Chamber (fissionTPC) [46] that allows for full 3D reconstruction of charged-particle tracks ranging from protons to fission fragments. This type of measurement is in contrast to fission chambers which usually only provide a pulse height or energy and, depending on the configuration, some angular information on the fission fragments. With 3D track reconstruction, the fissionTPC benefits from a direct measurement of several quantities needed to adequately correct cross section ratios, including beam and target uniformity and detector efficiency, eliminating the need to make certain assumptions or auxiliary measurements. A detailed and carefully documented analysis was conducted to understand all the relevant uncertainty sources and validate the analysis results [25]. In short, the fissionTPC produced a precision shape measurement that is largely uncorrelated with previous measurements and has some different systematic uncertainties. The shape of previous measurements and the ENDF/B-VIII.0 evaluation was generally verified, however, valuablel information was provided above 14 MeV, where several data sets are discrepant [10, 47–50].
2.4 Correlated fission modeling
CGMF is a Hauser-Feshbach fission fragment decay code [28] that calculates prompt fission observables and their correlations through the event-by-event de-excitation of fission fragments. As input for this de-excitation, information about the compound nucleus is needed, e.g., multi-chance fission probabilities and pre-fission neutron energies. The initial distributions of the primary fission fragments, prior to neutron emission, have to be sampled in mass, charge, total kinetic energy, spin, and parity—Y(A, Z, TKE, J, π).
The mass distribution is written as a sum of three Gaussians,
defined as
and
where Ac is the mass of the compound nucleus that undergoes fission, and the weights, means, and standard deviations of each Gaussian are energy dependent with
where c is defined by equating those two equations at E = E0. For 239Pu(n,f), TKE has no slope change, and E0 = b = 0 and a = c. For each mass, TKE(A) is defined as a Gaussian, with high-order polynomials for the mean and width,
For the optimization to the prompt neutron multiplicity, we consider the parameters in Table 2, for first-, second-, and third-chance fission. The initial parameters, p0, are the default CGMF parameters [28]. To calculate the model parameter uncertainties, δp0, we sample the Y(A|Einc), TKE(Einc),
where
2.5 Other evaluation input
2.5.1 Prompt fission neutron spectrum evaluation
The 239Pu PFNS evaluation for incident-neutron energies, Einc, 0.5–30 MeV differs from an earlier one of [53] by 1) the inclusion of Chi-Nu and CEA experimental data [22–24], 2) considering 239Pu PFNS at Einc = 2 MeV [54] that were extracted by Lestone similarly to [55], and 3) assumptions on the prior for Einc < 3 MeV. In general, the same prior as for [52] was used to obtain evaluated PFNS; the Los Alamos model [15] was paired with the exciton model [56] as well as the average total kinetic energy and energy release parametrizations based on [57, 58]. The only difference between the prior used for the evaluation of [53] and the one here is that the model correlation across Einc are set to zero for evaluating PFNS at Einc < 3 MeV—effectively evaluating PFNS one Einc at a time for this energy range. This choice was taken, as otherwise evaluated PFNS for Einc < 3 MeV are systematically lower than the experimental data for Eout > 8 MeV. This too low trend is caused by a rigid prior across Einc paired with a parameterization that is too far from Chi-Nu and CEA PFNS at the second-chance fission threshold.
2.5.1.1
In addition to the new Marini 239Pu
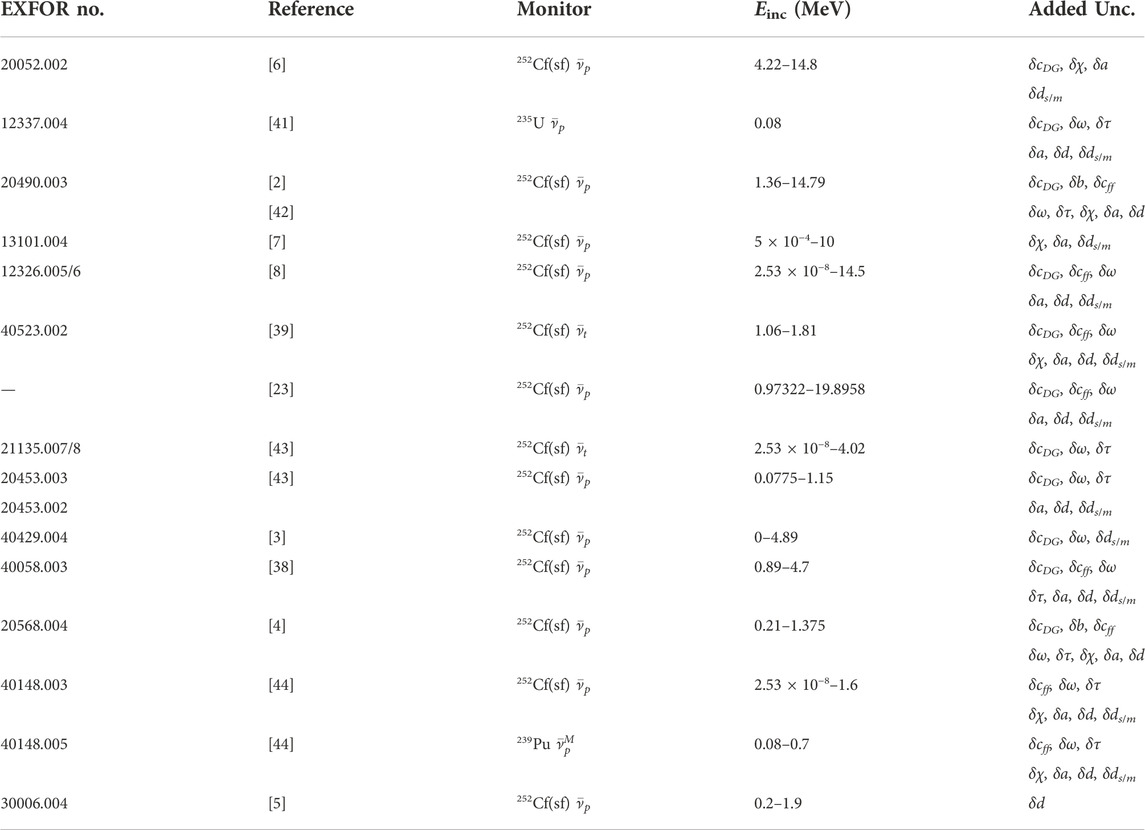
TABLE 1. Experimental 239Pu
Total covariances,
Nearly the same data as for the ENDF/B-VIII.0 evaluation of 239Pu
2.5.1.2 (n,f) cross sections
The 239Pu(n,f) cross section is evaluated as part of the Neutron Data Standards project with the code GMAP [63, 63]. We build here upon the data file related to the work of [11]. In this paper, all covariances of experimental 239Pu(n,f) cross sections were updated with templates of expected measurement uncertainties for this observable [11, 12]. Given that, all experimental data for the 239Pu(n,f) cross section should have a consistent weight compared to NIFFTE data. The only difference between this evaluation and the one used here is the inclusion of NIFFTE 239Pu/235U(n,f) and 238U/235U(n,f) cross section ratios [65, 66].
2.6 Evaluation methodology
The generalized least squares (GLS) algorithm [67], and the Kalman filter method [68] were employed to evaluate mean values, N, and covariances, CovN. Both algorithms are encoded in the same set of equations,
where the main difference lies in how the prior mean values, p, prior covariances, Covp, and sensitivities, S, are defined. The variables e and Cove encode all experimental data used for the evaluation and their covariances. The code GMAP [63, 64] is used for evaluating the (n,f) cross section via GLS; PFNS and
If the equations are applied for GLS, p and Covp are in the same physical space as for the observable to be evaluated. In GMAP, the previous standard values are used as p with a diagonal covariance matrix of 100%, i.e., an uninformative prior. The same approach is taken in ARIADNE to evaluate
The CGMF model was included into the
The experimental covariances were corrected for an effect termed “Peelle’s Pertinent Puzzle” (PPP) [69], where the mean value computed from strongly correlated data lies outside of the range of the input data due to an improperly formulated covariance matrix [70]. Both GMAP and ARIADNE use iterative linear least squares [71, 72] to mitigate the impact of PPP.
3 Discussion of evaluation and validation results
3.1 Evaluated results
3.1.1 Prompt fission neutron spectrum
The new evaluated PFNS in Figures 1, 2 interpolate between the high-precision 239Pu PFNS of CEA and Chi-Nu for all Einc, and closely follow Lestone data. In doing so, the evaluation differs noticeably from ENDF/B-VIII.0 highlighting that CEA and Chi-Nu PFNS provide decisive input. This is especially true for Einc > 2 MeV where past PFNS [73] were too uncertain to guide the evaluation. To be more specific, the evaluated PFNS are softer than ENDF/B-VIII.0 for Einc < 12 MeV. At Einc = 14 MeV, the new evaluation, distinctly different from ENDF/B-VIII.0, follows closely structures and shapes shown in CEA and Chi-Nu data. In fact, CEA and Chi-Nu data resolve for the first time physics expected structures expected at second and third-chance fission thresholds of the 239Pu PFNS: Characteristic structures from second-chance fission present themselves at Einc = 6–7 MeV as an increase in the PFNS for Eout = 0.1–0.8 MeV. Third-chance fission structures are less pronounced but are visible for Einc = 10–12 MeV for Eout = 0.1–0.8 MeV. In addition to that, the pre-equilibrium peak starts to emerge for Einc = 12 MeV at Eout > 5 MeV. While ENDF/B-VIII.0 correctly predicted the Einc and Eout of these structures, it incorrectly estimated their magnitude and the shape. Only CEA and Chi-Nu data enabled an accurate description of the PFNS physics there.
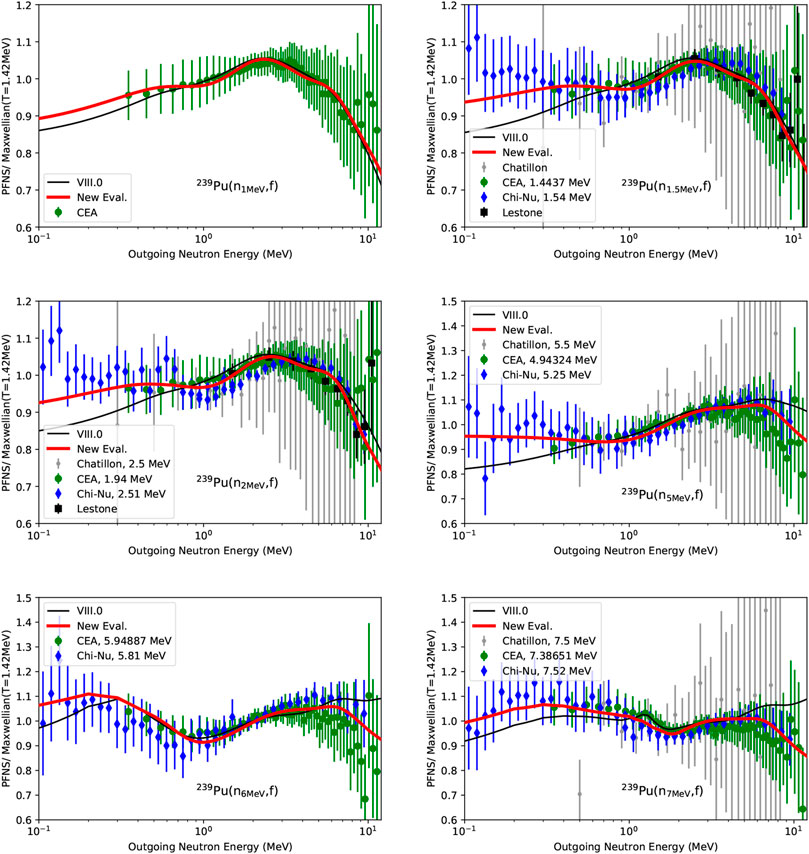
FIGURE 1. Evaluated 239Pu PFNS are shown in comparison to ENDF/B-VIII.0 and experimental data that were used for the evaluation, for incident neutron energies from 1 to 7 MeV.
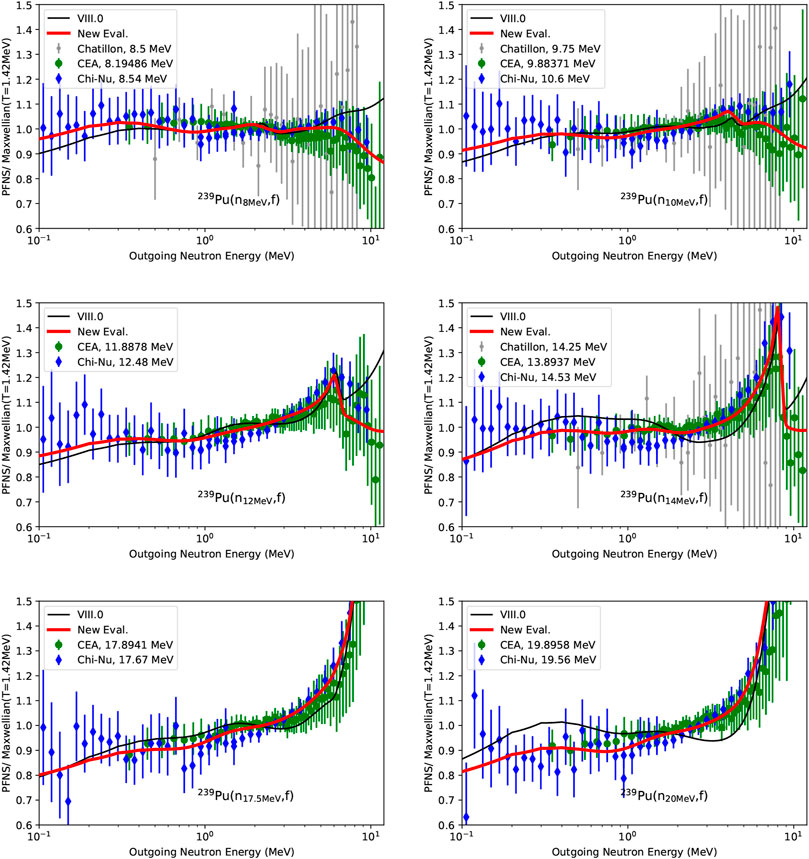
FIGURE 2. Same as Figure 1 for incident neutron energies from 8 to 20 MeV.
The changes in the PFNS can be also observed in the first two plots of Figure 3 showing the mean energy of the PFNS—that is the first moment of the PFNS—as a function of Einc. The new evaluated mean energy integrated for Eout = 0.01–10 MeV follows CEA and Chi-Nu data closely but is softer (by approximately 20 keV) than ENDF/B-VIII.0 up to 5 MeV. ENDF/B-VIII.0 also did not capture the mean energy close to second-and third-chance fission thresholds due to lack of experimental information. Non-linear behavior in the average mean energy in Figure 3 from thermal (calculated from INDEN PFNS [13]; [73]) to 1 MeV can be observed. The challenge we faced was that evaluated PFNS at Einc = 1, 1.5 and 2 MeV in Figure 1, based on the CEA, Chi-Nu, and Lestone data, gave evaluated mean energies in Figure 3. On the other hand, the INDEN PFNS at thermal [13]; [73], based on stringently-reviewed data at thermal [14], decreased mean energies versus ENDF/B-VIIII.0. If we had prioritized a smooth trend in the mean energy for Einc from thermal to 2.5 MeV, this would have been in contradiction to the aforementioned PFNS; i.e., we might have had to have a hotter spectrum at thermal or a softer spectrum at Einc = 1 MeV than the data called for. Our decision was to not under-value the 1 MeV PFNS data, while adopting also the new thermal assessment, and this led to the non-linear structures in the mean energies from thermal to 1 MeV. While the true Einc dependence of the mean energy is expected to be smooth from 0 to 2.5 MeV, it reflects our priorities to accurately represent the CEA and Chi-Nu PFNS in this fast range. Over time, we hope future measurements will better inform this evaluation decision, but such experiments typically take many years.
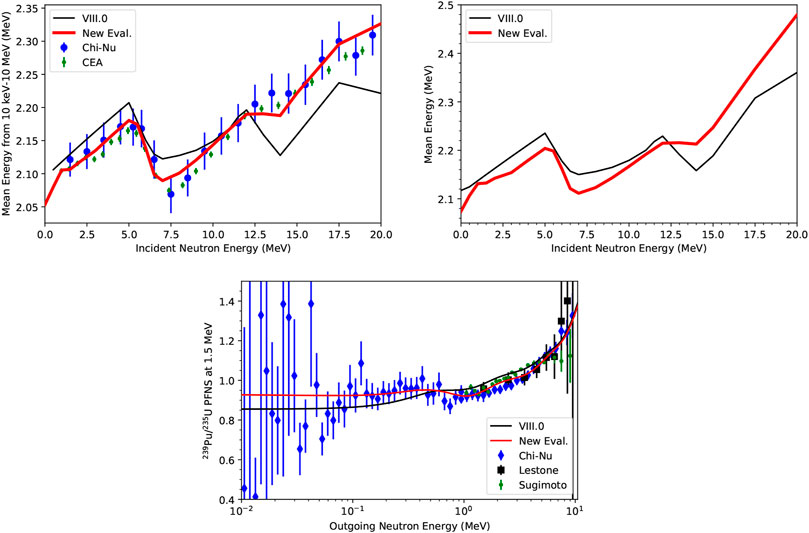
FIGURE 3. Further validation of evaluated PFNS is shown: (Top, right) Mean energies calculated from the PFNS from 100 keV to 10 MeV are compared for this evaluation, ENDF/B-VIII.0 and those from CEA and Chi-Nu experimental data. At thermal, the PFNS from INDEN is adopted [13, 73]. (Top, left) The same as the first plot but calculated mean energies are shown integrated over all Eout. (Bottom) Ratio of 239Pu/235U PFNS at Einc = 1.5 are shown for ENDF/B-VIII.0, this evaluation and one for 235U including Chi-Nu PFNS, Chi-Nu, Lestone and Sugimoto experimental data.
Further evidence on the consistency of the evaluated PFNS across isotopes is provided in the bottom of Figure 3 where the ratio of this evaluated PFNS to a new 235U PFNS [75], which also includes new Chi-Nu data [35], at Einc = 1.5 MeV compares well to experimental ratio data by [22, 24, 35, 55, 76].
3.1.2 Average prompt fission neutron multiplicity,
Three
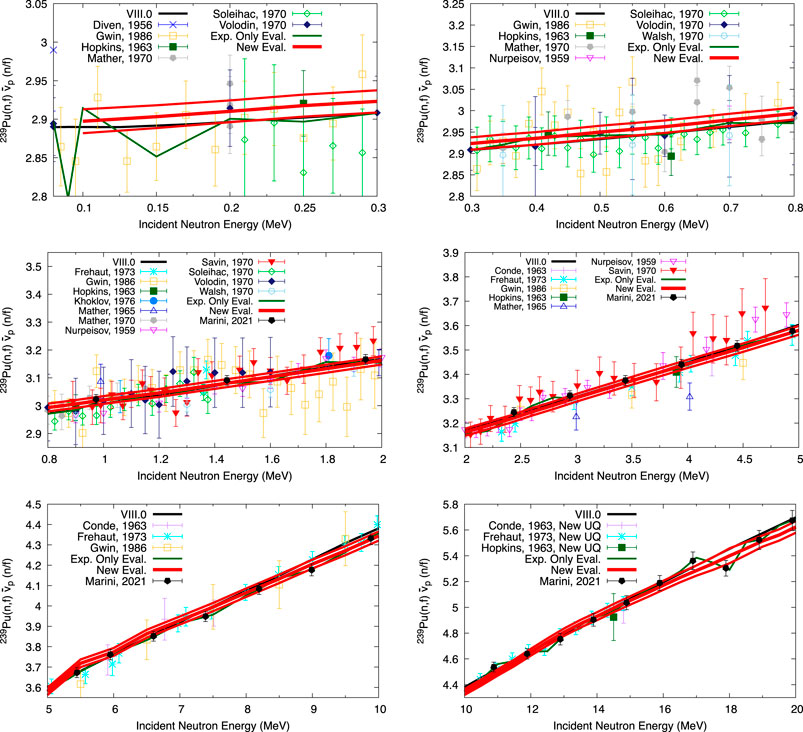
FIGURE 4. Evaluated 239Pu
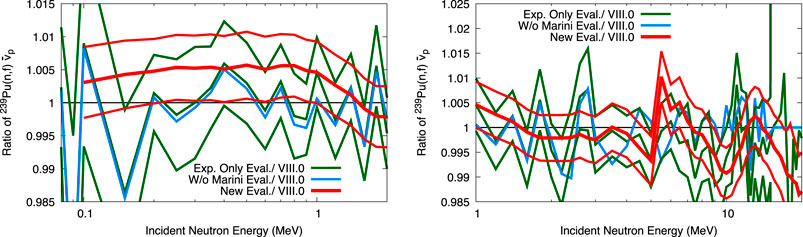
FIGURE 5. 239Pu
For ENDF/B-VIII.0 239Pu
If Marini data are included,
Including the CGMF prior via the Kalman filter smooths the evaluated
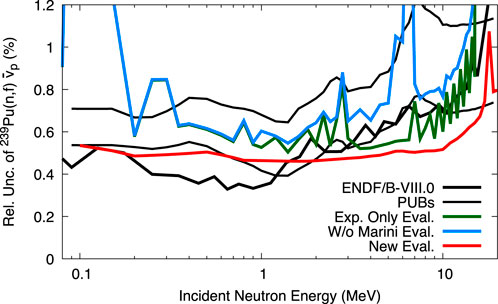
FIGURE 6. Evaluated uncertainties with and without Marini, and including CGMF are compared to ENDF/B-VIII.0 uncertainties and PUBs bounds.
The uncertainties of evaluation (1) are larger than those of ENDF/B-VIII.0 in Figure 6 from up to 15 MeV. It was shown via the Physical Uncertainty Bounds (PUBs) method [45, 77, 78] that ENDF/B-VIII.0
3.1.3 (n,f) cross section
Three evaluations are discussed: 1) The 2018 standards evaluation (Std. 2018) that is in ENDF/B-VIII.0 from 0.04 to 20 MeV [10], (2) an evaluation building upon (1) from [11] differing in 239Pu(n,f) cross section experimental covariances updated by templates of expected measurement uncertainties, and (3) evaluation (2) updated with NIFFTE TPC data. These evaluations differ by a maximum of 0.5% until 14 MeV, as shown in the bottom of Figure 7. However, most of the previous data were measured with fission chambers, while NIFFTE TPC shape data were obtained with a time-projection chamber which allows accurate tracking of charged particles in three dimensions. Hence, this small difference up to 14 MeV in the shape of evaluations (2) and (3) indicates that the TPC confirms the shape obtained from a bulk of data measured with fission chambers.
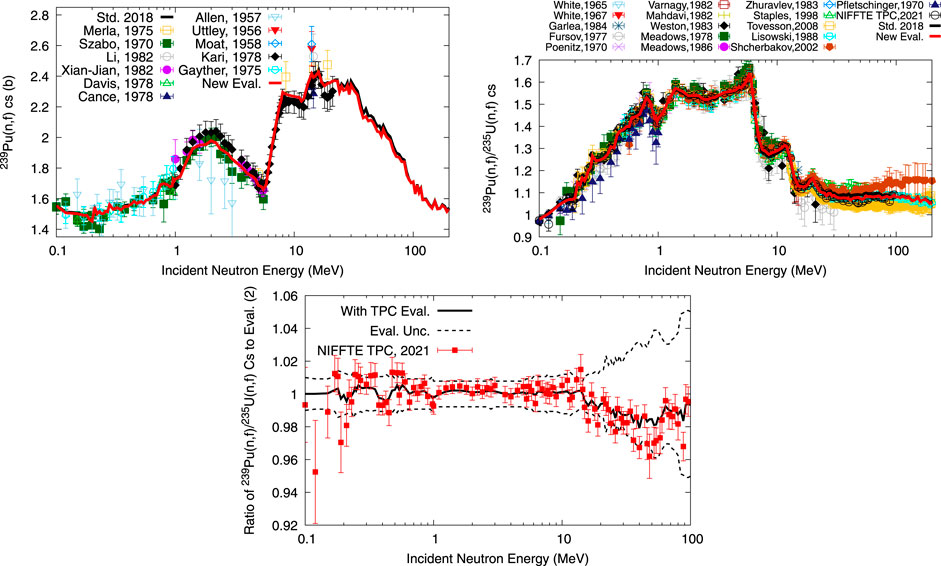
FIGURE 7. The 239Pu(n,f) cross section and 239Pu(n,f)/235U(n,f) cross section ratio obtained in the nuclear data evaluations (1) and (3) are compared to experimental data in the top two plots. In the bottom plot, NIFFTE TPC data are compared to evaluated data with and without NIFFTE TPC data [evaluations (2) and (3)].
Above 14 MeV, the evaluated (n,f) cross section of evaluation (3), with NIFFTE TPC data, is systematically lower by 2% than without, evaluation (2), but within the GMAP uncertainties. In this energy range, the exact value of the (n,f) cross section was not well defined [10] given discrepancies in previous data sets [47–50]. NIFFTE TPC data support the shape of Lisowski [47] data rather than the higher ones of Shcherbakov [49] and Staples [50]. No integral experiments exist that allow to conclusively validate whether evaluations (1) or (3) of the (n,f) cross section are more realistic from 10 to 15 MeV. While LLNL pulsed spheres [32] are sensitive to nuclear data from 5 to 15 MeV, changes in the 239Pu(n,f) cross section of less than 5% were shown in [79] to have minimal impact on their simulation. Hence, the new NIFFTE TPC measurement is an important clue to accurately define the (n,f) cross section above 14 MeV.
3.2 Validation with respect to various fission quantities
The evaluated parameters listed in Table 2 were used not only to calculate the evaluated
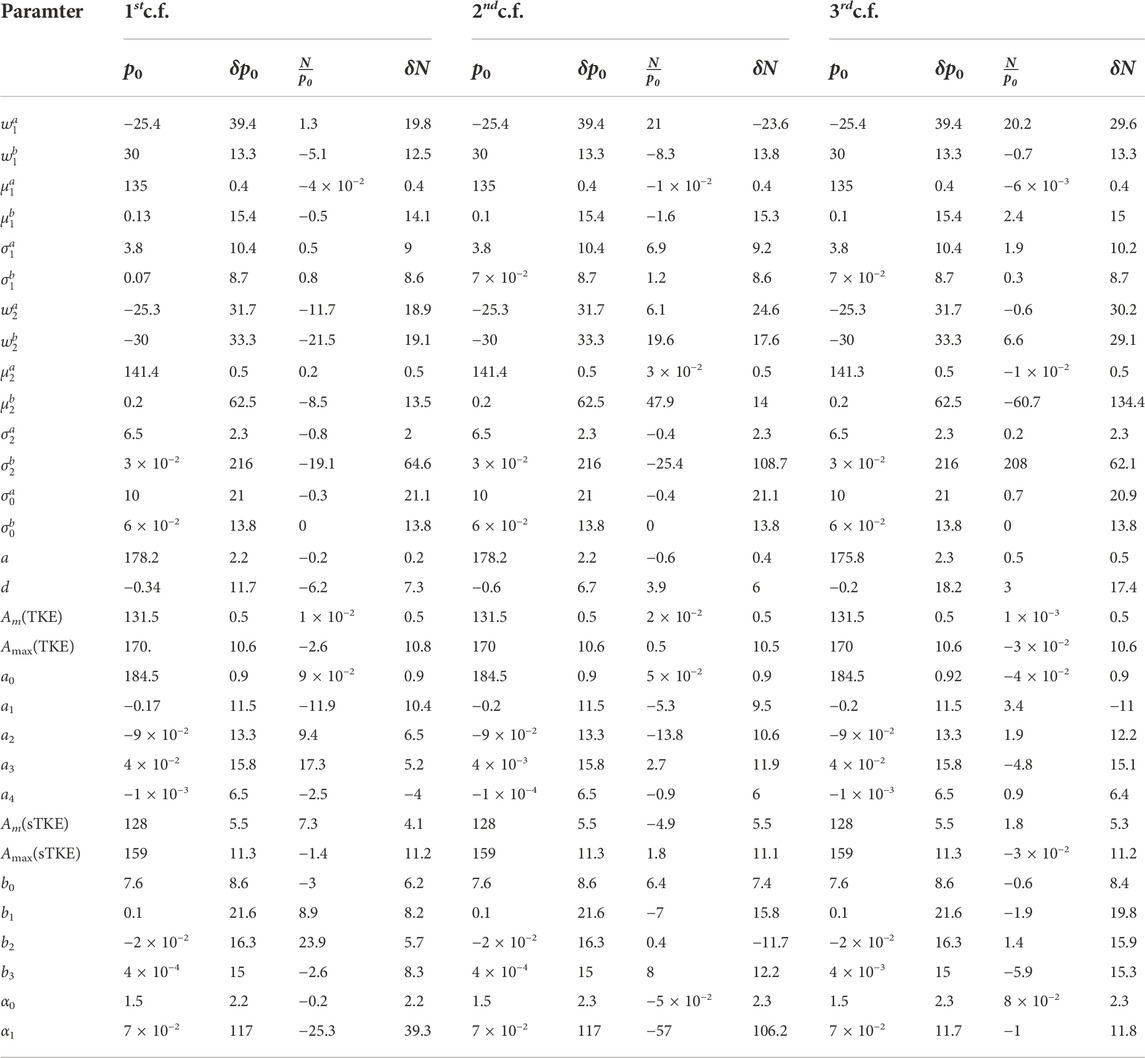
TABLE 2. Prior CGMF parameter values, p0, for the
As these are potentially large parameter changes, we use the evaluated parameters to calculate other fission observables in CGMF to ensure their consistency. The mass distributions in the first chance energy range, shown in Figure 8, differ only little from prior estimates despite changes of 10%–20% in parameter values. However, seemingly small changes
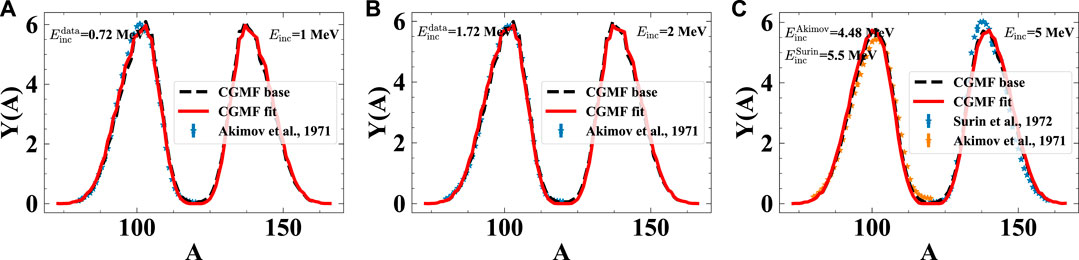
FIGURE 8. Comparison of the baseline CGMF calculation (black dashed), evaluated CGMF calculation (red solid) and experimental data (filled symbols) for the pre-neutron emission mass distributions, Y(A), at incident neutron energies of 1, 2, and 5 MeV.
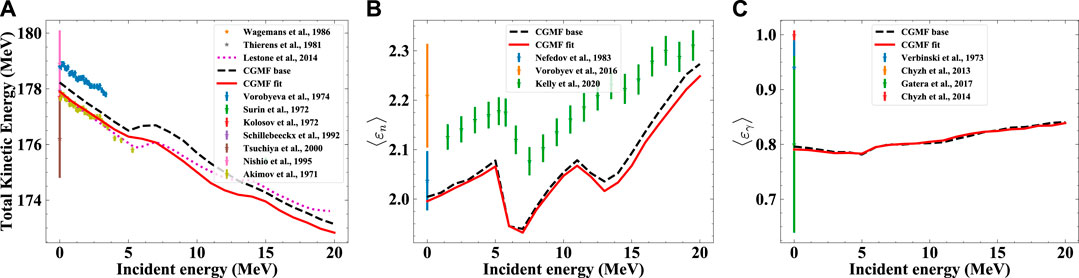
FIGURE 9. CGMF baseline calculation, evaluated CGMF calculation, and experimental data are compared for several observables: (Left) Total kinetic energy, TKE, as a function of incident neutron energy. The curve of Lestone et al. is a phenomenological model calculation informed by experimental data. (Center) Average outgoing energies of the prompt neutrons and (right) γ rays as a function of incident neutron energy.
The predicted prompt fission observables are all well in line with experimental data except for the known discrepancies in the mean energies of the PFNS. This close agreement of fission data beyond
3.3 Validation with respect to integral experiments
The evaluated 239Pu
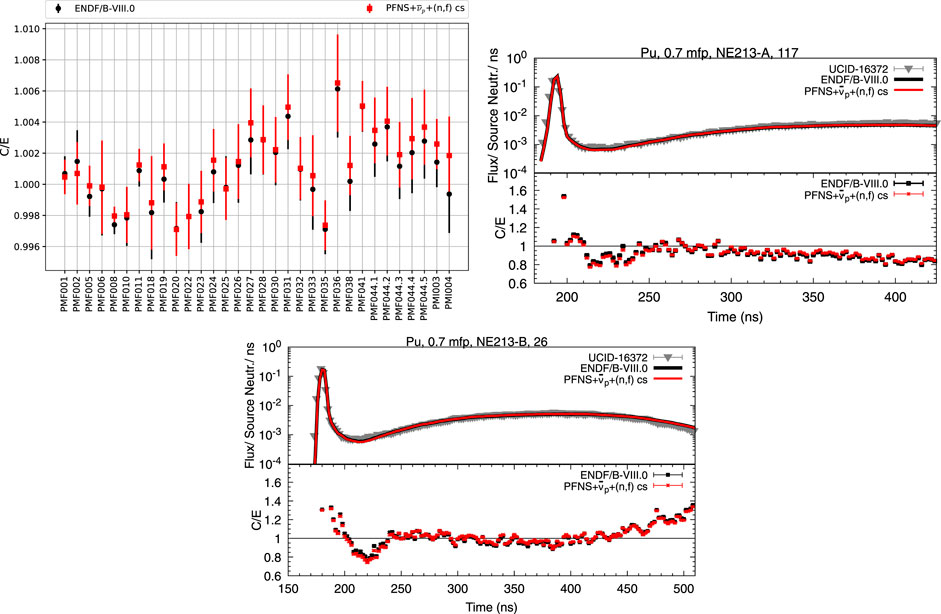
FIGURE 10. Simulated values (“C”) for keff of PMF and PMI assemblies (left) and two Pu LLNL pulsed sphere neutron leakage spectra (other two plots) are depicted for ENDF/B-VIII.0 versus the new fission source term. Experimental data (“E”) are shown for comparison.
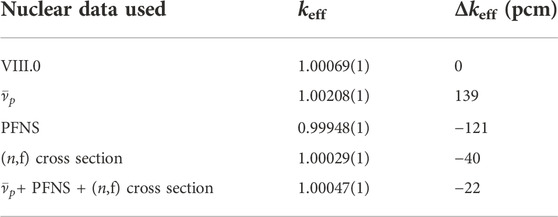
TABLE 3. Calculated values of PMF-001rev.4 keff are shown for ENDF/B-VIII.0 and ENDF/B-VIII.0 with different combinations of nuclear data. Δkeff is the difference between keff using new nuclear data identified with the same row and ENDF/B-VIII.0.
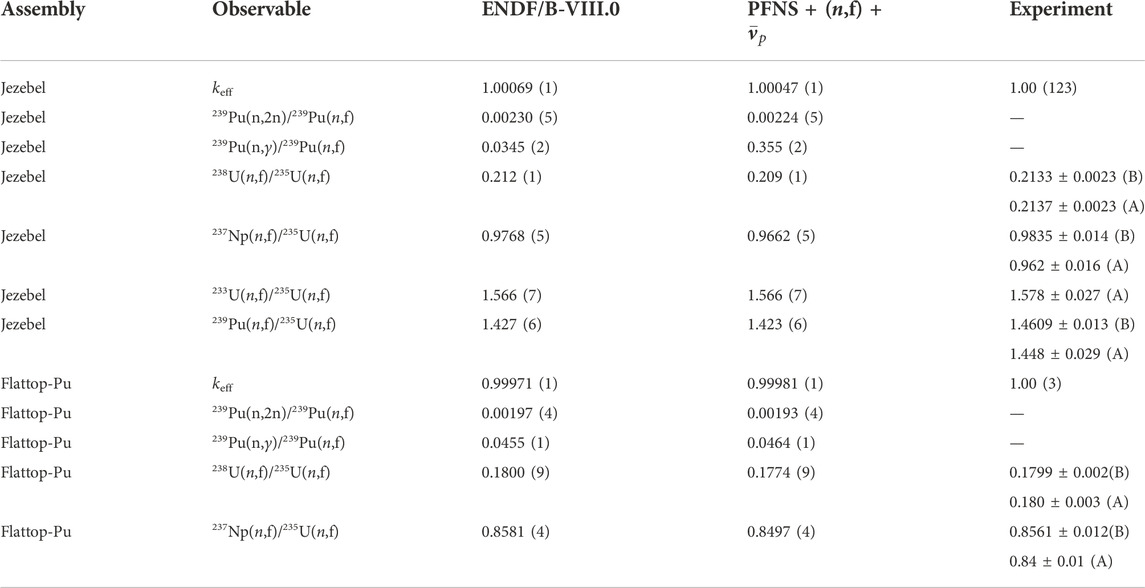
TABLE 4. Calculated values are shown for reaction rates of various reactions in Jezebel and Flattop-Pu critical assemblies. Calculated values are given for ENDF/B-VIII.0 as well as the 239Pu fission source term. Experimental values were taken from Table XXXIX of Ref. [85].
We have assessed the impact of changing each fission source term observable on simulated keff values of PMF001v.4 (Jezebel) by swapping them into ENDF/B-VIII.0 and comparing them to ENDF/B-VIII.0 simulated results in Table 3. The simulated keff values change distinctly: keff decreases by 121 pcm if the new PFNS is used. This large change, largely driven by including CEA and Chi-Nu data, is counterbalanced by the new
Similarly to what was seen for changing the fission source term for predicting PMF001.v4, keff values of several PU-MET-FAST (PMF) and PU-MET-INT (PMI) assemblies simulated with new nuclear data are close to ones predicted with ENDF/B-VIII.0: the mean bias calculated from ENDF/B-VIII.0 C/E, calculated over experimental, values is 18 pcm, and increases to only 58 pcm for the file including the new nuclear data. The keff value of benchmarks with harder spectra are predicted slightly better than with ENDF/B-VIII.0. For instance, Jezebel (PMF001v.4), dirty Jezebel (PMF002), and Flattop-Pu (PMF006) keff values predicted with the new fission source term are closer to experimental values, while PMI and PMF assemblies with a softer spectrum (011, 018, 019, 021.1, 021.2, 024, 027, 031, 032, 033, 036, 038, and all cases of 044) have worse C/E for the new file than when simulated with ENDF/B-VIII.0. This difference could point to the need for a lowering of the
The differences in using ENDF/B-VIII.0 and the new fission source term for simulating plutonium LLNL pulsed spheres [32] are modest. These experiments validate 239Pu fission and neutron scattering nuclear data from approximately 5–15 MeV, but little impact was expected from changes in the (n,f) cross section and
4 Summary and outlook
Recently, new high-precision experimental fission data and detailed modeling became available that refined our understanding of 239Pu prompt fission neutron spectra, PFNS, average prompt-fission neutron multiplicity,
• The LANL Chi-Nu and CEA teams provided two data sets, that covered for the first time 239Pu PFNS for broad incident and outgoing energy ranges with high precision. These show that the 239Pu PFNS should be softer for Einc < 5 MeV than in ENDF/B-VIII.0, and resolved, for the first time, predicted structures in the PFNS due to multiple chance fission and the pre-equilibrium component. While the data confirmed the incident and outgoing energies where theory predicted these structures, the experimental data led to corrections in the magnitude of these effects.
• The average prompt fission neutron multiplicity,
• The NIFFTE TPC collaboration measured 239Pu(n,f)/235U(n,f) cross sections, with high precision using a new detector type, a time-projection chamber. To date, these data are recommended to be treated as shape data. These data confirmed the shape of previous evaluated data that were mostly driven by fission chamber measurements below 14 MeV. The new data resolved a question triggered by discrepant data above 14 MeV and lowered the evaluated cross section by 2%.
The detailed fission theory and new high precision experiments distinctly changed the evaluated nuclear data. These changes balance each other, without the need for tweaks, such that their combined impact on the simulated effective neutron multiplication factors of ICSBEP critical assemblies is small. Given that the new evaluations are backed by new high precision experimental data and detailed fission modeling, it is likely that compensating errors between the fission source term observables in ENDF/B-VIII.0 are reduced.
Future work could focus on predicting PFNS and
Data availability statement
The evaluated data generated as part of this study can be found in https://www-nds.iaea.org/INDEN/ under Tab “Pu-239“. The code GMAP is available on https://github.com/IAEA-NDS/gmapy. The code CGMF is available on https://github.com/lanl/CGMF. The code ARIADNE is currently under review for release at LANL. It cannot be made available before this review is successfully finalized per LANL rules. The code containing the exciton and Los Alamos model is a code by another LANL employee and cannot be made available by the authors per LANL rules. The MCNP code is distributed to its worldwide user community by the Radiation Safety Information Computational Center (RSICC), which is based at the Oak Ridge National Laboratory in Oak Ridge, Tennessee. Because the MCNP code is export controlled, the distribution through RSICC is governed by US laws and Department of Energy regulations. Information can be found on: https://mcnp.lanl.gov/how\_to\_get\_the\_mcnp\_code.html.
Author contributions
DN undertook the evaluations, uncertainty quantification of input data, and integral-experiment analysis. AL provided the prior and fission-observable validation for the
Funding
Work at LANL was carried out under the auspices of the National Nuclear Security Administration (NNSA) of the U.S. Department of Energy (DOE) under contract 89233218CNA000001. Research on compensating errors mentioned in this publication was supported by the U.S. Department of Energy LDRD program at Los Alamos National Laboratory.
Acknowledgments
DN thanks N. Gibson (LANL) for his help in assembling the 239Pu file for integral-experiment validation. We gratefully acknowledge partial support of the Advanced Simulation and Computing program at LANL and the DOE Nuclear Criticality Safety Program, funded and managed by NNSA for the DOE.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Footnotes
1The liquid scintillator array was used to measure PFNS above 200 keV, while an extrapolation was used to approximate the PFNS below (which constitutes 0.3% of the PFNS for Einc = 1–3 MeV and, therefore, keeps the uncertainty due to the extrapolation low).
References
1. Chadwick MB. Nuclear science for the manhattan project and comparison to today’s ENDF data. Nucl Technology (2021) 207:S24–S61. doi:10.1080/00295450.2021.1901002
2. Fréhaut J, Mosinski G, Soleilhac M. Recent results in v̄p measurements between 1.5 and 15 MeV. In: v̄p The average Number of Emitted Neutrons in Fission, Contributions to the EANDC Topical Conference held on Novembre 29 (1973).
3. Nurpeisov B, Volodin K, Nesterov VG, Smirenkin G, Turchin Y. Dependence of \overline\nu on neutron energies up to 5 MeV for 233U, 238U, and 239Pu. At Energy (1975) 39:807–13. doi:10.1007/bf01122383
4. Soleilhac M, Fréhaut J, Gauriau J, Mosinski G. Average number of prompt neutrons and relative fission cross-sections of U-235 and Pu-239 in the 0.3 to 1.4 MeV range. Nucl Data Reactors Conf (1970) 2:145–56.
5. Walsh R, Boldeman J. The energy dependence of νp for 233U, 235U and 239Pu below 5⋅ 0 MeV. J Nucl Energ (1971) 25:321–30. doi:10.1016/0022-3107(71)90064-5
6. Condé H, Hansén J, Holmberg M. Prompt ν in neutron-induced fission of 239Pu and 241Pu. J Nucl Energ (1968) 22:53–60. doi:10.1016/0022-3107(68)90064-6
7. Gwin R, Spencer R, Ingle R. Measurements of the energy dependence of prompt neutron emission from 233U, 235U, and 239Pu for en = 0.0005 to 10 MeV relative to emission from spontaneous fission of 252Cf. Nucl Sci Eng (1986) 94:365–79. doi:10.13182/nse86-a18347
8. Hopkins J, Diven B. Prompt neutrons from fission. Nucl Phys (1963) 48:433–42. doi:10.1016/0029-5582(63)90182-2
9. Neudecker D, Lewis AM, Matthew E. Templates of expected measurement uncertainties. Tech. Rep. LA-UR-19-31156. Los Alamos, MN: Los Alamos National Laboratory (2019).
10. Carlson A, Pronyaev V, Capote R, Hale G, Chen Z-P, Duran I, et al. Evaluation of the Neutron Data StandardsSpecial issue on nuclear reaction data. Nucl Data Sheets (2018) 148:143–88. doi:10.1016/j.nds.2018.02.002
11. Neudecker D, Smith D, Tovesson F, Capote R, White M, Bowden N, et al. Applying a template of expected uncertainties to updating 239Pu(n, f) cross-section covariances in the neutron data standards database. Nucl Data Sheets (2020) 163:228–48. doi:10.1016/j.nds.2019.12.005
12. Neudecker D, Hejnal B, Tovesson F, White MC, Smith DL, Vaughan D, et al. Template for estimating uncertainties of measured neutron-induced fission cross-sections. EPJ Nucl Sci Technol (2018) 4:21. doi:10.1051/epjn/2018026
13. Capote R, Chen Y-J, Hambsch F-J, Kornilov N, Lestone J, Litaize O, et al. Prompt fission neutron spectra of ActinidesSpecial issue on nuclear reaction data. Nucl Data Sheets (2016) 131:1–106. doi:10.1016/j.nds.2015.12.002
14. Neudecker D, Taddeucci T, Haight R, Lee H, White M, Rising M. The need for precise and well-documented experimental data on prompt fission neutron spectra from neutron-induced fission of 239Pu. Nucl Data Sheets (2016) 131:289–318. doi:10.1016/j.nds.2015.12.005
15. Madland D, Nix J. New calculation of prompt fission neutron spectra and average prompt neutron multiplicities. Nucl Sci Eng (1982) 81:213–71. doi:10.13182/nse82-5
16. Kornilov N. The scale method as an approach for prompt fission neutron spectra analysis and EvaluationSpecial issue on nuclear reaction data. Nucl Data Sheets (2019) 155:75–85. doi:10.1016/j.nds.2019.01.004
17. Kawano T. CoH3: The coupled-channels and hauser-feshbach code. Springer Proc Phys (2021) 254:28–34. doi:10.1007/978-3-030-58082-7
18. Vladuca G, Tudora A. Improved Los Alamos model applied to the neutron induced fission of 239Pu and 240Pu and to the spontaneous fission of Pu isotopes239Pu and 240Pu and to the spontaneous fission of Pu isotopes, journal = Annals of Nuclear Energy. Ann Nucl Energ (2001) 28:689–700. doi:10.1016/s0306-4549(00)00083-9
19. Kahler A, MacFarlane R, Mosteller R, Kiedrowski B, Frankle S, Chadwick M, et al. ENDF/B-VII.1 neutron cross section data testing with critical assembly benchmarks and reactor experiments. Nucl Data Sheets (2011) 112:2997–3036. doi:10.1016/j.nds.2011.11.003
20.ICS. International handbook of evaluated criticality safety benchmark experiments/nuclear energy agency. Tech. Rep. (NEA;7328). Paris: OECD Nuclear Energy Agency (2019).
21. Chadwick M, Capote R, Trkov A, Herman M, Brown D, Hale G, et al. CIELO collaboration summary results: International evaluations of neutron reactions on uranium, plutonium, iron, oxygen and hydrogen. Nucl Data Sheets (2018) 148:189–213. doi:10.1016/j.nds.2018.02.003
22. Kelly KJ, Devlin M, O’Donnell JM, Gomez JA, Neudecker D, Haight RC, et al. Measurement of the 239Pu(n, f) prompt fission neutron spectrum from 10 keV to 10 MeV induced by neutrons of energy 1–20 MeV. Phys Rev C (2020) 102:034615. doi:10.1103/physrevc.102.034615
23. Marini P, Taieb J, Laurent B, Bélier G, Chatillon A, Etasse D, et al. Prompt-fission-neutron spectra in the 239Pu(n, f ) reaction. Phys Rev C (2020) 101:044614. doi:10.1103/physrevc.101.044614
24. Kelly K, Marini P, Taieb J, Devlin M, Neudecker D, Haight R, et al. Comparison of results from recent NNSA and CEA measurements of the 239Pu(n, f) prompt fission neutron spectrum. Nucl Data Sheets (2021) 173:42–53. doi:10.1016/j.nds.2021.04.003
25. Snyder L, Anastasiou M, Bowden N, Bundgaard J, Casperson R, Cebra D, et al. Measurement of the 239Pu(n, f)/235U(n, f) cross-section ratio with the NIFFTE fission time projection chamber. Nucl Data Sheets (2021) 178:1–40. doi:10.1016/j.nds.2021.11.001
26. Monterial M, Schmitt K, Prokop C, Leal-Cidoncha E, Anastasiou M, Bowden N, et al. Measurement of material isotopics and atom number ratio with α-particle spectroscopy for a NIFFTE fission Time Projection Chamber actinide target. Nucl Instr Methods Phys Res Section A: Acc Spectrometers, Detectors Associated Equipment (2022) 1021:165864. doi:10.1016/j.nima.2021.165864
27. Marini P. Energy dependence of prompt fission neutron multiplicity in the 239Pu(n,f) reaction (2021).
29. Verbeke J, Randrup J, Vogt R. Fission reaction event yield algorithm FREYA 2.0.2. Computer Phys Commun (2018) 222:263–6. doi:10.1016/j.cpc.2017.09.006
30. Litaize O, Serot O, Berge L. Fission modelling with FIFRELIN. Eur Phys J A (2015) 51:177. doi:10.1140/epja/i2015-15177-9
31. Schmidt K-H, Jurado B, Amouroux C, Schmitt C. General description of fission observables: GEF model code. Nucl Data Sheets (2016) 131:107–221. doi:10.1016/j.nds.2015.12.009
32. Wong C, Anderson J, Brown P, Hansen L, Kammerdiener J, Logan C, et al. Livermore pulsed sphere program: Program summary through july 1971. LLNL Ucrl-51144 Rev (1972) 1.
33. Wu CY, Henderson RA, Haight RC, Lee HY, Taddeucci TN, Bucher B, et al. A multiple parallel-plate Avalanche counter for fission-fragment detection. Nucl Instr Methods Phys Res Section A: Acc Spectrometers Detectors Associated Equipment (2015) 794:76–9. doi:10.1016/j.nima.2015.05.010
34. Kelly KJ, Kawano T, O’Donnell JM, Gomez JA, Devlin M, Neudecker D, et al. Preequilibrium asymmetries in the 239Pu(n, f) prompt fission neutron spectrum. Phys Rev Lett (2019) 122:072503. doi:10.1103/physrevlett.122.072503
35. Kelly KJ, Gomez JA, Devlin M, O’Donnell JM, Neudecker D, Lovell AE, et al. Measurement of the 235U(n, f) prompt fission neutron spectrum from 10 keV to 10 MeV induced by neutrons of energy 1–20 MeV. Phys Rev C (2022) 105:044615. doi:10.1103/physrevc.105.044615
36. Devlin M, Kelly KJ. Prompt neutron emission from fission: Recent experimental results. Front Phys (2022).
37. Laurent B, Taieb J, Bélier G, Marini P, Morfouace P. New developments of a fission chamber for very high radioactivity samples. Nucl Instr Methods Phys Res Section A: Acc Spectrometers, Detectors Associated Equipment (2021) 990:164966. doi:10.1016/j.nima.2020.164966
38. Savin M, Khokhlov Y, Zamjatnin Y, Paramonova I. The average number of prompt neutrons in fast neutron induced fission of 235U and 239Pu. Nucl Data Reactors Conf. (1970) 2:157–65.
39. Savin M, Khokhlov Y, Savelév A, Paramonova I. Energy dependence of v̄ in the fission of U235 by fast neutrons. Soviet J Nucl Phys (1973) 16:638–40.
40. Haight R, Lee H, Taddeucci T, O’Donnell J, Perdue B, Fotiades N, et al. Two detector arrays for fast neutrons at LANSCE. J Instrum (2012) 7:C03028. doi:10.1088/1748-0221/7/03/c03028
41. Diven BC, Martin HC, Taschek RF, Terrell J. Multiplicities of fission neutrons. Phys Rev (1956) 101:1012–5. doi:10.1103/physrev.101.1012
42. Soleilhac M, Frehaut J, Gauriau J. Energy dependence of ν̄p for neutron-induced fission of 235U, 238U and 239Pu from 1.3 to 15 MeV. J Nucl Energ (1969) 23:257–82. doi:10.1016/0022-3107(69)90060-4
43. Mather D, Fieldhouse P, Moat A. Measurement of prompt ν for the neutron-induced fission of Th232, U233, U234, U238 and Pu239. Nucl Phys (1965) 66:149–60. doi:10.1016/0029-5582(65)90139-2
44. Bolodin K, Kuznetsov V, Nesterov V, Nurpeisov B, Prokhorova L, Turchin Y, et al. Average number of prompt neutrons in Pu239 fission. At Energy (1972) 33:1045–50. doi:10.1007/bf01124606
45. Neudecker D, White M, Vaughan D, Srinivasan G. Validating nuclear data uncertainties obtained from a statistical analysis of experimental data with the ”Physical Uncertainty Bounds” method. EPJ Nucl Sci Technol (2020) 6:19. doi:10.1051/epjn/2020007
46. Heffner M, Asner D, Baker R, Baker J, Barrett S, Brune C, et al. A time projection chamber for high accuracy and precision fission cross-section measurements. Nucl Instr Methods Phys Res Section A: Acc Spectrometers, Detectors Associated Equipment (2014) 759:50–64. doi:10.1016/j.nima.2014.05.057
47. Lisowski P, Ullman J, Balestrini S, Carlson A, Wasson O, Hill N. Neutron induced fission cross section ratios for 232Th, 235, 238U, 237Th and 239Pu from 1 to 400 MeV. Proc Conf Nucl Data Sci Technol Mito (1988) 1988:97–9.
48. Tovesson F, Hill T. Cross sections for 239Pu(n, f) and 241Pu(n, f) in the range en = 0.01 eV to 200 MeV. Nucl Sci Eng (2010) 165:224–31. doi:10.13182/nse09-41
49. Shcherbakov O, Donets A, Evdokimov A, Fomichev A, Fukahori T, Hasegawa A, et al. Neutron-induced fission of 233U, 238U, 232Th, 239Pu, 237Np, natPb and 209Bi relative to 235U in the energy range 1–200 MeV. J Nucl Sci Technol (2002) 39:230–3. doi:10.1080/00223131.2002.10875081
50. Staples P, Morley K. Neutron-induced fission cross-section ratios for 239Pu, 240Pu, 242Pu, and 244Pu relative to 235U from 0.5 to 400 MeV. Nucl Sci Eng (1998) 129:149–63. doi:10.13182/nse98-a1969
52. Duke DL. Fission fragment mass distributions and total kinetic energy release of 235-uranium and 238-uranium in neutron-induced fission at intermediate and fast neutron energies. Ph.D. thesis. Golden, CO: Colorado School of Mines (2015).
53. Neudecker D, Talou P, Kawano T, Kahler A, White M, Taddeucci T, et al. Evaluations of energy spectra of neutrons emitted promptly in neutron-induced fission of 235U and 239Pu. Nucl Data Sheets (2018) 148:293–311. doi:10.1016/j.nds.2018.02.006
54. Chadwick M, Herman M, Obložinský P, Dunn M, Danon Y, Kahler A, et al. ENDF/B-VII.1 nuclear data for science and Technology: Cross sections, covariances, fission product yields and decay DataSpecial issue on ENDF/B-VII.1 library. Nucl Data Sheets (2011) 112:2887–996. doi:10.1016/j.nds.2011.11.002
55. Lestone J, Shores E. Uranium and plutonium average prompt-fission neutron energy spectra (PFNS) from the analysis of NTS NUEX data. Nucl Data Sheets (2014) 119:213–6. doi:10.1016/j.nds.2014.08.059
57. Lestone J, Strother T. Energy dependence of plutonium and uranium average fragment total kinetic energies. Nucl Data Sheets (2014) 118:208–10. doi:10.1016/j.nds.2014.04.038
58. Madland D. Total prompt energy release in the neutron-induced fission of 235U, 238U, and 239Pu. Nucl Phys A (2006) 772:113–37. doi:10.1016/j.nuclphysa.2006.03.013
59. Otuka N, Dupont E, Semkova V, Pritychenko B, Blokhin A, Aikawa M, et al. Towards a more complete and accurate experimental nuclear reaction data library (EXFOR): International collaboration between nuclear reaction data centres (NRDC). Nucl Data Sheets (2014) 120:272–6. doi:10.1016/j.nds.2014.07.065
60. Neudecker D, Lovell A, Talou P. Producing ENDF/B-quality Evaluations of 239Pu(n,f) and 235U(n,f) average prompt neutron Multiplicities using the CGMF model. Tech. Rep. LA-UR-21–29906. Los Alamos, MN: Los Alamos National Laboratory (2021).
61. Neudecker D. ARIADNE—A program estimating covariances in detail for neutron experiments. EPJ Nucl Sci. Technol. (2018) 4:34. doi:10.1051/epjn/2018012
62. Young P, Chadwick M, MacFarlane R, Talou P, Kawano T, Madland D, et al. Evaluation of neutron reactions for ENDF/B-vii: 232−241U and 239Pu. Nucl Data Sheets (2007) 108:2589–654. doi:10.1016/j.nds.2007.11.002
63. Poenitz W, Aumeier S. The simultaneous evaluation of the standards and other cross-sections of importance for Technology. Tech. Rep. ANL/NDM-139. Chicago, IL: Argonne National Laboratory Report (1997).
64. Badikov S, Chen Z, Carlson A. International evaluation of neutron cross-section standards. Tech. Rep. STI/PUB/1291. Vienna, Austria: International Atomic Energy Agency (2007).
65. Neudecker D, Pronyaev V, Snyder L. Including238U(n,f)/235U(n,f) and239Pu(n,f)/235U(n,f) NIFFTE fissionTPC Cross-sections into the Neutron Data Standards Database. Los Alamos, MN: Los Alamos National Laboratory (2021). Tech. Rep. LA-UR-21–24093.
66. Neudecker D, Otuka N, Casperson R, Bowden N, Snyder L, Schmitt K, et al. Information files of 238U(n,f)/235U(n,f) NIFFTE fissionTPC cross-sections for the neutron data standards project. Tech. Rep. LA-UR-18–23788. Los Alamos, MN: Los Alamos National Laboratory (2018).
67. Carlson A, Pronyaev V, Smith D, Larson N, Chen Z, Hale G, et al. International evaluation of neutron cross section StandardsSpecial issue on nuclear reaction data. Nucl Data Sheets (2009) 110:3215–324. doi:10.1016/j.nds.2009.11.001
68. Herman MW. Covariance data in the fast neutron region. Tech. Rep. NEA/NSC/WPEC/DOC(2010)427. Paris, France: Organization for Economic Co-operation and Development-Nuclear Energy Agency (2011).
70. Neudecker D, Frühwirth R, Leeb H. Peelle’s pertinent puzzle: A fake due to improper analysis. Nucl Sci Eng (2012) 170:54–60. doi:10.13182/nse11-20
71. Chiba S, Smith D. A suggested procedure for resolving an anomaly in least-squares data analysis known as ”peelle’s pertinent puzzle” and the general implications for nuclear data evaluation. Chicago, IL: Argonne National Laboratory}, (1991). doi:10.2172/10121367
72. Grosskopf M, Vander Wiel S. On using fully-correlated relative covariance for catpuring systematic uncertainty (2022).
73. Chatillon A, Bélier G, Granier T, Laurent B, Morillon B, Taieb J, et al. Measurement of prompt neutron spectra from the 239Pu(n, f) fission reaction for incident neutron energies from 1 to 200 MeV. Phys Rev C (2014) 89:014611. doi:10.1103/physrevc.89.014611
74. Trkov A, Capote R, Pronyaev V. (2015 current issues in nuclear data evaluation methodology: 235U prompt fission neutron spectra and multiplicity for thermal neutrons. Nucl Data Sheets (2015) 123:8–15. doi:10.1016/j.nds.2014.12.003
75. Neudecker D, Kelly KJ. Including chi-nu 235U PFNS experimental Data into an ENDF/B-VIII. 1 release candidate evaluation. Tech. Rep. LA-UR-22–22220. Los Alamos, MN: Los Alamos National Laboratory (2022).
76. Sugimoto M, Smith AB, Guenther PT. Ratio of the prompt fission neutron spectrum of 239pu to that of 235u. Nucl Sci Eng (1987) 97:235–8. doi:10.13182/nse87-a23505
77. Vaughan DE, Preston DL. Physical uncertainty bounds (PUB). Los Alamos, MN: Los Alamos National Laboratory (2014).
78. Neudecker D, White MC. Report on validating ENDF/B-VIII.0 239Pu average prompt fission neutron multiplicity. Los Alamos, MN: Los Alamos National Laboratory (2019).
79. Neudecker D, Cabellos O, Clark A, Grosskopf M, Haeck W, Herman M, et al. Informing nuclear physics via machine learning methods with differential and integral experiments. Phys Rev C (2021) 104:034611. doi:10.1103/PhysRevC.104.034611
80. Werner C, Armstrong J, Brown F, Bull J, Casswell L, Cox L, et al. MCNP users manual - code version 6.2. Tech. Rep. LA-UR-17-29981. Los Alamos, MN: Los Alamos National Laboratory (2017).
81. Neudecker D, Cabellos O, Clark A, Haeck W, Capote R, Trkov A, et al. Which nuclear data can be validated with LLNL pulsed-sphere experiments? Ann Nucl Energy (2021) 159:108345. doi:10.1016/j.anucene.2021.108345
82. Mumpower M, Neudecker D, Kawano T, Herman M, Kleedtke N, Lovell AE, et al. The Los Alamos evaluation of 239Pu neutron-induced reactions in the fast energy range. Tech. Rep. LA-UR-22-24121. Los Alamos, MN: Los Alamos National Laboratory (2022).
83. Aguilar GP, Descalle M, Kravvaris K, Ormand W, Beck B, Mattoon C, et al. LLNL Evaluation of n +239Pu. Tech. Rep. LLNL-MI-834591. Lawrence Livermore National Laboratory (2022).
84. Capote R, Trkov A, Pigni M, Neudecker D, Herman M, Kelly K, et al. INDEN evaluation of neutron induced reactions on Pu-239. EPJ Web of conferences (2022).
Keywords: 239Pu, average prompt fission neutron multiplicity, prompt fission neutron spectrum, fission cross section, CGMF
Citation: Neudecker D, Lovell AE, Kelly KJ, Marini P, Snyder L, White MC, Talou P, Devlin M, Taieb J and Chadwick MB (2023) Shedding light on the 239Pu fission source term with new high-precision experiments and advanced fission modeling. Front. Phys. 10:1056324. doi: 10.3389/fphy.2022.1056324
Received: 28 September 2022; Accepted: 07 November 2022;
Published: 06 January 2023.
Edited by:
Anabella Tudora, University of Bucharest, RomaniaReviewed by:
Satoshi Chiba, Tokyo Institute of Technology, JapanAntonio Caciolli, University of Padua, Italy
Copyright © 2023 Neudecker, Lovell, Kelly, Marini, Snyder, White, Talou, Devlin, Taieb and Chadwick. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: D. Neudecker, ZG5ldWRlY2tlckBsYW5sLmdvdg==
 D. Neudecker
D. Neudecker A. E. Lovell1
A. E. Lovell1 P. Marini
P. Marini M. Devlin
M. Devlin M. B. Chadwick
M. B. Chadwick