- 1School of Physics and Electronics Science, Hunan University of Science and Technology, Xiangtan, China
- 2Hunan Provincial Key Laboratory of Intelligent Sensors and Advanced Sensor Materials, Xiangtan, China
- 3School of Physics and Electronics, Gannan Normal University, Ganzhou, China
- 4Institute of Theoretical Physics, Lanzhou University, Lanzhou, China
We investigate the single-photon quantum routing composed of two infinite waveguides coupled to two giant two-level atoms. The exact expressions of the single-photon transmission and reflection amplitudes are derived with the real-space approach. It is found that the single photon scattering behavior is strongly dependent on the phase difference between the two adjacent atom-waveguide coupling points, the frequency detuning, the coupling strength between the two giant atoms, and the interaction strengths between the giant atoms and the waveguides. Our studies show that an ideal single photon router with unit efficiency can be realised by designing the size of the giant atom, and the frequency detuning or adjusting the interaction strengths between the atoms and the waveguides. The results suggest the potential to effectively control the single-photon quantum routing based on the giant-atom setup.
1 Introduction
The design and realization of scalable quantum information processing systems rely on quantum networks [1]. As an essential ingredient in a quantum network, quantum routers can be used to transfer the quantum information from one channel to others, distributing it in the network. Due to their fastness, very low loss and long-playing coherence [2–4], photons are considered as ideal candidates of carriers of quantum information and thus quantum routing of photons has drawn more attentions in recent years. Numerous theoretical and experimental researches on quantum routing or photon transport have been made based on several different structures, such as coupled-resonator waveguides [5–16], whispering-gallery-mode resonators [17–20], waveguide-emitter systems [21–29], superconducting circuit [30–36].
Recently, giant atoms, as an emerging playground in quantum optics, have attracted a plethora of research interest because they exhibit several striking new phenomena, such as frequency-dependent relaxation rate and Lamb shift [37,38], oscillating bound states [39–43], decoherence-free interaction [44–46], chiral quantum optics [47,48], and phase-controlled frequency conversions [49,50]. For a traditional small atom, the size of the atom is very smaller than the wavelength of the field, and thus it can be well described with the dipole approximation. However, a giant atom couples to a waveguide at multiple points, and the distance between these points is no longer negligible compared with the waveguides of propagating fields in the waveguide. Such a giant-atom structure can be realized in several systems, such as superconducting quits coupled to either surface acoustic waves [51–54] or microwave transmission lines [4,44,55–57], cold atoms interacting with optical lattices [58]. In the giant-atom setup, the multiple coupling points lead to additional interference effects that are not present in quantum optics with conventional small atoms [37,39,45,59,60].
It is very interesting to study the issue that how to mediate single-photon scattering by the giant atoms. Some pioneering works have been reported in this area [42,50,61–65]. Reference [42] investigated the single-photon scattering properties in a one-dimensional coupled-resonator waveguide, where a giant two-level atom is nonlocally coupled to the waveguide via two or multiple resonators. The results showed that a giant atom can be treated as a controller to manipulate the propagation of the photon by introducing the interference effect. In a giant-molecule waveguide-QED system consisting of two coupled giant atoms and an infinite waveguide, the single-photon scattering in both the Markovian and non-Markovian regimes was studied. In this system, the asymmetric Fano line-shapes and the Rabi splitting-like phenomenon were observed [61]. Zhao et.al., reported that single photon scattering in a one-dimensional waveguide can be dynamically controlled by the periodic phase modulation via changing the size of the giant atom and a tunable Autler-Townes splitting can be achieved with the giant atom [62]. Furthermore, a chiral giant-atom model in both the Markovian and the non-Markovian regimes was focused, and it was shown that intriguing interference effects induced by a giant-atom structure result in exotic quantum phenomena such as ultranarrow scattering window [50].
Very recently, the strong dependence of single photon routing properties on the size of a giant atom coupling to two waveguides was revealed. To improve the routing efficiency, a perfect mirror was placed into the non-target waveguide to form a boundary and then the routing efficiency can reach unity [63]. An alternative approach was proposed in Ref. [21] to achieve a high transfer-rate routing, which is to place an atomic mirror aside the input channel but not to terminate it. Inspired by these works, we show an extension of the single photon router based on a single giant atom to the router with two coupled giant atoms, one of which serves as an atomic mirror. With the real-space approach, the exact expressions of the single-photon transmission and reflection amplitudes are derived. We explore the dependence of the single photon properties on the phase shift between two atom-waveguide coupling points, the frequency detuning between the incident photon and the atoms, the coupling strength between the two giant atoms, and the interaction strengths between the atoms and the waveguides. It is found that the single photon incident from one waveguide can be redirected in the other waveguide with a 100% probability by well designing the size of the giant atom and the frequency detuning or adjusting the ratio between the two atom-waveguide coupling strengths.
The paper is organized as follows: In Section 2, we present theoretical model and give the exact expressions of the single-photon transmission and reflection amplitudes with the real-space approach. In Section 3, we discuss the effects of the phase shift between two adjacent coupling points, the frequency detuning, the atomic interaction, and the coupling strengths between the giant atoms and the waveguides on the single photon routing properties. Finally, we conclude with a brief summary of the results in Section 4.
2 Theoretical model
As shown in Figure 1, we consider a single-photon router composed of two infinite linear waveguides and two coupled giant two-level atoms. The giant atom a simultaneously couples to the two waveguides, waveguide m and waveguide n, at two points x = 0 and x = x0, respectively, while the giant atom b only interacts the waveguide m at x = 2x0 and x = 3x0. For simplicity, we assume here that the distances between any two neighboring connection points are identical. With rotating-wave approximation [66,67], the real-space Hamiltonian of the system could be written as (ℏ = 1)
where Hw represents the free Hamiltonian of the two waveguides, Hab describes the two coupled giant atoms, HI is the interaction Hamiltonian between the atoms and the waveguides. The expressions of these Hamiltonian are written as follows:
where
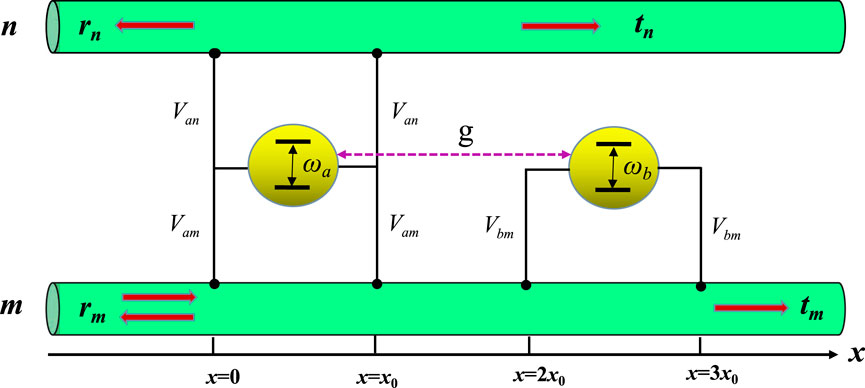
FIGURE 1. Schematic configuration of routing single photons in two channels made of two infinite linear waveguides. The giant two-level atom a couples twice with the waveguide m (waveguide n) at x = 0 and x = x0 with strength Vam (Van), and the giant two-level atom b only interacts the waveguide m at x = 2x0 and x = 3x0 with strength Vbm. The purple dashed line indicates an interatomic interaction with strength g. Initially, a single photon is launched from the left side of waveguide m and then is reflected, transmitted, or transferred to waveguide n.
We assume that initially a single photon with energy υgk is injected from the far left of the waveguide m. In the single-excitation subspace, the eigenstate of the system can be written as
where |∅⟩ is the vacuum state, which indicates zero photon in any waveguide and the two giant atoms in their ground states. ua (ub) is excitation amplitude of the atom a (b) in the excite state |e⟩a (|e⟩b).
where θ(x) is the Heaviside step function. tm (tn) and rm (rn) are, respectively, the transmission and reflection coefficients in the waveguide m (n). tmj (tnj) and rmj (rnj) represent the probability amplitudes for right-going and left-going photons between x = (j − 1)x0 and x = jx0 (j = 1, 2, 3) in the waveguide m (n), respectively.
Solving the eigenvalue equation H|ω⟩ = ω|ω⟩ with the expressions in Eqs 2–9, one can obtain a set of equations
where Δa = ω − ωa and Δb = ω − ωb are the frequency detunings between the incident photon and the atom a and b, respectively. θ = kx0, describes an accumulated phase of single photon traveling between any two adjacent coupling points. Then one can get the transmission and reflection amplitudes
where
Based on Eqs 11–13, the single-photon transmission and reflection rates could be defined by
One can obtian the relations Rn = Tn and Rm + Tm + Rn + Tn = 1 for probability conservation.
3 Single photon scattering mediated by two giant atoms
Now, we explore the single photon routing properties between the two waveguides mediated by the two giant atoms. Here, we interest in the quantum transfer efficiency Rn + Tn from the waveguide m to n, and only focus on Tn due to the relation Rn = Tn. The simple case with Δa = Δb = Δ, Γa = Γb = Γ and g = 0 is considered firstly. In this case, the transmission and reflection amplitudes in Eqs 11–13 can be simplified as
where
Figure 2 displays the transmission rates Tm and Tn versus the detuning Δ between the incident photon and the atoms, and the phase shift θ between two adjacent atom-waveguide coupling points. Here, the coupling strength between the two atoms is not taken into account, i.e., g = 0. Obviously, these spectra vary periodically as θ with a period of 2π. Note that the value of Tm is always zero when Δ = 2Γ sin θ, except for some special phases θ = (2j − 1)π (j = 1, 2, 3 … ) by analyzing Eq. 15. A dark purple sinusoidal shape appears at Δ/Γ = 2 sin θ, indicating Tm = 0, as shown in Figure 2A. Similar transmitted behavior have also been demonstrated in other giant-atom setups [50,62,68]. In the case of θ = (2j − 1)π (j = 1, 2, 3 … ), we have Rm = Tn = Rn = 0 (Rm and Rn not shown in Figure 2) with the factor 1 + eiθ = 0 in the expressions of Eqs 16, 17 but Tm = 1. The perfect transmission of the single photon arises from the quantum interferences among the multiple connection points [45]. Figure 2B displays that Tn can reach a maximum value of 0.48 (Rn = Tn = 0.48), which can be verified by numerical calculation based on Eq. 17. The results indicate that the maximum total quantum routing probability (Rn + Tn) from waveguide m to waveguide n is about 0.96.
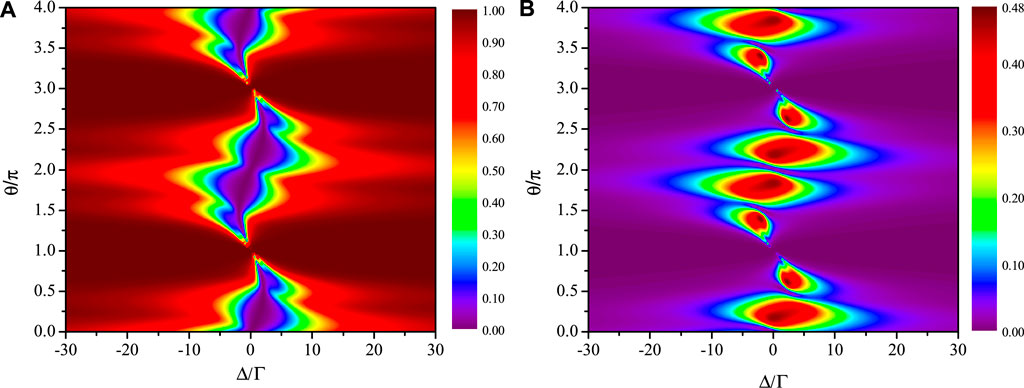
FIGURE 2. Transmission rates Tm (A) and Tn (B) as a function of the detuning Δ and the phase shift θ, in which the frequency detunings are equal (Δa = Δb = Δ), and the two atom-waveguide coupling strengths are the same (Γa = Γb = Γ). A dark purple sinusoidal shape implies Tm = 0, and Tn can reach its maximum value of 0.48. The transferred rate Tn + Rn (Rn = Tn) of the photon from the input waveguide m into the targeted waveguide n is 0.96. The other parameter is g = 0.
As shown in Figures 3, 4, we plot the effect of the coupling strength between the two giant atoms on single-photon routing properties. We also assume Δa = Δb = Δ and Γa = Γb = Γ. Figure 3 exhibits the transmission rates Tm and Tn as a function of the detuning Δ and the coupling strength g. One can see that there are two valleys or peaks, which are more clearly demonstrated by the profiles of Figure 3, as depicted in Figure 4. When g = 0, there is a single valley or peak in these scattering spectra, but for g ≠ 0 two valleys or peaks appear in these spectra. As g increases, the separation of the two valleys or peaks gradually increases and the intensities also change. The results indicate that the coupling strength between the two atoms can control the single-photon scattering in the two waveguide channels. However, an increase of the coupling strength leads to decreasing of Tn. Consequently, when the coupling strength g = 0 the maximum total quantum routing probability with 0.88 can reach.
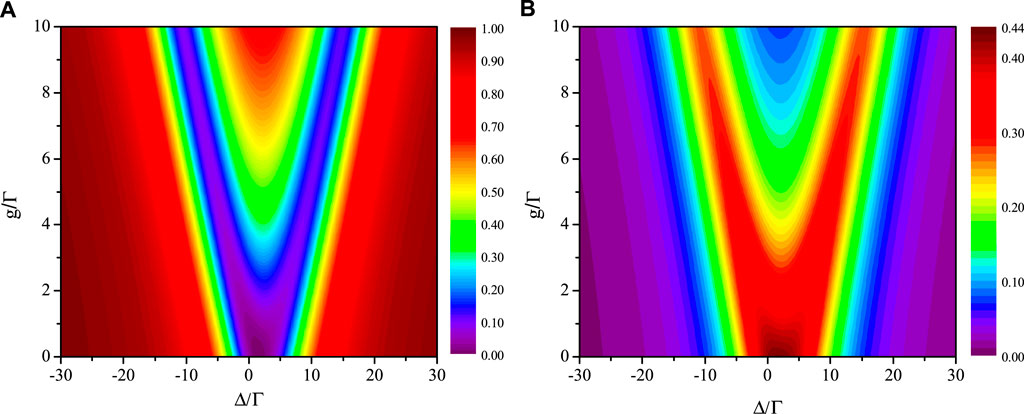
FIGURE 3. Transmission rates Tm (A) and Tn (B) as a function of the detuning Δ and the coupling strength g between the two atoms under the same atom-waveguide interaction strengths (Γa = Γb = Γ). The spectra show V-type shapes, indicating the existence of two valleys or peaks. The phase shift between two adjacent coupling points is fixed to θ = π/4.
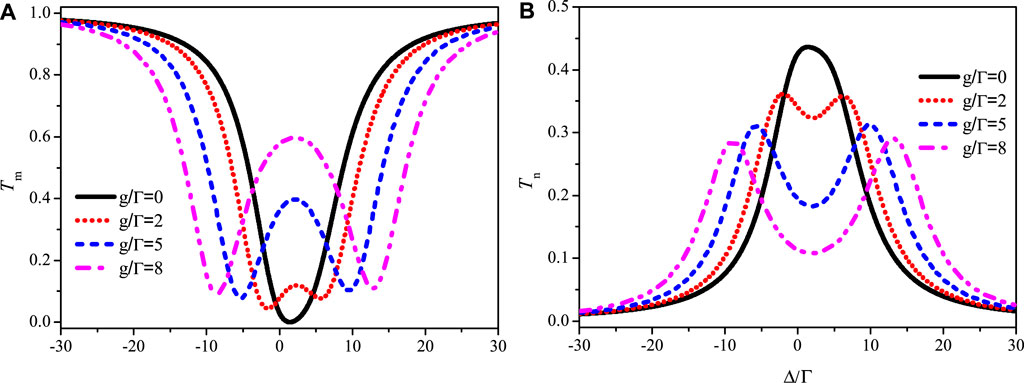
FIGURE 4. The transmitted curves Tm (A) and Tn (B) show the profiles of Figure 3. The effect of the coupling strength g between the atom a and b on the single-photon scattering is revealed. The number of valleys or peaks varies from one to two as g changes from zero to non-zero.
Next, the influence of the atom-waveguide coupling strengths on single-photon routing properties is investigated. Here, we also set Γa = Γ, serving as the unit of other parameters, but change the value of Γb by adjusting the ratio Γb/Γa = η. Moreover, the interatomic coupling is turned off, i.e., g = 0. To explore a possible unit transfer efficiency from the waveguide m to n, we let Δ = 2Γb sin θ = 2Γη sin θ [θ ≠ (2j − 1)π, j = 1, 2, 3 … ] to ensure Tm = 0, meanwhile, seek the condition of Rm = 0. After analyzing Eqs 11, 12, both Tm = 0 and Rm = 0 are guaranteed when the following conditions are satisfied simultaneously:
To clearly demonstrate possible extremum values of Tn and Rm, we plot Tn and Rm as a function of θ and η by substituting g = 0 and Δ = 2Γb sin θ into Eqs 11–13. One can see that there are six extremum points with Tn = 0.5 and Rm = 0 marked with white dots in Figures 5A,B, respectively, and they are symmetric about θ = π. The exact locations of the six extreme points are obtained based on the numerical analysis of Eqs 18–20, as shown in Table 1. We plot Tm, Rm and Tn versus Δ where the values of the other parameters are provided in the Table. It is worth noting that each pair of spectra (i.e., Figures 6A–F) with the same values of η are symmetric with respect to the vertical line Δ = 0. In fact, we have Tm [η, − Δ, 2π − (2j − 1)π/8] = Tm [η, Δ (2j − 1)π/8], Rm [η, − Δ, 2π − (2j − 1)π/8] = Rm [η, Δ (2j − 1)π/8] and Tn [η, − Δ, 2π − (2j − 1)π/8] = Tn [η, Δ (2j − 1)π/8] (j = 2, 3, 4, 5, 6, 7). In addition, two peaks appear in the reflected spectra Rm but not in other spectra. The locations of the two peaks are derived as
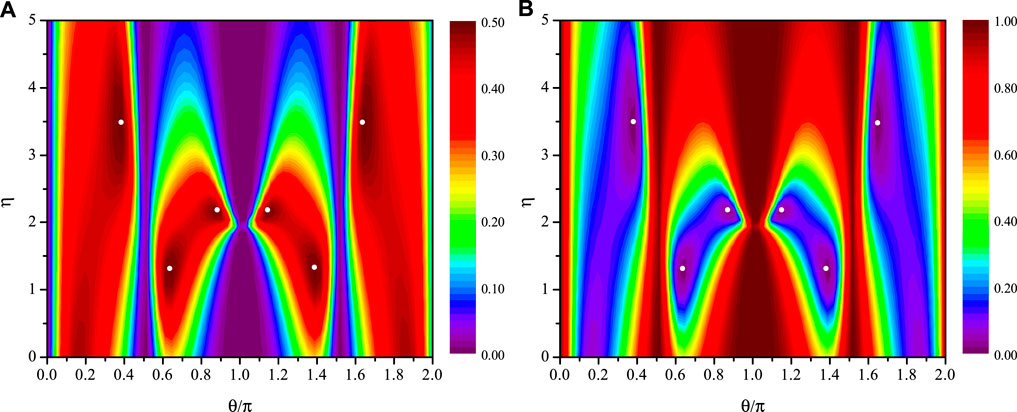
FIGURE 5. The extreme values of Tn (A) and Rm (B) for various phase shift θ and the ratio η between the two atom-waveguide coupling strengths. White dots represent extremum points with Tn = 0.5 or Rm = 0, showing symmetric about θ = π. The values of the parameters at the six extreme points are listed in Table 1. The interatomic interaction is fixed to g = 0.

TABLE 1. The values of the parameters θ, η and Δ at extremum points with Tn = Rn = 0.5 and Tm = Rm = 0 in Figures 5, 6.
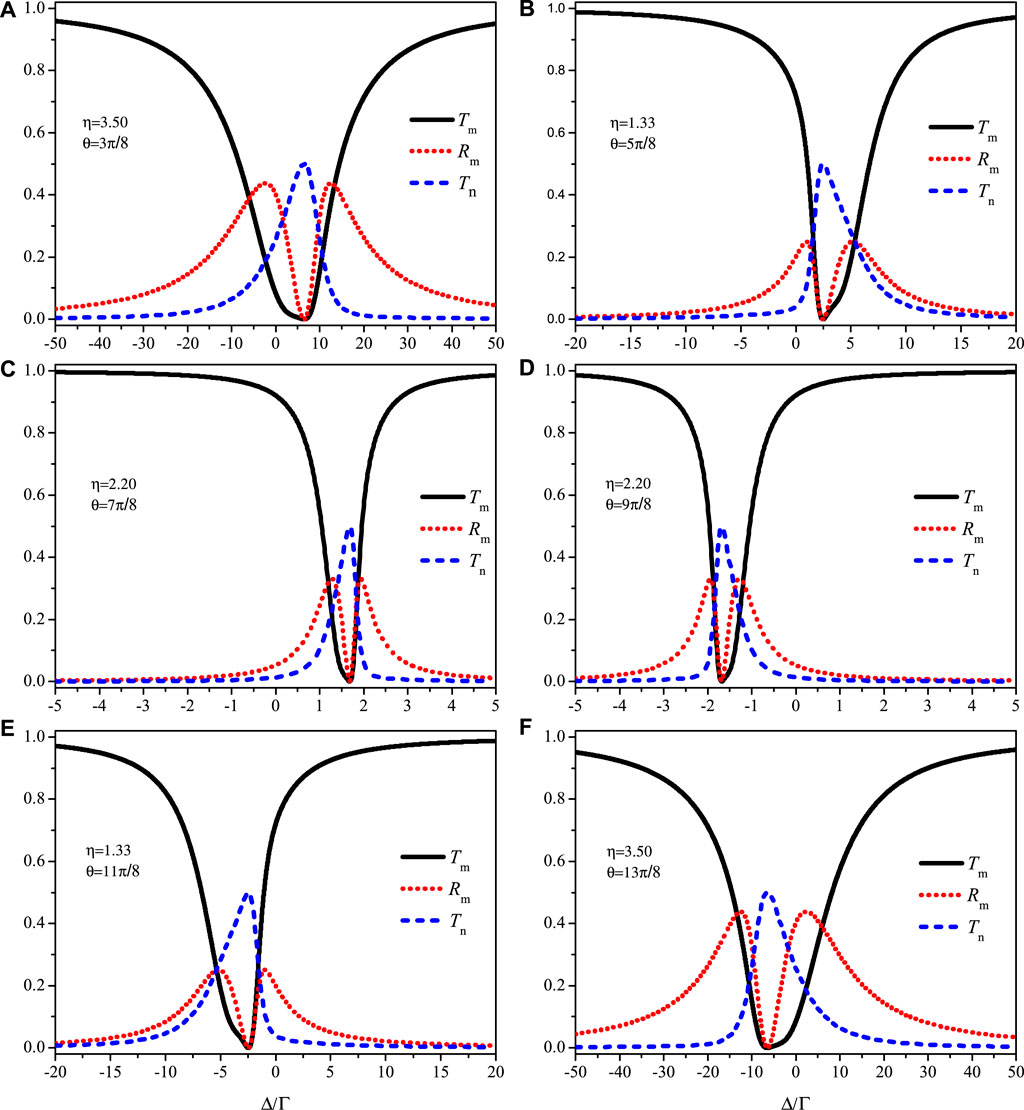
FIGURE 6. Transmission and reflection rates Tm (dark solid line), Tn (blue dashed line) and Rm (red dotted line) as a function of Δ around the six extreme points shown in Figure 5. (A) η = 3.50, θ = 3π/8, (B) η = 1.33, θ = 5π/8, (C) η = 2.20, θ = 7π/8, (D) η = 2.20, θ = 9π/8, (E) η = 1.33, θ = 11π/8, (F) η = 3.50, θ = 13π/8. The transmitted spectra of Tm and Tn show a single valley or peak, while the reflected spectrum of Rm exhibits two peaks. The values of η and θ are provided by Table 1 and the interatomic interaction is not considered (g = 0).
Finally, we explore the effects of the detunings Δa and Δb on the single photon quantum routing. After analyzing Eqs 11–13 and letting g = 0, Γa = Γb = Γ, a single photon router with unit efficiency may be achieved when the following equations are fulfilled
The calculation and analysis for the above equations show that there are eight solutions of θ meeting the conditions, specially, θ = (2j − 1)π/8, (j = 1, 2, 3, 4, 5, 6, 7, 8), and the other parameters are listed in Table 2. One can find that there is the relation Tn [ − Δa, − Δb, 2π − (2j − 1)π/8] = Tn [Δa, Δb, (2j − 1)π/8]. As a consequence, any two transmitted spectra with θ = (2j − 1)π/8 and 2π − (2j − 1)π/8 show central symmetry with respect to the origin (Δa = 0, Δb = 0). Figure 7 shows the transmission rate Tn versus Δa and Δb with some given values of θ provided by Table 2. This indicates that a single photon router with unit efficiency can be also realised by tuning the phase shift of two adjacent connection points and the frequency detuning between the single photon and the atoms.

TABLE 2. The values of the parameters θ, Δa and Δb with Tn = Rn = 0.5 and Tm = Rm = 0 in Figure 7.
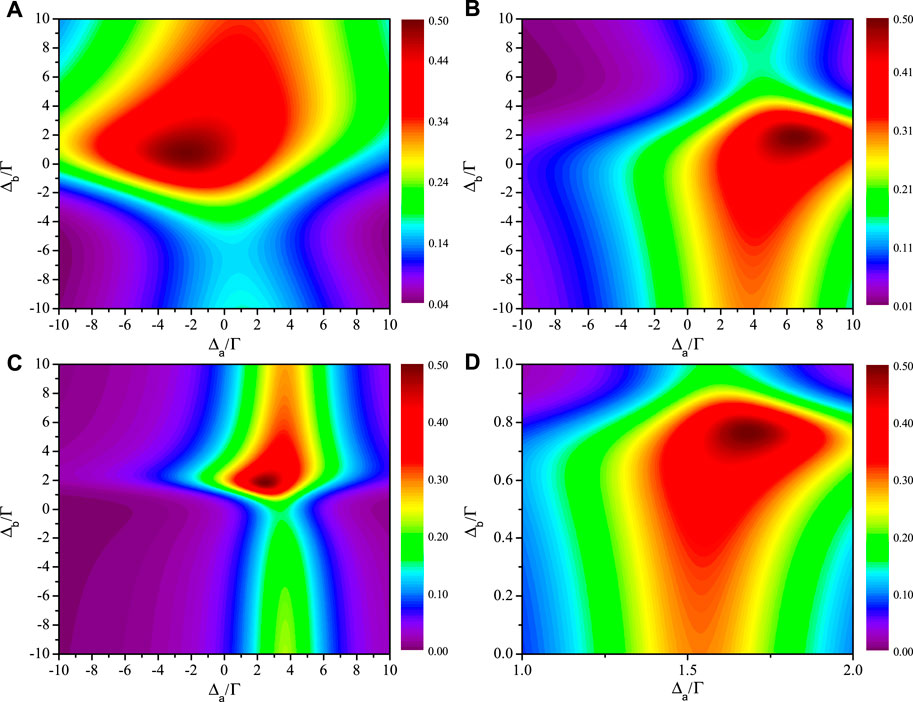
FIGURE 7. Transmission rate Tn as a function of Δa and Δb, in which the four values of the phase shift θ are given by Table 2. Specially, (A) θ = π/8, (B) θ = 3π/8, (C) θ = 5π/8, (D) θ = 7π/8. The transmitted spectra with the other four values of θ are not presented here. The total transfer efficiency from the waveguide m to n can achieve 100% by adjusting the detunings. The other parameters are Γa = Γb = Γ, g = 0.
4 Conclusion
We have studied the influence of two coupled giant two-level atoms on the modulation of single photon quantum routing in two channels composed of two infinite waveguides, and derived the exact expressions of the single-photon transmission and reflection amplitudes with the real-space approach. Our studies show the single photon scattering can be mediated by the atomic phase difference, the frequency detuning, the interatomic interaction, and the coupling strengths between the giant atoms and the waveguides. In the two-giant-atom scheme, it is found that the giant atom located between the two waveguides plays a role in transferring the single photon from the input waveguide to the output waveguide, and the other one interacting with the non-target waveguide is equivalent to a giant-atom mirror, inducing additional interferences. Importantly, a single photon router with unit efficiency can be realised by designing a proper size of the giant atom and adjusting the ratio of the coupling strength and the frequency detuning. Our work may provide a feasible approach to design an efficient quantum router and manipulate photon transport at the single-photon level using the giant-atom setup.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Author contributions
YZ and ZZ conceived the physical model and the idea of the study, and ZZ and ZP performed the numerical calculation and numerical analysis. ZZ and WY contributed to writing the manuscript. All authors contributed to manuscript revision, read, and approved the submitted version.
Funding
This work was partly supported by Scientific Research Fund of Hunan Provincial Education Department under Grant Nos 19B206, 21B0485, the National Natural Science Foundation of China under Grant Nos 11704115, 11504104, 51867002, 61835013, and the Hunan Provincial Natural Science Foundation of China Grant No. 2021JJ40188.
Acknowledgments
The authors thank C. X. Jia and C. L. Jiang for helpful discussions.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
2. O’Brien JL, Furusawa A, Vučković J. Photonic quantum technologies. Nat Photon (2009) 3:687–95. doi:10.1038/nphoton.2009.229
3. Astafiev O, Zagoskin AM, Abdumalikov JA, Pashkin YA, Yamamoto T, Inomata K, et al. Resonance fluorescence of a single artificial atom. Science (2010) 327:840–3. doi:10.1126/science.1181918
4. Hoi IC, Wilson CM, Johansson G, Palomaki T, Peropadre B, Delsing P. Demonstration of a single-photon router in the microwave regime. Phys Rev Lett (2011) 107:073601. doi:10.1103/PhysRevLett.107.073601
5. Zhou L, Dong H, Liu YX, Sun CP, Nori F. Quantum supercavity with atomic mirrors. Phys Rev A (Coll Park) (2008) 78:063827. doi:10.1103/PhysRevA.78.063827
6. Zhou L, Yang S, Liu YX, Sun CP, Nori F. Quantum Zeno switch for single-photon coherent transport. Phys Rev A (Coll Park) (2009) 80:062109. doi:10.1103/PhysRevA.80.062109
7. Zhou L, Chang Y, Dong H, Kuang LM, Sun CP. Inherent Mach-Zehnder interference with “which-way” detection for single-particle scattering in one dimension. Phys Rev A (Coll Park) (2012) 85:013806. doi:10.1103/PhysRevA.85.013806
8. Zhou L, Yang LP, Li Y, Sun CP. Quantum routing of single photons with a cyclic three-level system. Phys Rev Lett (2013) 111:103604. doi:10.1103/PhysRevLett.111.103604
9. Lu J, Zhou L, Kuang LM, Nori F. Single-photon router: Coherent control of multichannel scattering for single photons with quantum interferences. Phys Rev A (Coll Park) (2014) 89:013805. doi:10.1103/PhysRevA.89.013805
10. Liao JQ, Gong ZR, Zhou L, Liu YX, Sun CP, Nori F. Controlling the transport of single photons by tuning the frequency of either one or two cavities in an array of coupled cavities. Phys Rev A (Coll Park) (2010) 81:042304. doi:10.1103/PhysRevA.81.042304
11. Huang JS, Wang JW, Wang Y, Li YL, Huang YM. Control of single-photon routing in a T-shaped waveguide by another atom. Quan Inf Process (2018) 17:78–15. doi:10.1007/s11128-018-1850-9
12. Huang JS, Wang JW, Li YL, Wang Y, Huang YM. Tunable quantum routing via asymmetric in tercavity couplings. Quan Inf Process (2019) 18:59–15. doi:10.1007/s11128-019-2176-y
13. Liu L, Zhang JH, Jin L, Zhou L. Transport properties of the non-Hermitian T-shaped quantum router. Opt Express (2019) 27:13694–705. doi:10.1364/OE.27.013694
14. Ahumada M, Orellana PA, Domínguez-Adame F, Malyshev AV. Tunable single-photon quantum router. Phys Rev A (Coll Park) (2019) 99:033827. doi:10.1103/PhysRevA.99.033827
15. Du XP, Cao Q, Dang N, Tan L. Quantum router modulated by two Rydberg atoms in a X-shaped coupled cavity array. Eur Phys J D (2021) 75:79–8. doi:10.1140/epjd/s10053-021-00085-9
16. Tang JS, Nie W, Tang L, Chen MY, Su X, Lu YQ, et al. Nonreciprocal single-photon band structure. Phys Rev Lett (2022) 128:203602. doi:10.1103/PhysRevLett.128.203602
17. Cao C, Duan YW, Chen X, Zhang R, Wang TJ, Wang C. Implementation of single-photon quantum routing and decoupling using a nitrogen-vacancy center and a whispering-gallery-mode resonator-waveguide system. Opt Express (2017) 25:16931–46. doi:10.1364/OE.25.016931
18. Aoki T, Parkins AS, Alton DJ, Regal CA, Dayan B, Ostby E, et al. Efficient routing of single photons by one atom and a microtoroidal cavity. Phys Rev Lett (2009) 102:083601. doi:10.1103/PhysRevLett.102.083601
19. Yang H, Qin GQ, Zhang H, Mao X, Wang M, Long GL. Multimode interference induced optical routing in an optical microcavity. Annalen der Physik (2021) 533:2000506. doi:10.1002/andp.202000506
20. Tang L, Tang JS, Chen MY, Nori F, Xiao M, Xia KY. Quantum squeezing induced optical nonreciprocity. Phys Rev Lett (2022) 128:083604. doi:10.1103/PhysRevLett.128.083604
21. Li XM, Wei LF. Designable single-photon quantum routings with atomic mirrors. Phys Rev A (Coll Park) (2015) 92:063836. doi:10.1103/PhysRevA.92.063836
22. Carlos GB, Esteban M, Francisco JGV, Alejandro GT. Nonreciprocal few-photon routing schemes based on chiral waveguide-emitter couplings. Phys Rev A (Coll Park) (2016) 94:063817. doi:10.1103/PhysRevA.94.063817
23. Huang JS, Zhong JT, Li YL, Xu ZH, Xiao QS. Efficient single-photon routing in a double-waveguide system with a mirror. Quan Inf Process (2020) 19:290. doi:10.1007/s11128-020-02789-0
24. Yan GA, Lu H. Realization of tunable highly-efficient quantum routing in chiral waveguides. Front Phys (2022) 227:880117. doi:10.3389/fphy.2022.880117
25. Yan CH, Li Y, Yuan HD, Wei LF. Targeted photonic routers with chiral photon-atom interactions. Phys Rev A (Coll Park) (2018) 97:023821. doi:10.1103/PhysRevA.97.023821
26. Poudyal B, Mirza IM. Collective photon routing improvement in a dissipative quantum emitter chain strongly coupled to a chiral waveguide QED ladder. Phys Rev Res (2020) 2:043048. doi:10.1103/PhysRevResearch.2.043048
27. Li XM, Xin J, Li GL, Lu XM, Wei LF. Quantum routings for single photons with different frequencies. Opt Express (2021) 29:8861–71. doi:10.1364/OE.418414
28. Kim NC, Ko MC, Ryom JS, Choe H, Choe IH, Ri SR, et al. Single plasmon router with two quantum dots side coupled to two plasmonic waveguides with a junction. Quan Inf Process (2021) 20:5–14. doi:10.1007/s11128-020-02884-2
29. Dong MX, Xia KY, Zhang WH, Yu YC, Ye YH, Li EZ, et al. All-optical reversible single-photon isolation at room temperature. Sci Adv (2021) 7:eabe8924. doi:10.1126/sciadv.abe8924
30. Lemr K, Bartkiewicz K, Cernoch A, Soubusta J. Resource-efficient linear-optical quantum router. Phys Rev A (Coll Park) (2013) 87:062333. doi:10.1103/PhysRevA.87.062333
31. Xia K, Jelezko F, Twamley J. Quantum routing of single optical photons with a superconducting flux qubit. Phys Rev A (Coll Park) (2018) 97:052315. doi:10.1103/PhysRevA.97.052315
32. Wen PY, Kockum AF, Ian H, Chen JC, Nori F, Hoi IC. Reflective amplification without population inversion from a strongly driven superconducting qubit. Phys Rev Lett (2018) 120:063603. doi:10.1103/PhysRevLett.120.063603
33. Wen PY, Lin KT, Kockum AF, Suri B, Ian H, Chen JC, et al. Large collective Lamb shift of two distant superconducting artificial atoms. Phys Rev Lett (2019) 123:233602. doi:10.1103/PhysRevLett.123.233602
34. Wen PY, Ivakhnenko OV, Nakonechnyi MA, Suri B, Lin JJ, Lin WJ, et al. Landau-Zener-Stückelberg-Majorana interferometry of a superconducting qubit in front of a mirror. Phys Rev B (2020) 102:075448. doi:10.1103/PhysRevB.102.075448
35. Wang ZL, Wu YK, Bao ZH, Li Y, Ma C, Wang HY, et al. Experimental realization of a deterministic quantum router with superconducting quantum circuits. Phys Rev Appl (2021) 15:014049. doi:10.1103/PhysRevApplied.15.014049
36. Ren Y, Ma S, Xie J, Li XK, Cao MT, Li FL. Nonreciprocal single-photon quantum router. Phys Rev A (Coll Park) (2022) 105:013711. doi:10.1103/PhysRevA.105.013711
37. Kockum AF, Delsing P, Johansson G. Designing frequency-dependent relaxation rates and Lamb shifts for a giant artificial atom. Phys Rev A (Coll Park) (2014) 90:013837. doi:10.1103/PhysRevA.90.013837
38. Guo L, Grimsmo AL, Kockum AF, Pletyukhov M, Johansson G. Giant acoustic atom: A single quantum system with a deterministic time delay. Phys Rev A (Coll Park) (2017) 95:053821. doi:10.1103/PhysRevA.95.053821
39. Wang X, Liu T, Kockum AF, Li HR, Nori F. Tunable chiral bound states with giant atoms. Phys Rev Lett (2021) 126:043602. doi:10.1103/PhysRevLett.126.043602
40. Guo L, Kockum AF, Marquardt F, Johansson G. Oscillating bound states for a giant atom. Phys Rev Res (2020) 2:043014. doi:10.1103/PhysRevResearch.2.043014
41. Guo S, Wang Y, Purdy T, Taylor J. Beyond spontaneous emission: Giant atom bounded in the continuum. Phys Rev A (Coll Park) (2020) 102:033706. doi:10.1103/PhysRevA.102.033706
42. Zhao W, Wang ZH. Single-photon scattering and bound states in an atom-waveguide system with two or multiple coupling points. Phys Rev A (Coll Park) (2020) 101:053855. doi:10.1103/PhysRevA.101.053855
43. Vega C, Bello M, Porras D, Gonzlez-Tudela A. Qubit-photon bound states in topological waveguides with long-range hoppings. Phys Rev A (Coll Park) (2021) 104:053522. doi:10.1103/PhysRevA.104.053522
44. Kannan B, Ruckriegel MJ, Campbell DL, Kockum AF, Braumuller J, Kim DK, et al. Waveguide quantum electrodynamics with superconducting artificial giant atoms. Nature (2020) 583:775–9. doi:10.1038/s41586-020-2529-9
45. Kockum AF, Johansson G, Nori F. Decoherence-free interaction between giant atoms in waveguide quantum electrodynamics. Phys Rev Lett (2018) 120:140404. doi:10.1103/PhysRevLett.120.140404
46. Carollo A, Cilluffo D, Ciccarello F. Mechanism of decoherence-free coupling between giant atoms. Phys Rev Res (2020) 2:043184. doi:10.1103/PhysRevResearch.2.043184
47. Soro A, Kockum AF. Chiral quantum optics with giant atoms. Phys Rev A (Coll Park) (2022) 105:023712. doi:10.1103/PhysRevA.105.023712
48. Wang X, Li HR. Chiral quantum network with giant atoms. Quan Sci Technol (2022) 7:035007. doi:10.1088/2058-9565/ac6a04
49. Du L, Li Y. Single-photon frequency conversion via a giant Λ-type atom. Phys Rev A (Coll Park) (2021) 104:023712. doi:10.1103/PhysRevA.104.023712
50. Du L, Chen YT, Li Y. Nonreciprocal frequency conversion with chiral Λ-type atoms. Phys Rev Res (2021) 3:043226. doi:10.1103/PhysRevResearch.3.043226
51. Gustafsson MV, Aref T, Kockum AF, Ekström MK, Johansson G, Delsing P. Propagating phonons coupled to an artificial atom. Science (2014) 346:207–11. doi:10.1126/science.1257219
52. Aref T, Delsing P, Ekstrom MK, Kockum AF, Gustafsson MV, Johansson G, et al. Quantum acoustics with surface acoustic waves. In: RH Hadfield, and G Johansson, editors. Superconducting devices in quantum optics. Cham: Springer (2016). p. 217–44.
53. Manenti R, Kockum AF, Patterson A, Behrle T, Rahamim J, Tancredi G, et al. Circuit quantum acoustodynamics with surface acoustic waves. Nat Commun (2017) 8:975–6. doi:10.1038/s41467-017-01063-9
54. Andersson G, Suri B, Guo L, Aref T, Delsing P. Non-exponential decay of a giant artificial atom. Nat Phys (2019) 15:1123–7. doi:10.1038/s41567-019-0605-6
55. Vadiraj AM, Ask A, McConkey TG, Nsanzineza I, Chang CS, Kockum AF, et al. Engineering the level structure of a giant artificial atom in waveguide quantum electrodynamics. Phys Rev A (Coll Park) (2021) 103:023710. doi:10.1103/PhysRevA.103.023710
56. Blais A, Grimsmo AL, Girvin SM, Wallraff A. Circuit quantum electrodynamics. Rev Mod Phys (2021) 93:025005. doi:10.1103/RevModPhys.93.025005
57. Gu X, Kockum AF, Miranowicz A, Liu YX, Nori F. Microwave photonics with superconducting quantum circuits. Phys Rep (2017) 718:1–102. doi:10.1016/j.physrep.2017.10.002
58. González-Tudela A, Muñoz CS, Cirac JI. Engineering and harnessing giant atoms in high-dimensional baths: A proposal for implementation with cold atoms. Phys Rev Lett (2019) 122:203603. doi:10.1103/PhysRevLett.122.203603
59. Kockum AF, Nori F. Quantum bits with josephson junctions. In: F Tafuri, editor. Fundamentals and Frontiers of the josephson effect. Cham: Springer (2019). p. 703–41.
60. Du L, Zhang Y, Wu JH, Kockum AF, Li Y. Giant atoms in a synthetic frequency dimension. Phys Rev Lett (2022) 128:223602. doi:10.1103/PhysRevLett.128.223602
61. Yin XL, Liu YH, Huang JF, Liao JQ. Single-photon scattering in a giant-molecule waveguide-QED system. Phys Rev A (Coll Park) (2022) 106:013715. doi:10.1103/PhysRevA.106.013715
62. Zhao W, Zhang Y, Wang ZH. Phase-modulated Autler-Townes splitting in a giant-atom system within waveguide QED. Front Phys (Beijing) (2022) 17:42506–11. doi:10.1007/s11467-021-1135-0
63. Wang C, Ma XS, Cheng MT. Giant atom-mediated single photon routing between two waveguides. Opt Express (2021) 29:40116–24. doi:10.1364/OE.444096
64. Liu N, Wang X, Wang X, Ma XS, Cheng MT. Tunable single photon nonreciprocal scattering based on giant atom-waveguide chiral couplings. Opt Express (2022) 30:23428–38. doi:10.1364/OE.460255
65. Chen YT, Du L, Guo LZ, Wang ZH, Zhang Y, Li Y, et al. Nonreciprocal and chiral single-photon scattering for giant atoms. Commun Phys (2022) 5:215. doi:10.1038/s42005-022-00991-3
66. Peng JS, Li GX. Effects of the dipole-dipole interaction on dynamic properties and atomic coherent trapping of a two-atom system. Phys Rev A (Coll Park) (1993) 47:4212–8. doi:10.1103/PhysRevA.47.4212
67. Shen JT, Fan SH. Theory of single-photon transport in a single-mode waveguide. I. Coupling to a cavity containing a two-level atom. Phys Rev A (Coll Park) (2009) 79:023837. doi:10.1103/PhysRevA.79.023837
Keywords: giant two-level atom, single photon, qantum routing, phase difference, waveguide
Citation: Zhang YQ, Zhu ZH, Chen KK, Peng ZH, Yin WJ, Yang Y, Zhao YQ, Lu ZY, Chai YF, Xiong ZZ and Tan L (2022) Controllable single-photon routing between two waveguides by two giant two-level atoms. Front. Phys. 10:1054299. doi: 10.3389/fphy.2022.1054299
Received: 26 September 2022; Accepted: 11 October 2022;
Published: 25 October 2022.
Edited by:
Bernard Gelloz, Nagoya University, JapanReviewed by:
Lingzhen Guo, Max Planck Institute for the Science of Light, GermanyF. Nori, RIKEN, Japan
Copyright © 2022 Zhang, Zhu, Chen, Peng, Yin, Yang, Zhao, Lu, Chai, Xiong and Tan. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Y. Q. Zhang, bGFuemhvdWd4QDE2My5jb20=
 Y. Q. Zhang
Y. Q. Zhang Z. H. Zhu1,2
Z. H. Zhu1,2 Z. Y. Lu
Z. Y. Lu