High-flux positron generation via the ultra-intense laser irradiating density-modulated plasmas

To investigate plasma density during the Breit–Wheeler positron generation, a comparative study of four plasma targets is performed via the PIC (particle-in-cell) code EPOCH. When an ultra-intense laser ($2.8\times {10}^{23}{\mathrm{W}\mathrm{c}\mathrm{m}}^{-2}$) is incident, more positrons with high energy are generated in the increasing density plasmas. The positron yield is already $1.5\times {10}^8$ with a cutoff energy of 2 GeV at $\mathrm{t}=37{\mathrm{T}}_0$. It is demonstrated that increasing density plasmas will enhance gamma photon radiation and positron generation. In increasing density plasmas, under-dense plasmas favor electron acceleration, and over-dense plasmas will induce laser reflection. Cross sections of the Compton back-scattering and the BW positron generation are both increased via high-energy electrons colliding with the reflected laser. In addition, increasing the laser intensity will directly enhance positron generation. This investigation will further facilitate high-flux positron generation and application.

1 Introduction

As a result of the quick development of laser technology, a peak intensity of ${10}^{24}\mathrm{W}\mathrm{c}{\mathrm{m}}^{-2}$ will soon be realized [1]. Under such laser intensity, the quantum electrodynamics (QED) effect dominates the laser–plasma interaction which results in positron creation. The laser-induced positron source has drawn great attention and research interests due to its unique properties such as ultra-short duration, high energy, low divergence, high flux, and density [2]. Positrons have extensive application prospects in material science for defect and phase transition, new radiation source, and laboratory astrophysics [3–5]. For example, based on coherent gamma rays emitted by the stimulated annihilation of electron–positron pairs, researchers are trying to build a new gamma laser [6]. High-density electron–positron pairs (>10²⁶ m⁻³) are required in the Bose–Einstein condensate (BEC) of positroniums and in the gamma-ray burst (GRB) in the laboratory [7]. However, the required density is still beyond that obtained in state-of-the-art laser facilities.

According to creation mechanisms, laser-induced positron generation includes two ways: an indirect way and a direct way [8]. In the indirect way, high-energy electrons are obtained via the laser–plasma interaction first. Then, these electrons are shot into a second-class target to produce positrons. For example, the trident process and the BH (Bethe–Heitler) process belong to the indirect way [9]. The indirect way always requires a thick, solid target for transition [10], and the required laser intensity can be afforded by current large laser facilities. When an ultra-short (∼1 ps) and ultra-intense ($\sim {10}^{20}\mathrm{W}\mathrm{c}{\mathrm{m}}^{-2}$) laser pulse is incident obliquely onto a ∼1-mm-thick gold foil [7], $2\times {10}^{10}s{r}^{-1}$ positrons with a density of $\sim {10}^{12}\mathrm{c}{\mathrm{m}}^{-3}$ are obtained in the laboratory. In the direct way, laser irradiates a target directly to generate positrons, such as the multi-photon BW (Breit–Wheeler) process [11]. First, photon radiation can be described as $\mathrm{e}+\mathrm{m}{\gamma }_{\mathrm{l}}\to \mathrm{e}+{\gamma }_{\mathrm{r}}$ on behalf of an energetic electron (e) interacting with laser photons (${\gamma }_{\mathrm{l}}$) to radiate a high-energy gamma photon (${\gamma }_{\mathrm{r}}$) [12, 13]. Second, the BW process is initiated to generate positrons when these radiated gamma photons further interact with laser photons, which is ${\gamma }_{\mathrm{r}}+\mathrm{n}{\gamma }_{\mathrm{l}}\to \mathrm{e}+{\mathrm{e}}^{+}$. It is to be noted that the BW process is a highly nonlinear multi-photon process. Provided that the energy of the generated positron is high enough, an avalanche is initiated [14]. Compared with the indirect way, positrons produced in the BW process have unique characteristics of high yield, high density, and high energy. However, the driven laser intensity required is too high to be realized in state-of-the-art laser facilities. Recent investigations have focused on the enhancement of positron generation and lowering the required laser intensity. When a 12.5 PW laser is tightly focused on a $1-\mu \mathrm{m}$-thick aluminum foil [15], the BW process is greatly enhanced with ${10}^{10}$ positrons generated. The maximal positron density is as high as $\sim {10}^{26}{\mathrm{m}}^{-3}$. Positron yield and density will be further increased if a 320 PW laser is employed. Head-on collisions of an electron and laser (photon and photon) are demonstrated to be an effective way for the enhancement of positron generation. When two collimated $\gamma$-ray pulses driven by 10 PW lasers collide, $3.2\times {10}^8$ positrons with a divergence angle of $7°$ are created per shot [16]. The head-on collision can lower laser intensity required for the BW process to $\sim {10}^{22}\mathrm{W}\mathrm{c}{\mathrm{m}}^{-2}$ [17]. Our previous reports also show that positron generation can be enhanced via modulating the incident laser profile, optimizing the plasma target, and employing two laser pulses for collision [18–20]. However, further investigations of plasma density on positron generation are still needed.

In this work, taking an ultra-intense laser irradiating foam-like plasmas into account, the influence of plasma density on the BW positron generation is studied. Laser intensity is also discussed in the optimized plasmas. Results show that the increasing density plasma favors positron generation and acceleration, and increasing the incident laser intensity is still an effective way to enhance positron generation. This work will promote the investigation of the laser-induced positron source and its further applications.

2 Methods and model

When a laser pulse propagates in under-dense plasmas, a plasma density that matched the laser pulse favors electron acceleration. Taking the bubble regime, for example, a bubble is formed only when the normalized laser amplitude ${\mathrm{a}}_0=\mathrm{e}\mathrm{A}/{\mathrm{m}}_{\mathrm{e}}{\mathrm{c}}^2$ and the plasma frequency ${\omega }_{\mathrm{p}}={\left(\frac{4\pi {\mathrm{e}}^2{\mathrm{n}}_{\mathrm{e}}}{{\mathrm{m}}_{\mathrm{e}}{\mathrm{c}}^2}\right)}^{1/2}$ follow $\mathrm{R}{\omega }_{\mathrm{p}}/c\approx \sqrt{a_0}$ [21, 22]. Here, ${\mathrm{n}}_{\mathrm{e}}$ is the plasmas’ density, e and ${\mathrm{m}}_{\mathrm{e}}$ are the electric field and mass of an electron, respectively, R is the bubble radius, and c is the light speed in the vacuum. Self-focusing and reflection are induced when the laser propagates in dense plasmas. The critical power for laser self-focusing is ${\mathrm{P}}_{\mathrm{c}}\approx 16.4{\omega }_{\mathrm{l}}^2/{\omega }_{\mathrm{p}}^2\mathrm{G}\mathrm{W}$, where ${\omega }_{\mathrm{l}}$ is the laser frequency [23]. To investigate the effects of non-uniform density plasmas on laser propagation and positron generation, four types of plasmas are taken into account: linearly increasing density plasmas (type I), linearly decreasing density plasmas (type D), first increasing and then decreasing density plasmas (type A), and first decreasing and then increasing density plasmas (type V). As schematically shown in Figure 1, plasmas whose density varies linearly in the x-direction are distributed between $0\mu \mathrm{m}$ and $30\mu \mathrm{m}$. The minimal density is $0.1{\mathrm{n}}_{\mathrm{c}}$, while the maximum is $4{\mathrm{n}}_{\mathrm{c}}$, where ${\mathrm{n}}_{\mathrm{c}}\approx \frac{1.1\times {10}^{21}}{{\lambda }_0^2\left[\mu \mathrm{m}\right]}\mathrm{c}{\mathrm{m}}^{-3}$ is the critical density according to the pulse wavelength ${\lambda }_0=1\mu \mathrm{m}$. In the y-direction, plasmas are uniformly distributed. The simulation box is $\mathrm{x}\times \mathrm{y}=33\mu \mathrm{m}\times 16\mu \mathrm{m}$, being sampled by $3300\times 1600$ cells. Thus, the cell size is $0.01\mu \mathrm{m}$, being comparable to the relativistic corrected skin depth. The boundary is set at “simple_outflow” to prevent the field and particles from being reflected into the region of interest. A circularly polarized Gaussian laser pulse is incident from the left boundary with an intensity of $\mathrm{I}=2.8\times {10}^{23}\mathrm{W}\mathrm{c}{\mathrm{m}}^{-2}$, the corresponding normalized amplitude of which is ${\mathrm{a}}_0\approx 320$. The laser is tightly focused with a focal spot radius of $2\mu \mathrm{m}$, and the laser focal positon is at the left surface of the plasmas. All simulations are realized with the two-dimension PIC (particle-in-cell) code EPOCH, in which the QED module is implemented [24]. In order to save the computational source, 77 macro-particles are initially put in each cell. As the incident laser is ultra-intense, the pre-pulse will ionize the target as soon as irradiating onto its surface. Thus, fully ionized nitrogen plasmas are employed with ${\mathrm{N}}^{7+}$ ions and electrons to simplify the model.

FIGURE 1

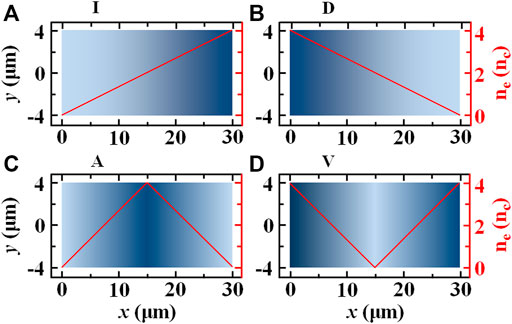
FIGURE 1. Schematics of four types of plasmas: type I is linearly increasing density plasmas (A); type D is linearly decreasing density plasmas (B); type A is first increasing and then decreasing density plasmas (C); and type V is first decreasing and then increasing density plasmas (D).

3 Results and discussion

As the laser is ultra-intense and ultra-short and foam-like plasmas are employed, the multi-photon BW process dominates positron generation in the laser–plasma interaction. When the laser propagates in plasmas, electrons are accelerated to radiate high-energy gamma photons. These photons further interact with laser photons, resulting in positron generation. Figure 2A shows the evolution of positron yield in four types of plasmas. It can be seen from the figure that the positron yield gradually reaches its maximum in A- and D-type plasmas. Even though the positron yield is small at first, it increases quickly and keeps increasing in I-and V-type plasmas. In the I-type plasmas, whose density increases linearly, the positron yield is the highest among these four plasma targets. At $\mathrm{t}=37{\mathrm{T}}_0$, $1.5\times {10}^8$ positrons have already been generated with a maximal density of $7.1\times {10}^{25}$ m⁻³. Here, ${\mathrm{T}}_0$ is the laser period. The BW process continues to generate more positrons as the interaction is sustained. When comparing the positron yield in the A-type plasmas and in the V-type plasmas, it is to be noted that the positron yield increases slowly as the laser propagates from high- to low-density plasmas. However, it increases quickly as the laser propagates into denser plasmas. It is demonstrated that increasing density plasmas favor positron generation.

FIGURE 2

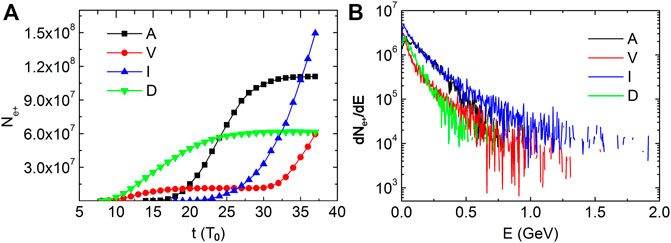
FIGURE 2. Evolutions of the positron yield (A) and spectra of positrons (B) at $\mathbf{t}=\mathbf{37}{\mathbf{T}}_{\mathbf{0}}$ in simulations with different types of plasmas.

When the laser propagates in increasing density plasmas, on the one hand, the under-dense plasmas favor electron acceleration. High-energy electrons are obtained, and they propagate along with the laser pulse. On the other hand, when plasmas get denser, partial laser is reflected [18]. It is to be noted that gamma photon radiation is controlled by $\eta \approx \frac{\gamma }{{\mathrm{E}}_{\mathrm{s}}}\left|{\overrightarrow{E}}_{\perp }+\overrightarrow{v}\times \overrightarrow{B}\right|$, where $\gamma$ is the Lorentz factor, ${\mathrm{E}}_{\mathrm{s}}=1.3\times {10}^{18}{\mathrm{V}\mathrm{m}}^{-1}$ is the Schwinger field, ${\overrightarrow{E}}_{\perp }$ is the component of the laser electric field perpendicular to the electron velocity $\overrightarrow{v}$, and $\overrightarrow{B}$ is the laser magnetic field [25]. When electrons move in the same direction as the laser, ${\overrightarrow{E}}_{\perp }$ is almost canceled by $\overrightarrow{v}\times \overrightarrow{B}$, resulting in few photon radiations. However, when electrons collide with the reflected laser, the Compton back-scattering is initiated, resulting in plenty of gamma photon radiations as $\eta$ reaches its maximum. The emission direction of these gamma photons is parallel to the electron velocity. Furthermore, high-energy gamma photons collide with the reflected laser, and positron generation is also enhanced as the controlling parameter $\chi =\frac{\hslash {\omega }_{\gamma }}{2{\mathrm{m}}_{\mathrm{e}}{\mathrm{c}}^2}\left|{\overrightarrow{E}}_{\perp }+\overrightarrow{k}\times \mathrm{c}\overrightarrow{B}\right|$ also reaches its maximum [26]. Here, $\mathrm{\hslash }{\omega }_{\gamma }$ is the photon energy, and $\overrightarrow{k}$ is the unit vector in the photon radiation direction.

Figure 2B shows the spectra of positrons at $\mathrm{t}=37{\mathrm{T}}_0$. First, it is also to be noted that there are more positrons generated in I-type plasmas. Second, the cutoff energy of positrons in the I-type plasmas is $\sim 2\mathrm{G}\mathrm{e}\mathrm{V}$, which is higher than that in the other plasmas. High-energy electrons accelerated in the under-dense plasmas induce high-energy gamma photon radiations, and thus high-energy positrons are generated. Provided high enough of the generated electron–positron pair energy, second-class photons are radiated to join in the positron generation, and thus an avalanche is initiated.

For more details, the energy density distributions of gamma photons and the location of the laser pulse are provided in Figure 3. It can be seen from the figure that high-energy density gamma photons are well focused in the I-type plasmas when compared with those in the other plasmas. Also, these high-energy density gamma photons are distributed in the center of the laser pulse, where the laser field is the strongest. In the positron generation-controlling parameter, higher ${\overrightarrow{E}}_{\perp }$ and $\overrightarrow{B}$ induce higher $\chi$, which favors positron generation. The maximal energy density of photons is 1,327.8 $\mathrm{M}\mathrm{e}\mathrm{V}\bullet {\mathrm{n}}_{\mathrm{c}}$ in the I-type plasmas at $\mathrm{t}=35{\mathrm{T}}_0$. When the laser pulse propagates to the denser region in the I-type plasmas, an electron-free channel is formed. Electrons are accelerated along with the laser in the channel. The higher the plasma density, the smaller the channel radius. Thus, electrons are well focused in the channel, resulting in well-focused and high-energy density gamma photons. It is also to be noted from the simulation result that the positron density in I-type plasmas is also the highest of these four plasma targets.

FIGURE 3

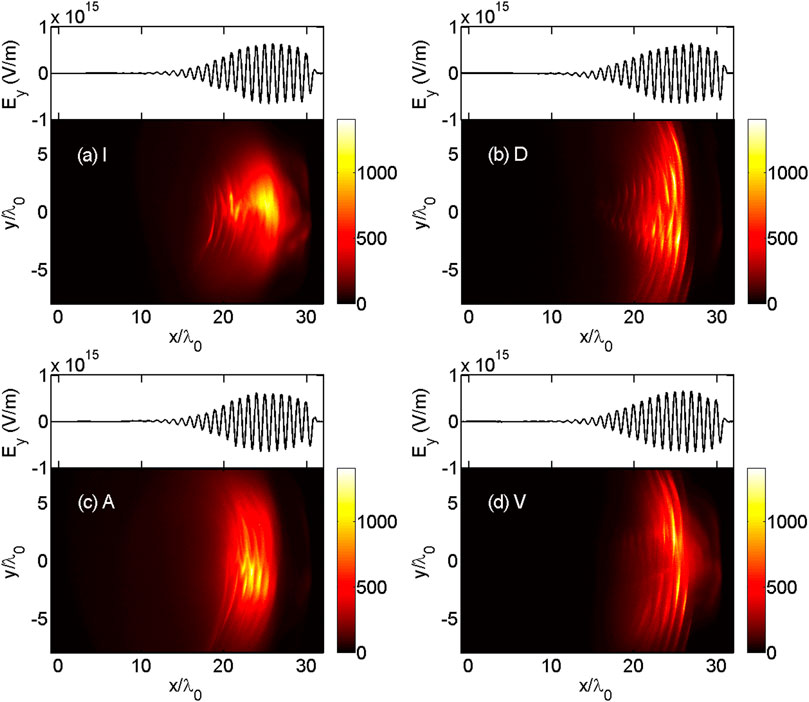
FIGURE 3. Energy density ($\mathbf{M}\mathbf{e}\mathbf{V}\bullet {\mathbf{n}}_{\mathbf{c}}$) distributions of radiated photons at $\mathbf{t}=\mathbf{35}{\mathbf{T}}_{\mathbf{0}}$ in simulations with different types of plasmas and the profile of the transverse electric field ${\mathbf{E}}_{\mathbf{y}}$ (V/m) at $\mathbf{t}=\mathbf{35}{\mathbf{T}}_{\mathbf{0}}$ in each simulation.

Laser intensity plays an important role in electron acceleration, photon radiation, and positron generation. Taking the positron generation process into account, laser intensity even induces different mechanisms. Provided that the Schwinger field is realized, the vacuum will break down to generate electron–positron pairs. However, that field is too strong to be realized in a laboratory. Researchers are concerned with the feasibility of experiments in state-of-the-art laser facilities. In the following, simulations of different intensity lasers irradiating plasmas are performed. The normalized laser amplitude ${\mathrm{a}}_0$ ranges from 260 to 500, while all the other laser parameters remain unchanged. In consideration of its benefit in high-flux and high-density positron generation, the I-type plasma target is employed. All parameters of the target and the simulation box remain the same as previously described.

Figure 4 provides simulation results for different intensity lasers irradiating the I-type plasma target at $\mathrm{t}={33\mathrm{T}}_0$. Gamma photon radiations are gradually enhanced as the incident laser intensity increases (Figure 4A). The photon number is proportional to the normalized laser amplitude. It is also to be noted that the cutoff energy and the mean energy of photons are both increased with the laser. Taking the Compton back-scattering process for photon radiation into account, increasing the laser intensity results in high-energy electron acceleration and strong laser field reflection. High-flux and high-energy photons induce the enhancement of positron generation. The positron yield increases exponentially with the laser intensity. When ${\mathrm{a}}_0=500$, the positron yield is $\sim 8.6\times {10}^8$, while the maximal density is $1.2\times {10}^{26}{\mathrm{m}}^{-3}$ at $\mathrm{t}=33{\mathrm{T}}_0$. In addition, there are $\sim 2.0\times {10}^7$ positrons generated with a maximal density of $5.2\times {10}^{25}{\mathrm{m}}^{-3}$, even though the normalized laser amplitude is 260. With the quick development of laser technology, this scheme can be realized experimentally in the foreseeable future. Figure 4D shows positron spectra at $\mathrm{t}=33{\mathrm{T}}_0$ in simulations with different intensity lasers. It can be seen that positron energy increases quickly at first and then slows down. The cutoff energy exceeds $4\mathrm{G}\mathrm{e}\mathrm{V}$ when the normalized laser amplitude is 500. On the one hand, these high-energy positrons further radiate second-class gamma photons, which prevents the cutoff energy from increasing. On the other hand, photons radiated from generated pairs interact with laser photons to produce more positrons. The avalanche induces a rapid increase in positron yield (Figure 4C).

FIGURE 4

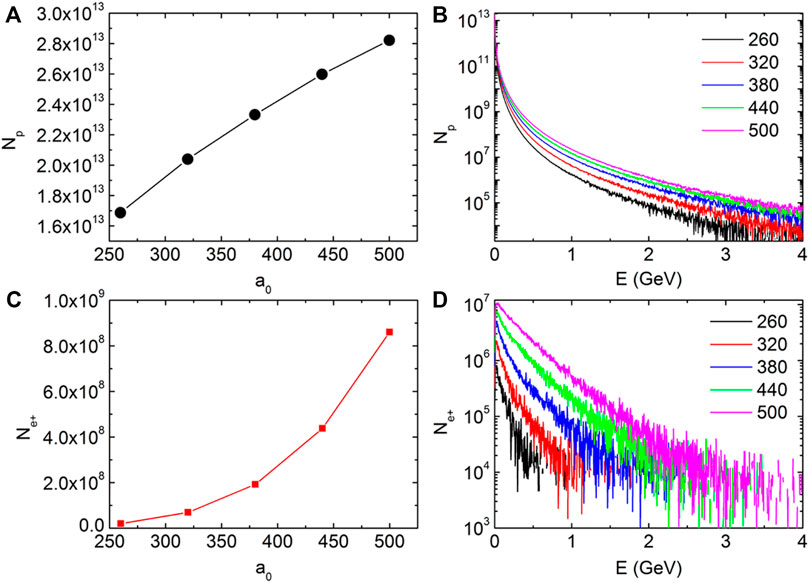
FIGURE 4. Photon yield (A) and positron yield (C) as a function of the normalized laser amplitude; spectra of photons (B) and positrons (D) at $\mathbf{t}=\mathbf{33}{\mathbf{T}}_{\mathbf{0}}$ in simulations with different intensity lasers.

4 Conclusion

In conclusion, a comparative study of four plasma targets in the BW process for positron generation is performed. It is found that increasing density plasmas favor high-flux and high-density positron generation. When an ultra-intense laser irradiates increasing density plasmas, under-dense plasmas will contribute to electron acceleration, and dense plasmas will reflect the laser in order to collide with high-energy electrons. The Compton back-scattering is enhanced as a result of the collision, followed by the enhancement of positron generation. When different intensity lasers irradiate increasing density plasmas, it is found that increasing the normalized laser amplitude induces exponential growth of positron yield. High-flux and high-density positrons are generated even with lower laser intensities. This investigation provides a feasible basis for obtaining positrons experimentally via the BW process.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

All authors took part actively in carrying out all simulations, in the analysis of results, and in the writing of the article. In particular, W-QD, T-YL, and XW prepared the proposal for simulations. H-BJ, T-PY, and J-XL contributed to the analysis of simulation results. J-XL and TG prepared the manuscript.

Funding

This work was financially supported by the National Natural Science Foundation (Grant Nos 11805278 and 11875319), the Youth Promotion Project of Early Warning Academy, the Science and Technology Innovation Program of Hunan Province (Grant No. 2020RC4020), and the Fok Ying-Tong Education Foundation (Grant No. 161007).

Acknowledgments

The authors wish to thank the Centre for Fusion, Space, and Astrophysics at the University of Warwick for allowing the usage of EPOCH.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Turcu I., Shen B., Neely D., Sarri G., Tanaka K. A., Mckenna P., et al. Quantum electrodynamics experiments with colliding petawatt laser pulses. High Power Laser Sci.Eng. (2019) 7(1):e10. doi:10.1017/hpl.2018.66

CrossRef Full Text | Google Scholar

2. Chen H., Wilks S., Meyerhofer D., Bonlie J., Chen C., Chen S., et al. Relativistic quasimonoenergetic positron jets from intense laser-solid interactions. Phys Rev Lett (2010) 105:015003. doi:10.1103/physrevlett.105.015003

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Jiang J., Wu Y. C., Liu X. B., Wang R. S., Nagai Y., Inoue K., et al. Microstructural evolution of RPV steels under proton and ion irradiation studied by positron annihilation spectroscopy. J Nucl Mater (2015) 458:326–34. doi:10.1016/j.jnucmat.2014.12.113

CrossRef Full Text | Google Scholar

4. Yu T. P., Hu L. X., Yin Y., Shao F. Q., Zhuo H. B., Ma Y. Y., et al. Bright tunable femtosecond x-ray emission from laser irradiated micro-droplets. Appl Phys Lett (2014) 105:114101. doi:10.1063/1.4895928

CrossRef Full Text | Google Scholar

5. Ruffini R., Vereshchagin G., Xue S. Electron-positron pairs in physics and astrophysics: From heavy nuclei to black holes. Phys Rep (2010) 487:1–140. doi:10.1016/j.physrep.2009.10.004

CrossRef Full Text | Google Scholar

6. Müller C., Keitel C. H. Antimatter: Abundant positron production. Nat Photon (2009) 3:245–6. doi:10.1038/nphoton.2009.56

CrossRef Full Text | Google Scholar

7. Chen H., Wilks S. C., Bonlie J. D., Liang E. P., Myatt J., Price D. F., et al. Relativistic positron creation using ultraintense short pulse lasers. Phys Rev Lett (2009) 102:105001. doi:10.1103/physrevlett.102.105001

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Yan Y., Zhang B., Wu Y., Dong K., Yao Z., Gu Y. Comparison of direct and indirect positron-generation by an ultra-intense femtosecond laser. Phys Plasmas (2013) 20:103114. doi:10.1063/1.4826219

CrossRef Full Text | Google Scholar

9. Sarri G., Schumaker W., Di Piazza A., Vargas M., Dromey B., Dieckmann M. E., et al. Table-top laser-based source of femtosecond, collimated, ultrarelativistic positron beams. Phys Rev Lett (2013) 110:255002. doi:10.1103/physrevlett.110.255002

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Breit G., Wheeler J. A. Collision of two light quanta. Phys Rev (1934) 46:1087–91. doi:10.1103/physrev.46.1087

CrossRef Full Text | Google Scholar

11. Yan Y., Dong K., Wu Y., Zhang B., Yao Z., Gu Y. Numerical simulation study of positron production by intense laser-accelerated electrons. Phys Plasmas (2013) 20:103106. doi:10.1063/1.4824107

CrossRef Full Text | Google Scholar

12. Burke D. L., Field R. C., Horton-Smith G., Spencer J. E., Walz D., Berridge S. C., et al. Positron production in multiphoton light-by-light scattering. Phys Rev Lett (1997) 79:1626–9. doi:10.1103/physrevlett.79.1626

CrossRef Full Text | Google Scholar

13. Liu J. X., Ma Y. Y., Zhao J., Yu T. P., Yang X. H., Gan L. F., et al. High-flux low-divergence positron beam generation from ultra-intense laser irradiated a tapered hollow target. Phys Plasmas (2015) 22:103102. doi:10.1063/1.4932997

CrossRef Full Text | Google Scholar

14. Jirka M., Klimo O., Bulanov S. V., Esirkepov T. Z., Gelfer E., Bulanov S. S., et al. Electron dynamics andγande−e+production by colliding laser pulses. Phys Rev E (2016) 93:023207. doi:10.1103/physreve.93.023207

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Ridgers C. P., Brady C. S., Duclous R., Kirk J., Bennett K., Arber T., et al. Dense electron-positron plasmas and bursts of gamma-rays from laser-generated quantum electrodynamic plasmas. Phys Plasmas (2013) 20:056701. doi:10.1063/1.4801513

CrossRef Full Text | Google Scholar

16. Yu J. Q., Lu H. Y., Takahashi T., Hu R. H., Yan X. Q., Ma W., et al. Creation of electron-positron pairs in photon-photon collisions driven by 10-PW laser pulses. Phys Rev Lett (2019) 122:014802. doi:10.1103/physrevlett.122.014802

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Zhu X-L., Yu T-P., Sheng Z-M., Yin Y., Turcu I. C. E., Pukhov A. Dense GeV electron–positron pairs generated by lasers in near-critical-density plasmas. Nat Commun (2016) 7:13686. doi:10.1038/ncomms13686

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Jian-Xun L., Yan-Yun M., Tong-Pu Y., Jun Z., Xiao-Hu Y., Long-Fei G., et al. Enhanced electron–positron pair production by ultra intense laser irradiating a compound target. Plasma Phys Control Fusion (2016) 58:125007. doi:10.1088/0741-3335/58/12/125007

CrossRef Full Text | Google Scholar

19. Jian-Xun L., Yan-Yun M., Tong-Pu Y., Jun Z., Xiao-Hu Y., De-Bin Z., et al. Dense pair plasma generation by two laser pulses colliding in a cylinder channel. Chin Phys B (2017) 26:035202. doi:10.1088/1674-1056/26/3/035202

CrossRef Full Text | Google Scholar

20. Liu J. X., Zhao Y., Wang X. P., Quan J. Z., Yu T. P., Zhang G. B., et al. High-flux positrons generation via two counter-propagating laser pulses irradiating near-critical-density plasmas. Phys Plasmas (2018) 25:103106. doi:10.1063/1.5043627

CrossRef Full Text | Google Scholar

21. Lu W., Tzoufras M., Joshi C., Tsung F. S., Mori W. B., Vieira J., et al. Generating multi-GeV electron bunches using single stage laser wakefield acceleration in a 3D nonlinear regime. Phys Rev Spec Top Acc Beams (2017) 10:061301. doi:10.1103/physrevstab.10.061301

CrossRef Full Text | Google Scholar

22. Lu W., Huang C., Zhou M., Mori W. B., Katsouleas T. Nonlinear theory for relativistic plasma wakefields in the blowout regime. Phys Rev Lett (2006) 96:165002. doi:10.1103/physrevlett.96.165002

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Gahn C., Tsakiris G., Pretzler G., Witte K., Thirolf P., Habs D., et al. Generation of MeV electrons and positrons with femtosecond pulses from a table-top laser system. Phys Plasmas (2002) 9:987–99. doi:10.1063/1.1446879

CrossRef Full Text | Google Scholar

24. Arber T. D., Arber T. D., Bennett K., Bennett K., Brady C. S., Brady C. S., et al. Contemporary particle-in-cell approach to laser-plasma modelling. Plasma Phys Control Fusion (2015) 57:113001. doi:10.1088/0741-3335/57/11/113001

CrossRef Full Text | Google Scholar

25. Ridgers C. P., Brady C. S., Duclous R., Kirk J., Bennett K., Arber T., et al. Dense electron-positron plasmas and ultraintenseγrays from laser-irradiated solids. Phys Rev Lett (2012) 108:165006. doi:10.1103/physrevlett.108.165006

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Piazza A. D., Müller C., Hatsagortsyan K. Z., Keitel C. H. Extremely high-intensity laser interactions with fundamental quantum systems. Rev Mod Phys (2011) 84:1177–228. doi:10.1103/RevModPhys.84.1177

CrossRef Full Text | Google Scholar