- 1Dipartimento di Fisica “E. Fermi”, Università di Pisa, Pisa, Italy
- 2Theory Center, Jefferson Lab, Newport News, Virginia, United States
- 3Istituto Nazionale di Fisica Nucleare, Pisa, Italy
- 4Physics Department, Washington University, St. Louis, MO, United States
- 5McDonnell Center for the Space Sciences at Washington University in St. Louis, St. Louis, MO, United States
The muon capture reaction μ− + d → n + n + νμ in the doublet hyperfine state is studied using nuclear potentials and consistent currents derived in the chiral effective field theory, which are local and expressed in coordinate space (the so-called Norfolk models). Only the largest contribution due to the 1S0 nn scattering state is considered. Particular attention is given to the estimate of theoretical uncertainty, for which four sources have been identified: 1) the model dependence, 2) the chiral-order convergence for the weak nuclear current, 3) the uncertainty in the single-nucleon axial form factor, and 4) the numerical technique adopted to solve the bound and scattering A = 2 systems. This last source of uncertainty has turned out to be essentially negligible. For the 1S0 doublet muon capture rate
1 Introduction
The muon capture on a deuteron, i.e. the process
is one of the few weak nuclear reactions involving light nuclei which, on one side, are experimentally accessible, and, on the other, can be studied using ab initio methods. Furthermore, it is a process closely linked to the proton–proton weak capture, the so-called pp reaction,
which, although being of paramount importance in astrophysics, is not experimentally accessible due to its extremely low rate and can only be calculated. Since the theoretical inputs to study reaction (2) and reaction (1) are essentially the same, the comparison between the experiment and theory for muon capture provides a strong test for the pp studies.
The muon capture reaction (1) can take place in two different hyperfine states, f = 1/2 and 3/2. Since it is well known that the doublet capture rate is about 40 times larger than the quartet one (see, for instance, Ref. [1]), we will consider the f = 1/2 state only, and we will focus on the doublet capture rate, ΓD. The experimental situation for ΓD is quite confused, with available measurements which are relatively old. These are the ones of Refs. [2–5], 365 (96) s−1, 445 (60) s−1, 470 (29) s−1, and 409 (40) s−1, respectively. All these data are consistent with each other within the experimental uncertainties, which are, however, quite large. To clarify the situation, an experiment with the aim of measuring ΓD with 1% accuracy is currently performed at the Paul Scherrer Institute, in Switzerland, by the MuSun Collaboration [6].
Many theoretical studies are available for the muon capture rate ΓD. A review of the available literature from up to about 10 years ago can be found in Ref. [7]. Here, we focus on the work conducted in the past 10 years. To the best of our knowledge, the capture rate ΓD has been studied in Refs. [8–12]. The studies of Refs. [9, 11] were performed within the phenomenological approach, using phenomenological potentials and currents. In Ref. [9], the first attempt to use the chiral effective field theory (χEFT) was presented, within the so-called hybrid approach, where a phenomenological nuclear interaction is used in conjunction with χEFT weak nuclear charge and current operators. In the study we present in this contribution, though, we are interested not only in the determination of ΓD but also an assessment of the theoretical uncertainty. This can be grasped more comfortably and robustly within a consistent χEFT approach. Therefore, we review only the theoretical works of Refs. [8, 10, 12], which were performed within a consistent χEFT. The studies of Refs. [8, 10] were essentially performed in parallel. They both employed the latest (at those times) nuclear chiral potentials and consistent weak current operators. In Ref. [8], the doublet capture rate was found to be ΓD = 388.1 (4.3) s−1, when the NN chiral potentials of Ref. [13], obtained up to the next-to-next-to-next-to-leading order (N3LO) in the chiral expansion, were used. When only the
The most recent and systematic study of reaction (1) in χEFT, even if only retaining the
The chiral nuclear potentials involved in all the aforementioned studies are highly non-local and expressed in momentum space. This is less desirable than the r-space in the case of the pp reaction, where the treatment in the momentum space of the Coulomb interaction and the higher-order electromagnetic effects is rather cumbersome. To overcome these difficulties, local chiral potentials expressed in the r-space would be highly desirable. These have been developed only in recent years, as discussed in the recent review of Ref. [18]. These potentials are very accurate and have proven to be extremely successful in describing the structure and dynamics of light and medium-mass nuclei. In particular, we are interested in the work of the models of Ref. [19], the so-called Norfolk potentials, for which, in these years, consistent electromagnetic and weak transition operators have been constructed [20–22]. This local chiral framework has been used to calculate energies [23] and charge radii [24] and various electromagnetic observables in light nuclei, as the charge form factors in A = 6, 12 [24] and the magnetic structure of few-nucleon systems [22]. It has also been used to study weak transitions in light nuclei [25, 26], the muon captures on A = 3, 6 nuclei [27], neutrinoless double β-decay for A = 6, 12 [28] and the β-decay spectra in A = 6 [29], and, finally, the equation of the state of pure neutron matter [30, 31]. However, the use of the Norfolk potentials to study the muon capture on a deuteron and the pp reaction is still lacking. One of the aims of this work is to start this path. Given the fact that
where the dots indicate higher-order terms, which are typically disregarded, and rA is the axial charge radius, its square being given by
The paper is organized as follows: Section 2 presents the theoretical formalism, providing a schematic derivation for
2 Theoretical formalism
We discuss, in this section, the theoretical formalism developed to calculate the muon capture rate. In particular, Section 2.1 gives the main steps of the formalism used to derive the differential and the total muon capture rate on a deuteron in the initial doublet hyperfine state. A through discussion is given by Ref. [9]. Section 2.2 reports the main characteristics of the nuclear potentials and currents we used in the present study. Finally, Section 2.3 presents the variational and the Numerov methods used to calculate the deuteron bound and nn scattering wave functions.
2.1 Observables
The differential capture rate in the doublet initial hyperfine state dΓD/dp can be written as [9]
where p is the nn relative momentum, and
with mμ, mn, and md being the muon, neutron, and deuteron masses, respectively. The transition amplitude
where f, fz indicate the initial hyperfine state, fixed here to be f = 1/2, while s1, s2, and hν denote the spin z-projection for the two neutrons and the neutrino helicity state, respectively. In turn, TW (f, fz; s1, s2, hν) is given by
with
and
Here, the leptonic momentum transfer q is defined as q = kμ − kν ≃ − kν. Furthermore, Ψd (sd) and
where ψ1s (0) denotes the Bohr wave function for a point charge e evaluated at the origin, μμd is the reduced mass of the (μ, d) system, and α = 1/137.036 is the fine-structure constant.
The final nn wave function can be expanded in partial waves as
where
Using standard techniques described in Refs. [9, 35], a multipole expansion of the weak charge, ρ(q), and current, j(q), operators can be performed, resulting in
where λ = ±1, and
To calculate the differential capture rate dΓD/dp in Eq. 4, we need to integrate over
where pmax is the maximum value of the momentum p. To find the smallest needed number of grid points on p to reach convergence, we computed the capture rate by integrating over several grids starting from a minimum value of 20 points up to a maximum of 80. We verified that the results obtained by integrating over 20 or 40 points differ by about 0.1 s−1, while the ones obtained with 40, 60, and 80 points differ by less than 0.01 s−1. Therefore, we have used 60 grid points in all the studied cases mentioned below.
2.2 Nuclear potentials and currents
In this study, we consider four different nuclear interaction models and consistent weak current operators derived in χEFT. We decided to concentrate our attention on the recent local r-space potentials of Ref. [19] (see also Ref. [18] for a recent review). The motivation behind this choice is that, in the future, we plan to use this same formalism to the pp reaction, for which the Coulomb interaction and also electromagnetic higher-order contributions play a significant role at the accuracy level reached by theory. The possibility to work in the r-space is clearly an advantage compared with the momentum space, which would be the unavoidable choice when using non-local potentials. However, in the momentum space, the full electromagnetic interaction between the two protons is not easy to be taken into account. The potentials of Ref. [19], which we will refer to as Norfolk potentials (denoted as NV), are chiral interactions that also include, beyond pions and nucleons, Δ-isobar degrees of freedom explicitly. The short-range (contact) part of the interaction receives contributions at the leading order (LO), next-to-leading order (NLO), and next-to-next-to-next-to-leading order (N3LO), while the long-range components arise from one- and two-pion exchanges, and are retained up to the next-to-next-to-leading order (N2LO). By truncating the expansion at N3LO, there are 26 LECs which have been fitted to the NN Granada database [36–38], obtaining two classes of Norfolk potentials, depending on the range of laboratory energies over which the fits have been carried out: the NVI potentials have been fitted in the range 0–125 MeV, while for the NVII potentials, the range has been extended up to 200 MeV. For each class of potential, two cutoff functions
with aL ≡ RL/2. Two different sets of cutoff values have been considered, (RS; RL) = (0.7; 1.0) and (0.8; 1.2), and the resulting models have been labeled “a” and “b,” respectively. All these potentials are very accurate: in fact, the χ2/datum for the NVIa, NVIIa, NVIb, and NVIIb potentials are 1.05, 1.37, 1.07, and 1.37 [19], respectively. It should be noted that in Ref. [19], another set of NV potentials labeled NVIc and NVIIc was constructed, with (RS; RL) = (0.6; 0.8). The reason for not considering these potential models in this work is that they have been found to lead to a poor convergence in the hyperspherical harmonics method used to calculate the 3H and 3He wave functions needed to predict the Gamow–Teller matrix element in tritium β-decay. This study is, in turn, necessary to fit the aforementioned dR LEC (see as follows and Ref. [20]). Therefore, for the NVIc and NVIIc potentials, consistent currents are not available, and we have disregarded them in this work.
We now turn our attention to the weak transition operators. When only the
Therefore, we will review the various contributions to the electromagnetic current, even if we are interested only in their isovector components. The electromagnetic current operators up to one loop have been most recently reviewed in Ref. [22]. Here, we only give a synthetic summary. Following the notation of Ref. [22], we denote with Q the generic low-momentum scale. The LO contribution, at the order Q−2, consists of the single-nucleon current, while at the NLO or order Q−1, there is the one-pion-exchange (OPE) contribution. The relativistic correction to the LO single-nucleon current provides the first contribution of order Q0 (N2LO). Furthermore, since the Norfolk interaction models retain explicitly Δ-isobar degrees of freedom, we take into account also the N2LO currents originating from explicit Δ intermediate states. Finally, the currents at order Q1 (N3LO) consist of 1) terms generated by minimal substitution in the four-nucleon contact interactions involving two gradients of the nucleon fields and by non-minimal couplings to the electromagnetic field; 2) OPE terms induced by γπN interactions of sub-leading order; and 3) one-loop two-pion-exchange terms. A thorough discussion of all these contributions as well as their explicit expressions is given in Ref. [22]. Here, we only remark that 1) the various contributions are derived in momentum space and have power–law behavior at large momenta, or short range. Therefore, they need to be regularized. The procedure adopted here, as in Ref. [22], is to carry out first the Fourier transforms of the various terms. This results in r-space operators which are highly singular at vanishing inter-nucleon separations. Then, the singular behavior is removed by multiplying the various terms by appropriate r-space cutoff functions, identical to those of the Norfolk potentials of Ref. [19]. More details are given in Refs. [21, 22]. 2) There are 5 LECs in the electromagnetic currents which do not enter the nuclear potentials and need to be fitted using electromagnetic observables. These LECs enter the current operators at N3LO; in particular, two of them are present in the currents arising from non-minimal couplings to the electromagnetic field, and three of them are present in the sub-leading isoscalar and isovector OPE contributions. In this study, these LECs are determined by a simultaneous fir to the A = 2–3 nuclei magnetic moments and the deuteron threshold electrodisintegration at backward angles over a wide range of momentum transfers [22]. In this work, we used the LECs labeled with set A in Ref. [22].
The axial current operators used in the present work are the ones of Ref. [20]. They include the LO term of order Q−3, which arises from the single-nucleon axial current, and the N2LO and N3LO terms (scaling as Q−1 and Q0, respectively), consisting of the relativistic corrections and Δ contributions at N2LO, and of OPE and contact terms at N3LO. It should be noted that at NLO, here of order Q−2, there is no contribution in χEFT. The explicit r-space expression of these operators is given in Ref. [20]. Here, we only remark that all contributions have been regularized at a short and long range consistently with the regulator functions used in the Norfolk potentials. Furthermore, the N3LO contact term presents a LEC, here denoted by z0 (but essentially equal to the dR LEC mentioned in Section 1), defined as
Here, gA = 1.2723 (23) is the single-nucleon axial coupling constant, m = 938.9 MeV is the nucleon mass, mπ = 138.04 MeV and fπ = 97.4 MeV are the pion mass and decay constant, respectively, Λχ ∼ 1 GeV is the chiral-symmetry breaking scale, and c3 = −0.79 and c4 = 1.33 are two LECs entering the ππN Lagrangian at N2LO and taken from the fit of the pion-nucleon scattering data with Δ-isobar as explicit degrees of freedom [39]. As mentioned previously, cD is one of the two LECs which enter the three-nucleon interaction, the other being denoted by cE. The two LECs cD (and consequently z0) and cE have been fitted to simultaneously reproduce the experimental trinucleon binding energies and the central value of the Gamow–Teller matrix element in tritium β-decay. The explicit values for cD are −0.635, −4.71, −0.61, and −5.25 for the NVIa, NVIb, NVIIa, and NVIIb potentials, respectively.
The nuclear axial charge has a much simpler structure than the axial and vector currents, and we have used the operators as derived in Ref. [40]. At LO, i.e., at the order Q−2, it retains the one-body term, which gives the most important contribution. At NLO (order Q−1), the OPE contribution appears, which, however, has been found to be almost negligible in this study. The N2LO contributions (order Q0) exactly vanish, and at N3LO (order Q1), there are two-pion-exchange terms and new contact terms where new LECs appear. N3LO has not been included in the calculation, since the new LECs have not been fixed yet. However, we have found the contribution of C1(A) to be two orders of magnitude smaller than the one from the other multipoles. Therefore, the effect of the axial current correction at N3LO can be safely disregarded.
All the axial charge and current contributions are multiplied by the single-nucleon axial coupling constant,
where the variable
with
The value for
Alternatively, it is possible to obtain
2.3 Nuclear wave functions
The calculation of the nuclear wave functions of the deuteron and nn systems was, first of all, performed using the variational method described in Ref. [9], where all the details of the calculation can be found. Here, we summarize only the main steps.
The deuteron wave function can be written as
where the channels α ≡ (l; s; J; t) denote the deuteron quantum numbers, with the combination (l = 0, 2; s = 1; J = 1; t = 0) corresponding to α = 1, 2, respectively, and the functions
The M radial functions fi(r), normalized to unity, with i = 0, …, M − 1, are written as
where γ is a non-variational parameter chosen to be [9] γ = 0.25 fm−1 and (2)Li (γr) are the Laguerre polynomials of the second type [42]. The unknown coefficients cα,i are obtained using the Rayleigh–Ritz variational principle, i.e., imposing the condition
where H is the Hamiltonian and Bd is the deuteron binding energy. This reduces to an eigenvalue–eigenvector problem, which can be solved with standard numerical techniques [9].
The nn wave function
where fi(r) and
The asymptotic wave function Ψa(p) describes the nn scattering system in the asymptotic region, where the nuclear potential is negligible. Consequently, it can be written as a linear combination of regular (Bessel) and irregular (Neumann) spherical functions, denoted as jL(pr), nL(pr), respectively, i.e.,
where RLL’ is the reactance matrix, and
so that they are well defined for p → 0 and r → 0. The function
To determine the coefficients di(p) in Eq. 28 and the reactance matrix RLL’ in Eq. 29, we use the Kohn variational principle [43], which states that the functional
is stationary with respect to di(p) and RLL’. In Eq. 32, E is the nn relative energy (E = p2/mn, mn being the neutron mass) and H is the Hamiltonian operator. Performing the variation, a system of linear inhomogeneous equations for di(p) and a set of algebraic equations for RLL’ are derived. These equations are solved by standard techniques. The variational results presented in the following section are obtained using M = 35 for both the deuteron and the nn scattering wave functions.
To test the validity of the variational method and its numerical accuracy, in this work, we also used the Numerov method for the deuteron and the nn wave functions.
For the deuteron wave function, we used the so-called renormalized Numerov method, based on the work of Ref. [44]. Within this method, the Schrödinger equation is rewritten as
where I is the identity matrix and Q(x) is a matrix defined as
and Ψ(x) is also a matrix whose columns are the independent solutions of the Schrödinger equation with non-assigned boundary conditions on the derivatives. In Eq. 34, μ is the np reduced mass, E ≡ − Bd, and V(x) is the sum of the np nuclear potential Vnp(x) and the centrifugal barrier, i.e.,
The Schrödinger equation is evaluated on a finite and discrete grid with a constant step h. The boundary conditions require knowing the wave function at the initial and final grid points, given by x0 = 0 and xN = Nh, respectively. Specifically, it is assumed that Ψ(0) = 0 and Ψ(Nh) = 0. No conditions on first derivatives are imposed.
Equation 33 can be rewritten equivalently as [44]
where xn ∈ A,
It should be noted that Eq. 36 is, in fact, the natural extension to a matrix formulation of the ordinary Numerov algorithm (see Eq. 65 as follows).
By introducing the matrix F (xn) as [44]
where the matrix U (xn) is given by
Furthermore, we introduce the matrices R (xn) and
and their inverse matrices as
By using definitions (41) and (42), it is possible to derive from Eq. 39 the following recursive relations:
We now notice that, since Ψ(0) = 0, Eq. 38 implies that F (0) = 0 and, consequently, from Eq. 43, it follows that R−1 (0) = 0. Similarly, since Ψ(Nh) = 0, from Eqs 38, 44 we obtain
where l and r are two unknown vectors. Multiplying Eq. 48 by
Similarly, from Eq. 47, we can write
Using Eq. 41 with xn = xm for the outgoing solution and Eq. 42 with xn = xm+1 for the incoming solution, we can write
By replacing Eqs 51, 52 with Eq. 49 and using Eq. 50, we obtain that
or equivalently that
A non-trivial solution is only admitted if the aforementioned equation satisfies the following condition:
This determinant is a function of the energy E, i.e.,
Therefore, we proceed as follows: starting from an initial trial value E1, we calculate det (E1). Fixing a tolerance factor ϵ, for example ϵ = 10–16, if det (E1) ≤ ϵ, we assume E1 being the eigenvalue, otherwise we compute the determinant for a second energy value E2. If det (E2) ≤ ϵ, we take the deuteron binding energy as Bd = −E2, otherwise it is necessary to repeat the procedure iteratively until det (Ei) ≤ ϵ. For the iterations after the second one, the energy is chosen through the relation
which follows from a linear interpolation procedure. The procedure stops when det (Ei) ≤ ϵ, and the deuteron binding energy is taken to be Bd = −Ei.
To calculate the S- and D-wave components of the reduced radial wave function, denoted as u0 (xn) and u2 (xn), respectively, we notice that they are the two components of the vector ψ(xn), defined in Eq. 47 at the point xm. The starting point is to assign an arbitrary value to one of the two components of the vector function f (xm) (see Eq. 50). Since R (xm) and
where n = m − 1, …, 0. Similarly, we can proceed with the incoming function. By defining it as f (xn) = F (xn) ⋅r, from Eq. 42 we have
where n = m + 1, …, N. At this point, the vector function f (xn) can be calculated
Finally, the deuteron wave function is normalized to unity.
The single-channel Numerov method, also known as a three-point algorithm, is used to calculate the nn wave function. Although the method is quite well known, to provide a comprehensive review of all the approaches to the A = 2 systems, we briefly summarize its main steps. Again, we start by defining a finite and discrete interval I, with constant step h, characterized by the initial and final points, x0 = 0 and xN = Nh, respectively. Then, the Schrödinger equation can be cast in the form
where
with V (xn) being the nuclear potential and p the nn relative momentum. To solve Eq. 61, it is convenient to introduce the function z (xn), defined as
By replacing Eq. 61 with Eq. 63, z (xn) can be rewritten as
By expanding z (xn−1) and z (xn+1) in an interval around the point xn in a Taylor series up to O (h4), and adding together the two expressions, we obtain
This is a three-point relation: once the z (xn−1) and z (xn) values are known, after calculating u″(xn) using Eq. 61, we can compute z (xn+1) at the order O (h6).
By fixing the values u (0) = 0 and u(h) = h, we consequently know z (0) and z(h), i.e.,
and u″(h) is obtained by Eq. 61. Then, z (2h) is obtained from Eq. 65, and consequently,
where W (2h) is given by Eq. 62. Equation 68 can be used again to determine the u(3h) value, and, proceeding iteratively, the S-wave scattering reduced radial wave function is fully determined except for an overall normalization factor. This means that for a sufficiently large value of xn ∈ A, denoted as
where N is the sought normalization constant, and the phase shift δ0 can be computed by taking the ratio between Eq. 69 written for
Finally, using Eq. 69, the normalization constant N is given by
so that the function u(xn) turns out to be normalized to unitary flux.
To compare the results obtained with the variational and the Numerov methods, Table 1 shows the deuteron binding energies and the nn phase shifts at the indicative relative energy E = 5 MeV for the four chiral potentials under consideration. In the table, we can see an excellent agreement between the two methods, with a difference well below 1 keV for the binding energies. The phase shifts calculated with the two methods are also in excellent numerical agreement. Furthermore, Figure 1 shows the deuteron and the nn wave functions, still at E = 5 MeV as an example, for the NVIa potential. The results obtained with the other chiral potentials present similar behavior. In the figure, we can see that the variational method fails to reproduce the u0(r) function for r > 20 fm. However, it should be noticed that in this region, the function is almost two orders of magnitude smaller than in the dominant range of r ∼ 0–5 fm. As we will see in the following section, we already anticipate that these discrepancies in the deuteron wave functions will have no impact on the muon capture rate.
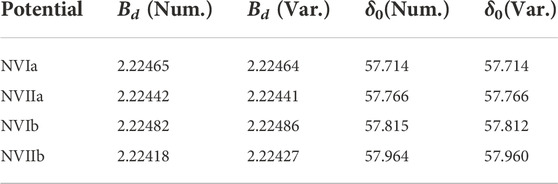
TABLE 1. Deuteron binding energies Bd, in MeV, and nn S-wave phase shift δ0 at E =5 MeV, in deg, calculated with the Numerov (Num.) or the variational (Var.) methods using the four Norfolk chiral potentials NVIa, NVIIa, NVIb, and NVIIb. Here, we report the results up to the digit from which the two methods start to differ. The experimental value for Bd is
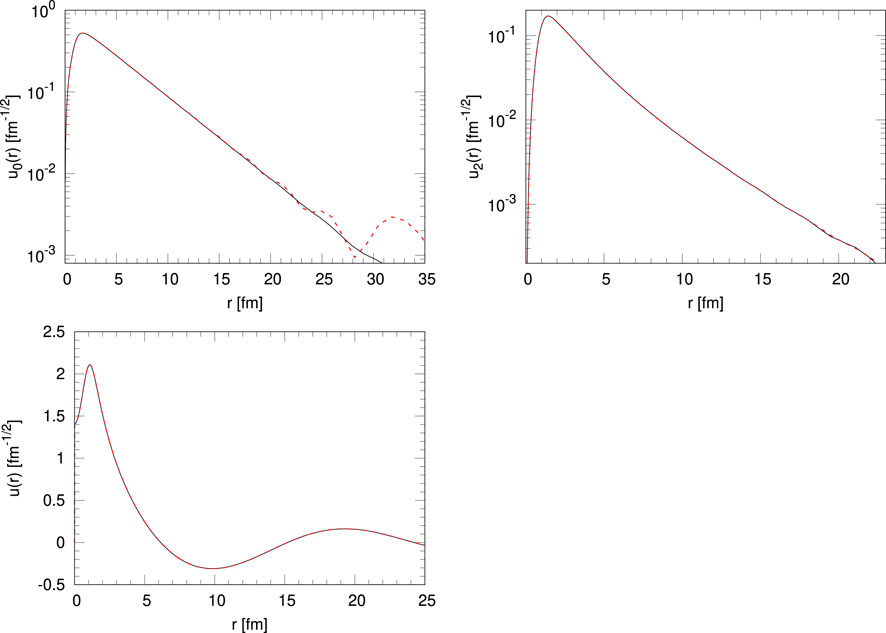
FIGURE 1. Deuteron u0(r) (left top panel) and u2(r) (right top panel) functions, and the
3 Results
We present, in this section, the results for the
First, we begin by proving that the uncertainty arising from the numerical method adopted to study the deuteron and the nn scattering states is well below the 1% level. In fact, Table 2 shows the results obtained with the NVIa potential and currents with up to N3LO contributions, using either the variational or the Numerov method to solve the two-body problem (see Section 2.3). The function
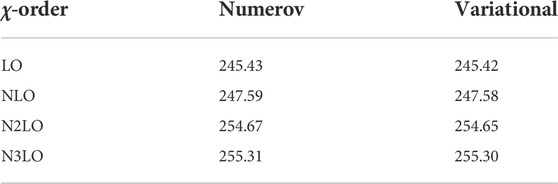
TABLE 2. Total doublet capture rate in the
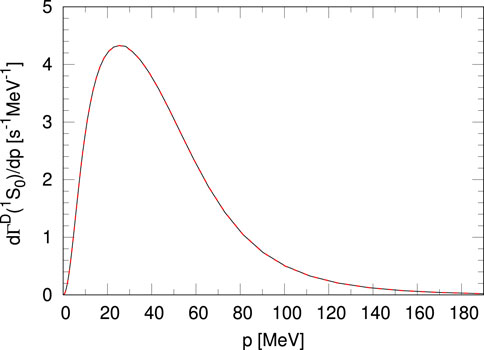
FIGURE 2. Differential doublet capture rate in the
Table 3 shows the results for
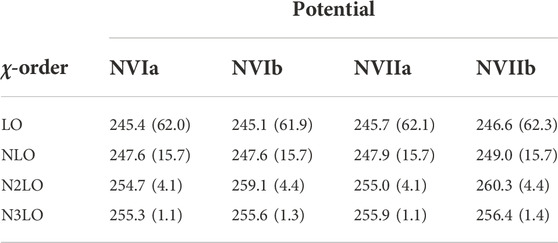
TABLE 3. Total doublet capture rate in the
From this, we obtain
From Table 3, we can conclude that the chiral-order convergence seems to be quite well under control for all the potential models. In fact, in going from LO to NLO,
The theoretical uncertainty arising from the chiral-order convergence of the nuclear weak transition operators can be studied using the prescription of Ref. [45]. Here, we report the formula for the error at N2LO only. At this order, for each energy, we define the error for the differential capture rate (to simplify the notation from now on we use
where we assumed
as in Ref. [46] for the case of the np ↔ dγ reaction. Here, p is the relative momentum of the nn system and we assume a value of Λ ≃ 550 MeV, which is of the order of the cutoff of the adopted interactions. Analogous formulas have been used to study the other orders (see Ref. [45] for details).
In Figure 3, we show the error on
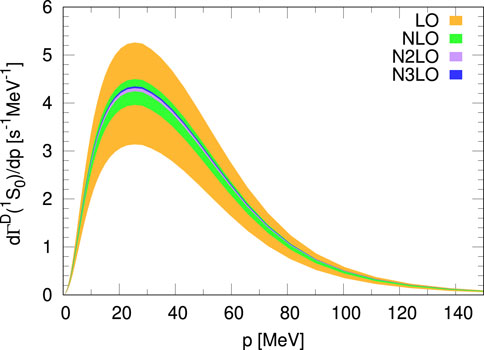
FIGURE 3. Differential doublet capture rate in the
Note that here we assumed the distribution of the truncation error to be uniform, this being a systematic error. Therefore, we do not square it in Eq. 75. Table 3 also shows for each order the error relative to the chiral truncation of the electroweak currents. To be the most conservative as possible, we keep as error the largest obtained with the various interaction models. In the same spirit, we consider the error computed at N2LO, since the calculation at N3LO does not contain all the contributions of the axial charge (see discussion Section 2.2). Therefore, we obtain
Finally, Table 4 shows the results obtained with all the interactions and consistent currents up to N3LO for the three values of the axial charge radius,
where maxpot indicates that we take the maximum value among the different interactions considered. From the table, we can conclude that
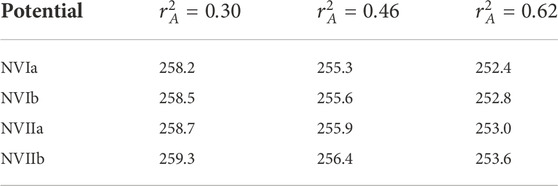
TABLE 4. Total doublet capture rate in the
In conclusion, our final result for
where the three uncertainties arise from model dependence, chiral convergence, and the experimental error in the axial charge radius rA. The overall systematic uncertainty becomes 5.0 s−1 when the various contributions are summed. The uncertainty on
4 Conclusion and outlook
We investigated, for the first time, with local nuclear potential models derived in χEFT and consistent currents, the muon capture on deuteron, in the
Our final result is
Given the success of this calculation in determining
Data availability statement
The original contributions presented in the study are included in the article; further inquiries can be directed to the corresponding author.
Author contributions
LC and LM shared the idea, the formula derivation, and the computer code implementation of this work. LM was mainly responsible for the drafting of the manuscript. AG contributed to reviewing the codes and running them in order to obtain the final results presented here, while MP and MV gave valuable suggestions during the setting up of the calculation. All the authors contributed equally to reviewing and correcting the draft of the manuscript.
Funding
AG acknowledges the support provided by the U.S. Department of Energy, Office of Nuclear Science, under Contract No. DE-AC05-06OR23177, while MP acknowledges the support from the U.S. Department of Energy through the FRIB Theory Alliance Award No. DE-SC0013617.
Acknowledgments
The authors also acknowledge the Istituto Nazionale di Fisica Nucleare (INFN), Sezione di Pisa, for providing the computational resources. The final calculation was performed using resources of the National Energy Research Scientific Computing Center (NERSC), a U.S. Department of Energy Office of Science User Facility located at Lawrence Berkeley National Laboratory, operated under Contract No. DE-AC02-05CH11231.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Measday DF. The nuclear physics of muon capture. Phys Rep (2001) 354:243–409. doi:10.1016/s0370-1573(01)00012-6
2. Wang IT, Anderson EW, Bleser EJ, Lederman LM, Meyer SL, Rosen JL, et al. Muon capture in (p μ d)+ molecules. Phys Rev (1965) 139:B1528–38. doi:10.1103/physrev.139.b1528
3. Bertin A, Vitale A, Placci A, Zavattini E. Muon capture in gaseous deuterium. Phys Rev D (1973) 8:3774–93. doi:10.1103/physrevd.8.3774
4. Bardin G, Duclos J, Martino J, Bertin A, Capponi M, Piccinini M, et al. A measurement of the muon capture rate in liquid deuterium by the lifetime technique. Nucl Phys A (1986) 453:591–604. doi:10.1016/0375-9474(86)90253-8
5. Cargnelli M, et al. Workshop on fundamental μ physics, los alamos, 1986, LA 10714C. In: M Morita, H Ejiri, H Ohtsubo, and T Sato, editors. Nuclear weak process and nuclear structure, Yamada Conference XXIII. Singapore: World Scientific (1989). p. 115.
7. Marcucci LE. Muon capture on deuteron and 3He: A personal review. Int J Mod Phys A (2012) 27:1230006. doi:10.1142/s0217751x12300062
8. Adam J, Tater M, Truhlik E, Epelbaum E, Machleidt R, Ricci P. Calculation of doublet capture rate for muon capture in deuterium within chiral effective field theory. Phys Lett B (2012) 709:93–100. doi:10.1016/j.physletb.2012.01.065
9. Marcucci LE, Piarulli M, Viviani M, Girlanda L, Kievsky A, Rosati S, et al. Muon capture on deuteron and 3He. Phys Rev C (2011) 83:014002. doi:10.1103/physrevc.83.014002
10. Marcucci LE, Kievsky A, Rosati S, Schiavilla R, Viviani M. Chiral effective field theory predictions for muon capture on deuteron and 3He. Phys Rev Lett (2012) 108:052502. [Erratum: Phys. Rev. Lett. 121, (2018) 049901]. doi:10.1103/physrevlett.108.052502
11. Golak J, Skibiński R, Witała H, Topolnicki K, Elmeshneb AE, Kamada H, et al. Break-up channels in muon capture on 3He. Phys Rev C (2014) 90:024001. [Addendum: Phys.Rev.C 90, 029904 10.1103/physrevc.90.029904(2014)].
12. Acharya B, Ekström A, Platter L. Effective-field-theory predictions of the muon-deuteron capture rate. Phys Rev C (2018) 98:065506. doi:10.1103/physrevc.98.065506
13. Entem DR, Machleidt R. Accurate charge dependent nucleon nucleon potential at fourth order of chiral perturbation theory. Phys Rev C (2003) 68:041001. doi:10.1103/physrevc.68.041001
14. Machleidt R, Entem DR. Chiral effective field theory and nuclear forces. Phys Rep (2011) 503:1–75. doi:10.1016/j.physrep.2011.02.001
15. Gazit D, Quaglioni S, Navrátil P. Three-nucleon low-energy constants from the consistency of interactions and currents in chiral effective field theory. Phys Rev Lett (2009) 103:102502. [Erratum: Phys. Rev. Lett. 122, (2019) 029901]. doi:10.1103/physrevlett.103.102502
16. Carlsson BD, Ekström A, Forssén C, Strömberg DF, Jansen GR, Lilja O, et al. Uncertainty analysis and order-by-order optimization of chiral nuclear interactions. Phys Rev X (2016) 6:011019. doi:10.1103/physrevx.6.011019
17. Acharya B, Ekström A, Odell D, Papenbrock T, Platter L. Corrections to nucleon capture cross sections computed in truncated Hilbert spaces. Phys Rev C (2017) 95:031301. doi:10.1103/physrevc.95.031301
18. Piarulli M, Tews I. Local nucleon-nucleon and three-nucleon interactions within chiral effective field theory. Front Phys (2020) 7:245. doi:10.3389/fphy.2019.00245
19. Piarulli M, Girlanda L, Schiavilla R, Kievsky A, Lovato A, Marcucci LE, et al. Local chiral potentials with Δ-intermediate states and the structure of light nuclei. Phys Rev C (2016) 94:054007. doi:10.1103/physrevc.94.054007
20. Baroni A, Schiavilla R, Marcucci LE, Girlanda L, Kievsky A, Lovato A, et al. Local chiral interactions, the tritium Gamow-Teller matrix element, and the three-nucleon contact term. Phys Rev C (2018) 98:044003. doi:10.1103/physrevc.98.044003
21. Schiavilla R, Baroni A, Pastore S, Piarulli M, Girlanda L, Kievsky A, et al. Local chiral interactions and magnetic structure of few-nucleon systems. Phys Rev C (2019) 99:034005. doi:10.1103/physrevc.99.034005
22. Gnech A, Schiavilla R. Magnetic structure of few-nucleon systems at high momentum transfers in a χEFT approach (2022). arXiv:2207.05528.
23. Piarulli M, Baroni A, Girlanda L, Kievsky A, Lovato A, Lusk E, et al. Light-nuclei spectra from chiral dynamics. Phys Rev Lett (2018) 120:052503. doi:10.1103/PhysRevLett.120.052503
24. Gandolfi S, Lonardoni D, Lovato A, Piarulli M. Atomic nuclei from quantum Monte Carlo calculations with chiral EFT interactions. Front Phys (2020) 8:117. doi:10.3389/fphy.2020.00117
25. King GB, Andreoli L, Pastore S, Piarulli M, Schiavilla R, Wiringa RB, et al. Chiral effective field theory calculations of weak transitions in light nuclei. Phys Rev C (2020) 102:025501. doi:10.1103/physrevc.102.025501
26. King GB, Andreoli L, Pastore S, Piarulli M. Weak transitions in light nuclei. Front Phys (2020) 8:363. doi:10.3389/fphy.2020.00363
27. King GB, Pastore S, Piarulli M, Schiavilla R. Partial muon capture rates in A=3 and A=6 nuclei with chiral effective field theory. Phys Rev C (2022) 105:L042501. doi:10.1103/physrevc.105.l042501
28. Cirigliano V, Dekens W, De Vries J, Graesser ML, Mereghetti E, Pastore S, et al. Renormalized approach to neutrinoless double- β decay. Phys Rev C (2019) 100:055504. doi:10.1103/physrevc.100.055504
29. King GB, Baroni A, Cirigliano V, Gandolfi S, Hayen L, Mereghetti E, et al. Ab initio calculation of the β decay spectrum of 6He (2022). ArXiv:2207.11179.
30. Piarulli M, Bombaci I, Logoteta D, Lovato A, Wiringa RB. Benchmark calculations of pure neutron matter with realistic nucleon-nucleon interactions. Phys Rev C (2020) 101:045801. doi:10.1103/physrevc.101.045801
31. Lovato A, Bombaci I, Logoteta D, Piarulli M, Wiringa RB. Benchmark calculations of infinite neutron matter with realistic two- and three-nucleon potentials. Phys Rev C (2022) 105:055808. doi:10.1103/physrevc.105.055808
32. Acharya B, Platter L, Rupak G. Universal behavior of p-wave proton-proton fusion near threshold. Phys Rev C (2019) 100:021001. doi:10.1103/physrevc.100.021001
33. Marcucci LE, Schiavilla R, Viviani M. Proton-proton weak capture in chiral effective field theory. Phys Rev Lett (2013) 110:192503. [Erratum: Phys. Rev. Lett. 123, (2019) 019901]. doi:10.1103/physrevlett.110.192503
34. Hill RJ, Kammel P, Marciano WJ, Sirlin A. Nucleon axial radius and muonic hydrogen—A new analysis and review. Rep Prog Phys (2018) 81:096301. doi:10.1088/1361-6633/aac190
36. Navarro Pérez R, Amaro JE, Ruiz Arriola E. Erratum: Coarse-grained potential analysis of neutron-proton and proton-proton scattering below the pion production threshold [Phys. Rev. C88, 064002 (2013)]. Phys Rev C (2013) 88:064002. [Erratum: Phys. Rev. C 91, (2015) 029901]. doi:10.1103/physrevc.91.029901
37. Navarro Pérez R, Amaro JE, Ruiz Arriola E. Coarse grained nn potential with chiral two-pion exchange. Phys Rev C (2014) 89:024004. doi:10.1103/physrevc.89.024004
38. Navarro Pérez R, Amaro JE, Ruiz Arriola E. Statistical error analysis for phenomenological nucleon-nucleon potentials. Phys Rev C (2014) 89:064006. doi:10.1103/physrevc.89.064006
39. Krebs H, Epelbaum E, Meissner U. Nuclear forces with Δ excitations up to next-to-next-to-leading order, part I: Peripheral nucleon-nucleon waves. Eur Phys J A (2007) 32:127–37. doi:10.1140/epja/i2007-10372-y
40. Baroni A, Girlanda L, Pastore S, Schiavilla R, Viviani M. Nuclear axial currents in chiral effective field theory. Phys Rev C (2016) 93:015501. doi:10.1103/physrevc.93.015501
41. Meyer AS, Betancourt M, Gran R, Hill RJ. Deuterium target data for precision neutrino-nucleus cross sections. Phys Rev D (2016) 93:113015. doi:10.1103/physrevd.93.113015
42. Abramowitz M, Stegun IA. Handbook of mathematical functions with formulas, graphs, and mathematical tables, vol. 55. Washington, DC, USA: US Government printing office (1964).
43. Kohn W. Variational methods in nuclear collision problems. Phys Rev (1948) 74:1763–72. doi:10.1103/physrev.74.1763
44. Johnson BR. The renormalized Numerov method applied to calculating bound states of the coupled-channel Schroedinger equation. J Chem Phys (1978) 69:4678–88. doi:10.1063/1.436421
45. Epelbaum E, Krebs H, Meißner UG. Improved chiral nucleon-nucleon potential up to next-to-next-to-next-to-leading order. Eur Phys J A (2015) 51:53. doi:10.1140/epja/i2015-15053-8
46. Acharya B, Bacca S. Gaussian process error modeling for chiral effective-field-theory calculations of np ↔ dγ at low energies. Phys Lett B (2022) 827:137011. doi:10.1016/j.physletb.2022.137011
47. Marcucci LE, Dohet-Eraly J, Girlanda L, Gnech A, Kievsky A, Viviani M. The hyperspherical harmonics method: A tool for testing and improving nuclear interaction models. Front Phys (2020) 8:69. doi:10.3389/fphy.2020.00069
48. Gnech A, Viviani M, Marcucci LE. Calculation of the 6Li ground state within the hyperspherical harmonic basis. Phys Rev C (2020) 102:014001. doi:10.1103/physrevc.102.014001
49. Gnech A, Marcucci LE, Schiavilla R, Viviani M. Comparative study of 6He β-decay based on different similarity-renormalization-group evolved chiral interactions. Phys Rev C (2021) 104:035501. doi:10.1103/physrevc.104.035501
50. Marcucci LE, Schiavilla R, Viviani M, Kievsky A, Rosati S, Beacom JF. Weak proton capture on 3He. Phys Rev C (2001) 63:015801. doi:10.1103/physrevc.63.015801
51. Park TS, Marcucci LE, Schiavilla R, Viviani M, Kievsky A, Rosati S, et al. Parameter free effective field theory calculation for the solar proton fusion and hep processes. Phys Rev C (2003) 67:055206. doi:10.1103/physrevc.67.055206
Keywords: muon capture, deuteron, chiral effective field theory, ab initio calculation, error estimate
Citation: Ceccarelli L, Gnech A, Marcucci LE, Piarulli M and Viviani M (2023) Muon capture on deuteron using local chiral potentials. Front. Phys. 10:1049919. doi: 10.3389/fphy.2022.1049919
Received: 21 September 2022; Accepted: 07 November 2022;
Published: 11 January 2023.
Edited by:
Sonia Bacca, Johannes Gutenberg University Mainz, GermanyReviewed by:
Chen Ji, Central China Normal University, ChinaBijaya Acharya, Oak Ridge National Laboratory (DOE), United States
Copyright © 2023 Ceccarelli, Gnech, Marcucci, Piarulli and Viviani. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: L. E. Marcucci, bGF1cmEuZWxpc2EubWFyY3VjY2lAdW5pcGkuaXQ=
 L. Ceccarelli1
L. Ceccarelli1 A. Gnech
A. Gnech L. E. Marcucci
L. E. Marcucci M. Piarulli
M. Piarulli M. Viviani
M. Viviani