Broadband low-frequency sound absorption in open tunnels with deep sub-wavelength Mie resonators

We report both experimentally and numerically that near-perfect absorption of low-frequency sound is realized in an open tunnel embedded with two deep sub-wavelength (0.085 λ) Mie resonators. The resonators are composed of a multiple-cavity structure and an outer frame on three sides. In the eigenmode analysis, we obtain two types of monopolar Mie resonance modes (MMR I&II) in a single resonator around 250 Hz. The eigenfrequency of MMR I is mainly determined by the Helmholtz resonance of each cavity in the multiple-cavity structure, while that of MMR II is closely related to the coupling between the multiple-cavity structure and its outer frame, showing high performances of coupling and sound absorption. Based on the thermal viscous loss of sound energy in the channels created by the mutual coupling of MMR II of both Mie resonators with different diameters, the near-perfect sound absorption through the open tunnel is realized around 283 Hz. More interestingly, by increasing the number of Mie resonators in the tunnel, a broadband near-perfect sound absorption is observed, and the fractional bandwidth can reach about 0.25 and 0.46 for the tunnels with 6 and 13 resonators, The proposed deep sub-wavelength Mie resonator and its associated near-perfect sound absorptions have great potential applications in architectural acoustics and mechanical engineering.

Introduction

Sound absorbers have attracted considerable interest from both the physics and engineering communities due to their important potential applications, such as noise control and architectural acoustics. Recent advancement of metamaterials [1–20] with the ability of manipulating wave propagation in unprecedented ways, has motivated a variety of sound absorber designs, which show superior absorptive features than conventional structures, such as porous and fibrous materials and micro-perforated plates. The demonstrated sound absorbers based on the acoustic metamaterials are usually composed of deep sub-wavelength resonant unit cells to absorb and dissipate sound energy inside, such as Helmholtz resonators [21–26], coiled Fabry-Perot resonators [27–29], sound membranes [30–33], acoustic metasurfaces [34–36], split-ring-resonators [37–39], Mie resonators [40, 41], etc. But in most of these types of absorbers, the structures are almost closed, which would inevitably affect the exchange of media between both sides, including heat, air, light and water.

To realize sound absorbers with an open structure, the coherent perfect sound absorbers [42–45] are proposed by using two sound beams with the same amplitudes and opposite phases which propagate into two ports simultaneously. Furthermore, by introducing lossy Bragg stacks or hybrid membrane resonators in two-port open systems [46, 47], the sound absorption can also be obtained. However, these systems usually impose high requirements in the structure design (such as loss factor and surface tensor). By attaching Helmholtz resonators with different sizes on both sides of an open tunnel, the sound absorption can be realized with a simpler structure [48]. However, these selected Helmholtz resonators inevitably require larger sizes for the absorption of low-frequency sound, which significantly affect their practical applications. Thus, the design of open structures for low-frequency sound absorption with deep sub-wavelength resonators still remain a technical challenge.

In this work, we demonstrate an open tunnel of near-perfect sound absorption with two deep sub-wavelength Mie resonators composed of a multiple-cavity structure and an outer frame on three sides. We find that two types of monopolar Mie resonance (MMR) modes exist in a single resonator around 250 Hz, and the eigenfrequency of MMR II decreases greatly by the coupling between the multiple-cavity structure and its outer frame. Based on the thermal viscous loss in the channels created by the mutual coupling of MMR II of both Mie resonators with different diameters, we can realize the near-perfect sound absorption through the open tunnel at 283 Hz. Additionally, by increasing the number of Mie resonators, we further increase the bandwidth of near-perfect sound absorption, and the fractional bandwidth can reach about 0.25 and 0.46 for the cases of 6 and 13 resonators, The measured results also demonstrate the characteristics of near-perfect sound absorption through the designed open tunnel, which agree with the simulated ones. The proposed deep sub-wavelength Mie resonator and its associated near-perfect sound absorption could potentially be applied in architectural acoustics, mechanical engineering, and noise reduction.

Design and performance of unit cell of Mie resonance

Figure 1A shows the photograph of the unit cell of Mie resonance, which consists of a circular multiple-cavity structure with the outer and inner radii R and r surrounded by hard sound boundaries with a thickness e on three sides. The bottom side of the unit cell is open with a length L. The unit cell is made of epoxy resin by the three-dimensional (3D) printing technology, and the background medium is air. The multiple-cavity structure is composed of a central circular cavity, surrounded by 8 interconnected cavities, which are divided by 4 channels. The thickness of all frames is t, the width of 4 channels is w, and the open width and radial length of all cavities are b and l, respectively. In our work, the sound absorption is caused by the visco-thermal loss inside the unit cell. When the acoustic wave propagates into the deep sub-wavelength resonators with narrow channels, the sound energy is attenuated owing to the thermal and viscous losses. Thus, we use the Thermoviscous Acoustic-Solid Interaction module of COMSOL Multiphysics software to numerically simulate sound characteristics. In the model, the structure parameters e = 10.0 mm, t = b = 1.2 mm, w = 2.0 mm, and l = 17.6 mm, and the other parameters R, r and L are variables, in which their relations are r = R-2.0 cm and L = 2R + 0.4 cm. The material parameters of epoxy resin are the density ρ = 1,050 kg/m³, the Young’s modulus E = 5.08 GPa, and the Poisson ratio v = 0.35, and the material parameters of air are calculated as density $\rho =p_{0}M/R_{0}T$ and sound speed $c=\sqrt{\gamma R_{0}T/M}$, respectively, where γ = 1.4, M = 28.97 × 10⁻³ kg/mol, R₀ = 8.31 J/(mol/K), p₀ = 101.325 kPa, and T = 293 K. Here, it is noted that the proposed sound absorber can also be applied in a 3D open tunnel via 3D Mie resonators [49]. In this work, we mainly design a two-dimensional open tunnel of sound absorption based on the proposed Mie resonator.

FIGURE 1

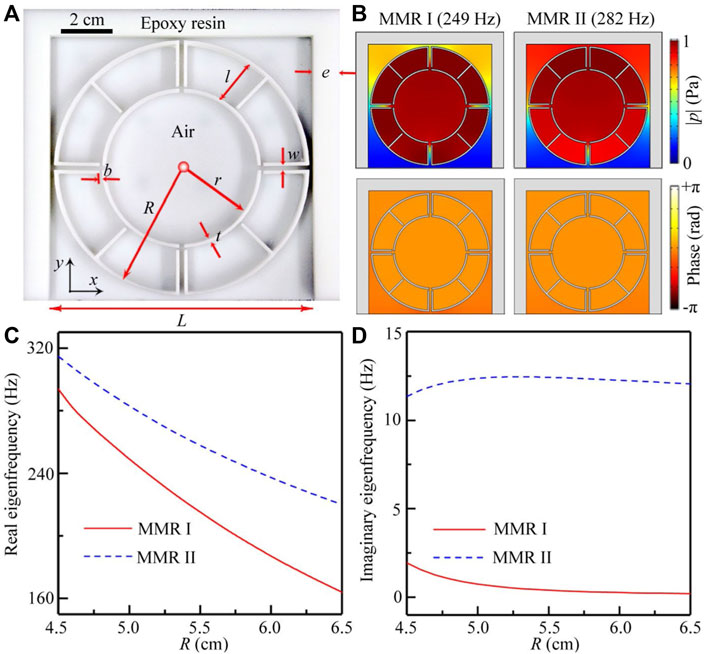
FIGURE 1. (A) Photograph of the unit cell of Mie resonance. (B) Simulated pressure and phase eigenfunctions of the unit cell with R = 5.0 cm. Eigenmodes of MMR I and II can be observed at 249 and 282 Hz, respectively. (C) Real and (D) imaginary parts of the eigenfrequencies for MMR I and II with different values of R.

Figure 1B shows the simulated pressure amplitude and phase eigenfunctions of the unit cell with R = 5.0 cm. We can see that the pressure amplitude and phase distributions of both eigenmodes exhibit typical characteristics of monopolar Mie resonance (MMR), denoting as MMR I and II. Here, note that the sound amplitude outside the multiple-cavity structure for MMR II is much larger than that for MMR I, indicating that the coupling effect between the multiple-cavity structure and outer frame for MMR II is stronger. Furthermore, we simulate the real and imaginary eigenfrequencies of both MMR modes with different values of R, in which the parameters t, b, w and l are the same as those in Figure 1B. As shown in Figure 1C, with the increase of R, the real eigenfrequencies of both modes decrease gradually. However, the imaginary eigenfrequencies of MMR I are around zero (shown in Figure 1D), which is much lower than those of MMR II, showing that performance of sound absorption for MMR II is much higher than that for MMR I.

Beyond that, we simulate both types of eigenmodes (MMR I’&II’) for the unit cell without outer frames (see Supplementary Material). It is worth noting that the real eigenfrequencies of MMR II’ are much larger than those of MMR II, but those of MMR I’ and MMR I are almost the same. Therefore, MMR II is closely related to the coupling between the multiple-cavity structure and outer frame, but MMR I is mainly created by Helmholtz resonances of each cavity in the multiple-cavity structure (see Supplementary Material). Based on the aforementioned results, we also demonstrate that the coupling of MMR II is much stronger than that of MMR I.

Performance and mechanism of open tunnel

Figure 2A shows the schematic of an open tunnel of sound absorption for the left incidence of sound, which is composed of a straight waveguide with a height h and two types of unit cells with different values of R. The distance between both unit cells is d, and the other parameters of the tunnel are h = 40 cm, R_I = 4.9 cm, R_II = 5.0 cm and d = 18.5 cm. Here, it is worth mentioning that the height ratio between the open tunnel and the resonator is about 4.0, which is much larger than those of the previously demonstrated absorber [48]. Beyond that, compared with other sound absorption structures in the open tunnel, the proposed Mie resonators have a smaller size. Figure 2B shows the absorption spectrum through the open tunnel. The absorption coefficient of sound is calculated as α = 1–R–T, in which R and T represent the acoustic reflectance and transmittance, respectively. We can see that, for the tunnel with both unit cells, three absorption peaks (denoted as A, B and C) can be observed, which corresponds to 249, 256, and 283 Hz, respectively. The absorption coefficient at the peak C can reach about 0.98, which is much larger than those at the peaks A and B. Therefore, the proposed open tunnel has a good practical applicability. Additionally, as shown in Figure 2C, the values of R and T through the tunnel with both unit cells are almost zero at the peak C, displaying a typical characteristic of near-perfect sound absorption in the open tunnel. To theoretically investigate the sound absorption performance at the peak C, we also calculate the relative impedance of the open tunnel by using an acoustic equivalent circuit, which is shown in Supplementary Material. We can see that, at the peak C (283 Hz), the real part of the relative impedance Z/Z₀ is close to 1, and its imaginary part is close to 0, further demonstrating the near-perfect sound absorption of the open tunnel.

FIGURE 2

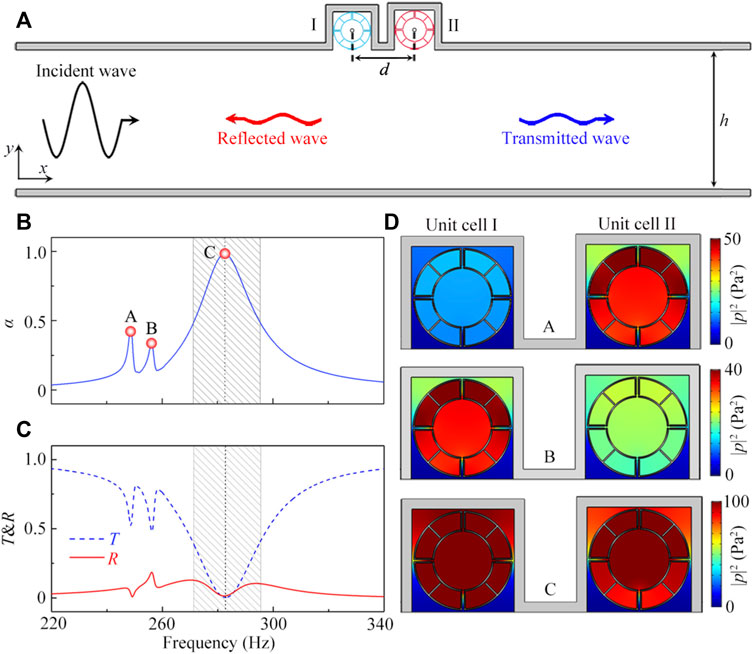
FIGURE 2. (A) Schematic of the open tunnel with the unit cells I and II, and the diameters of the unit cells I and II are R_I = 4.9 cm and R_II = 5.0 cm, respectively. (B) Simulated absorption spectra through the open tunnels. The frequencies of the peaks A, B and C in (B) are 249, 256 and 283 Hz, respectively. (C) Simulated transmittance and reflectance spectra through the tunnel with the unit cells I and II. (D) Simulated distributions of intensity field in both unit cells at 249, 256 and 283 Hz.

To investigate the mechanism of the three peaks, we simulate the distributions of intensity field in both unit cells created by the acoustic wave passing through the tunnel at three frequencies, which is shown in Figure 2D. We can see that, at the peaks A and B, the MMR of the unit cells II and I are excited, respectively, while those of both unit cells are obtained simultaneously at the peak C. Additionally, the frequencies of the peaks A and B are close to those of the MMR I for the unit cells II (249 Hz) and I (256 Hz), respectively, and the frequency of the peak C is between those of the MMR II of the unit cells II (282 Hz) and I (288 Hz). We therefore demonstrate that the absorption peaks A and B are created by the MMR I of the unit cells II and I, respectively, while the near-perfect sound absorption at the peak C is created by the coupling of the MMR II of both unit cells.

To verify this, we simulate the sound absorption spectra with different values of d, which is shown in Figure 3. We can see that, with the increase of d, the frequencies of both absorption peaks A and B remain unchanged, while the frequency of the peak C changes gradually. Thus, we further demonstrate that the peak C is created by the coupling of both unit cells I and II.

FIGURE 3

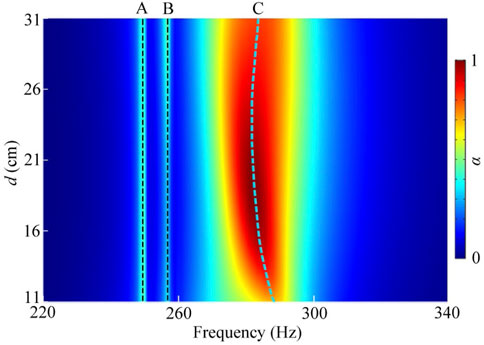
FIGURE 3. Simulated sound absorption spectra through the tunnel with different values of d. Dashed lines represent three absorption peaks A, B and C.

To further show the characteristic of near-perfect sound absorption at the peak C, we simulate the pressure amplitude distribution created by the acoustic wave passing through the tunnel, which is shown in Figure 4A. We can see from the sky blue arrows that almost all sound energy is absorbed into both unit cells, and MMR II of both unit cells are excited simultaneously. Meanwhile, there is almost no sound energy reaching the right side of the unit cell II, which is obviously shown in Figure 4B.

FIGURE 4

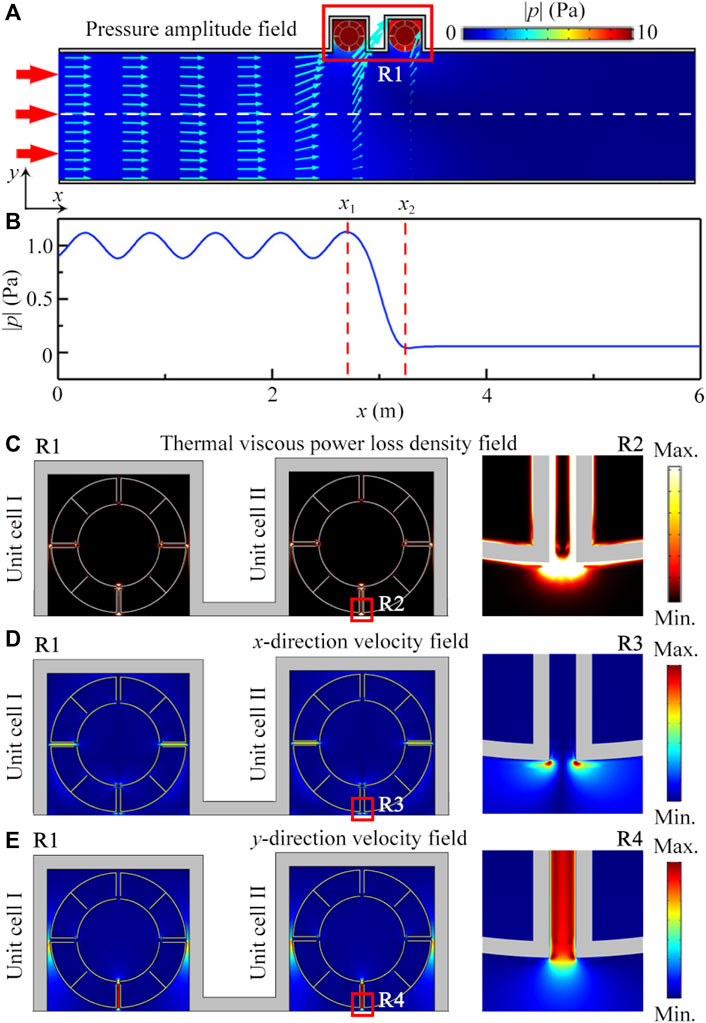
FIGURE 4. (A) Simulated pressure amplitude distribution created by the acoustic wave passing through the tunnel at 283 Hz. Red and sky blue arrows represent the directions of incident wave and propagating sound energy flux. (B) Simulated pressure amplitude distribution along the white dashed line in (A). x₁ and x₂ are the center positions of the unit cells I and II. (C) Simulated distributions of thermal viscous power density, (D) x-direction and (E) y-direction vibration velocity in R1 in (A). Zooms at the right side are the corresponding distributions in R2-R4.

Furthermore, we simulate the distributions of thermal viscous loss density in a red open rectangle R1 in Figure 4A, which is shown in Figure 4C. We can see that the viscous loss is mainly distributed on both sides and output port of the channels, especially the bottom three channels. This is because the viscous force is closely related to the vibration velocity gradient of sound, and so is the viscous loss. To demonstrate it, we present the corresponding vibration velocity of sound in x and y directions. We can see that, there exists a large velocity gradient in x direction at the output port (Figure 4D). For the case of the vibration velocity in y direction (Figure 4E), the value is large at the center, but is almost zero at the walls on both sides of the channel. Therefore, we deduce that the near-perfect sound absorption at the peak C is created by the thermal viscous loss of sound energy in the channels under the coupling of MMR II for both unit cells.

Beyond that, we also discuss the absorption performance through the open tunnel for the right incidence of sound, in which the parameters of the open tunnel remain constant. The simulated results show that the maximum absorption coefficient is only about 0.66, which is much smaller than that from the left incidence of sound (see Supplementary Material). Such a phenomenon arises from sound reflections created by the asymmetric design of both Mie resonators, and the proposed open tunnel of asymmetric sound absorption can be applied to exhaust pipes of cars with the need of unidirectional noise reduction. Additionally, we simulate the sound absorption through the open tunnel with a symmetric system of Mie resonators which is composed of a unit cell I and two unit cells II on both sides, and the maximum absorption coefficient is about 0.88, which is still lower than that in Figure 2B. The corresponding results are displayed in the Supplementary Material.

Bandwidth optimization of open tunnel

To optimize the bandwidth of sound absorption, we design another type of open tunnel by using 6 unit cells with different values of R, which is schematically shown in Figure 5A. The size of the open tunnel and the distance between adjacent unit cells are the same as those in Figure 2A, and the incident plane wave is still placed at the left port. Figure 5B shows the absorption spectra through the open tunnel around the peak C. It is found that, in the range 227–292 Hz (shaded region), the absorption coefficients of the open tunnel with 6 unit cells are larger than 0.5, and thus the fractional bandwidth can reach about 0.25. Beyond that, in the range 240–280 Hz, the absorption coefficient can exceed 0.9, and both coefficients R and T are close to zero (Figure 5C), showing the characteristic of broadband near-perfect sound absorption. Moreover, we can further broad the working bandwidth of the tunnel by increasing the number of the unit cells, and the fractional bandwidth can reach about 0.46 with 13 unit cells, which is shown in Supplementary Material.

FIGURE 5

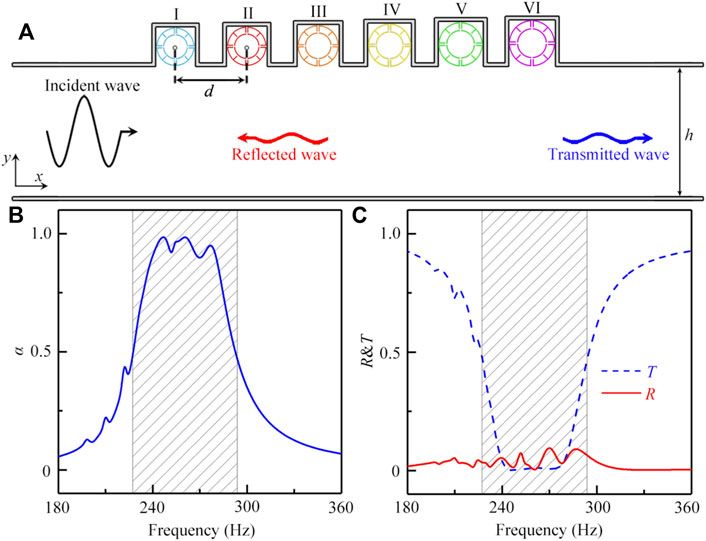
FIGURE 5. (A) Schematic of the open tunnel with 6 unit cells. The parameters t and w of the unit cells are fixed at 1.2 and 2.0 mm, and the diameters of the unit cells I-VI are R_I = 4.9 cm, R_II = 5.0 cm, R_III = 5.2 cm, R_IV = 5.4 cm, R_V = 5.6 cm and R_VI = 5.8 cm, respectively. (B) The absorption spectrum through the open tunnel with 6 unit cells. (C)Transmittance and reflectance spectra through the open tunnel with 6 unit cells.

Experimental demonstration

Finally, we experimentally demonstrate the near-perfect sound absorption of the two types of open tunnels, in which the detailed description of the experimental setup is shown in Supplementary Material. As shown in Figures 6A,B, the samples are placed at the left side of a planar waveguide composed of two parallel plexiglass plates (dimension 3.0 m × 0.4 m×3 cm), The height of sample is selected as 3 cm to match the height of the waveguide, in which the thicknesses of each unit cell and the cover plate on both sides are 2.7 and 0.15 cm, respectively. The other parameters of the unit cells in Figures 6A,B are the same as those in Figures 2A, 5A.

FIGURE 6

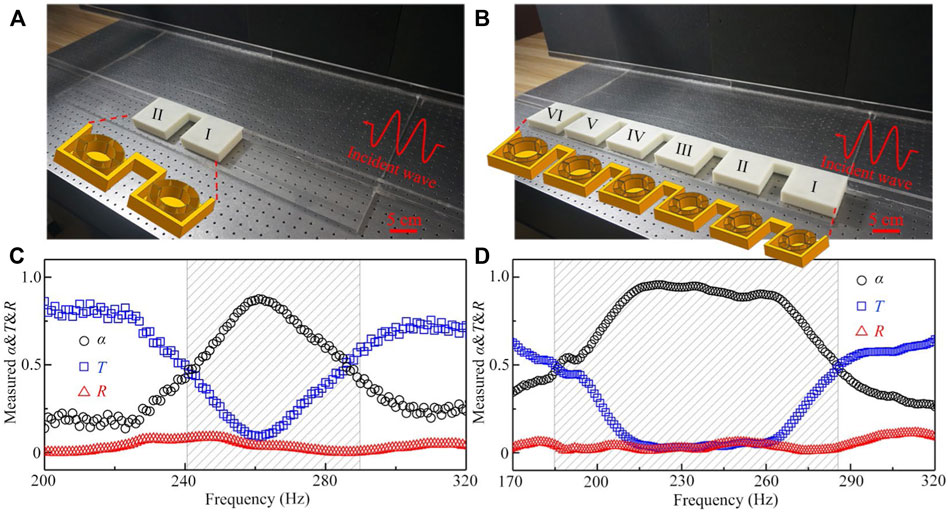
FIGURE 6. Photographs of the open tunnels with (A) 2 and (B) 6 unit cells in the experiment. Measured absorption, transmittance and reflectance spectra through the tunnels with (C) 2 and (D) 6 unit cells.

Figures 6C,D show the measured absorption, transmittance and reflectance spectra through the two types of tunnels. Note that both results show the typical characteristics of the near-perfect sound absorption. The measured maximum sound absorption coefficients in Figures 6C,D can reach about 0.88 and 0.96, respectively, while the measured transmittance and reflectance are close to zero around the absorption peaks. However, the measured frequency ranges of the near-perfect sound absorption are not consistent with the simulated results in Figures 2, 5. This is because the sound absorption is very sensitive to the structure parameters of each unit cell, and the measured parameters of the unit cells in both samples are different from those in the simulations due to the fabrication accuracy of 3D printing and the deformation of the unit cells with circular structure. The error analysis of experimental measurement is shown in Supplementary Material.

Conclusion

In conclusions, we have experimentally demonstrated an open tunnel of near-perfect sound absorption by using a type of deep sub-wavelength Mie resonator composed of a multiple-cavity structure and an outer frame on three sides. The results show that there exist two types of MMR modes in a single resonator around 250 Hz. The eigenfrequencies of MMR I and II are mainly determined by the Helmholtz resonance of each cavity in the multiple-cavity structure and the coupling between the multiple-cavity structure and its outer frame, respectively. By combining the two Mie resonators with R_I = 4.9 cm and R_II = 5.0 cm, we can observe the near-perfect sound absorption through the open tunnel at 283 Hz, which arises from the thermal viscous loss of sound energy in the channels created by the mutual coupling of MMR II of both Mie resonators. Moreover, by increasing the number of Mie resonators in the tunnel, the broadband near-perfect sound absorption is realized, and the fractional bandwidths can reach about 0.25 and 0.46 for the cases of 6 and 13 resonators, respectively. Finally, we experimentally demonstrate the near-perfect sound absorption through the two types of tunnels with 2 and 6 Mie resonators, in which the measured results agree with the simulated ones. The proposed Mie resonator has the advantages of deep sub-wavelength size (L/λ ∼ 0.085) and high coupling performance, which has certain application prospect in the fields of architectural acoustics and mechanical engineering. It also advanced the deep sub-wavelength coupling resonance with versatile applications in sound communication, bio-sensing, and noise reduction.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding authors.

Author contributions

J-PX, Y-YS, and Y-JG contributed equally to this work. All authors contributed to the article and approved the submitted version.

Funding

This work was supported by National Natural Science Foundation of China (Grant Nos. 12174159, 12274183, 11834008, 11974176, and 12174188), the National Key Research and Development Program of China (Grant No. 2020YFC1512403).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2022.1047892/full#supplementary-material

References

1. Liu Z, Zhang X, Mao Y, Zhu YY, Yang Z, Chan CT, et al. Locally resonant sonic materials. Science (2000) 289:1734–6. doi:10.1126/science.289.5485.1734

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Lai Y, Wu Y, Sheng P, Zhang ZQ. Hybrid elastic solids. Nat Mater (2011) 10:620–4. doi:10.1038/nmat3043

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Christensen J, Javier García de Abajo F. Anisotropic metamaterials for full control of acoustic waves. Phys Rev Lett (2012) 108:124301. doi:10.1103/PhysRevLett.108.124301

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Liang Z, Li J. Extreme acoustic metamaterial by coiling up space. Phys Rev Lett (2012) 108:114301. doi:10.1103/PhysRevLett.108.114301

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Cheng Y, Zhou C, Yuan BG, Wu DJ, Wei Q, Liu XJ. Ultra-sparse metasurface for high reflection of low-frequency sound based on artificial Mie resonances. Nat Mater (2015) 14:1013–9. doi:10.1038/NMAT4393

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Cummer SA, Christensen J, Alù A. Controlling sound with acoustic metamaterials. Nat Rev Mater (2016) 1:16001. doi:10.1038/natrevmats.2016.1

CrossRef Full Text | Google Scholar

7. Xie BY, Tang K, Cheng H, Liu ZY, Chen SQ, Tian JG. Metasurfaces: Coding acoustic metasurfaces. Adv Mater (2017) 29:1603507. doi:10.1002/adma.201603507

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Bai L, Dong HY, Song GY, Cheng Q, Huang B, Jiang WX, et al. Impedance-matching wavefront-transformation lens based on acoustic metamaterials. Adv Mater Technol (2018) 3:1800064. doi:10.1002/admt.201800064

CrossRef Full Text | Google Scholar

9. Tian ZH, Shen C, Li JF, Reit E, Gu YY, Fu H, et al. Programmable acoustic metasurfaces. Adv Funct Mater (2019) 29:2006376. doi:10.1002/adfm.202006376

CrossRef Full Text | Google Scholar

10. Quan L, Sounas DL, Alu A. Nonreciprocal willis coupling in zero-index moving media. Phys Rev Lett (2019) 123:064301. doi:10.1103/PhysRevLett.123.064301

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Nikkhah MR, Hiranandani M, Kishk A. Rotman lens design with wideband DRA array. Prog Electromagn Res (2020) 169:45–57. doi:10.2528/PIER20050801

CrossRef Full Text | Google Scholar

12. Kumar S, Lee HP. Labyrinthine acoustic metastructures enabling broadband sound absorption and ventilation. Appl Phys Lett (2020) 116:134103. doi:10.1063/5.0004520

CrossRef Full Text | Google Scholar

13. Allen KW, Dykes DJP, Reid DR, Lee RT. Multi-objective genetic algorithm optimization of frequency selective metasurfaces to engineer ku-passband filter responses. Prog Electromagn Res (2020) 167:19–30. doi:10.2528/PIER19112609

CrossRef Full Text | Google Scholar

14. Zhu YF, Merkel A, Donda K, Fan SW, Cao LY, Assouar B. Nonlocal acoustic metasurface for ultrabroadband sound absorption. Phys Rev B (2021) 103:064102. doi:10.1103/PhysRevB.103.064102

CrossRef Full Text | Google Scholar

15. Jia D, Wang Y, Ge Y, Yuan SQ, Sun HX. Tunable topological refractions in valley sonic crystals with triple valley hall phase transitions. Prog Electromagn Res (2021) 172:13–22. doi:10.2528/PIER21102002

CrossRef Full Text | Google Scholar

16. Shen L, Zhu YF, Mao FL, Gao SY, Su ZH, Luo ZT, et al. Broadband low-frequency acoustic metamuffler. Phys Rev Appl (2021) 16:064057. doi:10.1103/PhysRevApplied.16.064057

CrossRef Full Text | Google Scholar

17. Gao NS, Zhang ZC, Deng J, Guo XY, Cheng BZ, Hou H. Acoustic metamaterials for noise reduction: A review. Adv Mater Technol (2022) 7:2100698. doi:10.1002/admt.202100698

CrossRef Full Text | Google Scholar

18. Yan QH, Chen HS, Yang YH. Non-hermitian skin effect and delocalized edge states in photonic crystals with anomalous parity-time symmetry. Prog Electromagn Res (2021) 172:33–40. doi:10.2528/PIER21111602

CrossRef Full Text | Google Scholar

19. Zhou ZL, Huang SB, Li DT, Zhu J, Li Y. Broadband impedance modulation via non-local acoustic metamaterials. Natl Sci Rev (2022) 9:nwab171. doi:10.1093/nsr/nwab171

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Liu L, Xie LX, Huang WC, Zhang XJ, Lu MH, Chen YF. Broadband acoustic absorbing metamaterial via deep learning approach. Appl Phys Lett (2022) 120:251701. doi:10.1063/5.0097696

CrossRef Full Text | Google Scholar

21. Quan L, Zhong X, Liu XZ, Gong XF, Johnson PA. Effective impedance boundary optimization and its contribution to dipole radiation and radiation pattern control. Nat Commun (2014) 5:3188. doi:10.1038/ncomms4188

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Li JF, Wang WQ, Xie YB, Popa BI, Cummer SA. A sound absorbing metasurface with coupled resonators. Appl Phys Lett (2016) 109:091908. doi:10.1063/1.4961671

CrossRef Full Text | Google Scholar

23. Romero-Garcia V, Theocharis G, Richoux O, Merkel A, Tournat V, Pagneux V. Perfect and broadband acoustic absorption by critically coupled sub-wavelength resonators. Sci Rep (2016) 6:19519. doi:10.1038/srep19519

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Jimenez N, Huang W, Romero-Garcia V, Pagneux V, Groby JP. Ultra-thin metamaterial for perfect and quasi-omnidirectional sound absorption. Appl Phys Lett (2016) 109:121902. doi:10.1063/1.4962328

CrossRef Full Text | Google Scholar

25. Cheng Y, Jin YB, Zhou YK, Hao T, Li Y. Distinction of acoustically induced transparency and autler-townes splitting by Helmholtz resonators. Phys Rev Appl (2019) 12(4):044025. doi:10.1103/PhysRevApplied.12.044025

CrossRef Full Text | Google Scholar

26. Gu TY, Cheng Y, Wen ZH, Boudouti EHE, Jin YB, Li Y, et al. Induced transparency based subwavelength acoustic demultiplexers. J Phys D Appl Phys (2021) 54(17):175301. doi:10.1088/1361-6463/abe07c

CrossRef Full Text | Google Scholar

27. Zhang C, Hu X. Three-dimensional single-port labyrinthine acoustic metamaterial: Perfect absorption with large bandwidth and tunability. Phys Rev Appl (2016) 6:064025. doi:10.1103/PhysRevApplied.6.064025

CrossRef Full Text | Google Scholar

28. Jimenez N, Romero-Garcia V, Pagneux V, Groby JP. Rainbow-trapping absorbers: Broadband, perfect and asymmetric sound absorption by subwavelength panels for transmission problems. Sci Rep (2017) 7:13595. doi:10.1038/s41598-017-13706-4

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Yang M, Chen SY, Fuab CX, Sheng P. Optimal sound-absorbing structures. Mater Horiz (2017) 4:673–80. doi:10.1039/c7mh00129k

CrossRef Full Text | Google Scholar

30. Mei J, Ma GC, Yang M, Yang ZY, Wen WJ, Sheng P. Dark acoustic metamaterials as super absorbers for low-frequency sound. Nat Commun (2012) 3:756. doi:10.1038/ncomms1758

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Ma GC, Yang M, Xiao SW, Yang ZY, Sheng P. Acoustic metasurface with hybrid resonances. Nat Mater (2014) 13:873–8. doi:10.1038/NMAT3994

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Yang M, Meng C, Fu CX, Li Y, Yang ZY, Sheng P. Subwavelength total acoustic absorption with degenerate resonators. Appl Phys Lett (2015) 107:104104. doi:10.1063/1.4930944

CrossRef Full Text | Google Scholar

33. Yang M, Li Y, Meng C, Fu CX, Mei J, Yang ZY, et al. Sound absorption by subwavelength membrane structures: A geometric perspective. Comptes Rendus Mecanique (2015) 343:635–44. doi:10.1016/j.crme.2015.06.008

CrossRef Full Text | Google Scholar

34. Cai XB, Guo QQ, Hu GK, Yang J. Ultrathin low-frequency sound absorbing panels based on coplanar spiral tubes or coplanar Helmholtz resonators. Appl Phys Lett (2014) 105:121901. doi:10.1063/1.4895617

CrossRef Full Text | Google Scholar

35. Li Y., Assouar B. Acoustic metasurface-based perfect absorber with deep subwavelength thickness Appl. Phys Lett. (2016) 108: 063502. doi:10.1063/1.4941338

CrossRef Full Text | Google Scholar

36. Donda K, Zhu YF, Fan SW, Cao LY, Li Y, Assouar B. Extreme low-frequency ultrathin acoustic absorbing metasurface. Appl Phys Lett (2019) 115:173506. doi:10.1063/1.5122704

CrossRef Full Text | Google Scholar

37. Wu XX, Fu CX, Li X, Meng Y, Gao YB, Tian JX, et al. Low-frequency tunable acoustic absorber based on split tube resonators. Appl Phys Lett (2016) 109:043501. doi:10.1063/1.4959959

CrossRef Full Text | Google Scholar

38. Long HY, Cheng Y, Tao JC, Liu XJ. Perfect absorption of low-frequency sound waves by critically coupled subwavelength resonant system. Appl Phys Lett (2017) 110:023502. doi:10.1063/1.4973925

CrossRef Full Text | Google Scholar

39. Xu ZX, Meng HY, Chen A, Yang J, Liang B, Cheng JC. Tunable low-frequency and broadband acoustic metamaterial absorber. J Appl Phys (2021) 129:094502. doi:10.1063/5.0038940

CrossRef Full Text | Google Scholar

40. Long HY, Gao SX, Cheng Y, Liu XJ. Multiband quasi-perfect low-frequency sound absorber based on double-channel Mie resonator. Appl Phys Lett (2018) 112:033507. doi:10.1063/1.5013225

CrossRef Full Text | Google Scholar

41. Sun YY, Xia JP, Sun HX, Yuan SQ, Ge Y, Liu XJ. Dual-band fano resonance of low-frequency sound based on artificial Mie resonances. Adv Sci (Weinh) (2019) 6:1901307. doi:10.1002/advs.201901307

PubMed Abstract | CrossRef Full Text | Google Scholar

42. Wei PJ, Croenne C, Chu ST, Li JS. Symmetrical and anti-symmetrical coherent perfect absorption for acoustic waves. Appl Phys Lett (2014) 104:121902. doi:10.1063/1.4869462

CrossRef Full Text | Google Scholar

43. Meng C, Zhang XN, Tang ST, Yang M, Yang ZY. Acoustic coherent perfect absorbers as sensitive null detectors. Sci Rep (2017) 7:43574. doi:10.1038/srep43574

PubMed Abstract | CrossRef Full Text | Google Scholar

44. Ghaffarivardavagh R, Nikolajczyk J, Anderson S, Zhang X. Ultra-open acoustic metamaterial silencer based on fano-like interference. Phys Rev B (2019) 99:024302. doi:10.1103/PhysRevB.99.024302

CrossRef Full Text | Google Scholar

45. Dong RZ, Mao DX, Wang X, Li Y. Ultrabroadband Acoustic ventilation barriers via hybrid-functional metasurfaces. Phys Rev Appl (2021) 15:024044. doi:10.1103/PhysRevApplied.15.024044

CrossRef Full Text | Google Scholar

46. Long HY, Cheng Y, Zhang T, Liu XJ. Wide-angle asymmetric acoustic absorber based on one-dimensional lossy Bragg stacks. J Acoust Soc Am (2017) 142:EL69–EL74. doi:10.1121/1.4991677

PubMed Abstract | CrossRef Full Text | Google Scholar

47. Fu CX, Zhang XN, Yang M, Xiao SW, Yang Z. Hybrid membrane resonators for multiple frequency asymmetric absorption and reflection in large waveguide. Appl Phys Lett (2017) 110:021901. doi:10.1063/1.4973821

CrossRef Full Text | Google Scholar

48. Long HY, Cheng Y, Liu XJ. Asymmetric absorber with multiband and broadband for low-frequency sound. Appl Phys Lett (2017) 111:143502. doi:10.1063/1.4998516

CrossRef Full Text | Google Scholar

49. Zhang T, Bok E, Tomoda M, Matsuda O, Guo JZ, Liu XJ, et al. Compact acoustic metamaterial based on the 3D Mie resonance of a maze ball with an octahedral structure. Appl Phys Lett (2022) 120:161701. doi:10.1063/5.0084030

CrossRef Full Text | Google Scholar