Andreev reflection mediated by Majorana zero modes in T-shaped double quantum dots

We theoretically study the Andreev reflection processes in T-shaped double quantum dots (TDQDs) in terms of the nonequilibrium Green’s function technique. It is considered that one of the TDQDs is coupled to the Majorana zero modes (MZMs) prepared at the ends of a topological superconductor nanowire and simultaneously to one metallic and one superconductor lead. Our numerical results show that the in-gap state originated from the proximity effect due to the superconductor lead being sensitive to the existence of MZMs. The local density of states (LDOS) of the spin-up electrons, which are directly coupled to the MZMs, has a Fano antiresonance at the in-gap state. Meanwhile, the local density of the spin-down electrons, which are free from hybridization to the MZMs due to the helical property of the latter, has a Lorentzian resonance at the same state. The differential Andreev conductance of both the spin directions exhibits Fano-type resonance but with different tails’ directions. The in-gap state is also significantly influenced by the energy level and coupling strength of the other side-coupled dot, as well as the MZM–MZM interaction.

1 Introduction

Recent developments in nano-fabrication techniques have enabled the implementation of hybrid devices composed of different materials, such as semiconductor quantum dots (QDs) and metallic or superconductor leads [1–5]. The most important aspect of interest in such a system is the construction of quantum bits relying on the Andreev bound states [6, 7], which are superpositions of the QDs’ energy levels and Bogoliubov states in the superconductor leads. In some earlier work, systems with one or multiple QDs connected to one metallic and one superconductor lead were intensively studied, taking the electron–electron interaction that is responsible for the Coulomb blockade and Kondo effects into consideration [3, 8–10]. In macroscopic structures, it is known that the Coulomb interaction between electrons will suppress local pairing and then enhance intersite superconductivity through mechanisms such as spin-exchange processes. However, the relationship between the Coulomb interaction and local pairing is quite difficult to be uncovered, either theoretically or experimentally. Fortunately, this limitation can be overcome in nanoscale structures by varying the isolated energy levels or interaction strength between electrons. These will change the charge transport and result in a controllable adjustment of the Kondo effect and the opposite case determined by the electron pairing on the QDs. There was also some work concerning joint influences of the quantum interference and proximity effect on electronic transport in multiple QDs, such as T-shaped double quantum dots (TDQDs) sandwiched between one conducting and one superconducting lead [9, 11–13]. It was found that in the subgap regime, i.e., when the external bias voltage is smaller than the energy gap of the superconductor lead [9, 10], the electron transfer is determined by the anomalous Andreev reflections when an electron entering into the dot from the metallic lead is converted into the Cooper pair accompanied by the simultaneous reflection of a hole back to the metallic lead. The transmittance of this Andreev reflection is promising in detecting on-dot pairing induced by the proximity effect and the quantum interference, as well as the Coulomb blockade or Kondo effects. In the presence of on-dot pairing due to the superconductor lead, the quantum interference processes are doubled as compared to similar structures without the superconductor lead. In particular, for TDQD systems, the side-coupled QD induces resonance or antiresonance at particular dot levels controllable by the gate voltage. As a result of it, the Fano effect emerges on the condition that the coupling strength between the two dots is much weaker than that between the dot and the metallic lead [9]. With increasing inter-dot coupling strength, the Fano-type resonance disappears and finally evolves into the Lorentzian resonance due to spreading out of the on-dot pairing from the central dot to the side-coupled dot.

Recent theoretical and experimental works have proved that Majorana zero modes (MZMs) may emerge as exotic quasiparticles at opposite ends of one-dimensional topological superconductors. The MZMs were first predicted in the Kitaev chain of the p-wave superconductor as the degenerate ground state obeying non-Abelian statistics [14, 15]. They are protected by the topological gap and are robust against local perturbations, which makes them promising in fault-tolerant quantum computation [15–17]. Since the spinless Kitaev chain and p-wave superconductor are rare in nature, various theoretical and experimental schemes were then subsequently proposed, such as the hybridized one-dimensional semiconductor–superconductor nanowire under a large enough magnetic field, which is usually called a Majorana nanowire [2, 18]. A p-wave superconductor is realized from the s-wave superconductor due to the proximity effect, given that the semiconductor nanowire has a strong Rashba-type spin-orbit coupling. Unlike the MZMs in the Kitaev chain, others prepared at the ends of the Majorana wire are spinful and may interact with electrons of both the spin directions. To detect the MZMs invasively, researchers also proposed to couple the MZMs to QDs sandwiched between metallic leads [18, 19]. Some interesting phenomena were then found, such as half of the quantum value of the electron conductance [19] and sign reversion of the thermopower [20–22]. There were also some works concerning MZMs hybridized to QDs with metallic and superconductor leads [23–25]. It was found that in the absence of the intradot Coulomb interaction, there is destructive (constructive) interference for spin-up (spin-down) electrons at the in-gap states. Such an interference effect, combined with the MZMs, exerts significant influence on the transport processes and can be inferred from the local density of states (LDOS) of the QDs and the in-gap Andreev conductance.

In the present article, we study transport through TDQDs side-coupled to the Majorana nanowire having one metallic and one superconductor lead. We concentrate on the influences of the MZMs on the LDOS and Andreev differential conductance within the in-gap regime. Our numerical results show that the LDOS of the spin-up electrons which are directly coupled to the MZMs have an asymmetrical Fano line shape. However, the spin-down electrons that are not directly hybridized to the MZMs have a Lorentzian line shape at the same state. Both spin-up and spin-down differential Andreev conductances have Fano-type resonance at the in-gap state but with different directions of the tails in the line shape. The direct hybridization between the MZMs and side-coupled dots will significantly change the Fano effect.

2 Model and methods

The system is composed of TDQDs connected to one metallic and one superconductor lead, and a nanowire hosting MZMs can be modeled by the following Hamiltonian[9, 10, 19]:

$H=H_{\mathit{TDQD}}+H_N+H_S+H_T+H_{\mathit{MZMs}},(1)$

in which the Hamiltonian for the TDQDs in the absence of the intradot Coulomb interaction is $H_{\mathit{TDQD}}={\sum }_{i,\sigma }{\epsilon }_{di}{d}_{i\sigma }^{†}{d}_{i\sigma }+(t_c{d}_{1\sigma }^{†}{d}_{2\sigma }+H.c)$. The creation (annihilation) operator $d_{i\sigma }^{†}(d_{i\sigma })$ is for an electron with the energy level ɛ_di (i = 1, 2 individually for the central and side-coupled dots) and spin-σ with t_c the coupling strength between electrons on different dots. The Hamiltonian $H_N={\sum }_{k\sigma }{\epsilon }_{kN}{c}_{kN\sigma }^{†}{c}_{kN\sigma }$ is for the normal metallic lead coupled to the central dot with $c_{kN\sigma }^{†}(c_{kN\sigma })$ creating (annihilating) an electron of momentum k and energy ɛ_kN. The superconductor lead is represented by $H_S={\sum }_{k\sigma }{\epsilon }_{kS}{c}_{kS\sigma }^{†}{c}_{kS\sigma }+{\sum }_k(\mathrm{\Delta }{c}_{kS\uparrow }^{†}{c}_{-kS\downarrow }^{†}+{\mathrm{\Delta }}^{*}{c}_{-kS\downarrow }{c}_{kS\uparrow })$ with the isotropic energy gap Δ. In the present work, we focus our attention on the deep subgap regime |ɛ|≪Δ, and then, the Hamiltonian of the superconductor lead is replaced by the creation and annihilation of Cooper pairs [9, 10].

$H_{\mathit{Cooper}}={\mathrm{\Gamma }}_S\left(d_{1\uparrow }^{†}{d}_{1\downarrow }^{†}+d_{1\downarrow }{d}_{1\uparrow }\right),(2)$

where Γ_S = ∑_k|V_kS|²δ(ɛ − ɛ_kS) denotes the line-width function of the central dot and the superconductor lead with V_kS the electron’s tunneling amplitude contained in the Hamiltonian for tunneling between the central dot and the leads $H_T={\sum }_{k\sigma ,\beta =N,S}(V_{k\beta }{c}_{k\beta \sigma }^{†}{d}_{1\sigma }+H.c)$. The replacement of the complex function of the superconductors by a constant line-width function is called the atomic superconducting limit, which can be seen in [9]. The last term in Eq. 1 represents the MZMs at the ends of the nanowire coupled to the central dot and is given by [19]

$H_{\mathit{MZMs}}=i{\delta }_M{\eta }_1{\eta }_2+\sum \lambda \left(d_{1\uparrow }-d_{1\uparrow }^{†}\right){\eta }_1,(3)$

in which δ_M is the interaction strength between the MZMs with operators satisfying ${\eta }_j={\eta }_j^{†}(j=\mathrm{1,2})$ and {η_i, η_j} = δ_i,j. λ is for hybridization between the MZM and the spin-up electrons on the central dot. Here, we calculate the physical quantities related to transport processes, such as the LDOS and the Andreev differential conductance, with the help of the nonequilibrium Green’s function technique. By using the equation of the motion technique and Dyson’s equation method, Green’s function is obtained in the following form [9, 19, 26]:

${\mathbf{G}}^{r-1}=\left(\begin{array}{cccccc}\hfill g_{1,\uparrow }^{r-1}+i{\mathrm{\Gamma }}_N/2\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill -{\mathrm{\Gamma }}_S/2\hfill & \hfill -\lambda \hfill & \hfill -\lambda \hfill \\ \hfill 0\hfill & \hfill {\tilde{g}}_{1,\uparrow }^{r-1}+i{\mathrm{\Gamma }}_N/2\hfill & \hfill {\mathrm{\Gamma }}_S/2\hfill & \hfill 0\hfill & \hfill \lambda \hfill & \hfill \lambda \hfill \\ \hfill 0\hfill & \hfill {\mathrm{\Gamma }}_S/2\hfill & \hfill g_{1,\downarrow }^{r-1}+i{\mathrm{\Gamma }}_N/2\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill -{\mathrm{\Gamma }}_S/2\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill {\tilde{g}}_{1,\downarrow }^{r-1}+i{\mathrm{\Gamma }}_N/2\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill -\lambda \hfill & \hfill \lambda \hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill g_M^{r-1}\hfill & \hfill 0\hfill \\ \hfill -\lambda \hfill & \hfill \lambda \hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill {\tilde{g}}_M^{r-1}\hfill \end{array}\right),(4)$

where Green’s function of electrons on the TDQDs free from the interaction between the leads and the MZMs is given by $g_{1,\sigma }^r=1/[\epsilon -{\epsilon }_{d1}+t_c^2/(\epsilon -{\epsilon }_{d2})]$ and that of the hole is ${\tilde{g}}_{1,\sigma }^r=1/[\epsilon +{\epsilon }_{d1}+t_c^2/(\epsilon +{\epsilon }_{d2})]$. Similarly, the electron and hole Green’s function of the MZMs are individually given by $g_M^r=1/(\epsilon -{\delta }_M)$ and ${\tilde{g}}_M^r=1/(\epsilon +{\delta }_M)$. The LDOS is thus obtained by ρ_↑(↓) = −(1/π)ImG₁₁₍₃₃₎(ɛ)^r, and the Andreev differential conductance at zero temperature is $G_{A\uparrow (\downarrow )}={\mathrm{\Gamma }}_N^2|G_{23(14)}{(\epsilon )}^r{|}^2$ [9].

3 Results and discussion

In this section, we present numerical results by choosing the coupling strength between the central dot and the metallic lead Γ_N ≡ 1 as an energy unit with fixed Γ_S = 4Γ_N. Such a choice of the line-width functions enables the transport processes through the system to be dominated by on-dot pairing arising from the interaction between the dot and the superconductor lead [9, 10]. Otherwise, for Γ_S ≪Γ_N, the electronic states are determined by the Kondo effect arising from the Coulomb repulsion between the spin-up and spin-down electrons, which is neglected in the present paper. Figure 1 presents the spin-dependent LDOS as a function of electron energy ɛ for different values of dot-MZM coupling strength λ. For λ = 0, the spin-up LDOS in Figure 1A shows the typical four-peak structure. The peaks formed at the effective quasiparticle states $\epsilon =\pm \sqrt{{\epsilon }_{d1}^2+{({\mathrm{\Gamma }}_S/2)}^2}$ originate from the on-dot pairing by the proximity effect of the superconductor lead. The width of the two peaks is determined by the value of Γ_N, whereas their distance in energy is Γ_S, which also indicates the particle-hole splitting of the quasiparticle states [9]. For the present chosen parameters (ɛ_d1 = 0), the two states (corresponding peaks in the LDOS) are exactly at ɛ = ±Γ_N/2. The other pair of peaks emerge at ɛ = ±ɛ_d2 due to the quantum interference effect resulting from the side-coupled dot. These two peaks correspond to the Fano resonance at −ɛ_d2 and antiresonance at +ɛ_d2, respectively. It is worth noting that if the central dot is coupled to two metallic leads, there is just one Fano structure located at ɛ_d2, which can be found in some previous works [27].

FIGURE 1

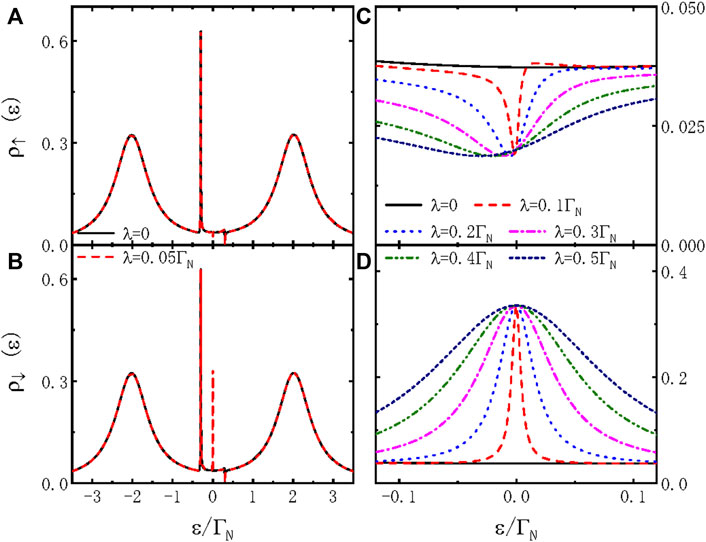
FIGURE 1. (Color online) Spin-dependent LDOS ρ_σ varying with respect to the electron energy ɛ for different values of dot-MZM hybridization strength λ. The tunneling strength between the central dot and the side-coupled dot is fixed as t_c = 0.2Γ_N. The energy levels of the two dots are ɛ_d1 = 0 and ɛ_d2 = 0.3Γ_N, respectively. Direct hybridization between the MZMs is ɛ_M = 0.

Turning on the coupling between the spin-up electrons on the central dot and one mode of the MZMs formed at the ends of the nanowire (λ ≠ 0), a dip (peak) emerges in the spin-up (spin-down) LDOS when the electrons’ energy ɛ is aligned to the Fermi energy in the normal metallic lead μ = 0 (see the red lines in Figures 1A,B). Such a result is the consequence of the combined effect of MZMs and the on-dot pairing due to the superconductor lead. There are two new features in the present TDQDs with one metallic and one superconductor lead as compared to the case of the TDQDs coupled to two normal metallic leads. First, the zero-energy LDOS develops a dip other than a peak that occurred in the latter case. This is due to the combined effects of the quantum interference from the side-coupled dot and on-dot pairing from the superconductor lead. Second, if the spin-down electrons are decoupled from the MZMs, a resonant peak emerges at ɛ = 0 for nonzero λ. The interaction between the spin-up and spin-down electrons can be understood by examining the off-diagonal elements of the self-energy. If the central dot is coupled to both metallic leads, the spin-down electrons will not be influenced by the MZMs, and the LDOS is solely determined by the quantum interference effect due to the side-coupled dot. The present result is interesting for both detecting the existence of the MZMs and distinguishing electrons of the different spin components, provided there is hybridization between the central dot and the MZMs. As was mentioned previously, searching for the detection scheme for the MZMs is still an important issue in current condensed matter physics. The phenomenon found here may provide a new feasible way for the aforementioned task. With increasing λ, the widths of the dip (peak) in spin-up (spin-down) LDOS become wider with a fixed value of ρ_↑(↓)(ɛ = 0). Meanwhile, the spin-up and spin-down LDOS remain in the asymmetrical Fano-type and Lorentzian line shape, respectively.

Combined functions of the MZMs, quantum interference, and proximity effect can also be studied by measuring the tunneling current through the system. In Figure 2 we show the dependence of the differential Andreev conductance G_Aσ(V) = dI_Aσ/dV at zero temperature on the bias voltage V. Only a relative narrow bias regime covering the in-gap quasiparticle peak is presented. The quasiparticle peaks at $eV=\pm \sqrt{{\epsilon }_{d1}^2+{({\mathrm{\Gamma }}_S/2)}^2}$ are similar to those in Figure 1 and then are neglected. For λ = 0, the Andreev differential conductance of the two spin components is the same, and they have a pair of Fano-type resonance at eV = ±ɛ_d2 but with different directions of the tail [9]. For this simple case, the Andreev differential conductance can be expressed as G_Aσ = G_0σ(x + q)²/(x² + 1) + G_1σ, where x = |eV + ɛ_d2| and q are the asymmetric factors depending on the choice of t_c. With increasing t_c, the value of q is decreased, and the Fano line shape evolves into a Lorentzian line shape. Therefore, here, we choose a relatively small t_c = 0.2Γ_N to show the Fano effect. In the presence of MZMs (λ ≠ 0), the Fano resonance in spin-up (spin-down) Andreev differential conductance at positive (negative) bias voltage is drastically changed, whereas that at a negative (positive) bias regime remains almost unchanged. For a sufficiently large value of λ, the directions of the tails in spin-up and spin-down conductances are interchanged. This phenomenon provides an efficient means to detect the existence of the MZMs and is also important in spintronics devices. Moreover, a zero-bias abnormal Fano-type dip emerges at both spin-up and spin-down Andreev differential conductance but with different directions of the tail in the Fano line shape. With increasing λ, the positions of the Fano resonance and antiresonance are interchanged, and then, the directions of the tails in the line shape are reversed, accordingly. This interesting result is fundamentally different from that in the system of QDs coupled to two normal metal leads, in which a zero-bias anomaly (ZBA) in the conductance peak is brought about by the interaction between the QDs and the MZMs [18, 19]. This ZBA is a reliable evidence of the existence of the MZMs. However, in the present system of the QDs coupled to one metallic and one superconductor lead, the ZBA evolves into a zero-bias abnormal dip due to the pairing state by the superconductor lead. If the MZMs are replaced by regular fermions, such as another QD, the structure then becomes triple QDs coupled to two leads, which has been studied before. Then, there will be newly emerged Fano peaks in the LDOS and the differential conductance, whose positions are determined by the coupling strengths between the dots and their energy levels. In the present structure, however, the MZMs mainly influence the properties of the structure around the zero-energy point. This is determined by the exotic zero-energy property of the MZMs.

FIGURE 2

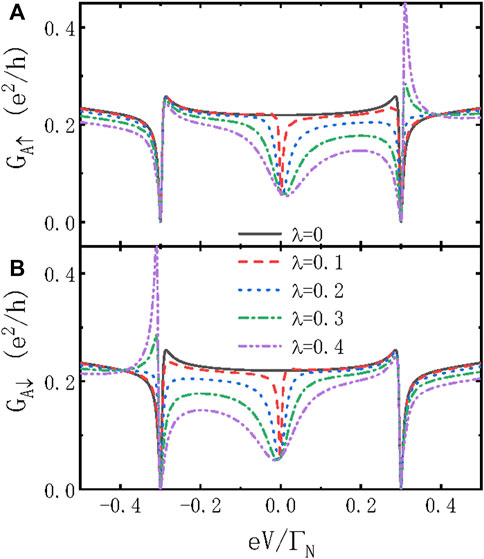
FIGURE 2. (Color online) Spin-resolved Andreev differential conductance G_Aσ as a function of the bias voltage eV for the same parameters adopted in Figure 1.

In Figure 3, we present the impacts of the interdot coupling t_c and dot level ɛ_d2 on the LDOS. Figure 3A shows that the spin-up LDOS has a Lorentzian-type dip when the electron energy ɛ is aligned to the dot level ɛ_d1 = 0 for a small value of t_c = 0.05Γ_N (the solid line). The spin-down LDOS in Figure 3B, however, has a Lorentzian-type peak at ɛ = 0. With increasing t_c, the quantum interference effect brought about by the additional dot is strengthened, and thus, the spin-up LDOS in Figure 3A shows the Fano line shape. The spin-down LDOS remains in the Lorentzian line shape with a lower peak height. Figures 3C,D show that the LDOS of both the spin-up and spin-down electrons has a symmetrical double-peak configuration, with ρ_σ(0) ≡ 0 for ɛ_d2 = 0. For non-zero ɛ_d2, a Fano (Lorentzian)-type resonance emerges in the zero-energy spin-up (spin-down) LDOS due to the quantum interference effect. These results are consistent with those in Figures 3A,B. It should be noted that the MZMs are quasiparticles of Majorana fermions, which are characterized by the zero-energy property. Therefore, the MZMs will induce a sharp peak in the spectral function located at the zero-energy level or the zero-bias peak in electrical conductance, which are the most reliable signatures of the existence of MZMs for far. Apart from the zero-energy state, there are no distinct peaks or valleys in spectral function, and then, these states are relatively less important as compared to the zero-energy state. In the presence of the Coulomb repulsive interaction between electrons on the QD, there are two energy states without the external magnetic field. One is at the Fermi level (which is usually at zero-energy), and the other is aligned to the Fermi energy plus the strength Coulomb interaction. As was discussed previously, the state concerning the Coulomb interaction is less influenced by the MZMs, and then, we neglect the Coulomb interaction in the QDs.

FIGURE 3

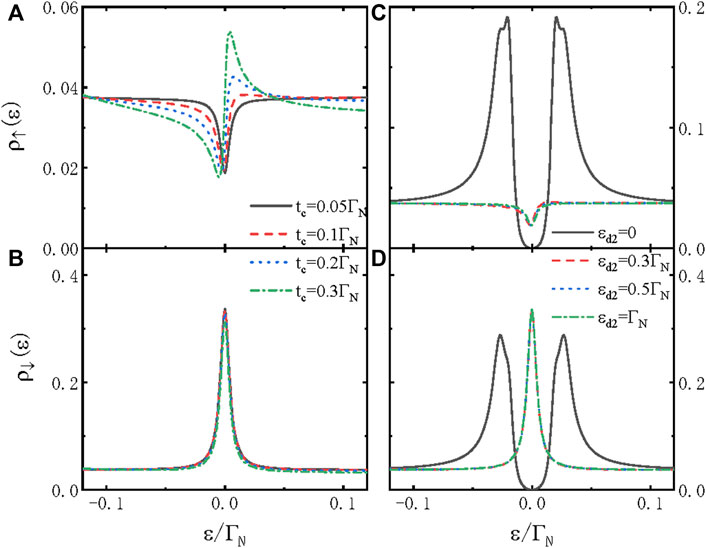
FIGURE 3. (Color online) Spin-dependent LDOS as a function of the electron energy ɛ for different values of t_c in (A) and (B), and different ${\epsilon }_{\left(\right.}d2$) in (C) and (D). Unless indicated, other parameters are as in Figure 1.

The two modes of the MZMs will interact with each other with a strength of δ_M, which depends on the length of the nanowire hosting the MZMs. The MZM–MZM hybridization δ_M exerts significant influences on the electronic transport properties [19–21, 28–30]. For example, the half-fermionic nature of the MZMs (the zero-energy linear conductance of the QD side-coupled to the MZMs is half of its quantum value G (eV = 0) = e²/2h) is destroyed by δ_M [19]. It can also induce a sign reversion in the thermopower of the QD side-coupled to the MZMs [20, 21]. Figure 4 shows that the MZM–MZM hybridization split the single Fano (Lorentzian) resonance in spin-up (spin-down) LDOS for the case of δ_M = 0 into double Fano (Lorentzian) resonance configuration, which is centered at ɛ = ±δ_M. This result is qualitatively consistent with that in [19]. The main difference in the LDOS between the present system and that of [19] is the disappearance of the central peak due to the presence of the superconductor lead. With increasing δ_M, the Fano peaks in the spin-up LDOS become more asymmetric in the negative energy regime, but that in the positive energy regime evolves into a Lorentzian one. For the spin-down electrons, their LDOS is less changed by the variation of δ_M. This is because the spin-down electrons are not directly coupled to the MZMs in the present structure. At last, we note that in experiments, the two modes may interact with the QD simultaneously. [19] Usually, the coupling of the QD to both the modes will enhance or suppress the impacts of the MZMs depending on the arrangement of the coupling strength of different modes. Such a case generally will not change the qualitative functions of the MZMs on the LDOS or the Andreev differential conductance. Another impact of the coupling between the dots with the two modes of the MZMs is the introduction of a phase factor arising from the closed geometry. This phase factor will also exert important influences on the quantum interference effect and is worth discussing in the future.

FIGURE 4

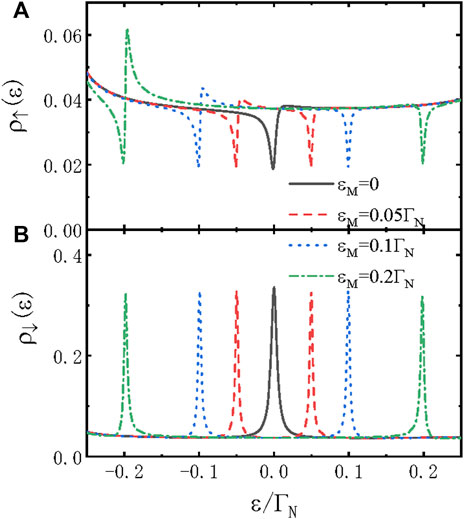
FIGURE 4. (Color online) Spin-dependent LDOS changing with the electron energy for different values of the direct overlap between the MZMs ɛ_M. Other parameters are as in Figure 1.

4 Summary

In summary, we have studied electronic transport through T-shaped DQDs with the central dot coupled to one normal metallic and one superconductor lead, as well as to a nanowire hosting MZMs. Our numerical results show that the combined effects of the QD–MZM interaction and the on-dot pairing from the superconductor lead exert significant impacts on the LDOS and the Andreev differential conductance. Under some conditions, a Fano- or Lorentzian-type resonance emerges in the spin-resolved LDOS or conductance, which depends on whether the electrons are coupled to the MZMs. Either the position or the strength of the resonance can be efficiently tuned by the quantities related to the MZMs, such as QD-MZMs or MZM–MZM hybridization strengths. The quantum interference arising from the side-coupled dot will change the molecular states induced by the MZMs and the superconductor lead, thus providing an effective means to adjust the system’s transport properties.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author contributions

L-LS derived the formulae, performed the numerical calculations, and wrote the original manuscript. JL helped derive the formulae and explain the physical mechanisms of the results.

Funding

The authors gratefully acknowledge the financial support from the R&D Program of Beijing Municipal Education Commission (KM201910009002) and the NSFC (Grant No. 12264037).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Deacon RS, Tanaka Y, Oiwa A, Sakano R, Yoshida K, Shibata K, et al. Tunneling spectroscopy of andreev energy levels in a quantum dot coupled to a superconductor. Phys Rev Lett (2010) 104:076805. doi:10.1103/PhysRevLett.104.076805

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Mourik V, Zuos K, Frolovs M, Plissarde R, Bakkers PAM, Kouwenhoven LP. Signatures of majorana fermions in hybrid superconductor-semiconductor nanowire devices. Science (2012) 336:1003–7. doi:10.1126/science.1222360

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Weymann I, Wojcik KP. Andreev transport in a correlated ferromagnet-quantum-dot-superconductor device. Phys Rev B (2015) 92:245307. doi:10.1103/PhysRevB.92.245307

CrossRef Full Text | Google Scholar

4. Sun QF, Guo H, Wang J. Hamiltonian approach to the ac josephson effect in superconducting-normal hybrid systems. Phys Rev B (2002) 65:075315. doi:10.1103/PhysRevB.65.075315

CrossRef Full Text | Google Scholar

5. Sun QF, Wang J, Lin TH. Photon-assisted andreev tunneling through a mesoscopic hybrid system. Phys Rev B (1999) 59:13126–38. doi:10.1103/PhysRevB.59.13126

CrossRef Full Text | Google Scholar

6. Rodero AM, Yeyati AL. Josephson and andreev transport through quantum dots. Adv Phys X (2011) 60:899–958. doi:10.1080/00018732.2011.624266

CrossRef Full Text | Google Scholar

7. Larsen TW, Petersson KD, Kuemmeth F, Jespersen TS, Krogstrup P, Nygard J, et al. Semiconductor-nanowire-based superconducting qubit. Phys Rev Lett (2015) 115:127001. doi:10.1103/PhysRevLett.115.127001

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Sun QF, Guo H, Lin TH. Excess kondo resonance in a quantum dot device with normal and superconducting leads: The physics of andreev-normal co-tunneling. Phys Rev Lett (2001) 87:176601. doi:10.1103/PhysRevLett.87.176601

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Baranski J, Domanski T. Fano-type interference in quantum dots coupled between metallic and superconducting leads. Phys Rev B (2011) 84:195424. doi:10.1103/PhysRevB.84.195424

CrossRef Full Text | Google Scholar

10. Baranski J, Domanski T. In-gap states of a quantum dot coupled between a normal and a superconducting lead. J Phys : Condens Matter (2013) 25:435305. doi:10.1088/0953-8984/25/43/435305

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Baranski J, Domanski T. Decoherence effect on fano line shapes in double quantum dots coupled between normal and superconducting leads. Phys Rev B (2012) 85:205451. doi:10.1103/PhysRevB.85.205451

CrossRef Full Text | Google Scholar

12. Calle AM, Pacheco M, Martins GB, Apel VM, Lara GA, Orellana PA. Fano–Andreev effect in a T-shape double quantum dot in the Kondo regime. J Phys : Condens Matter (2017) 29:135301. doi:10.1088/1361-648X/aa58c1

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Li YX, Choi HY, Lee HW, Liu JJ. Andreev reflection with spin-flip scattering through a t-shaped double quantum dot. J Appl Phys (2007) 101:103918. doi:10.1063/1.2724832

CrossRef Full Text | Google Scholar

14. Fu L, Kane CL. Superconducting proximity effect and majorana fermions at the surface of a topological insulator. Phys Rev Lett (2008) 100:096407. doi:10.1103/PhysRevLett.100.096407

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Nayak C, Simon SH, Stern A, Freedman M, Das Sarma S. Non-abelian anyons and topological quantum computation. Rev Mod Phys (2008) 80:1083–159. doi:10.1103/RevModPhys.80.1083

CrossRef Full Text | Google Scholar

16. Alicea J, Oreg Y, Refael G, von Oppen F, Fisher MPA. Non-abelian statistics and topological quantum information processing in 1d wire networks. Nat Phys (2011) 7:412–7. doi:10.1038/nphys1915

CrossRef Full Text | Google Scholar

17. Karzig T, Knapp C, Lutchyn RM, Bonderson P, Hastings MB, Nayak C, et al. Scalable designs for quasiparticle-poisoning-protected topological quantum computation with majorana zero modes. Phys Rev B (2017) 95:235305. doi:10.1103/PhysRevB.95.235305

CrossRef Full Text | Google Scholar

18. Ricco LS, de Souza M, Figueira MS, Shelykh IA, Seridonio AC. Spin-dependent zero-bias peak in a hybrid nanowire-quantum dot system: Distinguishing isolated majorana fermions from andreev bound states. Phys Rev B (2019) 99:155159. doi:10.1103/PhysRevB.99.155159

CrossRef Full Text | Google Scholar

19. Liu DE, Baranger HU. Detecting a majorana-fermion zero mode using a quantum dot. Phys Rev B (2011) 84:201308. doi:10.1103/PhysRevB.84.201308

CrossRef Full Text | Google Scholar

20. López R, Lee M, Serra L, Lim J. Thermoelectrical detection of majorana states. Phys Rev B 89 (2014) 205418. doi:10.1103/PhysRevB.89.205418

CrossRef Full Text | Google Scholar

21. Hong L, Chi F, Fu ZG, Hou YF, Wang Z, Li KM, et al. Large enhancement of thermoelectric effect by majorana bound states coupled to a quantum dot. J Appl Phys 127 (2020) 124302. doi:10.1063/1.5125971

CrossRef Full Text | Google Scholar

22. Chi F, Fu ZG, Liu J, Li K, Wang Z, Zhang P. Thermoelectric effect in a correlated quantum dot side-coupled to majorana bound states. Nanoscale Res Lett 15 (2020) 79. doi:10.1186/s11671-020-03307-y

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Majek P, Gorski G, Domanski T, Weymann I. Hallmarks of majorana mode leaking into a hybrid double quantum dot. arXiv:2202.09227v1 (2022). doi:10.48550/arXiv.2202.09227

CrossRef Full Text | Google Scholar

24. Feng GH, Zhang HH. Probing robust majorana signatures by crossed andreev reflection with a quantum dot. Phys Rev B (2022) 105:035148. doi:10.1103/PhysRevB.105.035148

CrossRef Full Text | Google Scholar

25. Zhang P, Wu H, Chen J, Khan SA, Krogstrup P, Pekker D, et al. Signatures of andreev blockade in a double quantum dot coupled to a superconductor. Phys Rev Lett (2022) 128:046801. doi:10.1103/PhysRevLett.128.046801

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Chi F, Wang J, He TY, Fu ZG, Zhang P, Zhang XW, et al. Quantum interference effects in quantum dot molecular with majorana bound states. Front Phys 8 (2021) 631031. doi:10.3389/fphy.2020.631031

CrossRef Full Text | Google Scholar

27. Zitko R. Fano-kondo effect in side-coupled double quantum dots at finite temperatures and the importance of two-stage kondo screening. Phys Rev B (2010) 81:115316. doi:10.1103/PhysRevB.81.115316

CrossRef Full Text | Google Scholar

28. Jiang C, Zheng YS. Fano effect in the andreev reflection of the aharonov–bohm–fano ring with majorana bound states. Solid State Commun (2015) 212:14–8. doi:10.1016/j.ssc.2015.04.001

CrossRef Full Text | Google Scholar

29. Zeng QB, Chen S, Lü R. Fano effect in an ab interferometer with a quantum dot side-coupled to a single majorana bound state. Phys Lett A (2016) 380:951–7. doi:10.1016/j.physleta.2015.12.026

CrossRef Full Text | Google Scholar

30. Chi F, He TY, Wang J, Fu ZG, Liu LM, Liu P, et al. Photon-assisted transport through a quantum dot side-coupled to majorana bound states. Front Phys 8 (2020) 2541. doi:10.3389/fphy.2020.00254

CrossRef Full Text | Google Scholar