Acoustic wavefront manipulation via transmission-type labyrinth structure

In this work, a transmission-type labyrinth structure (LS) is proposed to construct subwavelength acoustic functional metasurfaces, through which various desirable acoustic wavefront manipulation can be achieved in a broadband from 2,700 Hz to 3,900 Hz. By utilizing the excellent guiding property of LS, an invisibility cloak is designed to shield the target scattering body in the transmitted field. In addition, gradient metasurfaces composed of several LSs with different phase responses are constructed to obtain broadband beam deflection and focusing. Moreover, binary coding approach is adopted to further simplify the design philosophy of the metasurfaces by taking advantage of only two kinds of LS with opposite phase responses. Numerous wavefront manipulations including acoustic splitting beam and self-bending beam can be realized by using corresponding coding sequences. Our work provides a solution for multifunctional acoustic wavefront manipulation in a broadband, which may have potential applications in acoustic communication, detection and holography.

1 Introduction

Acoustic wavefront manipulation is desirable in numerous engineering applications such as acoustic communication, detection, holography and bioimaging. Three wavefront categories including reflection wave, absorption wave and transmission wave are essential for target pattern of the acoustic field. It is easy to manipulate the reflection wave by groove structures with different depths [1–4]⁾. To achieve tunable and broadband reflected wavefront modulation, Fan et al. [5] proposed a helical metasurface, through which many interesting acoustic phenomena including anomalous reflection, arbitrary focusing and self-bending beams were realized. They also designed a tunable lossy metsurface to achieve multi-plane acoustic holograms [6]. Weng et al. [7] adopted multiple resonant elements to construct an ultrathin planar metasurface with wavelength-dependent manipulation. Meanwhile, porous materials are investigated to achieve perfect absorption [8, 9]. For transmission wave, although using phased array transducers is an effective approach to generate arbitrary transmission wavefront, it has disadvantages in large scale, complex circuit and high cost.

In past decade, the development of acoustic metamaterial and metasurface provides another method to manipulate the transmission wavefront by artificial passive structures [10–17]. By utilizing the band characteristics of the phononic crystals, some abnormal acoustic phenomena for instance negative refraction [18], beam focusing [19] and topological energy transport [20] have been widely reported. Meanwhile, multiple fascinating acoustic wavefront modulations including splitting beam [21], vortex beam [22], Airy beam [23], focusing beam [24], and acoustic illusion [25] have been realized by taking advantage of the Helmholtz resonators [26], spiral cavities [27] and coiling waveguides [28]. For example, Zhu et al. [29] reported an investigation of multiplexed acoustic holograms at both audio and ultrasonic frequencies via a rationally designed transmission-type metamaterial. Wang et al. [30] proposed a tunable flat acoustic metasurface composed of fan-shaped annular resonator arrays. However, both the phononic crystals and resonant cavities are suffering from the limitation of bandwidth. In addition, the structure designed by phononic crystals has a large size, while that by resonant cavities needs a complicated configuration. Therefore, a simple design method for the realization of broadband acoustic wavefront manipulation is needed to be sought.

In this work, we propose a transmission-type labyrinth structure (LS) with sub-wavelength scale to achieve various acoustic wavefront manipulations. By changing the interdigital length of the LS, the phase response of the transmission wave can cover a full range from 0 to 2π under a high transmittance. Thanks to the excellent guiding property of LS to the transmission acoustic waves, a stealth structure is constructed to shield target scattering body. Meanwhile, a metasurface composed of several LSs with gradient phase responses is designed to achieve broadband beam deflection and beam focusing. Owing to the linear relation between operating frequency and phase shift, the metasurface showing a low dispersion feature for wavefront manipulation. Moreover, by taking advantage of the binary design, broadband splitting beam and self-bending beam are realized as well, which further simplify the design philosophy of the metasurface. Our work provides a solution for multifunctional acoustic wavefront manipulation in a broadband, which may have potential applications in acoustic communication, detection and holography.

2 Model design and analysis

As shown in Figure 1A, the LS designed in our work is a rectangular cavity with several interdigital plates. The length, height, and thickness of the LS are L = 55.5 mm, H = 15.5 mm, and T = 10 mm. The air gaps between two adjacent interdigital plates are G₁ = 6.4 mm, G₂ = 2 mm, and G₃ = 1 mm. The thickness and heights of interdigital plate at different positions are w = 0.5 mm and H₁ = 8.6 mm, H₂ = 11.3 mm, H₃ = 12 mm, respectively. The LS is a mirror symmetrical structure, and the lengths of each composing cavity are L₁ = L₃ = 14 mm, L₂ = 27.5 mm. Here, we adopt finite element software COMSOL Multiphysics to calculate the transmission information of the LS. The acoustic velocity and density of the air are c = 343 m/s and ρ = 1.29 kg/m³. Hard acoustic field conditions are set along the upper and lower boundaries of the LS, and plane wave radiation conditions are used in left and right boundaries of the LS to avoid unwanted echo interference. When we adjust the height of middle interdigital plate (H₃), as shown in Figure 1C, the transmission information including transmittance and phase responses of the LS can be modulated correspondingly at 3,430 Hz. The phase shift can nearly cover a full range from 0 to 2π under a high transmittance when H₃ changes from 8.3 mm to 14 mm, exhibiting an excellent performance for wavefront modulation by LS with subwavelength scale. The high transmittance steams from resonance effect of the LS and the phase shift originates from the change of equivalent acoustic velocity (or propagation length) caused by different shield heights. According to the acoustic pressure distributions shown in Figures 1A,B gradient phase response (ϕ = 0.4π, 0.8π, 1.2π, 1.6π, 2.0π) is generated by five LSs with different parameters (H₃ = 13.30 mm, 11.53 mm, 10.12 mm, 8.97 mm, 8.30 mm) for plane wave incidence at 3,430 Hz, which verifies the ability of phase modulation for transmission wave. In addition, as illustrated in Figure 1D, the phase shift is linear with the operating frequency in a broadband of 2,700 Hz–3900 Hz, and the transmittance of the LS is relatively high (near unity) within this band. Therefore, as shown in Figures 1E,F), the gradient of the phase delay can be linear in a frequency range of 2,700 Hz–3900 Hz under a high transmission coefficient when H₃ > 7.6 mm, providing an opportunity to achieve broadband acoustic wavefront manipulation.

FIGURE 1

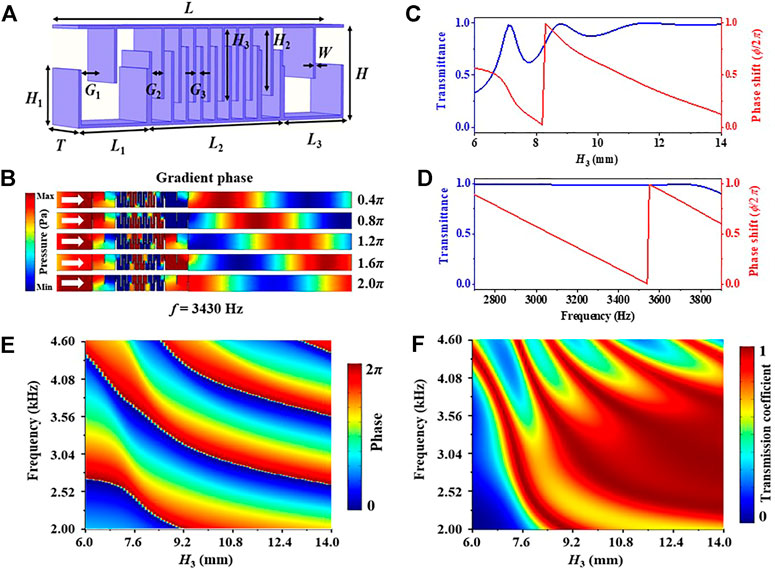
FIGURE 1. (A) The three-dimensional schematic of LS. (B) The acoustic pressure distributions of the LS with different interdigital length (H₃ = 13.30 mm, 11.53 mm, 10.12 mm, 8.97 mm, 8.30 mm) at 3,430 Hz. (C) The relation between the interdigital length and transmission information (transmittance and phase shift) for LS. (D) The relation between the operating frequency and transmission information (transmittance and phase shift) for LS. (E) The relation between phase shift and incident frequency with the increase of parameter H₃. (F) The relation between transmission coefficient and incident frequency with the increase of parameter H₃.

3 Results and discussions

The LS proposed here is flexible, which can control the acoustic propagation path of the transmission wavefront by rotating different angles. As shown in Figure 2A, the LSs with rotation angles of 30°, 45°, and 60° have identical transmission wavefront under the same incident condition (normal incidence at 3,430 Hz). With the increase of rotation angle, the acoustic propagation path moves up gradually, making it is suitable for LS to construct invisibility cloak. As shown in Figure 2B, when the plane acoustic wave normally incident on the LS array, the shape of wavefront in the transmission field is the same as that in the incident field. The result is applicable to both plane wave incidence and spherical wave incidence, indicating a zero refractive property of the LS array. Taking a circular scattering body as an example, as shown in Figure 2C, the transmission wavefront is damaged and disorderly when the scattering body is placed in a free air space for normal incidence, making it is easy to be detected under this circumstance. As a comparison, when the scattering body is surrounded by LS array, the incident acoustic waves propagate along the designed path and bypass the scattering body. In this case, the shape of transmission wavefront remains unchanged, and the scattering body is invisible. To further verify the stealth performance of the LS array, as shown in Figure 2D, the acoustic amplitude and pressure distribution along the cut-line 1 marked in Figure 1C is periodic and uniform. The target scattering body is hardly to be detected since the waveform in the transmission field is identical to that in the incident field. For acoustic amplitude and pressure distributions along the cut-line 2 marked in Figure 1C, it is uneven and visible owing to the strong scattering by rigid body. Therefore, the acoustic cloak designed by LS array can extremely improve the security of the acoustic target.

FIGURE 2

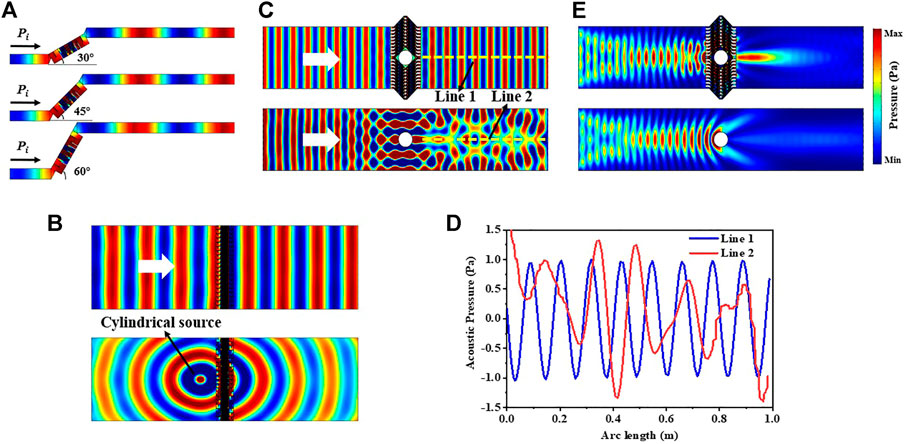
FIGURE 2. Acoustic pressure distributions of (A) the waveguide designed by LS with different rotation angles, (B) the array of LS stimulated by plane and cylindrical sources, and (C) the circular scattering body surrounded by LS array and without LS array at 3,430 Hz. (D) Acoustic pressure distributions along Lines one and 2 marked by yellow dashed lines in Panel 2C. (E) Acoustic intensity distributions of the circular scattering body surrounded by LS array and without LS array at 3,430 Hz.

Next, we construct a gradient metasurface composed of periodic LS arrays to achieve desirable acoustic beam shaping. Similar to the generalized Snell’s law in optics [31], if the acoustic wave with a frequency f is incident from one medium to another, the generalized Snell’s law in acoustics can be expressed as follows:

$k_t\sin {\theta }_t-k_i\sin {\theta }_i=d\varphi \left(x\right)/dx(1)$

$k_i=2\pi f/c_i(2)$

$k_t=2\pi f/c_t(3)$

where θ_i and θ_t represent the incident angle and refraction angle; c_i and c_t represent the acoustic velocities of the incident medium and transmitted medium, respectively; dϕ(x)/dx represents the phase gradient along the metasurface. To be simplified, we consider the case of θ_i = 0, and Eq. 1 is rewritten as

$k_t\sin {\theta }_t=d\varphi \left(x\right)/dx(4)$

Following Eq. 4, the refraction property of the metasurface is closely related to the phase gradient along the metasurface. As shown in Figures 3A supercell composed of ten LSs is constructed as a periodic unit. The rectangular blocks with different colors correspond to distinct phase responses. The phase shifts from left to right are 0.4π, 0.4π, 0.8π, 0.8π, 1.2π, 1.2π, 1.6π, 1.6π, 2.0π, 2.0π. The design principle of the period length should be longer than incident wavelength, otherwise the surface acoustic wave will appear [32]. In Figure 3A, the period length is set as D = 155 mm, and it can be adjusted by altering the number of LS. When plane acoustic waves are normally incident on the metasurface, the propagation direction of the transmission wavefront is changed. The simulated acoustic pressure distributions verify that the desirable acoustic beam deflection is generated by a gradient metasurface. Meanwhile, the metasurface can work well in a broadband within 2,700 Hz–3900 Hz, showing an excellent wavelength tolerance.

FIGURE 3

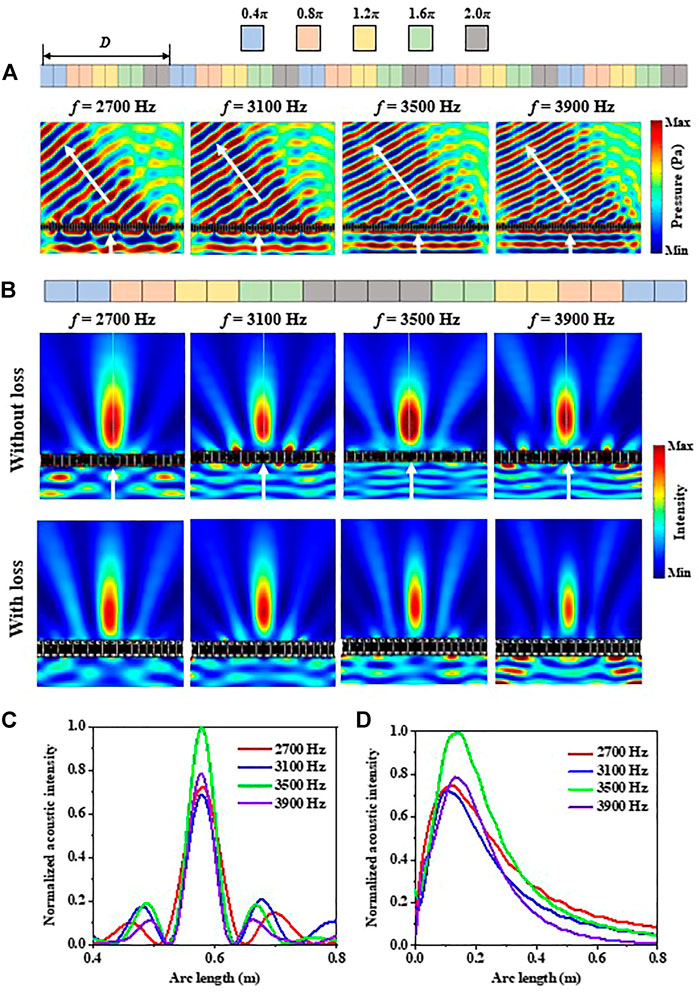
FIGURE 3. (A) Acoustic pressure distributions and (B) intensity distributions of the metasurface composed of LS with different interdigital length at 2,700 Hz, 3,100 Hz, 3,500 Hz and 3,900 Hz. Normalized acoustic intensities along (C) horizontal and (D) vertical cut-lines in Panel 3B.

The function of the metasurface can be changed if we adopt other arrangements of LS. As shown in Figures 3A,B mirror symmetrical structure composed of 20 LSs is constructed to serve as an acoustic lens. From left to right, the phase responses of 20 LSs are 0.4π, 0.4π, 0.8π, 0.8π, 1.2π, 1.2π, 1.6π, 1.6π, 2.0π, 2.0π, 2.0π, 2.0π, 1.6π, 1.6π, 1.2π, 1.2π, 0.8π, 0.8π, 0.4π, 0.4π. Owing to the symmetrical distributions of the phase response, interference superposition of acoustic intensity is generated in the transmitted field. The acoustic intensity distributions of the metasurface shown in Figure 3B confirms that the incident plane acoustic waves are converted into focusing beams after passing through the designed lens, and the metasurface can work in a broadband from 2,700 Hz to 3900 Hz. Figure 3B also illustrates the acoustic intensity distribution of the metasurface with thermal viscosity loss, it can be seen that although the intensity of the focus is reduced compared with that in lossless case, the ability of beam focusing exists. In addition, note that the refraction angle of the transmission wave shown in Figure 3A and the focal length of the focus shown in Figure 3B are independent of incident frequencies. Following the linear relation between transmitted phase response and incident frequency shown in Figure 1D, the change of incident wavelength and gradient phase response along the metasurface can be offset, exhibiting a low dispersion feature for gradient metasurface. Figure 3C shows the normalized acoustic intensity distributions along the cut-line of y = 0.15 m marked in Figure 3B, apparent acoustic wave convergence can be observed at this position. The peak intensity value of the focus is at 3,500 Hz, which near the center frequency (3,430 Hz) of the LS. Moreover, the performance of the beam focusing can also be verified by plotting the normalized acoustic intensity distributions along the cut-line of x = 0 m marked in Figure 3B. From Figure 3D it can be seen that the beam focusing for different incident frequencies from 2,700 Hz to 3,900 Hz is generated at the position of y = 0.15 m, and the high intensity value of the focus is at 3,500 Hz, which agrees well with the results shown in Figure 3C. Therefore, the gradient metasurfaces designed by LSs not only can work in a broadband, but also have a low dispersion feature for acoustic wavefront manipulation [33].

As another feasible approach to realize broadband acoustic wavefront manipulation, binary design for functional metasurface can further simplify the design philosophy since only two kinds of coding units with high transmittance and opposite phase responses are needed [34–39]. We define LS with parameters of H₃ = 10 mm and H₃ = 14 mm as coding bits ‘0’ and ‘1’, respectively. Following the relation between phase shift of the LS and parameter H₃ shown in Figure 1C, coding bit ‘0’ has a phase response of 1.2π and coding bit ‘1’ has a phase response of 0.2π, which meets the requirement of opposite phase response for the design of binary metasurface. As shown in Figure 4A, an acoustic beam splitter is composed of two coding bits ‘0’ and ‘1’ with a periodic coding sequence of 01/01/01 … 01/01/01, and the cycle length is set as D = 160 mm. According to the generalized Snell’s law, the diffraction orders of n = 0, 1, -1 are all open for normal incidence when the reciprocal lattice vector (G = 2π/D) is smaller than the wavenumber in air background. However, the diffraction orders of n = 1, -1 is preferential to the n = 0 order, leading to a beam splitting stemming from the transmission channel of the n = 1, -1 orders for normal incidence. The simulated acoustic pressure distributions display apparent beam splitting at four different frequencies (2,700 Hz, 3,100 Hz, 3,500 Hz and 3,900 Hz), verifying the broadband performance of the beam splitter.

FIGURE 4

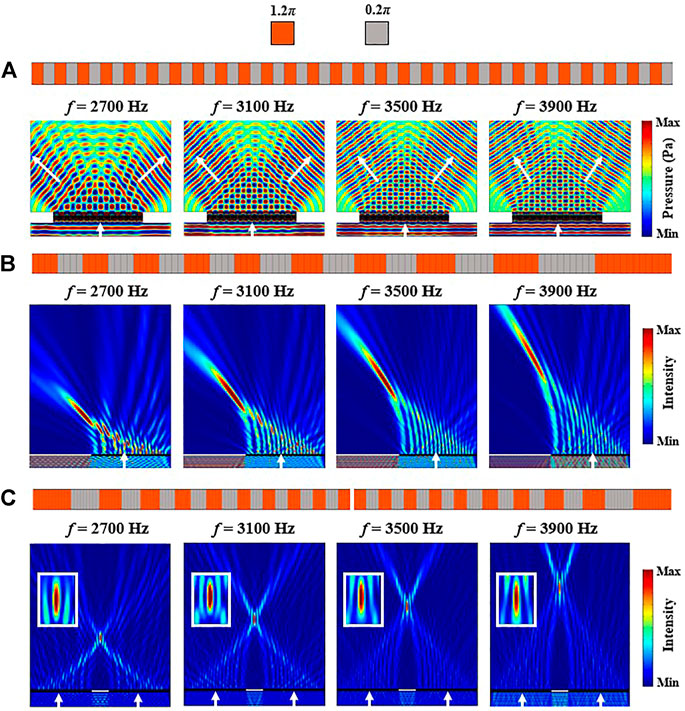
FIGURE 4. (A) Acoustic pressure distributions and (B), (C) intensity distributions of the binary metasurfaces at 2,700 Hz, 3,100 Hz, 3,500 Hz and 3,900 Hz.

Meanwhile, the function of the metasurface can be customized by adopting different coding sequences. Taking acoustic self-bending beam as an example, as shown in Figure 4B, the coding sequence of the metasurface is a staggered arrangement composed of coding bits ‘0’ (orange blocks) and ‘1’ (grey blocks). From left to right, the numbers of the coding bit are 4, 4, 4, 4,4,4,4,4,4,5,5,5,5,5,6,6,7,9,12. The incident plane acoustic wave can be converted into self-bending beam at this time. The intensity of the transmitted wave is localized in the main lobe, and the trajectory of transmission wave is curved. Similar to the beam splitter, the acoustic self-bending beam generator can work in a broadband of 2,700 Hz–3900 Hz as well. Moreover, if we place two self-bending beam generators in a mirror symmetrical manner, as shown in Figure 4C, acoustic beam focusing can be obtained owing to the interference superposition from two identical self-bending beams with opposite radiation directions, which further expends the function of binary metasurface designed by LSs.

4 Conclusion

In summary, a labyrinth structure (LS) is proposed in this work for transmitted acoustic wavefront manipulation. Owing to the excellent guiding property of LS, an invisibility cloak is designed to achieve acoustic stealth for scattering body. The transmission information including phase response and transmittance of the LS can be modulated by the height of interdigital plate, and there exists a linear relation between phase shift and incident wavelength, which can be adopted to construct gradient acoustic metasurfaces to achieve beam deflection and focusing in a broadband from 2,700 Hz to 3,900 Hz. Moreover, a binary design for acoustic metasurface is utilized to further simplify the design philosophy by using only two kinds of LS with opposite phase responses. Two binary metasurfaces with different coding sequences are constructed to play the roles of acoustic beam splitter and self-bending beam generator, through which the broadband wavefront manipulation has been obtained. The acoustic metasurface constructed by LS has the advantages of simple design, subwavelength scale and broadband response, which may have potential applications in acoustic communication, detection and holography.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

RW conceived the presented idea, performed the calculations and simulations and drafted the manuscript. All authors discussed the results and contributed to the final manuscript.

Funding

This work was supported by the National Natural Science Foundation of China (61972363).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Zhang Y, Cheng H, Tian J, Chen S. Frequency-Selected bifunctional coding acoustic metasurfaces. Phys Rev Appl (2020) 14:064057. doi:10.1103/physrevapplied.14.064057

CrossRef Full Text | Google Scholar

2. Zhu Y, Assouar B. Multifunctional acoustic metasurface based on an array of Helmholtz resonators. Phy Rev B (2019) 99:174109. doi:10.1103/physrevb.99.174109

CrossRef Full Text | Google Scholar

3. Zhang Y, Xie B, Liu W, Cheng H, Chen S, Tian J. Anomalous reflection and vortex beam generation by multi-bit coding acoustic metasurfaces. Appl Phys Lett (2019) 114:091905. doi:10.1063/1.5087636

CrossRef Full Text | Google Scholar

4. Song X, Chen T, Huang W, Chen C. Frequency-selective modulation of reflected wave fronts using a four-mode coding acoustic metasurface. Phys Lett A (2021) 394:127145. doi:10.1016/j.physleta.2021.127145

CrossRef Full Text | Google Scholar

5. Fan S, Zhao S, Chen A, Wang Y, Assouar B, Wang Y. Tunable broadband reflective acoustic metasurface. Phys Rev Appl (2019) 11:044038. doi:10.1103/physrevapplied.11.044038

CrossRef Full Text | Google Scholar

6. Fan S, Zhu Y, Cao L, Wang Y, Chen A, Merkel A, et al. Broadband tunable lossy metasurface with independent amplitude and phase modulations for acoustic holography. Smart Mater Struct (2020) 29:105038. doi:10.1088/1361-665x/abaa98

CrossRef Full Text | Google Scholar

7. Weng J, Zhu Y, Liang B, Yang J, Cheng J. Wavelength-dependent multi-functional wavefront manipulation for reflected acoustic waves. Appl Phys Express (2020) 13:094003. doi:10.35848/1882-0786/abb062

CrossRef Full Text | Google Scholar

8. Gao N, Zhang Z, Tang L, Hou H, Chen K. Optimal design of broadband quasi-perfect sound absorption of composite hybrid porous metamaterial using TLBO algorithm. Appl Acoust (2021) 183:108296. doi:10.1016/j.apacoust.2021.108296

CrossRef Full Text | Google Scholar

9. Gao N, Wu J, Lu K, Zhong H. Hybrid composite meta-porous structure for improving and broadening sound absorption. Mech Syst Signal Process (2021) 154:107504. doi:10.1016/j.ymssp.2020.107504

CrossRef Full Text | Google Scholar

10. Ju F, Xiong W, Liu C, Cheng Y, Liu X. Acoustic accelerating beam based on a curved metasurface. Appl Phys Lett (2019) 114:113507. doi:10.1063/1.5087544

CrossRef Full Text | Google Scholar

11. Li X, Zhou H, Wang Y, Wang Y. Modulation of acoustic self-accelerating beams with tunable curved metasurfaces. Appl Phys Lett (2021) 118:023503. doi:10.1063/5.0035286

CrossRef Full Text | Google Scholar

12. Tang S, Ren B, Feng Y, Song J, Jiang Y. The generation of acoustic Airy beam with selective band based on binary metasurfaces: Customized on demand. Appl Phys Lett (2021) 119:071907. doi:10.1063/5.0060032

CrossRef Full Text | Google Scholar

13. Li Y, Shen C, Xie Y, Li J, Wang W, Cummer S, et al. Tunable asymmetric transmission via lossy acoustic metasurfaces. Phys Rev Lett (2017) 119:035501. doi:10.1103/physrevlett.119.035501

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Xia J, Zhang X, Sun H, Yuan S, Qian J, Ge Y. Broadband tunable acoustic asymmetric focusing lens from dual-layer metasurfaces. Phys Rev Appl (2018) 10:014016. doi:10.1103/physrevapplied.10.014016

CrossRef Full Text | Google Scholar

15. Zhang C, Cao W, Wu L, Ke J, Jing Y, Cui T, et al. A reconfigurable active acoustic metalens. Appl Phys Lett (2021) 118:133502. doi:10.1063/5.0045024

CrossRef Full Text | Google Scholar

16. Tang S, Ren B, Feng Y, Song J, Jiang Y. Asymmetric acoustic beam shaping based on monolayer binary metasurfaces. Appl Phys Express (2021) 14:085504. doi:10.35848/1882-0786/ac15bf

CrossRef Full Text | Google Scholar

17. Zhao J, Ye H, Huang K, Chen Z, Li B, Qiu C. Manipulation of acoustic focusing with an active and configurable planar metasurface transducer. Sci Rep (2014) 4:6257. doi:10.1038/srep06257

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Li X, Gao J, Liu S, Zhou K, Huang B. Acta Phys Sin (2010) 59:376.

19. Tang S, Wang R, Han J. Acoustic focusing imaging characteristics based on double negative locally resonant phononic crystal. IEEE Access (2019) 7:112598–604. doi:10.1109/access.2019.2932419

CrossRef Full Text | Google Scholar

20. Fleury R, Khanikaev A, Alu A. Floquet topological insulators for sound. Nat Commun (2016) 7:11744. doi:10.1038/ncomms11744

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Li W, Meng F, Huang X. Coding metalens with helical-structured units for acoustic focusing and splitting. Appl Phys Lett (2020) 117:021901. doi:10.1063/5.0012784

CrossRef Full Text | Google Scholar

22. Jiang X, Li Y, Liang B, Cheng J, Zhang L. Convert acoustic resonances to orbital angular momentum. Phys Rev Lett (2016) 117:034301. doi:10.1103/physrevlett.117.034301

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Fan X, Huang X, Kang Y, Li C, Li N, Weng C. Ultra-broadband bending beam and bottle beam based on acoustic metamaterials. Appl Sci (Basel) (2022) 12:3025. doi:10.3390/app12063025

CrossRef Full Text | Google Scholar

24. Fan X, Zhu Y, Liang B, Yang J, Cheng J. Broadband convergence of acoustic energy with binary reflected phases on planar surface. Appl Phys Lett (2016) 109:243501. doi:10.1063/1.4971795

CrossRef Full Text | Google Scholar

25. Fan X, Liang B, Yang J, Cheng J. Illusion for airborne sound source by a closed layer with subwavelength thickness. Sci Rep (2019) 9:1750. doi:10.1038/s41598-018-38424-3

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Li Y, Jiang X, Liang B, Cheng J, Zhang L. Metascreen-Based acoustic passive phased array. Phys Rev Appl (2015) 4:024003. doi:10.1103/physrevapplied.4.024003

CrossRef Full Text | Google Scholar

27. Li K, Liang B, Yang J, Cheng J. Broadband transmission-type coding metamaterial for wavefront manipulation for airborne sound. Appl Phys Express (2018) 11:077301. doi:10.7567/apex.11.077301

CrossRef Full Text | Google Scholar

28. Ghaffarivardavagh R, Nikolajczyk J, Holt R, Anderson S, Zhang X. Horn-like space-coiling metamaterials toward simultaneous phase and amplitude modulation. Nat Commun (2018) 9:1349. doi:10.1038/s41467-018-03839-z

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Zhu Y, Gerard N, Xia X, Stevenson G, Cao L, Fan S, et al. Systematic design and experimental demonstration of transmission‐type multiplexed acoustic metaholograms. Adv Funct Mater (2021) 31:2101947. doi:10.1002/adfm.202101947

CrossRef Full Text | Google Scholar

30. Wang X, Yang J, Liang B, Cheng J. Tunable annular acoustic metasurface for transmitted wavefront modulation. Appl Phys Express (2020) 13:014002. doi:10.7567/1882-0786/ab59a5

CrossRef Full Text | Google Scholar

31. Yu N, Genevet P, Kats M, Aieta F, Tetienne J, Capasso F, et al. Light propagation with phase discontinuities: Generalized laws of reflection and refraction. Science (2011) 334:333–7. doi:10.1126/science.1210713

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Mei J, Wu Y. Controllable transmission and total reflection through an impedance-matched acoustic metasurface. New J Phys (2014) 16:123007. doi:10.1088/1367-2630/16/12/123007

CrossRef Full Text | Google Scholar

33. Dong H, Shen C, Zhao S, Qiu W, Zheng H, Zhang C, et al. Natl Sci Rev Nwac030 (2022).

34. Tang S, Wu J, Lü C, Song J, Jiang Y. Functional acoustic metamaterial using shortcut to adiabatic passage in acoustic waveguide couplers. Phys Rev Appl (2022) 18:014038. doi:10.1103/physrevapplied.18.014038

CrossRef Full Text | Google Scholar

35. Xie B, Cheng H, Tang K, Liu Z, Chen S, Tian J. Multiband Asymmetric transmission of airborne sound by coded metasurfaces. Phys Rev Appl (2017) 7:024010. doi:10.1103/physrevapplied.7.024010

CrossRef Full Text | Google Scholar

36. Tang S, Lü C, Wu J, Song J, Jiang Y. Wavelength-selected bifunctional beam shaping for transmitted acoustic waves via coding metasurface. Appl Acoust (2022) 194:108786. doi:10.1016/j.apacoust.2022.108786

CrossRef Full Text | Google Scholar

37. Tang S, Ren B, Feng Y, Song J, Jiang Y. Broadband acoustic focusing via binary rectangular cavity/Helmholtz resonator metasurface. J Appl Phys (2021) 129:155307. doi:10.1063/5.0049407

CrossRef Full Text | Google Scholar

38. Fu Y, Tao J, Song A, Liu Y, Xu Y. Controllably asymmetric beam splitting via gap-induced diffraction channel transition in dual-layer binary metagratings. Front Phys (Beijing) (2020) 15:52502. doi:10.1007/s11467-020-0968-2

CrossRef Full Text | Google Scholar

39. Tang S, Wu J, Lü C, Wang X, Song J, Jiang Y. Acoustic wavelength-selected metamaterials designed by reversed fractional stimulated Raman adiabatic passage. Phys Rev B (2022) 105:104107. doi:10.1103/physrevb.105.104107

CrossRef Full Text | Google Scholar