Solar data uncertainty impacts on MCMC methods for r-process nucleosynthesis

In recent work, we developed a Markov Chain Monte Carlo (MCMC) procedure to predict the ground state masses capable of forming the observed Solar r-process rare-earth abundance peak. By applying this method to nucleosynthesis calculations which make use of distinct astrophysical conditions and comparing our results to the latest precision mass measurements, we are able to shed light on the conditions/masses capable of producing a rare-earth peak which matches Solar data. Here we examine how our mass predictions change when using a few different sets of r-process Solar abundance residuals that have been reported in the literature. We explore how the differing error estimates of these Solar evaluations propagate through the Markov Chain Monte Carlo to our mass predictions. We find that Solar data which reports the rare-earth peak to have its highest abundance at mass number A = 162 can require distinctly different mass predictions from data with the peak centered at A = 164. Nevertheless, we find that two important general conclusions from past work, regarding the inconsistency of ‘cold’ astrophysical outflows with current mass measurements and the need for local stability at N = 104 in ‘hot’ scenarios, remain robust in the face of differing Solar data evaluations. Additionally, we show that the masses our procedure finds capable of producing a peak at A < 164 are not in line with the latest precision mass measurements.

The study of the origin of the heaviest elements has in recent years been buzzing with new discussions surrounding the interpretation of the multi-messenger neutron star merger event GW170817 [1–3]. This event was first detected in gravitational waves and then followed-up by the telescope community to be observed across the electromagnetic spectrum [4, 5]. The prospect of learning from real-time nucleosynthesis events such as this is indeed a direction in which the field will grow for years to come. However, if such single events are to be connected back to our own Solar System origins, the importance of messengers of heavy element synthesis closer to home, that is Solar spectroscopic data and meteorites, must continue to be recognized. From these sources the Solar isotopic pattern, that is the relative amounts of species of a given mass number, is able to be determined [6]. This bit of observational information is unique to our Solar System with only elemental abundance patterns being available for other stars through spectroscopy [7]. The Solar isotopic pattern serves as an important benchmark for studies of the rapid neutron capture process (r-process), with it being common practice to compare these abundances to nucleosynthesis predictions in order to sort out the possible contributions a given astrophysical scenario or the plausibility of a given set of nuclear inputs (e.g. [8–11]). In recent work [12–17], rather than proceeding with the Solar isotopic pattern as solely a final point of comparison, we have instead made use of these abundances as the starting point for Markov Chain Monte Carlo (MCMC) methods aiming to work backwards toward deriving fundamental nuclear physics quantities. This approach is possible due to the clear impact of the properties of neutron-rich nuclei on astrophysical abundances, as evidenced by the second and third r-process abundance peaks seen in the Solar data at A ∼130 and A ∼195 from the closed neutron shells at N = 82 and N = 126 respectively [18]. Our approach therefore exploits this interplay between nuclear physics and observables by focusing on an abundance feature of uncertain origin, the r-process rare-earth abundance peak [19, 20], in order to probe previously unmeasured nuclear masses of rare-earth species.

Our MCMC method considers the masses needed in order to form the rare-earth abundance peak by applying the mass parameterization:

$M\left(Z,N\right)=M_{DZ}\left(Z,N\right)+a_N{e}^{-{\left(Z-C\right)}^2/2f}(1)$

where M_DZ corresponds to the masses predicted by the Duflo-Zuker (DZ) mass model [21] and a_N values are the parameters being determined by the MCMC. In these calculations we set f = 10 based on fits to mass trends of the Atomic Mass Evaluation (AME) 2012 data [22] and set C = 58 or C = 60 as was determined by numerous initial runs in which this parameter was allowed to float (see [15] for a detailed discussion). Following our mass adjustments we then calculate neutron capture, β-decay, and photodissociation rates corresponding to the mass changes before performing the nucleosynthesis calculation. Additionally, as discussed in [15], we perform external checks on quantities, such as the one neutron pairing metric and the σ_rms deviation with respect to AME2012 mass values, in order to ensure that we do not explore unphysical solutions.

Since the astrophysical conditions present during the nucleosynthesis impact the formation of abundance features, in past work we considered our MCMC approach along with several distinct astrophysical outflows. We consider an outflow ‘hot’ if neutron capture and photodissociation undergo an extended equilibrium during the synthesis. If rather photodissociation falls out of equilibrium early leaving neutron capture to compete with β-decay, we consider this a ‘cold’ outflow. As can be seen in Figure 1, we predict distinct mass surface trends to be needed to form the rare-earth peak for each of the distinct astrophysical outflows. Here note that since our mass predictions M are illustrated via the mass difference with respect to DZ (M−M_DZ) a positive value implies our MCMC requires masses less tightly bound than DZ and a negative value implies a more tightly bound system than is predicted by DZ. Since the nucleosynthesis outcome is sensitive to how the properties of a given nucleus relate to the properties of its neighbors, the most influential mass surface features will be ones that introduce strong local differences, such as the drop in the red band from positive to negative M−M_DZ from N = 102 to N = 104 which creates a region of ‘enhanced stability’ at N = 104 relative to neighboring nuclei. Independent mass measurements performed by the Canadian Penning Trap (CPT) at the CAlifornium Rare Isotope Breeder Upgrade (CARIBU) of which the MCMC calculation was not informed are found to be most consistent with the masses need in hot astrophysical outflows. Therefore this method can ultimately point to the type of astrophysical conditions which dominantly produced the lanthanide elements we see in the Solar System, which can then be traced back to candidate sites such as neutron star mergers or magneto-rotationally driven supernovae through comparisons with hydrodynamics predictions (e.g. [23–28]) and multi-messenger observations.

FIGURE 1

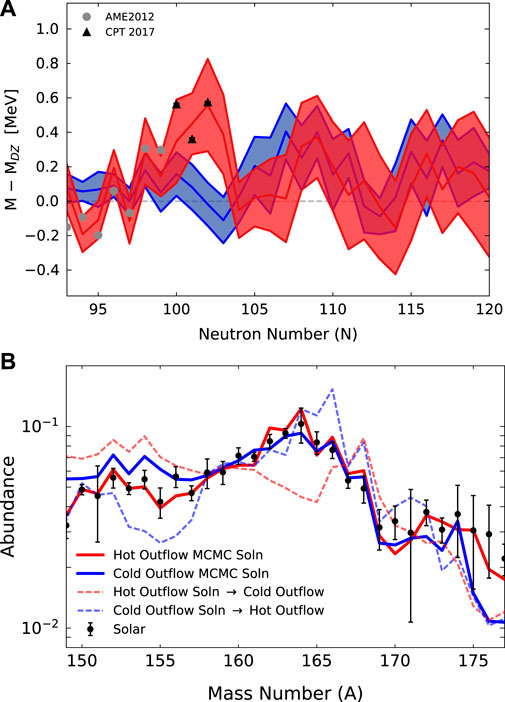
FIGURE 1. (A) The MCMC predicted masses for samarium (Z =62), relative to the DZ mass model, given two distinct moderately neutron-rich (Y_e =0.2) astrophysical outflows that could be found in accretion disk winds: a hot case which undergoes an extended (n,γ)⇄(γ,n) equilibrium (red band) and a cold case (blue band) for which photodissociation falls out of equilibrium early (adapted from Figure 20 of [15]). The AME2012 data [22] used to guide the calculation is shown along with CPT at CARIBU [14] data of which the calculation was not informed. All bands were determined from the average and standard deviation of 50 parallel, independent MCMC runs (B) Demonstration that the mass solutions are uniquely tied to the astrophysical conditions, with the solid red line showing the abundance results using the MCMC masses of top panel and the dotted red line showing the results when these masses are applied in a nucleosynthesis calculation with the cold trajectory. Likewise the blue solid line shows the abundances predicted by the blue band in the top panel along with the resultant abundances when this mass solution is applied to the hot trajectory (Figure 2 of [16]). Note that results in the top panel were determined from runs which applied symmetrized Solar data derived from Arnould+07 [29] (described in [15]) which is shown as black points in the bottom panel.

This exciting prospect to use advancements in statistical methods in order to progress our understanding of the origins of Solar System elements however hinges on how precisely we know the r-process content of the Solar System. The so-called ‘Solar r-process residuals’ are derived from subtracting out the predicted contribution to the Solar System for the slow neutron capture process (s-process). This is accepted as the standard approach since the s process occurs closer to stable species and so the nuclear data of importance to this process is significantly better understood than the data of relevance to the r process. Such ‘s-process subtractions’ have been performed over the years, taking into account new nuclear data measurements or new information on the conditions present at the astrophysical site of the s process, Asymptotic Giant Branch (AGB) stars. However very few of these independent Solar data evaluation sets from the literature report error estimates. The few that do report errors do so via propagating uncertainties from multiple sources including the observational data, neutron capture and β-decay measurement uncertainties, as well as estimates of the astrophysical variations which may be present in s-process sites (e.g. [30]). This procedure can thus yield different predictions for the relative abundances of neighboring nuclei as well as big differences in the reported errors depending on the error propagation treatment. Such considerations are highly relevant for our r-process MCMC calculations since the absolute value (Y_⊙(A)) and error (ΔY_⊙(A)) of the Solar r-process residuals at a given mass number dictates how our Markov chains evolve. This is because whether or not new masses of given step are adopted is determined by the likelihood ratio $R=\frac{{\mathcal{L}}_j}{{\mathcal{L}}_i}$ with j being the new step, i being the previous step, and the likelihood function being $\mathcal{L}\sim e^{-{\chi }^2/2}$ with χ² defined by

${\chi }^2=\sum _{A=150}^{180}\frac{{\left(Y_{\odot }\left(A\right)-Y\left(A\right)\right)}^2}{{\left(\mathrm{\Delta }{Y}_{\odot }\left(A\right)\right)}^2}.(2)$

Here we consider the Solar data impact on our MCMC mass predictions by applying two evaluations which report error estimates, those of Arnould+07 [29] and those of Beer+97 [31], and the data set of Sneden+08 [32] which does not report error estimates. As can be seen from Figure 2, Arnould+07 and Beer+97 not only have distinctly different trends in the shape of the relative abundances of the rare-earths, but also very different error estimates with the Beer+97 set being the case considered here with the smallest reported error. Even though the Sneden+08 dataset does not come with its own unique error estimate, this is an important set to consider given its frequent use as a comparison point for nucleosynthesis calculations in the literature. To utilize the Sneden+08 set in our MCMC approach, we must assign an abundance uncertainty in order to calculate χ². For our purposes, the most intriguing feature of the Sneden+08 dataset is the location of the peak of the rare-earth abundances since our calculations must find nuclear properties which can pile up nuclei at the needed mass number. Therefore for this case we take the error to be the average error of the Arnould+07 set applied equally to all points so that our MCMC analysis can investigate sensitivity to peak location rather than overall error. Thus the Beer+97 case will be most informative of the impact of error estimates and the Sneden+08 case will serve to observe how much the relative abundances and exactly placement of the highest peak point influence our MCMC.

FIGURE 2

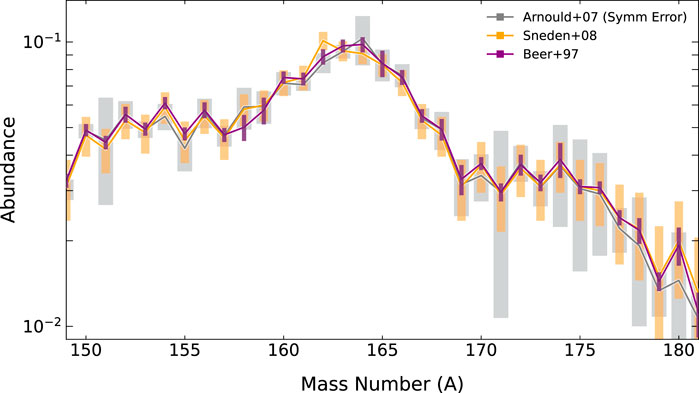
FIGURE 2. The Solar r-process abundance residuals for the rare-earth peak (∼ A =150−180) given several evaluations and error estimates. The set applied in previous MCMC work (grey) were derived from those in Arnould+07 [29, 30] by performing a symmetrization procedure as described in [15]. Also shown is the Solar data evaluation of Beer+97 [31] (purple) which reports significantly smaller error estimates. Another set considered is the popular Sneden+08 Solar data evaluation [32] (orange) which does not report errors. For this Sneden+08 set, the average error on abundances between A =150−180 from [29, 30] was applied.

In Table 1 we compare the χ² fits for each astrophysical scenario/Solar data combination reported in this work. Note that we report unnormalized χ² values because of the difficulty in defining the number of degrees of freedom due to the nature of how our MC parameters propagate through to the abundance values. We use 28 a_N parameters to adjust the masses of $\sim 300$ nuclei that are then inputs for the neutron capture rates, photodissociation rates, and β-decay rates that ultimately determine the abundances entering the χ² calculation for A = 150–180 (30 data points). Propagation of our 28 parameters to reaction rates introduces non-trival correlations amongst the 30 abundances being investigated, and the number of correlations introduced is a necessary ingredient to define the number of degrees of freedom (for instance standard deviations require dividing by N-1 where N is the number of points and one degree of freedom is subtracted since the average of N values enters the calculation and thus introduces one correlation). See the discussion in [15] for further details.

TABLE 1

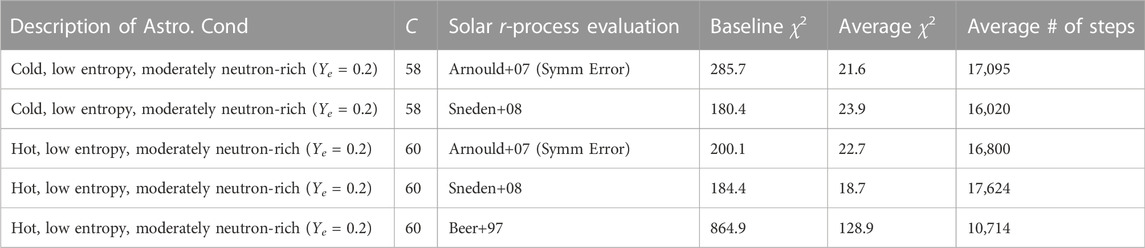
TABLE 1. Summary of the χ² for the DZ baseline and MCMC results for all cases presented in this work.

As can be seen in Table 1, since the errors we assume for the Sneden+08 Solar data set are based on the average of the Arnould+07 set, the χ² for the initial baseline nucleosynthesis abundance is similar, being between 180–286 for both the hot and cold astrophysical scenarios. The set considered here with the smallest errors, that is Beer+97, is distinct in having a much larger initial χ² abundance baseline of 865 for the hot astrophysical outflow. This leads to the MCMC not being able to achieve as low of χ² solutions as could be found in the Arnould+07 and Sneden+08 cases, despite the fact that the average number of steps taken by MCMC runs with Beer+97 was more than 10,000. Note that a few preliminary runs considered another Solar evaluation dataset in the literature of Arlandini+99 [33] which does report an error estimate for the r-process residuals. However in this case the error bars are especially small when compared to the sets pursued here, leading to a very large initial χ² of 6941.8. Such a high initial χ² implies that our Duflo-Zuker baseline mass model produces abundances very far off from the targeted Solar data, reported to be very precise in the Arlandini+99 case. Such a big initial discrepancy produced challenges to our current approach with all preliminary runs having a low acceptance rate. Such challenges could be overcome by, for example, exploring new baselines, but we leave such investigations to future work. Thus we concentrated our computational time on the Sneden+08 and Beer+97 cases since these already permit us to explore the influence of the unique features of each evaluation in terms of their error size and overall shape of the rare-earth peak. To provide a sense of the computational cost of a given MCMC result, we note that there are two main factors determining this: 1) the time to run the β-decay code which calculates the β-delayed neutron emission probabilities (∼30 s) and 2) the time to run the nucleosynthesis network (PRISM), with both being performed for every timestep. Runtime for the network can take between 30 s and 3 min depending on whether we are considering an astrophysical scenario in which the fission products must be included in the network. Therefore a single MCMC run which takes 10,000 steps can translate into anywhere from ∼2,000–10,000 core-hours depending on the speed of network calculation and the set-up of the computing cluster (this work made use of three distinct computing facilities). Therefore a 50 run band result ultimately requires ∼100,000 to 500,000 core-hours depending on the scenario.

We now evaluate whether the Solar data applied modifies our previous conclusions regarding cold astrophysical scenarios being inconsistent with the latest mass measurements. As can be seen in Figure 3, the MCMC calculations with Arnould+07 and Sneden+08 give similar mass predictions in the cold case, with the mass surface behavior at N = 103 and N = 108 as the main features forming the peak consistently appearing in the trends of both calculations. As discussed in [15], the time evolution of peak formation in the cold case first starts with a shifted peak with highest abundance at A = 162, which is moved via late time neutron capture to having highest abundance at A = 164 as predicted by Arnould+07. Thus in the case of Sneden+08 data which peaks instead at A = 162, the MCMC mass solution does not have to be significantly modified as it can already accommodate an abundance pile-up at A = 162, leading to relatively minor mass differences near N = 100 where the Sneden+08 case requires some enhancement in the stability of such nuclear species in order to keep the highest abundance from shifting beyond A = 162. Most importantly, we find that the differing peak placement of these distinct r-process Solar residual evaluations does not present an avenue towards resolving the tension between the predicted masses and the latest mass measurements given this cold astrophysical outflow.

FIGURE 3

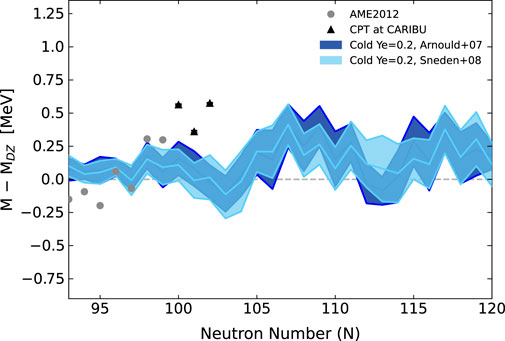
FIGURE 3. The MCMC predicted masses for samarium (Z =62) given the cold, moderately neutron-rich outflow with different sets of Solar data applied: those from Arnould+07 [29, 30] with symmeterized errors (as described in [15]) (dark blue, band derived from 50 runs) as well as the Solar residuals from Sneden+08 [32] (light blue, band derived from 25 runs) which differ in their prediction for the location of highest abundance in the rare-earths (A = 162 for [32] and A = 164 for [29, 30]).

We next consider the impact of the Solar data on mass solutions in the hot astrophysical scenario. Our uncertainty bands are derived from 50 MCMC runs when applying Arnould+07 and Sneden+08 Solar data and in the case of Beer+97 data are determined from 25 runs. As can be seen in Figure 3 of [15], previous investigations demonstrated that a 20 run result can underestimate the total uncertainty band by at most 0.26 MeV or 0.05 MeV on average when considering the N = 93–110 range which influences rare-earth peak formation most strongly. For the 30 run case we find this underestimate to be only at most 0.06 MeV or 0.02 MeV on average. Therefore we estimate that our 25 run results likely underrepresent the reported total uncertainty by roughly 0.035–0.16 MeV, but still adequately capture the overall mass surface trends.

As discussed in [15], peak formation in the hot case centers around nuclei being held at neutron number N = 104 during the time evolution of the synthesis. To achieve this, in the case of Arnould+07 data, we require a strong difference in the predicted masses at N = 102 and N = 104 which can be seen as a dive in the mass surface shown in Figure 4. The latest precision measurements agree with this predicted N = 102 rise, however measurements fall just short of providing information on mass behavior at N = 104. Contrary to the result using Arnould+07 Solar data, the MCMC predictions when Sneden+08 data is applied show the drop in the mass surface is needed to instead begin at neutron number N = 100 in order for the highest abundance peak to be produced instead at A = 162. This behavior is also present in the predicted MCMC solution using the Solar data of Beer+97 since this case also requires higher abundances than Arnould+07 at A = 162, 163 and a lower abundance than Arounld+07 at A = 164. Since this drop in the predicted masses after N = 100 is inconsistent with CPT measurements, we find that Solar evaluations in which the rare-earth peak has its highest abundance at A < 164 to be in tension with the latest mass data. Additionally, from Figure 4 we can see directly the influence of the size of the Solar data error bars. The case with Sneden+08 and Arnould+07 data show very similarly sized mass surface bands whereas significantly tighter mass surface bands are predicted in the Beer+97 case (even with accounting for the slight underestimate of the bands due to the smaller statistics of a 25 run result) which is consistent with expectations given that this set has the smallest error on average. Interestingly, we find that regardless of the differences in the Solar data values and overall errors, all MCMC solutions in hot scenarios predict a local region of enhanced stability at N = 104.

FIGURE 4

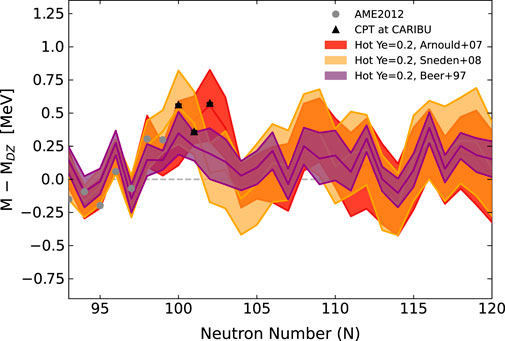
FIGURE 4. The MCMC predicted masses for samarium (Z =62) given the hot, moderately neutron-rich outflow with different sets of Solar data applied: those from Arnould+07 [29, 30] with symmeterized errors (as described in [15]) (red, band derived from 50 runs), those from Sneden+08 [32] (orange, band derived from 50 runs), and those reported in Beer+97 [31] (purple, band derived from 25 runs).

Here we demonstrated that studies, such as the MCMC work presented, which seek to be quantitative when using Solar abundance data are directly dependent upon a careful accounting of abundance uncertainties. The Solar r-process abundances are regularly used as a comparison point with theoretical nucleosynthesis calculations, however often the associated error on these abundances is not considered. Since the Solar r-process abundances are in actuality the ‘residual’ abundances remaining after subtracting the predicted s-process contribution from the total Solar inventory, our understanding of the Solar System r-process content is directly dependent on uncertainties in s-process nucleosynthesis predictions. More recent evaluations have demonstrated the importance of accounting for new neutron capture measurements [34] and more sophisticated treatments of the s-process astrophysical site [35]. Nevertheless, the r-process community remains in need of updated Solar s-process subtractions which put together all such new information while also carefully propagating the uncertainties associated with the meteoritic and spectroscopic data which are used to determine the total abundances of Solar System heavy elements.

The application of distinct Solar data evaluations reveals that the mass predictions of our MCMC are sensitive to both the location of the highest peak abundance as well as the abundance error estimates, such that both the predicted uncertainty bands and overall mass trends can be affected. Nevertheless, two important general conclusions from utilizing Arnould+07 Solar data in our previous MCMC work [15] remain robust, that is: (1) cold astrophysical outflows remain inconsistent with the latest mass measurements and (2) hot astrophysical outflows consistently point to a local enhancement in stability at N = 104 as the mechanism by which the rare-earth peak forms. This consistency further argues for the importance of mass measurements at this neutron number, as may be possible in the future at Argonne National Laboratory’s N = 126 Factory, the Facility for Rare Isotopes Beams (FRIB), or the Advanced Rare Isotope Laboratory (ARIEL) at TRIUMF.

Since we have demonstrated that our MCMC method is sensitive to the overall shape and errors of the r-process abundances, our calculations permit us to consider what the masses of neutron-rich nuclei can teach us about Solar r-process evaluations. We find that in the case of Solar evaluations which predict the highest abundance of the rare-earth peak to occur before A = 164, our method points to the need for masses which are not consistent with the most recent measurements. Therefore, this result favors Solar r-process evaluations with the highest abundance of the rare-earth peak located at A = 164 as those which can be readily replicated given the latest nuclear data. We note that robust conclusions regarding Solar r-process abundances from such an MCMC approach require more exhaustively considering the uncertainties of all nuclear data inputs such as the β-decay strength function and neutron capture model. Therefore, since the interplay between β-decay, neutron capture, and photodissociation is at the heart of peak formation, future MCMC studies which consider other β-decay and neutron capture treatments when propagating mass changes to astrophysical reaction and decay rates could yield even more robust statements on whether the highest rare-earth peak abundance can occur at A < 164. We leave these investigations to future work, but note that such an approach could apply a more global analysis with both mass and β-decay measurements guiding the Markov chains and therefore informing uncertainty estimates. Nevertheless, the work presented here highlights how statistical methods such as our MCMC procedure can be used to explicitly link nuclear data and astrophysical observations, thereby serving to inform and drive progress in both nuclear physics and astrophysics communities.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

Development of the MCMC code was performed by MM and NV. The MCMC calculations and the analysis of results were performed by NV. NV was the primary author of the manuscript, with MM, GM, and RS participating in the writing process.

Funding

The work of NV acknowledges the support of the Natural Sciences and Engineering Research Council of Canada (NSERC). The work of NV, GM, MM, and RS was partly supported by the Fission In R-process Elements (FIRE) topical collaboration in nuclear theory, funded by the U.S. Department of Energy. RS and GM also acknowledge support by the US Department of Energy from grant LA22-ML-DE-FOA-2440. Additional support was provided by the U.S. Department of Energy through contract numbers DE-FG02-02ER41216 (GM), DE-FG02-95-ER40934 (R.S.), and DE-SC0018232 (SciDAC TEAMS collaboration, RS). RS and GM also acknowledge support by the National Science Foundation N3AS Hub Grant No. PHY-1630782 and Physics Frontiers Center No. PHY-2020275. MM was supported by the US Department of Energy through the Los Alamos National Laboratory. Los Alamos National Laboratory is operated by Triad National Security, LLC, for the National Nuclear Security Administration of U.S. Department of Energy (Contract No. 89233218CNA000001). This work was partially enabled by the National Science Foundation under Grant No. PHY-1430152 (JINA Center for the Evolution of the Elements). This manuscript has been released via Los Alamos National Laboratory report number LA-UR-22-29364.

Acknowledgments

This work utilized the computational re- sources of the Laboratory Computing Resource Center at Argonne National Laboratory (ANL LCRC), the University of Notre Dame Center for Research Computing (ND CRC), as well as TRIUMF laboratory’s Theory Group Cluster Oak (TRIUMF Oak). We specifically acknowledge the assistance of Stanislav Sergienko (ANL LCRC), Scott Hampton (ND CRC), and Kel Raywood (TRIUMF Oak).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Abbott BP. Erratum: Upper limits on the stochastic gravitational-wave background from advanced LIGO's first observing run. Phys Rev Lett (2017) 119:029901. doi:10.1103/PhysRevLett.119.029901

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Abbott BP, Abbott R, Abbott TD, Acernese F, Ackley K, Adams C, et al. Multi-messenger observations of a binary neutron star merger. ApJL (2017) 848:L12. doi:10.3847/2041-8213/aa91c9

CrossRef Full Text | Google Scholar

3. Abbott BP, Abbott R, Abbott TD, et al. Erratum: Tests of general relativity with GW150914. Phys Rev Lett (2018) 121:129902. arXiv:1805.11581 [gr-qc]. doi:10.1103/PhysRevLett.121.129902

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Villar VA, Guillochon J, Berger E, Metzger BD, Cowperthwaite PS, Nicholl M, et al. The combined ultraviolet, optical, and near-infrared light curves of the kilonova associated with the binary neutron star merger GW170817: Unified data set, analytic models, and physical implications. Astrophys J (2017) 851:L21. doi:10.3847/2041-8213/aa9c84

CrossRef Full Text | Google Scholar

5. Cowperthwaite PS, Berger E, Villar VA, Metzger BD, Nicholl M, Chornock R, et al. Electromagnetic counterpart of the binary neutron star merger LIGO/Virgo GW170817. II. UV, optical, and near-infrared light curves and comparison to kilonova models. ApJL (2017) 848:L17. doi:10.3847/2041-8213/aa8fc7

CrossRef Full Text | Google Scholar

6. Lodders K. Principles and perspectives in cosmochemistry. Astrophysics Space Sci Proc (2010) 16:379.

Google Scholar

7. Frebel A. From nuclei to the cosmos: Tracing heavy-element production with the oldest stars. Annu Rev Nucl Part Sci (2018) 68:237–69. doi:10.1146/annurev-nucl-101917-021141

CrossRef Full Text | Google Scholar

8. Mumpower MR, Surman R, Fang DL, Beard M, Möller P, Kawano T, et al. Impact of individual nuclear masses onr-process abundances. Phys Rev C (2015) 92:035807. doi:10.1103/physrevc.92.035807

CrossRef Full Text | Google Scholar

9. Eichler M, Arcones A, Kelic A, Korobkin O, Langanke K, Marketin T, et al. The role of fission in neutron star mergers and its impact on ther-process peaks. ApJ (2015) 808:30. doi:10.1088/0004-637x/808/1/30

CrossRef Full Text | Google Scholar

10. Goriely S. Towards more accurate and reliable predictions for nuclear applications. Eur Phys J A (2015) 51:172. doi:10.1140/epja/i2015-15172-2

CrossRef Full Text | Google Scholar

11. Vassh N, Vogt R, Surman R, Randrup J, Sprouse TM, Mumpower MR, et al. Using excitation-energy dependent fission yields to identify key fissioning nuclei in r-process nucleosynthesis. J Phys G: Nucl Part Phys (2019) 46:065202. doi:10.1088/1361-6471/ab0bea

CrossRef Full Text | Google Scholar

12. Mumpower MR, McLaughlin GC, Surman R, Steiner AW. The link between rare-earth peak formation and the astrophysical site of therprocess. ApJ (2016) 833:282. doi:10.3847/1538-4357/833/2/282

CrossRef Full Text | Google Scholar

13. Mumpower MR, McLaughlin GC, Surman R, Steiner AW. Reverse engineering nuclear properties from rare Earth abundances in therprocess. J Phys G: Nucl Part Phys (2017) 44:034003. doi:10.1088/1361-6471/44/3/034003

CrossRef Full Text | Google Scholar

14. Orford R, Vassh N, Clark JA, McLaughlin GC, Mumpower MR, Savard G, et al. Precision mass measurements of neutron-rich neodymium and samarium Isotopes and their role in understanding rare-earth peak formation. Phys Rev Lett (2018) 120:262702. doi:10.1103/physrevlett.120.262702

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Vassh N, McLaughlin GC, Mumpower MR, Surman R. Markov chain Monte Carlo predictions of neutron-rich lanthanide properties as a probe of r-process dynamics. ApJ (2021) 90798(2021):98. doi:10.3847/1538-4357/abd035

CrossRef Full Text | Google Scholar

16. Orford R, Vassh N, Clark JA, McLaughlin GC, Mumpower MR, Ray D, et al. Searching for the origin of the rare-Earth peak with precision mass measurements across Ce–Eu isotopic chains. Phys Rev C (2022) 105:L052802. doi:10.1103/physrevc.105.l052802

CrossRef Full Text | Google Scholar

17. Vassh N, McLaughlin GC, Mumpower MR, Surman R. The need for a local nuclear physics feature in the neutron-rich rare-earths to explain Solar r-process abundances. arXiv e-prints, arXiv:2202.09437 (2022). doi:10.48550/arxiv.2202.09437

CrossRef Full Text | Google Scholar

18. Burbidge EM, Burbidge GR, Fowler WA, Hoyle F. Synthesis of the elements in stars. Rev Mod Phys (1957) 29:547–650. doi:10.1103/revmodphys.29.547

CrossRef Full Text | Google Scholar

19. Surman R, Engel J, Bennett JR, Meyer BS. Source of the rare-earth element peak inr-process nucleosynthesis. Phys Rev Lett (1997) 79:1809–12. doi:10.1103/physrevlett.79.1809

CrossRef Full Text | Google Scholar

20. Mumpower MR, McLaughlin GC, Surman R. Formation of the rare-Earth peak: Gaining insight into late-timer-process dynamics. Phys Rev C (2012) 85:045801. doi:10.1103/physrevc.85.045801

CrossRef Full Text | Google Scholar

21. Duflo J, Zuker AP. Microscopic mass formulas. Phys Rev C (1995) 52:R23–7. doi:10.1103/physrevc.52.r23

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Audi G, Wang M, Wapstra AH, Kondev FG, MacCormick M, Xu X, et al. The Ame2012 atomic mass evaluation. Chin Phys C (2012) 36:1287–602. doi:10.1088/1674-1137/36/12/002

CrossRef Full Text | Google Scholar

23. Perego A, Rosswog S, Cabezón RM, Korobkin O, Käppeli R, Arcones A, et al. Neutrino-driven winds from neutron star merger remnants. Mon Not R Astron Soc (2014) 443:3134–56. doi:10.1093/mnras/stu1352

CrossRef Full Text | Google Scholar

24. Just O, Bauswein A, Pulpillo RA, Goriely S, Janka H-T. Comprehensive nucleosynthesis analysis for ejecta of compact binary mergers. Mon Not R Astron Soc (2015) 448:541–67. doi:10.1093/mnras/stv009

CrossRef Full Text | Google Scholar

25. Radice D, Perego A, Hotokezaka K, Fromm SA, Bernuzzi S, Roberts LF. Binary neutron star mergers: Mass ejection, electromagnetic counterparts, and nucleosynthesis. ApJ (2018) 869:130. doi:10.3847/1538-4357/aaf054

CrossRef Full Text | Google Scholar

26. Foucart F, Duez MD, Hebert F, Kidder LE, Pfeiffer HP, Scheel MA. Monte-carlo neutrino transport in neutron star merger simulations. Astrophys J (2020) 902:L27. doi:10.3847/2041-8213/abbb87

CrossRef Full Text | Google Scholar

27. Reichert M, Obergaulinger M, Eichler M, Aloy MÁ, Arcones A. Mon Not R Astron Soc (2021) 501:5733.

28. Mösta P, Roberts LF, Halevi G, Ott CD, Lippuner J, Haas R, et al. r-Process nucleosynthesis from three-dimensional magnetorotational core-collapse supernovae. ApJ (2018) 864:171. doi:10.3847/1538-4357/aad6ec

CrossRef Full Text | Google Scholar

29. Arnould M, Goriely S, Takahashi K. The r-process of stellar nucleosynthesis: Astrophysics and nuclear physics achievements and mysteries. Phys Rep (2007) 450:97–213. doi:10.1016/j.physrep.2007.06.002

CrossRef Full Text | Google Scholar

30. Goriely S. Astron Astrophys (1999) 342:881.

31. Beer H, Corvi F, Mutti P. Neutron capture of the bottleneck Isotopes¹³⁸Ba and ²⁰⁸Pb, s-process studies, and ther-process abundance distribution. Astrophys J (1997) 474:843–61. doi:10.1086/303480

CrossRef Full Text | Google Scholar

32. Sneden C, Cowan JJ, Gallino R. Neutron-capture elements in the early galaxy. Annu Rev Astron Astrophys (2008) 46:241–88. doi:10.1146/annurev.astro.46.060407.145207

CrossRef Full Text | Google Scholar

33. Arlandini C, Käppeler F, Wisshak K, Gallino R, Lugaro M, Busso M, et al. Neutron capture in low-mass asymptotic giant Branch stars: Cross sections and abundance signatures. Astrophys J (1999) 525:886–900. arXiv:astro-ph/9906266 [astro-ph]. doi:10.1086/307938

CrossRef Full Text | Google Scholar

34. Pritychenko B. Determination of solar system R-process abundances using ENDF/B-VIII.0 and TENDL-2015 libraries. aXiv e-prints, aXiv e-prints, arXiv:2012.06728 [astro-ph.SR] (2020). doi:10.48550/arxiv.2012.06728

CrossRef Full Text | Google Scholar

35. Prantzos N, Abia C, Cristallo S, Limongi M, Chieffi A. Chemical evolution with rotating massive star yields II. A new assessment of the solar s- and r-process components. Mon Not R Astron Soc (2020) 491:1832. arXiv:1911.02545 [astro-ph.GA]

Google Scholar