State-to-state dynamics of the C+(2P) + SH(X2Π) → H(2S) + CS+(X2Σ+) reaction using a time-dependent wave packet and quasi-classical trajectory methods

The time-dependent quantum wave packet (TDWP) and quasi-classical trajectory (QCT) are the basic research methods of reaction dynamics. Utilizing these two methods, the total reaction probability (J = 0), integral cross section (ICS), and rate parameter for the C⁺(²P) + SH(X²Π)(v = 0, 1, 2, 3) → H(²S) + CS⁺(X²Σ⁺) reactions are calculated on an accurate potential energy surface [Zhang et al. Phys. Chem. Chem. Phys. 2022, 24, 1007]. The results of QCT are slightly different from those of the TDWP in value, but the trend is consistent. They are also weakly dependent on the initial vibrational excitation of SH. The state-to-state reaction probability and ICS at fixed collision energies (0.1, 0.3, 0.5, and 0.7 eV) are first calculated using QCT methods. It is hoped that our work can attract experimentalists to study the dynamics of this interesting but rarely discussed system.

1 Introduction

The ion-neutral collisions in the interstellar medium play essential roles in the field of molecular physics and astrophysics [1, 2]. Also, the interaction between the C⁺ ion and SH radical is considered to be significant in the production of carbon monosulfide ions. The precise dynamics information on this reaction requires a full-dimensional analytical potential energy surface (PES) of high quality.

The research on HCS⁺(X¹Σ⁺) could date back to 1978 when Bruna et al. [3] found that the global minimum HCS⁺ is a linear structure with CS⁺ = 2.814 a₀ and CH = 2.062 a₀, and one of its isomer, HSC⁺, is located 4.770 eV above HCS⁺. The equilibrium structure of HCS⁺ was also calculated by Botschwina and Sebald [4], who reported the intensities of the stretching vibrations simultaneously. Wong et al. [5] found a tiny barrier (about 0.104 eV) between HCS⁺ and HSC⁺, and HSC⁺ is 3.089 eV above HCS⁺. Puzzarini [6] accurately investigated the structural and energetic characteristics of HCS⁺ and HSC⁺ using the coupled cluster method with single and double excitations with a perturbative treatment of the connected triples [CCSD(T)] method, and the results are in good agreement with the experimental results. Kaur and Kumar [7, 8] computed the various energy transfer channels of the collision between atomic H and CS⁺ molecular ions and 3D ab initio PESs of the ground state and low-lying excited states of the HCS⁺ system. Recently, the analytical global three-dimensional PES of HCS⁺(X¹Σ⁺) for the C⁺(²P) + SH(X²Π) → H(²S) + CS⁺(X²Σ⁺) reaction was first constructed by Zhang et al. [9]. This PES is fitted by a grid of 7,907 ab initio energy points computed at a multi-reference configuration interaction level plus the Davidson correction [MRCI(Q)] [10, 11] with aug-cc-pV(5 + d)Z basis sets [12, 13]. The MRCI method uses the full-valence complete active space self-consistent field (CASSCF) [14] wave function as a reference. By using this PES of high accuracy, with a final root mean square error of 0.0419 eV and a maximum error of 0.0251 eV, the structures and locations of the global minimum HCS⁺, local minimum HSC⁺, and transition states are obtained. Scrutiny of the HCS⁺(X¹Σ⁺) PES shows that the isomeric HSC⁺ is in a potential well, 3.178 eV above the most stable HCS⁺ structure, but it is separated from HCS⁺ only with a tiny barrier (0.139 eV). According to the PES, the most likely minimum energy path for the C⁺(²P) + SH(X²Π) → H(²S) + CS⁺(X²Σ⁺) reaction and the energies of relative stationary points are displayed in Figure 1. The reaction is found to be exothermic (≈ 2.555 eV) and barrierless relative to the entrance channel.

FIGURE 1

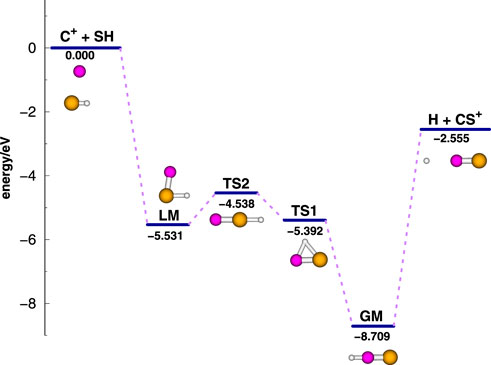
FIGURE 1. Energy diagram for the reaction pathway and relative stationary points of the C⁺( [2]P) + SH(X²Π) → H( [2]S) + CS⁺(X²Σ⁺) reaction. Energies are given relative to the C⁺( [2]P) + SH(X²Π) asymptote with the unit of eV.

The reaction probability and integral cross section (ICS) were first calculated by Zhang et al. [9] with a time-dependent quantum wave packet (TDWP) and quasi-classical trajectory (QCT) methods [9]. The calculated reaction probabilities for total angular momentum J = 0, 10, 60, and 120 by the TDWP and QCT are consistent with each other at high collision energies. Although the divergence in the ICSs obtained from the two methods is evident, the evolutional trend is consistent. Substantial dynamic information on the title reaction should be deduced with a more time-saving QCT method in the high-energy region in comparison with the time-consuming TDWP calculations. Finally, the type of the title reaction is given by using the QCT method. The complex with a long life easily formed in the title reaction is attributed to a distinct potential well in the path of reaction. Therefore, the indirect reaction is the primary mechanism for C⁺(²P) + SH(X²Π) → H(²S) + CS⁺(X²Σ⁺).

In the present work, both the TDWP and QCT methods are applied to study the C⁺(²P) + SH(X²Π) → H(²S) + CS⁺(X²Σ⁺) reaction on the PES of Zhang et al. [9] at the state-to-state level. The paper is structured as follows. Section 2 gives a brief survey of the TDWP and QCT theoretical methods used in this work. The results and discussion, and conclusions are explained in Section 3 and Section 4, respectively.

2 Theory

2.1 Time-dependent quantum wave packet

The TDWP [15–20] method is applied to calculate the accurate dynamic information on the C⁺(²P) + SH(X²Π) → H(²S) + CS⁺(X²Σ⁺) reaction. The core idea is to get the numerical solution to the Schrödinger equation through the split-operator propagation scheme. The Hamiltonian is expressed in reactant Jacobi coordinates as follows:

$H=-\frac{\hslash }{2{\mu }_R}\frac{{\partial }^2}{\partial R^2}+\frac{{\left(\mathit{J}-\mathit{j}\right)}^2}{2{\mu }_R{R}^2}+\frac{{\mathit{j}}^2}{2{\mu }_r{r}^2}+V\left(R,r,\gamma \right)+h\left(r\right),(1)$

where r, R, and γ are the bond length of the reactant molecule, the distance from the atom to the center-of mass of the diatomic, and the angle between the R and r vectors, respectively. μ_R and μ_r are the reduced masses between the center-of-mass of the diatomic and atom and the reduced mass of the reactant molecule, respectively. J and j are the total angular momentum operators and the rotational angular momentum operator of BC, respectively. V(R, r, and γ) is the potential energy (total energy deducted from the diatomic potential energy), and h(r) is the diatomic reference of Hamiltonian defined as follows:

$h\left(r\right)=-\frac{\hslash }{2{\mu }_r}\frac{{\partial }^2}{\partial r^2}+V\left(r\right),(2)$

where V(r) is the diatomic reference potential usually used as an asymptotic diatomic potential.

In this calculation, the initial wave packet is usually chosen as the product of a localized translational wave packet and a specific rovibrational eigenfunction [18, 21]. After the wave packet is propagated into the product region, the reaction probability and ICS can be calculated as follows:

$P_{\mathit{vjk}}^J\left(E\right)=\frac{\hslash }{{\mu }_r}\mathrm{I}\mathrm{m}\left[⟨\mathrm{\Psi }\left(E\right)|\delta \left(r-r_0\right)\frac{\partial }{\partial r}|\mathrm{\Psi }\left(E\right)⟩\right],(3)$

${\sigma }_{vj}\left(E\right)=\frac{1}{2j_0+1}\frac{\pi }{k^{\prime 2}}\sum _{Jk}\left(2J+1\right)P_{\mathit{vjk}}^J\left(E\right),(4)$

where v and j are the vibrational and rotational quantum numbers of the reactant, and k is the projection quantum number of j. Ψ(E) can be derived from the Fourier transform of the time-dependent wave function Ψ(t). $k^{\prime }=\sqrt{2{\mu }_{r}E}$, with E being the collision energy. To get convergence results, a lot of test calculations are carried out for each parameter. Table 1 lists the parameters used in the quantum calculations of the C⁺(²P) + SH(X²Π) → H(²S) + CS⁺(X²Σ⁺) reaction.

TABLE 1

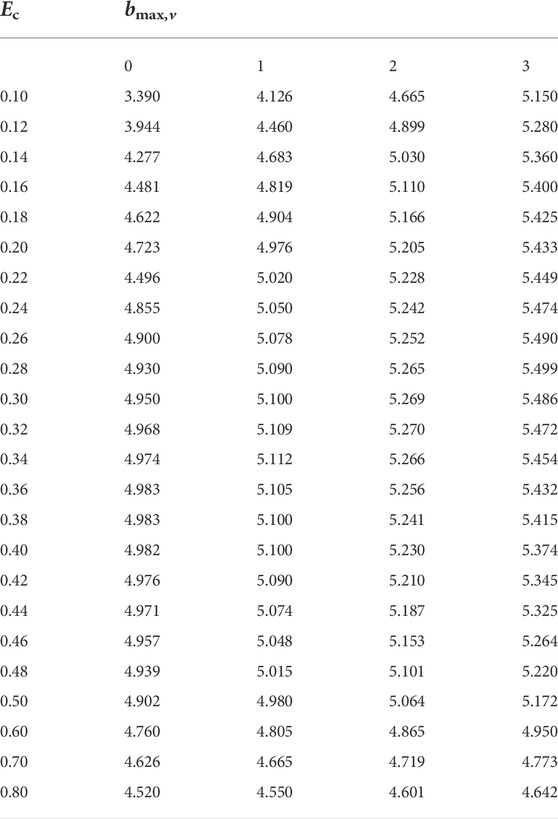
TABLE 1. Numerical parameters used in the present quantum wavepacket calculations (atomic units unless the number of argument).

The rate constant determined by the ICS σ_vj(E) is as follows:

$k_{vj}\left(T\right)=g_e\left(T\right){\left(\frac{8}{\pi {\mu }_R{\left(k_{B}T\right)}^3}\right)}^{\frac{1}{2}}{\int }_0^{\infty }E{\sigma }_{vj}\left(E\right){\mathrm{e}}^{-E/k_{B}T}dE,(5)$

where k_B is the Boltzmann constant and g_e(T) is the electronic partition function with a form, which is as follows:

$g_e\left(T\right)=\frac{1}{\left(2+4{\mathrm{e}}^{-91.25/T}\right)\left(2+2{\mathrm{e}}^{-542.36/T}\right)}.(6)$

2.2 Quasi-classical trajectory

The QCT method [22–27] has been widely applied to explore chemical reaction dynamics [28–33]. Here, only the details pertinent to the present work are summarized. In the QCT calculation [34–37], the distance from the atom C⁺ to the center-of-mass of S and H is set to 20 $\mathring{\mathrm{A}}$ for the conservation of total energy and angular momentum. The total 100,000 trajectories are introduced for the C⁺(²P) + SH(X²Π) → H(²S) + CS⁺(X²Σ⁺) reaction, with the time step being 0.1 fs. The impact parameter b_max,v tabulated in Table 2 is simulated at each pair of E and v in the collision energy ranging from 0.1 eV to 0.8 eV and the initial vibrational quantum number ranges from 0 to 3. In the calculations, b_max,v is obtained by systematically increasing the value of the impact parameter, b, until no reaction trajectory is found for each trajectory at a given collision energy and initial vibrational quantum number. The ICS can be given as follows:

${\sigma }_v=\pi b_{\text{max,}v}^2{P}_v,(7)$

where $P_v=\frac{N_r}{N}$ is the average reaction probability, with N being the total trajectory number and N_r the reactive trajectory number.

TABLE 2

TABLE 2. Values of b_max (in Å) for the C⁺ + SH(v = 0 − 3, j = 0) → H + CS⁺ reaction.

3 Results and discussion

3.1 Total and state-to-state reaction probabilities at J = 0

Figure 2 depicts the evolution of total reaction probability (J = 0) with collision energy obtained by employing the TDWP and QCT methods for C⁺ + SH(v = 0–3, j = 0) reactions. The reaction probabilities selected initially (v = 0–3; j = 0) illustrate that the title reaction is typically exothermic without threshold characteristics; in other words, the reaction is barrierless and the probability decreases with the increase of collision energy. A deep potential well in the reaction path makes the TDWP reaction probability in the upper panel a fluctuating decline. It is easily found that the reaction probability seems to decrease first with initial v from 0 to 2 and then hardly changes with v at higher collision energies. With the increase in the vibrational energy level, the reaction probability becomes more and more gentle with the collision energy, and when v = 3, the probability is the most gentle. This is because, at higher vibration energy levels, the effect of the collision energy is weaker on the reaction probability. The QCT reaction probability (lower panel) perfectly reproduces the overall shape of the TDWP in the whole collision energy range (from v = 0 to 3).

FIGURE 2

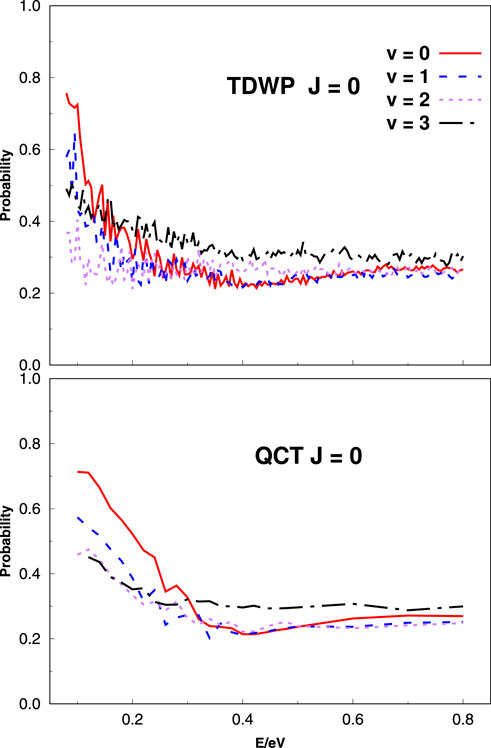
FIGURE 2. Total reaction probabilities at J = 0 as a function of collision energy calculated using the TDWP (top panel) and QCT (bottom panel) methods for various initial vibrational states of the SH for the title reaction.

Figure 3 reveals the QCT reaction probability of product vibrational distributions at J = 0 for the reaction of C⁺ + SH(v = 0, j = 0) → H + CS⁺(v′) at certain collision energies (0.1, 0.3, 0.5, and 0.7 eV). It is easily found in a great number of vibrational excitation products with a distinguished population inversion. At E_c = 0.1 eV, the distribution is bimodal, peaking at v′ = 11 and v′ = 13 and the highest vibrational excitation product at v′ = 19. The vibrational distributions get hotter and wider as the collision energy increases. Also, the v′ state-resolved reaction probability decreases gradually when the collision energy increases, consistent with the total probability.

FIGURE 3

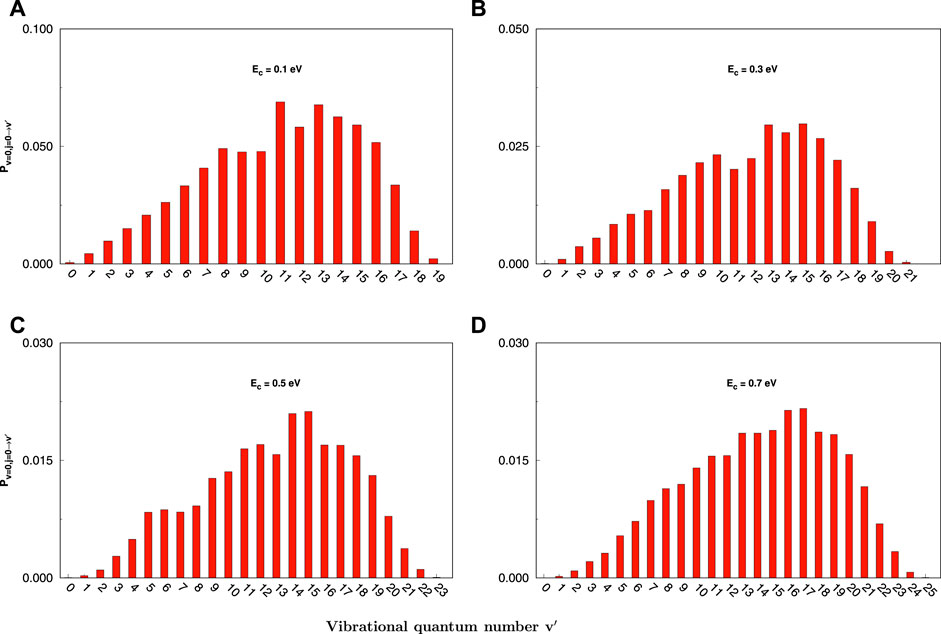
FIGURE 3. Final v′ state-resolved reaction probabilities at J = 0 for the C⁺ + SH(v = 0, j = 0) → H + CS⁺(v′) reaction at selected collision energies (0.1, 0.3, 0.5, and 0.7 eV) obtained with the QCT method. (A) for 0.1 eV, (B) for 0.3 eV, (C) for 0.5 eV, (D) for 0.7 eV.

Figure 4 displays the final j′ state-resolved reaction probabilities for the most populated product vibrational quantum states, i.e., v′ = 13, 14, and 15, at the four selected collision energies. Similarly, the higher the collision energy, the higher the rotational energy level and the more obvious the population inversion are. Meanwhile, the shapes of probabilities for each v′ state resemble each other as explained. On the whole, the QCT product rotational distribution shows a significant oscillatory behavior, particularly at the low collision energy for low final rotational quantum states. It clearly appears that the lower the vibrational excitation, the higher the rotational excitation of products with the same collision energy is. For instance, at 0.1eV, the maximum product rotational energy level j′ is 64 when the vibrational energy level of the product v′ = 13, while for v′ = 14 and v′ = 15, the maximum of j′ is 61 and 55, respectively, which is consistent with the energy conservation.

FIGURE 4

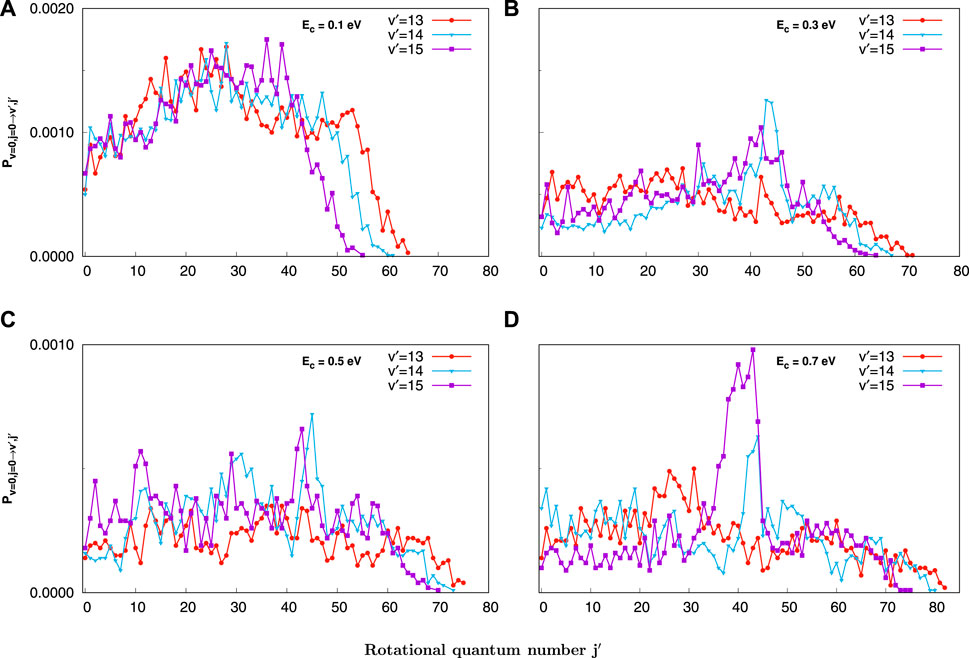
FIGURE 4. Final j′ state-resolved reaction probabilities at J = 0 for the C⁺ + SH(v = 0, j = 0) → H + CS⁺(v′ = 13, 14, 15) reaction at selected collision energies (0.1, 0.3, 0.5, and 0.7 eV) obtained with the QCT method. (A) for 0.1 eV, (B) for 0.3 eV, (C) for 0.5 eV, (D) for 0.7 eV.

QCT vibrational state-resolved reaction probabilities at the various collision energies for C⁺ + SH(v = 0–3, j = 0) → H + CS⁺ are shown in Figure 5. The distinguishing feature of the vibrational distributions for the reaction is that because of the rise of v or collision energy, the distribution curve becomes wider and the peak value shifts rightward. The distributions are oscillatory, especially at lower collision energies. Moreover, the shapes of reaction probability curves for each v are similar to each other. Analogously, the reaction probability gradually decreases when the collision energy increases, consistent with the total probability.

FIGURE 5

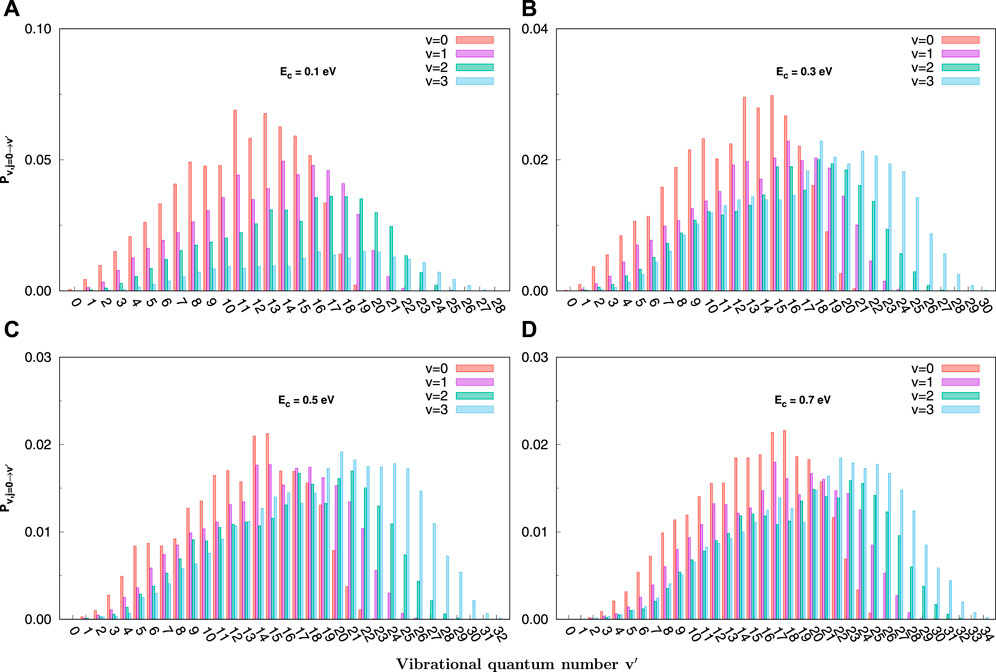
FIGURE 5. Final v′ state-resolved reaction probabilities at J = 0 for the C⁺ + SH(v = 0 − 3, j = 0) → H + CS⁺(v′) reaction at selected collision energies (0.1, 0.3, 0.5, and 0.7 eV) obtained with the QCT method. (A) for 0.1 eV, (B) for 0.3 eV, (C) for 0.5 eV, (D) for 0.7 eV.

3.2 Total and state-to-state integral cross sections

Figure 6 indicates the TDWP and QCT ICSs as a function of collision energy for C⁺ + SH(v = 0–3, j = 0) → H + CS⁺. The ICSs calculated both with the TDWP and QCT methods climb over a mountain and gradually reach a plateau with increasing collision energy. The behavior is the common characteristic of barrierless exothermic reactions and similar to the same type reactions such as H + CH [38–40], S⁺ + H₂ [41], and C + SH [30, 42]. First, we find that the shapes of ICSs for C⁺ + SH(v = 0–3, j = 0) are analogous in four panels obtained by the TDWP and QCT methods, indicating that the ICSs are insensitive to the vibrational quantum state of reactant SH. Then, it is distinguished that the QCT ICSs are slightly higher than the TDWP ICSs, particularly at low collision energies. The reason may be that in the present TDWP calculation, the zero-point energy (ZPE) is considered naturally, whereas in the QCT calculation, the ZPE is not taken into account, which leads to the larger ICS of the QCT than the TDWP calculation in the low energy range for such an exothermic reaction. In other words, the quantum effect cannot be ignored, especially at low collision energies. The error bars are calculated and added in Figure 6 for the QCT method. We find that the uncertainties of ICSs for the title reactions are very small in the entire collision energy ranges, so their accuracy can be warranted. Since the trend of the ICSs obtained by these two methods is consistent and as the two cases gradually approach the vibrational quantum state of SH increases, the QCT method can be used for further study due to the low time consumption.

FIGURE 6

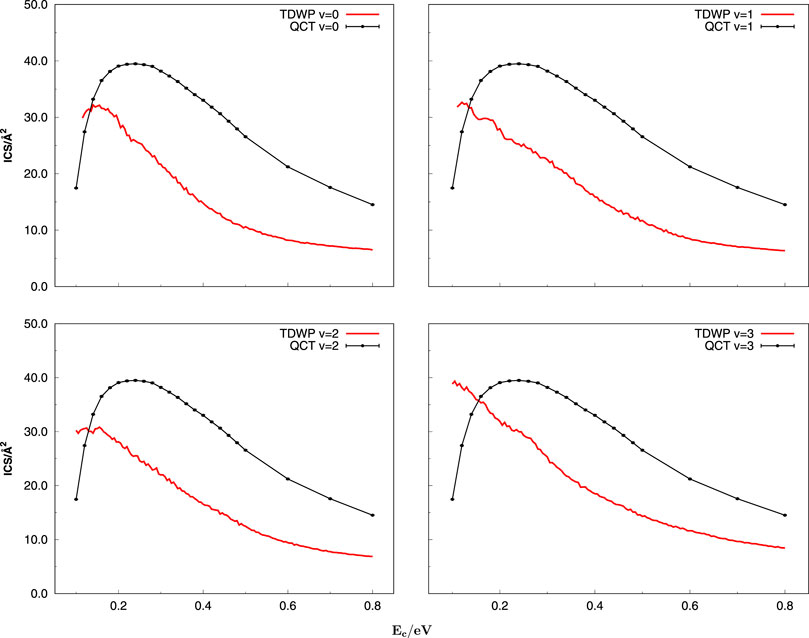
FIGURE 6. Integral cross sections as a function of collision energy for the C⁺ + SH(v = 0 − 3, j = 0) → H + CS⁺(v′) reaction obtained with the TDWP and QCT methodologies.

The vibrational state-resolved ICSs computed by the QCT method at various collision energies (0.1, 0.3, 0.5, and 0.7 eV) for C⁺ + SH(v = 0–3, j = 0) → H + CS⁺ are shown in Figure 7. The most obvious feature is a population inversion of the vibrational distribution peak at a low value of v′. An increase in collision energy and the initial vibrational quantum number can make the ICS distributions wider. The distributions become hotter along with the enlargement of the initial vibrational quantum number. However, the distributions become colder as collision energy increases, at variance with the effect of the initial vibrational quantum number.

FIGURE 7

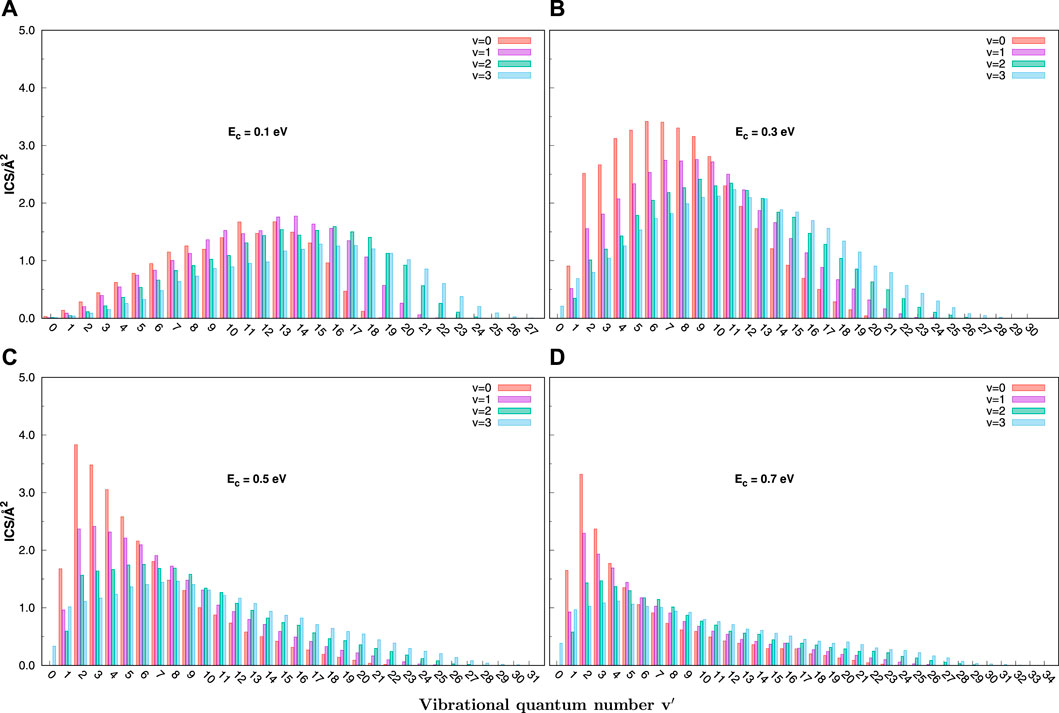
FIGURE 7. Final v′ state-resolved integral cross sections for the C⁺ + SH(v = 0 − 3, j = 0) → H + CS⁺(v′) reaction at selected collision energies (0.1, 0.3, 0.5, and 0.7 eV) obtained with the QCT method. (A) for 0.1 eV, (B) for 0.3 eV, (C) for 0.5 eV, (D) for 0.7 eV.

3.3 Rate constants

The initial state-selected rate constants shown in Figure 8 are calculated by the TDWP (in upper panel) and QCT (in lower panel) methods in a large temperature range from 1200 to 92000 K for C⁺ + SH(v = 0–3, j = 0) → H + CS⁺. The current rate constants are calculated by numerical integration over the collision energy in the range of 0.10–0.80 eV. As revealed in Figure 8, both the TDWP and QCT rate constants rise slightly with increasing temperature until reaching a plateau. The increase in the QCT rate constants at a lower temperature is much faster than those of TDWP. In addition, the QCT rate constants are a little higher than the TDWP rate constants; meanwhile, the distributions are consistent with the TDWP and QCT ICSs as a function of collision energy. The TDWP state-selected rate constants are slightly positively correlated with the initial vibrational quantum number of the reagent molecule SH. Nevertheless, the QCT rate constants are insensitive to v, which is analogous to the cross-section results of Figure 6. In conclusion, the rate constants obtained by the TDWP and QCT methods are in essential agreement, especially in the high-temperature region.

FIGURE 8

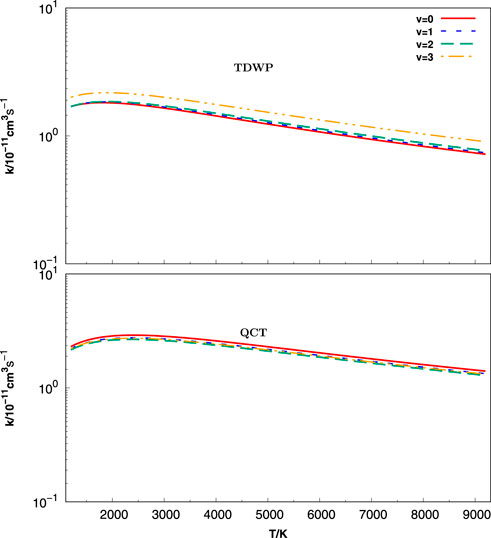
FIGURE 8. Vibrationally state-specific rate constants as a function of temperature for the C⁺ + SH(v = 0 − 3, j = 0) → H + CS⁺ reaction calculated with the TDWP (top panel) and QCT (bottom panel) methods.

In the present work, we provided a new and reliable rate constant for the C⁺ + SH(v = 0–3, j = 0) → H + CS⁺ reaction. Although there are no other theoretical and experimental results for the title reaction on the HCS⁺(X¹Σ⁺) PES, the vibrational distribution information is of deep value for further study of this system.

4 Conclusion

This study presents the initial state-selected reaction probabilities, ICSs, and rate constants calculated with both the QCT and TDWP methods. The QCT reaction probability perfectly reproduces the overall shape of the TDWP results in the whole collision energy region for v = 0 to 3. The ICSs obtained by the QCT are slightly higher than those obtained by the TDWP, and as the initial vibrational quantum state increases, the ICSs obtained by these two methods are in more substantial agreement. The QCT rate constants are slightly higher than those of the TDWP, and ICSs obtained from the two methods show a similar relationship. Overall, the aforementioned QCT results are consistent with those of the TDWP, both showing practical independence with the initial vibrational excitation. The QCT method is employed to obtain the state-to-state reaction probabilities and product state-resolved ICSs at fixed collision energies (0.1, 0.3, 0.5, and 0.7 eV). The probability distributions are hotter, wider, and peak at higher v′ values at higher collision energy and a larger vibrational quantum number. An increase in collision energy and the initial vibrational quantum number can also make the ICS distributions wider. The ICS distributions become hotter along with the enlargement of v, while the collision energy has the opposite effect. Considering the time cost, the QCT method can well describe this reaction. We hope that our work can attract the attention of experimentalists to this fascinating but scarcely studied system.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author contributions

DL wrote the original manuscript and performed the QCT calculations. DL and JZ performed the TDWP calculations. YS and QM proposed the idea, supervised the research work, and revised the manuscript. DL, WW, QM, and LZ discussed and analyzed the results.

Funding

The present work was supported by the National Natural Science Foundation of China (Grant Nos. 12004216, 11904394, 12274265, and 11874241) and the Natural Science Foundation of Shandong Province, China (Grant Nos. ZR2020QA064, ZR2021MA069, and ZR2022MA006).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Thaddeus P, Guelin M, Linke RA. Three new ″nonterrestrial″ molecules. Astrophys J (1981) 246:L41. doi:10.1086/183549

CrossRef Full Text | Google Scholar

2. Margulès L, Lewen F, Winnewisser G, Botschwina P, Müller HSP. The rotational spectrum up to 1 THz and the molecular structure of thiomethylium, HCS⁺. Phys Chem Chem Phys (2003) 5:2770–3. doi:10.1039/b303260d

CrossRef Full Text | Google Scholar

3. Bruna PJ, Peyerimhoff SD, Buenker RJ. Ab initio SCF and CI study of the HCS⁺ − CSH⁺ system: Potential surfaces for hydrogen abstraction and internuclear bending for ground and excited states and vertical spectrum for HCS⁺. Chem Phys (1978) 27:33–43. doi:10.1016/0301-0104(78)85159-3

CrossRef Full Text | Google Scholar

4. Botschwina P, Sebald P. Spectroscopic properties of CS and HCS⁺ from ab initio calculations. J Mol Spectrosc (1985) 110:1–18. doi:10.1016/0022-2852(85)90207-3

CrossRef Full Text | Google Scholar

5. Wong MW, Nobes RH, Radom L. The [HCS]⁺ and \mathrm{[H_2CS]}^{2+} potential energy surfaces: Predictions of bridged equilibrium structures. J Mol Struct THEOCHEM (1988) 163:151–61. doi:10.1016/0166-1280(88)80387-7

CrossRef Full Text | Google Scholar

6. Puzzarini C. The HCS/HSC and HCS⁺/HSC⁺ systems: Molecular properties, isomerization, and energetics. J Chem Phys (2005) 123:024313. doi:10.1063/1.1953367

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Kaur R, Kumar TD. Nonadiabatic couplings and charge transfer study in H + CS⁺ collision using time-dependent quantum dynamics. Mol Phys (2015) 113:3271–81. doi:10.1080/00268976.2015.1017021

CrossRef Full Text | Google Scholar

8. Kaur R, Dhilip Kumar T. Ab initio potential energy surfaces of HCS⁺: A study of the ground and the low-lying excited electronic states. Chem Phys (2016) 479:36–41. doi:10.1016/j.chemphys.2016.09.015

CrossRef Full Text | Google Scholar

9. Zhang LL, Zhao J, Liu D, Wang W, Yue DG, Song YZ, et al. A new global analytical ab initio potential energy surface for the dynamics of the C⁺(²P) + SH(X²Π) reaction. Phys Chem Chem Phys (2022) 24:1007–15. doi:10.1039/d1cp04948h

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Werner HJ, Knowles PJ. An efficient internally contracted multiconfiguration–reference configuration interaction method. J Chem Phys (1988) 89:5803–14. doi:10.1063/1.455556

CrossRef Full Text | Google Scholar

11. Werner HJ, Knowles PJ. An efficient method for the evaluation of coupling coefficients in configuration interaction calculations. Chem Phys Lett (1988) 145:514–22. doi:10.1016/0009-2614(88)87412-8

CrossRef Full Text | Google Scholar

12. Dunning TH. Gaussian basis sets for use in correlated molecular calculations. I. The atoms boron through neon and hydrogen. J Chem Phys (1989) 90:1007–23. doi:10.1063/1.456153

CrossRef Full Text | Google Scholar

13. Woon D, Dunning TH. Gaussian basis sets for use in correlated molecular calculations. III. The atoms aluminum through argon. J Chem Phys (1993) 98:1358–71. doi:10.1063/1.464303

CrossRef Full Text | Google Scholar

14. Knowles PJ, Werner HJ. An efficient second order MCSCF method for long configuration expansions. Chem Phys Lett (1985) 115:259–67. doi:10.1016/0009-2614(85)80025-7

CrossRef Full Text | Google Scholar

15. Zhang DH, Zhang JZH. Full-dimensional time-dependent treatment for diatom-diatom reactions: The H₂ + OH reaction. J Chem Phys (1994) 101:1146–56. doi:10.1063/1.467808

CrossRef Full Text | Google Scholar

16. Varandas AJC, Chu TS, Han KL, Caridade PJ. Accurate rate constant and quantum effects for N(²D) + H₂ reaction. Chem Phys Lett (2006) 421:415–20. doi:10.1016/j.cplett.2006.01.073

CrossRef Full Text | Google Scholar

17. Chu TS, Han KL. Nonadiabatic time-dependent wave packet study of theD⁺ + H₂ reaction system. J Phys Chem A (2005) 109:2050–6. doi:10.1021/jp0451391

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Zhang Y, Cao E, Gao SB, Huang X, Meng QT, Song YZ. Exploring the reaction dynamics of O(³P) + ${\mathrm{H}}_2^{+}$ (X²${\Sigma }_g^{+}$) → OH⁺ (X³Σ⁻) + H(²S) reaction with time-dependent wave packet method. Int J Quan Chem (2017) 117:e25343. doi:10.1002/qua.25343

CrossRef Full Text | Google Scholar

19. Mao Y, Buren B, Yang ZJ, Chen MD. Time-dependent wave packet dynamics study of the resonances in the H + LiH⁺(v = 0, j = 0) → Li⁺ + H₂ reaction at low collision energies. Phys Chem Chem Phys (2022) 24:15532–9. doi:10.1039/d1cp05601h

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Zhang WY, Meng QT, Gao SB, Song YZ. Theoretical insight into the vibrational excitation effect of the S⁺(⁴S) + H₂(X¹${\Sigma }_g^{+}$) reaction. Chem Phys Lett (2021) 764:138257. doi:10.1016/j.cplett.2020.138257

CrossRef Full Text | Google Scholar

21. Gao SB, Zhang J, Song YZ, Meng QT. Cross sections for vibrational inhibition at low collision energies for the reaction H + Li₂(X¹${\Sigma }_g^{+}$) → Li + LiH (X¹Σ⁺). Eur Phys J D (2015) 69:111. doi:10.1140/epjd/e2015-50772-9

CrossRef Full Text | Google Scholar

22. Han KL, Zheng XG, Sun BF, He GZ, Zhang RQ. Chemical reaction dynamics of barium atom with alkyl bromides. Chem Phys Lett (1991) 81:474–8. doi:10.1016/0009-2614(91)90383-k

CrossRef Full Text | Google Scholar

23. Ju LP, Han KL, Zhang JZH. Global dynamics and transition state theories: Comparative study of reaction rate constants for gas-phase chemical reactions. J Comput Chem (2009) 30:305–16. doi:10.1002/jcc.21032

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Chu TS, Han KL. Effect of Coriolis coupling in chemical reaction dynamics. Phys Chem Chem Phys (2008) 10:2431–41. doi:10.1039/b715180b

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Lin SY, Han KL, Zhang JZH. Accurate quantum-mechanical calculation for O(¹D)+DCl reaction. Chem Phys Lett (2000) 324:122–6. doi:10.1016/s0009-2614(00)00590-x

CrossRef Full Text | Google Scholar

26. Chu TS, Zhang Y, Han KL. The time-dependent quantum wave packet approach to the electronically nonadiabatic processes in chemical reactions. Int Rev Phys Chem (2006) 25:201–35. doi:10.1080/01442350600677929

CrossRef Full Text | Google Scholar

27. Xin R, Xiang HP, Tian L, Rong L, Song HW. Kinetic and dynamic studies of the F(²P) + ND₃ → DF + ND₂ reactio. J Phys Chem A (2021) 125:8025–32. doi:10.1021/acs.jpca.1c06515

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Liu D, Zhang LL, Zhao J, Zhang Q, Song YZ, Meng QT. Quantum and quasiclassical dynamics of C(³P) + H₂(¹${\Sigma }_g^{+}$) → H(²S) + CH(² Π). Chin Phys B (2022) 31:043102. doi:10.1088/1674-1056/ac3989

CrossRef Full Text | Google Scholar

29. Yue DG, Zhang LL, Zhao J, Song YZ, Meng QT. Stereo-dynamics of the reaction C + SH(D, T)(v = 0, j = 0) → H(D, T) + CS based on a recent excited state potential energy surface. Comput Theor Chem (2019) 1155:82–9. doi:10.1016/j.comptc.2019.03.028

CrossRef Full Text | Google Scholar

30. Zhang LL, Gao SB, Song YZ, Meng QT. The manifestation of vibrational excitation effect in reactions C + SH(v = 0 − 20, j = 0) → H + CS, S + CH. J Phys B: Mol Opt Phys (2018) 51:065202. doi:10.1088/1361-6455/aaae2e

CrossRef Full Text | Google Scholar

31. Wu H, Duan ZX, Yin SH, Zhao GJ. State-resolved dynamics study of the H + HS reaction on the 3A′ and 3A”states with time-dependent quantum wave packet method. J Chem Phys (2016) 145:124305. doi:10.1063/1.4962543

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Yao CX, Zhao GJ. Energy-dependent stereodynamics for the H(²S)+NH(X³Σ) → H2(X¹${\Sigma }_g^{+}$) + N(⁴S) reaction on the improved ZH potential energy surface. Can J Chem (2013) 91:387–91. doi:10.1139/cjc-2012-0404

CrossRef Full Text | Google Scholar

33. Yao CX, Zhao GJ. Quasiclassical trajectory theoretical study on the chemical stereodynamics of the O(¹D) +H2 → OH+H reaction and its isotopic variants (HD, D2). Chin Phys B (2013) 22:083403. doi:10.1088/1674-1056/22/8/083403

CrossRef Full Text | Google Scholar

34. Wang ML, Han KL, He GZ. Product rotational polarization in the photoinitiated bimolecular reaction A+BC → AB+C on attractive, mixed and repulsive surfaces. J Chem Phys (1998) 109:5446–54. doi:10.1063/1.476522

CrossRef Full Text | Google Scholar

35. Chen MD, Han KL, Lou NQ. Theoretical study of stereodynamics for the reactions Cl+H₂/HD/D₂. J Chem Phys (2003) 118:4463–70. doi:10.1063/1.1545112

CrossRef Full Text | Google Scholar

36. Chen MD, Han KL, Lou NQ. Vector correlation in the H+D2 reaction and its isotopic variants: Isotope effect on stereodynamics. Chem Phys Lett (2002) 357:483–90. doi:10.1016/s0009-2614(02)00585-7

CrossRef Full Text | Google Scholar

37. Wang ML, Han KL, He GZ. Product rotational polarization in photo-initiated bimolecular reactions A+BC: Dependence on the character of the potential energy surface for different mass combinations. J Phys Chem A (1998) 102:10204–10. doi:10.1021/jp981738u

CrossRef Full Text | Google Scholar

38. Zhang LL, Liu D, Yue DG, Song YZ, Meng QT. Dynamics of H(²S) + CH(X²Π) reactions based on a new CH₂(X³A′′) surface via extrapolation to the complete basis set limit. J Phys B: Mol Opt Phys (2020) 53:095202. doi:10.1088/1361-6455/ab7641

CrossRef Full Text | Google Scholar

39. Liu D, Zhao J, Wang LF, Song YZ, Meng QT, Zhang LL. Exploring reaction mechanism and vibrational excitation effect in H+CH(v, j = 0) reaction. Chem Phys Lett (2020) 749:137398. doi:10.1016/j.cplett.2020.137398

CrossRef Full Text | Google Scholar

40. Zhang LL, Liu D, Song YZ, Gao F, Meng QT. Examining the isotope effect on CH decay and H exchange reactions: H(²S) + CH (D/T)(²Π). Phys Scr (2020) 96:015404. doi:10.1088/1402-4896/abc20d

CrossRef Full Text | Google Scholar

41. Zhang LL, Gao SB, Meng QT, Pan J, Song YZ. Accurate potential energy surface of H₂S⁺(X²A′′) via extrapolation to the complete basis set limit and its use in dynamics study of S⁺(²D)+H₂(X¹${\Sigma }_g^{+}$) reaction. J Chem Phys (2018) 149:154303. doi:10.1063/1.5046315

PubMed Abstract | CrossRef Full Text | Google Scholar

42. Zhang LL, Song YZ, Gao SB, Meng QT. Globally accurate potential energy surface for HCS(A²A′′) by extrapolation to the complete basis set limit. J Phys Chem A (2018) 122:4390–8. doi:10.1021/acs.jpca.8b02131

PubMed Abstract | CrossRef Full Text | Google Scholar