Cherenkov radiation emitted by Kuznetsov–Ma solitons

Cherenkov radiation emitted by Kuznetsov–Ma soliton (KMS) with an arbitrary propagation constant in the presence of higher-order dispersions is studied analytically and numerically. We show that the third-order dispersion (TOD) yields asymmetric radiated bands, while the fourth-order dispersion (FOD) gives rise to symmetric radiated bands only when the value of FOD is positive. In contrast to radiations emitted by other localized waves, such a radiation emerges periodically in propagation, and can exhibit multi-frequency bands which depends strongly on the propagation constant of the KMS. We presented radiation conditions to calculate different frequency bands, which shows great agreement with numerical simulations. Important radiation features such as radiation frequencies, velocities, and distances are shown in phase diagrams. Our results could be helpful for controllable radiations in nonlinear fiber and other nonlinear systems.

1 Introduction

The ability of solitons to emit dispersive radiation also known as Cherenkov radiation is a property vividly expressing their wave nature. Although radiation emission by solitons has been well known in the 1990s [1–3], such a radiation is confirmed to be one of the key nonlinear frequency conversion mechanisms of coherent supercontinuum generation [4]. This allows a substantial increase in the spectral bandwidth of pulsed laser sources [5]. In particular, recent studies confirmed that soliton radiation leads to broader optical frequency combs on a photonic chip which can help refine time standards [5–7].

Cherenkov radiation in nonlinear optics is caused by the higher-order dispersion. The latter continues to pose major challenges in our understanding of nonlinear phenomena despite being vigorously investigated [8]. Indeed, owing to precise dispersion engineering, recent studies demonstrated that fourth-order dispersion (FOD) can give rise to gener ation of a new class of solitons, i.e., pure-quartic solitons [9, 10]. This opens a novel path for the design of pure-quartic soliton laser [11] and the exploration of pattern transition of modulation instability [12].

In addition to radiation emission by solitons, recent studies revealed radiation properties of shock waves [13, 14] as well as nonlinear “breathing” waves including Akhmediev breathers [15] and Peregrine rogue waves [16]. It has been shown that the symmetry-breaking dynamics of modulation instability (MI) spectrum induced by third-order dispersion (TOD) [17] turns out to be the radiation emission by Akhmediev breathers [15]. This radiation can also lead to disappearances and recoveries of the Fermi-Pasta-Ulam recurrence [18]. Furthermore, higher-order nonlinear effects, such as the spontaneous Raman scattering and self-steepening terms can also break the spectrum symmetry of breathers [19–21]. However, there exists another type of “breathing” wave—Kuznetsov-Ma soliton (KMS) [22, 23] that has attracted considerable attention recently [24–30]. KMS is oscillating due to the coherent interaction with a constant background [24, 28]. In contrast to Akhmediev breathers and Peregrine rogue waves, KMS describes not only the MI in the small amplitude regime, but also the interference between bright soliton and plane wave in the large amplitude regime [28]. When the amplitude of the background tends to zero, the period of oscillations increases and in the zero limit the KMS turns into an ordinary bright soliton [24]. The periodic evolution in propagation of the KMS has been observed experimentally both in fiber optics [25] and in hydrodynamics [26]. It has also been predicted in a microfabricated optomechanical array [27]. Even in dissipative optical systems, the KMS solution provides a basis in clarifying many experimental and numerical observations of oscillating phenomena [31, 32].

In this paper, we study Cherenkov radiation emitted by KMS with an arbitrary propagation constant in the presence of higher-order dispersions including TOD and FOD. Distinctive periodic radiation by KMS can be observed. We show such radiation depends on the propagation constant. The radiation frequencies can be calculated via the wavenumber-matching condition.

2 Physical model and radiation conditions

We consider the pulse propagation in optical fiber ruled by the nonlinear Schrödinger equation in the presence of the TOD and FOD. It reads in dimensionless form [8]:

$\frac{\partial \psi }{\partial z}+\frac{\alpha }{2}\psi -\frac{i{\beta }_2}{2}\frac{{\partial }^2\psi }{\partial t^2}+\frac{{\beta }_3}{6}\frac{{\partial }^3\psi }{\partial t^3}-i\frac{{\beta }_4}{24}\frac{{\partial }^4\psi }{\partial t^4}=i\gamma {|\psi |}^2\psi ,(1)$

where, in nonlinear fiber system, ψ denotes the slowly varying pulse envelope of optical field, z is the evolution distance, t is the retarded time, β₃ and β₄ denote the third and fourth order dispersions, α is the gain or loss, and γ stands for the nonlinear parameter. If β₃ = β₄ = 0, β₂ = 1, α = 0, and γ = 1. Eq. 1 admits the KMS solution [22, 23]:

$\psi \left(z,t\right)=\left[a-2\frac{\delta \cos \left(1/2\xi z\right)+ib\sqrt{\delta }\sin \left(1/2\xi z\right)}{b\cosh \left(2\sqrt{\delta }t\right)-a\cos \left(1/2\xi z\right)}\right]e^{\text{i}\left(1/2k_{b}z\right)},(2)$

where k_b = 2a², $\xi =4b\sqrt{\delta }$ with δ = b² − a². The parameter a is the background amplitude, while b (≥a) determines the KMS amplitude and the period (D_z = 2π/ξ) in propagation. In the limit case b → a, Eq. 2 reduces to the doubly localised Peregrine rogue wave with infinite period in z. The radiation properties of such limiting case induced by the TOD have been studies in Ref. [16]. In contrast, we consider here a general case of the KMS radiation with an arbitrary b. Such an additional degree of freedom induces nontrivial radiation properties of KMS.

We start with the phase of the KMSs. As the KMS is a particular nonlinear wave on the plane wave background, the total phase turns out to be the sum of the linear background contribution and the nonlinear KMS contribution. It reads explicitly:

${\varphi }_{\text{kms}}\left(z,t\right)=1/2k_{b}z+{\varphi }_{\text{nl}}\left(z,t\right).(3)$

where the nonlinear phase ϕ_nl is given by

${\varphi }_{\text{nl}}\left(z,t\right)={\tan }^{-1}\left[\frac{-2b\sqrt{\delta }\sin \left(2b\sqrt{\delta }z\right)}{ab\cosh \left(2\sqrt{\delta }t\right)+\left(a^2-2b^2\right)\cos \left(2b\sqrt{\delta }z\right)}\right].(4)$

Clearly, such a phase exhibits periodic profile in propagation; it has the maximum value at the pulse peak t = 0. The z-derivative maximum phase corresponds to the maximum wavenumber of the KMS. The latter is given by:

$k_{\text{kms}}\left(z\right)=\frac{d{\varphi }_{\text{kms}}\left(z,t=0\right)}{dz}=k_b+k_{\text{nl}}\left(z\right),(5)$

where

$k_{\text{nl}}=-\frac{2\sqrt{\delta }b\sin \left(4\sqrt{\delta }b\right)\mu +4\delta b^2\left(a^2-2b^2\right)z\sin \left(2\sqrt{\delta }bz\right)}{{\mu }^2+4\delta b^2+{\sin }^2\left(4\sqrt{\delta }b\right)},(6)$

and $\mu =ab+(a^2-2b^2)\cos (2\sqrt{\delta }bz)$. Here, k_nl denotes the nonlinear wavenumber of the KMS. The variation of k_kms(z) follows that of the KMS amplitude, exhibiting periodic profile in z.

Resonant radiation occurs as a result of interaction between the KMS and linear dispersive waves. The latter has the form exp (iωT + i1/2k_dwz), where T = t − 1/2v_gz with v_g being the group velocity, and k_dw is the wavenumber which constitutes the radiation from the soliton frequency. By inserting the term of linear waves in Eq. 1, we find the dispersion relationship:

$k_{\text{dw}}={\beta }_4{\omega }^4+{\beta }_3{\omega }^3-{\beta }_2{\omega }^2+v_g\omega .(7)$

From here, we have the radiative velocity of linear wave

$v_R=d{k}_{\text{dw}}/d\omega =4{\beta }_4{\omega }^3+3{\beta }_3{\omega }^2-2{\beta }_2\omega +v_g.(8)$

Resonant radiated frequencies can be obtained by imposing the matching condition of wavenumber. As the KMS admits both linear and nonlinear contributions of wavenumber, the resonant condition admits different forms. The simplest resonant condition reads

$k_{\text{dw}}=k_b.(9)$

Namely, only the linear (lowest-order) wavenumber of the KMS is considered. This has been used in the resonant radiation of Akhmediev breathers [15], where the associated Fermi-Pasta-Ulam recurrence can be well controlled by the value of TOD.

A more accurate estimate of the radiated frequencies is obtained by considering the total wavenumber of the KMS. It is given by

$k_{\text{dw}}=k_{\text{kms}}\left(z\right).(10)$

On the other hand, by considering an additional nonlinear correction arising from cross-phase modulation (induced by the intense background) [13], we obtain another radiation condition:

$k_{\text{dw}}=k_{\text{kms}}\left(z\right)-2k_b=k_{\text{nl}}\left(z\right)-k_b.(11)$

This condition is composed of the effective nonlinear contributions of the KMS wavenumber. It has been demonstrated that this radiation condition produces accurate description of radiated frequencies of the limiting case of KMSs (i.e., Peregrine rogue waves) [16].

Despite being different in form, all radiation conditions can admit multiple radiated frequencies. We will investigate below the properties of resonant radiation emitted by KMSs by considering the radiation condition [10]. The availability of three different radiation conditions will be also clarified.

Note that since k_dw must be evaluated in the frame where the KMS is stationary, in each radiation condition, v_g = 2dt/dz is equal to the velocity of the KMS induced by the odd-order dispersion. Moreover, as the KMS is a particular nonlinear periodic mode in propagation, resonant radiation can occur periodically. In particular, as b is large, KMS suffers acceleration in propagation [see Figures 1, 4]. Thus, for each cell of KMS, the velocity should be re-estimated carefully.

FIGURE 1

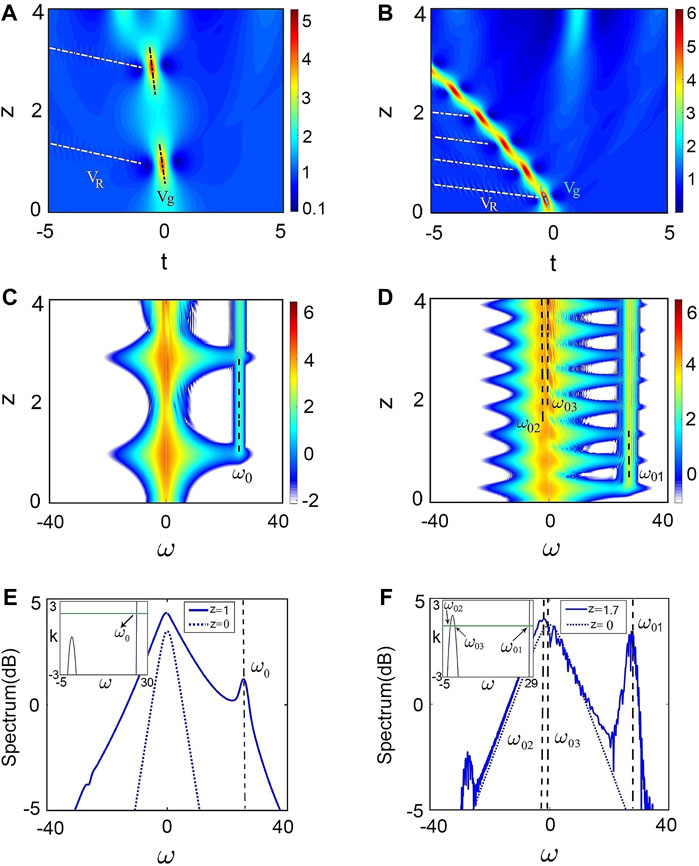
FIGURE 1. Characteristics of radiations emitted by KMSs induced by TOD in both time and frequency domains with different propagation constants b=1.5 (left column) and b=2.5 (right column). (A,B) show false color plots of spatio-temporal evolution; the dashed black line refers to KMS velocity v_g, and the dashed white line refers to radiation velocity v_R. (C,D) correspond to the evolution of the Fourier spectrum (log scale) of (A,B). The radiation frequencies are obtained exactly from the resonance condition [10]. Namely, ω₀=25.6748, ω₀₁=27.5391, ω₀₂=−2.11617, ω₀₃=−0.422941. (E,F) are output spectrums in log scale (solid blue) compared with the input spectrum (dashed blue). The intersection points in the insets correspond to the radiation frequencies. Other parameters are a =1, β₃=0.24.

Furthermore, for a given optical fiber system, i.e., the higher-order dispersion parameters are fixed, the radiation properties of KMSs depend strongly on the parameter b. Such radiation properties can be well described by four physical quantities, namely, radiation frequency ω_R, the initial radiation distance z₀, KMS velocity v_g and radiation velocity v_R. In the following, we will study these physical quantities with different b. All numerical results are obtained from the numerical integration of Eq. 1 by the split-step Fourier method.

3 Radiation induced by third-order dispersion

We first consider the radiation properties emitted by KMSs induced only by the TOD. As is well known, the TOD results in asymmetric spectral distribution in processes of modulation instability and Fermi-Pasta-Ulam recurrence [15]. TOD also causes asymmetric spectra for Peregrine rogue waves [16]. However, for KMSs with different parameters b, the radiation properties are different.

Figure 1 shows radiation characteristics emitted by KMSs with different b in both time and frequency domains. The initial condition is extracted from solution [2] at z = 0. We then consider two cases with b = 1.5 and b = 2.5. The other parameters are a = 1, β₂ = 1, β₃ = 0.24, and β₄ = 0. As can be seen from the figure, KMSs, in either case, generate distinctive radiation in propagation. The group velocity of KMSs is induced by the TOD. If one chooses the opposite value of TOD, the velocity will be opposite. In particular, the radiation occurs periodically at the particular (maximum-compressed) distance where KMSs have maximum amplitude. This can be clearly seen from the characteristic of spectral distributions.

An interesting result is that as b is small, the KMS has a unique group velocity as shown in Figure 1A. This results in that the radiation spectrum corresponds to a unique frequency ω₀. However, when b is large, KMSs suffer accelerating propagation [Figure 1B]. This means that for each cell of KMS shown in Figure 1B, the velocity v_g is different and should be re-estimated. Due to the difference of v_g in each cell of KMS, radiation frequency in each cell is also different. A slight deviation from the initial radiation frequency (ω₀₁) can be clearly observed in the spectral distribution. This leads to radiation band broadening as z increases. In addition to the dominating radiation band, there are two radiation lines (ω₀₂ and ω₀₃) which are not that obvious in the spectra. Such frequencies can be given by the cubic resonance equation. As can be seen, the appearance of these three radiation bands corresponds to different initial distances (z₀₁, z₀₂, and z₀₃).

Note that all these numerical results are completely consistent with the analytical results given by Eq. 10. This can be observed from the spectrum profiles shown in Figure 1. The intersection points in the insets correspond to the radiation frequencies obtained exactly from the resonance condition. As can be seen, such frequencies coincide with those obtained by numerical simulation.

To better understand the radiation phenomenon, we depict, in Figures 2A,B, the variations of radiation frequencies (ω_0j, j = 1, 2, 3), initial distances (z_0j), the group velocity of first cell of KMS (v_g), and the radiation velocity of dominating radiation band (v_R) as b increases. Interestingly, we numerically find a critical value of b, say b_c ≈ 2.45, that divides the regions into two parts. Namely, when b ≤ b_c, there is only one radiation frequency (ω₀₁) with its initial distance (z₀₁). As b increases, z₀₁ decreases sharply while ω₀₁ increases slightly. Instead, if b > b_c, three radiation frequencies (ω_0j) emerge from different initial distances (z_0j). However, due to the secondary radiation bands (ω₀₂ and ω₀₃) are always weak, only the radiation velocity of dominating radiation band v_R is shown in Figure 2B. As b increases, v_R decreases and |v_g| increases.

FIGURE 2

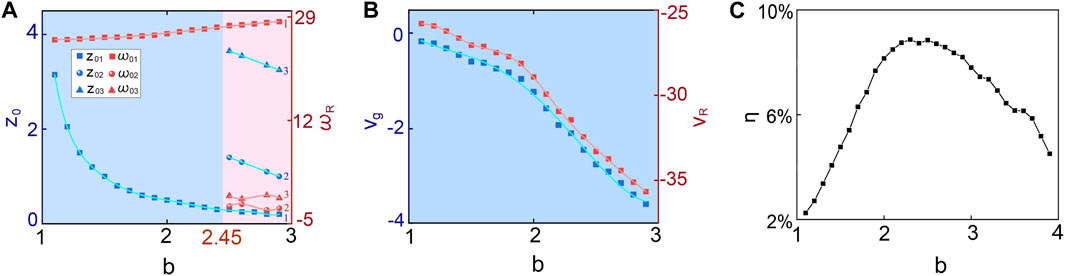
FIGURE 2. Variations of initial radiation distances (z_0j) (A), radiation frequencies (ω_0j, j = 1, 2, 3) (A), group velocity of first cell of KMS (v_g) (B), radiation velocity of dominating radiation band (v_R) (B), and radiation efficiency (η) (C) versus b.

In addition to the radiation frequency, the efficiency of radiation is also the crucial property that should be considered. Here we define radiation efficiency η = (S₁ − S₀)/S₀, where S₁ denotes the numerical integration of the spectrum with higher-order dispersion for given b, while S₀ stands for the numerical integration of the spectrum without higher-order dispersion. We then show the radiation conversion efficiency versus the propagation constant b. As shown in Figure 2C, the radiation efficiency increases and then decreases as b increases. The maximum efficiency occurs when b ≈ 2.4.

4 Radiation induced by fourth-order dispersion

Next, we consider the radiation properties induced only by the FOD. In contrast to the case of radiation induced by the TOD, FOD can result in radiation only when β₂ and β₄ have the same sign.

Figure 3 displays the evolution characteristics of KMSs with positive and negative FOD (β₄). One can see from the figure that in either case, KMSs propagate with zero group velocity v_g = 0. As shown in Figure 3A, KMS cannot produce radiation when FOD is negative. It propagates with zero group velocity just as the standard KMS. This is because that the quartic equation (radiation condition) has no real roots.

FIGURE 3

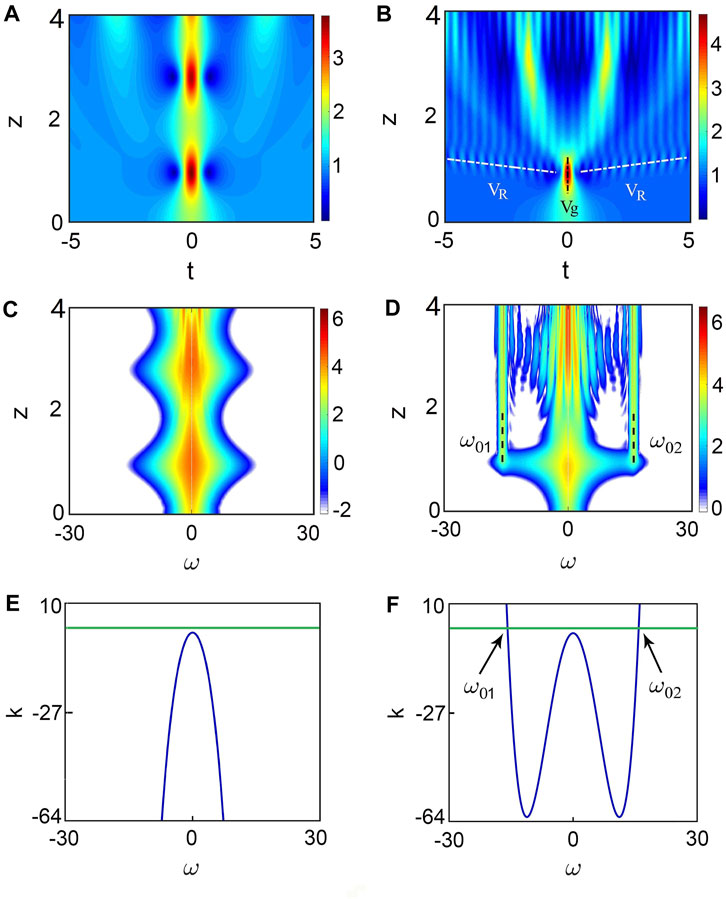
FIGURE 3. Propagation of perturbed KMS without radiations (β₄=−0.096, left column) and with radiations (β₄=0.096, right column). (A,B) show the false color plot of spatio-temporal evolution. In (B), the dashed black line refers to group velocity, and the dashed white line refers to radiation velocity. (C,D) are the corresponding evolution of Fourier spectrum (log scale). (E,F) are graphical solution of Eq. 10. ω_0j is given by the cross of the green horizontal line standing for k_dw, with the blue solid curve signifying the quartic dispersion relation.

On the contrary, when β₄ is positive, radiation waves appear in the first cell of the KMS, as shown in Figure 3B. Specifically, just as the case of TOD, radiation waves generate at the maximum-compressed distance where KMSs have maximum amplitude. Unlike the case of TOD, there are two radiation waves which are symmetrical about t = 0. Namely, they have opposite radiation velocity v_R. After the radiation, the KMS splits into several subwaves distributed symmetrically with respect to t = 0.

A further observation for resonance radiation in frequency domain shows that KMSs produce two symmetrical radiation bands with frequencies ω₀₁ and ω₀₂ (ω₀₁ = −ω₀₂). This corresponds to the linear waves with opposite radiation velocity v_R shown in time domain. We emphasize that these radiation frequencies fit the calculated frequencies accurately. In addition, with the value of FOD increasing, the two radiation bands get closer. Note that although the radiation condition yields a quartic equation, there are only two real roots that correspond to the radiation frequencies.

5 Radiation induced by third-order dispersion and fourth-order dispersion

Let us consider the radiation properties induced by the combined effects of TOD and FOD. In order to better understand this combined effects, we consider the radiation shown in Figure 1A but perturbed by a small positive value of FOD.

As shown in Figure 4, even when b is small, KMS can suffer accelerating propagation. This means that FOD enhances the group velocity of KMS. Clearly, the group velocity of the first cell is different from that of the second one, i.e., v_g1 ≠ v_g2. The radiation occurs in each cell of KMS. Due to the coexistence of TOD and FOD, linear radiation waves appear on two sides of the KMS with velocities v_R1, v_R2. However, they are asymmetric about the group velocity of KMS. The spectrum distribution reveals that the two radiation waves correspond to the frequencies ω₀₁, ω₀₂. The radiation bands become wider as z increases, since the variety of the group velocity of KMS causes the slight frequency shift. We perform the radiation condition for the first 2 cells of the KMS. Again, the analytical frequencies agree with those obtained by numerical simulations.

FIGURE 4

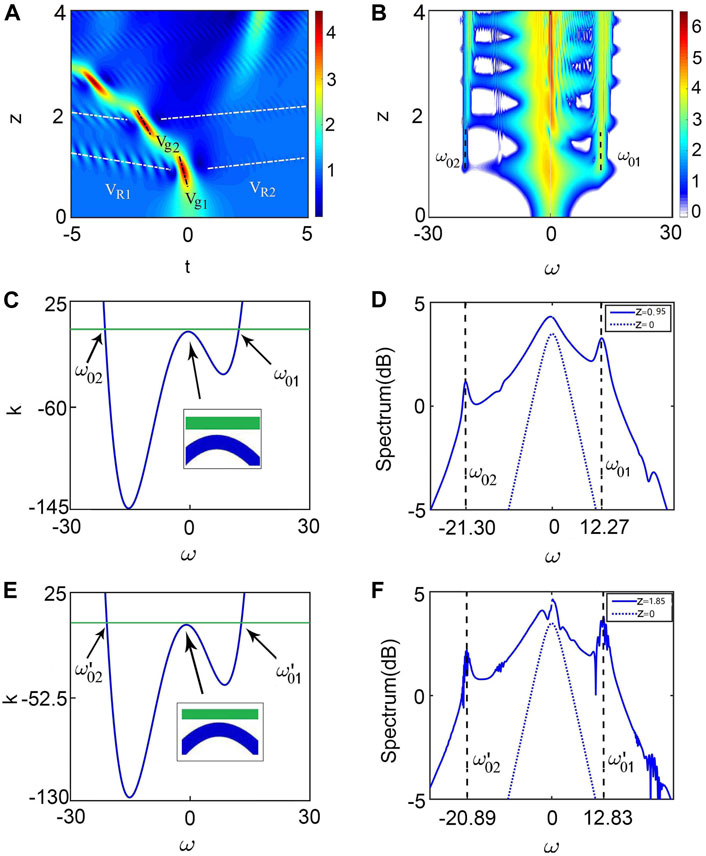
FIGURE 4. Radiation properties induced by the combined effects of TOD and FOD. (A,B) show false color plots of spatio-temporal evolution and spectra with two. In (A), the dashed black lines refer to group velocities of the first and second cell of KMS, v_g1=−0.92033, v_g2=−2. The dashed white lines refer to radiation velocities v_R1=−21.5271, v_R2=58.0662. (C,D) Radiation frequencies and spectra for the first cell of KMS with v_g1. (C) Graphical solutions of Eq. 10. ω₀₁ and ω₀₂ are the intersection points corresponding to the radiation frequencies obtained exactly from the resonance condition. (D) Output spectrum in log scale (solid blue) compared with the input spectrum (dashed blue). (E,F) Similar to (C,D) but for the second cell of KMS with v_g2. The parameters are β₃=0.24, β₄=0.096, and b = 1.5.

Figure 5 shows the variations of radiation frequencies (ω_0j), initial distances (z_0j), group velocity of first cell of KMS (v_g), and radiation velocities of two dominating radiation bands (v_R1, v_R2) as b increases. The critical value of b (b_c = 2.15) is obtained numerically. When b ≤ b_c, two radiation bands with frequencies (ω₀₁, ω₀₂) appear at initial distances (z₀₁, z₀₂). As b → 1, z₀₁ ≈ z₀₂. As b increases, both z₀₁ and z₀₂ decrease, and in particular, z₀₁ ≠ z₀₂. Correspondingly, ω₀₁ and ω₀₂ increase slightly. Instead, if b > b_c, two additional radiation bands with frequencies (ω₀₃, ω₀₄) emerge at different initial distances (z₀₃, z₀₄). The radiation efficiency in the presence of both TOD and FOD is shown in Figure 5C. As can be seen, the variation of the radiation efficiency is irregular as b increases due to the coexistence of TOD and FOD. This coexistence induces the difference of the initial radiation distances between two radiation bands.

FIGURE 5

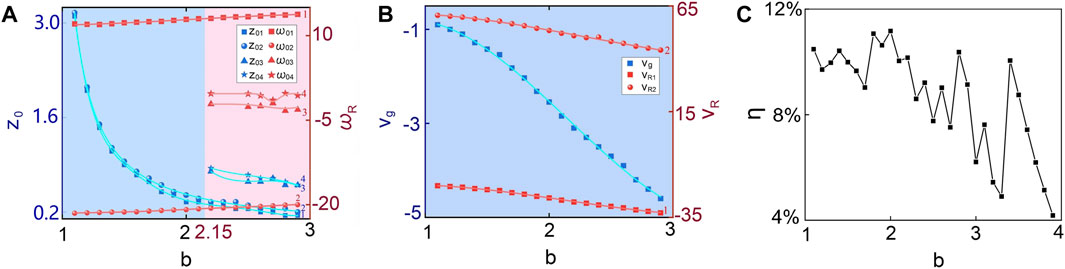
FIGURE 5. As in Figure 2 for β₃=0.24, and β₄=0.096. The variations of radiation distances (z_0j) (A), radiation frequencies (ω_0j) (A), group velocity of first cell of KMS (v_g) (B), radiation velocities of two dominating radiation bands (v_R1, v_R2) (B), and radiation efficiency (η) (C) versus b.

We point out that all results shown above are obtained by considering the radiation condition [10]. Let us clarify here the availability of the conditions [9, 11]. To do so, we numerically calculate the radiation frequencies under different conditions. We first show in Figure 6A, the variation of single dominant frequency (ω₀) induced by TOD as b increases. As can be seen, three curves obtained under different conditions are much close to each other. In the case of two dominant frequencies (ω₀₁, ω₀₂) induced by both TOD and FOD (Figures 6B,C), a slight difference can be observed for ω₀₁ when b is small, as shown in Figure 6C. We compare this difference with the numerical simulation. As shown in Figure 6D, the frequency ω₀₁ obtained under the condition [10] shows a greet agreement with the numerical simulation. This is because when b is small the dominant mechanism of KMS formation is the modulation instability (namely, the property of KMSs is similar with that of Peregrine rogue waves). In this case, the plane wave background plays a key role and the linear contribution of the wavenumber cannot be ignored. However, when b is large the dominant mechanism of KMS formation is the linear interference between solitons and a plane wave. The nonlinear contribution of the soliton wavenumber plays a dominant role in radiation. As shown in Figure 6E, when b = 2.8, we can see clearly that the condition [11] provides a better description of the radiation frequency.

FIGURE 6

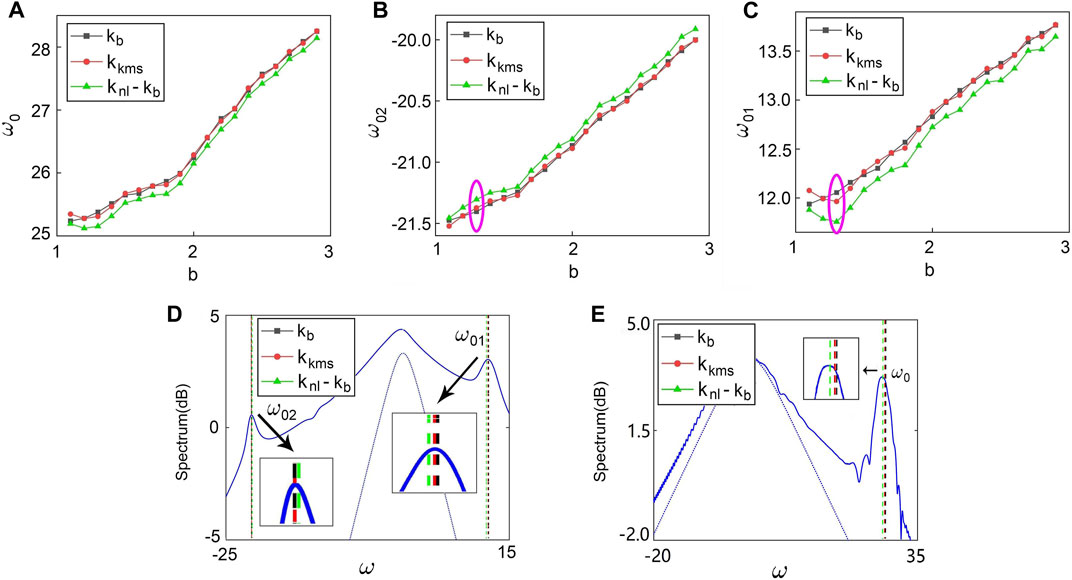
FIGURE 6. Dominant radiation frequencies under different radiation conditions [9]–[11]. (A) Variations of single radiation frequency (ω₀) induced by TOD. (B,C) Variations of two radiation frequency (ω₀₁, ω₀₂) induced by TOD and FOD. (D) Comparison between radiation frequencies (ω₀₁, ω₀₂) and the numerical simulations with a special b circled in (B) and (C). (E) Comparison of the frequency calculations for the three resonance conditions with b = 2.8 when β₃ = 0.24 and β₄ = 0.

6 Conclusion

We have studied analytically and numerically Cherenkov radiation emitted by KMSs with arbitrary propagation constant b in the presence of TOD and FOD. The radiation emerges periodically in propagation and can exhibit multi-frequency bands which depends strongly on the propagation constant. We presented radiation conditions to calculate different frequency bands, which shows great agreement with numerical simulations. All these results are available for the single-mode fiber. Breather emission can be extended into a generalized framework in a multimode fiber, where resonant radiations emitted by conical waves in a multimode fiber (so-called discretization of conical emission) have been revealed recently [33].

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

CL conceived the idea and presented the first draft of the manuscript. YZ preformed the numerical simulations. CL and YZ provided the physical analysis and interpretation of results.

Funding

This work was supported by the National Natural Science Foundation of China (Grant Nos 12175178, 12047502, and 12004309), the Major Basic Research Program of Natural Science of Shaanxi Province (Grant No. 2017KCT-12), and the Natural Science basic Research Program of Shaanxi Province (Grant No. 2022KJXX-71).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Wai PKA, Menyuk CR, Lee Y, Chen H. Nonlinear pulse propagation in the neighborhood of the zero-dispersion wavelength of monomode optical fibers. Opt Lett (1986) 11:464–6. doi:10.1364/ol.11.000464

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Karpman V. Radiation by solitons due to higher-order dispersion. Phys Rev E (1993) 47:2073–82. doi:10.1103/physreve.47.2073

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Akhmediev N, Karlsson M. Cherenkov radiation emitted by solitons in optical fibers. Phys Rev A (Coll Park) (1995) 51:2602–7. doi:10.1103/physreva.51.2602

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Skryabin DV, Gorbach AV. Colloquium: Looking at a soliton through the prism of optical supercontinuum. Rev Mod Phys (2010) 82:1287–99. doi:10.1103/revmodphys.82.1287

CrossRef Full Text | Google Scholar

5. Brasch V, Geiselmann M, Herr T, Lihachev G, Pfeiffer MH, Gorodetsky ML, et al. Photonic chip–based optical frequency comb using soliton Cherenkov radiation. Science (2016) 351:357–60. doi:10.1126/science.aad4811

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Akhmediev N, Devine N. How Cherenkov radiative losses can improve optical frequency combs. Science (2016) 351:340–1. doi:10.1126/science.aad8694

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Diddams SA, Vahala K, Udem T. Optical frequency combs: Coherently uniting the electromagnetic spectrum. Science (2020) 369:eaay3676. doi:10.1126/science.aay3676

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Agrawal GP. Nonlinear fiber optics. Nonlinear science at the dawn of the 21st century. Springer (2000). p. 195–211.

Google Scholar

9. Blanco-Redondo A, De Sterke CM, Sipe JE, Krauss TF, Eggleton BJ, Husko C. Pure-quartic solitons. Nat Commun (2016) 7:10427–9. doi:10.1038/ncomms10427

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Lo CW, Stefani A, de Sterke CM, Blanco-Redondo A. Analysis and design of fibers for pure-quartic solitons. Opt Express (2018) 26:7786–96. doi:10.1364/oe.26.007786

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Runge AF, Hudson DD, Tam KK, de Sterke CM, Blanco-Redondo A. The pure-quartic soliton laser. Nat Photon (2020) 14:492–7. doi:10.1038/s41566-020-0629-6

CrossRef Full Text | Google Scholar

12. Yao X, Liu C, Yang ZY, Yang WL. Heteroclinic-structure transition of the pure quartic modulation instability. Phys Rev Res (2022) 4:013246. doi:10.1103/physrevresearch.4.013246

CrossRef Full Text | Google Scholar

13. Conforti M, Trillo S. Radiative effects driven by shock waves in cavity-less four-wave mixing combs. Opt Lett (2014) 39:5760–3. doi:10.1364/ol.39.005760

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Conforti M, Baronio F, Trillo S. Resonant radiation shed by dispersive shock waves. Phys Rev A (Coll Park) (2014) 89:013807. doi:10.1103/physreva.89.013807

CrossRef Full Text | Google Scholar

15. Soto-Crespo JM, Ankiewicz A, Devine N, Akhmediev N. Modulation instability, Cherenkov radiation, and fermi–pasta–ulam recurrence. J Opt Soc Am B (2012) 29:1930–6. doi:10.1364/josab.29.001930

CrossRef Full Text | Google Scholar

16. Baronio F, Chen S, Trillo S. Resonant radiation from Peregrine solitons. Opt Lett (2020) 45:427–30. doi:10.1364/ol.381228

CrossRef Full Text | Google Scholar

17. Droques M, Barviau B, Kudlinski A, Taki M, Boucon A, Sylvestre T, et al. Symmetry-breaking dynamics of the modulational instability spectrum. Opt Lett (2011) 36:1359–61. doi:10.1364/ol.36.001359

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Mussot A, Kudlinski A, Droques M, Szriftgiser P, Akhmediev N. Fermi-pasta-ulam recurrence in nonlinear fiber optics: The role of reversible and irreversible losses. Phys Rev X (2014) 4:011054. doi:10.1103/physrevx.4.011054

CrossRef Full Text | Google Scholar

19. Xu G, McNiff J, Boardman A, Kibler B. Space–time evolution of optical breathers and modulation instability patterns in metamaterial waveguides. Wave Motion (2020) 93:102448. doi:10.1016/j.wavemoti.2019.102448

CrossRef Full Text | Google Scholar

20. Bu L, Baronio F, Chen S, Trillo S. Quadratic peregrine solitons resonantly radiating without higher-order dispersion. Opt Lett (2022) 47:2370–3. doi:10.1364/ol.456187

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Liu C, Wu YH, Chen SC, Yao X, Akhmediev N. Exact analytic spectra of asymmetric modulation instability in systems with self-steepening effect. Phys Rev Lett (2021) 127:094102. doi:10.1103/physrevlett.127.094102

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Kuznetsov EA. Solitons in a parametrically unstable plasma. Akademiia Nauk SSSR Doklady (1977) 236:575–7.

Google Scholar

23. Ma YC. The perturbed plane-wave solutions of the cubic Schrödinger equation. Stud Appl Maths (1979) 60:43–58. doi:10.1002/sapm197960143

CrossRef Full Text | Google Scholar

24. Akhmediev NN, Wabnitz S. Phase detecting of solitons by mixing with a continuous-wave background in an optical fiber. J Opt Soc Am B (1992) 9:236–42. doi:10.1364/josab.9.000236

CrossRef Full Text | Google Scholar

25. Kibler B, Fatome J, Finot C, Millot G, Genty G, Wetzel B, et al. Observation of Kuznetsov-Ma soliton dynamics in optical fibre. Sci Rep (2012) 2:463–5. doi:10.1038/srep00463

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Chabchoub A, Kibler B, Dudley JM, Akhmediev N. Hydrodynamics of periodic breathers. Phil Trans R Soc A (2014) 372:20140005. doi:10.1098/rsta.2014.0005

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Xiong H, Gan J, Wu Y. Kuznetsov-Ma soliton dynamics based on the mechanical effect of light. Phys Rev Lett (2017) 119:153901. doi:10.1103/physrevlett.119.153901

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Zhao LC, Ling L, Yang ZY. Mechanism of kuznetsov-ma breathers. Phys Rev E (2018) 97:022218. doi:10.1103/physreve.97.022218

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Che WJ, Chen SC, Liu C, Zhao LC, Akhmediev N. Nondegenerate Kuznetsov-Ma solitons of Manakov equations and their physical spectra. Phys Rev A (Coll Park) (2022) 105:043526. doi:10.1103/physreva.105.043526

CrossRef Full Text | Google Scholar

30. Wang W, Bu L, Cheng D, Ye Y, Chen S, Baronio F. Ultraslow kuznetsov-ma solitons and ahkmediev breathers in a cold three-state medium exposed to nanosecond optical pulses. OSA Continuum (2021) 4:1488–96. doi:10.1364/osac.422914

CrossRef Full Text | Google Scholar

31. Lucas E, Karpov M, Guo H, Gorodetsky M, Kippenberg TJ. Breathing dissipative solitons in optical microresonators. Nat Commun (2017) 8:736–11. doi:10.1038/s41467-017-00719-w

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Peng J, Boscolo S, Zhao Z, Zeng H. Breathing dissipative solitons in mode-locked fiber lasers. Sci Adv (2019) 5:eaax1110. doi:10.1126/sciadv.aax1110

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Kibler B, Béjot P. Discretized conical waves in multimode optical fibers. Phys Rev Lett (2021) 126:023902. doi:10.1103/physrevlett.126.023902

PubMed Abstract | CrossRef Full Text | Google Scholar