Non-degenerate rogue waves and multiple transitions in systems of three-wave resonant interaction

Non-degenerate rogue waves (RWs) and multiple transitions between RWs and solitons arising from vector three-wave resonant interaction are studied analytically and numerically. In contrast to the conventional degenerate RWs, such non-degenerate RWs consist of two fundamental RWs each with individual Lax spectral parameter. We show distinctive continuous transitions from bright (dark) RWs to four-petal RWs to dark (bright) solitons as the relative frequency between the wave components increases. The underlying mechanism of such processes is the non-monotonic variation of the energy exchanges between different components of the waves. We further reveal the transition dynamics of non-degenerate RWs. Finally, we confirm numerically the robustness of the transition dynamics in the presence of spontaneous modulation instability induced by white noise. Our results provide insights into the RW formation and the multiple transitions in systems with three-wave resonant interaction, and may offer the possibility of experimental observations in multi-component resonant processes.

1 Introduction

Three-wave resonant interaction (3WRI) enjoys a prominent status in various branches of nonlinear science [1–7]. It involves the simplest and lowest-order wave-wave coupling in weakly nonlinear and dispersive media [8–15]. The 3WRI has been extensively studied alongside with the development of nonlinear optics, since it applies to laser-plasma interaction [2], group-velocity pulse control [14, 16–19], ultrashort pulse train generation [7, 20], and frequency conversion [21].

The mathematical model that describes such interaction is commonly based on a coupled set of evolution equations [1, 22]. An integrable version of the latter was established in the early 1970s [1]. Just as the celebrated nonlinear Schrödinger equation (NLSE), an important point is that the integrable 3WRI system admits various exact localized wave solutions in analytic form. These contain the resonant solitons [1, 13–15, 20] as well as the “breathing waves” such as breathers [23, 24] and rogue waves (RWs) [23–28]. Physically, these localized waves correspond to different nonlinear excitations [29, 30]. Recently, significant progress has been made on the 3WRI solitons and RWs. In particular, the 3WRI velocity-locked solitons have been confirmed in both theory and experiment [14, 15], and the existence of fundamental and high-dimensional RWs has been predicted in theory recently [25–27]. However, just as the scalar NLSE case [31–33], all existing 3WRI RWs are the conventional degenerate solutions. Namely, the RWs correspond to an identical spectral parameter of the associated Lax pair [25, 26, 28]. Recently, a new type of RWs—nondegenerate RWs—has been demonstrated in the coupled NLSEs accounting for the dynamics of vector waves in weak resonant processes [34]. Such non-degenerate RWs consist of different fundamental RWs each with individual Lax spectral parameter. This possibility arises from the internal integrable structure of the coupled NLSEs where the Lax pair is a multidimensional matrix. Just like the coupled NLSEs, the 3WRI equations also admit multidimensional (3 × 3) Lax matrix. Unlike the coupled NLSEs, the 3WRI equations are the fundamental model accounting for the dynamics of vector waves in strong resonant processes. It is therefore relevant to find out whether nondegenerate RWs exist in the 3WRI system.

On the other hand, as two different types of localized excitations, transitions between the 3WRI RWs and solitons remain completely unexplored. Transitions between different types of nonlinear waves in both the scalar and vector nonlinear systems have been a subject of extensive research. Recent studies have demonstrated that the transitions between RWs (or breathers) and solitons only exhibit a simple transition process—from bright (dark) RWs to bright (dark) solitons [35–37]. Namely, all these results are limited to a relatively simple single transition. It has been shown that such single transition describes a continuous process of RW elongation, which corresponds to the monotonic decay of modulation instability (MI) gain [36, 37].

In this paper, we demonstrate the existence of nondegenerate RWs in the 3WRI system, and reveal multiple transitions which are different from the single transition reported before [35–37]. The nondegenerate RWs consist of two fundamental RWs each with individual Lax spectral parameter. We present the existence diagram. We show that the multiple transitions are closely connected with the inherent energy exchange between different wave components of the 3WRI system. The latter is forbidden in the coupled NLSE case [38]. The robustness of all transition dynamics in the presence of spontaneous MI induced by white noise is confirm numerically.

2 The three-wave resonant interaction system and rogue wave solutions

The 3WRI equations describing the propagation of three coupled waves in a weakly dispersive nonlinear medium [1, 8, 9], can be written as, in dimensionless form,

$\begin{array}{ccc}\hfill & u_{1t}+c_1{u}_{1z}=u_2{u}_3^{\ast },\hfill & \hfill \\ \hfill & u_{2t}+c_2{u}_{2z}=-u_1{u}_3,\hfill & \hfill \\ \hfill & u_{3z}=\left(c_2-c_1\right)u_1^{\ast }{u}_2,\hfill & \hfill \end{array}(1)$

where u_j(t, z), j = 1, 2, 3 are the slowly varying electric field envelopes of the three waves. If z is the evolution variable, then this system is the well-known 3WRI equation [1] where the three characteristic velocities are 1/c₁, 1/c₂, and 0; otherwise, if the evolution variable is t, this system models the nonlocal interaction of two waves, that is the transformation $u_3=(c_2-c_1)\int u_1^{\ast }{u}_2\mathrm{d}\mathrm{z}$ in system (1) [39, 40]. In optics, the 3WRI Eq. 1 describes optical pulses with second-harmonic generation in a KTP crystal [14–16].

Due to the resonant conditions for the frequencies and momenta [8], the initial plane-wave background of Eq. 1 can be expressed as

$\begin{array}{ccc}\hfill u_1^{\left[0\right]}& =\hfill & a_1\exp \left[i\left(k_{1}t+qz\right)\right],\hfill \\ \hfill u_2^{\left[0\right]}& =\hfill & a_2\exp \left[i\left(k_{2}t-qz\right)\right],\hfill \\ \hfill u_3^{\left[0\right]}& =\hfill & i{a}_3\exp \left[i\left(k_2-k_1\right)t-2qz\right],\hfill \end{array}(2)$

where

$k_1=-c_{1}q-a_2^2\delta ,k_2=c_{2}q-a_1^2\delta ,a_3=a_1{a}_2\delta ,\delta =\frac{c_2-c_1}{2q},$

with a_j, k_j, and q being the amplitudes, wavenumbers, and relative frequency of the vector plane-wave fields. The model (1) is integrable [1]. Namely, it admits various exact solutions. By solving the associated Lax pair (13), exact solutions describing localized nonlinear wave on the vector backgrounds (2) can be constructed by the Darboux transformation method [23]. The details are presented in Appendix. The first-order RW solutions $u_j^{[1]}$ of Eq. 1 are given by

$u_1^{\left[1\right]}=\left[1+\frac{2i\left({\lambda }^{\ast }-\lambda \right){\mathrm{\Psi }}_{11}^{\ast }{\mathrm{\Psi }}_{21}}{|{\mathrm{\Psi }}_{11}{|}^2+a_1^2|{\mathrm{\Psi }}_{21}{|}^2+a_2^2|{\mathrm{\Psi }}_{31}{|}^2}\right]u_1^{\left[0\right]},$

$u_2^{\left[1\right]}=\left[1+\frac{2i\left({\lambda }^{\ast }-\lambda \right){\mathrm{\Psi }}_{11}^{\ast }{\mathrm{\Psi }}_{31}}{|{\mathrm{\Psi }}_{11}{|}^2+a_1^2|{\mathrm{\Psi }}_{21}{|}^2+a_2^2|{\mathrm{\Psi }}_{31}{|}^2}\right]u_2^{\left[0\right]},(3)$

$u_3^{\left[1\right]}=\left[1+\frac{4q\left({\lambda }^{\ast }-\lambda \right){\mathrm{\Psi }}_{21}^{\ast }{\mathrm{\Psi }}_{31}}{|{\mathrm{\Psi }}_{11}{|}^2+a_1^2|{\mathrm{\Psi }}_{21}{|}^2+a_2^2|{\mathrm{\Psi }}_{31}{|}^2}\right]u_3^{\left[0\right]}.$

Here, the expressions of Ψ₁₁, Ψ₂₁ and Ψ₃₁ as shown in the Supplementary Appendix S7.1. These solutions depend on the free parameters A_j and the spectral parameter λ. Solutions (3) describe RWs when one of A_j vanishes; otherwise, they describe the interaction between RWs and breathers when A_j ≠ 0.

3 Non-degenerate rogue waves and transition dynamics

3.1 Spectral parameter analysis and characteristics of rogue waves

The spectral parameter λ in Eq. 3 is one of the complex roots of the discriminant condition:

${\left(i\lambda M_1-9N_1\right)}^2+4\left({\lambda }^2+3M_1\right)\left(M_1^2-3i\lambda N_1\right)=0,(4)$

where

$M_1={\lambda }^2+q^2+a_1^2+a_2^2,(5)$

$N_1=i\left[{\lambda }^3-\lambda q^2+a_1^2\left(\lambda -q\right)+a_2^2\left(\lambda +q\right)\right].(6)$

For simplicity, we set here a₁ = a₂ = a. The spectral parameter λ is given explicitly by

$\left\{\begin{array}{cc}{\lambda }_{\pm }=\pm \frac{i}{4q}\left(\sqrt{-{\mathrm{\Delta }}_1}-\sqrt{{\mathrm{\Delta }}_2}\right),\hfill & |q|<a/2,\hfill \\ {\lambda }_{\pm }=\pm \frac{1}{4q}\left[\sqrt{{\mathrm{\Delta }}_1}+i\sqrt{{\mathrm{\Delta }}_2}\right],\hfill & |q|>a/2,\hfill \end{array}\right.(7)$

with

$\begin{array}{ccc}\hfill {\mathrm{\Delta }}_1& =\hfill & 2q\sqrt{{\left(2a^2+q^2\right)}^3}-{\eta }^2-18q^2\left(a^2-q^2\right),\hfill \\ \hfill {\mathrm{\Delta }}_2& =\hfill & 2q\sqrt{{\left(2a^2+q^2\right)}^3}+{\eta }^2+18q^2\left(a^2-q^2\right),\hfill \end{array}$

and η = a² − 4q². The special case of |q| = a/2 has to be neglected to avoid singular solutions in Eq. 3.

We stress that, the spectral parameter λ plays a key role in the dynamics of localized waves. Namely, the imaginary part of λ determines the existence condition of the waves, while the real part determines the wave structures. In particular, the sign of the imaginary part has no effect on the waveform; while the sign of the real part induces different waveforms.

Eq. 7 shows the variety of the spectral parameter λ. Namely, for any given initial parameters we have two spectral parameters λ₊ and λ₋. Such variety provides possibilities for new RW formation.

Figure 1 shows the evolution of the spectral parameter λ verse the relative frequency q. In the region |q| < a/2, both λ₊ and λ₋ are purely imaginary (λ_+r = λ_−r = 0), and we have λ_+i = −λ_−i. Thus, RWs in this region are degenerate for any given a, q. Namely, $u_j^{[1]}({\lambda }_{+})=u_j^{[1]}({\lambda }_{-})$ when |q| < a/2. In contrast, in the region |q| > a/2, λ₊ and λ₋ are complex, and λ₊ = −λ₋. This makes it possible to have two different RWs in the same parameter range, which is absent in previous results [25, 26]. Such two RWs are non-degenerate.

FIGURE 1

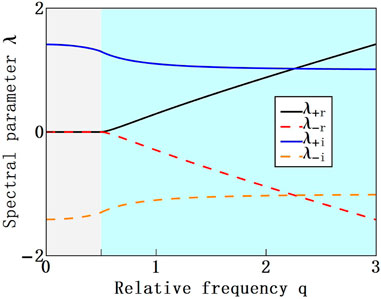
FIGURE 1. Evolution of the spectral parameter λ versus the relative frequency q. The gray and cyan areas correspond to the degenerate and non-degenerate regions, respectively. The parameters are a₁ = a₂ = a = 1.

Figure 2 shows the amplitude distributions of RWs in the degenerate and non-degenerate regions, respectively. As shown in Figure 2A, RWs with λ₊ and λ₋ in the degenerate region |q| < a/2 are identical, namely, $|u_j^{[1]}({\lambda }_{+})|=|u_j^{[1]}({\lambda }_{-})|$. Moreover, $|u_1^{[1]}|$ and $|u_2^{[1]}|$ feature standard bright RWs, while $|u_3^{[1]}|$ exhibits dark structure.

FIGURE 2

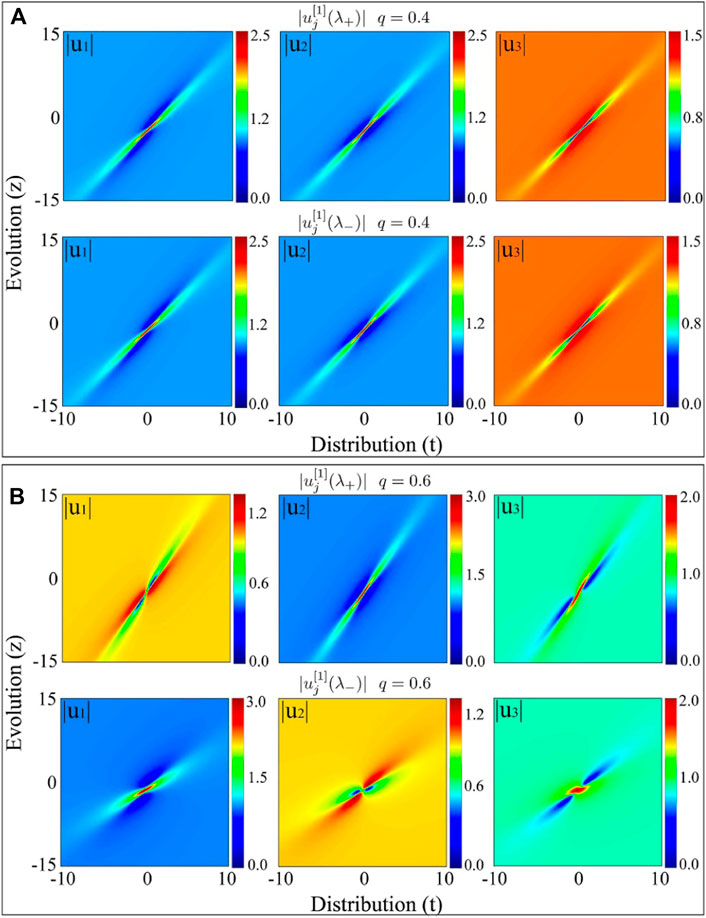
FIGURE 2. Amplitude distributions of RWs $|u_j^{[1]}({\lambda }_{+})|$, $|u_j^{[1]}({\lambda }_{-})|$ in the degenerate (A) and non-degenerate (B) regions. (A) RWs with q = 0.4 and (B) RWs with q = 0.6. The other parameters are a₁ = a₂ = 1, c₁ = 1, c₂ = 2, A₁ = A₂ = 1, and A₃ = 0. The spectral parameters λ_± are calculated by Eq. 7.

However, in the non-degenerate region, $|u_j^{[1]}({\lambda }_{+})|$ and $|u_j^{[1]}({\lambda }_{-})|$ are different not only in velocity but also in amplitude structure, as shown in Figure 2B. Specifically, $|u_j^{[1]}({\lambda }_{+})|$ exhibits vector four-petal-bright-bright RWs; while $|u_j^{[1]}({\lambda }_{-})|$ shows vector bright-four-petal-bright RWs.

Another remarkable result is that such RWs can exhibit the soliton structure when q is large. As shown in Figure 3, the vector RWs (Figure 3A) transform themselves to the vector solitons (Figure 3B) when q changes from 0.4 to 2. A comparison between the RWs (shown in Figure 2) and the solitons (shown in Figure 3) reveals a distinct type of transition between the bright (dark) RWs and the dark (bright) solitons. Examples are shown in the case of $u_{\mathrm{1,3}}^{[1]}({\lambda }_{+})$ and $u_{\mathrm{2,3}}^{[1]}({\lambda }_{-})$. This transition dynamics is different from the conventional transitions between bright (dark) RWs and bright (dark) solitons reported before [35–37].

FIGURE 3

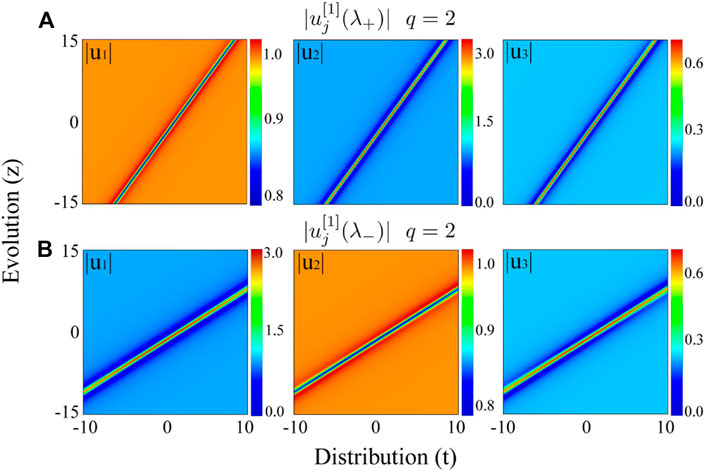
FIGURE 3. Amplitude distributions of solitons $|u_j^{[1]}({\lambda }_{+})|$, $|u_j^{[1]}({\lambda }_{-})|$ in the non-degenerate regions of q = 2. (A) Solitons with λ₊ and (B) solitons with λ₋. Other parameters are the same as in Figure 2.

3.2 Multiple transition of fundamental rogue waves

To better understand the transitions shown above, we focus our attention on $u_1^{[1]}({\lambda }_{+})$ with different frequencies. Figure 4 highlights the transition characteristics with the parameter variation from q = 0 to q = 2. The extremum of the amplitude profiles (at z = −2.35) versus the frequency are shown in Figure 4A. The maximum amplitude corresponds to the red and yellow curves, and the minimum amplitude is represented by the blue solid and dashed curves. The labels in Figure 4A correspond to the amplitude distributions of RWs in Figure 4B.

FIGURE 4

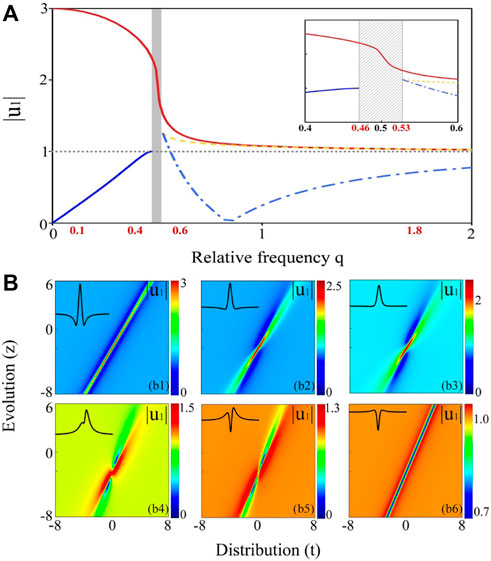
FIGURE 4. Characteristics of transitions on the certain range of frequency in the wave field $|u_1^{[1]}({\lambda }_{+})|$.(A) Variation in the extremum of the amplitude profiles of RWs versus the frequency at z = −2.35, including the maximum $|u_{1max}^{[1]}|$ (red and yellow curves) and the minimum $|u_{1min}^{[1]}|$ (blue solid and dashed curves). There is only one maximum in the range q ∈ (0.46, 0.53) (the gray area). Here the insert shows an enlargement of the gray area. Note that the amplitude profiles of RWs at z = −2.35 in this region have no minimum. As q ≥ 0.53, there are two maximums and one minimum. (B) Amplitude distributions $|u_1^{[1]}|$ for (b1) q = 0.1, (b2) q = 0.4, (b3) q = 0.46, (b4) q = 0.53, (b5) q = 0.6, and (b6) q = 2.5. The insert curves in upper left correspond to the amplitude profiles at z = −2.35. Other parameters are the same as Figure 2.

As can be seen, the structure of RWs is at first compressed then elongated with a continuously decreasing amplitude $|u_1^{[1]}({\lambda }_{+})|$ as q increases. Finally, the RW is transformed into a soliton-like wave. The corresponding localization increases at first and then decreases.

Clearly, this transition process (a bright RW to a dark soliton) contains multiple wave states, namely bright RW [Figure 4 (b1)], four-petal RW [Figure 4 (b4)] and dark soliton [Figure 4 (b6)]. This stands in sharp contrast to the simple single transition reported before [35–37].

3.3 Non-degenerate second-order rogue waves

As shown in Section 3.1, for any given parameters in the non-degenerate region, there exist two different RWs. Let us consider whether such two RWs can coexist in the same plane wave. To answer this question, we proceed to construct the second-order RW solution in the non-degenerate region. The details are given by Supplementary Appendix S7.2. The solution is obtained by using the second-order iteration of the Darboux transformation with two spectral parameters {λ₊, λ₋}. Each spectral parameter corresponds to a RW. Thus, this solution describes the dynamics of the non-degenerate second-order RW. This higher-order RW solution is different from the degenerate multi-RWs presented before [25, 26].

Figure 5 shows the characteristics of non-degenerate second-order RWs with different q. To better analyze the variation of each RW structure, we have separated the RWs by the relative separations in both z and t, i.e., z₁ = z − 1, t₁ = t + 1, z₂ = z + 1, t₂ = t − 1. As can be seen from the figure, the second-order RWs (Figures 5A,B) have two different fundamental RWs. In particular, such two RWs can both transform into two solitons (Figure 5C). Interestingly, in either $u_1^{[2]}$ or $u_2^{[2]}$ component, two different types of transitions appear simultaneously in the same wave component. One is the multiple transition from bright RW to four-petal RW then to dark soliton; another is the single transition from bright RW to bright soliton.

FIGURE 5

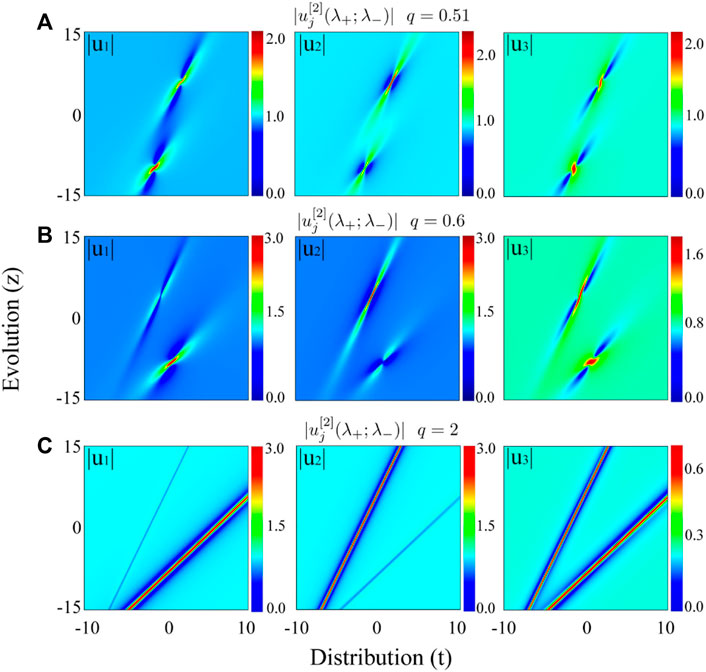
FIGURE 5. Amplitude distributions of non-degenerate second-order RWs, $|u_j^{[2]}({\lambda }_{+};{\lambda }_{-})|$ with (A) q = 0.51, (B) q = 0.6, and (C) q = 2. From (A) to (C), one can see clearly the transitions between non-degenerate RWs and solitons. The exact second-order solutions as shown in the Supplementary Appendix S7.2, other parameters are the same as Figure 2.

4 Mechanism explanation

In previous results, the mechanism of single state transitions is explained well by the MI analysis [35–37]. To better understand the multiple transition, we use here the combination analysis of the MI and the energy exchange between different wave components. The latter is an important physical quantity in 3WRI system that can be monitored in experiments. Such combination provides a solid interpretation for the transition mechanism.

We first pay attention to the standard modulation (linear) stability analysis. Adding a small-amplitude Fourier modes to the plane-wave solutions, we obtain

$u_j=u_j^{\left[0\right]}\left\{1+f_j{e}^{i\mathrm{\Omega }\left(t-\mu x\right)}+g_j{e}^{-i\mathrm{\Omega }\left(t-{\mu }^{\ast }x\right)}\right\},(8)$

where f_j and g_j are small amplitudes, and the propagation parameters Ω and μ are assumed to be real and complex, respectively. A substitution of these perturbed plane-wave solutions into Eq. 1, followed by linearization yields the dispersion relation

${\left[\left(\frac{a_1^2}{\mu c_1-1}+\frac{a_2^2}{\mu c_2-1}\right)\delta \mu -\frac{c_1-c_2}{\delta }\right]}^2+\frac{4\mu a_2^2\left(c_1-c_2\right)}{\mu c_1-1}-{\mathrm{\Omega }}^2{\mu }^2=0.(9)$

Considering the condition of RW formation, namely, Ω → 0 [29, 30], we have the solutions of μ from Eq. 9 as follows

${\mu }_1={\mu }_r+i{\mu }_{i_1},{\mu }_2={\mu }_r+i{\mu }_{i_2},(10)$

where μ_r denotes the real part, while ${\mu }_{i_1}$, ${\mu }_{i_2}$ are the imaginary parts. For simplicity, we set c₁ = 1 and c₂ = 2. Their explicit expressions are given by

${\mu }_r=\left\{\begin{array}{cc}{\varrho }_1\left[\varpi +3a^2\sqrt{a\eta }\right],\hfill & |q|<a/2,\hfill \\ {\varrho }_1\left[\varpi +2aq{\ell }_1\right],\hfill & |q|>a/2,\hfill \end{array}\right.$

and

${\mu }_{i_1}=\left\{\begin{array}{cc}\pm {\varrho }_1\left[2aq\sqrt{{\mathrm{\Gamma }}_2-{\mathrm{\Gamma }}_1}\right],\hfill & |q|<a/2,\hfill \\ \pm {\varrho }_1\left[3a^2\sqrt{-a\eta }-2aq{\ell }_2\right],\hfill & |q|>a/2,\hfill \end{array}\right.$

${\mu }_{i_2}=\left\{\begin{array}{cc}\pm {\varrho }_1\left[2aq\sqrt{{\mathrm{\Gamma }}_1+{\mathrm{\Gamma }}_2}\right],\hfill & |q|<a/2,\hfill \\ \pm {\varrho }_1\left[3a^2\sqrt{-a\eta }+2aq{\ell }_2\right],\hfill & |q|>a/2,\hfill \end{array}\right.$

where ϖ = 3η² + 18a²q², ${\varrho }_1={[4{\eta }^2+5a^4+16a^2{q}^2]}^{-1},{\mathrm{\Gamma }}_1=(a^2-40q^2)\sqrt{a\eta },{\mathrm{\Gamma }}_2={\eta }^3+3a^2{q}^2(17a^2-32q^2),$ and ${\ell }_1={[\frac{1}{2}\sqrt{{\mathrm{\Gamma }}_2^2-{\mathrm{\Gamma }}_1^2}-{\mathrm{\Gamma }}_2]}^{1/2},{\ell }_2={[\frac{1}{2}\sqrt{{\mathrm{\Gamma }}_2^2-{\mathrm{\Gamma }}_1^2}+{\mathrm{\Gamma }}_2]}^{1/2}$.

MI is described by the gain (growth rate). The latter is given by G_1,2 = |Im{μ_1,2}| ≠ 0. It means that small-amplitude perturbations suffer MI and grow exponentially as exp (Gx) at the expense of pump waves.

Note that there are two different forms of the MI gain, namely $G=|{\mu }_{i_1}|$ and $G=|{\mu }_{i_2}|$. The existence condition of MI is consistent with the imaginary part of spectral parameter given by Eq. 7. As MI is regarded as the origin of RWs [29, 30], the two MI gains correspond to two different families of RWs.

On the other hand, the effective energy exchanges take place between the waves in different components. The effective energy has the form [25, 26].

$E_j\left({\lambda }_{\pm }\right)=\frac{1}{2}{\int }_{-\infty }^{+\infty }\left(|u_j^{\left[1\right]}\left({\lambda }_{\pm }\right){|}^2-|u_j^{\left[0\right]}{|}^2\right)dt.(11)$

For RWs with different spectral parameters λ_±, we have E_j(λ_±). In each case, one can verify that the effective energy obeys the relation E₁ = E₃ = −2E₂.

Figure 6A shows the variations of both the MI gain $G=|{\mu }_{i_1}|$, $G=|{\mu }_{i_2}|$ versus q. As can be seen, both two MI gains exhibit non-monotonic variation. Specifically, as q increases, MI gain increases first and reaches its peak at a certain q = q_max. It is given by ∂|μ_i|/∂q = 0. MI gain then decreases gradually and approaches to zero when q is relatively large. This process corresponds to the transition between RWs and solitons reported above.

FIGURE 6

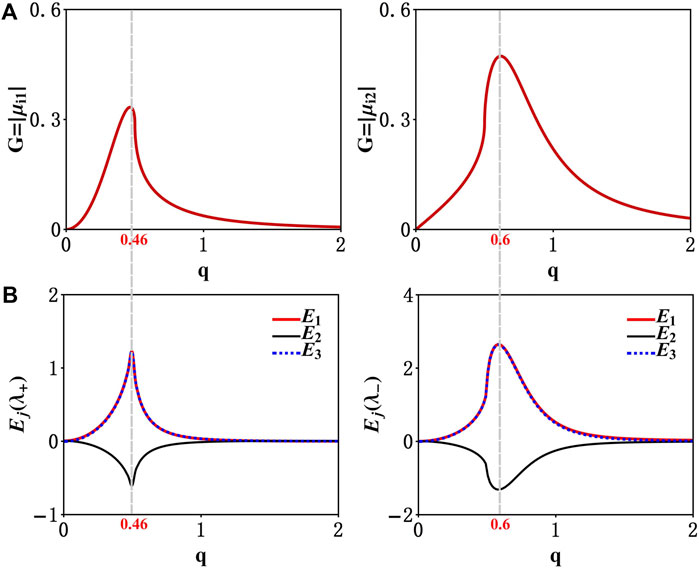
FIGURE 6. Non-monotonic variation of the MI gain (A) and effective energy (B) versus q, which can be obtained by Eqs 9, 11. Here the energy E_j (λ₊) trend consistent with MI gain G = |μ_i1|, and the extreme point corresponds to the most localized structures RWs for q = 0.46. Another case of MI gain G = |μ_i2| corresponding to the energy changes E_j (λ₋) that reaches an extreme at q = 0.6.

However, one should note that the two MI gains admit different maximums. For $G=|{\mu }_{i_1}|$, we obtain q_max = 0.46; for $G=|{\mu }_{i_2}|$, we obtain q_max = 0.6. This indicates that the variations of the MI gains are asynchronous. To better understand the property of MI, we further consider the characteristics of the effective energy of RWs.

Figure 6B shows the variations of the effective energy E_j (λ_±) versus q. All effective energies exhibit non-monotonic variation. For u₁ and u₃, the effective energies E₁ (λ_±) and E₃ (λ_±) increase first and reach the maximums. They then decrease and approach to zero. However, the reverse process proceeds for E₂ (λ_±) in u₂ wave component. This comes from the conservation law E₁ + E₂ = E₂ + E₃. A comparison between MI gains and the effective energy shows that the extreme point of E_j (λ₊) is completely consistent with that of $G=|{\mu }_{i_1}|$; the extreme point of E_j (λ₋) coincides with that of $G=|{\mu }_{i_2}|$. Thus, the multiple transition comes from the inherent non-monotonic variation of the effective energy in 3WRI system.

5 Numerical simulations

Finally, we discussed the robustness of the RWs and their transition dynamics. This can be done numerically by adding random noise to the initial states. Such perturbed initial states read

$u_p=u_j\left(t,z=z_0\right)\left\{1+m\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{d}\mathrm{o}\mathrm{m}\left[-\mathrm{1,1}\right]\right\},(12)$

where m is a small number denoting the amplitude of noise, u_j (t, z = z₀) denotes the exact vector solution at a certain distance z₀.

Figure 7 shows the numerical results of the fundamental RWs (a) and the transformed solitons (b). We take the initial states from the exact solutions $u_j^{[1]}({\lambda }_{+})(t,z_0=-10)$ (shown in Figures 2A, 3A) perturbed by the noise amplitude m = 0.001. As can be seen from the figures, both RWs and solitons can suffer the random noises and be well reproduced. The following chaotic states appear as the result of the spontaneous MI.

FIGURE 7

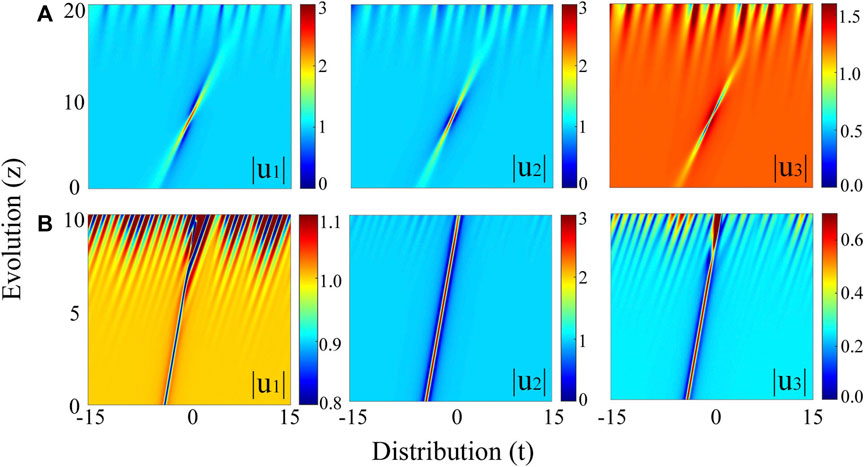
FIGURE 7. Numerical evolution of the transition between the fundamental RW (A) with q = 0.4 and soliton (B) with q = 2. The initial states are extracted from the exact solutions $u_j^{[1]}({\lambda }_{+})(t,z_0=-10)$ (shown in Figures 2A, 3A) perturbed by the noise amplitude m = 0.001.

Figure 8 shows the numerical results of the non-degenerate RWs (a) and the transformed solitons (b). The corresponding initial states are extracted from exact solutions $u_j^{[2]}({\lambda }_{+};{\lambda }_{-})(t,z_0=-15)$ (shown in Figures 5A,C) perturbed by the noise amplitude m = 0.0001. Despite being perturbed by random noises, the non-degenerate RWs and solitons are well reproduced. This result confirms the robustness of the non-degenerate RWs and solitons in 3WRI system.

FIGURE 8

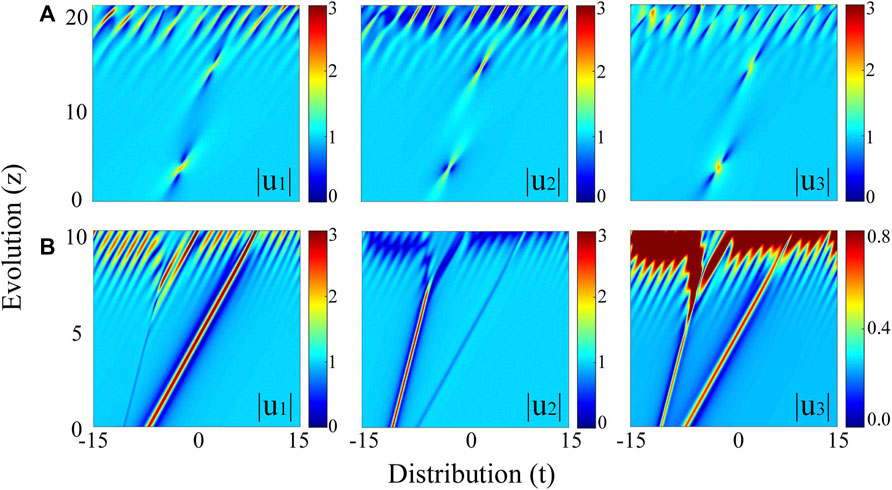
FIGURE 8. Numerical evolution of the transition between the nondegenerate RW (A) with q = 0.4 and (B) nondegenerate soliton with q = 2. The initial states are extracted from the exact solutions $u_j^{[2]}({\lambda }_{+};{\lambda }_{-})(t,z_0=-15)$ (shown in Figures 5A,C) perturbed by the noise amplitude m = 0.0001.

6 Conclusion

We demonstrated the existence, transition, formation mechanism, and stability of the nondegenerate RWs in the 3WRI system, which have not been reported before. The nondegenerate RWs consist of two fundamental RWs each with individual Lax spectral parameter. We present the existence diagram. We show that the multiple transitions are closely connected with the inherent energy exchange between different wave components of the 3WRI system, which is forbidden in the coupled NLSE systems. As the 3WRI equations are the fundamental model accounting for the dynamics of vector waves in strong resonant processes, our results could provide insights into the 3WRI RW formation, and may offer the possibility of experimental observations in multi-component resonant systems. On the other hand, the RW is just the limiting case of a breather with infinite period. Just like recent advances in nondegenerate breathers in coupled NLSEs [42, 43], we expect that 3WRI nondegenerate breathers will play a key role in understanding wave dynamics in strong resonant processes.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

CL conceived the ideal and wrote the first version of the manuscript. Y-HW presented the exact solutions of nonlinear excitations. All authors contributed to the physical analysis and revision of the manuscript.

Funding

This work is supported by the NSFC (Grants Nos 12275213, 12175178, 12004309, 12022513, and 12047502), the Major Basic Research Program of Natural Science of Shaanxi Province (No. 2017KCT-12), and the Natural Science basic Research Program of Shaanxi Province (Grant No. 2022KJXX-71).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2022.1043053/full#supplementary-material

References

1. Zakharov VE, Manakov SV. The theory of resonance interaction of wave packets in nonlinear media. Zh Exp Teor Fiz (1975) 69:1654–73.

Google Scholar

2. Malkin VM, Shvets G, Fisch NJ. Fast compression of laser beams to highly overcritical powers. Phys Rev Lett (1999) 82(22):4448–51. doi:10.1103/physrevlett.82.4448

CrossRef Full Text | Google Scholar

3. Lamb KG. Tidally generated near-resonant internal wave triads at a shelf break. Geophys Res Lett (2007) 34(18):L18607. doi:10.1029/2007gl030825

CrossRef Full Text | Google Scholar

4. Burlak G, Koshevaya S, Hayakawa M, Gutierrez-D E, Grimalsky V. Acousto-optic solitons in fibers. Opt Rev (2000) 7(4):323–5. doi:10.1007/s10043-000-0323-3

CrossRef Full Text | Google Scholar

5. Aubourg Q, Antoine C, Peureux C, Ardhuin F, Sommeria J, Viboud S, et al. Three-wave and four-wave interactions in gravity wave turbulence. Phys Rev Fluids (2017) 2(11):114802. doi:10.1103/physrevfluids.2.114802

CrossRef Full Text | Google Scholar

6. Deike L, Berhanu M, Falcon E. Experimental observation of hydroelastic three-wave interactions. Phys Rev Fluids (2017) 2(6):064803. doi:10.1103/physrevfluids.2.064803

CrossRef Full Text | Google Scholar

7. Cerullo G, De Silvestri S. Ultrafast optical parametric amplifiers. Rev scientific Instr (2003) 74(1):1–18. doi:10.1063/1.1523642

CrossRef Full Text | Google Scholar

8. Degasperis A, Lombardo S. Multicomponent integrable wave equations: Ii. soliton solutions. J Phys A: Math Theor (2009) 42(38):385206. doi:10.1088/1751-8113/42/38/385206

CrossRef Full Text | Google Scholar

9. Degasperis A, Conforti M, Baronio F, Wabnitz S, Lombardo S. The three-wave resonant interaction equations: Spectral and numerical methods. Lett Math Phys (2011) 96(1):367–403. doi:10.1007/s11005-010-0430-4

CrossRef Full Text | Google Scholar

10. Franken PA, Hill AE, el Peters CW, Gabriel W. Generation of optical harmonics. Phys Rev Lett (1961) 7(4):118–9. doi:10.1103/physrevlett.7.118

CrossRef Full Text | Google Scholar

11. Armstrong JA, Bloembergen N, Ducuing J, Pershan PS. Interactions between light waves in a nonlinear dielectric. Phys Rev (1962) 127(6):1918–39. doi:10.1103/physrev.127.1918

CrossRef Full Text | Google Scholar

12. Zernike F, Berman PR. Generation of far infrared as a difference frequency. Phys Rev Lett (1965) 15(26):999–1001. doi:10.1103/physrevlett.15.999

CrossRef Full Text | Google Scholar

13. Ibragimov E, Allan S. Second-harmonic pulse compression in the soliton regime. Opt Lett (1996) 21(19):1582–4. doi:10.1364/ol.21.001582

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Baronio F, Conforti M, De Angelis C, Degasperis A, Andreana M, Vincent C, et al. Velocity-locked solitary waves in quadratic media. Phys Rev Lett (2010) 104(11):113902. doi:10.1103/physrevlett.104.113902

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Degasperis A, Conforti M, Baronio F, Wabnitz S. Stable control of pulse speed in parametric three-wave solitons. Phys Rev Lett (2006) 97(9):093901. doi:10.1103/physrevlett.97.093901

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Picozzi A, Haelterman M. Parametric three-wave soliton generated from incoherent light. Phys Rev Lett (2001) 86(10):2010–3. doi:10.1103/physrevlett.86.2010

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Conforti M, Baronio F, Degasperis A, Wabnitz S. Inelastic scattering and interactions of three-wave parametric solitons. Phys Rev E (2006) 74(6):065602. doi:10.1103/physreve.74.065602

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Taranenko YN, Kazovsky LG. Three-wave envelope solitons: Can the speed of light in the fiber be controlled. IEEE Photon Technol Lett (1992) 4(5):494–7. doi:10.1109/68.136498

CrossRef Full Text | Google Scholar

19. Taranenko NL, Kazovsky LG, Taranenko YN. Three-wave envelope solitons: Possibility of controlling the speed of light in fiber. J Lightwave Technol (1994) 12(7):1101–11. doi:10.1109/50.301801

CrossRef Full Text | Google Scholar

20. Baronio F, Conforti M, Degasperis A, Wabnitz S. Three-wave trapponic solitons for tunable high-repetition rate pulse train generation. IEEE J Quan Electron (2008) 44(6):542–6. doi:10.1109/jqe.2008.917970

CrossRef Full Text | Google Scholar

21. Conforti M, Baronio F, Degasperis A, Wabnitz S. Parametric frequency conversion of short optical pulses controlled by a cw background. Opt Express (2007) 15(19):12246–51. doi:10.1364/oe.15.012246

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Romanova NN, Yu Annenkov S. Three-wave resonant interactions in unstable media. J Fluid Mech (2005) 539:57–91. doi:10.1017/s0022112005005665

CrossRef Full Text | Google Scholar

23. Degasperis A, Lombardo S. Rational solitons of wave resonant-interaction models. Phys Rev E (2013) 88(5):052914. doi:10.1103/physreve.88.052914

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Zhang G, Yan Z, Wen XY. Three-wave resonant interactions: Multi-dark-dark-dark solitons, breathers, rogue waves, and their interactions and dynamics. Physica D: Nonlinear Phenomena (2018) 366:27–42. doi:10.1016/j.physd.2017.11.001

CrossRef Full Text | Google Scholar

25. Baronio F, Conforti M, Degasperis A, Lombardo S. Rogue waves emerging from the resonant interaction of three waves. Phys Rev Lett (2013) 111(11):114101. doi:10.1103/physrevlett.111.114101

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Chen S, Baronio F, Soto-Crespo JM, Grelu P, Conforti M, Wabnitz S. Optical rogue waves in parametric three-wave mixing and coherent stimulated scattering. Phys Rev A (Coll Park) (2015) 92(3):033847. doi:10.1103/physreva.92.033847

CrossRef Full Text | Google Scholar

27. Yang B, Yang J. Rogue waves in (2+1)-dimensional three-wave resonant interactions. Physica D: Nonlinear Phenomena (2022) 432:133160. doi:10.1016/j.physd.2022.133160

CrossRef Full Text | Google Scholar

28. Chen S, Baronio F, Soto-Crespo JM, Grelu P, Mihalache D. Versatile rogue waves in scalar, vector, and multidimensional nonlinear systems. J Phys A: Math Theor (2017) 50(46):463001. doi:10.1088/1751-8121/aa8f00

CrossRef Full Text | Google Scholar

29. Baronio F, Conforti M, Degasperis A, Lombardo S, Onorato M, Wabnitz S. Vector rogue waves and baseband modulation instability in the defocusing regime. Phys Rev Lett (2014) 113(3):034101. doi:10.1103/physrevlett.113.034101

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Zhao LC, Ling L. Quantitative relations between modulational instability and several well-known nonlinear excitations. J Opt Soc Am B (2016) 33(5):850–6. doi:10.1364/josab.33.000850

CrossRef Full Text | Google Scholar

31. Akhmediev N, Adrian A, Soto-Crespo JM. Fundamental rogue waves and their superpositions in nonlinear integrable systems. Nonlinear Guided Wave Opt A Testbed Extreme Waves (2017).

Google Scholar

32. Akhmediev N. Waves that appear from nowhere: Complex rogue wave structures and their elementary particles. Front Phys (2021) 8:612318. doi:10.3389/fphy.2020.612318

CrossRef Full Text | Google Scholar

33. Mihalache D. Localized structures in optical and matter-wave media: A selection of recent studies. Rom Rep Phys (2021) 73(2):403.

Google Scholar

34. Liu C, Chen SC, Yao X, Akhmediev N. Non-degenerate multi-rogue waves and easy ways of their excitation. Physica D: Nonlinear Phenomena (2022) 433:133192. doi:10.1016/j.physd.2022.133192

CrossRef Full Text | Google Scholar

35. Zhao LC, Li SC, Ling L. Rational w-shaped solitons on a continuous-wave background in the sasa-satsuma equation. Phys Rev E (2014) 89(2):023210. doi:10.1103/physreve.89.023210

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Liu C, Yang ZY, Zhao LC, Yang WL. State transition induced by higher-order effects and background frequency. Phys Rev E (2015) 91(2):022904. doi:10.1103/physreve.91.022904

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Liu C, Yang ZY, Zhao LC, Yang WL. Transition, coexistence, and interaction of vector localized waves arising from higher-order effects. Ann Phys (2015) 362:130–8. doi:10.1016/j.aop.2015.06.008

CrossRef Full Text | Google Scholar

38. Yang J. Nonlinear waves in integrable and nonintegrable systems. Philadelphia, Pennsylvania, USA: SIAM (2010).

Google Scholar

39. Degasperis A. Integrable nonlocal wave interaction models. J Phys A: Math Theor (2011) 44(5):052002. doi:10.1088/1751-8113/44/5/052002

CrossRef Full Text | Google Scholar

40. Borgna JP, Degasperis A, Fernando De Leo M, Rial D. Integrability of nonlinear wave equations and solvability of their initial value problem. J Math Phys (2012) 53(4):043701. doi:10.1063/1.3699358

CrossRef Full Text | Google Scholar

41. Liu C, Chen SC, Yao XK, Akhmediev N. Modulation instability and non-degenerate akhmediev breathers of manakov equations. Chin. Phys. Lett. (2022) 39:094201.

CrossRef Full Text | Google Scholar

42. Che WJ, Chen SC, Liu C, Zhao LC, Akhmediev N. Nondegenerate kuznetsov-ma solitons of manakov equations and their physical spectra. Physical Review A (2022) 105(4):043526.

CrossRef Full Text | Google Scholar

43. Guo B, Ling L, Liu QP. Nonlinear Schrödinger equation: Generalized darboux transformation and rogue wave solutions. Phys Rev E (2012) 85(2):026607. doi:10.1103/physreve.85.026607

PubMed Abstract | CrossRef Full Text | Google Scholar