An opinion dynamics model based on affinity and social noise

Most previous works have studied the evolution of opinions based on the Hegselmann–Krause model, the Deffuant–Weisbuch model, and the Sznajd model. However, the influence of social influence on opinions is discussed less. Based on the social influence theory and the Hegselmann–Krause model of opinion dynamics, we introduce the affinity and social noise in the Hegselmann–Krause model of opinion dynamics and propose an affinity and social noise Hegselmann–Krause model (ASNHK). The influence of affinity degree, affinity threshold, social noise, and personnel heterogeneity on opinion evolution is discussed in experimental analysis. Experimental results show that the affinity between people can improve opinions to form a consensus positively, but the affinity threshold has a negative role contrarily. Moreover, when the social noise increases, the opinions will form a consensus. When it increases to a certain value, the opinion will be decentralized. Furthermore, personnel heterogeneity has different effects on opinion evolution. Open-minded individuals are more likely to form a unified opinion, while closed-minded individuals have difficulty unifying their opinions. Overall, this research provides a clearer explanation of the group opinion evolution from social influence.

1 Introduction

Opinion is people’s insights and understanding of something. It is a kind of idea, opinion, judgment, or emotion generally held by the public [1]. Exploring the evolution of public opinion can help people understand the evolution mechanism of opinion and behavior, respond to public opinion crises, and guide public opinion dissemination. At present, scholars have carried out relevant research on the evolution of ideas, but the behavior and opinions of the public still need to be further explored. For example, with the advent of COVID-19, it was believed that the Shuanghuanglian oral liquid can act on the COVID-19 virus, based on an internet finding, and then many people began to form opinions. What is the mechanism behind this phenomenon and how are the opinions affected and formed? What factors play a role? To our best knowledge, there is still no research that can provide a clear explanation.

Until now, scholars have researched group opinion dynamics from different perspectives [2–5]. According to the type of opinion, the opinion dynamic model can be divided into many types, such as the continuous model, the discrete model, and the continuous opinions and discrete actions model (CODA model). The common continuous model contains the Hegselmann–Krause model (HK model) [6–9], the Deffuant–Weisbuch model (DW model) [10–12], and other models. In terms of the Deffuant–Weisbuch model, [13] proposed an adaptation of the Deffuant–Weisbuch model that incorporates both implicit and explicit opinions; [14] discussed the higher-order interactions that destroy phase transitions in the Deffuant–Weisbuch opinion dynamics model; based on the Deffuant model, [1] considered attitude-hiding behaviors and proposed an agent-based model of opinion dynamics with attitude-hiding behaviors. The common discrete model contains the Sznajd model [15–18], the Voter model [19–21], and the Majority model [22, 23].

Current scholars have explored different opinion models from different perspectives. However, few researchers consider the social influence. In fact, the study of opinions is often inseparable from the individual and the environment in which the individual lives, but existing research has not observed this. Social influence theory indicates that proximity to others and the social environment can affect people’s opinions comprehensively. On one hand, people cannot survive independently, and it is necessary to establish a relationship with people around [24]; on the other hand, it is impossible for people to escape from the social environment. Therefore, relationship and social environment are two important factors that can influence people’s behavior [25]. To express conveniently, we use affinity and social noise to indicate the relationship and social environment. If the relationship among people is good, the affinity is large; on the contrary, if the relationship is not good, the affinity is small. Similarly, if the influence of the social environment is strong, the social noise is large; on the contrary, the social noise is small. To explore opinion evolution under the influence of social influence theory, this study discussed the evolution mechanism of group opinion by introducing affinity and social noise. Finally, an experimental analysis is carried out, and the simulation results are discussed. The illustration of the affinity and social noise Hegselmann–Krause model is shown in Figure 1.

FIGURE 1

FIGURE 1. Illustration of the affinity and social noise Hegselmann–Krause model.

There are the following contributions to this research. First, this study extends the Hegselmann–Krause model and conforms the opinion evolution more to human interaction activities. Second, affinity and social noise are introduced to the Hegselmann–Krause model based on the social influence theory. Third, this research will shed light on and help people understand the opinion evolution mechanism well. Moreover, distinct from the HK model, this research used mathematical models and equations to portray affinity and social noise, and it enriched the opinion dynamics model greatly and can be applied to the fields of public opinion governance, intervention, and control. The research considers interpersonal and environmental influences in the evolution of opinion and further extends the boundaries of opinion dynamics.

The article is arranged as follows: the introduction is shown in Section 1. In this part, we introduce the current research on the opinion dynamic models; the related works on the Hegselmann–Krause model, social influence theory, affinity in public, and social noise are introduced in Section 2; in Section 3, the affinity and social noise Hegselmann–Krause model (ASNHK) construction is described; section 4 presents the experimental analysis of the ASNHK model. Finally, we discuss the experimental results and summarize the conclusion in Section 5 and Section 6, respectively.

2 Related work

2.1 Opinion dynamics in the Hegselmann–Krause model

As a kind of bounded confidence group opinion dynamics, the HK model has attracted the research interests of many scholars since it was put forward by Hegselmann and Krause [6] in 2002. After that, scholars used different methods to extend this model. [26] integrated the Hegselmann–Krause model into the process of product improvement and explored the relationship among the evolution of opinion, product scheme, and design iteration; [27] proposed a bounded confidence model which considered the opinion priority of leaders and divided the group into “opinion leaders” and ordinary people groups; based on the HK model, [28] considered social learning and explored the agent’s opinion evolution when they are influenced by the truth or a conflicting source. In addition, some researchers discussed the consensus and convergence in the HK model [29, 30]. The aforementioned research provided some insights to the following scholars on the HK model, and these research studies broaden the research boundary of opinion dynamics.

2.2 Social influence theory

As a kind of sociological and psychological theory, social influence theory has been given more and more attention by scholars [31]. Social influence comes from two aspects. On one hand, an agent will be influenced by the role of another. Under the influence of others, an individual will more or less change in one way or another. On the other hand, the surrounding environment will form a kind of normative force, promoting members’ psychology to form a kind of group pressure and making its members be in line with the group [4, 32]. In terms of social influence, [33] explored the effect of social influence based on the Durkheimian opinion dynamics by constructing a social influence function with the social ranking (SR) and the distance; [34] also introduced individuals’ social influences in social networks to highlight the heterogeneity of individuals in opinion evolution; [35] considered the individuals’ influential power and explored the authority effect and the Matthew effect in opinion dynamics. In addition, some researchers also explored individuals’ social influence on themselves in opinion dynamics [36].

2.3 Affinity in public

As an indicator of people’s estrangement, affinity is an important factor that influences people’s attitudes and behavior. In opinion dynamics, [37] proposed a model to simulate the process of opinion formation and explored the role of mutual affinity between interacting agents; [38] developed a statistical method to find affinity relations in a large opinion network; [39] took the mutual affinity between agents into the model and explored the process of opinion formation in an open community; [40] used the opinion dynamics to explore the partisan conflicts in recent America and discuss the change of affinity among co-partisans; [41] explored the nonlinear interaction of ideological affinity with the psychological reaction of agents in the frame of a multiparametric mathematical model of opinion dynamics. It can be seen from the aforementioned research that affinity has gradually gained the attention of scholars and has been applied to sociology, opinion dynamics, and other fields.

2.4 Social noise

In addition, in the process of evolution, social noise can also influence people’s behavior or opinions [42]. At present, [43] explored the HK model under the influence of noise and found that the fragmentation of HK dynamics tends to vanish when persistent noise was present; [44] explored the influence of noise on the HK model and found that the system presented an orderly to disordered phase transition with the increase of noise in the HK model; [45] also found that noise was helpful in adjusting the split phenomenon of viewpoint through the study of HK model noise; [46] used an agent-based modeling and a computational social science approach to explore the opinion evolution with various noise levels; [47] introduced the noise into the Degroot framework and proposed a new Degroot-type social learning model.

The aforementioned scholars explored opinion dynamics from different perspectives. Few studies have explored the affinity and social noise in opinion dynamics based on social influence theory systematically. To bridge this gap, this study takes the affinity and noise into the HK model and constructs an affinity and social noise Hegselmann–Krause model. In this model, we explore opinion evolution and propose the evolutionary rules and algorithm. After that, experimental analysis is carried out, and some conclusions are discussed.

3 Model formulation

3.1 Introduction of the Hegselmann–Krause model

Within the limited confidence threshold, we assume that there is a set A, A = [1, 2, 3, … , i, j, N], the set A has N individuals, and the opinion of individuals i and j is assigned as $x_i^t$ and $x_j^t$ and $x_i^t$ and $x_j^t\in [\mathrm{0,1}]$, respectively; if $|x_i^t-x_j^t|\le \epsilon$, then:

$x_i^{t+1}=\sum _{j:|x_i^t-x_j^t|}{\alpha }_{ij}{x}_j^t,(1)$

where the aforementioned model [Eq. (1)] is the Hegselmann–Krause model of opinion dynamics[6], x indicates the individual’s opinion, α_ij is the influence weight of individual i on the individual j, α_ij ∈ [0, 1], and ${\sum }_{j=1}^N{\alpha }_{ij}=1$. If the α_ij is larger, it indicates that one individual’s influence on other individuals is more obvious; ɛ is the opinion threshold, and the smaller the ɛ is, it is difficult for an individual’s opinions to influence each other. In addition, the aforementioned model is a simplified model; it ignores the order in which ideas are presented and is suitable for simultaneous group updates, such as a group meeting and an exchange within a forum.

3.2 Affinity and social noise Hegselmann–Krause model

Based on the HK model, according to the group opinion dynamics’ characteristics, we focus on the affinity and social noise in the opinion evolution. Affinity always exists in the relationship among people. If the relationship between two individuals is good, the affinity is large; on the contrary, if the relationship between two individuals is bad, the affinity is small. To take into account the affinity, we use the $r_{ij}^t$ to indicate the degree of opinion influence:

$r_{ij}^t=\frac{\mathit{max}\left(R_{ij}-\left(|x_i^t-x_j^t|-{\epsilon }_i\right),0\right)}{\mathit{max}\left(|x_i^t-x_j^t|,\phi \right)},(2)$

where R_ij ∈ [0, 1] is a real number of N × N nonnegative and asymmetric matrix of R, and it indicates the affinity degree between people. If the R_ij is smaller, the relationship between them is worse; instead, if the R_ij is larger, the relationship between them is good. $x_i^t$ is the opinion value of i, and $x_j^t$ is the opinion value of j. $r_{ij}^t$ is the degree of opinion influence, which indicates the influence degree of individual j on i in the t round. φ is a number that is not equal to 0. To avoid the denominator being equal to 0, we set φ as a minimal number, here φ = 0.001. Especially, if $|x_i^t-x_j^t|>{\epsilon }_i\&R_{ij}<\delta$, the opinion influence weight is 0, and to measure the degree of opinion influence weight, we define ρ_ij is the opinion influence weight, which is given by Eq. 3. Here, the δ is the affinity threshold, and this parameter shows that if the opinion difference between two individuals does not exceed the opinion influence threshold, the affinity between individuals can also affect the evolution of opinion.

${\rho }_{ij}=\left\{\begin{array}{cc}{r}_{ij}^t,otherwise\hfill & \hfill \\ \hfill 0,if|x_i^t-x_j^t|>{\epsilon }_i\&R_{ij}<\delta \end{array}\right.(3)$

By standardizing the influence degree of the aforementioned opinions, the following ${\mathrm{\Phi }}_{ij}^{t+1}$ indicates the opinion influence weight of individual j on individual i.

${\mathrm{\Phi }}_{ij}^{t+1}=\left\{\begin{array}{c}\hfill 0,\sum _{\kappa \in N}{\rho }_{ik}^t=0\&i\ne j\\ \hfill \frac{{\rho }_{ij}^t}{{\sum }_{\kappa \in N}{\rho }_{ik}^t},\sum _{\kappa \in N}{\rho }_{ik}^t\ne 0\\ \hfill 1,\sum _{\kappa \in N}{\rho }_{ik}^t=0\&i=j\end{array}\right.(4)$

Furthermore, to take into account the social noise, the extended HK equation in opinion dynamics can be constructed as follows.

$x_i^{\ast }\left(t\right)={\mu }_i{x}_i\left(t\right)+\left(1-{\mu }_i\right)\sum _{j\in N\left(i,x\left(t\right)\right)}{\mathrm{\Phi }}_{ij}{x}_j\left(t\right)+{\xi }_i\left(t\right),(5)$

where μ_i indicates the initial opinion persistence, ξ_i is the social noise, and it obeys the random uniform distribution. Moreover, the social noise is independent and identically distributed (i.i.d.) with Eξ₁ (1) = 0, $E{\xi }_1^2(1)>0$ [48,49]. μ_i is the persistence of individual i, and 1 − μ_i indicates the sensitivity of individuals to the opinions of the public around them. The initial persistence generally follows the normal distribution, that is to say, most people’s persistence of opinions is neutral, and the persistence of few individuals is extreme. When the mean value of the normal distribution is large, it is easy to form multiple opinion clusters, but not easy to form a consensus. On the contrary, if the majority of people’s opinions is amiable, individuals’ opinions are easily influenced by other individuals and finally form a consistent opinion.

The conditions for the evolution of opinion are as follows:

$N\left(i,x\left(t\right)\right)=\left\{\left(j\in \nu \right)|x_j\left(t\right)-x_i\left(t\right)|\le \epsilon \right\},\epsilon \in \left(\mathrm{0,1}\right].(6)$

At the t + 1, the opinion evolution equation is as follows:

$x_i\left(t+1\right)=\left\{\begin{array}{cc}1,x_i^{\ast }\left(t\right)>1\hfill & \hfill \\ \hfill x_i^{\ast }\left(t\right),x\ast \in \left[\mathrm{0,1}\right],\forall i\in N,t\ge 0\\ \hfill 0,x_i^{\ast }\left(t\right)<0\end{array}\right.(7)$

To clearly explain the algorithm, we have shown the calculation process of the affinity and social noise Hegselmann–Krause model in Figure 2.

FIGURE 2

FIGURE 2. Algorithm of the affinity and social noise Hegselmann–Krause model.

Based on the aforementioned model construction, the affinity and social noise Hegselmann–Krause model is built, and the specific parameter note is shown in Table 1.

TABLE 1

TABLE 1. Parameters in the model.

4 Experimental analysis

4.1 Experiment setup

Generally speaking, in real life, the persistence of opinion is neutral, and the opinion of small people is extremely close to 0 or 1. Therefore, we can assume that the distribution of people’s opinion persistence belongs to normal distribution. Default settings for the parameters used in the experiments are shown in Table 2.

TABLE 2

TABLE 2. Default settings for the parameters used in the experiments.

4.2 Influence of affinity degree on opinion evolution

In the proposed model, the first analysis is performed by simulating the influence of affinity degree on opinion evolution. In terms of parameter setting, we set the affinity degree R_ij to 0.1, 0.5, and 0.9. At this moment, the threshold of the affinity is 0.8 and the opinion numbers are 100. Also, we keep other parameters unchanged, and the simulation result is shown in Figure 3.

FIGURE 3

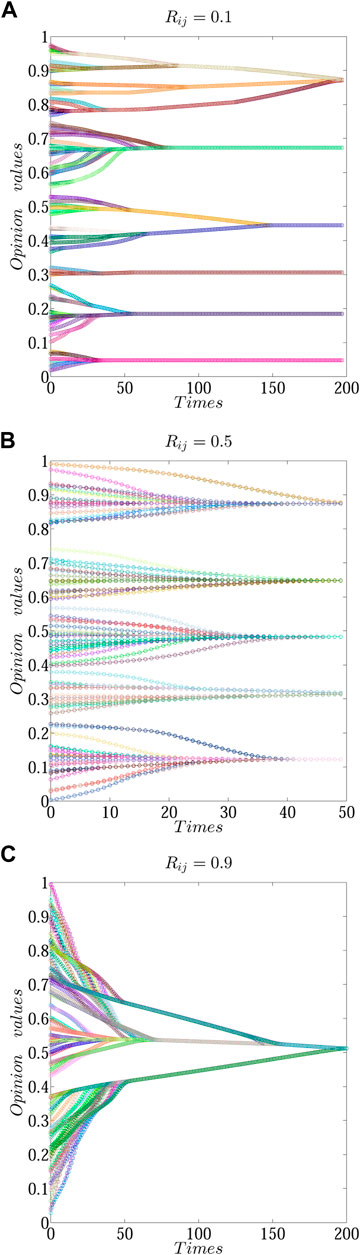
FIGURE 3. Opinion evolution result under the different affinities R_ij, (A) R_ij = 0.1, (B) R_ij = 0.5, and (C) R_ij = 0.9.

As shown in Figure 3A, we find that the opinion evolution is related to the affinity degree. In Figure 3A, when R_ij = 0.1, the opinion will be stable at 200 steps, and the opinion will form six opinion clusters; when R_ij = 0.5, the opinion will be stable at 50 steps, and the opinion will form five opinion clusters in Figure 3B; as the affinity continues to increase, when the affinity degree increases to 0.9, at this moment, the opinion will form one opinion cluster in Figure 3C. Based on the aforementioned simulation results, we can see that affinity can improve the opinion to tend to an agreement, and the result is also consistent with the social influence theory. Meanwhile, the aforementioned results indicate that affinity among people has a positive effect on opinions. If the affinity among individuals increases, the opinion will be easier to reach an agreement.

4.3 Influence of threshold of affinity on opinion evolution

Different thresholds of affinity may have different influences on opinion evolution. To further explore the influence of the threshold of affinity on opinion evolution, we carried out a related simulation about the threshold of affinity. In the simulation, we set the affinity as 0.5, and the thresholds of affinity are 0.5, 0.8, and 0.9. Keeping other parameters unchanged, the simulation result is shown in Figure 4.

FIGURE 4

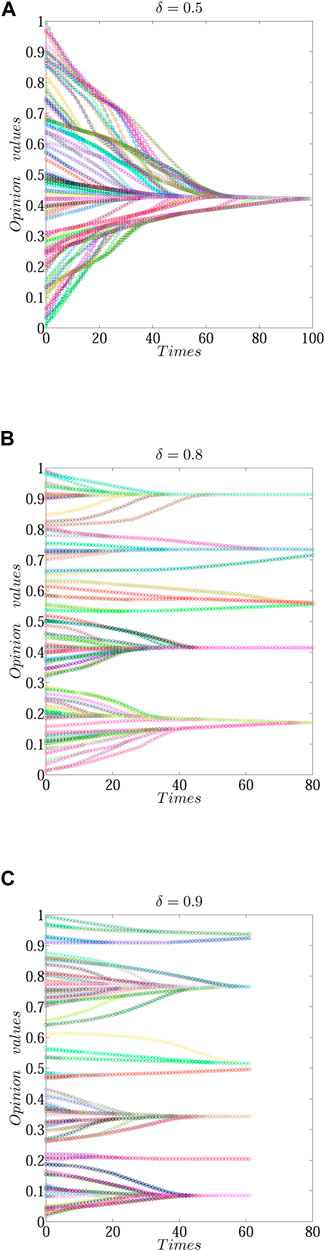
FIGURE 4. Opinion evolution result under different thresholds of affinity, (A)δ = 0.5, (B) δ = 0.8, and (C) δ = 0.9.

As shown in Figure 4, opinion evolution has different results when the threshold of affinity takes different values. In Figure 4A, when δ = 0.5, at this moment, the affinity is equal to the threshold of affinity, the opinion will be stable at 100, and the opinion will form one opinion cluster finally. As shown in Figure 4B, when the threshold increases, for instance, if δ = 0.8, we can find that the opinion will be stable at 80, and the opinion will form six opinion clusters, compared with Figure 4A. This result indicates that the larger difference between affinity and the threshold will prevent opinions from forming a consensus and lead to a split of opinion. In Figure 4C, when the δ = 0.9, at this moment, the difference between affinity and the threshold is increasing continuously, and the opinion will form more clusters. It indicates that if the difference between affinity and the threshold is larger, the opinion will be more dispersed.

4.4 Influence of social noise on opinion evolution

In the ASNHK model, social noise is an important factor that can affect opinion evolution. In terms of social noise, as an external factor, social noise can give individuals some pressure or influence and promote the evolution of individual opinion. To explore the influence mechanism of social noise, we set the affinity to 0.5, set the threshold to 0.8, and kept other parameters unchanged. Moreover, we set the interval of social noise distribution to ξ_i ∈ [ − 0.01, 0.01], ξ_i ∈ [ − 0.02, 0.02], and ξ_i ∈ [ − 0.03, 0.03] uniformly. The simulation result is shown in Figure 5.

FIGURE 5

FIGURE 5. Opinion evolution result under different social noises, (A) No noise, (B) ξ_i ∈[−0.01,0.01], (C) ξ_i ∈[−0.02,0.02], and (D) ξ_i ∈[−0.03,0.03].

As shown in Figure 5, we find that the opinion will form different evolution results when the social noise increases to different values. In Figure 5A, when there is no noise in opinion dynamics, the opinion will be stable at 95 steps and form five opinion clusters. Based on Figure 5A, when the interval of social noise distribution increases to [ − 0.01, 0.01], the simulation result is shown in Figure 5B. As shown in Figure 5B, the number of final opinion clusters is 4. This result indicates that social noise can urge the people to form more consensus opinions. Furthermore, in Figure 5C, when the interval of social noise distribution increases to [ − 0.02, 0.02], the number of the final opinion cluster is reduced from 4 to 3, and the opinion gets more close. As the social noise increases continuously, for example [ − 0.03, 0.03], the simulation result is shown in Figure 5D. From Figure 5D, we can find that the final opinion is disorderly, dispersed, and inconsistent. The possible explanation is that social noise has a critical influence. When social noise is greater than the critical value, an individual’s opinion will get dispersed. It also indicates that a phase transition exists under the influence of social influence. The aforementioned conclusions are also consistent with those of the research of Su et al.[43, 45].

4.5 Influence of personnel heterogeneity on opinion evolution

In the process of opinion evolution, because people have different characteristics, people react differently to opinions, that is to say, people’s character has certain heterogeneity [50]. According to the heterogeneity, people can be divided into three types roughly: closed, easygoing, and open. We set the opinion thresholds ɛ_i ∈ [0.01, 0.05], [0.2, 0.3], and [0.4, 0.5] separately. ɛ_i ∈ [0.01, 0.05] indicates that people are closed; ɛ_i ∈ [0.2, 0.3] indicates that people are easy-going; and ɛ_i ∈ [0.4, 0.5] indicates that people are open. To explore the influence of different heterogeneity in the opinion evolution and keep other parameters unchanged, we perform the related simulations on the personnel heterogeneity. In addition, to make the evolution of ideas clearer, we also use the histogram to display the result of opinion evolution. The specific result is shown in Figures 6, 7.

FIGURE 6

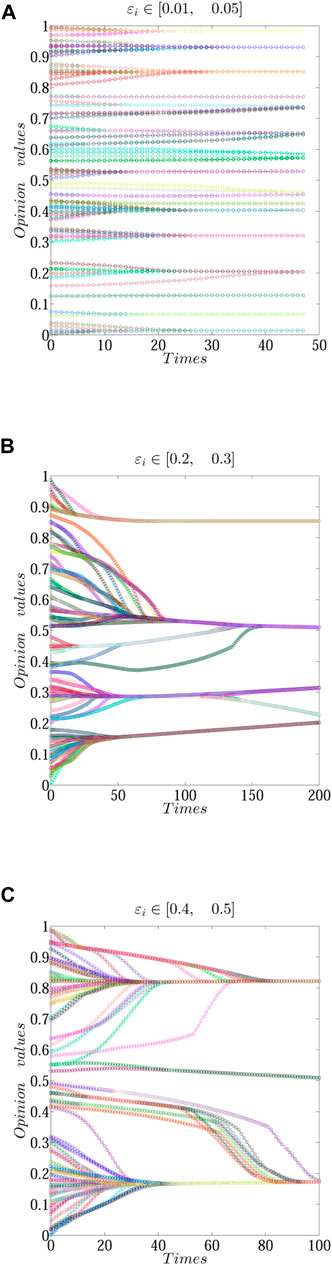
FIGURE 6. Opinion evolution result under different personnel heterogeneity, (A) ɛ_i ∈[0.01,0.05]; (B) ɛ_i ∈[0.2,0.3]; (C) ɛ_i ∈[0.4,0.5]; (A–C) are the results of the opinion evolution.

FIGURE 7

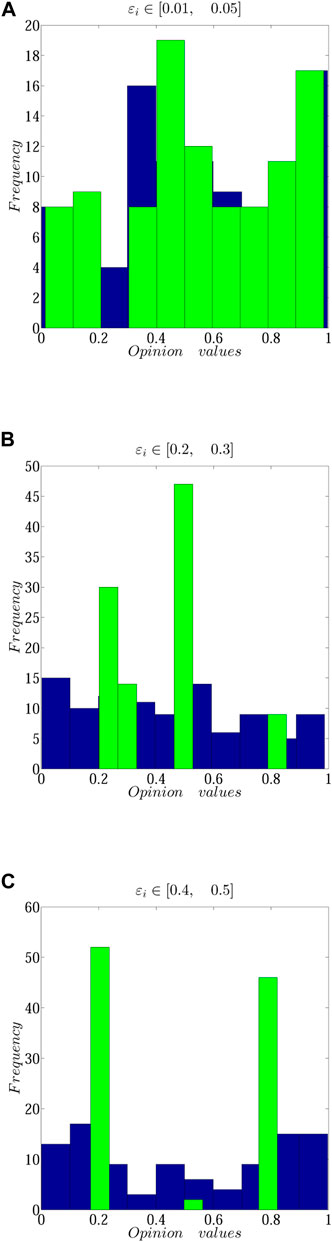
FIGURE 7. Opinion evolution result under different personnel heterogeneity, (A) ɛ_i ∈[0.01,0.05]; (B) ɛ_i ∈[0.2,0.3]; (C)ɛ_i ∈[0.4,0.5]; (A–C) are the histograms of the opinion evolution.

As shown in Figures 6, 7, we can find that different heterogeneity can cause different evolution results. In Figure 6A, when the opinion threshold ɛ_i ∈ [0.01, 0.05], it indicates that people are closed in the community. At this moment, the opinions will form nine clusters, and the convergence steps will stabilize at 49. We also find that the final opinion will distributed in [0, 1] almost uniformly in Figure 7A; From Figure 6B, when the opinion threshold increases continuously, for example, ɛ_i ∈ [0.2, 0.3]. This threshold indicates that people are easygoing in the community. The evolution result forms four opinion clusters, and convergence steps will stabilize at 200. The final opinions will be distributed around 0.5 in Figure 7B. In Figure 6C, when the opinion threshold ɛ_i ∈ [0.4, 0.5], it indicates that people are open in the community, the opinions will form three opinion clusters, and the steps will stabilize at 200. The final opinions are distributed around 0.2 and 0.8 in Figure 7C. At this moment, people’s opinions are easier to form an agreement.

5 Discussion

Opinion dynamics has been explored by most scholars in recent years [51–53]. However, few researchers explored the opinions of affinity and social noise systematically. As a kind of social influence, affinity and social noise affect an individual’s opinion and have an impact on others and the environment. Considering the aforementioned two factors, this study built an affinity and social noise Hegselmann–Krause model and explored the influence of affinity, the threshold of affinity, social noise, and personnel heterogeneity on opinion dynamics. The research result will extend the boundary of opinion dynamics and has certain practical significance. First, affinity has a positive effect on opinion dynamics. If the affinity among individuals increases, the opinion will quickly tend to be consistent. Compared with the HK model, the affinity can accelerate the integration and alignment of opinions. Thus, affinity is important to be considered in opinion evolution. Second, social noise has a critical influence on opinion dynamics. Within a certain range, when the social noise increases, the opinions will be convergent. Once the social noise exceeds the critical value, the opinions will be divergent [44], implying that social noise has an important influence on opinion dynamics, and it should be reasonably controlled and guided in public opinion management. Third, personnel heterogeneity has different effects on opinion evolution. When the opinion evolves, public opinion management should develop individualized strategies for guiding public opinion, as the heterogeneity of groups can affect the evolution of opinions.

6 Conclusion

Group opinion evolution is an interesting research topic. At present, scholars have carried out some research about it. However, few types of research focus on the influence of affinity and social noise comprehensively. Based on the Hegselmann–Krause model of opinion dynamics, this study constructs the ASNHK model by introducing affinity and social noise from the perspective of social influence. Then, it explores the influence of affinity degree, affinity threshold, social noise, and personnel heterogeneity on opinion evolution. The results show that first of all, affinity between people can improve the opinion to form a consensus positively, but the affinity threshold has a negative role on the contrary. When people’s affinity increases, it is easier for them to form an agreement on their opinions. Moreover, when the social noise increases, the opinions will form a consensus. When it increases to a certain value, the opinions will get decentralized. Furthermore, personnel heterogeneity has different effects on opinion evolution. Open-minded individuals are more likely to form a consistent opinion, while closed-minded personalities make it difficult to form a consensus. The research extends the opinion dynamics from social influence and will shed light on the interdisciplinary study of psychology, sociology, and opinion evolution dynamics.

This study explored opinion evolution based on the social influence theory. It introduced the affinity and social noise in the opinion dynamics model. In this research, the influence of affinity degree, affinity threshold, social noise, and personnel heterogeneity on opinion evolution is discussed. Although we obtained some valuable conclusions, there are still some limitations given as follows. First, in terms of research content, this study explored the influence of affinity, social noise, and personnel heterogeneity on opinion evolution. However, it does not consider the network structure of people. Different network structures of people may have a different social influence on opinion evolution. Thus, in the future, the network structures of people will be introduced to the model. Second, this study constructed a new model based on social influence theory and carried out some simulation analysis. However, no algebraic analysis was carried out. Future work will focus on the numerical analysis, and some convergence values will be calculated. Third, although some simulation analyses are mentioned in this article, the real data need to be considered in the opinion evolution. Future work will use real opinion data from some media to explore opinion evolution.

Overall, this research explored the model of opinion dynamics from social influence and provided some theoretical and practical insights for the following research. In theory, this study introduced the affinity and social noise in the Hegselmann–Krause model of opinion dynamics, provided a new perspective on the social influence theory, and enriched the application of this theory to opinion dynamics. In practice, this study explained the mechanism of influence of affinity in interpersonal relationships and social noise from the external environment. It provided some methods for managing public opinion; for example, improving interpersonal relationships and affinity between people can be conducive to a convergence of opinions. Moreover, reasonable control of external noise can facilitate a consistent opinion. In conclusion, this research can provide some new perspectives on the study of opinion dynamics and public opinion management.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding authors.

Author contributions

JL: conceptualization, methodology, software, writing—original draft, and investigation. JH: methodology, supervision, and validation. ZQ: methodology and Investigation. SH: supervision and validation.

Funding

This work was supported by the National Natural Science Foundation Project (grant no. 71871144) and the Science and Technology Development Program of the University of Shanghai for Science and Technology (grant no. 2020KJFZ046).

Conflict of interest

The authors declared that there was no competing financial interest, all authors made substantial contributions and agreed to the final manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Zhu J, Yao Y, Tang W, Zhang H. An agent-based model of opinion dynamics with attitude-hiding behaviors. Physica A: Stat Mech its Appl (2022) 603:127662. doi:10.1016/j.physa.2022.127662

CrossRef Full Text | Google Scholar

2. Shang L, Zhao M, Ai J, Su Z. Opinion evolution in the sznajd model on interdependent chains. Physica A: Stat Mech its Appl (2021) 565:125558. doi:10.1016/j.physa.2020.125558

CrossRef Full Text | Google Scholar

3. Hou J, Li W, Jiang M. Opinion dynamics in modified expressed and private model with bounded confidence. Physica A: Stat Mech its Appl (2021) 574:125968. doi:10.1016/j.physa.2021.125968

CrossRef Full Text | Google Scholar

4. Weimer CW, Miller J, Hill RR, Hodson DD. An opinion dynamics model of meta-contrast with continuous social influence forces. Physica A: Stat Mech its Appl (2022) 589:126617. doi:10.1016/j.physa.2021.126617

CrossRef Full Text | Google Scholar

5. Botte N, Ryckebusch J, Rocha LE. Clustering and stubbornness regulate the formation of echo chambers in personalised opinion dynamics. Physica A: Stat Mech its Appl (2022) 599:127423. doi:10.1016/j.physa.2022.127423

CrossRef Full Text | Google Scholar

6. Hegselmann R, Krause U. Opinion dynamics and bounded confidence models, analysis and simulation. J Artif Societies Soc Simulation (2002) 5:1–2.

Google Scholar

7. Su W, Gu Y, Wang S, Yu Y. Partial convergence of heterogeneous Hegselmann-Krause opinion dynamics. Sci China Technol Sci (2017) 60:1433–8. doi:10.1007/s11431-016-0615-x

CrossRef Full Text | Google Scholar

8. Zhao Y, Zhang L, Tang M, Kou G. Bounded confidence opinion dynamics with opinion leaders and environmental noises. Comput Operations Res (2016) 74:205–13. doi:10.1016/j.cor.2015.07.022

CrossRef Full Text | Google Scholar

9. Jiang L, Liu J, Zhou D, Zhou Q, Yang X, Yu G. Predicting the evolution of hot topics: A solution based on the online opinion dynamics model in social network. IEEE Trans Syst Man Cybern Syst (2018) 50:3828–40. doi:10.1109/TSMC.2018.2876235

CrossRef Full Text | Google Scholar

10. Deffuant G, Neau D, Amblard F, Weisbuch G. Mixing beliefs among interacting agents. Adv Complex Syst (2000) 03:87–98. doi:10.1142/S0219525900000078

CrossRef Full Text | Google Scholar

11. Zhang J, Hong Y. Opinion evolution analysis for short-range and long-range Deffuant–Weisbuch models. Physica A: Stat Mech its Appl (2013) 392:5289–97. doi:10.1016/j.physa.2013.07.014

CrossRef Full Text | Google Scholar

12. Chen G, Su W, Mei W, Bullo F. Convergence properties of the heterogeneous Deffuant–Weisbuch model. Automatica (2020) 114:108825. doi:10.1016/j.automatica.2020.108825

CrossRef Full Text | Google Scholar

13. Luo Y, Li K, Sun C, Cheng C. Adapted deffuant–weisbuch model with implicit and explicit opinions. Physica A: Stat Mech its Appl (2022) 596:127095. doi:10.1016/j.physa.2022.127095

CrossRef Full Text | Google Scholar

14. Schawe H, Laura H. Higher order interactions destroy phase transitions in deffuant opinion dynamics model. Commun Phys (2022) 5:32–9. doi:10.1038/s42005-022-00807-4–

CrossRef Full Text | Google Scholar

15. Sznajdweron K, Sznajd J. Opinion evolution in closed community. Int J Mod Phys C (2000) 11:1157–65. doi:10.1142/S0129183100000936

CrossRef Full Text | Google Scholar

16. Araujo MS, Vannucchi FS, Timpanaro AM, Prado CPC. Mean-field approximation for the Sznajd model in complex networks. Phys Rev E (2015) 91:022813. doi:10.1103/PhysRevE.91.022813

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Karan FSN, Srinivasan AR, Chakraborty S. Modeling and numerical simulations of the influenced Sznajd model. Phys Rev E (2017) 96:022310. doi:10.1103/PhysRevE.96.022310

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Calvelli M, Crokidakis N, Penna TJ. Phase transitions and universality in the sznajd model with anticonformity. Physica A: Stat Mech its Appl (2019) 513:518–23. doi:10.1016/j.physa.2018.09.023

CrossRef Full Text | Google Scholar

19. Hsu J, Huang D. Mean-field theory of modified voter model for opinions. Physica A: Stat Mech its Appl (2014) 416:371–7. doi:10.1016/j.physa.2014.09.009

CrossRef Full Text | Google Scholar

20. Tang S, Yan S, Pei S, Zheng Z. Evolutionary dynamics of the weighted voter model with opinion strength on complex networks. J Korean Phys Soc (2015) 66:1783–8. doi:10.3938/jkps.66.1783

CrossRef Full Text | Google Scholar

21. Klamser PP, Wiedermann M, Donges JF, Donner RV. Zealotry effects on opinion dynamics in the adaptive voter model. Phys Rev E (2017) 96:052315. doi:10.1103/PhysRevE.96.052315

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Pasi G, Yager RR. Modeling the concept of majority opinion in group decision making. Inf Sci (2006) 176:390–414. doi:10.1016/j.ins.2005.07.006

CrossRef Full Text | Google Scholar

23. Vilela ALM, Stanley HE. Effect of strong opinions on the dynamics of the majority-vote model. Sci Rep (2018) 8:8709. doi:10.1038/s41598-018-26919-y

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Javarone MA. Social influences in opinion dynamics: The role of conformity. Physica A: Stat Mech its Appl (2014) 414:19–30. doi:10.1016/j.physa.2014.07.018

CrossRef Full Text | Google Scholar

25. Nowak A, Szamrej J, Latané B. From private attitude to public opinion: A dynamic theory of social impact. Psychol Rev (1990) 97:362–76. doi:10.1037/0033-295x.97.3.362

CrossRef Full Text | Google Scholar

26. Dou R, Zhang Y, Nan G. Iterative product design through group opinion evolution. Int J Prod Res (2017) 55:3886–905. doi:10.1080/00207543.2017.1316020

CrossRef Full Text | Google Scholar

27. Zhu M, Xie G. Leader’s opinion priority bounded confidence model for network opinion evolution. In: AIP Conference Proceedings (2017). p. 020060. 1864. doi:10.1063/1.4992877

CrossRef Full Text | Google Scholar

28. Glass CA, Glass DH. Opinion dynamics of social learning with a conflicting source. Physica A: Stat Mech its Appl (2021) 563:125480. doi:10.1016/j.physa.2020.125480

CrossRef Full Text | Google Scholar

29. Bernardo C, Altafini C, Vasca F. Finite-time convergence of opinion dynamics in homogeneous asymmetric bounded confidence models. Eur J Control (2022) 100674. doi:10.1016/j.ejcon.2022.100674

CrossRef Full Text | Google Scholar

30. Lanchier N, Li H-L. Consensus in the hegselmann–krause model. J Stat Phys (2022) 187:20–13. doi:10.1007/s10955-022-02920-8

CrossRef Full Text | Google Scholar

31. Dong Y, Zhan M, Kou G, Ding Z, Liang H. A survey on the fusion process in opinion dynamics. Inf Fusion (2018) 43:57–65. doi:10.1016/j.inffus.2017.11.009

CrossRef Full Text | Google Scholar

32. Li C-Y. Persuasive messages on information system acceptance: A theoretical extension of elaboration likelihood model and social influence theory. Comput Hum Behav (2013) 29:264–75. doi:10.1016/j.chb.2012.09.003

CrossRef Full Text | Google Scholar

33. Kaur R, Kumar R, Bhondekar AP, Kapur P. Human opinion dynamics: An inspiration to solve complex optimization problems. Sci Rep (2013) 3:3008–7. doi:10.1038/srep03008

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Diao S-M, Liu Y, Zeng Q-A, Luo G-X, Xiong F. A novel opinion dynamics model based on expanded observation ranges and individuals’ social influences in social networks. Physica A: Stat Mech its Appl (2014) 415:220–8. doi:10.1016/j.physa.2014.07.072

CrossRef Full Text | Google Scholar

35. Lu X, Mo H, Deng Y. An evidential opinion dynamics model based on heterogeneous social influential power. Chaos, Solitons & Fractals (2015) 73:98–107. doi:10.1016/j.chaos.2015.01.007

CrossRef Full Text | Google Scholar

36. Glass CA, Glass DH. Social influence of competing groups and leaders in opinion dynamics. Comput Econ (2021) 58:799–823. doi:10.1007/s10614-020-10049-7

CrossRef Full Text | Google Scholar

37. Franco B, Carletti T, Duccio F, Alessio G, Andrea G. Dynamical affinity in opinion dynamics modeling. Phys Rev E (2007) 76:066105. doi:10.1103/PhysRevE.76.066105

CrossRef Full Text | Google Scholar

38. Blattner M, Zhang Y, Maslov S. Exploring an opinion network for taste prediction: An empirical study. Physica A: Stat Mech its Appl (2007) 373:753–8. doi:10.1016/j.physa.2006.04.121

CrossRef Full Text | Google Scholar

39. Carletti T, Fanelli D, Guarino A, Bagnoli F, Guazzini A. Birth and death in a continuous opinion dynamics model. Eur Phys J B (2008) 64:285–92. doi:10.1140/epjb/e2008-00297-3

CrossRef Full Text | Google Scholar

40. Ishii A, Okano N, Nishikawa M. Social simulation of intergroup conflicts using a new model of opinion dynamics. Front Phys (2021) 9:640925. doi:10.3389/fphy.2021.640925

CrossRef Full Text | Google Scholar

41. Abrica-Jacinto NL, Kurmyshev E, Juárez HA. Effects of the interaction between ideological affinity and psychological reaction of agents on the opinion dynamics in a relative agreement model. J Artif Soc Soc Simul (2017) 20:1–12. doi:10.18564/jasss.3377

CrossRef Full Text | Google Scholar

42. Pineda M, Toral R, Hernández-García E. The noisy hegselmann-krause model for opinion dynamics. Eur Phys J B (2013) 86:490–10. doi:10.1140/epjb/e2013-40777-7

CrossRef Full Text | Google Scholar

43. Su W, Chen G, Hong Y. Noise leads to quasi-consensus of Hegselmann–Krause opinion dynamics. Automatica (2017) 85:448–54. doi:10.1016/j.automatica.2017.08.008

CrossRef Full Text | Google Scholar

44. Wang C, Li Q, Weinan E, Chazelle B. Noisy hegselmann-krause systems: Phase transition and the 2R-conjecture. J Stat Phys (2016) 166:1209–25. doi:10.1007/s10955-017-1718-x

CrossRef Full Text | Google Scholar

45. Su W, Guo J, Chen X, Chen G, Li J. Robust fragmentation modeling of Hegselmann–Krause-type dynamics. J Franklin Inst (2019) 356:9867–80. doi:10.1016/j.jfranklin.2019.09.012

CrossRef Full Text | Google Scholar

46. Mansouri A, Taghiyareh F. Phase transition in the social impact model of opinion formation in log-normal networks. J Inf Syst Telecommunication (2021) 1:1–14. doi:10.52547/jist.9.33.1

CrossRef Full Text | Google Scholar

47. Vaidya T, Chotibut T, Piliouras G. Broken detailed balance and non-equilibrium dynamics in noisy social learning models. Physica A: Stat Mech its Appl (2021) 570:125818. doi:10.1016/j.physa.2021.125818

CrossRef Full Text | Google Scholar

48. Liu Y, Mo L. Noise-induced truth seeking of heterogeneous Hegselmann-Krause opinion dynamics. Adv Math Phys (2018) 2018:1–6. doi:10.1155/2018/8702152

CrossRef Full Text | Google Scholar

49. Su W, Wang X, Chen G, Yu Y, Hadzibeganovic T. Noise-based synchronization of bounded confidence opinion dynamics in heterogeneous time-varying communication networks. Inf Sci (2020) 528:219–30. doi:10.1016/j.ins.2020.04.018

CrossRef Full Text | Google Scholar

50. Su J, Liu B, Li Q, Ma H. Trust, evolution, and consensus of opinions in a social group. Acta Phys Sin (2014) 63:050501. doi:10.7498/aps.63.050501

CrossRef Full Text | Google Scholar

51. Liang H, Li C, Dong Y, Jiang Y. The fusion process of interval opinions based on the dynamic bounded confidence. Inf Fusion (2016) 29:112–9. doi:10.1016/j.inffus.2015.08.010

CrossRef Full Text | Google Scholar

52. Dong Y, Chen X, Liang H, Li C. Dynamics of linguistic opinion formation in bounded confidence model. Inf Fusion (2016) 32:52–61. doi:10.1016/j.inffus.2016.03.001

CrossRef Full Text | Google Scholar

53. Li K, Liang H, Kou G, Dong Y. Opinion dynamics model based on the cognitive dissonance: An agent-based simulation. Inf Fusion (2020) 56:1–14. doi:10.1016/j.inffus.2019.09.006

CrossRef Full Text | Google Scholar