Design of quasi-phase-matching nonlinear crystals based on quantum computing

Quasi-phase-matching (QPM) makes it possible to design domain engineered nonlinear crystals for highly efficient and multitasking nonlinear frequency conversion. However, finding the optimal crystal domain arrangement in a meaningful time is very challenging sometimes impossible by classical computing. In this paper, we proposed a quantum annealing computing method and used D-Wave superconducting quantum computer to design aperiodically poled lithium niobate (APPLN) for coupled third harmonic generation (CTHG). We converted the optical transformation efficiency function to an Ising model which can be solved by D-Wave quantum computer. The crystal design results were simulated by using nonlinear envelope equation (NEE), which showed very similar conversion efficiencies to the crystals designed by using simulated annealing (SA) method, demonstrating that quantum annealing computing is a powerful method for QPM crystal design.

Introduction

The wavelength generated from a laser depends on the energy level structure of the activated ions and is often limited in a small tuning range. A well-known Ti:sapphire laser has a tuning range of 650–1100 nm, but this is almost the widest span we can obtained in near infrared [1]. However, research in fields such as spectroscopy often requires wavelengths from the deep ultraviolet to the mid-infrared from a laser system as simple and efficient as possible. For example, currently there is no mature technology to obtain ultrashort 234 nm optical pulses directly from a laser for Al⁺ cooling in an optical clock [2]. Therefore, nonlinear frequency conversion is an important technique to obtain lights at various wavelengths flexibly.

Quasi-phase matching is a very popular second-order nonlinear frequency transformation technology. It avoids critical phase matching in a nonlinear crystal with a specific orientation and a specific polarization state. By artificially modulating the direction of each optical superlattice in a QPM crystal periodically or quasi-periodically, the nonlinear interaction can satisfy the phase matching condition where the crystal has the highest coefficient [3]. Periodically polarized nonlinear crystals, such as periodically polarized lithium niobate (PPLN), and periodically polarized potassium titanyl phosphate (PPKTP), are commonly used in quasi-phase matching second-order harmonic generation (SHG), sum-frequency generation (SFG), differential-frequency generation (DFG), and so on. However, a periodically polarized crystal normally only satisfies a specific frequency conversion with single process and narrow bandwidth. For nonlinear conversion of femtosecond laser pulse, especially when multiple nonlinear processes are expected in a single system, a more sophisticated design of QPM crystal should be employed.

In order to achieve CTHG from a single gain medium, Gu et al. demonstrated APPLN as a frequency conversion crystal, and used SA algorithm to realize the design of the APPLN [4]. The idea of this method is to set a small calculation step (a domain) in which the optical property is unified, select an appropriate objective function, and search the optimal domain orientations by using the SA algorithm. Since each crystal domain can take positive or negative polarization direction, the calculation may result in a crystal with different numbers of positively orientated domains adjacent and different numbers of negatively orientated domains adjacent, formed an APPLN with different lengths of positive and negative superlattices. For an APPLN with N domains, there are 2^N types of crystal domain arrangements, so increasing the number of calculation domains to obtain finer optical superlattice design and higher conversion efficiency is generally not practical by using SA algorithm.

Some other algorithms were also presented for APPLN design, including genetic algorithm [5], Lagrange multiplier method [6] and so on. These algorithms do not essentially solve the complexity problem, and can only obtain an approximate optimization result. Searching for optimal crystal domain orientations is essentially a combinatorial optimization problem. To solve this problem, it is necessary to improve the computing hardware essentially. Quantum computers are designed to solve such complex combinatorial optimization problems. Recent studies have shown that a large number of combinatorial optimization problems in the fields of medicine design [7], very-large-scale integrated circuit design [8], traffic planning [9], financial investment [10] can be solved using quantum computers. We are trying to adopt these methods to APPLN superlattice design, and to solve such combinatorial optimization problems in polynomial time.

In this paper, we demonstrated an APPLN design for CTHG by using the D-Wave superconducting quantum computer, which can only solve the minimum of the real number Ising model. We first convert the CTHG efficiency function into a complex Ising model, and then use the rotation-projection method to convert it into a series of real Ising models for D-Wave. The results show that with superconducting quantum computers, we can find fairly good solutions in a relatively short time. The method provides new ideas for the design of APPLN by using quantum computing.

Theoretical analysis

The quasi-phase matching technique compensates the phase mismatch in a nonlinear process by changing the sign of the nonlinear coefficient of the crystal within a coherent length, thereby realizing an effective and efficient nonlinear frequency transformation. As shown in Figure 1, the APPLN crystal is divided into numbers of domains of the same size, and each domain can have two polarization directions, either “up” or “down”.

FIGURE 1

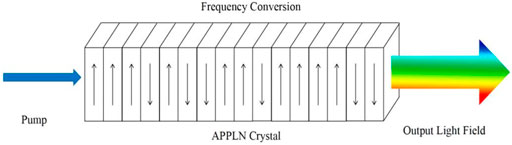
FIGURE 1. Schematic diagram of the structure of an APPLN. Lithium niobate crystals are divided into multiples of the same size of domains. The polarization direction of each crystal domain can be either “up” or “down”.

The CTHG process includes two nonlinear processes as SHG and SFG at the same time, its optical conversion efficiency is [4].

${\eta }_{THG}\equiv \frac{I_{3\omega }}{I_{\omega }}=\frac{144{\pi }^4{\left|d_{33}\right|}^4{I}_{\omega }^2{L}^4}{c^2{\epsilon }_0^2{\lambda }^4{n}_{\omega }^3{n}_{2\omega }^2{n}_{3\omega }}{\left(d_{eff}\right)}^2(1)$

where d₃₃ is nonlinear coefficient of the lithium niobate crystal in 33 direction, c is the speed of light in vacuum, I_ω is pump light intensity, I_3ω is light intensity of the third harmonic, L is the crystal length, and λ is pump wavelength, n_1ω, n_2ω, and n_3ω are refractive indices of the fundamental, second-harmonic and third-harmonic respectively, d_eff is effective nonlinear coefficient, which is defined as [4]:

$d_{eff}=\left|\frac{2}{L^2}{\int }_0^{L}dz{e}^{i\Delta k_{2}z}d\left(z\right)\times {\int }_0^{z}dx{e}^{i\Delta k_{1}x}d\left(x\right)\right|,(2)$

where i is the imaginary unit, Δk₁ and Δk₂ are phase mismatches of the SHG and SFG, respectively, $d\left(z\right)\in \left\{+1,-1\right\}$ is the reversal direction of the crystal domain at z position, where +1 represents “up” and -1 represents “down”. For a given pump wavelength and target signal wavelength, Δk₁ and Δk₂ can be calculated from the Sellmeier equation [11]. Eqs 1, 2 show that, to maximize η_THG, the task is to find an optimal set of domain arrangements d(z) such that the effective nonlinear coefficient d_eff is maximized.

Existing algorithms may fall into a local optimal solution, which cannot guarantee an optimal or near-optimal crystal design. Searching for optimal crystal domains is a combinatorial optimization problem. When N is large, to solve this problem is highly dependent on computing hardware. But quantum computers are designed to solve such complex combinatorial optimization problems. They are suitable for searching the maximum value of d_eff and its corresponding optimal crystal domain arrangement.

There are two main kinds of quantum computing: One is a general-purpose quantum computer, which requires the preparation of a large number of entangled quantum pairs for a long time; The other is to use the quantum annealing principle to solve Ising model. The low-temperature superconducting quantum Ising machine has mature technology and has been commercialized. In 2011, D-Wave company announced the world’s first commercial quantum computer. But it can only solve the minima of the Ising model, or equivalently, quadratic unconstrained binary optimization (QUBO) model. In other words, a quantum Ising machine can only solve for the minimum of a function of the form $H=-{\displaystyle \sum }_{i,j}{J}_{ij}{\sigma }_i{\sigma }_j-{\displaystyle \sum }_i{h}_i{\sigma }_i$, where ${\sigma }_i,{\sigma }_j\in \left\{+1,-1\right\}$, and the value and quantity of the coupling coefficient $J_{ij}$ and h_i can be set optionally.

To use D-Wave computer, we need to convert the effective nonlinear coefficient expressions into the Ising model. Each crystal domain has two polarization direction options in the Ising model: |↑⟩and |↓⟩. Assuming that the crystal of length L is divided into N equal segments, and the width of each domain is Δx, i.e. L = NΔx, then the effective nonlinear coefficient can be written as

$\begin{array}{l}{d}_{eff}^{THG}\propto \left|{\int }_0^{L}dz{e}^{i\Delta k_{2}z}d\left(z\right)\times {\int }_0^{z}dx{e}^{i\Delta k_{1}x}d\left(x\right)\right|\\ \approx \left|{\displaystyle \sum }_{m=1}^N{\int }_{\left(m-1\right)\Delta x}^{m\Delta x}dz{e}^{i\Delta k_{2}z}d\left(z\right)\times {\displaystyle \sum }_{n=1}^{m-1}{\int }_{\left(n-1\right)\Delta x}^{n\Delta x}dx{e}^{i\Delta k_{1}x}d\left(x\right)\right|\\ =\left|{\displaystyle \sum }_{m=1}^N\frac{1}{i\Delta k_2}\left[e^{i\Delta k_{2}m\Delta x}-e^{i\Delta k_2\left(m-1\right)\Delta x}\right]d\left(m\right)\times {\displaystyle \sum }_{n=1}^{m-1}\frac{1}{i\Delta k_1}\left[e^{i\Delta k_{1}n\Delta x}-e^{i\Delta k_1\left(n-1\right)\Delta x}\right]d\left(n\right)\right|\\ \propto \left|{\displaystyle \sum }_{m=1}^N\left[e^{i\Delta k_{2}m\Delta x}-e^{i\Delta k_2\left(m-1\right)\Delta x}\right]d\left(m\right)\times {\displaystyle \sum }_{n=1}^{m-1}\left[e^{i\Delta k_{1}n\Delta x}-e^{i\Delta k_1\left(n-1\right)\Delta x}\right]d\left(n\right)\right|\\ =\left|{\displaystyle \sum }_{m=1}^N{\displaystyle \sum }_{n=1}^{m-1}{J}_0\left(m,n\right)d\left(m\right)d\left(n\right)\right|\end{array},(3)$

where $J_0\left(m,n\right)$ is the coupling coefficient and written as:

$J_0\left(m,n\right)=\left(e^{i\Delta k_{2}m\Delta x}-e^{i\Delta k_2\left(m-1\right)\Delta x}\right)\cdot \left(e^{i\Delta k_{1}n\Delta x}-e^{i\Delta k_1\left(n-1\right)\Delta x}\right).(4)$

So the effective nonlinear coefficients is converted into an Ising model and a complex objective function is obtained:

$f\left(d_1,d_2,...,d_N\right)\equiv {\displaystyle \sum }_{m=1}^N{\displaystyle \sum }_{n=1}^{m-1}{J}_0\left(m,n\right)d_m{d}_n.(5)$

Now the problem becomes to find the maximum modulus of the complex objective function f (d₁,d₂,...d_N). But the D-Wave quantum computer can only solve the Ising model where the coupling coefficient J₀ is real. The real part of Eq. 5 is:

$\mathrm{R}\mathrm{e}\left[f\left(d_1,d_2,...,d_N\right)\right]={\displaystyle \sum }_{m=1}^N{\displaystyle \sum }_{n=1}^{m-1}\mathrm{R}\mathrm{e}\left[J_0\left(m,n\right)\right]d_m{d}_n.(6)$

The maximum of the f (d₁,d₂,...d_N) could not be replaced by that of Re [f (d₁,d₂,...d_N)] since there may be |f₁|>|f₂| but |Re [f₁]|<|Re [f₂]|. In order to solve this problem, we use rotation-projection method which projects the original objective function to r directed lines in 2π space, instead of only to real axis as usual (Figure 2 shows the case of r = 12). Projecting the objective function f onto the line Arg z = θ_j, where ${\theta }_j=\frac{2\pi }{r}\cdot j$, j = 0,1,2,..., (r-1), is equivalent to rotating f around the origin by -θ_j and then project onto the real axis, i.e. $f_j=\mathrm{R}\mathrm{e}\left(f\cdot e^{-i{\theta }_j}\right)$. Therefore, the projection of the function f on the line Arg z = θ_j is

$f_j\left(d_1,d_2,...,d_n\right)=\mathrm{R}\mathrm{e}\left[e^{-i{\theta }_j}{\displaystyle \sum }_{m=1}^N{\displaystyle \sum }_{n=1}^{m-1}{J}_0\left(m,n\right)d_m{d}_n\right]={\displaystyle \sum }_{m=1}^N{\displaystyle \sum }_{n=1}^{m-1}\mathrm{R}\mathrm{e}[e^{-i{\theta }_j}{J}_0\left(m,n\right)]d_m{d}_n(7)$

FIGURE 2

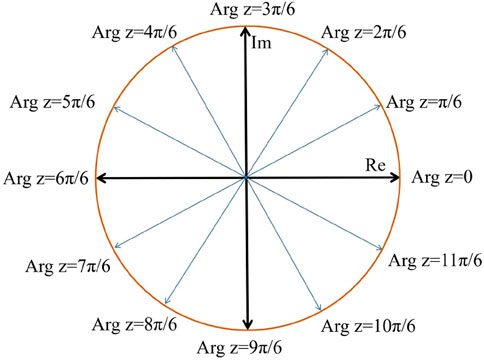
FIGURE 2. When the number of rotations r = 12, the rotation-projection method projects the objective function f to 12 directed lines in the complex plane. 12 Ising models f_j are generated, and the optimal crystal domains of each f_j are obtained respectively. Among these 12 crystal domain designs, the one that have the highest modulus of f is approximately the globally optimal design.

It should be noted that Arg z = θ_j and Arg z = θ_j+π represent two different directed lines. Because the projection of the function f on the line Arg z = θ_j is $\mathrm{R}\mathrm{e}\left(f\cdot e^{-i\theta }\right)$, the projection on the line Arg z = θ_j+π is $\mathrm{R}\mathrm{e}\left(f\cdot e^{-i\left({\theta }_j+\pi \right)}\right)=\mathrm{R}\mathrm{e}\left(f\cdot e^{-i{\theta }_j}\cdot e^{-i\pi }\right)=\mathrm{R}\mathrm{e}\left[\left(-f\right)\cdot e^{-i{\theta }_j}\right]$. Since $f\ne -f$, the Ising models obtained by projecting the objective function on the two directed lines Arg z = θ_j and Arg z = -θ_j are not equivalent.

Using the D-Wave quantum computer, we can obtain r groups of crystal domain arrangement {d}₀, {d}₁, ...{d}_r-1, corresponding to the maximum modulus of the functions f₀, f₁, ...f_r-1 on each line, respectively. The maximum value of f_j (j = 0∼r-1) is approximately equal to the global maximum of the objective function, ${\left|f\right|}_{\max }=\underset{\left\{d_n\right\}}{\max }\left|f\right|\approx \max \left\{\left|f\left(\{d{\}}_0\right)\right|,\left|f\left(\{d{\}}_1\right)\right|,\cdot \cdot \cdot ,\left|f\left(\{d{\}}_{r-1}\right)\right|\right\}$. It can be proved that the relative error between the maximum value obtained by the rotation-projection method and the true maximum value is $\delta d\le 1-\cos \frac{\pi }{r}\sim \frac{c}{r^2}$, where $c={\pi }^2/2\approx 4.93$. For example, if the rotation number r = 12, δd ≤ 3.4%. When r increases, δd tends to 0, but the computation time increases also. One must balance the accuracy and computing time when choosing proper number of r.

After converting the objective function into the Ising model, we can apply D-Wave’s quantum cloud computing platform Leap to solve the maximum value of the Ising model. In 2018, D-Wave System launched the quantum cloud computing platform Leap, which makes quantum computers more convenient for users around the world. First, the program is written in Python language on the terminal, and the code is sent to the quantum computer of D-Wave through the cloud for execution. After solving, the quantum computer returns results to the user through the control terminal. Users only need to upload the coupling coefficient J (m,n) of the Ising model to the quantum cloud server, and specify the type and parameters of the solver to solve it with a quantum computer.

D-Wave provides three kinds of solvers [12]: Classical Solver, Quantum Solver, and Hybrid Solver. Generally, the Classical Solver uses classical computer to solve, which is relatively slow when the number of variables of problem increase. The Quantum Solver uses the quantum processing unit (QPU), which is suitable for Ising model, but can only solve problems with a small number of variables as limited by the number of qubits currently. The Hybrid Solver takes advantages of combining a classical computer and a quantum processor collaboratively. In this article, we used the Hybrid Solver to search the maximum value of the object function f. The pseudocode of the algorithm can be found in the Supplementary material.

Simulation

We chose CTHG of 1404 nm light to 468 nm as an example to verify the proposed APPLN design method. This CTHG process was proposed to be a part of a scheme of 234 nm deep UV generation (Figure 3) for Al⁺ cooling [2].

FIGURE 3

FIGURE 3. Schematic diagram of the generation of deep UV light at 234 nm using a 1,040 nm fs fiber laser.

For the 1404 nm pumped CTHG, we used a 0.66 mm long crystal, and chose domain lengths of Δx as 1 μm and 0.5μm, corresponding to 660 (N = 660) and 1,320 (N = 1,320) crystal domains respectively. 0.66 mm is a fairly reasonable length of lithium niobate for CTHG when the pulse duration is about 200 fs The shorter the crystal domain (calculation step) is, the more accurate the design of the crystal will be. But that will cause dramatic increase in the demand for computing resource.

The first-process was a SHG process of 1404–702 nm, and the second was a SFG process of 1404 and 702 nm to obtain 468 nm. According to the Sellmeier equation [11] of lithium niobate crystal, the refractive indices of the interaction wavelengths are n₁₄₀₄ = 2.1350, n₇₀₂ = 2.1808, n₄₆₈ = 2.2574. Therefore the phase mismatch of the first process is $\Delta k_1=\frac{2\pi n_{702}}{{\lambda }_{702}}-2\cdot \frac{2\pi n_{1404}}{{\lambda }_{1404}}=4.0995\times {10}^5{m}^{-1}$ and the phase mismatch of the second process is $\Delta k_2=\frac{2\pi n_{468}}{{\lambda }_{468}}-\frac{2\pi n_{1404}}{{\lambda }_{1404}}-\frac{2\pi n_{702}}{{\lambda }_{702}}=1.2331\times {10}^6{m}^{-1}$. We adopted r = 12 for rotation-projection method, which makes the rotation angle $\theta =\frac{2\pi }{r}=\frac{\pi }{6}$.

By submitting the Python code to the D-Wave quantum computing cloud to start quantum computing, when Δx = 1 μm, we obtained the results in 366 s, in which the time for 12 quantum annealing calculations was 1.9 s, and the rest of the time was classical computing. The classical processing mainly included converting the Ising model to a form that can be solved by the quantum computer, configuring parameters. Figure 4A1 shows the objective function values obtained by 12 quantum annealing and post-processing optimizations. The maximum modulus of f_j (j = 0∼r-1) at different directions were various in a small range. The maximum was 26,041 at the rotation angle of π/3, and the corresponding crystal domain distribution is shown in Figure 4B1. The x-axis from left to right is the direction of light travel, and the red and blue means the “up” and “down” domain polarization, respectively. The y-axis is the length of the adjacent crystal domains with the same polarization. For example, the color of the first column is red and the number is 7, indicating that the polarization direction of the 1-seventh crystal domains of the APPLN crystal in the laser traveling direction was “up”, which formed the first optical superlattice of the APPLN crystal with length of 7 μm.

FIGURE 4

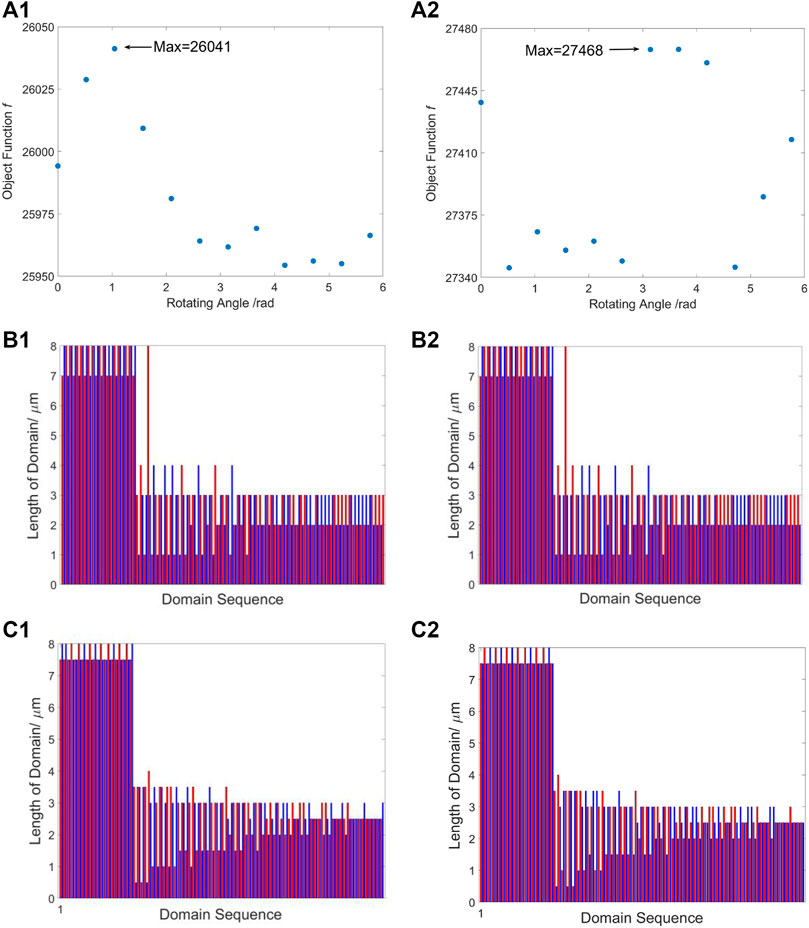
FIGURE 4. The results of the APPLN design. (A) The maximum modulus of the function f_i obtained at different rotation angles of θ by using the D-Wave quantum computer with Δx = 1 μm (A1) and 0.5 μm (A2) respectively. (B) The optimal domain distribution searched by using the D-wave (B1) and the classical computer (B2) when Δx = 1 μm. (C) The optimal domain distribution searched by using the D-wave (C1) and the classical computer (C2) when Δx = 0.5 μm.

When Δx = 0.5 μm, the solution time of D-Wave was 860s, in which the quantum annealing time was 2.2s. The optimized values of the objective function in 12 directions of the rotation-projection method was shown in Figure 4A2. The maximum was 27,468, obtained at $\theta =\frac{7\pi }{6}$. The corresponding crystal domains are shown in Figure 4C1.

In both cases of Figures 4B1, C1, the domain designing results were close to each other but with finer resolution of the length superlattice when Δx = 0.5 μm, which is obvious to our intuition. In the first part of the crystal, optical superlattices was about 7.5∼8 μm, which was approximately equal to the coherence length of SHG (7.664 μm), and the second part of the domain was about 2∼3 μm, which was approximately equal to the coherence length of SFG (2.548 μm). This indicates that in order to achieve the maximum THG efficiency, SHG should happen first. This auto-prioritization of coupled nonlinear processes demonstrates the power of the algorithms used for complex crystal design.

As a comparison, we searched for the optimal crystal domains using the traditional Simulated Annealing (SA) algorithm [4, 13] on a laptop computer. The initial temperature was T, the cooling coefficient of each time ΔT, and the minimum temperature T_min. In each loop, we randomly change a crystal domain. If the value of | f | corresponding to new crystal domain increases, then we accept the new domains; Otherwise accept the new domains with probability p = exp (-Δf/T), where Δf is the increasement of function | f |. If the temperature drops to $T^{\prime }=T\times ∆T$, then go to the next loop. The temperature decreases after each cycle and stops until the temperature falls below the minimum temperature T_min.

The initial temperature T was set as 1. In order to avoid falling into a local optimal solution, we used a lower minimum temperature T_min = 10⁻²⁰ and a slower cooling coefficient ΔT = 0.9995. The maximum number of loops was 100,000. The program was written in MATLAB language. The CPU of the computer is 2.7 GHz Intel(R) Core(TM) i7-7500U with maximum turbo frequency of 3.5GHz, and the memory is 8 GB. After 108s, the SA algorithm searched for an optimal crystal domain (Figure 4B2) for the case of Δx = 1 μm. The maximum value of the corresponding objective function f was 26,120. For Δx = 0.5μm, the solution time of SA was 187s, and the optimal crystal domains are shown in Figure 4C2 with objective function f as 27,456.

Comparing the optimal crystal domain obtained by quantum computing with SA, we find they are very similar, which proves the feasibility of using quantum computer to optimize the APPLN crystal design. For Δx = 1 μm, The maximum value of the objective function f obtained by the SA and quantum computing were 26,120 and 26,041 respectively; And for Δx = 0.5 μm, they were 27,456 and 27,468 respectively. Both values were not perfect solutions as SA gives only local maximum value, and quantum computing with r = 12 may cause a relative error within 3.4% as mentioned earlier. The two values we obtained have only 0.3% relative difference, and will lead to very similar conversion efficiencies as we will discuss in following text. As for solution time, the quantum computer used 366s (Δx = 1 μm) and 860s (Δx = 0.5 μm), in which the quantum annealing time was only 1.9s and 2.2s. The D-Wave quantum computer maps the Ising model to the Hamiltonian of the low-temperature superconducting circuit, realizes quantum annealing through the control of an external magnetic field, and finally stabilizes at the lowest energy state, obtaining the minimum value of the Ising model. This process is highly parallel.

We used nonlinear envelope equation (NEE) [14, 15] to simulate the optical conversion efficiency of the APPLN. The equation can be written as

$\frac{\partial A}{\partial z}+i\widehat{D}A=-i\frac{{\chi }^{\left(2\right)}{\omega }_0^2}{4{\beta }_0{c}^2}\left(1-\frac{i}{{\omega }_0}\frac{\partial }{\partial \tau }\right)\left[A^2{e}^{i{\omega }_0\tau -i\left({\beta }_0-{\beta }_1{\omega }_0\right)z}+2{\left|A\right|}^2{e}^{-i{\omega }_0\tau +i\left({\beta }_0-{\beta }_1{\omega }_0\right)z}\right],(8)$

where A is the light field envelop in time domain, z is the light propagation direction, $\widehat{D}={\displaystyle \sum }_{m=2}^{\infty }\frac{1}{m!}{\beta }_m{\left(-i\frac{\partial }{\partial t}\right)}^m$ and ${\beta }_m={\frac{{\partial }^{m}k}{\partial {\omega }^m}|}_{{\omega =\omega }_0}$ are the dispersion differential operator, $\tau =t-{\beta }_{1}z$ is group velocity delay, β₀ and β₁ are zero-order and first-order dispersion, and ω₀ is reference frequency. Through the step-Fourier method in the time domain, combined with the Runge-Kutta method, for a given pump light field and the arrangement of nonlinear crystal domains, we can simulate the distribution of the output field (including pump, signal, idler) through NEE simulation [14].

Assuming a Gaussian pump pulse with 1404 nm central wavelength, 200fs pulse duration and 4 × 10¹⁰ W/cm² peak intensity, the NEE simulation gave the output light field as shown in Figure 5 from the APPLN crystal designed by quantum annealing when Δx = 1 μm (see Figure 4B1). Simulation results of other crystal designs were very close so they were not plotted out. For Δx = 1μm, the conversion efficiency of the 468 nm light from 1404 nm pump was 28.37%. That was 28.38% by using the crystal in Figure 4B2 designed by SA algorithm. The two conversion efficiencies were almost the same.

FIGURE 5

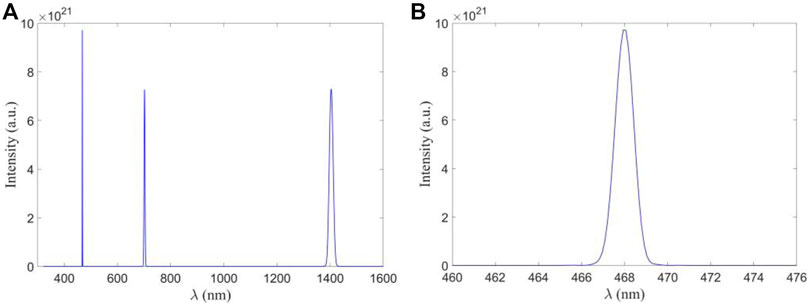
FIGURE 5. (A) Simulated output spectrum from the APPLN with crystal domains optimized by quantum computing as shown in Figure 4B1. (B) detailed output spectrum around 468 nm.

For the optimal domain of 0.5 μm (Figure 4C1), the THG efficiency calculated by the same method was 30.79%, which is higher than the case of Δx = 1 μm. This can be understood that with finer simulation steps, more flexible quasi-phase matching can be achieved, so higher THG efficiency can be expected. Detailed information can be seen in Table 1.

TABLE 1

TABLE 1. Calculation times and results for different domain lengths.

Conclusion

For an APPLN crystal design discussed in this paper, the number of crystal domains N corresponds to 2^N different possible arrangements of crystal domains, i.e. the size of the search space increases exponentially with the number N, leading to a exponential increase of the classical computation time. But a quantum computer breaks the limitation of the von Neumann system in terms of calculation principle, and calculates in a highly parallel manner, causing only linear increase of computation time. This is the essential feature that distinguishes quantum computers from classical computers.

Limited by the number of qubits available currently, we only adopted up to 1,320 crystal domains in our calculation. If there are more qubits available in the future, the crystal domain can be finer, say 0.1 μm, and one can naturally expect higher conversion efficiencies available based on fast parallel quantum computing.

Because of its high flexibility of designing and engineering, APPLN can also be used for white-light generation [16], simultaneous phase matching of multi-parameter processes [17], pulse compression [18], pulse shaping [19, 20] et al. Quantum computing is highly suitable to optimize the superlattice design for these purposes in a reasonably short time by converting these objective functions into Ising models.

In summary, this paper proposed a rotation-projection method to convert the effective nonlinear coefficients of the second-order nonlinear frequency transformation into the Ising model, and then demonstrated optimization of APPLN crystals for CTHG by using D-Wave superconducting quantum computer to solve the Ising model, which spent only 366s for Δx = 1μm and 860s for Δx = 0.5 μm respectively. The NEE simulation showed that the optical conversion efficiency were 28.37% (for Δx = 1 μm) and 30.79% (for Δx = 0.5 μm) respectively, indicating the validity of this quantum computation. In the future research, we will improve the models of APPLN design for situations where pulses have more complicated time-domain and frequency-domain details.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

ZZ and JS conceived the idea. ZZ and SY performed the quantum simulation and the data processing. DR supported the simulation. ZW supported the research group. ZZ and JS contributed to writing and editing the paper. All authors have approved the final version of the manuscript.

Funding

This work was supported by the Key Project of Basic Research and Applied Basic Research in Ordinary Universities of Guangdong Province, China (No. 2018KZDXM067), Department of Science and Technology of Guangdong Province, China (2020B1515120041), and research start-up funds of Dongguan University of Technology, China (No. KCYCXPT2017004).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2022.1038240/full#supplementary-material

References

1. Moulton PF. Spectroscopic and laser characteristics of Ti: Al₂O₃. J Opt Soc Am B (1986) 3(1):125–33. doi:10.1364/JOSAB.3.000125

CrossRef Full Text | Google Scholar

2. Wu H, Zhang Z, Chen S, Sun K, Sun J, Reid DT, et al. Development of a deep-ultraviolet pulse laser source operating at 234 nm for direct cooling of Al⁺ ion clocks. Opt Express (2021) 29(8):11468–78. doi:10.1364/OE.421684

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Boyd RW. Nonlinear optics. 3rd ed. Singapore: Elsevier (Singapore) Pte Ltd (2010). p. 84–8.

Google Scholar

4. Gu BY, Zhang Y, Dong BZ. Investigations of harmonic generations in aperiodic optical superlattices. J Appl Phys (2000) 87(11):7629–37. doi:10.1063/1.373433

CrossRef Full Text | Google Scholar

5. Lai JY, Liu YJ, Wu HY, Chen YH, Yang SD. Engineered multiwavelength conversion using nonperiodic optical superlattice optimized by genetic algorithm. Opt Express (2010) 18(5):5328–37. doi:10.1364/OE.18.005328

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Sapaev UK, Assanto G. Engineered quasi-phase matching for multiple parametric generation. Opt Express (2009) 17(5):3765–70. doi:10.1364/OE.17.003765

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Sakaguchi H, Ogata K, Isomura T, Utsunomiya S, Yamamoto Y, Aihara K. Boltzmann sampling by degenerate optical parametric oscillator network for structure-based virtual screening. Entropy (2016) 18(10):365. doi:10.3390/e18100365

CrossRef Full Text | Google Scholar

8. Barahona F, Grötschel M, Jünger M, Reinelt G. An application of combinatorial optimization to statistical physics and circuit layout design. Operations Res (1988) 36(3):493–513. doi:10.1287/opre.36.3.493

CrossRef Full Text | Google Scholar

9. Neukart F, Compostella G, Seidel C, Von Dollen D, Yarkoni S, Parney B. Traffic flow optimization using a quantum annealer. Front ICT (2017) 4:29. doi:10.3389/fict.2017.00029

CrossRef Full Text | Google Scholar

10. Rosenberg G, Haghnegahdar P, Goddard P, Carr P, Wu K, De Prado ML. Solving the optimal trading trajectory problem using a quantum annealer. IEEE J Sel Top Signal Process (2016) 10(6):1053–60. doi:10.1109/JSTSP.2016.2574703

CrossRef Full Text | Google Scholar

11. Gayer O, Sacks Z, Galun E, Arie A. Temperature and wavelength dependent refractive index equations for MgO-doped congruent and stoichiometric LiNbO₃. Appl Phys B (2008) 91(2):343–8. doi:10.1007/s00340-008-2998-2

CrossRef Full Text | Google Scholar

12.Author anonymous. Hybrid solvers (2022). Available at: https://docs.ocean.dwavesys.com/en/stable/overview/hybrid.html (Accessed June 1, 2022).

Google Scholar

13. Zhang Y, Gu BY. Optimal design of aperiodically poled lithium niobate crystals for multiple wavelengths parametric amplification. Opt Commun (2001) 192(3-6):417–25. doi:10.1016/S0030-4018(01)01220-2

CrossRef Full Text | Google Scholar

14. Conforti M, Baronio F, De Angelis C. Ultrabroadband optical phenomena in quadratic nonlinear media. IEEE Photon J (2010) 2(4):600–10. doi:10.1109/JPHOT.2010.2051537

CrossRef Full Text | Google Scholar

15. Reid DT. Ultra-broadband pulse evolution in optical parametric oscillators. Opt Express (2011) 19(19):17979–84. doi:10.1364/OE.19.017979

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Chen BQ, Zhang C, Hu CY, Liu RJ, Li ZY. High-efficiency broadband high-harmonic generation from a single quasi-phase-matching nonlinear crystal. Phys Rev Lett (2015) 115(8):083902. doi:10.1103/PhysRevLett.115.083902

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Lu M, Chen X. Multiple quasi-phase matching in engineered domain-inverted optical superlattice. J Nonlinear Optic Phys Mat (2007) 16(02):185–98. doi:10.1142/S0218863507003640

CrossRef Full Text | Google Scholar

18. Arbore MA, Marco O, Fejer MM. Pulse compression during second-harmonic generation in aperiodic quasi-phase-matching gratings. Opt Lett (1997) 22(12):865–7. doi:10.1364/OL.22.000865

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Imeshev G, Arbore MA, Fejer MM, Galvanauskas A, Fermann M, Harter D. Ultrashort-pulse second-harmonic generation with longitudinally nonuniform quasi-phase-matching gratings: Pulse compression and shaping. J Opt Soc Am B (2000) 17(2):304–18. doi:10.1364/JOSAB.17.000304

CrossRef Full Text | Google Scholar

20. Sapaev UK, Reid DT. General second-harmonic pulse shaping in grating-engineered quasi-phase-matched nonlinear crystals. Opt Express (2005) 13(9):3264–76. doi:10.1364/OPEX.13.003264

PubMed Abstract | CrossRef Full Text | Google Scholar