Spin-valley polarized edge states in quasi-one-dimensional asymmetric kagome lattice

The spin-valley-related electronic properties of quasi-one-dimensional kagome lattices with intrinsic spin-orbit coupling are studied, based on the tight-binding formalism. Three types of kagome-lattice nanoribbons along the x-direction with various geometric boundaries are proposed, including two symmetric nanoribbons and one asymmetric one. It is found that two nonequivalent Dirac cones and helical edge states exist in all the three types of kagome-lattice nanoribbons at 1/3 filling. Among them in the asymmetric nanoribbon, the spin and valley are found to be locked to each other due to inversion symmetry breaking, resulting in spin-valley polarized edge states. Band structure and probability density of wave function show that the spin-up/-down edge states locate at the K/K′ valley, with opposite propagation direction at the upper and lower boundaries. Spin-resolved real-space local current confirms the spin-valley polarized helical edge state in the asymmetric nanoribbon. The device application of the asymmetric kagome-lattice nanoribbon is worth further investigation.

1 Introduction

Kagome lattice is a two-dimensional network of corner-sharing triangles. Due to its special lattice geometric structure, an exotic band structure with flat band and Dirac cones has been theoretically demonstrated [1–6], as well as unconventional magnetism [7–9], Dirac metal [10] and quantum spin liquids [11, 12]. Experimentally, a lot of compounds with kagome lattice have been synthesized and studied. Among them, AV₃Sb₅ (A = K, Rb, Cs) is a novel superconductor coexisting with the charge density wave order [13–15], and RMn₆Sn₆ (R = Y, Tb, Dy, Ho) is a ferrimagnetic metal with anomalous Hall effect [16–20]. Besides, a number of well-known kagome magnets with exotic phenomenon have been reported to exhibit giant intrinsic anomalous Hall effect, such as ferromagnetic Fe₃Sn₂ with bilayer Fe kagome lattice [21–23], ferromagnetic Weyl semimetal Co₃Sn₂S₂ [24, 25], and noncollinear antiferromagnet Mn₃Sn [26]. The topological properties, like quantum Hall effect and quantum spin Hall effect, magnetic order and flat band of the kagome lattice have also been studied theoretically in recent years based on tight-binding model [1, 3, 27–33]. At 1/3 filling of kagome lattice, there are two nonequivalent Dirac points locating at the corners of the first Brillouin zone, and the system is a Dirac semi-metal. Similar to the Kane-Mele model on honeycomb lattices, the spin-orbit coupling (SOC) can open a non-trivial gap at the Dirac points and drive the system to a topological phase [34]. One could expect topological edge states at 1/3 filling of the kagome-lattice nanoribbon, like those of silicene nanoribbon [35, 36]. At 2/3 filling, the band crossing is quadratic and the instability toward the insulating phase occurs at infinitesimal (repulsive) interaction, making such system a promising candidate for a 2D topological insulator. Additionally, in the flat bands strong Coulomb interaction leads to the anti-ferromagnetism and the Wigner crystallization in these kagome systems.

Edge modes are very crucial to topological phases, and employing the bulk-edge correspondence is a powerful tool to determine the topology [37–40]. In graphene-like lattice, the edge states of nanoribbons with diffrent boundaries have been widely investigated, as well as their topological properties [35, 41, 42]. In this work, we study the edge states in quasi-one-dimensional kagome-lattice nanoribbons with intrinsic spin-orbit coupling via tight-binding model. Due to the triangle structure of kagome lattice, there are several geometric boundaries of kagome-lattice nanoribbons [43]. Three types of kagome-lattice nanoribbons along the x-direction with various boundaries are proposed and studied, which contains two symmetric nanoribbons and an asymmetric one. In the asymmetric nanoribbon, we find that the spin and valley are locked to each other at 1/3 filling by inversion symmetry breaking. Probability density of wave function and real-space local current confirm such helical spin-valley polarized edge states. The asymmetric kagome-lattice nanoribbon could have device application potential of spin-valley polarized current, where the selected current is both spin and valley dependent.

2 Model and methods

2.1 Tight-binding model

In this work, the tight-binding Hamiltonian for kagome lattice considering both the nearest-neighbor and second-nearest neighbor interactions can be written as [31].

$\begin{array}{c}\hfill H=-t_{\text{h}}\sum _{⟨i,j⟩\alpha }{c}_{i\alpha }^{†}{c}_{j\alpha }+\text{i}{\lambda }_{\text{SO}}\sum _{⟨⟨i,j⟩⟩\alpha \beta }{\nu }_{ij}{c}_{i\alpha }^{†}{\sigma }_{\alpha \beta }^z{c}_{j\beta }.\end{array}(1)$

In the first term, ⟨i, j⟩ means the hopping interaction with strength t_h occurring between the nearest neighbors, and $c_{i\alpha }^{†}$(c_iα) is the creation (annihilation) operator with spin α at site i. For most kagome materials, the hopping strength t_h varied from 0.07 to 0.1 eV [29, 44]. In this work, all the interaction parameters and related numerical results are in units of t_h. The second term is the SOC with strength λ_SO between the second-nearest-neighbor sites ⟨⟨i, j⟩⟩. ν_ij = +1 (ν_ij = −1) if the SOC hopping is anticlockwise (clockwise) with respect to the positive z axis, and the z component of Pauli matrix σ^z. Most kagome materials are composed of heavy atoms, which could lead to relatively large spin-orbit coupling. For example, in Fe₃Sn, the hopping parameter is t_h = 123 meV, and the SOC strength λ_SO = 9.24 meV [44]. Here, the SOC strength is set to be λ_SO = 0.1t_h, which is employed in most tight-bind studies and can well fit the first-principles calculations [31, 34]. Although the effects of second-nearest-neighbor hopping have been demonstrated [45], we only consider the nearest-neighbor hopping and second-nearest-neighbor SOC, which is widely employed in tight-binding models.

As shown in Figure 1A, there are three sublattices (A, B and C) in one unit cell, in momentum space the Hamiltonian turns to be 3 × 3 matrix

$\begin{array}{cc}\hfill {\mathcal{H}}_{\mathit{k}}& =-t_{\text{h}}\left(\begin{array}{ccc}\hfill 0\hfill & \hfill 1+e^{-\text{i}{k}_2}\hfill & \hfill 1+e^{\text{i}{k}_1}\hfill \\ \hfill 1+e^{\text{i}{k}_2}\hfill & \hfill 0\hfill & \hfill 1+e^{\text{i}{k}_3}\hfill \\ \hfill 1+e^{-\text{i}{k}_1}\hfill & \hfill 1+e^{-\text{i}{k}_3}\hfill & \hfill 0\hfill \end{array}\right)\hfill \\ \hfill & \pm \text{i}{\lambda }_{\text{SO}}\left(\begin{array}{ccc}\hfill 0\hfill & \hfill e^{\text{i}\left(k_2-k_3\right)}\hfill & \hfill e^{\text{i}\left(k_3-k_1\right)}\hfill \\ \hfill e^{\text{i}\left(k_3-k_2\right)}\hfill & \hfill 0\hfill & \hfill e^{\text{i}\left(k_1+k_2\right)}\hfill \\ \hfill e^{\text{i}\left(k_1-k_3\right)}\hfill & \hfill e^{\text{i}\left(-k_1-k_2\right)}\hfill & \hfill 0\hfill \end{array}\right),\hfill \end{array}(2)$

with k_n = k ⋅a_n. a_n are the unit lattice vectors with a the distance between nearest-neighbor sites, ${\mathit{a}}_1=a\widehat{x}+\sqrt{3}a\widehat{y}$, ${\mathit{a}}_2=a\widehat{x}+\sqrt{3}a\widehat{y}$, and a₃ = a₁ + a₂. Here the + ( − ) sign of the second term refers to spin-up (-down) electrons. Accordingly, the Brillouin zone (BZ) is shown in Figure 1B, with the reciprocal lattice vectors ${\mathit{b}}_1=\pi /a{\widehat{k}}_x+\pi /\sqrt{3}a{\widehat{k}}_y$ and ${\mathit{b}}_2=\pi /a{\widehat{k}}_x-\pi /\sqrt{3}a{\widehat{k}}_y$.

FIGURE 1

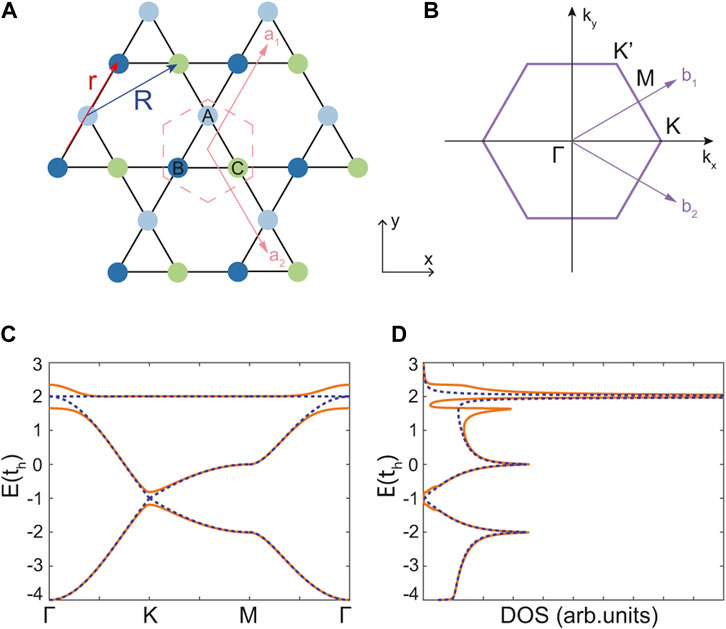
FIGURE 1. (A) Schematic of kagome lattice. The unit cell, formed by sublattice-A, B, and C, is indicated by red dashed hexagon, and ${\mathit{a}}_1=a\widehat{x}+\sqrt{3}a\widehat{y}$, ${\mathit{a}}_2=a\widehat{x}+\sqrt{3}a\widehat{y}$ are the unit lattice vectors with a the distance between nearest-neighbor sites. r is the position vector between nearest-neighbor sites, and R is the one between second-nearest-neighbor sites. (B) The Brillouin zone (BZ) with high-symmetry points and the reciprocal lattice vectors ${\mathit{b}}_1=\pi /a{\widehat{k}}_x+\pi /\sqrt{3}a{\widehat{k}}_y$ and ${\mathit{b}}_2=\pi /a{\widehat{k}}_x-\pi /\sqrt{3}a{\widehat{k}}_y$. (C) Energy spectrum along the high-symmetry lines in the BZ and (D) the density of states (DOS) with intrinsic spin-orbit coupling (SOC) strength λ_SO = 0 (dashed curves), λ_SO = 0.1t_h (solid curves).

Figures 1C,D show the energy spectrum along the high-symmetry lines in the BZ and the density of states (DOS) with SOC strength λ_SO = 0 (dashed curves) and λ_SO = 0.1t_h (solid curves). Without SOC, three doubly degenerate bands can be seen, which are two pairs of dispersing bands with two Dirac cones at K and K′ points and, an additional flat band. Gaps open in the two dispersing bands at the Dirac points and in the flat band at Γ point after introducing SOC. This formation of a bulk gap at the Dirac points induces a topological insulator phase in the kagome lattice system, since the SOC breaks the spin symmetries and possesses a nontrivial Z₂ invariant [31]. When the two-dimensional kagome lattice is cut into a quasi-one-dimensional nanoribbon along the x-direction, the two nonequivalent Dirac points could be preserved according to the BZ. One could expect the bulk-boundary correspondence and gapless edge states of the kagome nanoribbon similar to the case of silicene zigzag nanoribbon [35, 36].

2.2 Dc conductance and local current

The kagome-lattice nanoribbon can be viewed as a central device connected with two semi-infinite electrodes. The retarded Green’s function of the nanoribbon is obtained by ${\mathcal{G}}^{\alpha }(E)={\left[(E+\text{i}{0}^{+})-H^{\alpha }-{\mathrm{\Sigma }}_L^{\alpha }-{\mathrm{\Sigma }}_R^{\alpha }\right]}^{-1}$, where ${\mathrm{\Sigma }}_L^{\alpha }$ and ${\mathrm{\Sigma }}_R^{\alpha }$ are the spin-resolved self-energies of the semi-infinite left and right leads for spin α. According to Landauer-Büttiker formalism, the spin-resolved dc conductance is [46].

$G^{\alpha }\left(E\right)=\frac{e^2}{h}\text{Tr}\left[{\mathrm{\Gamma }}_R^{\alpha }{\mathcal{G}}^{\alpha }{\mathrm{\Gamma }}_L^{\alpha }{\mathcal{G}}^{\alpha †}\right],(3)$

where h and e are Planck’s constant and electron charge, respectively. ${\mathrm{\Gamma }}_{L/R}^{\alpha }=\text{i}\left[{\mathrm{\Sigma }}_{L/R}^{\alpha }-{\mathrm{\Sigma }}_{L/R}^{\alpha †}\right]$ is the imaginary part of the self-energy of the semi-infinite left/right lead. The spin-resolved local current between site i and j in the real space of the present nanoribbon is calculated by

$J_{ij}^{\alpha }\left(E\right)=H_{ji}^{\alpha }{\mathcal{G}}_{ij}^{<\alpha }-{\mathcal{G}}_{ji}^{<\alpha }{H}_{ij}^{\alpha \ast },(4)$

with the lesser Green’s function [47, 48] ${\mathcal{G}}^{<\alpha }=-\text{i}{\mathcal{G}}^{\alpha }{\mathrm{\Gamma }}_L^{\alpha }{\mathcal{G}}^{\alpha †}$.

3 Results and discussion

The two-dimensional kagome lattice can be cut into nanoribbons along the x-direction, with three different edge structures (types I, II, and III), as shown in Figure 2. We focus on the band structures at 1/3 filling of these nanoribbons, with edge states at two nonequivalent Dirac cones, K′ (k_x ∼ π/3a) and K (k_x ∼ 2π/3a) points. The type I and type II kagome-lattice nanoribbons in Figures 2A,B are of inversion symmetry with respect to a central point, while the type III in Figure 2C is inversion asymmetric. The upper and lower boundaries of type I are both formed by sublattice-B and sublattice-C, and the upper and lower boundaries of type II are both formed by sublattice-A. For the two-dimensional kagome lattice, a spin-independent lattice dimerization term was introduced to break the inversion symmetry [31]. As for the quasi-one-dimensional kagome-lattice nanoribbons, the inversion symmetry breaking is realized by composing different types of edge structures here. It has a much more significant effect on the edge state than that is induced by the bulk lattice dimerization or defect. As shown in Figure 2C, the upper boundary of type III is formed by sublattice-A, and the lower one is formed by sublattice-B and sublattice-C. Two symmetric nanoribbons have spin-degenerate band structure, though the SOC breaks the SU(2) spin symmetry. When the inversion symmetry and the SU(2) spin symmetry are broken simultaneously in the asymmetric nanoribbon, spin-up and spin-down band structures become nondegenerate, especially at 1/3 filling.

FIGURE 2

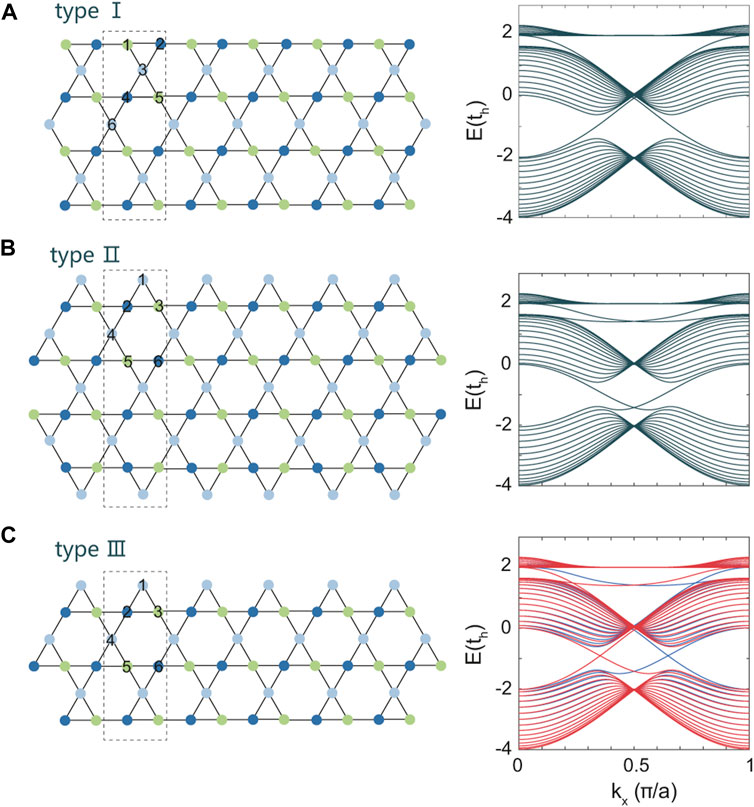
FIGURE 2. Three types of geometric edge structure for kagome-lattice nanoribbons along the x-direction and their band structures. The black dashed lines indicate unit cells of the three nanoribbons, and the numbers are the atom sites in one unit cell. In the right panel of (A,B), the spin-degenerate band structures are in black. In the right panel of (C), spin-up/-down band structures are in blue/red.

Let us first check the edge states at 1/3 filling of symmetric type I and type II nanoribbons, around E = −0.8t_h as labeled by black stars in Figure 3(a1) and (b1), respectively. Figure 3(a2) displays the probability density of the wave function of the three sublattice for spin-up (blue curves) and spin-down (red curves) edge states around K′ point, in the type I nanoribbon. One can clearly see that the spin-up edge states are formed on the upper boundary, while the spin-down ones are on the lower boundary. Both the right-moving edge states at upper and lower boundaries result from sublattice-B (blue star) and sublattice-C (green square), consistent with its geometric structure of boundaries. As shown in Figure 3(a3), the spin-up and spin-down edge states around K point have a left-moving direction, and locate at the opposite boundaries to the case of K′ point. The insets of Figure 3(a2) and (a3) show the propagation directions of the spin-degenerate helical edge modes, consisting of the counter propagating states with opposite spins on each boundary.

FIGURE 3

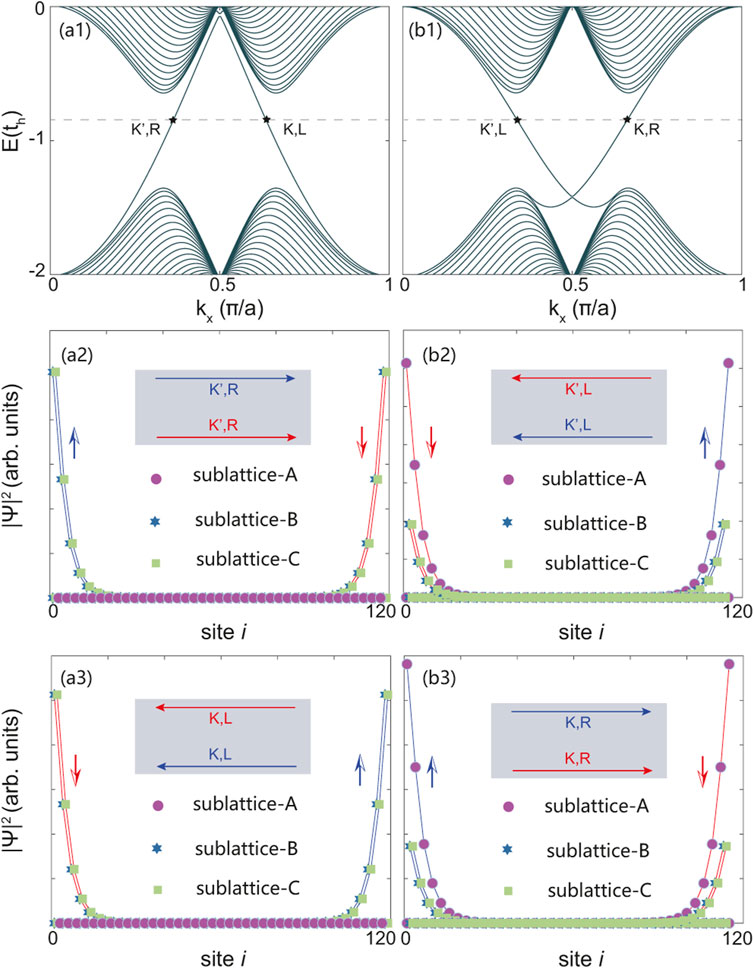
FIGURE 3. (a1/b1) The band structure of type I and II kagome-latttice nanoribbons, and corresponding squared wave function (probability density of wave function |Ψ|²) for three sublattices of the unit cell at 1/3 filling, at k_x ∼ π/3a (a2/b2) and k_x ∼ 2π/3a (a3/b3). Insets: the blue and red arrows denote the propagation directions (L/R is short for left/right) of the opposite spins at the boundaries. The number of atom sites along the y-direction, namely the width of the nanoribbons, is about 120.

Figure 3(b2/b3) shows the probability density of the wave function of three sublattices for spin-up (blue curves) and spin-down (red curves) edge states around K′/K point in the nanoribbon of type II. Comparing to the nanoribbon of type I around K′/K point, the spin-degenerate edge states have an opposite propagating direction and edge distribution. The left-/right-moving spin-up edge states are formed on the lower/upper boundary, and the left-/right-moving spin-down ones are at the upper/lower boundary. Sublattice-A (purple circle) mainly contributes to the edge states of both two boundaries. However, the sublattice-A at the boundaries is too sparse to form the edge states as shown in Figure 2B. Therefore, sublattice-B and sublattice-C close to the boundaries also have contributions, see the blue star and green square at boundary sites. In spite of the different propagation direction and edge distribution with nanoribbon of type I, one can find that the kagome nanoribbon of type II also possesses helical edge modes at 1/3 filling, as indicated in the insets of Figure 3(b2) and (b3).

Then we focus on the edge states at 1/3 filling of the type III asymmetric nanoribbon in Figure 4A. One can see that the spin-down edge states locate around the K′ point, and the spin-up ones around the K point, which implies that the spin and valley are locked to each other. Nevertheless, the spin-up and spin-down electrons are still degenerate with respect to energy. Thus, the spin-up and spin-down conductance of the nanoribbon are merged with each other as shown in Figure 4B. Figure 4C shows the probability density of the wave function for the edge states labeled by black stars in Figure 4A. As shown, near the K′ point, the spin-down edge states are formed on the two boundaries with opposite propagating directions, namely the edge states are spin- and valley-polarized simultaneously. Moreover, the edge states with left-moving Fermi velocity v = ∂E/∂k locate mainly at sublattice-A on the upper boundary, while right-moving ones at sublattice-B and sublattice-C on the lower boundary, as indicated in the inset of Figure 4C. As for the edge states around the K point, we show the probability density of the wave function in Figure 4D. Similarly, the spin-up edge states are locked to the K valley. The direction on the two boundaries are opposite to that of the spin-down states, i.e., the left-moving spin-down edge states locate at sublattice-B and sublattice-C on the lower boundary while the right-moving ones mainly locate at sublattice-A on the upper boundary. Note that in Figure 4A, the left-/right-moving spin-down/-up edge states at K′/K point is mainly contributed by sublattice-A on the upper boundary, while the right-/left-moving spin-down/-up edge states at K′/K point is contributed by sublattice-B and C on the lower boundary.

FIGURE 4

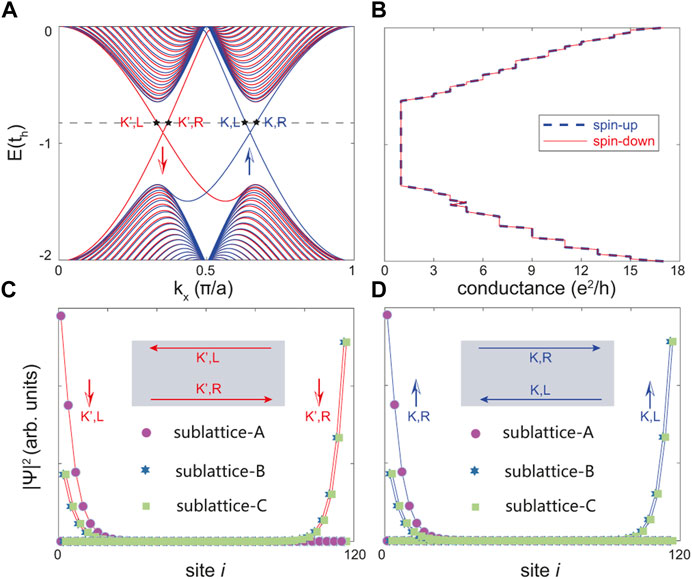
FIGURE 4. (A) The band structure and (B) conductance of kagome-latttice nanoribbons of Figure 2C at 1/3 filling, where the spin and valley are locked. (C/D) Squared wave function (probability density of wave function |Ψ|²) for three sublattice of the unit cell at K′/K point for spin-down/-up electrons. The blue and red arrows denote the propagation directions of the opposite spins at the boundaries. The number of atom sites along the y-direction, namely the width of the nanoribbons, is about 120.

To illustrate the anisotropic helical edge modes in the asymmetric kagome-lattice nanoribbon, we calculate the real-space local current at 1/3 filling, which shows the intensity and direction of current at each site. Figure 5 shows the spin-resolved local current at E = −0.8t_h of the three types kagome-lattice nanoribbons along the x-direction, consistent with the schematics in the inset of Figures 3, 4. Note that only in the asymmetric nanoribbon, the spin and valley are locked to each other as shown in Figure 5C. The spin-up and spin-down local currents are locked to the K and K′ valleys, respectively. For the right-moving modes, the spin-up/-down local current flows along the upper/lower boundary of the nanoribbon. On the other hand, the spin-up/-down local current for the left-moving modes prefers to flow along the lower/upper boundary. One can see that sublattice-A contributes to the current on the upper boundary due to its outmost site on the edge, while the sublattice-B and C not only have current contribution on the lower boundary but also contribute on the upper boundary. This could be owed to the direction of their connecting bonds, which is parallel to the current and, is easy for the current flowing. Interestingly, although the probability density of wave function of sublattice-A on the edge of type II and type III is larger than that of sublattice-B/C, the local current of sublattice-A contributes less than sublattice-B and sublattice-C. This phenomena may stem from the reflection of y-direction on the edge, which leads to large probability density of sublattice-A. However, it does not contribute to the local current in the x-direction transport. The spin-valley polarized edge state could have potential applications for electron manipulating in kagome-lattice nanodevice.

FIGURE 5

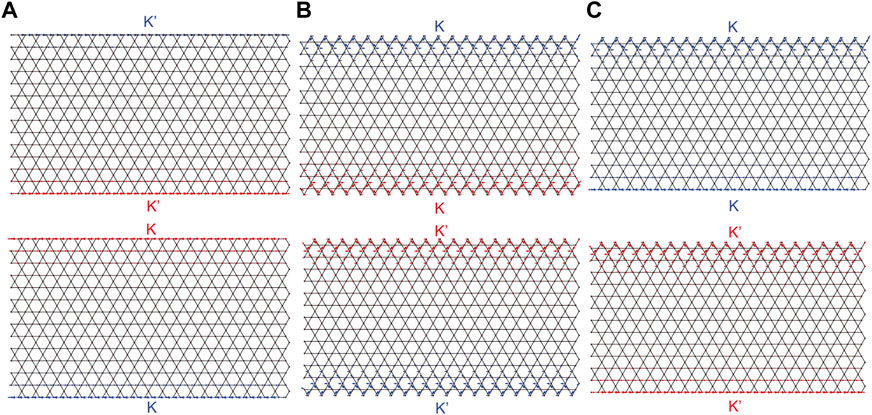
FIGURE 5. The real-space distribution of spin-up (blue arrows) and spin-down (red arrows) local current at E = −0.8t_h of the three types for (A) type I, (B) type II and (C) type III of kagome-lattice nanoribbns along the x-direction.

Finally, we study the size effect of the asymmetric type III kagome-lattice nanoribbon on the band structure and edge states, considering the device application based on the spin-valley polarized transport. Figures 6A–C show the band structure of the asymmetric type III kagome-lattice nanoribbons with atom sites 3, 9 and 15. As shown, one can find that an observable band gap is opened up at the K and K′ points when the nanoribbon is narrow. As the width of nanoribbon becomes wide, the gap is narrowed down gradually. Figure 6D shows the band gap as a function of nanoribbon width. According to the numerical results, when the width rises to 40 atom sites, the band gap could be vanishing zero. The gap opening in the narrow nanoribbon could be owed to the coupling of the edge states on the upper and lower boundaries via the tunnel effect. The narrow nanoribbon might be tuned by exchange field or photoirradiation to undergo topological phase transition, like a spin-polarized quantum anomalous Hall insulator as the case in honeycomb-lattices nanosystems [41, 49, 50].

FIGURE 6

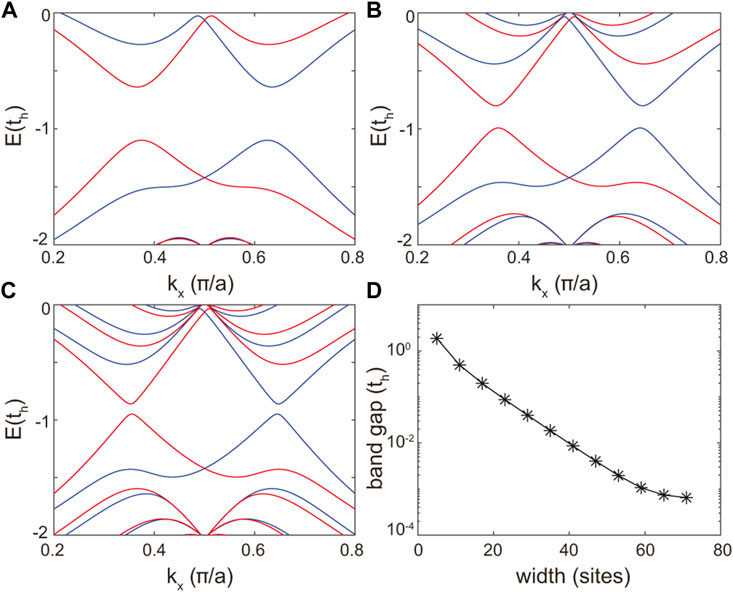
FIGURE 6. Band structures of the asymmetric kagome-lattice nanoribbons with width, namely atom sites (A) 3, (B) 9, and (C) 15. (D) Bang gap versus nanoribbon width.

4 Conclusion

In summary, we investigate the edge states of kagome-lattice nanoribbons with three types of boundary structures along the x-direction. Helical edge states can be observed in all the three types of nanoribbons at 1/3 filling, according to the analyses of the band structure and the probability density of wave function. Among them in the asymmetric nanoribbon, spin-valley polarized edge states induced by the asymmetric geometric structure are demonstrated. The spin-up/-down edge states locate at the K/K′ point with opposite propagation direction on the upper and lower boundaries, revealed by spin-resolved probability density of wave function and real-space local current. Such spin-valley polarized helical edge states in the asymmetric kagome-lattice nanoribbon could have application potential in various kinds of spin valley valves and filters. Additionally, in practical case, the effects of defect or disorder, and second-nearest-neighbor hopping for kagome lattice are worth study in the future.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

Y-LS and E-JY conceived the project. Y-LS and E-JY performed the tight-binding modeling and data analysis. Y-LS and E-JY wrote the manuscript with contributions from G-HC, S-CD, Z-BC, and Y-WZ. Y-LS and E-JY supervised the work.

Funding

Zhejiang Provincial Natural Science Foundation of China (Grant No. LQ19A040010), and National Natural Science Foundation of China (Grant Nos. 11604293 and 11504137).

Acknowledgments

The authors would like to acknowledge financial support from Zhejiang Provincial Natural Science Foundation of China and National Natural Science Foundation of China.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Zhuo L, He H, Huang R, Li Z, Qiu W, Zhuang F, et al. Flat band of Kagome lattice in graphene plasmonic crystals. J Phys D Appl Phys (2022) 55:065106. doi:10.1088/1361-6463/ac30fe

CrossRef Full Text | Google Scholar

2. Ohgushi K, Murakami S, Nagaosa N. Spin anisotropy and quantum Hall effect in the kagomé lattice: Chiral spin state based on a ferromagnet. Phys Rev B 62 (2000) R6065, 8, –R6068. doi:10.1103/PhysRevB.62.R6065

CrossRef Full Text | Google Scholar

3. Mizoguchi T, Udagawa M. Flat-band engineering in tight-binding models: Beyond the nearest-neighbor hopping. Phys Rev B (2019) 99:235118. doi:10.1103/PhysRevB.99.235118

CrossRef Full Text | Google Scholar

4. Zhang Y, Železný J, Sun Y, van den Brink J, Yan B. Spin Hall effect emerging from a noncollinear magnetic lattice without spin-orbit coupling. New J Phys (2018) 20:073028. doi:10.1088/1367-2630/aad1eb

CrossRef Full Text | Google Scholar

5. Graf A, Piéchon F. Designing flat-band tight-binding models with tunable multifold band touching points. Phys Rev B (2021) 104:195128. doi:10.1103/PhysRevB.104.195128

CrossRef Full Text | Google Scholar

6. Provenzano PP. Bringing order to the matrix. Nat Mater (2020) 19:130–1. doi:10.1038/s41563-019-0592-0

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Sachdev S. Kagomé- and triangular-lattice Heisenberg antiferromagnets: Ordering from quantum fluctuations and quantum-disordered ground states with unconfined bosonic spinons. Phys Rev B (1992) 45:12377–96. doi:10.1103/PhysRevB.45.12377

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Legendre J, Le Hur K. Magnetic topological kagome systems. Phys Rev Res (2020) 2:022043. doi:10.1103/PhysRevResearch.2.022043

CrossRef Full Text | Google Scholar

9. Reimers JN, Berlinsky AJ. Order by disorder in the classical Heisenberg kagomé antiferromagnet. Phys Rev B (1993) 48:9539–54. doi:10.1103/PhysRevB.48.9539

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Mazin, , Jeschke HO, Lechermann F, Lee H, Fink M, Thomale R, et al. Theoretical prediction of a strongly correlated Dirac metal. Nat Commun (2014) 5:4261. doi:10.1038/ncomms5261

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Balents L. Spin liquids in frustrated magnets. Nature (2010) 464:199–208. doi:10.1038/nature08917

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Zhou Y, Kanoda K, Ng TK. Quantum spin liquid states. Rev Mod Phys (2017) 89:025003. doi:10.1103/RevModPhys.89.025003

CrossRef Full Text | Google Scholar

13. Ortiz BR, Gomes LC, Morey JR, Winiarski M, Bordelon M, Mangum JS, et al. New kagome prototype materials: Discovery of kv₃sb₅, rbv₃sb₅, and csv₃sb₅. Phys Rev Mater (2019) 3:094407. doi:10.1103/PhysRevMaterials.3.094407

CrossRef Full Text | Google Scholar

14. Nakayama K, Li Y, Kato T, Liu M, Wang Z, Takahashi T, et al. Multiple energy scales and anisotropic energy gap in the charge-density-wave phase of the kagome superconductor csv₃sb₅. Phys Rev B (2021) 104:L161112. doi:10.1103/PhysRevB.104.L161112

CrossRef Full Text | Google Scholar

15. Zhou X, Li Y, Fan X, Hao J, Dai Y, Wang Z, et al. Origin of charge density wave in the kagome metal csv₃sb₅ as revealed by optical spectroscopy. Phys Rev B (2021) 104:L041101. doi:10.1103/PhysRevB.104.L041101

CrossRef Full Text | Google Scholar

16. Gao L, Shen S, Wang Q, Shi W, Zhao Y, Li C, et al. Anomalous Hall effect in ferrimagnetic metal RMn ₆ Sn ₆ (R = Tb, Dy, Ho) with clean Mn kagome lattice. Appl Phys Lett (2021) 119:092405. doi:10.1063/5.0061260

CrossRef Full Text | Google Scholar

17. Asaba T, Thomas SM, Curtis M, Thompson JD, Bauer ED, Ronning F. Anomalous hall effect in the kagome ferrimagnet gdmn₆sn₆. Phys Rev B (2020) 101:174415. doi:10.1103/PhysRevB.101.174415

CrossRef Full Text | Google Scholar

18. Chen D, Le C, Fu C, Lin H, Schnelle W, Sun Y, et al. Large anomalous hall effect in the kagome ferromagnet limn₆sn₆. Phys Rev B (2021) 103:144410. doi:10.1103/PhysRevB.103.144410

CrossRef Full Text | Google Scholar

19. Wang Q, Neubauer KJ, Duan C, Yin Q, Fujitsu S, Hosono H, et al. Field-induced topological hall effect and double-fan spin structure with a c-axis component in the metallic kagome antiferromagnetic compound Ymn₆sn₆. Phys Rev B (2021) 103:014416. doi:10.1103/PhysRevB.103.014416

CrossRef Full Text | Google Scholar

20. Ma W, Xu X, Yin JX, Yang H, Zhou H, Cheng ZJ, et al. Rare Earth engineering in rmn₆sn₆ (r = Gd − Tm, lu) topological kagome magnets. Phys Rev Lett (2021) 126:246602. doi:10.1103/PhysRevLett.126.246602

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Wang Q, Sun S, Zhang X, Pang F, Lei H. Anomalous hall effect in a ferromagnetic fe₃sn₂ single crystal with a geometrically frustrated fe bilayer kagome lattice. Phys Rev B (2016) 94:075135. doi:10.1103/PhysRevB.94.075135

CrossRef Full Text | Google Scholar

22. Yin JX, Zhang SS, Li H, Jiang K, Chang G, Zhang B, et al. Giant and anisotropic many-body spin-orbit tunability in a strongly correlated kagome magnet. Nature (2018) 562:91–5. doi:10.1038/s41586-018-0502-7

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Ye L, Kang M, Liu J, von Cube F, Wicker CR, Suzuki T, et al. Massive Dirac fermions in a ferromagnetic kagome metal. Nature (2018) 555:638–42. doi:10.1038/nature25987

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Liu E, Sun Y, Kumar N, Muechler L, Sun A, Jiao L, et al. Giant anomalous Hall effect in a ferromagnetic kagome-lattice semimetal. Nat Phys (2018) 14:1125–31. doi:10.1038/s41567-018-0234-5

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Wang Q, Xu Y, Lou R, Liu Z, Li M, Huang Y, et al. Large intrinsic anomalous Hall effect in half-metallic ferromagnet Co3Sn2S2 with magnetic Weyl fermions. Nat Commun (2018) 9:3681. doi:10.1038/s41467-018-06088-2

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Kuroda K, Tomita T, Suzuki MT, Bareille C, Nugroho AA, Goswami P, et al. Evidence for magnetic Weyl fermions in a correlated metal. Nat Mater (2017) 16:1090–5. doi:10.1038/nmat4987

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Wang Z, Zhang P. Quantum spin Hall effect and spin-charge separation in a kagomé lattice. New J Phys (2010) 12:043055. doi:10.1088/1367-2630/12/4/043055

CrossRef Full Text | Google Scholar

28. Zhang ZY. The quantum anomalous Hall effect in kagomé lattices. J Phys : Condens Matter (2011) 23:365801. doi:10.1088/0953-8984/23/36/365801

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Wang ZF, Su N, Liu F. Prediction of a two-dimensional organic topological insulator. Nano Lett (2013) 13:2842–5. doi:10.1021/nl401147u

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Bolens A, Nagaosa N. Topological states on the breathing kagome lattice. Phys Rev B (2019) 99:165141. doi:10.1103/PhysRevB.99.165141

CrossRef Full Text | Google Scholar

31. Guo HM, Franz M. Topological insulator on the kagome lattice. Phys Rev B (2009) 80:113102. doi:10.1103/PhysRevB.80.113102

CrossRef Full Text | Google Scholar

32. Thi Tran TM, Nguyen DB, Nguyen HS, Tran MT. Magnetic competition in topological kagome magnets. Mater Res Express (2021) 8:126101. doi:10.1088/2053-1591/ac433c

CrossRef Full Text | Google Scholar

33. Zhang ZY. Quantum Hall effect in kagomé lattices under staggered magnetic field. J Phys : Condens Matter (2011) 23:425801. doi:10.1088/0953-8984/23/42/425801

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Liu HD, Chen YH, Lin HF, Tao HS, Wu JH. Interaction and spin—Orbit effects on a kagome lattice at 1/3 filling. Chin Phys B (2014) 23:077101. doi:10.1088/1674-1056/23/7/077101

CrossRef Full Text | Google Scholar

35. Ezawa M, Nagaosa N. Interference of topologically protected edge states in silicene nanoribbons. Phys Rev B (2013) 88:121401. doi:10.1103/PhysRevB.88.121401

CrossRef Full Text | Google Scholar

36. Liu CC, Feng W, Yao Y. Quantum spin hall effect in silicene and two-dimensional germanium. Phys Rev Lett (2011) 107:076802. doi:10.1103/PhysRevLett.107.076802

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Bernevig BA, Hughes TL, Zhang SC. Quantum spin hall effect and topological phase transition in hgte quantum wells. Science (2006) 314:1757–61. doi:10.1126/science.1133734

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Xu C, Moore JE. Stability of the quantum spin Hall effect: Effects of interactions, disorder, andZ2topology topology. Phys Rev B (2006) 73:045322. doi:10.1103/PhysRevB.73.045322

CrossRef Full Text | Google Scholar

39. Hasan MZ, Kane CL. Colloquium: Topological insulators. Rev Mod Phys (2010) 82:3045–67. doi:10.1103/RevModPhys.82.3045

CrossRef Full Text | Google Scholar

40. Wu C, Bernevig BA, Zhang SC. Helical liquid and the edge of quantum spin hall systems. Phys Rev Lett (2006) 96:106401. doi:10.1103/PhysRevLett.96.106401

PubMed Abstract | CrossRef Full Text | Google Scholar

41. Lu WT, Sun QF, Li YF, Tian HY. Spin-valley polarized edge states and quantum anomalous Hall states controlled by side potential in two-dimensional honeycomb lattices. Phys Rev B (2021) 104:195419. doi:10.1103/PhysRevB.104.195419

CrossRef Full Text | Google Scholar

42. Brey L, Fertig HA. Electronic states of graphene nanoribbons studied with the Dirac equation. Phys Rev B (2006) 73:235411. doi:10.1103/PhysRevB.73.235411

CrossRef Full Text | Google Scholar

43. Ablowitz MJ, Cole JT. Topological insulators in longitudinally driven waveguides: Lieb and kagome lattices. Phys Rev A (Coll Park) (2019) 99:033821. doi:10.1103/PhysRevA.99.033821

CrossRef Full Text | Google Scholar

44. Wu T, Guo J. Performance potential of 2D kagome lattice interconnects. IEEE Electron Device Lett (2019) 40:1973–5. doi:10.1109/LED.2019.2947285

CrossRef Full Text | Google Scholar

45. Tang E, Mei JW, Wen XG. High-temperature fractional quantum Hall states. Phys Rev Lett (2011) 106:236802. doi:10.1103/PhysRevLett.106.236802

PubMed Abstract | CrossRef Full Text | Google Scholar

46. Datta S. Electronic transport in mesoscopic systems. United Kingdom: Cambridge University Press (1997).

Google Scholar

47. Nikolić BK, Zârbo LP, Souma S. Imaging mesoscopic spin hall flow: Spatial distribution of local spin currents and spin densities in and out of multiterminal spin-orbit coupled semiconductor nanostructures. Phys Rev B (2006) 73:075303. doi:10.1103/PhysRevB.73.075303

CrossRef Full Text | Google Scholar

48. Stegmann T, Szpak N. Current splitting and valley polarization in elastically deformed graphene. 2d Mater (2018) 6:015024. doi:10.1088/2053-1583/aaea8d

CrossRef Full Text | Google Scholar

49. He C, Zhang Z. Floquet topological phase transitions and chiral edge states in a kagome lattice. Phys Lett A (2014) 378:3200–4. doi:10.1016/j.physleta.2014.09.029

CrossRef Full Text | Google Scholar

50. Mei J, Shao L, Xu H, Zhu X, Xu N. Photomodulated edge states and multiterminal transport in silicenelike nanoribbons. Phys Rev B (2019) 99:045444. doi:10.1103/PhysRevB.99.045444

CrossRef Full Text | Google Scholar