A linear time series analysis of carbon price via a complex network approach

Identifying the essential characteristics and forecasting carbon prices is significant in promoting green transformation. This study transforms the time series into networks based on China’s pilots by using the visibility graph, mining more information on the structure features. Then, we calculate nodes’ similarity to forecast the carbon prices by link prediction. To improve the predicted accuracy, we notice the node distance to introduce the weight coefficient, measuring the impact of different nodes on future nodes. Finally, this study divides eight pilots into different communities by hierarchical clustering to study the similarities between these pilots. The results show that eight pilots are the “small world” networks except for Chongqing and Shenzhen pilots, all of which are “scale-free” networks except for Shanghai and Tianjin pilots. Compared with other predicted methods, the proposed method in this study has good predicted performance. Moreover, these eight pilots are divided into three clusters, indicating a higher similarity in their price-setting schemes in the same community. Based on the analysis of China’s pilots, this study provides references for carbon trading and related enterprises.

1 Introduction

To effectively control CO₂ emissions, an emission trading scheme (ETS) was established by the EU in 2005, as a commodity to excise emission rights based on greenhouse gas emission reductions [1]. Since its launch, the EU has continuously optimized the carbon trading mechanism and subsequently formed a mature trading system. It is the most successful carbon trading system, covering 31 countries, bringing many experiences to China’s ETS [2].

“The 14th Five-Year Plan” pointed out that carbon dioxide emissions will strive to achieve a “carbon peak” by 2030 and “carbon neutral” by 2060. During the 14th Five-Year Plan, a stronger trading policy will be introduced to accelerate the transformation of a high-carbon into a low-carbon nation, laying the foundation for “carbon neutrality” [3]. In the past 20 years, China’s CO₂ emissions have increased six times faster than other regions, accounting for about 70% of global CO₂ emissions. Since 2020, China’s per capita CO₂ emissions have exceeded the EU [4]. Therefore, introducing a carbon trading mechanism has become an urgent task [5]. Subsequently, China established the Shenzhen pilot, Shanghai pilot, Beijing pilot, Guangdong pilot, Tianjin pilot, Hubei pilot, Chongqing pilot, and Fujian pilot since 2013, which is an important means to address climate problems and fulfil the international emission reduction commitments [6].

Due to China’s ETS pilots’ late opening, the mechanism is not mature enough to be applied effectively [7]. Many professors studied EU ETS, whereas a few researchers analyzed China’s ETS pilots. In addition, there are lot of research works about the factors affecting carbon price, but they seldom predict it. Moreover, many studies have been conducted for one pilot and not eight pilots, resulting in a less in-depth analysis of the whole carbon market.

Recently, the complex network has attracted more attention. The visibility graph is a bridge between time series and complex networks, and the networks would retain the structural features of the time series [8]; [9]; [10]. However, if there are no direct links between two nodes, it is unknown whether they will create a connection in the future. To address this problem, the study in [11] proposed the link prediction based on the local random walk (LRW) to evaluate the similarity between two nodes, thus determining whether there is a link between them.

This study collects the daily carbon price in China’s eight pilots and transforms the time series into eight networks by visibility graph. Then, we analyze the network structures and forecast the carbon prices based on link prediction. However, we consider the importance of the node distance to introduce the weight coefficient, which improves the predicted performance further. Finally, this study divides these pilots into different communities by hierarchical clustering, providing a special perspective to study the similarity between eight pilots.

Compared with existing studies, our contributions and core work in this study are mainly in three aspects. (1) A few researchers have studied the eight pilots in China together, but we evaluate them as a whole. To further explore them, we introduce the visibility graph to transform the time series. Based on the network structure, we mine more node information to analyze the features. (2) Most scholars only predicted the carbon prices and did not analyze the network structure to extract more information. We predict the carbon prices by link prediction and analyze the predicted performance according to the network features. Moreover, this study considers the importance of the node distance to introduce the weights, improving the forecasting accuracy. (3) Few studies have classified these pilots into different communities, and this study divides them into several sub-markets and analyzes their similarities.

The rest of this article is organized as follows: Section 2 provides a literature review of China’s ETS analysis; Section 3 introduces some concepts about network science and link prediction. In Section 4, the proposed method and the data are illustrated in detail; Section 5 shows the results and analysis, and we conclude our work in Section 6.

2 Literature review

Most academic research on carbon prices has focused on the causes that affect it and made predictions about it. Therefore, we introduce the two aspects in Section 2.1 and Section 2.2. Moreover, to further study the changing dynamic of the carbon prices in China’s ETS pilots, we analyze the relevant research in Section 2.3.

2.1 The influencing factors of the carbon prices

Many researchers have analyzed the reasons that induce the dynamic of carbon prices, which are mainly divided into three categories: energy, climate, and macroeconomic events [12].

The study in [13] found that carbon prices are positive to crude oil and natural gas prices and insignificantly influenced by coal prices. In addition, they concluded that energy is the main influencing factor in carbon prices. The study in [14] used quantile regression to study the nonlinear effects of coal, oil, natural gas, and other energy prices on carbon prices.

Moreover, the study in [13] concluded that temperature extremes positively affect carbon prices. The study in [15] found that changes in temperature at freezing temperatures have a greater impact on carbon prices than shallow temperatures, and high temperatures do not have such an effect.

The authors of [16] thought the macroeconomic environment would affect carbon prices. When the economic situation arises, industrial production activities increase, the demand for carbon emission rights increases, and carbon prices increase accordingly. Conversely, carbon prices will also decrease when the financial situation declines. The study in [17] analyzed the impact of industrial output on carbon trading prices. They found that the only industries in the EU’s industrial output significantly affecting carbon prices are the combustion and steel industries.

2.2 The forecasting of the carbon prices

To further analyze carbon prices, many experts have predicted prices that provide some experiences to control CO₂ emissions. There are three main methods to forecast time series: statistical models, artificial intelligence algorithms, and ensemble models. Statistical models are the methods to forecast the samples’ trend, including the generalized auto-regressive conditional heteroskedasticity (GARCH) model, auto-regressive integrated moving average (ARIMA) model, grey model GM (1,1), and so on. The authors of the study in [18] made a comparative analysis based on the daily data of the Europe Climate Exchange by using the GARCH model. The process is simple in statistical models, but there are also unavoidable drawbacks; hence, they are not suitable for non-linearity and non-stationary problems.

To address the limits of the statistical models, artificial intelligence algorithms are widely used to capture samples’ features. They mainly include back-propagation neural networks (BPNN), least squares support vector regression (LSSVR), and long short-term memory networks (LSTM). The authors of the study in [2] thought that the dynamics of the carbon prices were chaotic and proposed a multi-layer perceptron network prediction model to forecast the third phase prices in the EU. The study in [19] used ARIMA and LSSVM models to predict carbon prices. Moreover, particle swarm optimization (PSO) is used to find the best parameters for LSSVM to improve predicted accuracy.

To obtain a better performance in forecasting carbon prices, ensemble models that decompose the time series are proposed. The ensemble models mainly conclude empirical mode decomposition (EMD), variational mode decomposition (VMD), and so on. The authors of the study in [20] forecasted the carbon prices in the Guangdong pilot by back-propagation (BP), support vector machines (SVM), and a hybrid model of EMD-BP-DNN, respectively. In addition, they compared the forecasting performances of these models.

2.3 Relevant studies on China’s ETS pilots

The existing research on China’s ETS pilots also considered two aspects: the influencing factors and predictions in the carbon prices. Although there is not much research on eight pilots, it still has reference values.

Unlike the EU market, China’s carbon prices are mainly affected by coal rather than crude oil. The authors of the study in [21] examined the relationship between China’s ETS pilot and its influencing variables: coal price, economy, temperature, and the EU’s carbon prices. The results show a long-term co-integration relationship between them, and coal prices are the dominant factor. The study in [22] discussed the price drivers in ETS pilots by structural mutation testing and an auto-regressive distributed lag model. They proved that oil prices are positively correlated with carbon prices, while coal prices are negatively correlated. The study in [23] studied the driving factors (macroeconomic risks, environmental factors, and energy) in China’s carbon prices by quantitative analysis and the causes affecting price by the dynamic correlation measurement method.

Moreover, there are many methods to predict carbon prices. The authors of the study in [24] proposed a model based on a combination of an empirical modal decomposition algorithm (EMD) and a generalized auto-regressive condition heteroscedasticity model (GARCH), which predicted five pilots’ prices after 2016. The authors of the study in [25] proposed a combination forecasting model based on the hybrid interval multi-scale decomposition method and its application to forecasting interval-valued carbon prices. To mine the relationship between these pilots, the authors of the study in [26] visually analyzed the seven pilots by visibility graph and studied the similarity and heterogeneity.

3 Preliminary

3.1 Visibility graph algorithm

The authors of the study in [27] proposed a visibility graph algorithm, transforming the time series into visibility graphs. In the study, China’s ETS daily carbon prices as the time series values were mapped to each visual node in the network and then the linkages between all nodes were constructed by using the visibility graph algorithm [28]. Assuming a given time series $T=\left\{(t_1,y_1),(t_2,y_2),\dots (t_N,y_N)\right\}$, y_N is the value at t_N correspondingly. If there is a node $\left(t_b,y_b\right)$ between node $\left(t_a,y_a\right)$ and $\left(t_c,y_c\right)$ and it satisfied t_a < t_b < t_c, then whether two nodes construct a link depends on the following equation:

$y_b<y_a+\left(y_c-y_a\right)\frac{\left(t_b-t_a\right)}{\left(t_c-t_a\right)}.(1)$

Commonly, if there is a link between two nodes in a histogram, they can also be linked in a network. For example, if any two vertical bars can see each other’s top, then these 2 bars are supposed to take a linkage [29]; [30]. Next, we can create an adjacent metric based on the corresponding time series. Finally, a network is constructed by network science, as shown in Figure 1.

FIGURE 1

FIGURE 1. Process of time series transforming to a network.

3.2 Topological measures of the VG

3.2.1 Average degree

The average degree is the average value of all the nodes’ degree in a network. K_i is the degree of node i, describing the number of nodes directly connected to it. Commonly, the larger the node degree, the more communication the node and the larger the average degree, demonstrating that the network is more frequently communicated. The average degree is calculated by Eq. 2 and denoted by $⟨k⟩$.

$⟨k⟩=\frac{1}{N}\sum _{i=0}^N{k}_i.(2)$

It also can be expressed as follows:

$⟨k⟩=\frac{2E}{N},(3)$

where E represents the number of edges in a network and N is the number of nodes in a network.

3.2.2 Network diameter

The network diameter is a measure that the maximum value of distance between all nodes in a network, denoted as D, and expressed as

$D=\mathit{max}\left(d_{ij}\right),(4)$

where d_ij is the shortest distance of node i and node j, which defined as the least number of edges from node i to node j.

3.2.3 Average path length

The average path length is a vital character in a network, meaning the average of the shortest distance between any two nodes, denoted by L. The smaller the average path length, the more frequent communication between all nodes in the network. The calculation formula is shown as follows:

$L=\frac{2}{N\left(N-1\right)}\sum _{i\ge j}{d}_{ij}.(5)$

3.2.4 Network density

The network density is used to measure the closeness in the network, denoted by D_g. The higher the D_g, the more tightly connected the network. D_g is expressed by

$D_g=\frac{E}{N\left(N-1\right)}.(6)$

3.2.5 Average clustering coefficient

The average clustering coefficient refers to the clustering coefficient of the whole network, denoted as $C(0\le C\le 1)$, which means that the clustering coefficients of all nodes are averaged. In a network, suppose node i is connected to k_i nodes and we denote the actual number of edges existing between these k_i nodes as E_i; then, we can define the clustering coefficient of node i as the ratio of E_i to the total maximum possible proportion of the number of edges k_i (k_i−1)/2, and the calculation formula of C_i is as follows:

$C_i=\frac{2E_i}{k_i\left(k_i-1\right)}.(7)$

Then, the average clustering coefficient is denoted by

$C=\frac{1}{N}\sum _{i=1}^N{C}_i.(8)$

3.2.6 Community structure

To further explore the network, we introduce the community structure. Nodes are tightly connected between the same communities while sparsely connected between different communities [31]. Usually, the modularity Q function is used to describe the accuracy of community division, which was devised by the authors of the study in reference [32]. The closer the Q takes to 1, the more obvious the community structure is [33], which is expressed as follows:

$Q=\frac{1}{2E}\sum _{i,j}\left(a_{ij}-\frac{k_i{k}_j}{2E}\right)\delta \left(g_i,g_j\right).(9)$

Moreover, the function δ(g_i, g_j) is defined as: if node i and node j belong to the same community, δ(g_i, g_j) = 1, otherwise δ(g_i, g_j) = 0 [34]

3.3 Link prediction

Link prediction is a method to forecast the likelihood of two unlinked nodes establishing a link in the future based on the existing network analysis. Since a time series converts into a network, then the time series prediction map into a network prediction. In addition, most link prediction methods are based on node similarity, such as common neighbors (CN), resource allocation index (RA), and so on. The authors of the study in [11] proposed a competitive prediction method based on the local random walk (LRW), which measures the similarity by a walker walking randomly in the network. Correspondingly, the higher similarity between two nodes, the higher probability they will connect in the future.

3.3.1 Local random walk

In the method, a visibility graph is described as an unweighted network G (V, E), where V is the set of nodes and E is the set of edges. Then, the transition probability matrix that a random walker stays at node x and moves to node y in one step, denoted by P_xy and obtained by

$P_{xy}=\frac{a_{xy}}{k_x},(10)$

where a_xy = 1 if node x is connected to node y, otherwise a_xy = 0. k_x is the degree of node x.

After t steps, the probability ${\vec{\pi }}_x(t)$ that the walker moves from node x to node y is calculated by

${\vec{\pi }}_x\left(t\right)=P^T{\vec{\pi }}_x\left(t\right),(11)$

where P^T is the transposition of matrix P. Suppose there is a N length time series and an N × 1 vector with the xth element equaling to one and others to 0, then the vector is devoted by ${\vec{\pi }}_x(0)$, representing that the walker starts walk from node x.

Then, the similarity between node x and node y based on LRW is calculated by

$S_{xy}^{\mathit{LRW}}\left(t\right)=\frac{k_x}{2E}{\pi }_{xy}\left(t\right)+\frac{k_y}{2E}{\pi }_{yx}\left(t\right).(12)$

However, there is a problem that a random walker will walk too far away from node x to node y even though node x is adjacent to node y, resulting in unsatisfactory predictions. To address the issue, a higher similarity method is proposed, which ensures a random walker walks in a local part rather than other parts of the network. Superposed random walk (SRW) similarity between node x to node y is denoted by $S_{xy}^{\mathit{LRW}}$, as follows:

$S_{xy}^{\mathit{SRW}}\left(t\right)=\sum _{l=1}^t{S}_{xy}^{\mathit{LRW}}\left(l\right).(13)$

Then, $S_{xy}^{\mathit{LRW}}(n)$ = $S_{yx}^{\mathit{LRW}}(n)$ and $S_{xy}^{\mathit{SRW}}(t)$ = $S_{yx}^{\mathit{SRW}}(t)$.

3.3.2 Node distance

According to the method proposed in [35] , the distance d_i→j between node t_i and node t_j is calculated by Eq. (14), which corresponding time values in point (t_i, y_i) and (t_j, y_j), respectively.

$d_{i\to j}=|t_i-t_j|.(14)$

4 Method and data

The method is proposed to predict carbon prices utilizing the visibility graph and link prediction, which will be illustrated in detail and divided into three parts. In Section 4.1, the preliminary work based on visibility graph and link prediction will be introduced. In Section 4.2, an initial prediction will be obtained based on the node similarity. In Section 4.3, node distance will be taken into consideration to improve initial predicted accuracy.

4.1 Preliminary work

The preliminary work including three main steps as follows:

Step 1: Transforming a time series to a visibility graph

A given time series $T=\left\{(t_1,y_1),(t_2,y_2),\dots (t_N,y_N)\right\}$ can map into a network by visibility graph algorithm, as illustrated in Eq. (1).

Step 2: Calculating the node similarity based on LRW

The similarity between any two nodes based on LRW model is first calculated by Eqs (10)–(12). Then, to sum, the results of S^SRW = [S_1N, S_2N, … S_((N−1)N)] will obtain the similarities between the last node N and all previous (N − 1) nodes by using Eq. 13.

Step 3: Finding out the most similar nodes

The maximum value of S^SRW is denoted by S_MN, and then node (t_M, y_M) is the most similar point to node (t_N, y_N).

4.2 Initial forecasting

Suppose to forecast the future node (t_N+1, y_N+1), and it is the closest to the last observed node (t_N, y_N), namely, it will be directly influenced by node (t_N, y_N). However, the future node is not only influenced by the nearest node but also previously observed values. In Section 4.1, the higher similarity node (t_M, y_M) is obtained, and it is the most similar point to node (t_N, y_N), meaning it represents the previous data. Therefore, it is considered to carry all the historical information to forecast the future nodes.

As node (t_M, y_M) and node (t_N, y_N) have the most similarity in the network, they will directly link to forecast the future node (t_N+1, y_N+1), the calculation of y_N+1 by Eq. 15 according to the study in [36].

$y_{N+1}=\frac{y_N-y_M}{t_N-t_M}\left(t_{N+1}-t_M\right)+y_M.(15)$

As shown in Figure 2, it describes the process of the linear approximation prediction. Clearly, node (t₃, y₃) are the most similar point to (t₆, y₆), which determines the future node (t₇, y₇).

FIGURE 2

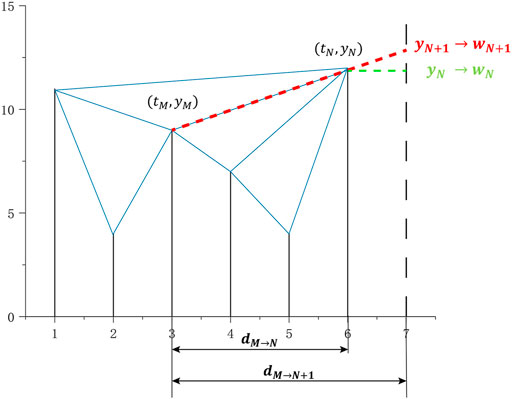
FIGURE 2. Process of linear approximation prediction. w_N+1 (red curve) is the weight coefficient of y_N+1, w_N (green curve) is the weight coefficient of y_N.

4.3 Improved forecasting

To improve the predicted accuracy, the node distance is considered to this method based on the initial forecasting, which determines the weight coefficients of y_N+1 and y_N, respectively.

Step 1: Calculating the node distance

The distance between node (t_M, y_M) and node (t_N, y_N) is determined by Eq. 16, denoted by d_M→N.

$d_{M\to N}=|t_M-t_N|,(16)$

where t_M and t_N are corresponding time values (M < N).

Similarly, the distance between node (t_M, y_M) and node (t_N+1, y_N+1), node (t_N, y_N), and node (t_N+1, y_N+1) is calculated by

$d_{M\to N+1}=|t_M-t_{N+1}|,(17)$

$d_{N\to N+1}=|t_N-t_{N+1}|.(18)$

Step 2: Determination of the weight coefficient

Furthermore, the closer the node (t_M, y_M) and node (t_N, y_N), the less importance the node (t_M, y_M). However, node (t_M, y_M) contains less historical information about past, which has the same effect as node (t_N, y_N) to predict future information. Conversely, if node (t_M, y_M) is far away from node (t_N, y_N), the importance of node (t_M, y_M) is higher because it carries more historical information for further predictions [37].

Then, the weight coefficients are defined by

$w_N=\frac{d_{M\to N}}{d_{M\to N+1}},(19)$

$w_{N+1}=1-w_N,(20)$

where w_N+1 denotes the weight coefficient of the predict value y_N+1 and w_N denotes the weight coefficient of the last observed value y_N. Figure 2 gives a more vivid interpretation.

Step 3: Final weighted prediction

Commonly, the larger the d_M→N, the larger d_M→N+1 and the smaller the w_N, demonstrating node (t_M, y_M) with more useful historical information. Therefore, the final predicted results are calculated by

${\widehat{y}}_{N+1}=w_{N+1}*y_{N+1}+w_N*y_N.(21)$

4.4 Data

The seven pilots’ carbon prices per day from January 2014 to June 2021 are collected from China’s Carbon Emission Trading Network (http://k.tanjiaoyi.com/) except the Fujian pilot. Because the Fujian pilot was constructed to operate in 2016, the pilot’s daily carbon prices are collected from January 2017 to June 2021. In addition, the transaction prices are used as the carbon prices except the Shenzhen pilot. Since six allowances (SZA-2013 to SZA-2019) traded in the Shenzhen market, it takes the average transaction prices as the carbon prices. Missing data are added by moving the average in the previous week. Therefore, these eight China pilots’ carbon prices are shown in Figure 3.

FIGURE 3

FIGURE 3. Carbon prices in China’s ETS pilots; the different colors represent different pilots.

5 Results and analysis

This section will analyze the data from January 2014 to June 2021 between China’s pilots. First, to realize the link prediction, this study transforms the time series into a visibility graph by the VG model and studies the network structures in the carbon price of eight pilots. In addition, we predict carbon prices by the proposed methods. To verify the predicted accuracy, the error indicators are used to analyze. Finally, we introduce hierarchical clustering to study the similarity between these eight pilots in China.

5.1 The network structure results

We construct eight networks by the data of Beijing, Fujian, Shanghai, Chongqing, Hubei, Shenzhen, Guangdong, and Tianjin pilots, respectively. After mapping the time series to eight networks by visibility graph, we calculate the characteristic statistics by Eqs 2-9, as shown in Table 1.

TABLE 1

TABLE 1. Characteristic statics of eight China’s ETS pilots.

Usually, the average degree reflects the importance of a node in networks. The average degree is the largest in Tianjin pilot, whereas Shanghai and Shenzhen pilots are small, reflecting that the carbon prices in Tianjin pilot are much affected by previous price fluctuations. The Shanghai pilot has the smallest diameter. The diameter of Chongqing and Shenzhen pilots is 13, indicating that the Shanghai pilot is easily influenced by the near prices. However, Chongqing and Shenzhen pilots are easily affected by earlier prices. Correspondingly, the changing trend of the average path length is as same as the diameter. In addition, the density is ranged from 0.004 to 0.017, which illustrates the tightness of the network. The average clustering coefficient indicates the aggregation of the network structure, ranging from 0.692 to 0.834. Moreover, the modularity of Beijing and Shenzhen pilots surpasses 0.8, reflecting that their community structures are apparent. The modularity in the Shanghai pilot is the lowest, indicating that the community structure is insignificant.

5.2 “Small world” and “scale-free” properties

As seen in Table 1, except Chongqing and Shenzhen pilots, these networks have a considerable average clustering coefficient and small average path length, showing “small world” characters. It reflects that the future carbon prices are easily affected by the historical prices, and are mainly influenced by the hubs in the networks.

Figure 4 and Table 2 show the power-law degree distribution of China’s ETS pilots, where γ is the exponent of the power-law degree distribution and R² is the fitting goodness. Clearly, the larger the fitting goodness, the more conforms to the “scale-free” properties. The “scale-free” network shows that only a few nodes have a large degree, whereas most nodes in the network have little linkage to other nodes, which reflects a severe heterogeneity in degree distribution. In this study, the properties indicate that future carbon prices will be affected easily by highly degree nodes, which have many linkages with other nodes in the network.

FIGURE 4

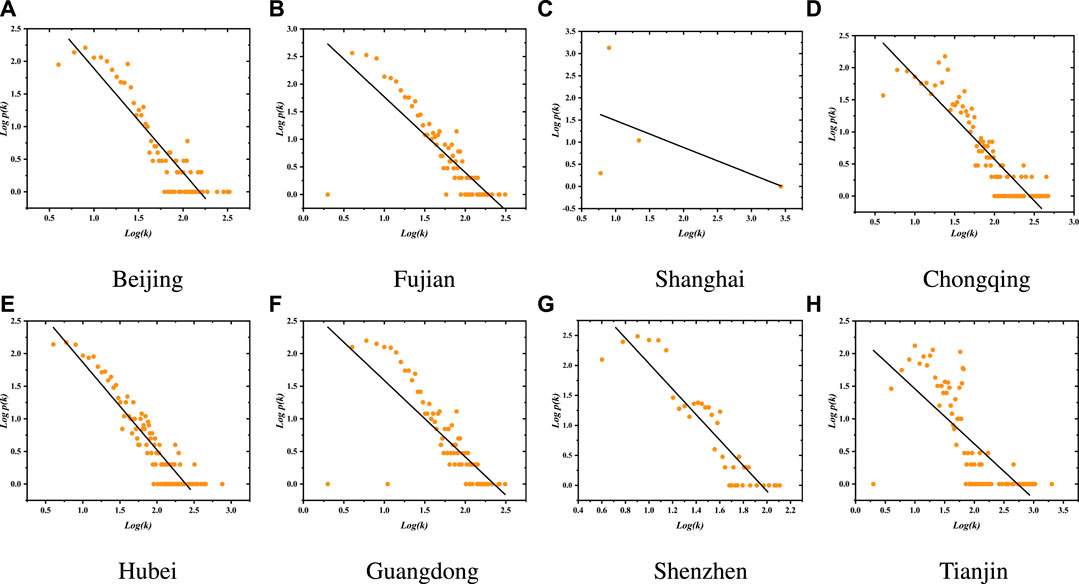
FIGURE 4. Degree distribution of the VGN of China’s ETS pilots. (A–H) The degree distribution of Beijing, Fujian, Shanghai, Chongqing, Hubei, Guangdong, Shenzhen, and Tianjin, respectively.

TABLE 2

TABLE 2. Exponent of power-law degree distribution and the fitting goodness.

Usually, the exponent γ is between 1 and 2. Beijing, Fujian, Chongqing, Hubei, Guangdong, and Shenzhen pilots are the “scale-free” network, except Shanghai and Tianjin pilots. To further mine their features, we analyze the topology network for Beijing and Shanghai pilots in Figure 5. However, the nodes’ degrees are described by different colors. The larger the degree, the large the node size is. Clearly, there are a few hubs and many low-degree nodes in the Beijing pilot, whereas there are many hubs and a few low-degree nodes in Shanghai. It proves that our experimental results are correct.

FIGURE 5

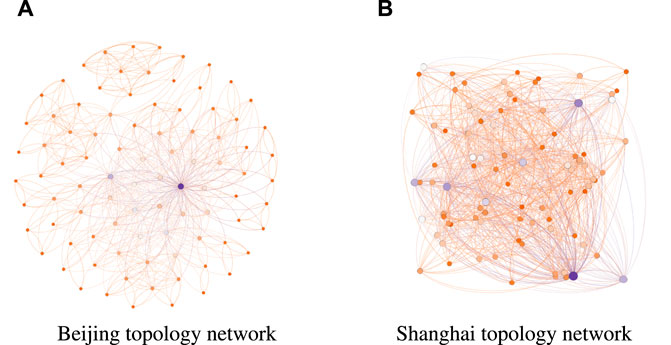
FIGURE 5. Different colors indicate nodes with different degree; the higher the degree, the larger the node size. (A) There are a few hubs and many low-degree nodes in Beijing. (B) There are a few low-degree nodes and many hubs in Shanghai.

The “scale-free” pilots show that the nodes with a high degree are easily affected by previous prices, and they also easily affect future carbon prices. Moreover, the carbon prices of pilots are not easily affected by events because there are a few hubs that would be influenced. Moreover, the fitting goodness of Fujian and Guangdong is about 60%, and others are all higher than 80%. Hubei shows the highest R², and the value is 0.866. However, in Shanghai and Tianjin pilots, γ is 0.606 and 0.844, respectively. In addition, Shanghai and Tianjin have a low R², meaning the fitting effect has a bad performance. As the financial technology center, the Shanghai topology network is different from others not with “scale-free” features. It communicates with many cities, and there are many carbon-reducing technologies here. Due to these characters, the carbon prices in Shanghai are easily affected by emergency events because there are many hubs that would be attacked.

5.3 Carbon price forecasting

In this section, we calculate the average carbon price in a month as the monthly price, and then the proposed method is adopted to forecast the monthly carbon prices in China’s pilots. Specifically, we divide China’s ETS pilots into a Universe dataset T from January 2014 to June 2021. First, the data from January 2014 to September 2015 are selected as a training set to predict October 2015. Then, the actual value of October 2015 will be added to the training set to forecast the next value. Above all, this process will be repeated until the value of June 2021 is predicted. Finally, we will obtain the predicted set from January 2016 to June 2021. Particularly, the Fujian pilot dataset is from January 2017 to June 2021. The training set is from January 2017 to September 2018, predicting the carbon prices from October 2018 to June 2021. The process of the method is shown in Algorithm 1.

Algorithm 1. Graph construction.

To verify the efficiency of the improved method, we compare two forecasting methods and the results in Figure 6. In this panel, (A–H) represents the predicted results in Beijing, Fujian, Shanghai, Chongqing, Hubei, Shenzhen, Guangdong, and Tianjin pilots, respectively.

FIGURE 6

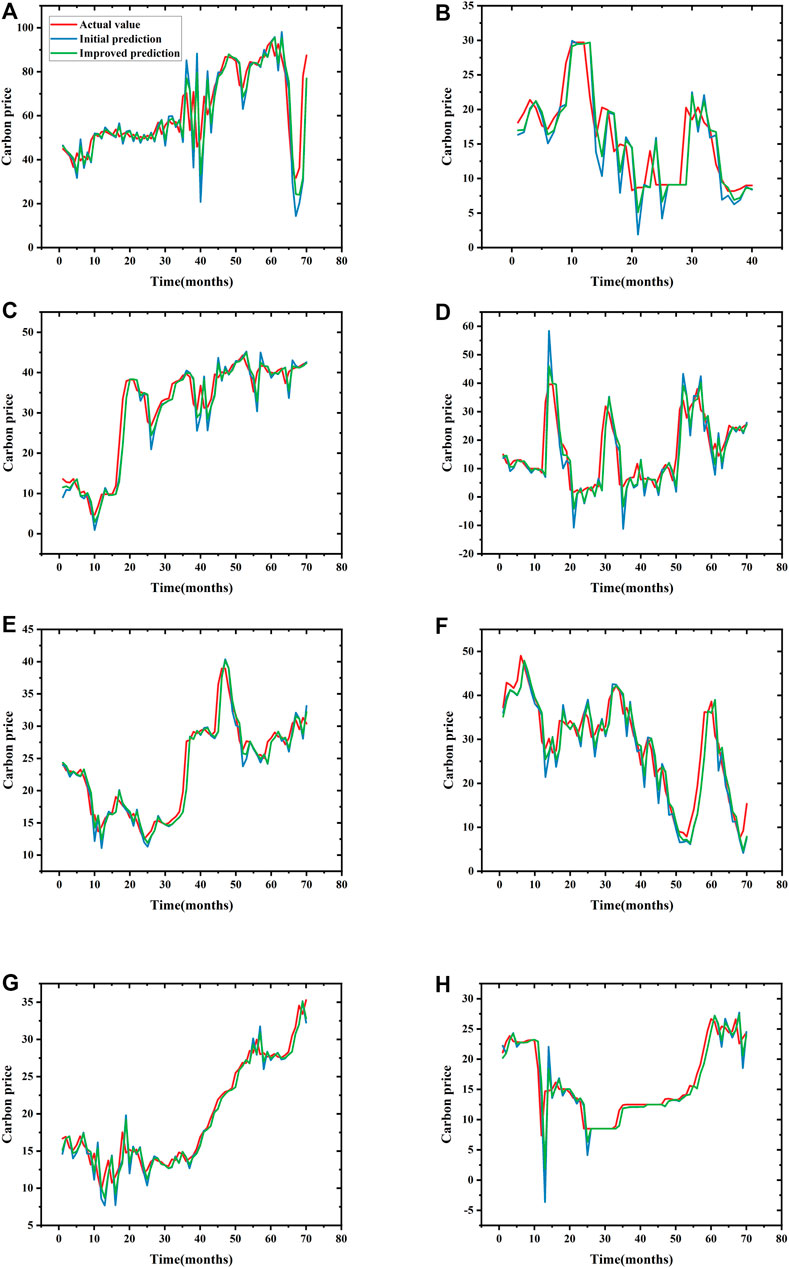
FIGURE 6. The forecasting results in panel. (A–H) The predicted results in Beijing, Fujian, Shanghai, Chongqing, Hubei, Shenzhen, Guangdong, and Tianjin pilots, respectively.

As can be seen, the blue line is the initial predicted values, the green line is the improved predictions, and the red line is the actual values. If the red line is close to the blue line or green line, indicating that the predicted accuracy of the proposed method is high. Conversely, the farther away the red line from the blue line, the worse the predicted accuracy. Moreover, if the green line is closer to the red line than the blue line, the improved method has a better predicted performance in a network.

To evaluate the predicted accuracy of the proposed method, this study adopts three error measures: mean absolute difference (MAD), root mean square error (RMSE), and mean absolute percentage error (MAPE). These error indicators are denoted by

$MAD=\frac{1}{N}\sum _{t=1}^N|{\widehat{y}}_t-y_t|,(22)$

$RMSE=\sqrt{\frac{1}{N}\sum _{t=1}^N{\left({\widehat{y}}_t-y_t\right)}^2},(23)$

$MAPE=\frac{1}{N}\sum _{t=1}^N\frac{|{\widehat{y}}_t-y_t|}{y_t},(24)$

where N is the number of predicted values, $\widehat{y}(t)$ represents the predicted value at t time, and y(t) is the actual value at t time.

The predicted accuracy is high if the results exhibit a low MAD, RMSE, or MAPE. Namely, the proposed method has a good prediction performance. To verify its forecasting performance further, we introduce the moving average (MA) method, a linear combination of residual terms to forecast. The order of MA is determined by ACF, which describes the correlation between the current and past values. Moreover, we compare three strategies of the initial predictions, the improved predictions, and the MA predictions in eight pilots, as shown in Table 3.

TABLE 3

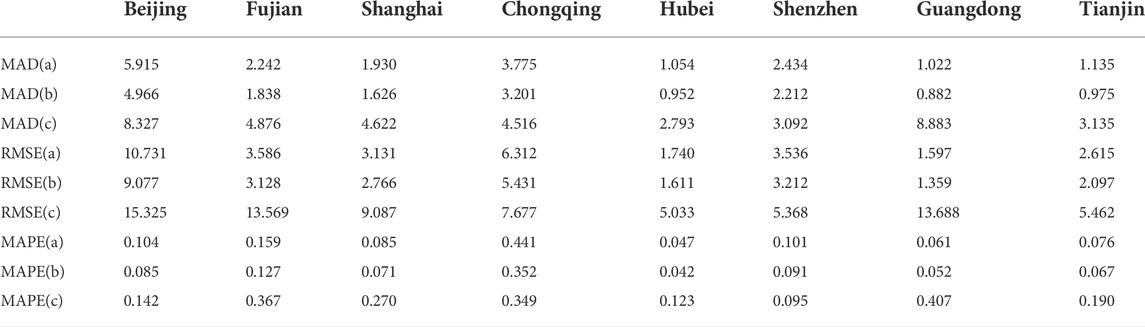
TABLE 3. Error measurements of carbon prices forecasting in eight pilots. (A–C) The initial forecasting method, improved forecasting method, and MA (2), respectively.

According to these data, the order of MA is 2. From Table 3, the performance of predicted values by MA(2) is worse than the method proposed by this study. The improved method has a better predicted capacity, showing that the node distance is also an important character in networks, so it is necessary to consider the weight coefficient. Moreover, the result explains that future prices will be affected by historical issues, not only recent events. The price fluctuations in the Hubei, Guangdong, and Tianjin pilots are flat, and the MAD(b) are all less than 1. These pilots start with a low price and actively encourage enterprises to reduce emissions. They are not easily affected by related events based on their “scale-free” features, so the carbon prices are stable to obtain a good forecasting performance.

Conversely, the forecasting performance in Beijing, Chongqing, and Shenzhen pilots is the worst, the RMSE(b) exceeds 3 because their prices fluctuate greatly. Beijing as the highest pilot with the worst MAD(b) and RMSE(b), 4.966 and 9.077, respectively. It cooperates with many enterprises with rich trading products, so there are a lot of uncertain factors to affect forecasting validity. Similarly, the Shenzhen pilot is the first carbon trading market, covering 40% of carbon emissions. In addition, it is one of the pilot areas with the largest number of enterprises and the most active transactions, so its prices are easily affected by other factors, such as coal, climate, and economic events. Moreover, Shenzhen and Chongqing pilots are not the “small world” networks with poor communication, inducing a bad predicted performance.

Besides, we have to consider the impact of the COVID-19 epidemic on carbon market trading, and the emergency has affected the predicted accuracy. Due to the abruptness of the COVID-19 outbreak, we cannot precisely estimate the trend of carbon prices. Thus, we cannot obtain a good forecasting performance.

5.4 Cluster results

Hierarchical clustering is a method to analyze the nodes’ similarity, measured by node distances. The steps are as follows:

Step 1: Each node is considered a cluster

Step 2: The distances between each cluster is calculated, and the two closet clusters are merged into a group

Step 3: The previous operations are repeated until all clusters are merged into a cluster

Step 4: The final cluster results are obtained

We divide eight pilots into three communities, which are seen as each sub-market, as shown in Figure 7. The higher the similarity between these pilots divided into a cluster, so they in the same sub-market are similar in price dynamics, and we use different colors to denote different groups. Beijing and Guangdong pilots are a community with the most similarity to China’s pilots because they encourage companies to save energy with a good performance to reduce emissions. Likewise, Shanghai and Shenzhen pilots belong to a cluster with a high GDP, illustrating that their operational mechanisms are similar. They cover the more comprehensive industries, and their penalties are also strict. Then, the rest of these pilots belong to a sub-market. They operate from a low price and trade in a single product with an inactive performance.

FIGURE 7

FIGURE 7. lustering results of China’s ETS pilots by hierarchical clustering; they are divided into three communities.

6 Conclusion

Carbon emission reduction has promoted the global carbon market development. To further control CO₂ emission effectively, this study analyzes the eight pilots in China based on network science. According to the network structures of eight pilots, we conclude that most pilots show the “scale-free” and “small world” features. Meanwhile, we predict the carbon prices by introducing the weight coefficient that measures the node distance, acquiring a better performance than before. We combine network science and link prediction, providing an effective method to forecast carbon prices. Finally, to study the similarity between these pilots, this study divides eight pilots into different communities by hierarchical clustering.

In this study, our analysis supplies experiences and policies among these pilots, providing crucial theoretical guidance for market participants to participate actively. The carbon pricing tool is a mechanism to stimulate markets to reduce emissions. Thus, it is important to predict carbon prices, which can stimulate innovation and improve productivity. However, the sudden outbreak of COVID-19 affects carbon market trading, so it is necessary to forecast carbon prices to change policies for decision makers. But, the uncontrollability and instability result in worse forecasting performance.

The subsequent research work would like to progress in the following areas: (1) This study predicts monthly carbon prices based on eight pilots. However, we will next consider forecasting the daily data in a pilot, maintaining more topology features to obtain a better predicted performance. (2) EEMD will be introduced to decompose the time series to mine the data features. After getting different IMFs and a residue, we predict them by different methods and integrate the results to obtain a final result. (3) To improve the accuracy, we can transform unweighted networks into weighted networks by different similarity indices in link prediction, even considering the reliability of the communication route.

To further respond effectively to global warming, China’s carbon market can be considered from the following aspects: First, the cooperation with the global carbon market should be deepened and we should start exploring the internationalization path, accelerating the internationalization of China’s pilots. At the same time, as the largest carbon market, China’s carbon market is expected to play a scale advantage in construction. Second, we should strengthen the construction of the basic legal system and improve the system specification. Third, we should take the carbon market as the leading market mechanism for coordinating energy conservation, emission reduction, and promote positive synergy.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author contributions

YH: visualization, drawing, writing, and software. CC: investigation and validation. PW: conceptualization and methodology. JH: writing—reviewing and editing and software.

Funding

This study was supported in part by the National Natural Science Foundation of China under Grant 71871159, in part by the Humanities and Social Science Foundation of the Chinese Ministry of Education under Grant 21YJA630096, in part by the second Fujian Young Eagle Program Youth Top Talent Program, in part by the Natural Science Foundation of Fujian Province, China, under Grant 2022J01075, and in part by the Fujian science and technology economic integration service platform.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2022.1029600/full#supplementary-material

References

1. Alberola E, Chevallier J, Chèze 1 B. The eu emissions trading scheme: The effects of industrial production and co2 emissions on carbon prices. Economie internationale (2008) n° 116:93–125. doi:10.3917/ecoi.116.0093

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Fan X, Li S, Tian L. Chaotic characteristic identification for carbon price and an multi-layer perceptron network prediction model. Expert Syst Appl (2015) 42:3945–52. doi:10.1016/j.eswa.2014.12.047

CrossRef Full Text | Google Scholar

3. Chen J, Li C, Ristovski Z, Milic A, Gu Y, Islam MS, et al. A review of biomass burning: Emissions and impacts on air quality, health and climate in China. Sci Total Environ (2017) 579:1000–34. doi:10.1016/j.scitotenv.2016.11.025

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Hu J, Chen J, Zhu P, Hao S, Wang M, Li H, et al. Difference and cluster analysis on the carbon dioxide emissions in China during Covid-19 lockdown via a complex network model. Front Psychol (2022) 12:795142. doi:10.3389/fpsyg.2021.795142

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Rong T, Zhang P, Zhu H, Jiang L, Li Y, Liu Z. Spatial correlation evolution and prediction scenario of land use carbon emissions in China. Ecol Inform (2022) 71:101802. doi:10.1016/j.ecoinf.2022.101802

CrossRef Full Text | Google Scholar

6. Adedoyin FF, Gumede MI, Bekun FV, Etokakpan MU, Balsalobre-Lorente D. Modelling coal rent, economic growth and co2 emissions: Does regulatory quality matter in brics economies? Sci Total Environ (2020) 710:136284. doi:10.1016/j.scitotenv.2019.136284

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Liu L, Chen C, Zhao Y, Zhao E China’s carbon-emissions trading: Overview, challenges and future. Renew Sustain Energ Rev (2015) 49:254–66. doi:10.1016/j.rser.2015.04.076

CrossRef Full Text | Google Scholar

8. Mao S, Hu Y, Yuan X, Zhang M, Qiu Q, Wu P Analysis of patent application attention: A network analysis method. Front Phys (2022):342.

CrossRef Full Text | Google Scholar

9. Hu J, Chu C, Xu L, Wu P, Lia H-J. Critical terrorist organizations and terrorist organization alliance networks based on key nodes founding. Front Phys (2021) 9:687883.

CrossRef Full Text | Google Scholar

10. Wang Y, Meng K, Wu H, Hu J, Wu P. Critical airports of the world air sector network based on the centrality and entropy theory. Int J Mod Phys B (2021) 35:2150081.

CrossRef Full Text | Google Scholar

11. Liu W, Lü L. Link prediction based on local random walk. Europhys Lett (2010) 89:58007. doi:10.1209/0295-5075/89/58007

CrossRef Full Text | Google Scholar

12. Ji C-J, Hu Y-J, Tang B-J. Research on carbon market price mechanism and influencing factors: A literature review. Nat Hazards (Dordr) (2018) 92:761–82. doi:10.1007/s11069-018-3223-1

CrossRef Full Text | Google Scholar

13. Mansanet-Bataller M, Pardo A, Valor E. Co2 prices, energy and weather. Energ J (2007) 28. doi:10.5547/issn0195-6574-ej-vol28-no3-5

CrossRef Full Text | Google Scholar

14. Hammoudeh S, Nguyen DK, Sousa RM. Energy prices and co2 emission allowance prices: A quantile regression approach. Energy policy (2014) 70:201–6. doi:10.1016/j.enpol.2014.03.026

CrossRef Full Text | Google Scholar

15. Alberola E, Chevallier J, Chèze B. Price drivers and structural breaks in European carbon prices 2005–2007. Energy policy (2008) 36:787–97. doi:10.1016/j.enpol.2007.10.029

CrossRef Full Text | Google Scholar

16. Christiansen AC, Arvanitakis A, Tangen K, Hasselknippe H. Price determinants in the eu emissions trading scheme. Clim Pol (2005) 5:15–30. doi:10.1080/14693062.2005.9685538

CrossRef Full Text | Google Scholar

17. Chèze B, Chevallier J, Alberola E. Climate change and energy policy. J Policy Modeling (2009) 31 (3):446–462. doi:10.1016/j.jpolmod.2008.12.004

CrossRef Full Text | Google Scholar

18. Byun SJ, Cho H. Forecasting carbon futures volatility using garch models with energy volatilities. Energ Econ (2013) 40:207–21. doi:10.1016/j.eneco.2013.06.017

CrossRef Full Text | Google Scholar

19. Zhu B, Chevallier J. Carbon price forecasting with a hybrid arima and least squares support vector machines methodology. In: Pricing and forecasting carbon markets. Berlin/Heidelberg, Germany; Springer (2017). p. 87–107.

CrossRef Full Text | Google Scholar

20. Yan M, Wang C. Prediction of carbon trading price based on multi-scale integrated model—Take guangzhou carbon emission trading centre as an example. J Tech Econ Manag (2020) 5:19–24.

Google Scholar

21. Zhao X, Zou Y, Yin J, Fan X. Cointegration relationship between carbon price and its factors: Evidence from structural breaks analysis. Energ Proced (2017) 142:2503–10. doi:10.1016/j.egypro.2017.12.190

CrossRef Full Text | Google Scholar

22. Ji C-J, Hu Y-J, Tang B-J, Qu S. Price drivers in the carbon emissions trading scheme: Evidence from Chinese emissions trading scheme pilots. J Clean Prod (2021) 278:123469. doi:10.1016/j.jclepro.2020.123469

CrossRef Full Text | Google Scholar

23. Wen F, Zhao H, Zhao L, Yin H. What drive carbon price dynamics in China? Int Rev Financial Anal (2022) 79:101999. doi:10.1016/j.irfa.2021.101999

CrossRef Full Text | Google Scholar

24. Li W, Lu C. The research on setting a unified interval of carbon price benchmark in the national carbon trading market of China. Appl Energ (2015) 155:728–39. doi:10.1016/j.apenergy.2015.06.018

CrossRef Full Text | Google Scholar

25. Liu J, Wang P, Chen H, Zhu J. A combination forecasting model based on hybrid interval multi-scale decomposition: Application to interval-valued carbon price forecasting. Expert Syst Appl (2022) 191:116267. doi:10.1016/j.eswa.2021.116267

CrossRef Full Text | Google Scholar

26. Fan X, Li X, Yin J, Tian L, Liang J. Similarity and heterogeneity of price dynamics across China’s regional carbon markets: A visibility graph network approach. Appl Energ (2019) 235:739–46. doi:10.1016/j.apenergy.2018.11.007

CrossRef Full Text | Google Scholar

27. Lacasa L, Luque B, Ballesteros F, Luque J, Nuno JC. From time series to complex networks: The visibility graph. Proc Natl Acad Sci U S A (2008) 105:4972–5. doi:10.1073/pnas.0709247105

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Hu J, Zhang Y, Wu P, Li H. An analysis of the global fuel-trading market based on the visibility graph approach. Chaos, Solitons & Fractals (2022) 154:111613. doi:10.1016/j.chaos.2021.111613

CrossRef Full Text | Google Scholar

29. Feng Q, Wei H, Hu J, Xu W, Li F, Lv P, et al. Analysis of the attention to covid-19 epidemic based on visibility graph network. Mod Phys Lett B (2021) 35:2150081.

CrossRef Full Text | Google Scholar

30. Cui X, Hu J, Ma Y, Wu P, Zhu P, Li H-J. Investigation of stock price network based on time series analysis and complex network. Int J Mod Phys B (2021) 35:2150171.

CrossRef Full Text | Google Scholar

31. Jiao J, Wang J, Jin F, Wang H. Impact of high-speed rail on inter-city network based on the passenger train network in China, 2003–2013. Acta Geogr Sin (2016) 71:265–80.

Google Scholar

32. Newman ME. Modularity and community structure in networks. Proc Natl Acad Sci U S A (2006) 103:8577–82. doi:10.1073/pnas.0601602103

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Hu J, Xia C, Li H, Zhu P, Xiong W. Properties and structural analyses of USA’s regional electricity market: A visibility graph network approach. Appl Maths Comput (2020) 385:125434. doi:10.1016/j.amc.2020.125434

CrossRef Full Text | Google Scholar

34. Cui M, Hu J, Wu P, Hu Y, Zhang X. Evolutionary analysis of international student mobility based on complex networks and semi-supervised learning. Front Phys (2022):538.

CrossRef Full Text | Google Scholar

35. Fei L, Wang H, Chen L, Deng Y. A new vector valued similarity measure for intuitionistic fuzzy sets based on owa operators. Iranian J Fuzzy Syst (2019) 16:113–26.

Google Scholar

36. Zhang R, Ashuri B, Shyr Y, Deng Y. Forecasting construction cost index based on visibility graph: A network approach. Physica A: Stat Mech Its Appl (2018) 493:239–52. doi:10.1016/j.physa.2017.10.052

CrossRef Full Text | Google Scholar

37. Xu H, Wang M. A novel carbon price fluctuation trend prediction method based on complex network and classification algorithm. Complexity (2021) 2021:1–19. doi:10.1155/2021/3052041

CrossRef Full Text | Google Scholar