Semi-quantum key distribution with two classical users

Semi-quantum key distribution (SQKD) is an important research issue which allows one quantum participant equipped with advanced quantum devices to distribute a shared secret key securely with one classical user who has restricted capabilities. In this paper, we propose a SQKD protocol which allows one quantum user to distribute two different private secret keys to two classical users respectively at the same time. Alice distributes two particle sequences from Bell states to Bob and Charlie respectively. Once the particles have been processed and returned, Alice can simultaneously detect reflected particles by Bob and Charlie based on Bell-state measurement and generate two different raw keys. To enable more participants in sharing keys, this protocol can be extended to the m + 1 party communication scheme by employing m-particle GHZ state. In large-scale communication networks, this extended model significantly reduces the complexity of communication compared to the traditional SQKD scheme. Security analyses show that the presented protocol is free from several general attacks, such as the entangle-measure attack, the modification attack, the double CNOT attack, and so on.

1 Introduction

It is known that the first quantum key distribution (QKD) protocol [1] was put forward by Bennett and Brassard in 1984, which allow two quantum participants to distribute a session key with unconditional security [2, 3]. Since then, many kinds of QKD protocols have been proposed [4–14]. However, these QKD protocols assumed that the participants possess unlimited quantum capabilities. Nowadays, most advanced quantum devices (e.g., quantum state generators and quantum storage) remain expensive and difficult to implement.

To improve the practicality of these protocols, Boyer et al. proposed a novel idea of quantum key distribution [15], where one of the player Alice has full quantum capabilities, while the other player Bob is classical. The “classical” Bob either measures the qubits Alice sent in classical basis (Z-basis) and resends it in the same state he found, or reflects the qubits without any change. They called the protocol as “quantum key distribution with classical Bob” or “semi-quantum key distribution(SQKD).” The idea was further extended in Ref . [16], where two similar protocols were presented based on measurement-resend and randomization-based environment. The “classical” users are restricted to perform the following operations: 1) generate Z-basis qubits, {|0⟩, |1⟩}, 2) measure the quantum state in the Z-basis, 3) reflect the qubits without disturbance, and 4) reorder the qubits via different delay lines. Due to the different operation types of classical users, two variants of SQKD environment was proposed. In the randomization-based SQKD protocol, the classical users can only to implement operations 2), 3) and 4), whereas in the measure-resend SQKD protocol, the classical participants are limited to perform 1), 2) and 3). In this regard, the idea of semi-quantum relieves users of the burden of quantum state generation and measurement, making it more convenient to participate in quantum key distribution.

Based on Boyer et al.’s study, various semi-quantum protocols have been proposed. Lu and Cai presented a SQKD protocol with classical Alice [17]. In 2009, Zou et al. [18] presented five SQKD protocols by employing less than four quantum states with complete robustness. Later, Wang et al. [19] proposed a SQKD protocol using entangle states. In 2014 and 2016, Yu et al. [20] and Li et al. [21] respectively proposed two authenticated semi-quantum key distribution (ASQKD) protocols. The ASQKD exploit the mechanism of a pre-shared key to transmit secret key without classical channels. In 2015, the mediated semi-quantum key distribution (MSQKD) protocol was first proposed by Krawec [22], which allows two classical participants to generate a secret key with the help of a quantum server. In 2018, Liu et al. [23] also proposed a MSQKD protocol without invoking quantum measurement for the classical users. Since then, Lin et al. [24] proposed a MSQKD protocol using single photons. Zhu et al. [25] devised two SQKD protocols with GHZ states involving a quantum server. One of these two protocols is to distribute keys between quantum users and classical users, and the other is to communicate between two classical users with the assistance of the quantum third party. Soon after, Chen et al. [26] also proposed two analogous SQKD protocols based on GHZ-like states. In 2020 and 2022, Ye et al. [27, 28] presented two SQKD protocols based on single photons in both polarization and spatial-mode degrees of freedom. Besides, security proofs, attack strategies, and improvement methods of SQKD protocols have been developed from information theory aspect in Refs [29–36].

However, under the above-mentioned protocols, the quantum user Alice can only share a private key with one classical user at a time or two classical parties distribute a session key with the help of a fully quantum server. Suppose a quantum server receives multiple distribution requests at the same time, the presented protocol is used to deal with this situation. In this paper, we are going to devise a semi-quantum key distribution protocol with two classical users. The presented protocol allows one quantum server to distribute two raw keys to these two classical users simultaneously. The proposed scheme greatly enhances the key distribution capability of the quantum server. Moreover, the proposed scheme can be expanded to m + 1 party SQKD.

The rest of this paper is organized as follows: Section 2 presents a SQKD protocol. The detailed security analyses are described in Section 3. Section 4 generalizes the proposed SQKD protocol to m + 1 party. An efficiency analysis and the comparison of our protocol to other SQKD protocols are provided in Section 5. This work is concluded in Section 6.

2 The designed semi-quantum key distribution protocol

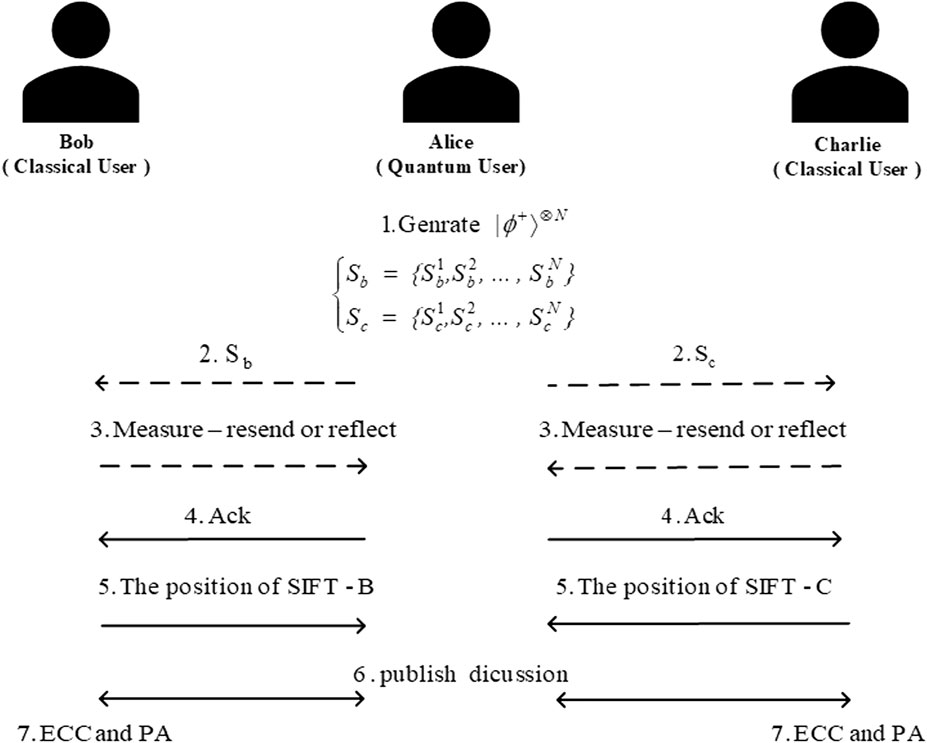
Suppose that quantum user Alice wants to distribute two different secret keys to classical user Bob and classical user Charlie separately at the same time. The following semi-quantum key distribution (SQKD) protocol is designed to make it possible. Here, the SIFT operation refers to measuring the received qubits in the Z-basis, {|0⟩, |1⟩}, and resending it in the same state as found; the CTRL operation refers to reflecting the received qubits back without any disturbance. The steps of the presented SQKD protocol are described as follows (as shown in Figure 1):

Step 1: Alice generates N = 8n(1 + δ) Bell states in $|{\varphi }^{+}\rangle =\frac{1}{\sqrt{2}}(|00\rangle +|11\rangle )$, where n is the desired length of INFO bits and δ is a fixed positive parameter. Then Alice respectively picks out the first particle, the second particle from every Bell state to construct two sequences

$\begin{array}{ll}\hfill S_b& =\left\{S_b^1,S_b^2,\dots ,S_b^N\right\},\hfill \\ \hfill S_c& =\left\{S_c^1,S_c^2,\dots ,S_c^N\right\}.\hfill \end{array}$

Step 2: Alice sends S_b to Bob and sends S_c to Charlie.

Step 3: For each coming qubits, Bob (Charlie) randomly chooses to SIFT or CTRL. For convenience, we denote the qubits reflected by Bob (Charlie) with CTRL-B (CTRL-C) qubits and the qubits resended by Bob (Charlie) with SIFT-B (SIFT-C) qubits.

Step 4: Alice stores the received qubits in two N-qubit quantum registers and informs Bob and Charlie.

Step 5: Bob and Charlie publish which particles they choose to SIFT.

Step 6: According to the published information by Bob and Charlie and Table 1, they check out the security of the quantum channel and produce INFO bits.

FIGURE 1

FIGURE 1. The proposed SQKD protocol.

TABLE 1

TABLE 1. Alice’s operation.

Case 1. Both Bob and Charlie perform the CTRL on some particles with the same superscript i, (i = 1, …, N). Alice performs the Bell-state measurement on the received quantum qubits. Alice checks the error rate on the Bell measurement results. If it is higher than predefined threshold P_CTRL (the threshold depends on the noise level of the quantum channel), they abort the protocol.

Case 2. Bob performs the SIFT on some particles $S_b^i$ and Charlie applies the operation CTRL on some particles $S_c^i$ with the same i in Step 3. Alice measures $S_b^i$ and $S_c^i$ with Z-basis respectively and examines whether the two corresponding measurement results are equal. If the error rate is less than P_TEST (the threshold depends on the noise level of the quantum channel), the protocol continues. Otherwise it is terminated. In this case, Alice will obtain 2n SIFT-B bits. Alice chooses at random n SIFT-B bits to be TEST-B bits and announces what are the chosen bits and the value of these TEST-B bits by the classical channel. Alice’s measurement results must be the states sent by Bob. Bob checks the error rate on the TEST bits. If it is higher than some predefined threshold P_TEST, Alice and Bob abort the protocol.

Case 3. Bob performs the operation CTRL on some particles $S_b^i$ and Charlie applies the operation SIFT on some particles $S_c^i$ with the same i in Step 3. Alice measures $S_b^i$ and $S_c^i$ with Z-basis respectively and examines whether the two corresponding measurement results are equal. If the error rate is less than P_TEST, the protocol continues. Otherwise it is terminated. In this case, Alice will capture 2n SIFT-C bits. Alice selects random n SIFT-C bits as the TEST-C bits and announces the positions of the TEST-C bits and the value of these bits to Charlie. Charlie compares his measurement results with TEST-C bits, if it is higher than some predefined threshold P_TEST, Alice and Charlie abort the protocol.

Case 4. Both Bob and Charlie perform the operation SIFT on some particles with the same superscript i, (i = 1, …, N). Alice measures $S_b^i$ and $S_c^i$ with Z-basis respectively and examines whether the two corresponding measurement results are equal. Alice aborts the protocol as the error rate is higher than the predefined threshold P_TEST. Alice requests measurement results from Bob and Charlie, and checks the error rate among these bits, if it is higher than the predefined threshold P_TEST, they abort the protocol.

Step 7: Alice and Bob select the n remaining SIFT-B bits in Case 2 to be used as INFO bits. Likewise, Alice and Charlie select the n remaining SIFT-C bits in Case 3 to be used as INFO bits. They abort the protocol as the number of remaining SIFT-B (SIFT-C) bits is less than n. Alice announces publicly the error correction code (ECC) and privacy amplification data [37–40]; Alice and Bob (Alice and Charlie) use them to extract the final key from the n-bit INFO string.

3 Security analysis

Basically, all existing SQKD protocols that adopt two-way quantum communication are suffer from the Trojan-horse attacks [41, 42]. To resist this kind of attacks, the photon number splitter device and the optical wavelength filter device could be equipped [43, 44]. Besides, identification should be employed to resist man-in-the-middle attack [45–47].

In this section, the security of the proposed protocol will be analyzed. Here, Eve is an outside attack and will try to perform the following possible attacks to reveal the secret key of the participants (as shown in Figure 2). Hence, the following five well-known attacks will be discussed.

FIGURE 2

FIGURE 2. Eve’s attack.

3.1 Entangle-measure attack

Assume Eve possesses full quantum computational power and takes control of the quantum channel, Eve will prepare an ancillary quantum state |E⟩ and performs an unitary operations, U_E, on the composite system |ρ⟩ ⊗|E⟩, where |ρ⟩ represents the transmitting qubit between participants. The effect of Eve’s unitary operation U_E on the |0⟩ or the |1⟩ can be expressed as

$U_E|0\rangle |E\rangle =a|0\rangle |e_0\rangle +b|1\rangle |e_1\rangle (1)$

$U_E|1\rangle |E\rangle =c|0\rangle |e_2\rangle +d|1\rangle |e_3\rangle (2)$

where |a|² + |b|² = 1, |c|² + |d|² = 1, ⟨e_i|e_i⟩ = 1 (i = 0, 1, 2, 3) and ⟨e₀|e₁⟩ = ⟨e₂|e₃⟩ = 0. When Eve captures the transit qubit on its return, Eve will implement another operation U_F. The following states are produced by implementing operation U_F on the states in Eqs 1, 2.

$U_F{U}_E|0\rangle |E\rangle =|0\rangle \left(a_1|f_0\rangle +b_1|f_1\rangle \right)+|1\rangle \left(c_1|f_2\rangle +d_1|f_3\rangle \right)(3)$

$U_F{U}_E|1\rangle |E\rangle =|0\rangle \left(a_2|f_4\rangle +b_2|f_5\rangle \right)+|1\rangle \left(c_2|f_6\rangle +d_2|f_7\rangle \right)(4)$

where |a_i|² + |b_i|² + |c_i|² + |d_i|² = 1 (i = 1, 2), and ⟨f_i|f_i⟩ = 1 (i = 0, 1, …, 7). At some point, Eve will measure the ancillary states to infer the private information based on the measurement of |E⟩. We will now prove security against entangle-measure attack, that is, there is no unitary operations that allows Eve to obtain information about the participant’s secret key without being detected.

When Alice prepares the Bell state and sends it through the quantum channel, Eve intercepts the particles sent by Alice and implements an unitary operation U_E on transmitted quantum state. The original Bell state will be transformed as

$\begin{array}{c}\hfill U_E|{\varphi }^{+}\rangle |E\rangle =\frac{1}{\sqrt{2}}\left(a|00\rangle |e_0\rangle +b|01\rangle |e_1\rangle +c|10\rangle |e_2\rangle +d|11\rangle |e_3\rangle \right)\end{array}(5)$

Then Eve distributes the contaminated quantum states to Bob and Charlie. If both Bob and Charlie perform SIFT, the participants will take the public discussion to check their measurement result in Step 6. Specifically, they will calculate the error rate on the TEST bits. If the error rate is lower than predefined threshold P_TEST, the process continues. Thus, in order to pass the detection on TEST qubits, Eve must modify the U_E to satisfy the following conditions

$b|e_1\rangle =c|e_2\rangle =\stackrel{\rightharpoonup }{0}(6)$

Therefore, Eq. 5 becomes

$\begin{array}{c}\hfill U_E|{\varphi }^{+}\rangle |E\rangle =\frac{1}{\sqrt{2}}\left(a|00\rangle |e_0\rangle +d|11\rangle |e_3\rangle \right)\end{array}(7)$

When Eve intercepts the returned qubits sent by Bob and Charlie, Eve will perform the second unitary operation U_F on the transmitted quantum state. The Eq. 7 will be disturbed as follows

$\begin{array}{cc}\hfill U_F{U}_E|{\varphi }^{+}\rangle |E\rangle & =\frac{1}{\sqrt{2}}\left[|00\rangle \left(a_1|f_0\rangle +b_1|f_1\rangle \right)\right.+|01\rangle \left(c_1|f_2\rangle +d_1|f_3\rangle \right)\hfill \\ \hfill & +|10\rangle \left(a_2|f_4\rangle +b_2|f_5\rangle \right)+\left.|11\rangle \left(c_2|f_6\rangle +d_2|f_7\rangle \right)\right]\hfill \end{array}(8)$

Then Eve sends the polluted quantum states to Alice. Eve can infer the participants’ measurement results through measuring his ancillary qubit. However, Alice will perform the Bell-state measurement on CTRL qubits in Step 6, and detect the presence of Eve if the error rate of CTRL qubits is higher than predefined threshold P_CTRL. Thus, Eve must set $a_2|f_4\rangle +b_2|f_5\rangle =c_1|f_2\rangle +d_1|f_3\rangle =\stackrel{}{0}$, and a₁|f₀⟩ + b₁|f₁⟩ = c₂|f₆⟩ + d₂|f₇⟩. According to the abovementioned setting, the transmission of quantum states is turned into

$\begin{array}{cc}\hfill U_F{U}_E|{\varphi }^{+}\rangle |E\rangle & =\frac{1}{\sqrt{2}}\left[|00\rangle \left(a_1|f_0\rangle +b_1|f_1\rangle \right)+|11\rangle \left(c_2|f_6\rangle +d_2|f_7\rangle \right)\right]\hfill \\ \hfill & =|{\varphi }^{+}\rangle \left(a_1|f_0\rangle +b_1|f_1\rangle \right)\hfill \end{array}(9)$

Based on the analysis of the above, the final quantum state of Eve’s probe |E⟩ is independent of the transmission of quantum entangled system, Eve can not obtain any information regarding INFO bits. In contrast, if Eve wishes to obtain useful information regarding the classical participants’s INFO bits, so the Eve’s attack will induce a detectable disturbance that increases the error rate P_TEST and P_CTRL. This gives participants a nonzero probability of detecting the Eve’s attack.

3.2 Modification attack

In the modification attack, the purpose of Eve is to enable the communicating parties to obtain inconsistent keys by using the unitary operation. For example, Eve can implement the unitary operation σ_x to flip the qubit, where

${\sigma }_x=|0\rangle \langle 1|+|1\rangle \langle 0|.(10)$

To completely analyze modification attack, we discuss the following three situations: 1) Eve would perform the unitary operation σ_x on the quantum channel between Alice and Bob, Alice and Charlie, simultaneously; 2) Eve would randomly perform the unitary operation σ_x on the channel only between Alice and Bob; 3) Eve would randomly perform the unitary operation σ_x on the channel only between Alice and Charlie. All the situations of Modification Attack are shown below.

• Eve intends to flip $S_b^i$ and $S_c^i$ simultaneously, the |ϕ⁺⟩ will be disturbed as follows

${\sigma }_x\otimes |{\varphi }^{+}\rangle =\frac{1}{\sqrt{2}}\left(|11\rangle +|00\rangle \right)(11)$

The above quantum state is the same as the primitive Bell state, so it has no effect on the conduct of the protocol.

• Eve merely flips $S_b^i$, the Bell state will be changed to

$\begin{array}{c}\hfill {\sigma }_x\otimes |{\varphi }^{+}\rangle =\frac{1}{\sqrt{2}}\left(|10\rangle +|01\rangle \right)\end{array}(12)$

Although Eve successfully changed the state, his sneaky action will be detected in Step 6. In case both Bob and Charlie select to CTRL, Alice will check the error rate on the CTRL qubits, if the error rate is higher than predefined threshold P_CTRL, Alice aborts the protocol. Besides, both Bob and Charlie select to SIFT, they will calculate the error rate on the TEST bits. Likewise, the presence of Eve can be detected. There is the probability of P₁ = 1 − 0.5ⁿ to detect Eve’s attack. It implies that if n is large enough, the detection probability will approach 1.

• Eve only flips $S_c^i$, the original Bell state will be transformed as

$\begin{array}{c}\hfill {\sigma }_x\otimes |{\varphi }^{+}\rangle =\frac{1}{\sqrt{2}}\left(|01\rangle +|10\rangle \right)\end{array}(13)$

Similar to the previous case, Eve’s operation will be detected in Step 6. Alice will find errors with a P₂ = 1 − 0.5ⁿ probability. When n is large enough, the probability of an eavesdropper being detected will approach 1.

In summary, the proposed scheme can successfully resist modification attack through detecting SIFT and CTRL qubits.

3.3 Intercept-resend attack

Eve attempts to implement an intercept-resend attack on the traveling particles in S_b, to obtain what Bob’s operation is. Firstly, Eve intercepts and saves the particle sequence S_b. Secondly, Eve sends the fake single photons randomly chosen from two different states (i.e., | + ⟩, | − ⟩). Finally, Eve tries to infer Bob’s operations through intercepting and measuring the returned particles by Bob in X-basis. That is, if the measurement result is different from the original state, the Bob’s operation is SIFT. Unfortunately, if the measurement result is the same as the initial state, Eve dan not distinguish Bob’s operation between SIFT and CTRL. Analogously, it is also useless for attacking S_c.

3.4 Measure-resend attack

In order to obtain SIFT-B bits and SIFT-C bits, Eve may intercept each traveling qubit of S_b and S_c and measure it with Z-basis. After Eve has performed the measurement operation on S_b and S_c, the initial Bell state generated by Alice is turned into |00⟩, |11⟩ with the same probability. Without loss of generality, assume that the original Bell state is collapsed into |00⟩. Once Eve measures the qubits which Bob or Charlie measures, he will acquire SIFT-B bits and SIFT-C bits. However, Eve measures the qubits which both Bob and Charlie reflect, this attack will destroy the entanglement of Bell state. Thus, Eve must measure the corresponding position in which measured by Bob or Charlie. However, Eve does not have any information about their operation. In Step 6, Alice implements the Bell measurement on qubits consist of CTRL-B qubits and CTRL-C qubits in Case 1. The measurement results may be |ϕ⁺⟩ or |ϕ⁻⟩ with the same probability. The probability that Bob and Charlie both reflect is $\frac{1}{4}$, hence, the probability of discover Eve’s fraudulent behavior is $\frac{1}{4}\ast \frac{1}{2}=\frac{1}{8}$. The reason Eve’s measure-resend attack can be detected lies in two aspects: on one hand, the entanglement correlation among different particles of the initial state is destroyed by Eve’s measurement; on the other hand, Bob and Charlie’s operations are random to Eve.

3.5 Double CNOT attack

Assume that Eve performs the Double CNOT attack to the proposed protocol trying to get the secret key. For example, Eve performs CNOT operation, U_CNOT = (|00⟩⟨00| + |01⟩⟨01| + |10⟩⟨10| + |11⟩⟨11|), with the particles sent to participants in Step 2 as the control bits the Eve’s ancillary particles as the target bits. Then, Eve perform the second CNOT operation with the particles sent from the participants in Step 3 as the control bits and Eve’s ancillary particles as the target bits. Eve tries to reveal Bob’s (Charlie’s) operation from the ancillary particles and then gets the secret key without being detected.

Alice’s quantum state is $|{\varphi }^{+}\rangle =\frac{1}{\sqrt{2}}(|00\rangle +|11\rangle )$, suppose Eve attacks the quantum channel between Alice and Bob. Eve generates a qubit |0⟩_E and performs a CNOT operation on Bell state and |0⟩_E, the qubit systems become the following:

$\begin{array}{c}\hfill U_{\mathit{CNOT}}|{\varphi }^{+}\rangle |0{\rangle }_E=\frac{1}{\sqrt{2}}\left(|00\rangle |0{\rangle }_E+|11\rangle |1{\rangle }_E\right)\end{array}(14)$

After the operation, Eve send’s the dirty qubits to Bob. According to the protocol, Bob either reflects it or resends a new one. Then, Eve intercepts each qubit send from Bob to Alice in Step 3 and performs the other CNOT operation on Bob’s qubits and the corresponding qubit kept by Eve. If Bob chose to CTRL in Step 3, the qubit systems become the following:

$\begin{array}{cc}\hfill U_{\mathit{CNOT}}\frac{1}{\sqrt{2}}\left(|00\rangle |0{\rangle }_E+|11\rangle |1{\rangle }_E\right)& =\frac{1}{\sqrt{2}}\left(|00\rangle |0{\rangle }_E+|11\rangle |0{\rangle }_E\right)\hfill \\ \hfill & =|{\varphi }^{+}\rangle |0{\rangle }_E\hfill \end{array}(15)$

If Bob chose to SIFT in Step 3, the qubits systems become the following:

$\begin{array}{cc}\hfill U_{\mathit{CNOT}}\left|0{\rangle }_B|0{\rangle }_E\right)& =|0{\rangle }_B|0{\rangle }_E\hfill \\ \hfill U_{\mathit{CNOT}}\left|1{\rangle }_B|1{\rangle }_E\right)& =|1{\rangle }_B|0{\rangle }_E\hfill \end{array}(16)$

The subscript B means the new qubit generated by Bob. According to Eqs 15, 16, whether Bob performs CTRL or SIFT operation, Eve measures his qubit in Z-bais, he will always get the measurement result |0⟩. That is, Eve cannot distinguish the current qubit is a reflected one or one generated by Bob. The analysis between Alice and Charlie is similar.

3.6 Key leakage problem

Assume Eve tries to eavesdrop on the Bob’s raw key from the traveling qubits. Eve may perform Z-basis measurement on the photon sequence sent by Alice, S_b. Eve obtains the measurement results of S_b (i.e., |0⟩, |1⟩). Suppose Shannon entropy is defined as E = −∑_iρ_i log₂ρ_i, where ρ_i denotes probability distribution. The entropy E₁ can be computed as $E_1=-2\times \frac{1}{2}{\log }_2\frac{1}{2}=1$ bit. However, the protocol provides an eavesdropping check, which limits the possibility of the measurement S_b being used as the raw key, hence the probability is $\frac{1}{8}$.(i.e., Bob receives S_b and performs SIFT operation or CTRL operation. Charlie receives S_c and performs SIFT operation or CTRL operation. Alice and Bob obtain raw key in case that Bob performs SIFT operation and Charlie implements CTRL operation. Alice and Bob select half of the transmitted photons as eavesdropping check. Eventually, the probability of Eve eavesdrops the raw key from the measurement results of S_b is $\frac{1}{2}\times \frac{1}{2}\times \frac{1}{2}=\frac{1}{8}$). Hence, the entire entropy denotes $\frac{1}{8}\times E_1=0.125$ bit. Even though Eve can obtain 0.125 bit by performing eavesdropping, eventually the attack will be detected by an eavesdropping check in Step 6. Even if Eve passes the eavesdropping check, one can still perform the privacy amplification process on the transmitted information to distill the private key, avoiding the key leakage problem. Thus, Eve cannot obtain any private key under an eavesdropping attack.

4 Extension of the proposed semi-quantum key distribution protocol

4.1 Extended m + 1 party semi-quantum key distribution protocol

In this subsection, we extend the proposed scheme to construct a semi-quantum key distribution network that involves one quantum user Alice and m classical participants P_i (i = 1, 2, …, m). The detailed process of the extended SQKD protocol is shown as follows:

Step 1: Alice generates N = 2n(m² + δ) m-particle GHZ states in $|\mathit{\Psi }\rangle =\frac{1}{\sqrt{2}}(\underset{m}{\underbrace{|00\dots 00\rangle }}+\underset{m}{\underbrace{|11\dots 11\rangle }})$ and divides the m-particle GHZ states into m sequences

$\begin{array}{ll}\hfill S_1& =\left\{S_1^1,S_1^2,\dots ,S_1^N\right\},\hfill \\ \hfill S_2& =\left\{S_2^1,S_2^2,\dots ,S_2^N\right\},\hfill \\ \hfill & ⋮\hfill \\ \hfill S_m& =\left\{S_m^1,S_m^2,\dots ,S_m^N\right\}.\hfill \end{array}$

Step 2: Alice sends S_i to P_i (i = 1, 2, …, m) respectively.

Step 3: For each coming qubits, every classical user P_i randomly chooses to SIFT or CTRL. For convenience, we denote the qubits resended by P_i with SIFT - P_i qubits.

Step 4: Alice stores the received qubits in m N-qubit quantum registers and informs all classical participants.

Step 5: All P_i publish which particles they choose to SIFT.

Step 6: According to the published information by all classical users, they check out the security of the quantum channel and produce INFO bits.

1) If all classical participants implement the operation CTRL on the kth m-particle GHZ state (k = 1, 2, …, N), Alice will perform m-particle GHZ measurement on the kth m-particle GHZ state. Alice checks the error rate on these measurement results. If it is higher than predefined threshold P_CTRL, they abort the protocol.

2) Only one classical participant P_i perform the operation SIFT, the others P_j apply the operation CTRL on kth m-particle GHZ state (k = 1, 2, …, N). Alice will measure these m particles with Z-basis respectively and examines whether these measurement results are equal. If the error rate is less than P_TEST, the protocol continues. Otherwise it is terminated. In this case, Alice will obtain 2n SIFT - P_i bits. Alice chooses at random n SIFT - P_i bits to be TEST - P_i bits and announces what are the chosen bits and the value of these TEST - P_i bits by the classical channel. P_i checks the error rate on the TEST bits. If it is higher than some predefined threshold P_TEST, Alice and P_i abort the protocol.

3) If all classical participants implement the operation SIFT on kth m-particle GHZ state (k = 1, 2, …, N), Alice will measure these m particles with Z-basis respectively and examines whether these measurement results are equal. Alice aborts the protocol as the error rate is higher than the predefined threshold P_TEST. Alice requests measurement results from all classical participants, and checks the error rate among these bits, if it is higher than the predefined threshold P_TEST, they abort the protocol.

4) Alice discards particles from other cases.

Step 7: Alice and P_i select the n remaining SIFT - P_i bits in above case 2 to be used as INFO bits. They abort the protocol as the number of INFO bits is less than n. Alice announces publicly the error correction code (ECC) and privacy amplification data, Alice and P_i use them to extract the final key from the n-bit INFO string.

4.2 Security analysis

4.2.1 Outside attack

In this part, we explain why an outside eavesdropper cannot learn the secrets in the extended scheme. In Step 2, qubits are transmitted and some usual attacks such as entangle-measure attack, intercept-resend attack and measure-resend attack may be launched by an outside eavesdropper. In Step 6, Alice will check the correctness of the returned particles from all classical participants. That is, an outside eavesdropper can be detected. Specifically, if Alice performs m-particle GHZ measurement on the kth m-particle GHZ state in case 1, her measurement result will be same as the initial entangle state. Once Eve has measured some reflected particles in case 1, he will be detected. Besides, Eve’s destructive operations will also be found in case 2 and case 3. The specific analysis is similar to the presented three-party protocol since the idea is the same.

4.1.2 Participant attack.

Participant attack, which was put forward in Ref. [48], is a kind of powerful attack by either one dishonest participant or more dishonest participants who conspire together. We will discuss these two cases separately.

First, we discuss the case that one dishonest classical participant, without loss of generality, P₁, wants to steal other participants’ secret. In our protocol, P_i’s secret is generated from case 2, that is, only P_i performed operation SIFT, other P_j(i ≠ j) applied operation CTRL. P₁ cannot steal other participant’s secrets since he performed operation CTRL. In step 5, P₁ can announce the erroneous information. For example, he declares a portion of SIFT as CTRL. He can obtain other participants’ measurement results by implementing operation SIFT. However, it will be detected in case 1 since Alice’s measurement result is different from original quantum state.

Second, we explain the more classical participants colluding together also cannot obtain others’ secret. Without of generality, we consider the extreme case in which there are m − 1 classical participants P₁, P₂, …, P_m−1 who collude together to steal the secret of classical user P_m. P₁, P₂, …, P_m−1 cannot obtain which particles P_m performs operation SIFT, the conspiring participants cannot obtain P_m’s key. If they publish misleading messages in step 5, Alice will find errors in case 1. Even though they can intercept the qubits from P_m, the conspiring participants can be put in light just like external attackers.

5 Comparison

In a quantum cryptographic protocol, we usually use the qubit efficiency to evaluate its performance of the communication protocol, which is defined as [49]

$\eta =\frac{b_s}{q_t}(17)$

where b_s represents the sum of the shared secret bits between the participants and q_t denotes the total number of generated qubits in the protocol. In the presented three-party protocol, Alice expects to share n bits secret messages to Bob and Charlie at the same time. Alice prepares 8n(1 + δ) Bell states and every Bell state have 2 particles, under the ideal conditions, δ = 0; Bob and Charlie generate 4n single photons in Z-basis respectively, hence, the efficiency η of the proposed three-party SQKD is $\frac{1}{12}$. Likewise, we can compute the efficiency of the extended m + 1 party SQKD is $\frac{1}{3m^2}$.

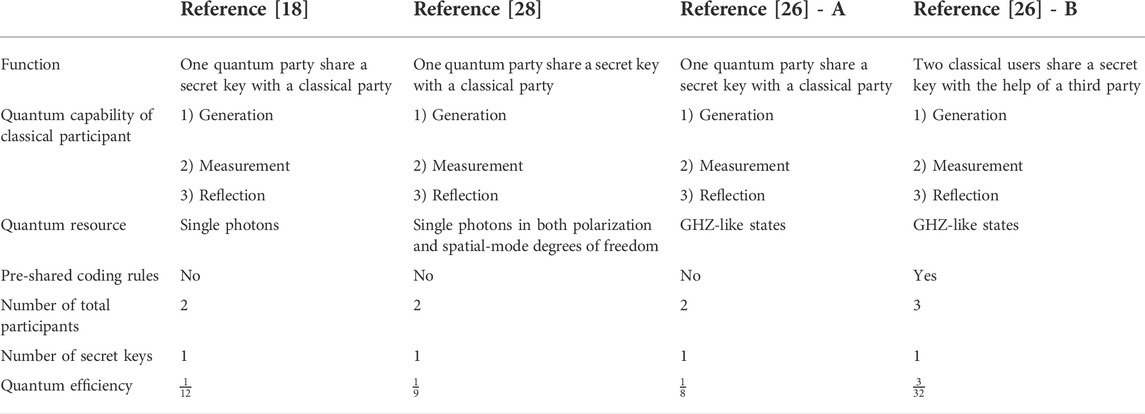
We will compare the proposed protocol with typical SQKD protocols in Tables 2, 3. Here, Ref. [26] - A refers to the two-party protocol in Ref. [26], and Ref. [26] - B refers to the three-party protocol in Ref. [26]. In the Ref. [18], quantum user Alice can only share a secret key with classical user Bob by employing single photons. Refs. [18, 28] and Ref. [26] - A can only distribute one secret message at a time, but Alice can distribute two different raw keys in our three-party protocol. Reference [26] - B additionally use the pre-shared coding rules, which increases the complexity of operations between participants and thus, decreases the time efficiency. In the protocol of Ref. [23], although the classical participants do not need quantum measurement devices, quantum memory or quantum delay line is required for reordering qubits. The Refs. [23, 24] allows two limited semi-quantum users to establish a shared secret key with the help of a fully quantum server. However, the proposed three-party protocol accomplishes one quantum server to share two different secret keys with two classical users respectively at a time. Furthermore, our scheme can be extended to multi-user key distribution. If there are n users who want to distribute keys to each other in quantum network, typical SQKD needs $\frac{n(n-1)}{2}$ times to achieve key distribution, such as Refs. [18, 23, 24, 26, 28]. But our extended m + 1 party protocol only needs n times.

TABLE 2

TABLE 2. Comparison results with other SQKD protocols.

TABLE 3

TABLE 3. Comparison results with other SQKD protocols.

6 Conclusion

As above, different from other SQKD protocols, the proposed protocol allows one quantum participant to distribute two different session keys to two classical participants respectively. This scheme is expanded to simultaneously distribute m keys. It provides a good idea for building quantum key distribution network. For example, we can build a key distribution center which is quantum, but the users only have classical capabilities. The quantum server can process up to m distribution requests at a time, greatly reducing distribution time. We validate that the proposed SQKD protocol can overcome the entangle-measurement attack, the modification attack, and the other typical attacks.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Bennett CH, Brassard G. Quantum cryptography: Public key distribution and coin tossing (2020). arXiv preprint arXiv:2003.06557.

Google Scholar

2. Lo HK, Chau HF. Unconditional security of quantum key distribution over arbitrarily long distances. science (1999) 283(5410):2050–6. doi:10.1126/science.283.5410.2050

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Shor PW, Preskill J. Simple proof of security of the bb84 quantum key distribution protocol. Phys Rev Lett (2000) 85(2):441–4. doi:10.1103/physrevlett.85.441

CrossRef Full Text | Google Scholar

4. Wang XB. Fault tolerant quantum key distribution protocol with collective random unitary noise. Phys Rev A (Coll Park) (2005) 72(5):050304. doi:10.1103/physreva.72.050304

CrossRef Full Text | Google Scholar

5. Lo HK, Curty M, Qi B. Measurement-device-independent quantum key distribution. Phys Rev Lett (2012) 108(13):130503. doi:10.1103/physrevlett.108.130503

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Sasaki T, Yamamoto Y, Koashi M. Practical quantum key distribution protocol without monitoring signal disturbance. Nature (2014) 509(7501):475–8. doi:10.1038/nature13303

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Yang CW. New probabilistic quantum key distribution protocol. Int J Theor Phys (Dordr) (2018) 57(12):3651–7. doi:10.1007/s10773-018-3878-0

CrossRef Full Text | Google Scholar

8. Bunandar D, Anthony L, Lee C, Cai H, Long CM, Boynton N, et al. Metropolitan quantum key distribution with silicon photonics. Phys Rev X (2018) 8(2):021009. doi:10.1103/physrevx.8.021009

CrossRef Full Text | Google Scholar

9. Aguado A, Lopez V, Lopez D, Peev M, Poppe A, Pastor A, et al. The engineering of software-defined quantum key distribution networks. IEEE Commun Mag (2019) 57(7):20–6. doi:10.1109/mcom.2019.1800763

CrossRef Full Text | Google Scholar

10. Kumar A, Dadheech P, Singh V, Poonia RC, Raja L. An improved quantum key distribution protocol for verification. J Discrete Math Sci Cryptography (2019) 22(4):491–8. doi:10.1080/09720529.2019.1637153

CrossRef Full Text | Google Scholar

11. Wu JZ, Yan L. Quantum key distribution protocol based on ghz like state and bell state. In: International Conference on Artificial Intelligence and Security. Berlin, Germany: Springer (2020). p. 298–306.

Google Scholar

12. Wang Y, Lou X, Zhou F, Wang S, Huang G. (t, n) Threshold Quantum Secret Sharing Using Rotation Operation n) threshold quantum secret sharing based on quantum walk. Int J Theor Phys (Dordr) (2022) 61(2):166–17. doi:10.1007/s10773-022-05121-x

CrossRef Full Text | Google Scholar

13. Tian-Yu Y, Jia-Li H. Quantum secure multiparty summation based on the phase shifting operation of d-level quantum system and its application. International Journal of Theoretical Physics (2021) 60(3):819–827.

Google Scholar

14. Tian-Yu Y, Hong-Kun L, Jia-Li H. Information leakage resistant quantum dialogue with single photons in both polarization and spatial-mode degrees of freedom. Quantum Information Processing (2021) 20(6):209

Google Scholar

15. Boyer M, Dan K, Mor T. Quantum key distribution with classical bob. In: 2007 First International Conference on Quantum, Nano, and Micro Technologies (ICQNM’07). Guadeloupe, French Caribbean: IEEE (2007). p. 10.

CrossRef Full Text | Google Scholar

16. Boyer M, Gelles R, Dan K, Mor T. Semiquantum key distribution. Phys Rev A (Coll Park) (2009) 79(3):032341. doi:10.1103/physreva.79.032341

CrossRef Full Text | Google Scholar

17. Lu H, Cai QY. Quantum key distribution with classical alice. Int J Quan Inform (2008) 6(06):1195–202. doi:10.1142/s0219749908004353

CrossRef Full Text | Google Scholar

18. Zou X, Qiu D, Li L, Wu L, Li L. Reply to “Comment on ‘Semiquantum-key distribution using less than four quantum states’ ”. Phys Rev A (Coll Park) (2009) 79(5):046302. doi:10.1103/physreva.83.046302

CrossRef Full Text | Google Scholar

19. Wang J, Zhang S, Zhang Q, Tang CJ. Semiquantum key distribution using entangled states. Chin Phys Lett (2011) 28(10):100301. doi:10.1088/0256-307x/28/10/100301

CrossRef Full Text | Google Scholar

20. Yu KF, Yang CW, Liao CH, Hwang T. Authenticated semi-quantum key distribution protocol using bell states. Quan Inf Process (2014) 13(6):1457–65. doi:10.1007/s11128-014-0740-z

CrossRef Full Text | Google Scholar

21. Li CM, Kun-Fei Y, Kao SH, Hwang T. Authenticated semi-quantum key distributions without classical channel. Quan Inf Process (2016) 15(7):2881–93. doi:10.1007/s11128-016-1307-y

CrossRef Full Text | Google Scholar

22. Krawec WO. Mediated semiquantum key distribution. Phys Rev A (Coll Park) (2015) 91(3):032323. doi:10.1103/physreva.91.032323

CrossRef Full Text | Google Scholar

23. Liu ZR, Hwang T. Mediated semi-quantum key distribution without invoking quantum measurement. Annalen der Physik (2018) 530(4):1700206. doi:10.1002/andp.201700206

CrossRef Full Text | Google Scholar

24. Lin PH, Tsai CW, Hwang T. Mediated semi-quantum key distribution using single photons. Annalen der Physik (2019) 531(8):1800347. doi:10.1002/andp.201800347

CrossRef Full Text | Google Scholar

25. Zhu KN, Zhou NR, Wang YQ, Wen XJ. Semi-quantum key distribution protocols with ghz states. Int J Theor Phys (Dordr) (2018) 57(12):3621–31. doi:10.1007/s10773-018-3875-3

CrossRef Full Text | Google Scholar

26. Chen LY, Gong LH, Zhou NR. Two semi-quantum key distribution protocols with g-like states. Int J Theor Phys (Dordr) (2020) 59(6):1884–96. doi:10.1007/s10773-020-04456-7

CrossRef Full Text | Google Scholar

27. Ye TY, Li HK, Hu JL. Semi-quantum key distribution with single photons in both polarization and spatial-mode degrees of freedom. Int J Theor Phys (Dordr) (2020) 59(9):2807–15. doi:10.1007/s10773-020-04540-y

CrossRef Full Text | Google Scholar

28. Ye TY, Geng MJ, Xu TJ, Chen Y. Efficient semiquantum key distribution based on single photons in both polarization and spatial-mode degrees of freedom. Quan Inf Process (2022) 21(4):123–1. doi:10.1007/s11128-022-03457-1

CrossRef Full Text | Google Scholar

29. Zhang W, Qiu D, Mateus P. Security of a single-state semi-quantum key distribution protocol. Quan Inf Process (2018) 17(6):135–21. doi:10.1007/s11128-018-1904-z

CrossRef Full Text | Google Scholar

30. Krawec WO. Security proof of a semi-quantum key distribution protocol. In: 2015 IEEE International Symposium on Information Theory (ISIT). Hong Kong, China: IEEE (2015). p. 686–90.

CrossRef Full Text | Google Scholar

31. Krawec WO. Restricted attacks on semi-quantum key distribution protocols. Quan Inf Process (2014) 13(11):2417–36. doi:10.1007/s11128-014-0802-2

CrossRef Full Text | Google Scholar

32. Tsai CL, Hwang T. Semi-quantum key distribution robust against combined collective noise. Int J Theor Phys (Dordr) (2018) 57(11):3410–8. doi:10.1007/s10773-018-3854-8

CrossRef Full Text | Google Scholar

33. Tsai CW, Yang CW. Cryptanalysis and improvement of the semi-quantum key distribution robust against combined collective noise. Int J Theor Phys (Dordr) (2019) 58(7):2244–50. doi:10.1007/s10773-019-04116-5

CrossRef Full Text | Google Scholar

34. Meslouhi A, Hassouni Y. Cryptanalysis on authenticated semi-quantum key distribution protocol using bell states. Quan Inf Process (2017) 16(1):18–7. doi:10.1007/s11128-016-1468-8

CrossRef Full Text | Google Scholar

35. Zhang W, Qiu D, Mateus P. Single-state semi-quantum key distribution protocol and its security proof. Int J Quan Inform (2020) 18(04):2050013. doi:10.1142/s0219749920500136

CrossRef Full Text | Google Scholar

36. Krawec WO. Security of a semi-quantum protocol where reflections contribute to the secret key. Quan Inf Process (2016) 15(5):2067–90. doi:10.1007/s11128-016-1266-3

CrossRef Full Text | Google Scholar

37. Reed IS, Solomon G. Polynomial codes over certain finite fields. J Soc Ind Appl Math (1960) 8(2):300–4. doi:10.1137/0108018

CrossRef Full Text | Google Scholar

38. Gallager R. Low-density parity-check codes. IEEE Trans Inf Theor (1962) 8(1):21–8. doi:10.1109/tit.1962.1057683

CrossRef Full Text | Google Scholar

39. Bennett CH, Brassard G, Claude C, Maurer UM. Generalized privacy amplification. IEEE Trans Inf Theor (1995) 41(6):1915–23. doi:10.1109/18.476316

CrossRef Full Text | Google Scholar

40. Bennett CH, Brassard G, Robert JM. Privacy amplification by public discussion. SIAM J Comput (1988) 17(2):210–29. doi:10.1137/0217014

CrossRef Full Text | Google Scholar

41. Deng FG, Zhou P, Li XH, Li CY, Zhou HY. Robustness of two-way quantum communication protocols against trojan horse attack (2005). arXiv preprint quant-ph/0508168.

Google Scholar

42. Cai QY. Eavesdropping on the two-way quantum communication protocols with invisible photons. Phys Lett A (2006) 351(1-2):23–5. doi:10.1016/j.physleta.2005.10.050

CrossRef Full Text | Google Scholar

43. Deng FG, Li XH, Zhou HY, Zhang ZJ. Improving the security of multiparty quantum secret sharing against trojan horse attack. Phys Rev A (Coll Park) (2005) 72(4):044302. doi:10.1103/physreva.72.044302

CrossRef Full Text | Google Scholar

44. Li XH, Deng FG, Zhou HY. Improving the security of secure direct communication based on the secret transmitting order of particles. Phys Rev A (Coll Park) (2006) 74(5):054302. doi:10.1103/physreva.74.054302

CrossRef Full Text | Google Scholar

45. Zhang Z, Zeng G, Zhou N, Jin X. Quantum identity authentication based on ping-pong technique for photons. Phys Lett A (2006) 356(3):199–205. doi:10.1016/j.physleta.2006.03.048

CrossRef Full Text | Google Scholar

46. Shi WM, Zhang JB, Zhou YH, Yang YG. A novel quantum deniable authentication protocol without entanglement. Quan Inf Process (2015) 14(6):2183–93. doi:10.1007/s11128-015-0994-0

CrossRef Full Text | Google Scholar

47. Zhou NR, Zhu KN, Bi W, Gong LH. Semi-quantum identification. Quan Inf Process (2019) 18(6):197–17. doi:10.1007/s11128-019-2308-4

CrossRef Full Text | Google Scholar

48. Gao F, Qin SJ, Wen QY, Zhu FC. A simple participant attack on the brádler-dušek protocol. Quan Inf Comput (2007) 7(4):329–34. doi:10.26421/qic7.4-4

CrossRef Full Text | Google Scholar

49. Cabello A. Quantum key distribution in the holevo limit. Phys Rev Lett (2000) 85(26):5635–8. doi:10.1103/physrevlett.85.5635

PubMed Abstract | CrossRef Full Text | Google Scholar