- 1Department of Mathematics, Art and Sciences Faculty, Yildiz Technical University, Istanbul, Turkey
- 2Independent Researcher, Eskisehir, Turkey
- 3Department of Mathematics, Faculty of Sciences, Al-Balqa Applied University, Al-Salt, Jordan
- 4Department of Mathematics and Statistics, American University of Sharjah, Sharjah, United Arab Emirates
The Fitzhugh–Nagumo equation is an important non-linear reaction–diffusion equation used to model the transmission of nerve impulses. This equation is used in biology as population genetics; the Fitzhugh–Nagumo equation is also frequently used in circuit theory. In this study, we give solutions to the fractional Fitzhugh–Nagumo (FN) equation, the fractional Newell–Whitehead–Segel (NWS) equation, and the fractional Zeldovich equation. We found the exact solutions of these equations by conformable derivatives. We have obtained the exact solutions within the time-fractional conformable derivative for these equations.
1 Introduction
Fractional differential equations (FDEs) are generalizations of known differential equations (ODEs). FPDEs are used effectively in many fields of science [1–4]. These equations are significant models to interpret plasma physics, relativistic physics, quantum mechanics, non-linear optics, etc. So, FPDE studies are getting more and more important. Recent developments and applications in fractional calculus have been discussed by many authors [5–9]. Many fractional models can be converted to a FODE, allowing us to use the power-series technique to find all open-series analytical solutions.
The fractional Fitzhugh–Nagumo equation is an important non-linear reaction–diffusion equation used to model the transmission of nerve impulses. This equation is used in biology as population genetics; the fractional Fitzhugh–Nagumo equation is also frequently used in circuit theory.
There are numerous effective ways to find solutions of PDEs. These methods are the
These equations we deal with in this study are effective equations that play a fundamental role in many phenomena such as plasma physics and optics. The non-linear phenomena of wave happen in different fields such as optical fiber, physics, and biology. It is necessary to gain the exact solutions of such models for the better understanding of non-linear wave phenomena.
In the second part, the conformable derivative is introduced. In the third part, the extended tanh–coth method is given. In the other sections, we found the exact solutions of the (1 + 1) dimensional time-fractional Fitzhugh–Nagumo (FN) equation, the Newell–Whitehead (NW) equation, and the Zeldovich equation via this method.
2 Conformable derivative
Definition 1. The basic limit definition of this derivative is [25]:
Some properties of this derivative are given in [26, 27].
Definition 2. Let g: (0, ∞) → R be a function. The conformable derivative of g for order α is defined by
for all k > 0, α ∈ (0, 1).
Theorem 3. If a function g: [0, ∞) → R is α − differentiable at t0 > 0, α ∈ (0, 1] and g is continuous at t0.
Theorem 4. Let f and g be α − differentiable at a point t > 0, α ∈ (0, 1]:
If g is differentiable,
Non-linear conformable partial differential equations (NCPDEs) with one independent variable are as follows:
The non-linear fPDE (5) can be converted to a non-linear ODE using Eq. 6:
Let us now discuss how we will approach solving the Fitzhugh–Nagumo equation, the Newell–Whitehead equation, and the Zeldovich equation.
3 The extended tanh–coth method
The tanh–coth approach can be summed up as follows in [28]:
The wave variable
u (x, t) = U(ξ) is a traveling wave solution. A non-linear ODE can be converted from the non-linear PDE (9):
From the derivatives of the independent variable Y,
The tanh method can be expressed as follows:
The following is an extension of Eq. 13 [29]:
4 Solutions of the Fitzhugh–Nagumo equation
The FN equation is an important non-linear reaction–diffusion equation used to model the transmission of nerve impulses. Also used in biology as population genetics, this equation is also frequently used in circuit theory, where x is the space variable and t is a time variable.
Since the FN equation is (1 + 1)-dimensional and time-fractional, using the wave variable
where c and v are constants. By balancing (U)3 with U″ in Eq. 16, we obtain the following:
The solution form is as follows:
Here a0 and a1, b1 are arbitrary constants. Eq. 19 is substituted into Eq. 16, and if the coefficients of Y are used to set the system of equations to zero, then
By solving this system of equations, we get the following cases.
Case 1:
Therefore, the exact solution is as follows:
Case 2:
The exact solution is as follows:
Case 3:
The exact solution is as follows:
Case 4:
The exact solution is as follows:
Case 5:
The exact solution is as follows:
Case 6:
The exact solution is as follows:
Case 7:
The exact solution is as follows:
Case 8:
The exact solution is as follows:
Case 9:
The exact solution is as follows:
5 Solutions of the Newell–Whitehead equation
If μ = −1 in Eq. 15, the NW equation is obtained by
Using the wave variable
where c and v are constants. By balancing, we obtain
The solution form is as follows:
Here, a0 and a1, b1 are arbitrary constants. Eq. 43 is substituted into Eq. 41, and if the coefficients of Y are used to set the system of algebraic equations to zero, then
By solving this system of equations, we get the following cases.
Case 1:
Therefore, the exact solution is as follows:
Case 2:
The exact solution is as follows:
Case 3:
The exact solution is as follows:
6 Solutions of the Zeldovich equation
If μ = 0 in Eq. 15, the Zeldovich equation is obtained:
Using the wave variable
where c and v are constants. From Eq. 52, we obtain
The solution form is as follows:
Here, a0 and a1, b1 are the arbitrary constants. Eq. 55 is substituted into Eq. 52, and if the coefficients of Y are used to set the system of equations to zero, then
By solving this system of equations, we get the following cases.
Case 1:
Therefore, the exact solution is as follows:
Case 2:
The exact solution is as follows:
Case 3:
The exact solution is as follows:
7 Conclusion
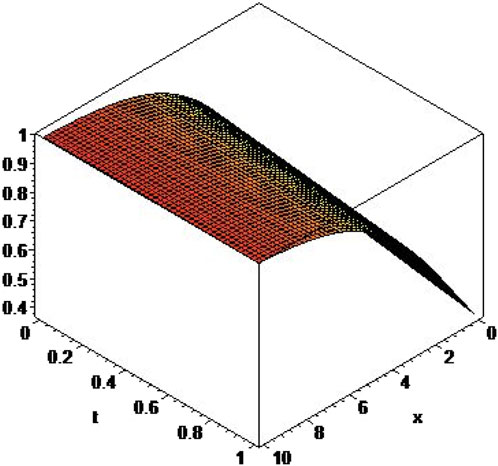
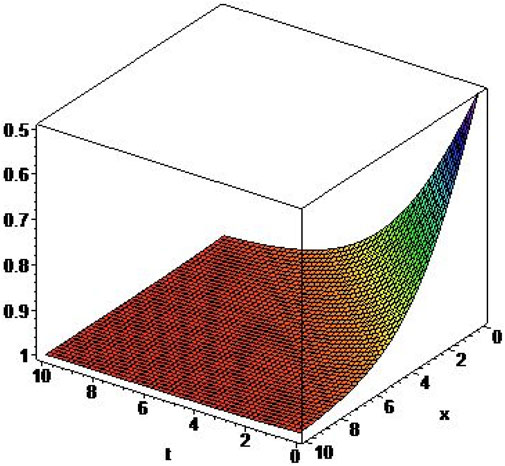
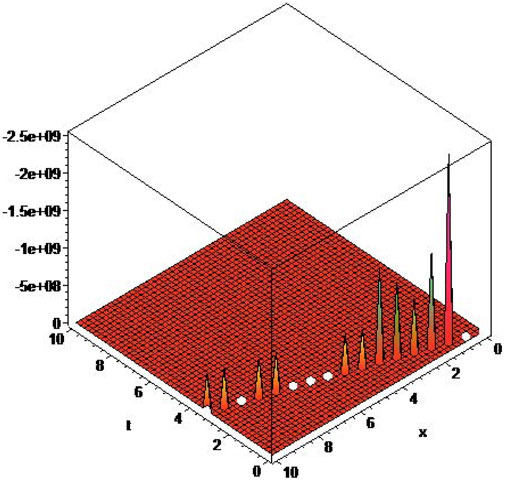
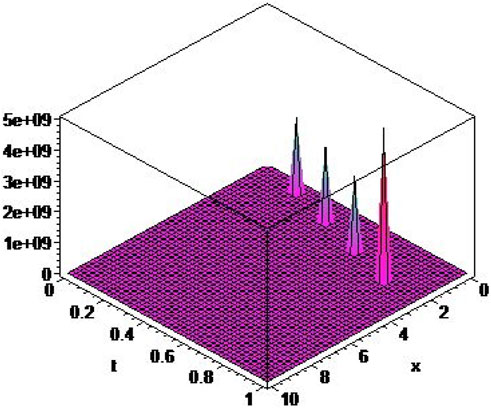
In this article, we present the extended tanh–coth method for solving non-linear space–time conformable PDEs. We found the exact and traveling wave solutions of some important space–time fPDEs via the extended tanh–coth method. We know many of the results obtained are new solutions that do not exist in the literature. The hyperbolic and trigonometric function solutions are significant to explain a variety of physical phenomena. This suggests that the extended tanh–coth method is more effective in finding the solutions of non-linear fPDEs. The 3D plots of the acquired solutions are presented by choosing appropriate values to the parameters in Figures 1–4. These are the advantages of the extended tanh–coth method. The offered method can be utilized to assist complicated models applicable to a wide variety of physical situations. We hope that the telecommunications industry and other such forms of waveguides will find this study to be beneficial.
Moreover, we come to the understanding that the newly obtained hyperbolic function and trigonometric function solutions in this study may help explain some complex physical aspects in non-linear physical sciences and are related to such physical properties. In future studies, these approaches can be easily used for other NFDEs, NFDE systems, fractional complex equations, fractional difference equations, etc.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.
Author contributions
ACC: Original Draft, Methodology, Validation; AB: Investigation, Supervision, Writing—Review and Editing; OAA: Conceptualization, Methodology, Writing; MA: Original Draft, Validation, Founding acquisition.
Funding
The work in this study was supported, in part, by the Open Access Program from the American University of Sharjah. This study represents the opinions of the authors and does not mean to represent the position or opinions of the American University of Sharjah
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Miller KS, Ross B. An introduction to the fractional calculus and fractional differential equations. New York: Wiley (1993).
3. Hilfer R. Applications of fractional calculus in physics. River Edge, NJ, USA: World Scientific Publishing (2000).
4. Kilbas AA, Srivastava HM, Trujillo JJ. Theory and applications of fractional differential equations. Amsterdam: Elsevier (2006).
5. Jajarmi A, Baleanu D, Vahid ZK, Pirouza HM, Asad JH. A new and general fractional Lagrangian approach: A capacitor microphone case study. Results Phys (2021) 31:104950. doi:10.1016/j.rinp.2021.104950
6. Acay B, Inc M, Mustapha UT, Yusuf A. Fractional dynamics and analysis for a lana fever infectious ailment with Caputo operator, Chaos. Solitons & Fractals (2022) 153:111605. doi:10.1016/j.chaos.2021.111605
7. Erturk VS, Godwe E, Baleanu D, Kumar P, Asad J, Jajarmi A. Novel fractional-order Lagrangian to describe motion of beam on nanowire. Acta Phys Pol A (2021) 140(3):265–72. doi:10.12693/aphyspola.140.265
8. Rawya A, Alquran M, Ali M, Yusuf A, Momani S. On group of Lie symmetry analysis, explicit series solutions and conservation laws for the time-fractional (2+1)-dimensional Zakharov-Kuznetsov (q,p,r) equation. J Geometry Phys (2022) 176:104512. doi:10.1016/j.geomphys.2022.104512
9. Baleanu D, Abadi MH, Jajarmi A, Vahid KZ, Nieto JJ. A new comparative study on the general fractional model of COVID-19 with isolation and quarantine effects. Alexandria Eng J (2022) 61(6):4779–91. doi:10.1016/j.aej.2021.10.030
10. Bekir A, Güner Ö, Ayhan B, Cevikel AC. Exact solutions for fractional differential-difference equations by (G’/G)-Expansion method with modified Riemann-Liouville derivative. Adv Appl Math Mech (2016) 8(2):293–305. doi:10.4208/aamm.2014.m798
11. Aksoy E, Cevikel AC, Bekir A. Soliton solutions of (2+1)-dimensional time-fractional Zoomeron equation. Optik (2016) 127(17):6933–42. doi:10.1016/j.ijleo.2016.04.122
12. Bekir A, Aksoy E, Cevikel AC. Exact solutions of nonlinear time fractional partial differential equations by sub-equation method. Math Methods Appl Sci (2015) 38(13):2779–84. doi:10.1002/mma.3260
13. Cevikel AC. New exact solutions of the space-time fractional KdV-Burgers and Non-Linear fractional Foam Drainage equation. Therm Sci (2018) 22:15–24. doi:10.2298/tsci170615267c
14. Bekir A, Güner Ö, Cevikel AC. The exp-function method for some time-fractional differential equations. Ieee/caa J Autom Sinica (2017) 4:315–21. doi:10.1109/jas.2016.7510172
15. Aksoy E, Bekir A, Cevikel AC. Study on fractional differential equations with modified Riemann-Liouville derivative via Kudryashov method. Int J Nonlinear Sci Numer Simulation (2019) 20(5):511–6. doi:10.1515/ijnsns-2015-0151
16. Rezazadeh H, Vahidi J, Zafar A, Bekir A. The functional variable method to find new exact solutions of the nonlinear evolution equations with dual-power-law nonlinearity. Int J Nonlinear Sci Numer Simulation (2020) 21(3-4):249–57. doi:10.1515/ijnsns-2019-0064
17. Cevikel AC, Bekir A, Akar M, San S. A Procedure to construct exact solutions of nonlinear evolution equations. Pramana - J Phys (2012) 79(3):337–44. doi:10.1007/s12043-012-0326-1
18. Taghizadeh N, Mirzazadeh M, Rahimian M, Akbari M. Application of the simplest equation method to some time-fractional partial differential equations. Ain Shams Eng J (2013) 4:897–902. doi:10.1016/j.asej.2013.01.006
19. Savaissou N, Gambo B, Rezazadeh H, Bekir A, Doka SY. Exact optical solitons to the perturbed nonlinear Schrodinger equation with dual-power law of nonlinearity. Opt Quan Electron (2020) 52:318. doi:10.1007/s11082-020-02412-7
20. Cevikel AC, Aksoy E. Soliton solutions of nonlinear fractional differential equations with their applications in mathematical physics. Revista Mexicana de Fisica (2021) 67(3):422–8. doi:10.31349/RevMexFis.67.422
21. Cevikel AC, Bekir A, Zahran EHM. Novel exact and solitary solutions of conformable Huxley equation with three effective methods. J Ocean Eng Sci (2022). doi:10.1016/j.joes.2022.06.010
22. Bekir A, Cevikel AC, Zahran EHM. New impressive representations for the soliton behaviors arising from the (2+1)-Boussinesq equation. J Ocean Eng Sci (2022). doi:10.1016/j.joes.2022.05.036
23. Cevikel AC. Traveling wave solutions of conformable Duffing model in shallow water waves. Int J Mod Phys B (2022) 36:2250164. doi:10.1142/s0217979222501648
24. Cevikel AC. New solutions for the high-dimensional fractional BLMP equations. J Ocean Eng Sci (2022). doi:10.1016/j.joes.2022.06.023
25. Khalil R, Al Horani M, Yousef A, Sababheh M. A new definition of fractional derivative. J Comput Appl Math (2014) 264:65–70. doi:10.1016/j.cam.2014.01.002
26. Abdeljawad T. On conformable fractional calculus. J Comput Appl Math (2015) 279:57–66. doi:10.1016/j.cam.2014.10.016
27. Eslami M, Rezazadeh H. The first integral method for Wu–Zhang system with conformable time-fractional derivative. Calcolo (2016) 53:475–85. doi:10.1007/s10092-015-0158-8
28. Cevikel AC, Bekir A. New solitons and Periodic solutions for (2+1)-dimensional Davey-Stewartson equations. Chin J Phys (2013) 51(1):1–13. doi:10.6122/CJP.51.1
Keywords: exact solutions, conformable derivative, the Fitzhugh-Nagumo equation, solitary wave solution, solitons
Citation: Cevikel AC, Bekir A, Abu Arqub O and Abukhaled M (2022) Solitary wave solutions of Fitzhugh–Nagumo-type equations with conformable derivatives. Front. Phys. 10:1028668. doi: 10.3389/fphy.2022.1028668
Received: 26 August 2022; Accepted: 06 October 2022;
Published: 26 October 2022.
Edited by:
Yakup Yildirim, Near East University, CyprusCopyright © 2022 Cevikel, Bekir, Abu Arqub and Abukhaled. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Ahmet Bekir, YmVraXJhaG1ldEBnbWFpbC5jb20=
 Adem C. Cevikel1
Adem C. Cevikel1 Ahmet Bekir
Ahmet Bekir Omar Abu Arqub
Omar Abu Arqub Marwan Abukhaled
Marwan Abukhaled