- 1Shanghai Aerospace Science and Industry Electric Appliance Research Institute Co., Ltd, Shanghai, China
- 2Shanghai Radio Equipment Research Institute, Shanghai, China
The physical process of stimulated Raman scattering (SRS) in the diamond and the performance of the Raman laser in the multi-phonon absorption band of 2.5–3 μm were theoretically studied. A theoretical model for the external-cavity diamond Raman laser emitting at the waveband was built based on the Raman coupled-wave equation and boundary conditions. Raman laser output characteristics such as lasing threshold, input–output, and temporal behavior of Stokes conversion were investigated and theoretically simulated by varying the values of the length of the diamond and the transmittance of the output coupler. The numerical modeling shows that to reduce the impact of the multi-phonon absorption and obtain a higher conversion efficiency, it is necessary to appropriately increase the output coupling of the cavity. Taking the 3 μm diamond Raman laser optimization as an example, it is predicted that the conversion efficiency of 10% could be obtained with a diamond length of 1 cm, a transmittance of 69%, and a pump intensity of 1.2 GWcm−2. The theoretical model also could be used to investigate other wavelengths of the external-cavity diamond Raman laser and be helpful for the optimum design of diamond Raman lasers in the mid-infrared band.
Introduction
Stimulated Raman scattering (SRS) has been widely used as an effective nonlinear frequency conversion technique with the advantages, such as beam cleanup, pulse compression, automatic phase-matching with no critical incident angle requirement, and narrow linewidth [1–6]. Efficient solid-state Raman lasers have been demonstrated with different configurations [7, 8]; among the various materials, the diamond possesses a high Raman gain coefficient (17 cmGW−1), record-high thermal conductivity (2,000 W m−1K−1), low thermal expansion coefficient (1.1 × 10–6 K−1), a broad optical transmission window (0.23–2.5 μm and >6.5 μm), and large Raman shift (1,332.3 cm−1) [9–11]. All of this means that diamond is a Raman medium with great potential and excellent performance.
Extensive studies on diamond Raman lasers have been demonstrated from ultraviolet to the mid-infrared spectral regime [12–20]. Combined with the ‘‘beam cleanup’’ of Raman conversion, an output power of 381 W and a conversion efficiency of 61% have been achieved in the diamond Raman laser at 1,234 nm [21]. Limited by the inevitable multi-phonon absorption in a 2.5–6.5-μm region, the conversion efficiency of 28.7% was obtained at 2.52 μm [22] and pumped by a narrow linewidth Q–switched Tm:YAP laser at 1.88 μm; the tunable diamond Raman laser was also achieved at 2.5 μm [23]. The diamond Raman laser operates in a 3.38–3.8-μm region with a pump source of 2.33–2.52 μm, and the conversion efficiency of 15% was generated at 3.075 μm [18].
Coupled-wave equations are powerful tools for analyzing laser performances and have been utilized to analyze and predict Raman lasers [24–29]. Analytical analysis of the external-cavity Raman laser was reported, which was consistent with the experimental results, but there was no analysis of the temporal pulse characteristics [30]. An analytical model for mid-infrared silicon Raman lasers was developed by J. Ma, and it could be applied in the theoretical analysis of diamond Raman lasers, provided that there was no multi-phonon absorption and the absorption coefficient of pump and Stokes were assumed to be equal in the model; due to multi-phonon absorption in 2.5–6.5 μm, the larger error would occur by the simplified model [31]. At present, the Tm or Ho-doped/co-doped solid-state laser has been rapidly developed [32–38]; if they are used as pump sources, combined with a diamond as the Raman medium, the Stokes of 2.5–3 μm mid-infrared high-power or high-energy pulsed laser would be obtained, which are located in the multi-phonon absorption band of the diamond. Therefore, we carried out a numerical simulation in order to be closer to the actual situation rather than the analytical solution for a more rational design of the diamond Raman laser in a multi-phonon absorption band.
In this study, we focus on our theoretical analysis of the diamond mid-infrared Raman laser based on the coupled-wave equations, which are located at the multi-phonon absorption band. The characteristics of the mid-infrared diamond Raman laser under different conditions are analyzed and discussed in detail, such as lasing threshold, input–output, and temporal behavior of Stokes conversion characteristics. The optimal laser resonator schemes are presented thoroughly, which is helpful for the optimum design of mid-infrared diamond Raman lasers.
Theoretical model
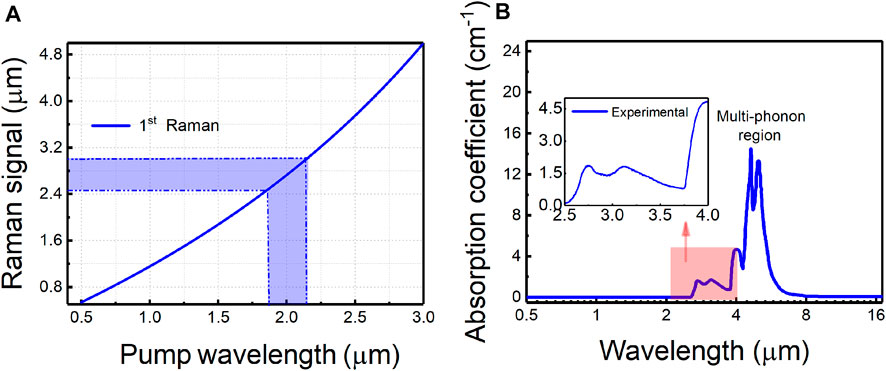
According to λs = (1/λp-vR/c)−1, where νR is the frequency in Hz of the Raman vibration, using a Tm or Ho-doped/co-doped solid-state pulsed laser as the pump source, the Stokes wavelength is 2.5–3 μm, as shown in Figure 1A. By neglecting the anti-Stokes waves, high-order Stokes and other nonlinear effects such as four-wave mixing, stimulated Brillouin scattering (SBS), the evolution of coupled-wave equations of the pump, and Stokes intensities with forward (+) and backward (−) propagation for the extra-cavity Raman laser are given by [27, 30, 31]
where z is the position in the cavity, n is the refractive index of the diamond, t is the time, g is the effective Raman gain coefficient, and αp and αs are the linear absorption loss coefficients at the pump (λp) and Stokes (λs) light, respectively. The corresponding boundary conditions are
where Iin is the input pump intensity, and Rm,n is the reflectivity of the resonator at both ends for the pump and Stokes. The absorption coefficient of the diamond is shown inFigure 1B, which was calculated by the following equation (39):
where R=(n-1)2/(n+1)2 and n is the refractive index of the diamond; T = 1-R, Tm is the transmittance measured using the Bruker OPTICS GmbH Fourier transform infrared spectrometer, and l is the length of diamond. It is to be noted here that the absorption parameters discussed in the following studies are all based on the measurements of the inset. The simulation analysis is directly realized by programming according to Eqs 1, 2, and the reliability of the program has been verified in [23], so there is no other formula derivation.
Simulation results and discussion
First, to more intuitively understand the process of the SRS in dynamic stability, the intensity distributions of the pump and Stokes in the resonator for an input intensity of Iin = 800 MWcm−2 are simulated, and the intra-cavity fields from the models as a function of distance along the cavity are shown in Figure 2A. Taking the output Stokes-shifted wavelength (λs) of 3 μm (αs = 1.58 cm−1) as the research object and the corresponding pump wavelength (λp) as 2.14 μm (αp = 0.11 cm−1), g = 1.59 cmGW−1. One observes that for L = 1 cm (the cavity length is equal to the length of the diamond, theoretically), the pump intensity is rapidly depleted due to the conversion to Stokes radiation and the linear absorption loss as it propagates along the diamond. After being reflected at the right end, the pump intensity propagates in the inverse direction and is damp continually (dotted line, black). As the pump intensity gradually decreases, the SRS process gradually decreases; therefore, the intensity distribution of Stokes (solid line, red) shows an upward and then downward trend. The output intensity of the Raman laser is the difference between the forward propagation and the backward propagation on the right end (output transmittance of 10%), and the output intensity is 6.5 MWcm−2 under these conditions.
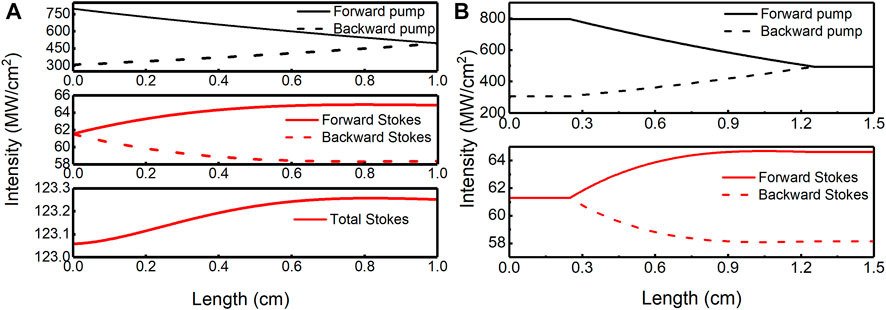
FIGURE 2. Intensity distributions of the pump and Stokes with the cavity. (A) 1-cm length of the cavity. (B) 1.5-cm length of the cavity.
Actually, the length of the cavity is longer than that of the Raman medium; therefore, the intensity distribution is simulated as the length of the cavity, and diamond lengths are 1.5 cm and 1 cm, respectively, as shown in Figure 2B. The straight line represents the intensity distribution that does not change within the distance between the mirrors and the diamond, which means that there is no SRS process in the absence of a Raman medium.
The input–output characteristics of Stokes relating to different parameters are presented, and the output intensity of Stokes Iout was defined as Iout = Is+(L) (1-Rsr), as shown in Figure 3. The pump intensity of 1 GWcm−2 is set in Figures 3A,C. Different optimal transmittances corresponding to different diamond lengths for the maximum output intensity are shown in Figure 3A. As can be seen, the optimal T is larger for the longer length of the diamond, but the output intensity is reduced. The output intensities of 57.1 MWcm−2 (L = 1 cm, T = 63%) and 29 MWcm−2 (L = 3 cm, T = 87%) are obtained, respectively. In Figure 3B, above the threshold intensity, the output intensity of the Raman laser increases linearly with the increase of the pump intensity. The slope of the output intensity increases with the increase of T, but the threshold intensity gets higher. The characteristic relationship between the output intensity and L with different T is studied, as shown in Figure 3C. The different optimal lengths of the diamond correspond to different T for the maximum output intensity. No Stokes is observed as the length of the diamond is less than 0.85 cm for T = 80%, which is due to the intensity of 1 GWcm−2 below the threshold intensity.
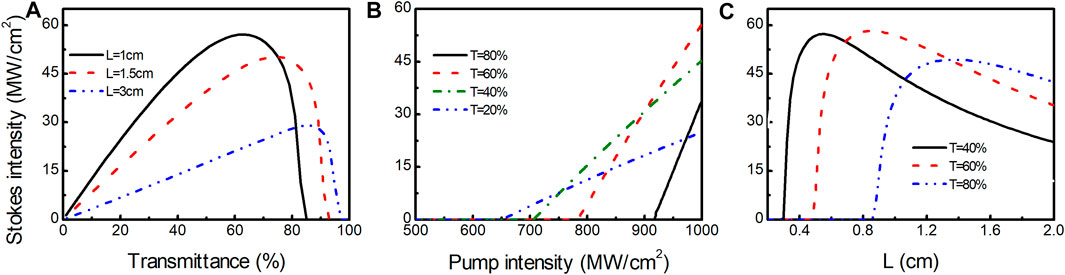
FIGURE 3. Input–output characteristics of the diamond Raman laser.(A) Output intensity versus T (B) Output intensity versus pump intensity (C) Output intensity versus L.
In addition to the parameters such as pump intensity, L, and T, the influence of linewidth on the laser performance also needs to be considered. The Raman gain can be measured by the relationships [40]:
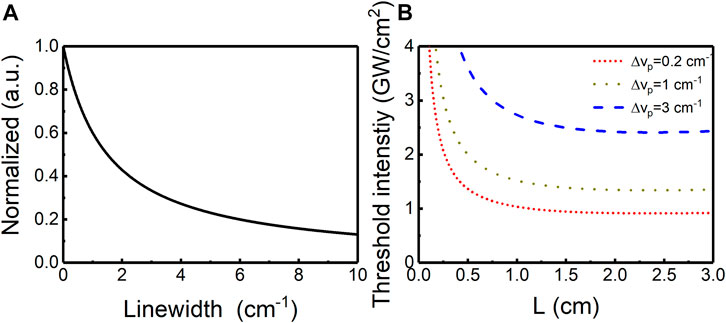
FIGURE 4. (A) Normalized effective Raman gain versus the linewidth. (B) Threshold intensity versus length for various linewidths.
By the coupled-wave equations and the boundary conditions, the threshold characteristics of the extra-cavity diamond Raman laser are calculated under different transmittances and pump wavelengths; the threshold intensity as a function of L for different parameters is shown in Figure 5. The simulation parameters in Figure 5 (an, n = 1, 2, and 3) are based on our measurement, and the parameters in Figure 5 (bn, n = 1, 2, and 3) are based on [10]. The measured linear propagation loss is larger than the reported linear propagation loss in [10]; this may be attributed to introduced impurities in the processing of diamond; therefore, the threshold intensity in Figure 5 (an, n = 1, 2, and 3) is larger than that in Figure 5 (bn, n = 1, 2, and 3) under the same conditions. The mid-infrared diamond cavities can oscillate for any given length if enough pump intensity is available, even if strong absorption occurs in these bands. In addition, it is evident that for a fixed T, there is an optimum L in which the lasing threshold reaches the minimum. According to [9], the Raman gain coefficient decreases with the increases in pump wavelength, that is, the gain of 2.2 μm is larger than the gain of 2.3 μm or 2.5 μm, but the threshold intensity is larger due to stronger absorption of Stokes in 3.11 μm (corresponding to the pump wavelength of 2.2 μm). The threshold intensity reaches GWcm−2 magnitude; it is not advisable to adopt the traditional method for reducing the Fresnel reflection loss by plating the antireflection film on both ends of the diamond, but the Brewster-cut diamond can be applied, which can effectively avoid the Fresnel reflection loss, and the diamond has a very high damage threshold (3–4 GWcm−2) [20].
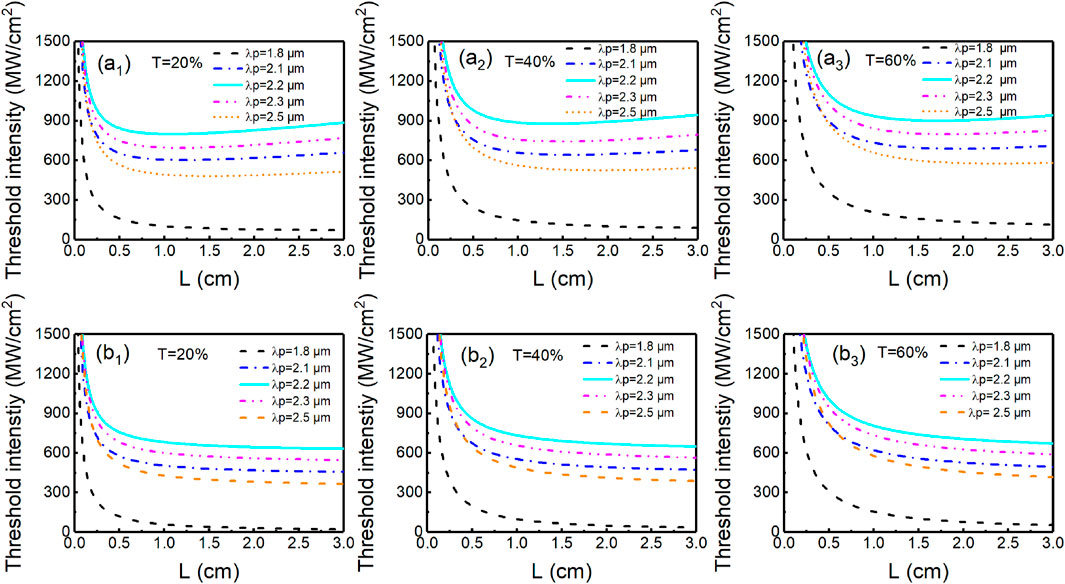
FIGURE 5. Threshold intensity versus L for various output facet transmittances with different pump wavelengths.
According to the previous analysis, the parameters need to be analyzed in detail. As shown in Figure 6, the influence of the resonator parameters, T and L, on the output intensity of the extra-cavity diamond lasers is studied and simulated with the 3D plot. As can be seen, the optimal L and T could be found under certain pump intensities. When the diamond length is fixed, different pump intensities correspond to different values of the optimal T and the optimal T increases with the increases in the pump intensity. When L is fixed, the gain in the resonator increases with the increases in the pump intensity; at the same time, the output efficiency can effectively be improved by increasing T, as shown in Figure 6.
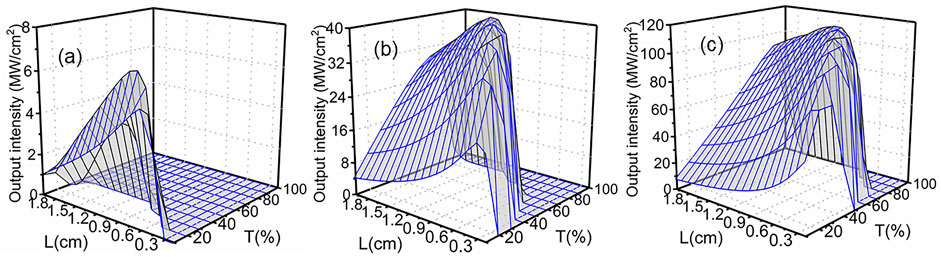
FIGURE 6. Output intensity versus output facet transmittance T and diamond length L for different pump intensities. (A) Ip = 750 MWcm−2, (B) Ip = 950 MWcm−2, and (C) Ip = 1.2 GWcm−2.
The output intensity of Stokes increases with the increases of the diamond length on the condition of the pump intensity, and T is constant and then reaches its highest intensity for a certain L. With further increasing diamond length, the output intensity decreases due to the overall net gain of the Raman laser and is reduced for the strong absorption loss in a longer diamond length. Due to the three-phonon absorption of the diamond at ∼3 μm, the output intensity could be effectively improved by properly increasing the T value of the resonator, but the smaller number of Stokes light photons are reflected into the resonator, and it is difficult to form the oscillation, which results in the higher threshold. For a low T of the resonator, more Stokes light photons are confined in the cavity, and multiple oscillations could be formed in the resonator; the output intensity is correspondingly reduced for the low T value, as shown in Figure 6. Therefore, to reduce the absorption loss of Stokes in the resonator, the larger T of the resonator is preferred for the stronger pump intensity in the multi-phonon absorption band. In this case, maximum conversion efficiencies of 10% are obtained at an input intensity of 1.2 GWcm−2 with L = 1 cm and T = 69%. Furthermore, increasing the length will result in lower conversion efficiency and higher lasing threshold simultaneously.
The temporal behavior of Stokes conversion could be analyzed by the output pulse shapes of the pump and Stokes with different pump intensities, as shown in Figure 7. In Figure 7A, no appearance of Stokes was observed with the pump intensity below the threshold intensity, and the residual pump intensity is equal to the incident pump intensity, theoretically, but it is not in Figure 7A; it is due to the linear absorption loss of the diamond. The pump intensity is rapidly converted to the Raman intensity once the threshold intensity is reached in the SRS process. This results in pump intensity decreases; however, the pump intensity does not continuously decrease, which corresponds to a depression in the residual pump, as shown in Figures 7B,C. Pulse-shortening is well known in the Raman lasers, and the consequence is that the Stokes pulses often have a much shorter duration than the pump pulses, sometimes by order of magnitude. The inset in Figure 7B is the temporal pulse of Stokes with the pump intensity of 750 MWcm−2. The Stokes pulse duration of 4.4 ns is obtained under the pump pulse duration of 10 ns in Figure 7 (c). The temporal pulse profiles share similar characteristics to those seen in [18, 41] and verify the correctness of our theoretical analysis.
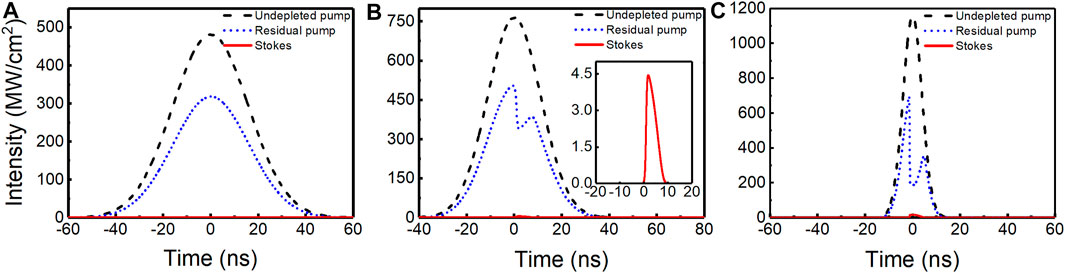
FIGURE 7. Temporal pulse behavior of the pump, residual pump, and Stokes. (A) Pump intensity below the threshold intensity. (B) Pump intensity is 750 MWcm−2. (C) Pump intensity is 1.2 GWcm−2.
Conclusion
In summary, we have modeled the characteristics of the extra-cavity diamond mid-infrared Raman laser based on the coupled-wave equation and boundary conditions with different parameters, which is helpful for understanding the physical process of SRS in the diamond. The input–output, threshold intensity, and temporal behavior of Stokes conversion characteristics of the Raman laser with different conditions are presented by numerically solving the coupled-wave equations. The performance of the length and the transmittance are simulated and discussed, which is helpful for the optimization of the diamond Raman laser in the mid-infrared regime.
Data availability statement
The original contributions presented in the study are included in the article/supplementary material; further inquiries can be directed to the corresponding author.
Author contributions
ZS conceived the project. HC conducted the simulation analysis. JC wrote the manuscript, and all authors contributed to discussions during its preparation. BL and ZS supervised the project.
Funding
This work was funded by the Shanghai Science and Technology Development Funds (22YF1416700).
Conflict of interest
ZS, HC, and JC were employed by Shanghai Aerospace Science and Industry Electric Appliance Research Institute Co., Ltd.
The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Pask HM. The design and operation of solid-state Raman lasers. Prog Quan Electron (2003) 27(1):3–56. doi:10.1016/s0079-6727(02)00017-4
2. Murray JT, Austin WL, Powell R C. Intracavity Raman conversion and Raman beam cleanup. Opt Mater (Amst) (1999) 11(4):353–71. doi:10.1016/s0925-3467(98)00033-0
3. Duan Y, Sun Y, Zhu H, Mao T, Zhang L, Chen X. YVO4 cascaded Raman laser for five-visible-wavelength switchable emission. Opt Lett (2020) 45(9):2564–7. doi:10.1364/ol.392566
4. Cerný P, Jelı́nková H, Zverev PG, Basiev TT. Solid state lasers with Raman frequency conversion. Prog Quan Electron (2004) 28(2):113–43. doi:10.1016/j.pquantelec.2003.09.003
5. Spence DJ. Spectral effects of stimulated Raman scattering in crystals. Prog Quan Electron (2017) 51:1–45. doi:10.1016/j.pquantelec.2016.11.001
6. Duan Y, Zhou Y, Zhu H, Li Z, Jin X, Tang D. Selective frequency mixing in a cascaded self-Raman laser with a critical phase-matched LBO crystal. J Lumin (2022) 118698. doi:10.1016/j.jlumin.2021.118698
7. Piper JA, Pask HM. Crystalline Raman lasers. IEEE J Sel Top Quan Electron (2007) 13(3):692–704. doi:10.1109/jstqe.2007.897175
8. Zverev PG, Basiev TT, Prokhorov AM. Stimulated Raman scattering of laser radiation in Raman crystals. Opt Mater (Amst) (1999) 11(4):335–52. doi:10.1016/S0925-3467(98)00032-9
9. Mildren RP. Intrinsic optical properties of diamond. Opt Eng Diamond (2013) 1–34. New Jersey: John Wiley&Sons. doi:10.1002/9783527648603.ch1
10. Friel I, Geoghegan SL, TwitchenDJ , Scarsbrook GA. Development of high quality single crystal diamond for novel laser applications. Proc SPIE (2010) 13:783819. doi:10.1117/12.864981
11. Balmer RS, Brandon JR, Clewes SL, Dhillon HK, Dodson JM, Friel I, et al. Chemical vapour deposition synthetic diamond: Materials, Technology and applications. J Phys : Condens Matter (2009) 21(36):364221. doi:10.1088/0953-8984/21/36/364221
12. Granados E, Spence DJ, Mildren RP. Deep ultraviolet diamond Raman laser. Opt Express (2011) 19(11):10857–63. doi:10.1364/oe.19.010857
13. Yang X, Kitzler O, Spence DJ, Williams RJ, Bai Z, Sarang S, et al. Single-frequency 620 nm diamond laser at high power, stabilized via harmonic self-suppression and spatial-hole-burning-free gain. Opt Lett (2019) 44(4):839–42. doi:10.1364/ol.44.000839
14. Reilly S, Savitski VG, Liu H, Gu E, Dawson MD, Kemp AJ. Monolithic diamond Raman laser. Opt Lett (2015) 40(6):930–3. doi:10.1364/OL.40.000930
15. Yang X, Kitzler O, Spence DJ, Bai Z, Feng Y, Mildren RP. Diamond sodium guide star laser. Opt Lett (2020) 45(7):1898–901. doi:10.1364/ol.387879
16. Li Y, Bai Z, Chen H, Jin D, Yang X, Qi Y, et al. Eye-safe diamond Raman laser. Results Phys (2020) 16:102853. doi:10.1016/j.rinp.2019.102853
17. Warrier AM, Lin J, Pask HM, Mildren RP, Coutts DW, Spence DJ. Highly efficient picosecond diamond Raman laser at 1240 and 1485 nm. Opt Express (2014) 22(3):3325–33. doi:10.1364/oe.22.003325
18. Sabella A, Piper JA, Mildren RP. Diamond Raman laser with continuously tunable output from 3.38 to 3.80 μm. Opt Lett (2014) 39(13):4037–40. doi:10.1364/ol.39.004037
19. Bai Z, Williams RJ, Jasbeer H, Sarang S, Kitzler O, Mckay A, et al. Large brightness enhancement for quasi-continuous beams by diamond Raman laser conversion. Opt Lett (2018) 43(3):563–6. doi:10.1364/ol.43.000563
20. Williams RJ, Kitzler O, Bai Z, Sarang S, Jasbeer H, McKay A, et al. High power diamond Raman lasers. IEEE J Sel Top Quan Electron (2018) 24(5):1–14. doi:10.1109/jstqe.2018.2827658
21. Williams RJ, Nold J, Strecker M, Kitzler O, McKay A, Schreiber T, et al. Efficient Raman frequency conversion of high-power fiber lasers in diamond. Laser Photon Rev (2015) 9(4):405–11. doi:10.1002/lpor.201500032
22. Demetriou G, Kemp AG, Savitski V. 100 kW peak power external cavity diamond Raman laser at 2.52 μm. Opt Express (2019) 27(7):10296–303. doi:10.1364/OE.27.010296
23. Shao Z, Li X, Shen Y, Shen D, Zhu H. Wavelength-tunable diamond Raman laser at 2.5 μm. Laser Phys Lett (2021) 18(7):075001. doi:10.1088/1612-202X/ac091a
24. Boyd G, Johnston W, Kaminow I. Optimization of the stimulated Raman scattering threshold. IEEE J Quan Electron (1969) 5(4):203–6. doi:10.1109/jqe.1969.1075751
25. Hellwarth R. Theory of stimulated Raman scattering. Phys Rev (1963) 130(5):1850–2. doi:10.1103/PhysRev.130.1850
26. Auyeung J, Yariv A. Theory of cw Raman oscillation in optical fibers. J Opt Soc Am (1979) 69(9):803–7. doi:10.1364/JOSA.69.000803
27. Ding S, Zhang X, Wang Q, Peng J, Chen Z, Liu B. Numerical optimization of the extracavity Raman laser with barium nitrate crystal. Opt Commun (2006) 267(2):480–6. doi:10.1016/j.optcom.2006.06.029
28. Ding S, Zhang X, Wang Q, Su F, Li S, Fan S, et al. Theoretical and experimental research on the multi-frequency Raman converter with KGd(WO4)2 crystal. Opt Express (2005) 13(25):10120–8. doi:10.1364/OPEX.13.010120
29. Chen H, Bai Z, Zhao C, Yang X, Ding J, Lu Z, et al. Numerical simulation of long-wave infrared generation using an external cavity diamond Raman laser. Front Phys (2021) 9(9):671559. doi:10.3389/fphy.2021.671559
30. Kitzler O, McKay A, Spence DJ, Mildren RP. Modelling and optimization of continuous-wave external cavity Raman lasers. Opt Express (2015) 23:8590–602. doi:10.1364/oe.23.008590
31. Ma J, Fathpour S. Pump-to-Stokes relative intensity noise transfer and analytical modeling of mid-infrared silicon Raman lasers. Opt Express (2012) 20(16):17962–72. doi:10.1364/OE.20.017962
32. Wang J, Song Q, Sun Y, Zhao Y, Zhou W, Li D, et al. High-performance Ho:YAG single-crystal fiber laser in-band pumped by a Tm-doped all-fiber laser. Opt Lett (2019) 44(2):455–8. doi:10.1364/OL.44.000455
33. Lagatsky AA, Antipov OL, Sibbett W. Broadly tunable femtosecond Tm:Lu2O3 ceramic laser operating around 2070 nm. Opt Express (2012) 20(17):19349–54. doi:10.1364/OE.20.019349
34. Brian C, Lew G. Highly efficient passively Q-switched Tm:YAP laser using a Cr:ZnS saturable absorber. Opt Lett (2017) 42(12):2259–62. doi:10.1364/OL.42.002259
35. Xu X, Wang X, Lin Z, Cheng Y, Li D, Cheng S, et al. Crystal growth, spectroscopic and laser properties of Tm:LuAG crystal. Laser Phys (2009) 9(11):2140–3. doi:10.1134/S1054660X09210129
36. Fonnum H, Lippert E, Haakestad MW. 550 mJ Q-switched cryogenic Ho:YLF oscillator pumped with a 100 W Tm:fiber laser. Opt Lett (2013) 38(11):1884–6. doi:10.1364/OL.38.001884
37. Li E, Tang J, Wang F, Shen D, Tang D, et al. High peak power acousto-optically Q-switched Ho:Y2O3 ceramic laser at 2117 nm. IEEE Photon Technol Lett (2020) 32(8):492–5. doi:10.1109/LPT.2020.2981642
38. Wang L, Cai X, Yang J, Wu X, Jiang H, Wang J. 520 mJ langasite electro-optically Q-switched Cr, Tm, Ho:YAG laser. Opt Lett (2012) 37(110):1986–8. doi:10.1364/OL.37.001986
39. Zhou T, Zhang L, Zhang J, Yang H, Liu P, Chen Y, et al. Improved conversion efficiency of Cr4+ ions in Cr: YAG transparent ceramics by optimization the particle sizes of sintering aids. Opt Mater (Amst) (2015) 50(14):11–4. doi:10.1016/j.optmat.2015.07.037
40. Ottusch JJ, Rockwell DA. Measurement of Raman gain coefficients of hydrogen, deuterium, and methane. IEEE J Quan Electron (1988) 24(10):2076–80. doi:10.1109/3.8545
Keywords: stimulated Raman laser, diamond, nonlinear optics, numerical simulation, midinfrared
Citation: Shao Z, Li B, Chen H and Cao J (2022) Numerical optimization of the extra-cavity diamond Raman laser in the multi-phonon absorption band. Front. Phys. 10:1027998. doi: 10.3389/fphy.2022.1027998
Received: 25 August 2022; Accepted: 22 September 2022;
Published: 12 October 2022.
Edited by:
Haiyong Zhu, Wenzhou University, ChinaReviewed by:
Zhenxu Bai, Hebei University of Technology, ChinaWeichao Yao, Ruhr University Bochum, Germany
Xuezong Yang, University of Chinese Academy of Sciences, China
Copyright © 2022 Shao, Li, Chen and Cao. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Zhenhua Shao, emhlbmh1YS5udW1iZXIxQDE2My5jb20=
 Zhenhua Shao
Zhenhua Shao Bei Li2
Bei Li2