- 1Collaboration Innovation Center for Molecular Imaging of Precision Medicine, Shanxi Medical University, Taiyuan, China
- 2Department of Physics, Shanxi Medical University, Taiyuan, China
- 3State Key Laboratory of Quantum Optics and Quantum Optics Devices, Institute of Laser Spectroscopy, Shanxi University, Taiyuan, China
- 4Collaborative Innovation Center of Extreme Optics, Shanxi University, Taiyuan, China
- 5Department of Medical Imaging, Shanxi Medical University, Taiyuan, China
- 6Department of Nuclear Medicine, First Hospital of Shanxi Medical University, Taiyuan, China
We investigate the input and propagation characteristics and geometric parametric instability of the partial Gaussian beam limited by the fiber face area in a graded-index multimode fiber. The theoretical simulation shows that the energy of the partial Gaussian beam and the coupling efficiency of the fiber face are restricted by the fiber face area for the different powers and spot sizes of the input Gaussian beam. The spot intensity pattern of the partial Gaussian beam exhibits a standard oscillating distribution in space as the beam undergoes periodic oscillations with propagation. Also, the dynamic evolution process from parametric sidebands to a supercontinuum is affected by the peak power, the spot size of the partial Gaussian beam, and the fiber length. Finally, the experimental output spectra with different powers of the partial Gaussian beam and fiber lengths in a graded-index multimode fiber confirm the prediction of theoretical simulations. This work provides practical guidance for optimizing supercontinuum source expansion and spectral power density.
Introduction
Multimode fibers (MMFs) have drawn renewed attention owing to their versatile platform to investigate the rich and complex phenomena in multimodal nonlinear environments such as spatiotemporal dynamics [1–3], spatial beam self-cleaning [4, 5], rogue waves [6], supercontinuum generation [7, 8], spatiotemporal mode-locking [9, 10], multimode solitons [11–13], and geometric parametric instability (GPI) [14, 15]. These studies are expected to enhance the bandwidth of telecom systems through space-division multiplexing as well as can offer a new route to mode-area scaling for high-power lasers in imaging systems [16–18], especially oriented toward the biomedical imaging domain [19–22].
Graded-index (GRIN) MMFs play an important role in the aforementioned studies for their arbitrary deviation of the refractive index profile, so as to the mode propagation constants happen to be equidistant [23, 24]. As a result, beam revivals in the form of compressions and expansions periodically occur during propagation. Under nonlinear conditions, these natural oscillating periodic behaviors can give rise to the special class of parametric instabilities that are called GPI. Recently, GPI in GRIN-MMFs has been studied extensively from various perspectives, including the first theoretical and experimental observation [14, 15], the adjustment of sideband positions [25], the rapid replication [26], Moiré-like patterns [27], rigorous analysis [28], modal perspective [29], correlation in energy [30], and higher-order dispersion effect [31]. These reports are all basically studied by using the injected field of a Gaussian beam.
Limited by the small face of the GRIN-MMFs, the incident of a large Gaussian spot will bring the result of partial Gaussian light injection, which makes the dynamic propagation complex. The partial Gaussian beam can be represented properly by the finite superposition of the Gaussian wavelet, and the propagation of the partial Gaussian beam was calculated [32]. The analytical expression for the kurtosis parameter of partially simplified general-type beams was derived based on the second- and fourth-order moment formalism [33]. The spatially partial Gaussian pulsed beam is combined with the conventional Gaussian pulsed beam decomposition method to enable the modeling of diffraction of a general ultrashort pulse from an arbitrarily shaped hard aperture [34]. Furthermore, when the partial Gaussian beam is transmitted in the GRIN-MMFs, the energy of the beam is partially transmitted because the Gaussian beam does not enter the fiber completely and unlike the self-similar transformation pattern of the complete Gaussian beam [35]. Accordingly, the generated GPI sidebands will also be affected by the partial Gaussian beam in transmission. However, there are no reports on the propagation characteristics of partial Gaussian beams in GRIN-MMFs to the best of our knowledge.
In this study, we investigate the input and propagation characteristics and GPI of the radially symmetric partial Gaussian beam in a GRIN-MMF by employing the (3 + 1) D NLSE in theory. The restriction of the fiber face area on the Gaussian beam results in partial Gaussian beam production. Meanwhile, the spatial distributions of the partial Gaussian beam in GRIN-MMFs are observed, and it is found that it is different from the case of a Gaussian beam. Also, the generations of GPI sidebands are further studied, and the influence of the power and spot size of the partial Gaussian beam on GPI sidebands is revealed. Furthermore, the generated spectrum of the partial Gaussian beam for different input powers and fiber lengths is observed realistically and experimentally.
Theoretical model
The propagation of a spatiotemporal optical beam inside a GRIN-MMF can be theoretically described by a (3 + 1) D NLSE in the presence of a parabolic potential [14, 15].
where
In general, it is assumed as an infinite parabolic profile such that the propagation constant of the modes is in equal spacing, but the highest-order modes do not have the equidistant feature arising from the effects of a cladded finite-size core. Thus, the lower-order sets of modes will remain linearly stable with periodic oscillations along the propagation [36], i.e., if a Gaussian mode beam is injected, the field remains approximately Gaussian [37]. To treat diverse practical cases, we here investigate the spatiotemporal dynamic while inputting a partial Gaussian beam in a GRIN-MMF. The analysis of nonlinear light propagation in an MMF becomes complex since it involves coupled spatial and temporal effects between hundreds or thousands of modes. From a theoretical aspect, solving the (3 + 1) D NLSE of Equation 1 is the most direct method, but it is computationally the most expensive method [11]. In this regard, several recent works have demonstrated with the neural network and deep-learning methods to improve the calculation speed [38–41]. More immediately, as suggested in [26], the (3 + 1) D problem of Eq. 1 can be approximately reduced to a (1 + 1) D NLSE through nonlinear pulse propagation. Along their lines, we take the form
Equation 2 is used to describe the self-imaging evolution of the beam, which preserves the nonlinearity term slightly different from [26]. Exterminating the transverse spatial dependence, Eq. 3 manages the temporal evolution of the small perturbation, which is influenced by the space field in the z-axis. If the self-imaging field is approximately linear in the aforementioned derivation, which means the absence of a nonlinearity term in Eq. 2, we can get the envelope
Thus, Eqs. 2–4 can manage the propagation of the partial Gaussian beam and the generated GPI sidebands in a GRIN-MMF, respectively.
Input and propagation of the partial Gaussian beam
First, we assume that the input field before entering the fiber face is an on-axis Gaussian spatial beam as follows:
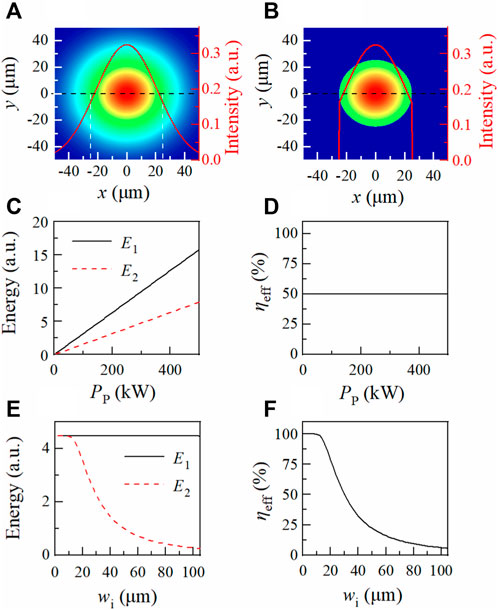
FIGURE 1. (Color inline) Spot intensity patterns before (A) and after (B) entering the fiber face with the fiber core radius
We next analyze the evolution of the partial Gaussian beam in a GRIN-MMF. The beam evolution in an MMF is a multimodal pattern process in which principal mode propagation is a localization of a group of guided modes and Gaussian mode represents the fundamental fiber mode [42]. Under the parabolic index profile of the MMF, any stationary nonlinear mode undergoes periodic oscillations (also named the periodic self-imaging phenomenon) with a spatial period of
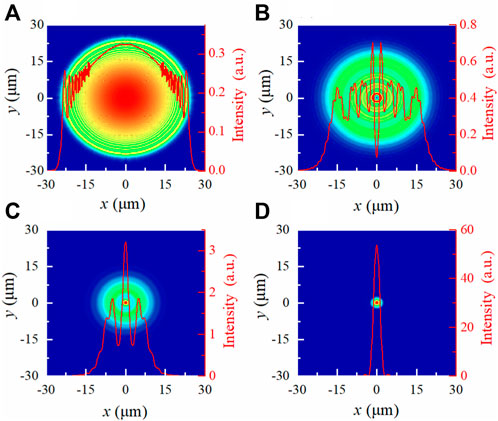
FIGURE 2. (Color inline) Evolution intensity patterns and the corresponding cross-section intensity profiles with the initial partial Gaussian beam [as shown in Figure 1B] at the distances (A)
We further demonstrate the periodic compressions and expansions of the partial Gaussian beam with four propagation cycles, as shown in Figure 3A. One can clearly find that the cross-section intensity profile shows a distinct oscillating distribution when the normalized intensity value is below about five. Furthermore, we can also see that the self-imaging is an approximately linear effect from Figure 3A although the nonlinearity term is preserved in Eq. 2 and the nonlinear Kerr coefficient
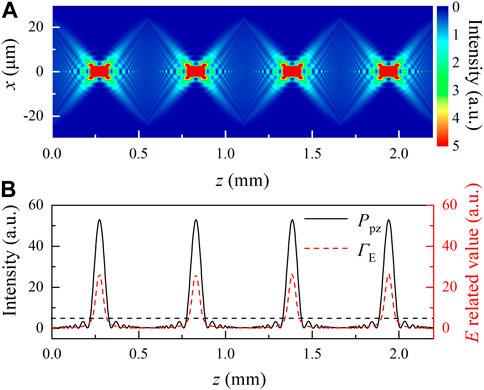
FIGURE 3. (Color inline) (A) Evolution of the spot cross-section intensity through a distance of 2.2 mm [the self-imaging period distance
The generated GPI sidebands
We next analyze the GPI sidebands in the GRIN-MMF, which play a prominent role in inciting supercontinuum generation. The GPI sidebands at different distances for two peak powers are obtained by solving Eq. 4 with a CW excitation, as shown in Figures 4A,B. One can see that for the case of high peak power, GPI first generates a series of narrow spectral sidebands, which then gradually broaden accompanying the increased intensity and eventually evolve into a supercontinuum. For the low peak power case, the GPI sidebands have the same evolutionary trend but at a slower rate. It is concluded that the spectrum is favorable to be broadened with higher peak power because of the enhanced self-phase modulation and four-wave mixing effects. It is worth noting that the frequency detuning of each sideband center
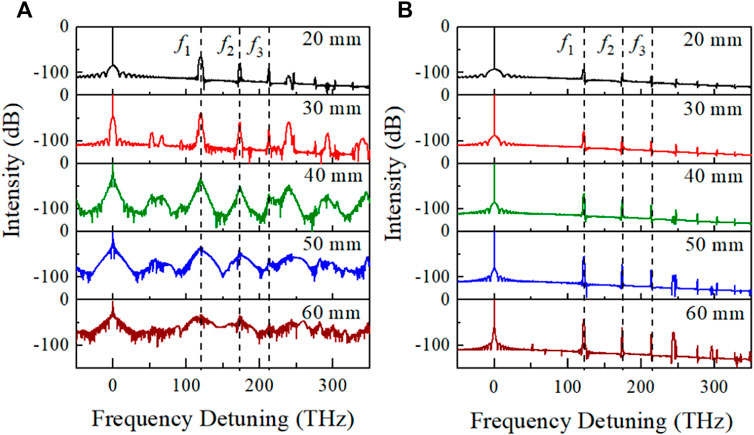
FIGURE 4. (Color online) Spectrum profile at different distances excited by the partial Gaussian beam with the peak power (A)
We further consider the dependence of the intensity and the frequency detuning of the sideband center
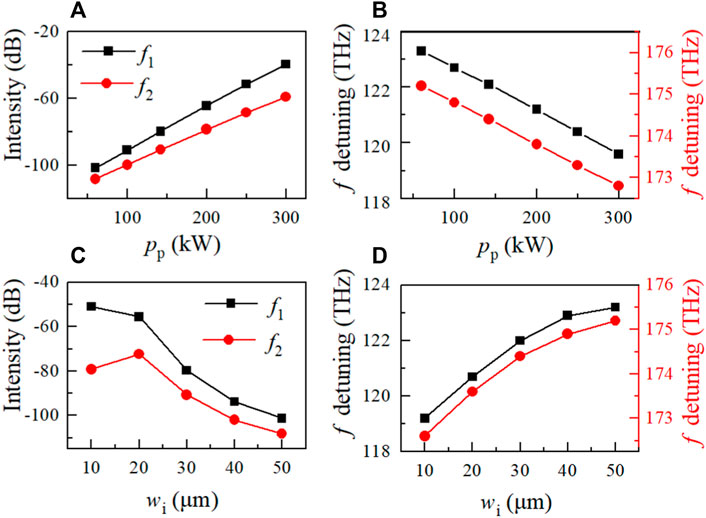
FIGURE 5. (Color online) Dependences of the intensity and frequency detuning of the first and second sideband center
Experimental observation of the frequency spectrum
In the experiment, an amplified Q-switched microchip laser is used as a pump source, which delivers 94 μJ pulses at 1,064 nm with a pulse duration of 400 ps and a repetition rate of 500 Hz. The linearly polarized Gaussian pump pulses are launched into the GRIN-MMF with a core diameter of 50 μm, NA = 0.200, and a refractive index contrast of 1.482 (Thorlabs, GIF50C). Three lenses with focal lengths of 50 mm, 50 mm, and 70 mm are used for beam focusing. At the input face of the fiber, the beam has a diameter of 200 μm, which is greater than the fiber core diameter. A large set of transverse spatial modes is excited at the fiber input by focusing the laser beam. Also, the output beam from the GRIN-MMF is detected by using an optical spectrum analyzer covering the spectral range from 600 to 1700 nm (Yokogawa, AQ6370C).
The experimentally observed spectra for different average powers and fiber lengths are shown in Figure 6. In the case of Figure 6A, the 400-ps pump pulse at 1,064 nm is launched into a 30-m GRIN-MMF, which has a free space coupling efficiency of 40%. It can be found that the pump pulse experiences tiny spectral broadening for relatively low average power (5 and 10 mW). Further spectral broadening is observed with the increasing average power. When the average power reaches 35 mW, no more obvious spectral broadening occurred. Similarly, in the case of Figure 6B, the pump pulse is launched into a 10-m GRIN-MMF with 60% free space coupling efficiency. It can be found that spectral broadening can be observed at a low average power. Meanwhile, the spectrum is further broadened with the increasing average power. The experimental results confirm the numerical simulation results of the influence of peak power on the spectral broadening as shown in Figure 4. The influence of the fiber length on spectrum broadening is not observed because the coupling efficiency of the 30-m fiber is lower than that of the 10-m fiber.
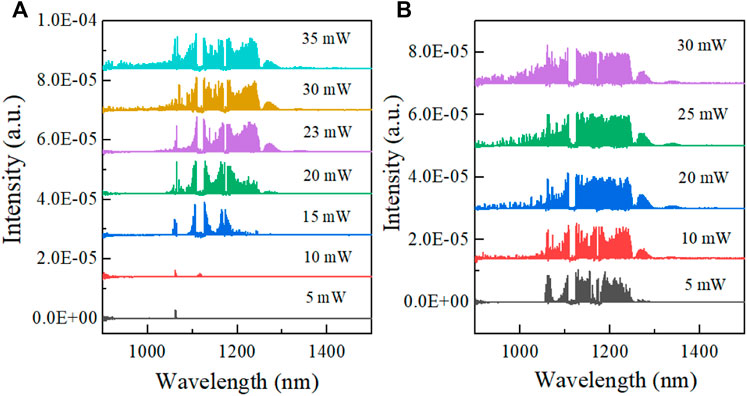
FIGURE 6. (Color online) Output spectra obtained from the (A) 30-m GRIN-MMF with 40% coupling efficiency and (B) 10-m GRIN-MMF with 60% coupling efficiency at different average powers.
Conclusion
In summary, we numerically explore the input and propagation characteristics and GPI sidebands of the partial Gaussian beam in GRIN-MMFs. The energy dependences of the complete and partial Gaussian beams and the coupling efficiency on the peak power and the spot size are shown, respectively. The partial Gaussian beam with a sharp boundary presents the spatial distribution of oscillation in propagation. Our studies indicate that each GPI sideband gradually strengthened and broadened with the increasing fiber length and finally formed a supercontinuum. Also, the intensity and frequency detuning of the sideband center frequency depend on the peak power and the spot size. Meanwhile, the generated supercontinuum spectra of the partial Gaussian beam in GRIN-MMFs are observed experimentally. Our studies provide actual operation guidance for optimizing the spectral extent and spectral power density of supercontinuum sources based on the GPI in GRIN-MMFs.
Data availability statement
The original contributions presented in the study are included in the article/supplementary material; further inquiries can be directed to the corresponding authors.
Author contributions
GY was the main author and responsible for the first draft of the manuscript. All authors provided reviews and comments on subsequent versions of the manuscript. GY, JY, and ZW conceived the idea. GY performed the numerical simulations. SW and JY performed the experiments. HZ conducted the data processing. GY, JY, ZW, and SL provided support with the setup, analysis, and interpretation of results.
Funding
The authors acknowledge support from the National Natural Science Foundation of China (Grant Nos. 61505101, 62005150, 82027804, 81971655, and 82102103), the Natural Science Foundation of Shanxi province (No. 201901D111212), and the Shanxi Scholarship Council of China (No. 2020-073).
Acknowledgments
The authors thank Fan O. Wu for fruitful discussions on the MMF theory. They also thank Helena E. Lopez Aviles for her help with the simulations.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Wright LG, Christodoulides DN, Wise FW. Controllable spatiotemporal nonlinear effects in multimode fibres. Nat Photon (2015) 9:306–10. doi:10.1038/nphoton.2015.61
2. Picozzi A, Millot G, Wabnitz S. Nonlinear virtues of multimode fibre. Nat Photon (2015) 9:289–91. doi:10.1038/nphoton.2015.67
3. Wabnitz S, Krupa K, Couderc V, Modotto D, Barthélémy A, Millot G, et al. Nonlinear dynamics in multimode optical fibers. Proc SPIE (2018) 10540:105402B. doi:10.1117/12.2287874
4. Krupa K, Tonello A, Shalaby BM, Fabert M, Barthélémy A, Millot G, et al. Spatial beam self-cleaning in multimode fibres. Nat Photon (2017) 11:237–41. doi:10.1038/nphoton.2017.32
5. Liu Z, Wright LG, Christodoulides DN, Wise FW. Kerr self-cleaning of femtosecond-pulsed beams in graded-index multimode fiber. Opt Lett (2016) 41:3675–8. doi:10.1364/ol.41.003675
6. Dudley JM, Dias F, Erkintalo M, Genty G. Instabilities, breathers and rogue waves in optics. Nat Photon (2014) 8(10):755–64. doi:10.1038/nphoton.2014.220
7. Lopez-Galmiche G, Eznaveh ZS, Eftekhar MA, Lopez JA, Wright LG, Wise F, et al. Visible supercontinuum generation in a graded index multimode fiber pumped at 1064 nm. Opt Lett (2016) 41:2553–6. doi:10.1364/ol.41.002553
8. Krupa K, Louot C, Couderc V, Fabert M, Guenard R, Shalaby BM, et al. Spatiotemporal characterization of supercontinuum extending from the visible to the mid-infraredin a multimode graded-index optical fiber. Opt Lett (2016) 41:5785–8. doi:10.1364/ol.41.005785
9. Guenard R, Krupa K, Dupiol R, Fabert M, Bendahmane A, Kermene V, et al. Nonlinear beam self-cleaning in a coupled cavity composite laser based on multimode fiber. Opt Express (2017) 25:22219–27. doi:10.1364/oe.25.022219
10. Wright LG, Christodoulides DN, Wise FW. Spatiotemporal mode-locking in multimode fiber lasers. Science (2017) 358:94–7. doi:10.1126/science.aao0831
11. Renninger WH, Wise FW. Optical solitons in graded-index multimode fibres. Nat Commun (2013) 4:1719. doi:10.1038/ncomms2739
12. Ahsan AS, Agrawal GP. Graded-index solitons in multimode fibers. Opt Lett (2018) 43(14):3345–8. doi:10.1364/OL.43.003345
13. Sun YF, Zitelli M, Ferraro M, Mangini F, Parra-Rivas P, Wabnitz S. Multimode soliton collisions in graded-index optical fibers. Opt Express (2022) 30:21710–4. doi:10.1364/OE.459447
14. Longhi S. Modulational instability and space time dynamics in nonlinear parabolic-index optical fibers. Opt Lett (2003) 28:2363–5. doi:10.1364/ol.28.002363
15. Krupa K, Tonello A, Barthélémy A, Couderc V, Shalaby BM, Bendahmane A, et al. Observation of geometric parametric instability induced by the periodic spatial self-imaging of multimode waves. Phys Rev Lett (2016) 116:183901. doi:10.1103/physrevlett.116.183901
16. Richardson DJ, Fini JM, Nelson LE. Space-division multiplexing in optical fibres. Nat Photon (2013) 7:354–62. doi:10.1038/nphoton.2013.94
17. Wright LG, Wabnitz SW, Christodoulides DN, Wise FW. Ultrabroadband dispersive radiation by spatiotemporal oscillation of multimode waves. Phys Rev Lett (2015) 115:223902. doi:10.1103/physrevlett.115.223902
18. Krupa K, Tonello A, Barthélémy A, Mansuryan T, Couderc V, Millot G, et al. Multimode nonlinear fiber optics, a spatiotemporal avenue. APL Photon (2019) 4(11):110901. doi:10.1063/1.5119434
19. Seddon AB, Napier B, Lindsay I, Lamrini S, Moselund PM, Stone N, et al. Prospective on using fibre mid-infrared supercontinuum laser sources for in vivo spectral discrimination of disease. Analyst (2018) 143:5874–87. doi:10.1039/c8an01396a
20. Zhang Y, Cao Y, Cheng JX. High-resolution photoacoustic endoscope through beam self-cleaning in a graded index fiber. Opt Lett (2019) 44(19):3841–4. doi:10.1364/ol.44.003841
21. Teng ZS, Gao F, Xia H, Chen WL, Li CX. In vivo pulse wave measurement through a multimode fiber diffuse speckle analysis system. Front Phys (2020) 8:613342. doi:10.3389/fphy.2020.613342
22. Wehbi S, Mansuryan T, Krupa K, Fabert M, Tonello A, Zitelli M, et al. Continuous spatial self-cleaning in GRIN multimode fiber for self-referenced multiplex CARS imaging. Opt Express (2022) 29:16104–14. doi:10.1364/oe.452384
23. Meunier JP, Pigeon J, Massot JN. Analyse perturbative des caractéristiques de propagation des fibres optiques à gradientd’ indice quasi-parabolique. Opt Quan Electron (1980) 12:41–9. doi:10.1007/bf00625497
24. Sammut RA, Ghatak AK. Perturbation theory of optical fibres with power-law core profile. Opt Quan Electron (1978) 10:475–82. doi:10.1007/bf00619848
25. Eznaveh ZS, Eftekhar MA, Lopez JEA, Kolesik M, Schlzgen A, Wise FW, et al. Tailoring frequency generation in uniform and concatenated multimode fibers. Opt Lett (2017) 42:1015–8. doi:10.1364/ol.42.001015
26. Conforti M, Arabi CM, Mussot A, Kudlinski A. Fast and accurate modeling of nonlinear pulse propagation in graded-index multimode fibers. Opt Lett (2017) 42(19):4004–7. doi:10.1364/ol.42.004004
27. Mas Arabí C, Kudlinski A, Mussot A, Conforti M. Geometric parametric instability in periodically modulated graded-index multimode fibers. Phys Rev A (Coll Park) (2018) 97(2):023803. doi:10.1103/physreva.97.023803
28. Lopez-Aviles HE, Wu FO, Sanjabi Eznaveh Z, Eftekhar MA, Wise F, Amezcua Correa R, et al. A systematic analysis of parametric instabilities in nonlinear parabolic multimode fibers. APL Photon (2019) 4(2):022803. doi:10.1063/1.5044659
29. He W, Dai J, Ma Q, Luo A, Hong W. Modal perspective on geometric parametric instability sidebands in graded-index multimode fibers. Opt Express (2021) 29:11353–60. doi:10.1364/oe.422667
30. Deng Z, Chen Y, Liu J, Zhao C, Fan D. Correlation between geometric parametric instability sidebands in graded-index multimode fibers. Chaos (2021) 31(1):013109. doi:10.1063/5.0028713
31. Bendahmane A, Conforti M, Vanvincq O, Arabi CM, Mussot A, Kudlinski A. Origin of spontaneous wave mixing processes in multimode GRIN fibers. Opt Express (2021) 29:30822–33. doi:10.1364/oe.436229
32. Cywiak M, Cywiak D, Yáñez E. Finite Gaussian wavelet superposition and Fresnel diffraction integral for calculating the propagation of truncated, non-diffracting and accelerating beams. Opt Commun (2017) 405:132–42. doi:10.1016/j.optcom.2017.08.015
33. Ouahid L, Nebdi H, Dalil-Essakali L. Kurtosis factor of truncated and non-truncated simplified general-type beams. Opt Quan Electron (2017) 49:91. doi:10.1007/s11082-017-0934-6
34. Worku NG, Gross H. Spatially truncated Gaussian pulsed beam and its application in modeling diffraction of ultrashort pulses from hard apertures. J Opt Soc Am A (2020) 37:317–26. doi:10.1364/josaa.382133
35. Deng ZX, Chen Y, Liu J, Zhao CJ, Fan DY. Emission of multiple resonant radiations by spatiotemporal oscillation of multimode dark pulses. Opt Express (2019) 27:36022–33. doi:10.1364/oe.27.036022
36. Longhi S, Janner D. Self-focusing and nonlinear periodic beams in parabolic index optical fibres. J Opt B: Quan Semiclass Opt (2004) 6:S303–8. doi:10.1088/1464-4266/6/5/019
37. Karlsson M, Anderson D, Desaix M. Dynamics of self-focusing and self-phase modulation in a parabolic index optical fiber. Opt Lett (1992) 17:22–4. doi:10.1364/ol.17.000022
38. Salmela L, Tsipinakis N, Foi A, Billet C, Dudley JM, Genty G. Predicting ultrafast nonlinear dynamics in fibre optics with a recurrent neural network. Nat Mach Intell (2021) 3:344–54. doi:10.1038/s42256-021-00297-z
39. Teğin U, Dinç NU, Moser C, Psaltis D. Reusability report: Predicting spatiotemporal nonlinear dynamics in multimode fibre optics with a recurrent neural network. Nat Mach Intell (2021) 3:387–91. doi:10.1038/s42256-021-00347-6
40. Wen XK, Wu GZ, Liu W, Dai CQ. Dynamics of diverse data-driven solitons for the three-component coupled nonlinear Schrödinger model by the MPS-PINN method. Nonlinear Dyn (2022) 109:3041–50. doi:10.1007/s11071-022-07583-4
41. Fang Y, Wu GZ, Wen XK, Wang YY, Dai CQ. Predicting certain vector optical solitons via the conservation-law deep-learning method. Opt Laser Technol (2022) 155:108428. doi:10.1016/j.optlastec.2022.108428
Keywords: graded-index multimode fiber, partial Gaussian beam, propagation characteristics, geometric parametric instability, supercontinuum
Citation: Yang G, Wang S, Yuan J, Zhou H, Wu Z and Li S (2022) Oscillating propagation and parametric instability of the partial Gaussian beam in graded-index multimode fibers. Front. Phys. 10:1027845. doi: 10.3389/fphy.2022.1027845
Received: 25 August 2022; Accepted: 26 September 2022;
Published: 12 October 2022.
Edited by:
Chengbo Mou, Shanghai University, ChinaReviewed by:
Chao-qing Dai, Zhejiang Agriculture and Forestry University, ChinaLi Zaidong, Tianjin University of Science and Technology, China
Huafeng Zhang, Huafeng Zhang, China
Copyright © 2022 Yang, Wang, Yuan, Zhou, Wu and Li. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Zhifang Wu, d3V6aGlmYW5nMDFAMTYzLmNvbQ==; Sijin Li, bGlzam5tMTIzQDE2My5jb20=
 Guangye Yang
Guangye Yang Sandan Wang3,4
Sandan Wang3,4 Jinpeng Yuan
Jinpeng Yuan Sijin Li
Sijin Li